karty

Čo je znakom kolmosti dvoch rovín. Prednáška z matematiky na tému "znamenie kolmosti dvoch rovín". Keď sú roviny kolmé

Ak jedna z dvoch rovín prechádza priamkou kolmou na druhú rovinu, potom sú dané roviny kolmé () (obr. 28)

α - rovina, V je na ňu kolmá priamka, β je rovina prechádzajúca priamkou V, A s je priamka, pozdĺž ktorej sa pretínajú roviny α a β.

Dôsledok. Ak je rovina kolmá na priesečník dvoch daných rovín, potom je kolmá na každú z týchto rovín

Úloha 1. Dokážte, že cez ktorýkoľvek bod priamky v priestore je možné nakresliť dve rôzne priamky kolmé naň.

dôkaz:

Podľa axiómy ja je tam bod, ktorý nie je na čiare A. Podľa vety 2.1 cez bod IN a priamy A možno nakresliť rovinu α. (Obr. 29) Podľa vety 2.3 cez bod A v rovine α možno nakresliť priamku A. Podľa axiómy C 1 existuje bod S, ktoré nepatria do α. Podľa vety 15.1 cez bod S a priamy A možno nakresliť rovinu β. V rovine β podľa vety 2.3 cez bod a možno nakresliť priamku s A.Čiary in a c majú podľa konštrukcie iba jeden spoločný bod A a obe sú kolmé

Úloha 2. Horné konce dvoch zvislo stojacich pilierov, vzdialených od seba 3,4 m, sú spojené priečkou. Výška jedného stĺpa je 5,8 m a druhého 3,9 m. Nájdite dĺžku priečnika.

AC= 5,8 m, BD= 3,9 m, AB- ? (obr.30)

AE = AC - CE = AC - BD= 5,8 - 3,9 = 1,9 (m)

Podľa Pytagorovej vety z ∆ AEB dostaneme:

AB 2 \u003d AE 2 + EB 2 \u003d AE 2 + CD 2 \u003d ( 1,9) 2 + (3,4) 2 \u003d 15,17 (m 2)

AB== 3,9 (m)

Úlohy

Cieľ. Naučte sa analyzovať relatívnu polohu objektov v priestore v najjednoduchších prípadoch, používať planimetrické fakty a metódy pri riešení stereometrických úloh.

1. Dokážte, že cez ktorýkoľvek bod priamky v priestore je možné nakresliť na ňu kolmú priamku.

2. Priamky AB, AC a AD sú na páry kolmé. Nájdite segment SD, ak:

1) AB = 3 cm , slnko= 7 cm, AD= 1,5 cm;

2) VD= 9 cm, AD= 5 cm, slnko= 16 cm;

3) AB = c, BC = a, AD = d;

4) BD = c, BC = a, AD = d

3. Bod A je vo vzdialenosti a z vrcholov rovnostranného trojuholníka so stranou A. Nájdite vzdialenosť od bodu A k rovine trojuholníka.

4. Dokážte, že ak je priamka rovnobežná s rovinou, tak všetky jej body sú v rovnakej vzdialenosti od roviny.

5. Telefónny drôt dlhý 15 m sa natiahne z telefónneho stĺpa, kde je pripevnený vo výške 8 m od zeme, k domu, kde je pripevnený vo výške 20 m. Nájdite vzdialenosť medzi domom a pól, za predpokladu, že drôt neklesne.

6. Z bodu do roviny sa narysujú dva naklonené 10 cm a 17 cm Rozdiel v priemetoch týchto naklonených je 9 cm Nájdite priemety naklonených.

7. Z bodu do roviny sú nakreslené dve naklonené čiary, z ktorých jedna je o 26 cm väčšia ako druhá. Výbežky šikmých sú 12 cm a 40 cm Nájdite šikmé.

8. Dve naklonené čiary sú nakreslené z bodu do roviny. Nájdite dĺžky šikmých plôch, ak sú v pomere 1:2 a priemety šikmých plôch sú 1 cm a 7 cm.

9. Dve naklonené čiary sú nakreslené z bodu do roviny, rovné 23 cm a 33 cm.

vzdialenosť od tohto bodu k rovine, ak sú priemetne šikmého pomeru 2:3.

10. Nájdite vzdialenosť od stredu úsečky AB k rovine, ktorá nepretína túto úsečku, ak vzdialenosť bodov a a B od roviny je: 1) 3,2 cm a 5,3 cm, 7,4 cm a 6,1 cm; 3) a a c.

11. Vyriešte predchádzajúcu úlohu za predpokladu, že úsečka AB pretína rovinu.

12. Úsečka dlhá 1 m pretína rovinu, jej konce sú od roviny vzdialené vo vzdialenosti 0,5 m a 0,3 m. Nájdite dĺžku priemetu úsečky do roviny ..

13. Z bodov A a B sa púšťajú kolmice na rovinu. Nájdite vzdialenosť medzi bodmi A a B, ak sú kolmice 3 ma 2 m, vzdialenosť medzi ich základňami je 2,4 m a úsečka AB nepretína rovinu.

14. Z bodov A a B, ležiacich v dvoch na seba kolmých rovinách, padnú kolmice AC a BD na priesečník rovín. Nájdite dĺžku segmentu AB, ak: 1) AC = 6 m, BD = 7 m, CD = 6 m; 2) AC = 3 m, BD = 4 m, CD = 12 m; 3) AD = 4 m, BC = 7 m, CD = 1 m; 4) AD = BC = 5 m, CD = 1 m; 4) AC = a, BD = b, CD = c; 5) AD = a, BC = b, CD = c.

15. Z vrcholov A a B rovnostranného trojuholníka ABC sú vzpriamené kolmice AA 1 a BB 1 na rovinu trojuholníka. Nájdite vzdialenosť od vrcholu C do stredu segmentu A 1 B 1, ak AB \u003d 2 m, CA 1 \u003d 3 m, CB 1 \u003d 7 m a segment A 1 B 1 nepretína rovinu trojuholník

16. Z vrcholov A a B ostrých uhlov pravouhlého trojuholníka ABC sú vzpriamené kolmice AA 1 a BB 1 na rovinu trojuholníka. Nájdite vzdialenosť od vrcholu C do stredu segmentu A 1 B 1, ak A 1 C \u003d 4 m, AA 1 \u003d 3 m, CB 1 \u003d 6 m, BB 1 \u003d 2 m a segment A 1 B 1 nepretína rovinu trojuholníka.

Pojem kolmých rovín

Keď sa pretínajú dve roviny, dostaneme uhly 4$. Dva z rohov sú $\varphi $ a ďalšie dva sú $(180)^0-\varphi $.

Definícia 1

Uhol medzi rovinami je najmenší z dihedrálnych uhlov tvorených týmito rovinami.

Definícia 2

Dve pretínajúce sa roviny sa nazývajú kolmé, ak je uhol medzi týmito rovinami rovný $90^\circ$ (obr. 1).

Obrázok 1. Kolmé roviny

Znak kolmosti dvoch rovín

Veta 1

Ak je priamka roviny kolmá na inú rovinu, potom sú tieto roviny navzájom kolmé.

Dôkaz.

Dostaneme roviny $\alpha $ a $\beta $, ktoré sa pretínajú pozdĺž priamky $AC$. Priamka $AB$ ležiaca v rovine $\alpha $ nech je kolmá na rovinu $\beta $ (obr. 2).

Obrázok 2

Keďže priamka $AB$ je kolmá na rovinu $\beta $, je kolmá aj na priamku $AC$. Dodatočne nakreslíme priamku $AD$ v rovine $\beta $, kolmú na priamku $AC$.

Dostaneme, že uhol $BAD$ je lineárny uhol dihedrálneho uhla rovný $90^\circ$. To znamená, že podľa definície 1 je uhol medzi rovinami rovný $90^\circ$, čo znamená, že tieto roviny sú kolmé.

Veta bola dokázaná.

Z tejto vety vyplýva nasledujúca veta.

Veta 2

Ak je rovina kolmá na priamku, pozdĺž ktorej sa pretínajú dve ďalšie roviny, potom je tiež kolmá na tieto roviny.

Dôkaz.

Dajme nám dve roviny $\alpha $ a $\beta $ pretínajúce sa pozdĺž priamky $c$. Rovina $\gama $ je kolmá na priamku $c$ (obr. 3)

Obrázok 3

Keďže priamka $c$ patrí rovine $\alpha $ a rovina $\gamma $ je kolmá na priamku $c$, potom podľa vety 1 sú roviny $\alpha $ a $\gamma $ kolmé.

Keďže priamka $c$ patrí rovine $\beta $ a rovina $\gamma $ je kolmá na priamku $c$, potom podľa vety 1 sú roviny $\beta $ a $\gamma $ kolmé.

Veta bola dokázaná.

Pre každú z týchto teorém platia aj opačné tvrdenia.

Príklady úloh

Príklad 1

Dostaneme obdĺžnikový box $ABCDA_1B_1C_1D_1$. Nájdite všetky dvojice kolmých rovín (obr. 5).

Obrázok 4

Riešenie.

Podľa definície kvádra a kolmých rovín vidíme nasledujúcich osem párov rovín navzájom kolmých: $(ABB_1)$ a $(ADD_1)$, $(ABB_1)$ a $(A_1B_1C_1)$, $(ABB_1) $ a $(BCC_1) $, $(ABB_1)$ a $(ABC)$, $(DCC_1)$ a $(ADD_1)$, $(DCC_1)$ a $(A_1B_1C_1)$, $(DCC_1)$ a $(BCC_1)$, $(DCC_1)$ a $(ABC)$.

Príklad 2

Dajme nám dve navzájom kolmé roviny. Z bodu v jednej rovine sa nakreslí kolmica do inej roviny. Dokážte, že táto priamka leží v danej rovine.

Dôkaz.

Dajme nám $\alpha $ a $\beta $ kolmé na roviny a pretínajúce sa pozdĺž priamky $c$. Z bodu $A$ roviny $\beta $ sa nakreslí kolmica $AC$ na rovinu $\alpha $. Predpokladajme, že $AC$ neleží v rovine $\beta $ (obr. 6).

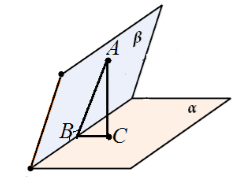
Obrázok 5

Zvážte trojuholník $ABC$. Je obdĺžnikový s pravým uhlom $ACB$. Preto $\angle ABC\ne (90)^0$.

Ale na druhej strane $\uhol ABC$ je lineárny uhol dihedrálneho uhla, ktorý tvoria tieto roviny. To znamená, že dihedrálny uhol tvorený týmito rovinami sa nerovná 90 stupňom. Dostaneme, že uhol medzi rovinami sa nerovná $90^\circ$. Rozpor. $AC$ teda leží v rovine $\beta $.

Konštrukcia dvoch vzájomne kolmých rovín. Ako je známe, Rovina je kolmá, ak je priamka v jednej rovine kolmá na inú rovinu. Preto môže byť rovina kolmá na danú rovinu vedená cez priamku kolmú na danú rovinu alebo kolmú na priamku ležiacu v danej rovine.

Znázornené na obr. 4.12 roviny (rovina trojuholníka ABC a rovina P) sú navzájom kolmé, keďže rovina P je kolmá na priamku A1 ležiacu v rovine trojuholníka. Znázornené sú priemety roviny P prechádzajúcej priamkou s priemetmi m 2 n 2, m 1 n 1 a kolmej na rovinu danú priemetmi a 2 b 2 c 2, a 1 b 1 c 1 trojuholníka. na obr. 4.12.

Konštrukcia: 1. Nakreslite hlavné čiary roviny, C1 - horizontálne, C2 - čelné.

2. Cez ľubovoľný bod E (umiestnený mimo trojuholníka ABC) nakreslite priamku EF kolmú na hlavné priamky roviny (c 2 f 2 je kolmá na c 2 2 2 a c 1 f 1 je kolmá na 1 1 1 ).

3. Cez bod N nakreslite ľubovoľnú priamku EM pretínajúcu sa s EF, dostaneme rovinu P danú dvoma pretínajúcimi sa priamkami (EM X EF).

Rovina P(ME X EF) je teda kolmá na rovinu Q(trojuholník ABC).

Treba poznamenať, že pre vzájomne kolmé roviny vo všeobecnej polohe nie sú ich stopy rovnakého mena nikdy kolmé. Ak je ale jedna z daných rovín (alebo obe) rovinou všeobecnej polohy, potom vzájomná kolmosť na diagrame jednej dvojice ich stôp udáva kolmosť rovín v priestore.

18) Priamku priesečníka dvoch rovín možno určiť ich dvoma spoločnými bodmi. Na tento účel určte priesečníky akýchkoľvek dvoch priamok jednej roviny s inou rovinou alebo priesečníky priamky na každej z rovín s inou rovinou.

Postupnosť stavby:

Priesečník dvoch rovín nájdeme pri riešení pomocou pomocných rezných rovín. Zvyčajne sa vyberajú projekčné roviny (často horizontálne alebo čelné)

Zvolí sa ľubovoľná sečnica pomocná horizontálna rovina Ф1, ktorá pretína dané roviny pozdĺž priamok (12 a 34), ktoré sa (na n1 pretínajú v bode k)

Druhá sečná horizontálna rovina pretína dané roviny aj pozdĺž horizontál, tie sa zasa pretínajú v bode E

Priamka KE je priesečníkom daných rovín.

Zvážte riešenie tohto problému na plochom výkrese.

1. etapa riešenia Na zostrojenie bodu M bola použitá vodorovne premietnutá rovina - prostredník ("), v ktorej je uzavretá strana AB trojuholníka ABC.

2. etapa riešenia Zostrojíme priesečník (na výkrese je daný bodmi 1 a 2) medziroviny (“) a roviny DEK.

3. fáza riešenia Nájdite bod M priesečníka priamky 1 - 2 s priamkou AB.

Nájdený jeden bod M požadovanej priesečníkovej čiary.

Na zostrojenie bodu N sa používa vodorovne premietajúca rovina  (“), v ktorej je uzavretá strana AC trojuholníka ABC.

Konštrukcie sú podobné predchádzajúcim.

Definícia viditeľnosti v rovine H sa robí pomocou horizontálne konkurujúcich bodov 4 a 8

Bod 4 sa nachádza nad bodom 8 (4" a 8"), preto v rovine H časť trojuholníka DEK, ktorá sa nachádza smerom k bodu 4, prekrýva časť trojuholníka ABC, ktorá sa nachádza od priesečníka smerom k bodu 8. Pomocou a dvojica čelne konkurujúcich bodov 6 a 7 je definovaná viditeľnosť v rovine V.

Priesečník dvoch čelne vyčnievajúcich rovín (?)

Priesečník dvoch vodorovne vyčnievajúcich rovín (?)

19) Rez je obraz predmetu mentálne rozrezaný jednou alebo viacerými rovinami, zatiaľ čo mentálna disekcia objektu sa vzťahuje iba na tento rez a nespôsobuje zmenu v iných obrazoch toho istého objektu. Sekcia ukazuje čo sa nachádza v rovine rezu a čo sa nachádza za ňou.

V závislosti od počtu rovín rezu je sekcia rozdelená na:

Jednoduché (s jednou rovinou rezu)

Komplexné (s niekoľkými rovinami rezu)

V závislosti od polohy roviny rezu vzhľadom na horizontálnu rovinu projekcie sú sekcie rozdelené na:

HORIZONTÁLNA - rovina rezu je rovnobežná s horizontálnou premietacou rovinou

VERTIKÁLNA - rovina rezu je kolmá na horizontálnu projekčnú rovinu

ŠIKM - rovina rezu je nejaký nepravý uhol s vodorovnou rovinou =) ZVISLÝ rez je tzv čelný ak je rovina rezu rovnobežná s prednou projekčnou rovinou. A špecializovaný ak je rovina rezu rovnobežná s rovinou premietania profilu.

KOMPLEXNÉ rezy sú POZDĹŽNE, ak sú rezné roviny nasmerované po dĺžke alebo výške predmetu. A PRIECNE, AK sú roviny rezu nasmerované KOLMO na dĺžku alebo výšku predmetu.

KROK - ak sú sečné roviny navzájom rovnobežné

POLYLINES - ak sa sečné roviny navzájom pretínajú.

LOCAL rezy sa používajú na odhalenie vnútornej štruktúry objektu na samostatnom obmedzenom mieste. LOCAL SECTION je v pohľade zvýraznený ako plná, zvlnená, tenká čiara.

Označenie rezov - Poloha roviny rezu je označená otvorenou čiarou rezu. Začiatočný a koncový ťah čiary rezu nesmie prekročiť obrys príslušného obrázku. Šípky označujúce smer pohľadu by mali byť umiestnené na počiatočnom a poslednom ťahu.Šípky by mali byť aplikované vo vzdialenosti 2 ... 3 mm od vonkajšieho konca ťahu.

PRE KOMPLEXNÝ REZ sa ťahy otvorenej línie rezu vykonávajú aj na zlomoch čiary rezu.

V BLÍZKOSTI šípok označujúcich smer pohľadu sú z vonkajšej strany rohu použité veľké písmená ruskej abecedy. Označenia písmen sa priraďujú v abecednom poradí bez opakovania a bez vynechávania.

Samotný rez by mal byť označený nápisom typu A-A

Ak sa rovina rezu zhoduje s rovinou symetrie objektu a rez je vedený v mieste zodpovedajúceho pohľadu v projekčnom vzťahu, potom pre horizontálne, čelné a profilové rezy nie je potrebné označovať polohu rezu. rovina a rez nie je doplnený nápisom.

Ak sa obrysová čiara objektu zhoduje s osou symetrie, potom je hranica medzi pohľadom a rezom označená vlnovkou, ktorá je nakreslená tak, aby sa zachoval obraz hrany.

Táto lekcia pomôže tým, ktorí chcú získať predstavu o téme "Znak kolmosti dvoch rovín." Na jeho začiatku si zopakujeme definíciu dihedrálneho a lineárneho uhla. Potom zvážime, ktoré roviny sa nazývajú kolmé, a dokážeme kritérium kolmosti dvoch rovín.

Téma: Kolmosť priamok a rovín

Lekcia: Znak kolmosti dvoch rovín

Definícia. Dihedrálny uhol je útvar tvorený dvoma polrovinami, ktoré nepatria do tej istej roviny, a ich spoločnou priamkou a (a je hrana).

Ryža. 1

Uvažujme dve polroviny α a β (obr. 1). Ich spoločná hranica je l. Tento údaj sa nazýva dihedrálny uhol. Dve pretínajúce sa roviny zvierajú štyri dihedrálne uhly so spoločnou hranou.

Dihedrálny uhol sa meria jeho lineárnym uhlom. Zvolíme ľubovoľný bod na spoločnej hrane l uhlu klinu. V polrovinách α a β z tohto bodu nakreslíme kolmice a a b na priamku l a získame lineárny uhol dihedrálneho uhla.

Priamky a a b zvierajú štyri uhly rovné φ, 180° - φ, φ, 180° - φ. Pripomeňme, že najmenší z týchto uhlov sa nazýva uhol medzi čiarami.

Definícia. Uhol medzi rovinami je najmenší z dihedrálnych uhlov tvorených týmito rovinami. φ - uhol medzi rovinami α a β, ak

Definícia. Dve pretínajúce sa roviny sa nazývajú kolmé (vzájomne kolmé), ak uhol medzi nimi je 90°.

Ryža. 2

Na hrane l sa zvolí ľubovoľný bod M (obr. 2). Narysujme dve kolmé priamky MA = a a MB = b na hranu l v rovine α a v rovine β. Dostali sme uhol AMB. Uhol AMB je lineárny uhol dihedrálneho uhla. Ak je uhol AMB 90°, potom sa hovorí, že roviny α a β sú kolmé.

Priamka b je konštrukciou kolmá na priamku l. Priamka b je kolmá na priamku a, pretože uhol medzi rovinami α a β je 90°. Dostaneme, že priamka b je kolmá na dve pretínajúce sa priamky a a l z roviny α. Čiara b je teda kolmá na rovinu α.

Podobne sa dá dokázať, že priamka a je kolmá na rovinu β. Priamka a je konštrukciou kolmá na priamku l. Priamka a je kolmá na priamku b, pretože uhol medzi rovinami α a β je 90°. Dostaneme, že priamka a je kolmá na dve pretínajúce sa priamky b a l z roviny β. Čiara a je teda kolmá na rovinu β.

Ak jedna z dvoch rovín prechádza priamkou kolmou na druhú rovinu, potom sú tieto roviny kolmé.

dokázať:

Ryža. 3

dôkaz:

Nech sa roviny α a β pretínajú pozdĺž priamky AC (obr. 3). Aby ste dokázali, že roviny sú navzájom kolmé, musíte medzi nimi zostrojiť lineárny uhol a ukázať, že tento uhol sa rovná 90 °.

Priamka AB je podľa podmienky kolmá na rovinu β, a teda aj na priamku AC ležiacu v rovine β.

Narysujme priamku AD kolmú na priamku AC v rovine β. Potom BAD je lineárny uhol dihedrálneho uhla.

Priamka AB je kolmá na rovinu β, a teda aj na priamku AD ležiacu v rovine β. Takže lineárny uhol BAD je 90°. Roviny α a β sú teda kolmé, čo sa malo dokázať.

Rovina kolmá na priamku, pozdĺž ktorej sa pretínajú dve dané roviny, je kolmá na každú z týchto rovín (obr. 4).

dokázať: