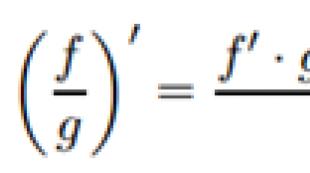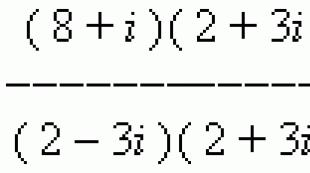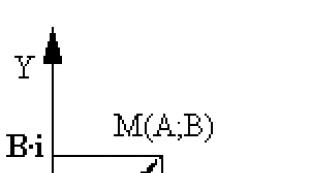Нарийн төвөгтэй тоо

Төсөөлөл Тэгээд нийлмэл тоо. Абсцисса ба ординат

нийлмэл тоо. Нийлмэл комплекс тоо.

Комплекс тоотой үйлдлүүд. Геометр

комплекс тоонуудын төлөөлөл. нарийн төвөгтэй хавтгай.

Комплекс тооны модуль ба аргумент. тригонометр

нийлмэл тооны хэлбэр. Цогцолбортой үйл ажиллагаа

тригонометрийн хэлбэрээр тоонууд. Мойврын томъёо.

тухай үндсэн мэдээлэл төсөөлөлтэй Тэгээд нийлмэл тоо "Төсөөлөл ба нийлмэл тоо" хэсэгт өгөгдсөн. Квадрат тэгшитгэлийг шийдвэрлэх үед эдгээр шинэ төрлийн тоонуудын хэрэгцээ гарч ирэвД< 0 (здесь Дквадрат тэгшитгэлийн дискриминант). Удаан хугацааны туршид эдгээр тоонууд нь биет хэрэглээг олж чадаагүй тул "төсөөлөл" тоо гэж нэрлэгддэг байсан. Гэсэн хэдий ч одоо тэд физикийн янз бүрийн салбарт маш өргөн хэрэглэгддэг.

ба технологи: цахилгаан инженерчлэл, гидро- ба аэродинамик, уян хатан байдлын онол гэх мэт.

Нарийн төвөгтэй тоо дараах байдлаар бичигдсэн байна.a+bi. Энд аТэгээд б – бодит тоо , А би – төсөөллийн нэгж.д. би 2 = –1. Тоо адуудсан абсцисса, a б - ординатнийлмэл тооa + b.Хоёр комплекс тооa+biТэгээд а-би дуудсан коньюгатнийлмэл тоо.

Үндсэн хэлэлцээрүүд:

1. Бодит тооАхэлбэрээр ч бичиж болнонийлмэл тоо:a + 0 биэсвэл а - 0 би. Жишээлбэл, 5 + 0 оруулгуудбиба 5 - 0 биижил тоо гэсэн үг 5 .

2. Цогцолбор тоо 0 + бидуудсан цэвэр төсөөлөл тоо. Бичлэг хийж байнаби0-тэй ижил утгатай + би.

3. Хоёр комплекс тооa+bi Тэгээдc + дибайвал тэнцүү гэж үзнэa = cТэгээд b = d. Үгүй бол нийлмэл тоонууд тэнцүү биш.

Нэмэлт. Комплекс тоонуудын нийлбэрa+biТэгээд c + дицогц тоо гэж нэрлэдэг (a+c ) + (б+д ) би .Тиймээс, нэмэх үед нийлмэл тоо, тэдгээрийн абсцисса ба ординатыг тус тусад нь нэмнэ.

Энэхүү тодорхойлолт нь энгийн олон гишүүнттэй харьцах дүрмийг дагаж мөрддөг.

Хасах. Хоёр комплекс тооны ялгааa+bi(багасгасан) ба c + ди(хасах) -ийг цогцолбор тоо гэж нэрлэдэг (а-в ) + (б-д ) би .

Тиймээс, нийлмэл хоёр тоог хасахдаа тэдгээрийн абсцисса ба ординатыг тус тусад нь хасна.

Үржүүлэх. Комплекс тоонуудын үржвэрa+biТэгээд c + ди нийлмэл тоо гэж нэрлэдэг.

(ac-bd ) + (ad+bc ) би .Энэхүү тодорхойлолт нь хоёр шаардлагаас үүдэлтэй:

1) тоо a+biТэгээд c + диалгебрийн адил үржих ёстойхоёр гишүүн,

2) тоо биүндсэн өмчтэй:би 2 = – 1.

ЖИШЭЭ ( a + bi )(а-би) = a 2 +б 2 . Тиймээс, ажил

хоёр хосолсон комплекс тоо нь бодиттой тэнцүү байна

эерэг тоо.

Хэлтэс. Комплекс тоог хуваахa+bi (хуваагдах) нөгөөдc + ди(хуваагч) - гурав дахь тоог олох гэсэн үгe + fi(чат), үүнийг хуваагчаар үржүүлэхэдc + ди, үүний үр дүнд ногдол ашигa + b.

Хэрэв хуваагч нь тэг биш бол хуваах боломжтой.

ЖИШЭЭ Хай (8+би ) : (2 – 3 би) .

Шийдэл Энэ харьцааг бутархай болгон дахин бичье.

Түүний тоо ба хуваагчийг 2 + 3-аар үржүүлэхби

БА Бүх өөрчлөлтийг хийсний дараа бид дараахь зүйлийг авна.

Комплекс тоонуудын геометрийн дүрслэл. Бодит тоонуудыг тооны шулуун дээрх цэгүүдээр илэрхийлнэ.

Гол нь энд байна Атоо -3, цэг гэсэн үгБнь 2 тоо бөгөөд О- тэг. Үүний эсрэгээр комплекс тоо нь координатын хавтгай дээрх цэгүүдээр илэрхийлэгдэнэ. Үүний тулд бид хоёр тэнхлэгт ижил масштабтай тэгш өнцөгт (картезиан) координатуудыг сонгоно. Дараа нь комплекс тооa+bi цэгээр дүрслэгдэх болно абсцисс бүхий P а ба ординат b (зураг харна уу). Энэ координатын системийг нэрлэдэг нарийн төвөгтэй хавтгай .

модуль комплекс тоог векторын урт гэнэOP, координат дээр комплекс тоог дүрсэлсэн ( цогц) онгоц. Комплекс тооны модульa+bi| гэж тэмдэглэсэн a+bi| эсвэл захидал r

Квадрат тэгшитгэлийг авч үзье.

Үүний үндсийг тодорхойлъё.

Квадрат нь -1 гэсэн бодит тоо байхгүй. Гэхдээ хэрэв томъёо нь операторыг тодорхойлдог бол битөсөөллийн нэгжийн хувьд энэ тэгшитгэлийн шийдийг хэлбэрээр бичиж болно . Хаана Тэгээд - нийлмэл тоо, үүнд -1 нь бодит хэсэг, 2 эсвэл хоёр дахь тохиолдолд -2 нь төсөөллийн хэсэг юм. Төсөөллийн хэсэг нь мөн бодит (бодит) тоо юм. Төсөөллийн хэсэг нь төсөөллийн нэгжээр үржүүлсэн нь аль хэдийн гэсэн үг юм төсөөллийн тоо.

Ерөнхийдөө комплекс тоо нь хэлбэртэй байдаг

z = x + iy ,

Хаана x, yнь бодит тоо, төсөөллийн нэгж юм. Олон тооны хэрэглээний шинжлэх ухаанд, жишээлбэл, цахилгаан инженерчлэл, электроник, дохионы онолд төсөөллийн нэгжийг дараах байдлаар тэмдэглэдэг. j. Бодит тоо x = Re(z)Тэгээд у=би(z)дуудсан Бодит ба төсөөллийн хэсгүүдтоо z.илэрхийлэл гэж нэрлэдэг алгебрийн хэлбэркомплекс тооны тэмдэглэгээ.

Аливаа бодит тоо нь хэлбэрийн нийлмэл тооны онцгой тохиолдол юм . Төсөөллийн тоо нь мөн нийлмэл тооны онцгой тохиолдол юм. .

Комплекс тооны олонлогийн тодорхойлолт C

Энэ илэрхийллийг дараах байдлаар уншина: set ХАМТгэх мэт элементүүдээс бүрдсэн xТэгээд yбодит тоонуудын багцад хамаарна Рбөгөөд энэ нь төсөөллийн нэгж юм. гэх мэтийг анхаарна уу.

Хоёр комплекс тоо Тэгээд бодит ба төсөөллийн хэсгүүд нь тэнцүү байх тохиолдолд л тэнцүү байна, өөрөөр хэлбэл. Мөн .

Цогцолбор тоо, функцийг шинжлэх ухаан, технологи, ялангуяа механик, хувьсах гүйдлийн хэлхээний шинжилгээ, тооцоо, аналог электроник, дохионы онол ба боловсруулалт, автомат удирдлагын онол болон бусад хэрэглээний шинжлэх ухаанд өргөн ашигладаг.

1. Комплекс тооны арифметик

Хоёр нийлмэл тоог нэмэх нь тэдгээрийн бодит ба төсөөллийн хэсгүүдийг нэмэх явдал юм.

Үүний дагуу хоёр цогц тооны зөрүү

Нарийн төвөгтэй тоо дуудсан цогцолбор коньюгаттоо z=x +i.y.

z ба z * нийлмэл нийлмэл тоо нь төсөөллийн хэсгийн шинж тэмдгээр ялгаатай. Энэ нь ойлгомжтой

.

Хэрэв энэ тэгш байдал хаа сайгүй байгаа бол нарийн төвөгтэй илэрхийллийн хоорондох аливаа тэгш байдал хүчинтэй хэвээр байна би-аар сольсон - би, өөрөөр хэлбэл холбогч тоонуудын тэгш байдал руу оч. Тоонууд биТэгээд – биучир нь алгебрийн хувьд ялгагдахгүй .

Хоёр цогц тооны үржвэрийг (үржүүлэх) дараах байдлаар тооцоолж болно.

Хоёр комплекс тооны хуваагдал:

Жишээ:

1. Нарийн төвөгтэй онгоц

Комплекс тоог тэгш өнцөгт координатын системд графикаар дүрсэлж болно. Хавтгайд тэгш өнцөгт координатын системийг байгуулъя (x, y).

тэнхлэг дээр ҮхэрБид жинхэнэ хэсгүүдийг зохион байгуулах болно x, гэж нэрлэдэг бодит (бодит) тэнхлэг, тэнхлэг дээр Өө- төсөөллийн хэсгүүд yнийлмэл тоо. Тэр нэрийг нь авсан төсөөллийн тэнхлэг. Түүгээр ч барахгүй нийлмэл тоо бүр нь онгоцны тодорхой цэгтэй тохирч, ийм хавтгайг нэрлэдэг нарийн төвөгтэй хавтгай. цэг Ацогц хавтгай нь вектортой тохирно О.А.

Тоо xдуудсан абсциссанийлмэл тоо, тоо y – ординат.

Бодит тэнхлэгт тэгш хэмтэй байрлалтай хос нийлмэл нийлмэл тоог цэг хэлбэрээр харуулав.

Хэрэв онгоцонд суулгасан бол туйлын координатын систем, дараа нь комплекс тоо бүр zтуйлын координатаар тодорхойлогддог. Хаана модультоо нь цэгийн туйлын радиус ба өнцөг юм - түүний туйлын өнцөг буюу комплекс тооны аргумент z.

Комплекс тооны модуль үргэлж сөрөг биш. Комплекс тооны аргумент нь өвөрмөц байдлаар тодорхойлогддоггүй. Аргументийн гол утга нь нөхцөлийг хангасан байх ёстой . Нарийн төвөгтэй хавтгайн цэг бүр нь аргументийн нийт утгатай тохирч байна. 2π-ийн үржвэрээр ялгаатай аргументуудыг тэнцүү гэж үзнэ. 0 тооны аргумент тодорхойлогдоогүй байна.

Аргументийн гол утгыг дараах илэрхийллээр тодорхойлно.

Энэ нь ойлгомжтой

Хаана
, .

Цогцолбор тооны төлөөлөл zзэрэг

дуудсан тригонометрийн хэлбэрнийлмэл тоо.

Жишээ.

1. Комплекс тооны экспоненциал хэлбэр

задрал Маклаурин цувралбодит аргумент функцүүдийн хувьд харагдаж байна:

Комплекс аргументийн экспоненциал функцийн хувьд zзадрал нь ижил төстэй юм

.

Төсөөллийн аргументын экспоненциал функцийн Маклаурин цувралын өргөтгөлийг дараах байдлаар илэрхийлж болно.

Үр дүнд нь таних тэмдэг гэж нэрлэдэг Эйлерийн томъёо.

Сөрөг аргументийн хувьд энэ нь харагдаж байна

Эдгээр илэрхийлэлүүдийг нэгтгэснээр бид синус болон косинусын дараах илэрхийллийг тодорхойлж чадна

.

Комплекс тоонуудын дүрслэлийн тригонометрийн хэлбэрээс Эйлерийн томъёог ашиглан

боломжтой харуулах шинж чанартай(экпоненциал, туйл) цогц тооны хэлбэр, i.e. хэлбэрээр түүний төлөөлөл

,

Хаана - тэгш өнцөгт координат бүхий цэгийн туйлын координат ( x,y).

Комплекс тооны нэгдлийг экспоненциал хэлбэрээр дараах байдлаар бичнэ.

Экспоненциал хэлбэрийн хувьд нийлмэл тоог үржүүлэх, хуваах дараах томъёог тодорхойлоход хялбар байдаг.

Өөрөөр хэлбэл экспоненциал хэлбэрээр комплекс тоонуудын үржвэр, хуваагдал нь алгебрийн хэлбэрээс илүү хялбар байдаг. Үржүүлэх үед хүчин зүйлийн модулиудыг үржүүлж, аргументуудыг нэмнэ. Энэ дүрэм нь хэд хэдэн хүчин зүйлд хамаарна. Ялангуяа нийлмэл тоог үржүүлэхэд zдээр бивектор zцагийн зүүний эсрэг 90-ээр эргэдэг

Хуваахдаа хуваагчийн модулийг хуваагчийн модулиар хувааж, хуваагчийн аргументыг хуваагч аргументаас хасна.

Комплекс тоонуудын экспоненциал хэлбэрийг ашиглан сайн мэддэг тригонометрийн илэрхийлэлүүдийг олж авах боломжтой. Жишээлбэл, таних тэмдэгээс

Эйлерийн томъёог ашиглан бид бичиж болно

Энэ илэрхийлэл дэх бодит ба төсөөллийн хэсгүүдийг тэнцүүлэхдээ бид өнцгийн нийлбэрийн косинус ба синусын илэрхийлэлийг олж авна.

1. Комплекс тоонуудын зэрэглэл, үндэс, логарифм

Комплекс тоог натурал зэрэгт хүргэх nтомъёоны дагуу үйлдвэрлэсэн

Жишээ. Тооцоолох .

Тоогоор төсөөлөөд үз дээ тригонометрийн хэлбэрээр

’

Экспонентацын томъёог ашигласнаар бид олж авна

Илэрхийлэлд утгыг оруулах r= 1, бид гэж нэрлэгддэг зүйлийг авдаг Де Мойврын томъёо, үүний тусламжтайгаар та олон өнцгийн синус ба косинусын илэрхийллийг тодорхойлж болно.

Үндэс nкомплекс тооны 0-р зэрэглэл zБайгаа nилэрхийллээр тодорхойлогддог өөр өөр утгууд

Жишээ. Олъё.

Үүнийг хийхийн тулд бид комплекс тоог () тригонометрийн хэлбэрт илэрхийлнэ

.

Комплекс тооны үндсийг тооцоолох томъёоны дагуу бид олж авна

Комплекс тооны логарифм zтоо юм w, Үүний төлөө . Комплекс тооны натурал логарифм нь хязгааргүй тооны утгатай бөгөөд томъёогоор тооцоологддог

Бодит (косинус) ба төсөөлөл (синус) хэсгүүдээс бүрдэнэ. Ийм стрессийг уртын вектор хэлбэрээр илэрхийлж болно У м, эхний үе шат (өнцөг), өнцгийн хурдаар эргэлддэг ω .

Түүнээс гадна, хэрэв нарийн төвөгтэй функцүүдийг нэмбэл тэдгээрийн бодит ба төсөөлөл хэсгүүдийг нэмнэ. Хэрэв нийлмэл функцийг тогтмол эсвэл бодит функцээр үржүүлбэл түүний бодит ба төсөөллийн хэсгүүдийг ижил хүчин зүйлээр үржүүлнэ. Ийм нарийн төвөгтэй функцийг ялгах/интеграцчилал нь бодит ба төсөөллийн хэсгүүдийг ялгах/интеграцчилал болгон бууруулна.

Жишээлбэл, нийлмэл стрессийн илэрхийлэлийг ялгах

-ээр үржүүлэх явдал юм iω нь f(z) функцийн бодит хэсэг ба нь функцийн төсөөллийн хэсэг юм. Жишээ нь: .

Утга zкомплекс z хавтгай дахь цэг, харгалзах утгаараа илэрхийлэгдэнэ w- цогц хавтгай дахь цэг w. Үзүүлсэн үед w = f(z)хавтгай шугамууд zонгоцны шугам руу шилжинэ w, нэг хавтгайн дүрсийг нөгөөгийн дүрс болгон хувиргах боловч шугам эсвэл дүрсийн хэлбэр ихээхэн өөрчлөгдөж болно.

		Комплекс тоог бичих алгебрийн хэлбэр ............................................. ... ...................
		Комплекс тоонуудын хавтгай ............................................. ................................................................... ................... ...
		Цогцолбор нийлмэл тоо ............................................. ................ ................................. ...............
	Алгебрийн хэлбэрийн комплекс тоотой үйлдлүүд ............................................. ................... ....
		Комплекс тооны нэмэх ................................................. ................................................................... ...................
		Комплекс тоонуудыг хасах ................................................ ................................................................ ............
		Комплекс тоог үржүүлэх ................................................ ................................................................ .........
		Комплекс тоонуудын хуваагдал.................................. ................ ................................. ............... ...
	Комплекс тооны тригонометрийн хэлбэр ............................................. .............. ..............
	Тригонометрийн хэлбэрийн комплекс тоотой үйлдлүүд ............................................. ............
		Комплекс тоог тригонометрийн хэлбэрээр үржүүлэх................................................. .........................
		Комплекс тоог тригонометрийн хэлбэрээр хуваах ................................................ ................... ...
		Комплекс тоог эерэг бүхэл тоо болгон өсгөх
		Комплекс тооноос эерэг бүхэл тооны язгуурыг гаргаж авах
		Комплекс тоог рациональ зэрэгт хүргэх ............................................. .........................
		Цогцолбор цуврал ................................................. ................................................. ................................................
		Цогцолбор тооны цуваа .............................................. ................ ................................. ...............
		Нарийн төвөгтэй хавтгай дахь хүч чадлын цуваа ................................................ ................................................................
		Нарийн төвөгтэй хавтгай дахь хоёр талт эрчим хүчний цуваа ...................................... ...................... ...
		Комплекс хувьсагчийн функцууд ............................................. ................................................................ ...................
		Үндсэн үндсэн функцууд ................................................. ................... ................................... ............
		Эйлерийн томьёо................................................. .. ................................................. .................................
		Комплекс тоог илэрхийлэх экспоненциал хэлбэр ...................................... ...... .
		Тригонометр ба гипербол функцүүдийн хоорондын хамаарал ......................................
		Логарифм функц ................................................. ................................................. ................. ...
		Ерөнхий экспоненциал ба ерөнхий чадлын функцууд ............................................. ................................................
	Комплекс хувьсагчийн функцүүдийн ялгаварлал...................................... .........................
		Коши-Риманы нөхцөл ................................................ ...................... ................................................. ......... ............
		Деривативыг тооцоолох томъёо ................................................ ............. .................................
		Ялгаварлах ажиллагааны шинж чанар ................................................ .............. .................................
		Аналитик функцийн бодит ба төсөөллийн хэсгүүдийн шинж чанарууд ...................................... .........

	Комплекс хувьсагчийн функцийг бодит болон төсөөллөөс нь сэргээх
		Аргын дугаар 1. Муруй шугаман интеграл ашиглах ................................................ ......... .........
		Аргын дугаар 2. Коши-Риманы нөхцлийн шууд хэрэглээ......................................
		Аргын дугаар 3. Хүссэн функцийн деривативаар ................................................. ................... .........
	Комплекс хувьсагчийн функцүүдийн интеграцчлал...................................... ...................... ............
	Кошигийн интеграл томьёо ............................................. ................................................ . ..
	Тейлор ба Лорентын цувралын функцүүдийн өргөтгөл ............................................. .... .........................
	Комплекс хувьсагчийн функцын тэг ба ганц цэгүүд ...................................... ............
		Комплекс хувьсагчийн функцын тэг ............................................. ................ .................................
		Комплекс хувьсагчийн функцийн тусгаарлагдсан ганц цэгүүд ...................................... ......

14.3 Хязгааргүй цэгийг комплекс хувьсагчийн функцийн ганц цэг болгон заана

	Татан авалт ................................................. ................................................ . ...................................................
		Төгсгөлийн цэгийн хасалт ................................................ ............. ................................................ ............ ......
		Хязгааргүй цэг дэх функцийн үлдэгдэл ...................................... ................... .................
	Үлдэгдэл ашиглан интегралыг тооцоолох ................................... ................................................................
	Өөрийгөө шалгах асуултууд ............................................. ................................................. ................. .......
	Уран зохиол.................................................. ................................................ . ................................
	Сэдвийн индекс................................................. ................................................ . .............

Өмнөх үг

Шалгалт эсвэл модулийн баталгаажуулалтын онолын болон практик хэсгүүдэд бэлтгэхэд цаг хугацаа, хүчин чармайлтыг зөв хуваарилах нь нэлээд хэцүү байдаг, ялангуяа хичээлийн үеэр үргэлж хангалттай цаг байдаггүй. Практикаас харахад хүн бүр үүнийг даван туулж чаддаггүй. Үүний үр дүнд шалгалтын үеэр зарим оюутнууд асуудлыг зөв шийдвэрлэдэг боловч хамгийн энгийн онолын асуултуудад хариулахад хэцүү байдаг бол зарим нь теоремыг томьёолж чаддаг ч түүнийгээ хэрэгжүүлж чаддаггүй.

Цогц хувьсагчийн функцын онол (TFV) хичээлийн шалгалтанд бэлтгэх арга зүйн зөвлөмж нь энэхүү зөрчилдөөнийг шийдвэрлэх оролдлого бөгөөд хичээлийн онолын болон практик материалыг нэгэн зэрэг давтахыг баталгаажуулах оролдлого юм. "Практикгүй онол үхсэн, онолгүй практик сохор" гэсэн зарчмыг удирдлага болгон эдгээр нь тухайн хичээлийн онолын байр суурийг тодорхойлолт, томъёоллын түвшинд багтаасан бөгөөд онолын байр суурь тус бүрийн хэрэглээг харуулсан жишээнүүдийг агуулдаг. санах, ойлгоход илүү хялбар байдаг.

Санал болгож буй арга зүйн зөвлөмжийн зорилго нь сурагчийг шалгалтанд анхан шатны түвшинд бэлтгэхэд нь туслах явдал юм. Өөрөөр хэлбэл, TFKT-ийн хичээлийн хичээлд хэрэглэгдэх, гэрийн даалгавар хийх, хяналтын үйл ажиллагаанд бэлтгэхэд шаардлагатай гол санааг агуулсан өргөтгөсөн ажлын гарын авлагыг эмхэтгэсэн болно. Оюутны бие даасан ажлаас гадна энэхүү цахим боловсролын хэвлэлийг цахим самбар ашиглан интерактив хэлбэрээр хичээл явуулах эсвэл зайны сургалтын системд байрлуулахад ашиглаж болно.

Энэхүү бүтээл нь сурах бичиг, лекцийн тэмдэглэлийг орлохгүй гэдгийг анхаарна уу. Материалыг гүнзгийрүүлэн судлахын тулд Москвагийн Улсын Техникийн Их Сургуульд хэвлэгдсэн нийтлэлийн холбогдох хэсгүүдэд хандахыг зөвлөж байна. Н.Э. Бауманы үндсэн сурах бичиг.

Гарын авлагын төгсгөлд санал болгож буй уран зохиолын жагсаалт, текстэд онцолсон бүх зүйлийг багтаасан сэдвийн индекс байна. тод налуунөхцөл. Индекс нь эдгээр нэр томъёог хатуу тодорхойлсон эсвэл тайлбарласан хэсгүүдэд зориулсан гипер холбоосуудаас бүрддэг бөгөөд тэдгээрийн хэрэглээг харуулах жишээнүүд байдаг.

Энэхүү гарын авлага нь МУБИС-ийн бүх факультетийн 2-р курсын оюутнуудад зориулагдсан болно. Н.Э. Бауман.

1. Комплекс тоо бичих алгебрийн хэлбэр

z \u003d x + iy хэлбэрийн бичлэг, энд x, y нь бодит тоо, i нь төсөөллийн нэгж (өөрөөр хэлбэл i 2 = − 1)

z цогцолбор тооны алгебрийн хэлбэр гэж нэрлэдэг. Энэ тохиолдолд x-ийг цогцолбор тооны бодит хэсэг гэж нэрлээд Re z (x \u003d Re z), y-г комплекс тооны төсөөлөл гэж нэрлэдэг ба Im z (y \u003d Im z) гэж тэмдэглэнэ.

Жишээ. z = 4 − 3i цогцолбор тооны бодит хэсэг нь Re z = 4, төсөөлөл нь Im z = − 3 байна.

2. Комплекс тоонуудын хавтгай

IN нийлмэл хувьсагчийн функцүүдийн онолуудыг авч үздэгкомплекс тооны хавтгай, аль нэгийг нь тэмдэглэсэн, эсвэл z, w гэх мэт нийлмэл тоог илэрхийлдэг үсгүүдийг ашигладаг.

Нарийн төвөгтэй хавтгайн хэвтээ тэнхлэгийг нэрлэдэг бодит тэнхлэг, z = x + 0 i = x бодит тоонууд үүн дээр байрлана.

Нарийн төвөгтэй онгоцны босоо тэнхлэгийг төсөөллийн тэнхлэг гэж нэрлэдэг, энэ нь байдаг

3. Нийлмэл нийлмэл тоо

z = x + iy ба z = x − iy тоонуудыг дуудна нарийн төвөгтэй коньюгат. Нарийн төвөгтэй хавтгайд тэдгээр нь бодит тэнхлэгт тэгш хэмтэй цэгүүдтэй тохирч байна.

4. Алгебрийн хэлбэрээр нийлмэл тоотой үйлдлүүд

4.1 Комплекс тоонуудын нэмэх

Хоёр комплекс тооны нийлбэр

z 1 = x 1 + iy 1

ба z 2 = x 2 + iy 2-г комплекс тоо гэнэ

z1 + z2

= (x 1 + iy 1 ) + (x 2 + iy 2 ) = (x 1 + x 2 ) + i (y 1 + y 2 ) .

үйл ажиллагаа

нэмэлтүүд

нийлмэл тоо нь алгебрийн биномуудыг нэмэхтэй төстэй.

Жишээ. z 1 = 3 + 7i ба z 2 хоёр цогц тооны нийлбэр

= −1 +2 i

нийлмэл тоо байх болно

z 1 + z 2 = (3 +7 i ) +(−1 +2 i ) = (3 −1 ) +(7 +2 ) i = 2 +9 i .

Мэдээжийн хэрэг,

цогцолбор дахь нийлбэр

хосолсон

байна

хүчинтэй

z + z = (x + iy) + (x − iy) = 2 x = 2 Rez .

4.2 Комплекс тоог хасах

Хоёр комплекс тооны зөрүү z 1 = x 1 + iy 1

X 2 +iy 2

дуудсан

цогц

тоо z 1 − z 2 = (x 1 + iy 1 ) − (x 2 + iy 2 ) = (x 1 - x 2 ) + i (y 1 - y 2 ) .

Жишээ. Хоёр комплекс тооны ялгаа

z 1 = 3 −4 i

болон z2

= −1 +2 i

цогц байх болно

z 1 − z 2 = (3 − 4i ) − (− 1+ 2i ) = (3 − (− 1) ) + (− 4 − 2) i = 4 − 6i тоо.

ялгаа

нарийн төвөгтэй коньюгат

байна

z − z = (x + iy) − (x − iy) = 2 iy = 2 i Im z .

4.3 Комплекс тоог үржүүлэх

Хоёр комплекс тооны үржвэр

z 1 = x 1 + iy 1

ба z 2 = x 2 + iy 2

цогцолбор гэж нэрлэдэг

z 1z 2 = (x 1 + iy 1 )(x 2 + iy 2 ) = x 1x 2 + iy 1x 2 + iy 2 x 1 + i 2 y 1 y 2

= (x 1x 2 − y 1 y 2 ) + i (y 1x 2 + y 2 x ) .

Иймд i 2 = − 1 гэдгийг харгалзан нийлмэл тоог үржүүлэх үйлдэл нь алгебрийн биномийг үржүүлэх үйлдэлтэй төстэй.

ТОДОРХОЙЛОЛТ

Комплекс тооны алгебрийн хэлбэр нь \(\ z \) цогц тоог \(\ z=x+i y \) хэлбэрээр бичих бөгөөд \(\ x \) ба \(\ y \) нь бодит тоо, \ (\ i \ ) нь \(\ i^(2)=-1 \) харьцааг хангадаг төсөөллийн нэгж юм.

\(\ x \) тоог \(\ z \) цогц тооны бодит хэсэг гэж нэрлэдэг бөгөөд \(\ x=\operatorname(Re) z \) гэж тэмдэглэнэ.

\(\ y \) тоог \(\ z \) цогцолбор тооны төсөөллийн хэсэг гэж нэрлэдэг бөгөөд \(\ y=\operatorname(Im) z \) гэж тэмдэглэнэ.

Жишээлбэл:

Комплекс тоо \(\ z=3-2 i \) ба түүнтэй холбогдох тоо \(\ \overline(z)=3+2 i \) алгебрийн хэлбэрээр бичигдсэн.

\(\ z=5 i \) төсөөллийн утгыг алгебрийн хэлбэрээр бичнэ.

Үүнээс гадна, шийдэж буй асуудлаас хамааран нийлмэл тоог тригонометр эсвэл экспоненциал тоо болгон хувиргаж болно.

Даалгавар

\(\ z=\frac(7-i)(4)+13 \) тоог алгебрийн хэлбэрээр бичээд түүний бодит ба төсөөллийн хэсгүүдийг, түүнчлэн нийлмэл тоог ол.

Шийдэл.

Бутархай хуваах нэр томъёо ба бутархай нэмэх дүрмийг ашигласнаар бид дараахь зүйлийг олж авна.

\(\ z=\frac(7-i)(4)+13=\frac(7)(4)+13-\frac(i)(4)=\frac(59)(4)-\frac( 1)(4) би \)

Иймд \(\ z=\frac(5 g)(4)-\frac(1)(4) i \) цогц тооны бодит хэсэг нь \(\ x=\operatorname(Re) z= тоо юм. \frac(59) (4) \) , төсөөллийн хэсэг нь тоо \(\ y=\operatorname(Im) z=-\frac(1)(4) \)

Холболтын дугаар: \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)

Хариулт

\(\ z=\frac(59)(4)-\frac(1)(4) i \), \(\ \операторын нэр(Re) z=\frac(59)(4) \), \(\ \operatorname(Im) z=-\frac(1)(4) \), \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)

Алгебрийн хэлбэрийн харьцуулалт дахь комплекс тоонуудын үйлдлүүд

\(\ x_(1)=x_(2) \), \(\ y_(1)= y_ бол \(\ z_(1)=x_(1)+i y_(1) \) хоёр цогц тоо тэнцүү байна. (2) \) i.e. Тэдний бодит ба төсөөллийн хэсгүүд тэнцүү байна.

Даалгавар

\(\ z_(1)=13+y i \) ба \(\ z_(2)=x+5 i \) x ба y хоёр нийлмэл тоонуудын аль нь тэнцүү болохыг тодорхойл.

Шийдэл

Тодорхойлолтоор, хоёр цогц тоо нь тэдгээрийн бодит ба төсөөллийн хэсгүүд тэнцүү бол тэнцүү байна, i.e. \(\ x=13 \), \(\ y=5 \).

Хариулт \(\ x=13 \), \(\ y=5 \)

нэмэлт

\(\ z_(1)=x_(1)+i y_(1) \) нийлмэл тоог нэмэх нь бодит ба төсөөллийн хэсгүүдийн шууд нийлбэрээр хийгддэг.

\(\ z_(1)+z_(2)=x_(1)+i y_(1)+x_(2)+i y_(2)=\зүүн(x_(1)+x_(2)\баруун) +i\left(y_(1)+y_(2)\баруун)\)

Даалгавар

\(\ z_(1)=-7+5 i \), \(\ z_(2)=13-4 i \) цогц тоонуудын нийлбэрийг ол.

Шийдэл.

\(\ z_(1)=-7+5 i \) цогц тооны бодит хэсэг нь \(\ x_(1)=\operatorname(Re) z_(1)=-7 \) тоо, төсөөлөл хэсэг нь тоо \( \ y_(1)=\mathrm(Im) \), \(\ z_(1)=5 \) . \(\ z_(2)=13-4 i \) цогц тооны бодит ба төсөөллийн хэсгүүд нь \(\ x_(2)=\operatorname(Re) z_(2)=13 \) ба \(\ y_) байна. (2 )=\операторын нэр(Im) z_(2)=-4 \) .

Тиймээс комплекс тоонуудын нийлбэр нь:

\(\ z_(1)+z_(2)=\зүүн(x_(1)+x_(2)\баруун)+i\зүүн(y_(1)+y_(2)\баруун)=(-7+ 13)+i(5-4)=6+i\)

Хариулт

\(\z_(1)+z_(2)=6+i \)

Комплекс тоо нэмэх талаар тусдаа нийтлэлээс уншина уу: Комплекс тоо нэмэх.

Хасах

\(\ z_(1)=x_(1)+i y_(1) \) ба \(\ z_(2)=x_(2)+i y_(2) \) нийлмэл тоог хасах үйлдлийг шууд Бодит ба төсөөллийн хэсгүүдийг хасах:

\(\ z_(1)-z_(2)=x_(1)+i y_(1)-\зүүн(x_(2)+i y_(2)\баруун)=x_(1)-x_(2) +\left(i y_(1)-i y_(2)\баруун)=\зүүн(x_(1)-x_(2)\баруун)+i\зүүн(y_(1)-y_(2)\баруун )\)

Даалгавар

нийлмэл тоонуудын ялгааг ол \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \)

Шийдэл.

\(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \) нийлмэл тоонуудын бодит ба төсөөллийн хэсгийг ол:

\(\ x_(1)=\operatorname(Re) z_(1)=17, x_(2)=\operatorname(Re) z_(2)=15 \)

\(\ y_(1)=\операторын нэр(Im) z_(1)=-35, y_(2)=\операторын нэр(Im) z_(2)=5 \)

Тиймээс комплекс тоонуудын ялгаа нь:

\(\ z_(1)-z_(2)=\зүүн(x_(1)-x_(2)\баруун)+i\зүүн(y_(1)-y_(2)\баруун)=(17-15 )+i(-35-5)=2-40 i \)

Хариулт

\(\ z_(1)-z_(2)=2-40 i \) үржүүлэх

\(\ z_(1)=x_(1)+i y_(1) \) ба \(\ z_(2)=x_(2)+i y_(2) \) нийлмэл тоог үржүүлэх үйлдлийг шууд гүйцэтгэнэ. \(\ i^(2)=-1 \) төсөөллийн нэгжийн шинж чанарыг харгалзан алгебрийн хэлбэрээр тоо үүсгэх:

\(\ z_(1) \cdot z_(2)=\зүүн(x_(1)+i y_(1)\баруун) \cdot\left(x_(2)+i y_(2)\баруун)=x_ (1) \cdot x_(2)+i^(2) \cdot y_(1) \cdot y_(2)+\left(x_(1) \cdot i y_(2)+x_(2) \cdot i y_(1)\баруун)= \)

\(\ =\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2) ) \cdot y_(1)\баруун) \)

Даалгавар

Комплекс тоонуудын үржвэрийг ол \(\ z_(1)=1-5 i \)

Шийдэл.

Комплекс тоонуудын цогцолбор:

\(\ z_(1) \cdot z_(2)=\зүүн(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\баруун)+i\зүүн(x_(1) \cdot y_(2)+x_(2) \cdot y_(1)\баруун)=(1 \cdot 5-(-5) \cdot 2)+i(1 \cdot 2+(-5) \cdot 5 )=15-23 би \)

Хариулт

\(\ z_(1) \cdot z_(2)=15-23 i \) хуваах

Комплекс тооны коэффициент \(\ z_(1)=x_(1)+i y_(1) \) ба \(\ z_(2)=x_(2)+i y_(2) \)-ийг үржүүлж тодорхойлно. хуваагчтай нийлмэл тоонд хуваагч ба хуваагч:

\(\ \frac(z_(1))(z_(2))=\frac(x_(1)+i y_(1))(x_(2)+i y_(2))=\frac(\зүүн (x_(1)+i y_(1)\баруун)\зүүн(x_(2)-i y_(2)\баруун))(\зүүн(x_(2)+i y_(2)\баруун)\зүүн (x_(2)-i y_(2)\баруун))=\frac(x_(1) \cdot x_(2)+y_(1) \cdot y_(2))(x_(2)^(2) +y_(2)^(2))+i \frac(x_(2) \cdot y_(1)-x_(1) \cdot y_(2))(x_(2)^(2)+y_(2) )^(2)) \)

Даалгавар

1-ийн тоог комплекс тоонд хуваах \(\ z=1+2 i \).

Шийдэл.

Бодит 1-ийн төсөөллийн хэсэг нь тэг тул хүчин зүйл нь:

\(\ \frac(1)(1+2 i)=\frac(1 \cdot 1)(1^(2)+2^(2))-i \frac(1 \cdot 2)(1^( 2)+2^(2))=\frac(1)(5)-i \frac(2)(5) \)

Хариулт

\(\ \frac(1)(1+2 i)=\frac(1)(5)-i \frac(2)(5) \)

Хичээлийн төлөвлөгөө.

1. Зохион байгуулалтын мөч.

2. Материалын танилцуулга.

3. Гэрийн даалгавар.

4. Хичээлийг дүгнэх.

Хичээлийн үеэр

I. Зохион байгуулалтын мөч.

II. Материалын танилцуулга.

Урам зориг.

Бодит тоонуудын багцыг өргөжүүлэх нь бодит тоон дээр шинэ тоо (төсөөлөл) нэмэгдэх явдал юм. Эдгээр тоонуудын танилцуулга нь бодит тооны олонлог дахь сөрөг тооноос үндсийг гаргаж авах боломжгүйтэй холбоотой юм.

Комплекс тооны тухай ойлголтын танилцуулга.

Бодит тоог нэмдэг төсөөлөлтэй тоонууд дараах байдлаар бичигдэнэ би, Хаана бинь төсөөллийн нэгж бөгөөд i 2 = - 1.

Үүний үндсэн дээр бид комплекс тооны дараах тодорхойлолтыг олж авна.

Тодорхойлолт. Комплекс тоо нь хэлбэрийн илэрхийлэл юм a+bi, Хаана аТэгээд ббодит тоонууд юм. Энэ тохиолдолд дараахь нөхцлийг хангасан болно.

a) Хоёр комплекс тоо a 1 + b 1 iТэгээд a 2 + b 2 iзөвхөн хэрэв л бол тэнцүү a 1 = a 2, b1=b2.

б) Комплекс тоонуудын нэмэгдлийг дараах дүрмээр тодорхойлно.

(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.

в) Комплекс тоонуудын үржвэрийг дараах дүрмээр тодорхойлно.

(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.

Комплекс тооны алгебрийн хэлбэр.

Комплекс тоог маягтаар бичих a+biнийлмэл тооны алгебрийн хэлбэр гэж нэрлэгддэг, энд А- бодит хэсэг бинь төсөөллийн хэсэг бөгөөд ббодит тоо юм.

Нарийн төвөгтэй тоо a+biХэрэв түүний бодит ба төсөөлөл хэсгүүд нь тэгтэй тэнцүү бол тэгтэй тэнцүү гэж үзнэ. a=b=0

Нарийн төвөгтэй тоо a+biцагт b = 0бодит тоо гэж үздэг а: a + 0i = a.

Нарийн төвөгтэй тоо a+biцагт a = 0цэвэр төсөөлөл гэж нэрлэдэг ба тэмдэглэсэн байна би: 0 + би = би.

Хоёр комплекс тоо z = a + biТэгээд = a – bi, зөвхөн төсөөллийн хэсгийн тэмдгээр л ялгаатай байгаа нь коньюгат гэж нэрлэгддэг.

Алгебрийн хэлбэрийн комплекс тоон дээрх үйлдлүүд.

Комплекс тоон дээр алгебрийн хэлбэрээр дараах үйлдлүүдийг хийж болно.

1) Нэмэлт.

Тодорхойлолт. Комплекс тоонуудын нийлбэр z 1 = a 1 + b 1 iТэгээд z 2 = a 2 + b 2 iнийлмэл тоо гэж нэрлэдэг z, бодит хэсэг нь бодит хэсгүүдийн нийлбэртэй тэнцүү байна z1Тэгээд z2, мөн төсөөллийн хэсэг нь тоонуудын төсөөллийн хэсгүүдийн нийлбэр юм z1Тэгээд z2, тэр бол z = (a 1 + a 2) + (b 1 + b 2)i.

Тоонууд z1Тэгээд z2нэр томъёо гэж нэрлэдэг.

Комплекс тоог нэмэх нь дараахь шинж чанартай байдаг.

1º. Солих чадвар: z1 + z2 = z2 + z1.

2º. Нийгэмлэг: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).

3º. Нарийн төвөгтэй тоо -а -бинийлмэл тооны эсрэг гэж нэрлэдэг z = a + bi. Комплекс тооны эсрэг талын нийлмэл тоо z, тэмдэглэсэн -z. Комплекс тоонуудын нийлбэр zТэгээд -zтэгтэй тэнцүү: z + (-z) = 0

Жишээ 1: Нэмэх (3 - i) + (-1 + 2i).

(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Хасах.

Тодорхойлолт.Комплекс тооноос хасах z1нийлмэл тоо z2 z,Юу z + z 2 = z 1.

Теорем. Нарийн төвөгтэй тоонуудын ялгаа байдаг бөгөөд үүнээс гадна өвөрмөц юм.

Жишээ 2: Хасах (4 - 2i) - (-3 + 2i).

(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.

3) Үржүүлэх.

Тодорхойлолт. Комплекс тоонуудын үржвэр z 1 =a 1 +b 1 iТэгээд z 2 \u003d a 2 + b 2 iнийлмэл тоо гэж нэрлэдэг zтэгшитгэлээр тодорхойлогддог: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.

Тоонууд z1Тэгээд z2хүчин зүйл гэж нэрлэдэг.

Комплекс тоог үржүүлэх нь дараахь шинж чанартай байдаг.

1º. Солих чадвар: z 1 z 2 = z 2 z 1.

2º. Нийгэмлэг: (z 1 z 2)z 3 = z 1 (z 2 z 3)

3º. Нэмэлттэй холбоотой үржүүлгийн тархалт:

(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.

4º. z \u003d (a + bi) (a - bi) \u003d a 2 + b 2бодит тоо юм.

Практикт нийлбэрийг нийлбэрээр үржүүлж, бодит болон төсөөллийн хэсгүүдийг салгах дүрмийн дагуу нийлмэл тоог үржүүлдэг.

Дараах жишээнд нийлмэл тоог дүрмээр болон нийлбэрийг нийлбэрээр үржүүлэх гэсэн хоёр аргаар үржүүлэхийг авч үзье.

Жишээ 3: Үржүүлэх (2 + 3i) (5 - 7i).

1 арга зам. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15) )i = 31 + i.

2 арга зам. (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.

4) хэлтэс.

Тодорхойлолт. Комплекс тоог хуваах z1комплекс тоо руу z2, ийм цогц тоог олно гэсэн үг z, Юу z z 2 = z 1.

Теорем.Комплекс тоонуудын категори нь байгаа бөгөөд хэрэв байгаа бол өвөрмөц байна z2 ≠ 0 + 0i.

Практикт нийлмэл тоонуудын хуваагчийг хуваагч болон хуваагчаар үржүүлэх замаар олдог.

Болъё z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, Дараа нь

.

Дараах жишээнд бид хуваалтыг томъёогоор болон хуваагчийн нэгдэлээр үржүүлэх дүрмийг гүйцэтгэдэг.

Жишээ 4. Хэсэлтийг ол .

5) Эерэг бүхэл тоо руу өсгөх.

a) Төсөөллийн нэгдлийн хүч.

Тэгш байдлын давуу талыг ашиглах би 2 \u003d -1, төсөөллийн нэгжийн эерэг бүхэл тоог тодорхойлоход хялбар байдаг. Бидэнд байгаа:

би 3 \u003d би 2 би \u003d -i,

би 4 \u003d i 2 i 2 \u003d 1,

би 5 \u003d би 4 би \u003d би,

би 6 \u003d i 4 i 2 \u003d -1,

би 7 \u003d би 5 би 2 \u003d -i,

би 8 = би 6 би 2 = 1гэх мэт.

Энэ нь градусын утгыг харуулж байна би н, Хаана n- эерэг бүхэл тоо, индикатор нэмэгдэхэд үе үе давтагдана 4 .

Тиймээс тоог нэмэгдүүлэх биэерэг бүхэл тоонд индексийг хуваана 4 мөн босгоно биилтгэгч нь хуваагдлын үлдэгдэл болох хүчинд.

Жишээ 5 Тооцоол: (би 36 + би 17) би 23.

i 36 = (i 4) 9 = 1 9 = 1,

i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 i = i.

i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 i 3 = - i.

(i 36 + i 17) i 23 \u003d (1 + i) (- i) \u003d - i + 1 \u003d 1 - i.

б) Комплекс тоог эерэг бүхэл тоо болгон өсгөх нь ижил цогцолбор хүчин зүйлийг үржүүлэх онцгой тохиолдол тул биномийг харгалзах зэрэгт өсгөх дүрмийн дагуу явагдана.

Жишээ 6 Тооцоол: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.