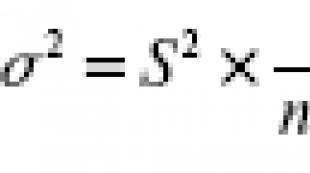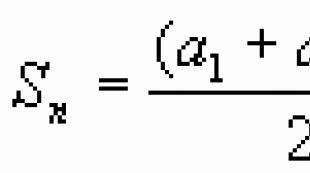Բոլոր բանաձևերը թվաբանական պրոգրեսիայում են: Թվաբանական առաջընթաց: Թվերի հաջորդականության մեկ այլ տեսակ երկրաչափական է

Մաթեմատիկան ունի իր գեղեցկությունը, ինչպես նկարչությունն ու պոեզիան:

Ռուս գիտնական, մեխանիկ Ն.Ե. Ukուկովսկին

Թվաբանական առաջընթացի հայեցակարգի հետ կապված խնդիրները շատ տարածված խնդիրներ են մաթեմատիկայի ընդունելության քննությունների ժամանակ: Նման խնդիրները հաջողությամբ լուծելու համար անհրաժեշտ է լավ իմանալ թվաբանական առաջընթացի հատկությունները և ունենալ դրանց կիրառման որոշակի հմտություններ:

Նախ հիշում ենք թվաբանական առաջընթացի հիմնական հատկությունները և ներկայացնում ամենակարևոր բանաձևերը, կապված այս հայեցակարգի հետ:

Սահմանում. Թվերի հաջորդականություն, որոնցում յուրաքանչյուր հաջորդ տերմին նախորդից տարբերվում է նույն թվով, կոչվում է թվաբանական առաջընթաց: Ավելին, թիվըկոչվում է առաջընթացի տարբերություն:

Թվաբանական առաջընթացի համար վավեր են հետևյալ բանաձևերը

, (1)

որտեղ Բանաձևը (1) կոչվում է թվաբանական առաջընթացի ընդհանուր տերմինի բանաձև, իսկ բանաձևը (2) թվաբանական առաջընթացի հիմնական հատկությունն է. Առաջընթացի յուրաքանչյուր տերմին համընկնում է նրա հարևան տերմինների թվաբանական միջինին և.

Նկատի ունեցեք, որ հենց այս հատկության պատճառով է դիտարկվող առաջընթացը կոչվում «թվաբանություն»:

Վերը նշված բանաձևերը (1) և (2) ընդհանրացված են հետևյալ կերպ.

(3)

Գումարը հաշվարկելու համարառաջին թվաբանական պրոգրեսիայի անդամներսովորաբար բանաձևը կիրառվում է

(5) որտեղ և.

Հաշվի առնելով բանաձևը (1), ապա բանաձեւը (5) ենթադրում է

Եթե ​​նշենք, ապա

որտեղ Քանի որ, ապա (7) և (8) բանաձևերը համապատասխան բանաձևերի ընդհանրացում են (5) և (6):

Մասնավորապես , բանաձեւը (5) ենթադրում է, ինչ

Թվաբանական առաջընթացի հատկությունը, որը ձևակերպված է հետևյալ թեորեմի միջոցով, ուսանողների մեծ մասի համար քիչ հայտնի է:

Թեորեմ.Եթե, ապա

Ապացույց.Եթե, ապա

Թեորեմն ապացուցված է:

Օրինակ , օգտագործելով թեորեմը, դա կարելի է ցույց տալ

Անցնենք «Թվաբանական առաջընթաց» թեմայով խնդիրների լուծման բնորոշ օրինակների դիտարկմանը:

Օրինակ 1.Թող և. Գտնել:

Լուծում:Կիրառելով բանաձևը (6) ՝ մենք ստանում ենք: Քանի որ, ապա, կամ.

Օրինակ 2.Թող այն լինի երեք անգամ ավելի, և երբ գործակիցով բաժանվում ենք, ստանում ենք 2 և մնացորդ 8. Որոշեք և.

Լուծում:Օրինակի վիճակը ենթադրում է հավասարումների համակարգ

Քանի որ ,, և, ապա հավասարումների համակարգից (10) մենք ստանում ենք

Այս հավասարումների համակարգի լուծումը և.

Օրինակ 3.Գտեք, եթե և.

Լուծում:Ըստ բանաձևի (5) մենք ունենք կամ. Այնուամենայնիվ, օգտագործելով գույքը (9), մենք ձեռք ենք բերում:

Քանի որ, և հետո ՝ հավասարությունից հետեւում է հավասարումըկամ .

Օրինակ 4.Գտնել, եթե.

Լուծում:Ըստ բանաձևի (5) մենք ունենք

Այնուամենայնիվ, օգտագործելով թեորեմը, կարելի է գրել

Սրանից և բանաձևից (11) մենք ստանում ենք.

Օրինակ 5. Հաշվի առնելով. Գտնել:

Լուծում:Այդ ժամանակվանից. Այնուամենայնիվ, հետևաբար.

Օրինակ 6.Թող, և. Գտնել:

Լուծում:Օգտագործելով բանաձևը (9), մենք ստանում ենք. Հետեւաբար, եթե, ապա կամ.

Քանի որ և, ապա այստեղ մենք ունենք հավասարումների համակարգ

Լուծելով, մենք ստանում ենք և.

Հավասարման բնական արմատըէ

Օրինակ 7.Գտեք, եթե և.

Լուծում:Քանի որ (3) բանաձևով մենք ունենք դա, ապա խնդրի վիճակից այն հետևում է հավասարումների համակարգին

Եթե ​​փոխարինեք արտահայտությունըհամակարգի երկրորդ հավասարման մեջ, ապա մենք ստանում ենք կամ.

Քառակուսի հավասարման արմատներն ենեւ.

Դիտարկենք երկու դեպք:

1. Թող, ուրեմն: Քանի որ, և հետո:

Այս դեպքում, ըստ բանաձևի (6), մենք ունենք

2. Եթե, ապա, և

Պատասխան ՝ և.

Օրինակ 8.Յայտնի է որ եւ. Գտնել:

Լուծում:Հաշվի առնելով բանաձևը (5) և օրինակի վիճակը, մենք գրում ենք և.

Հետևաբար հետևում է հավասարումների համակարգին

Եթե ​​համակարգի առաջին հավասարումը բազմապատկենք 2 -ով, ապա ավելացնենք երկրորդ հավասարումին, կստանանք

Ըստ բանաձևի (9) մենք ունենք... Այս կապակցությամբ (12) -ից հետևում էկամ .

Քանի որ, և հետո:

Պատասխան.

Օրինակ 9.Գտեք, եթե և.

Լուծում:Քանի որ, և պայմանով, ապա կամ.

Բանաձևից (5) հայտնի է, ինչ . Այդ ժամանակվանից.

Հետեւաբար, այստեղ մենք ունենք գծային հավասարումների համակարգ

Այսպիսով, մենք ստանում ենք և. Հաշվի առնելով բանաձևը (8) ՝ գրում ենք.

Օրինակ 10.Լուծի՛ր հավասարումը:

Լուծում:Տրված հավասարումից հետևում է, որ. Ենթադրենք, որ ,, և. Այս դեպքում .

Ըստ բանաձևի (1), կարող եք գրել կամ.

Քանի որ, ապա հավասարումը (13) ունի մեկ հարմար արմատ:

Օրինակ 11.Գտեք առավելագույն արժեքը, եթե և.

Լուծում:Քանի որ թվաբանական առաջընթացը նվազում է: Այս առումով արտահայտությունը ստանում է առավելագույն արժեք, երբ դա առաջընթացի նվազագույն դրական տերմինի թիվն է:

Մենք օգտագործում ենք բանաձևը (1) և փաստը, ինչպես Հետո մենք ստանում ենք դա կամ.

Քանի որ, ապա կամ ... Այնուամենայնիվ, այս անհավասարության մեջամենամեծ բնական թիվը, ուստի.

Եթե ​​արժեքները և փոխարինված են բանաձևով (6), ապա մենք ստանում ենք:

Պատասխան.

Օրինակ 12.Որոշեք բոլոր երկնիշ բնական թվերի գումարը, որոնք 6-ի բաժանելիս տալիս են 5-ի մնացորդ:

Լուծում:Եկեք բոլոր երկնիշ բնական թվերի բազմությամբ նշենք, այսինքն. ... Հաջորդը, մենք կառուցում ենք բազմության այն տարրերից (թվերից) բաղկացած ենթաբազմություն, որը 6 -ի բաժանելիս տալիս է մնացած 5 -ը:

Դժվար չէ հաստատել, ինչ . Ակնհայտորեն , որ հավաքածուի տարրերըձևավորել թվաբանական առաջընթաց, որում և.

Հավաքածուի կարդինալությունը (տարրերի թիվը) հաստատելու համար մենք ենթադրում ենք, որ. Քանի և, ապա (1) բանաձևից այն հետևում է կամ. Հաշվի առնելով բանաձևը (5) ՝ մենք ստանում ենք.

Խնդիրների լուծման վերը նշված օրինակները ոչ մի կերպ չեն կարող պնդել, որ սպառիչ են: Այս հոդվածը գրված է տվյալ թեմայով բնորոշ խնդիրների լուծման ժամանակակից մեթոդների վերլուծության հիման վրա: Թվաբանական առաջընթացի հետ կապված խնդիրների լուծման մեթոդների ավելի խորը ուսումնասիրման համար նպատակահարմար է անդրադառնալ առաջարկվող գրականության ցանկին:

1. Մաթեմատիկայի խնդիրների հավաքածու տեխնիկական քոլեջների դիմորդների համար / Էդ. Մ.Ի. Սկանավի. - Մ .: Խաղաղություն և կրթություն, 2013 թ.- 608 էջ

2. Suprun V.P. Մաթեմատիկա ավագ դպրոցի աշակերտների համար. Դպրոցական ծրագրի լրացուցիչ բաժիններ: - Մ .: Լենանդ / URSS, 2014 թ.- 216 էջ

3. Մեդինսկի Մ.Մ. Խնդիրների և վարժությունների տարրական մաթեմատիկայի ամբողջական դասընթաց: Գիրք 2. Թվերի հաջորդականություններ և առաջընթացներ: - Մ .: Էդիթուս, 2015 թ.- 208 էջ

Դեռ հարցեր ունե՞ք:

Դաստիարակից օգնություն ստանալու համար գրանցվեք:

կայքը, նյութի ամբողջական կամ մասնակի պատճենմամբ, անհրաժեշտ է հղում դեպի աղբյուրը:

Դասի տեսակը.սովորել նոր նյութ:

Դասի նպատակները.

• թվաբանական առաջընթացի միջոցով լուծված խնդիրների վերաբերյալ ուսանողների պատկերացումների ընդլայնում և խորացում; ուսանողների որոնողական գործունեության կազմակերպում ՝ թվաբանական առաջընթացի առաջին n անդամների գումարի բանաձևի հիման վրա.
• նոր գիտելիքներ ինքնուրույն ձեռք բերելու հմտությունների զարգացում, առաջադրված նպատակին հասնելու համար արդեն ձեռք բերված գիտելիքների օգտագործում.
• ձեռք բերված փաստերը ընդհանրացնելու ցանկության և անհրաժեշտության զարգացում, անկախության զարգացում:

Առաջադրանքներ.

• ընդհանրացնել և համակարգել «Թվաբանական առաջընթաց» թեմայի վերաբերյալ առկա գիտելիքները.
• ածանցել թվաբանական առաջընթացի առաջին n պայմանների գումարի հաշվարկման բանաձևեր.
• սովորեցնել, թե ինչպես կիրառել ստացված բանաձևերը տարբեր խնդիրներ լուծելիս.
• ուսանողների ուշադրությունը հրավիրել գործողությունների կարգի վրա ՝ թվային արտահայտության արժեքը գտնելիս:

Սարքավորումներ:

• խմբերով և զույգերով աշխատելու առաջադրանքներով քարտեր.
• գնահատման թուղթ;
• ներկայացում«Թվաբանական առաջընթաց»:

I. Հիմնական գիտելիքների թարմացում:

1. Անկախ աշխատանք զույգերով:

1 -ին տարբերակ.

Տվեք թվաբանական առաջընթացի սահմանում: Գրեք ռեկուրսիվ բանաձևը, որն օգտագործում եք թվաբանական առաջընթացը սահմանելու համար: Ողջույն, թվաբանական առաջընթացի օրինակ և նշեք դրա տարբերությունը:

2 -րդ տարբերակ.

Գրեք թվաբանական առաջընթացի n -րդ տերմինի բանաձևը: Գտեք թվաբանական առաջընթացի 100 -րդ տերմինը ( a n}: 2, 5, 8 …
Այս պահին գրատախտակի հետևում գտնվող երկու ուսանող պատրաստում են նույն հարցերի պատասխանները:
Ուսանողները գնահատում են գործընկերոջ աշխատանքը տախտակի դեմ: (Պատասխաններով թերթերը հանձնվում են):

2. Խաղի պահ:

Exորավարժություններ 1.

Ուսուցիչ.Ես թվաբանական առաջընթաց եմ պատկերացրել: Ուղղակի ինձ երկու հարց տվեք, որպեսզի պատասխաններից հետո կարողանաք արագ անվանել այս առաջընթացի 7 -րդ տերմինը: (1, 3, 5, 7, 9, 11, 13, 15 ...)

Ուսանողների հարցերը:

1. Ո՞րն է առաջընթացի վեցերորդ տերմինը և ո՞րն է տարբերությունը:
2. Ո՞րն է առաջընթացի ութերորդ տերմինը և ո՞րն է տարբերությունը:

Եթե ​​այլևս հարցեր չկան, ապա ուսուցիչը կարող է դրանք խթանել `« արգելել »դ (տարբերություն), այսինքն ՝ չի թույլատրվում հարցնել, թե որն է տարբերությունը: Կարող եք հարցեր տալ. Ո՞րն է առաջընթացի 6 -րդ և որքա՞ն առաջադիմության 8 -րդ տերմինը:

Առաջադրանք 2.

Գրատախտակին գրված է 20 թիվ. 1, 4, 7 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58.

Ուսուցիչը մեջքով կանգնած է գրատախտակին: Ուսանողները զանգում են համարի համարին, իսկ ուսուցիչը ակնթարթորեն զանգում է հենց իրեն: Բացատրեք, թե ինչպես եմ դա անում:

Ուսուցիչը հիշում է 9 -րդ կիսամյակի բանաձևը a n = 3n - 2և փոխարինելով n- ի տրված արժեքները, գտնում է համապատասխան արժեքները a n

II. Կրթական խնդրի հայտարարություն:

Ես առաջարկում եմ լուծել հնագույն խնդիրը, որը թվագրվում է մ.թ.ա.

Առաջադրանք.«Թող ձեզ ասեն. 10 չափաբաժին գարի բաժանեք 10 մարդու միջև, յուրաքանչյուր անձի և նրա հարևանի միջև տարբերությունը հավասար է չափման 1/8 -ի»:

• Ինչպե՞ս է այս առաջադրանքը կապված թվաբանական առաջընթացի թեմայի հետ: (Յուրաքանչյուր հաջորդ ստանում է չափման 1/8 ավելին, ինչը նշանակում է տարբերություն d = 1/8, 10 մարդ, ինչը նշանակում է n = 10):
• Ձեր կարծիքով, ի՞նչ է նշանակում 10 թիվը: (Առաջընթացի բոլոր անդամների գումարը):
• Էլ ի՞նչ պետք է իմանաք, որպեսզի հեշտ և պարզ դարձնեք գարի բաժանումը ըստ առաջադրանքի պայմանի: (Առաջընթացի առաջին տերմինը):

Դասի նպատակ- առաջադիմության անդամների գումարի կախվածությունը նրանց թվից, առաջին տերմինից և տարբերությունից, և ստուգելը, թե արդյոք խնդիրը ճիշտ է լուծվել հին ժամանակներում:

Մինչև բանաձևի եզրակացություն անելը, եկեք տեսնենք, թե ինչպես հին եգիպտացիները լուծեցին խնդիրը:

Եվ նրանք լուծեցին հետևյալ կերպ.

1) 10 միջոցառում `10 = 1 միջոց` միջին մասնաբաժին;
2) 1 միջոց = 2 միջոց ՝ կրկնապատկված միջինբաժանել:
Կրկնապատկվել է միջինբաժնեմասը 5 -րդ և 6 -րդ մարդկանց բաժնետոմսերի գումարն է:
3) 2 միջոց `1/8 միջոց = 1 7/8 միջոց` հինգերորդ անձի բաժնեմասի երկու անգամ:
4) 1 7/8: 2 = 5/16 - հինգերորդի մասնաբաժինը. և այլն, կարող եք գտնել յուրաքանչյուր նախորդ և հաջորդ անձի մասնաբաժինը:

Մենք ստանում ենք հաջորդականությունը.

III. Խնդրի լուծում:

1.Խմբային աշխատանք

I խումբ.Գտեք 20 հաջորդական բնական թվերի գումարը. S 20 = (20 + 1) ∙ 10 = 210:

Ընդհանրապես

II խումբ.Գտեք 1 -ից 100 բնական թվերի գումարը (The Little Legend of the Little Gauss):

S 100 = (1 + 100) ∙ 50 = 5050

Արդյունք:

III խումբ.Գտեք 1 -ից 21 բնական թվերի գումարը:

Լուծում. 1 + 21 = 2 + 20 = 3 + 19 = 4 + 18 ...

Արդյունք:

IV խումբ.Գտեք 1 -ից 101 բնական թվերի գումարը:

Արդյունք:

Քննարկված խնդիրների լուծման այս մեթոդը կոչվում է «Գաուսի մեթոդ»:

2. Յուրաքանչյուր խումբ գրատախտակին ներկայացնում է խնդրի լուծումը:

3. Կամայական թվաբանական առաջընթացի համար առաջարկվող լուծումների ընդհանրացում.

a 1, a 2, a 3, ..., a n-2, a n-1, a n:
S n = a 1 + a 2 + a 3 + a 4 +… + a n-3 + a n-2 + a n-1 + a n.

Եկեք այս գումարը գտնենք ՝ հիմնավորելով նույն ձևով.

4. Մենք լուծե՞լ ենք առաջադրանքը:(Այո)

IV. Ստացված բանաձևերի առաջնային ըմբռնումը և կիրառումը խնդիրների լուծման մեջ:

1. Հին խնդրի լուծման ստուգում բանաձևի միջոցով:

2. Բանաձեւի կիրառում տարբեր խնդիրներ լուծելիս:

3. Խնդիրներ լուծելիս բանաձեւը կիրառելու ունակություն ձեւավորելու վարժություններ:

Ա) թիվ 613

Հաշվի առնելով: ( ա ն) -թվաբանական առաջընթաց;

(a n) ՝ 1, 2, 3, ..., 1500

Գտնել: Ս 1500

Լուծում. , a 1 = 1, a 1500 = 1500,

Բ) Տրված է ՝ ( ա ն) -թվաբանական առաջընթաց;
(ա ն) ՝ 1, 2, 3, ...
S n = 210

Գտնել: n
Լուծում.

V. Անկախ աշխատանք փոխադարձ ստուգմամբ:

Դենիսը աշխատանքի գնաց որպես սուրհանդակ: Առաջին ամսվա ընթացքում նրա աշխատավարձը կազմում էր 200 ռուբլի, յուրաքանչյուր հաջորդ ամսվա ընթացքում այն ​​ավելանում էր 30 ռուբլով: Որքա՞ն է նա վաստակել մեկ տարվա ընթացքում:

Հաշվի առնելով: ( ա ն) -թվաբանական առաջընթաց;
a 1 = 200, d = 30, n = 12
Գտնել: Ս 12
Լուծում.

Պատասխան. Դենիսը մեկ տարվա ընթացքում ստացել է 4380 ռուբլի:

Vi. Տնային աշխատանքի ճեպազրույց:

1. էջ 4.3 - սովորեք բանաձևի ածանցումը:
2. №№ 585, 623 .
3. Ստեղծեք խնդիր, որը կլուծվեր ՝ օգտագործելով թվաբանական առաջընթացի առաջին n պայմանների գումարը:

Vii. Ամփոփելով դասը:

1. Գնահատման թերթիկ

2. Շարունակիր նախադասությունները

• Այսօր իմ սովորած դասին ...
• Սովորած բանաձևեր ...
• Ես կարծում եմ, որ …

3. Կարո՞ղ եք գտնել 1 -ից 500 թվերի գումարը: Ի՞նչ մեթոդ եք օգտագործելու այս խնդիրը լուծելու համար:

Մատենագիտություն.

1. Հանրահաշիվ, 9 -րդ դաս. Դասագիրք ուսումնական հաստատությունների համար: Էդ. Գ.Վ. Դորոֆեևա.Մ .: «Կրթություն», 2009 թ.

Այո, այո. Թվաբանական առաջընթացը խաղալիք չէ ձեզ համար :)

Դե, ընկերներ, եթե կարդում եք այս տեքստը, ապա ներքին գլխարկի ակնհայտությունն ինձ ասում է, որ դեռ չգիտեք, թե ինչ է թվաբանական առաջընթացը, բայց իսկապես (ոչ, այսպես. SOOOOO!) Ուզում եք իմանալ: Հետևաբար, ես ձեզ չեմ տանջի երկար ներածություններով և անմիջապես գործի կանցնեմ:

Սկսենք մի քանի օրինակով: Հաշվի առեք թվերի մի շարք.

• 1; 2; 3; 4; ...
• 15; 20; 25; 30; ...
• $ \ sqrt (2); \ 2 \ sqrt (2); \ 3 \ sqrt (2); ... $

Ի՞նչ ընդհանրություն ունեն այս բոլոր հավաքածուները: Առաջին հայացքից ՝ ոչինչ: Բայց իրականում ինչ -որ բան կա: Այսինքն: յուրաքանչյուր հաջորդ տարր տարբերվում է նախորդից նույն թվով.

Ինքներդ դատեք: Առաջին հավաքածուն պարզապես հաջորդական թվեր են, յուրաքանչյուր հաջորդը ավելի շատ, քան նախորդը: Երկրորդ դեպքում հարակից թվերի տարբերությունն արդեն հավասար է հինգի, սակայն այս տարբերությունը դեռ հաստատուն է: Երրորդ դեպքում ՝ արմատներն ընդհանրապես: Այնուամենայնիվ, $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $, և $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, այսինքն. և այս դեպքում յուրաքանչյուր հաջորդ տարր պարզապես ավելանում է $ \ sqrt (2) $ (և մի վախեցեք, որ այս թիվը իռացիոնալ չէ):

Այսպես. Բոլոր նման հաջորդականությունները կոչվում են թվաբանական առաջընթացներ: Եկեք հստակ սահմանում տանք.

Սահմանում. Թվերի հաջորդականությունը, որոնցում յուրաքանչյուր հաջորդը նախորդից տարբերվում է նույն չափով, կոչվում է թվաբանական առաջընթաց: Հենց այն թիվը, որով թվերը տարբերվում են, կոչվում է առաջընթացի տարբերություն և առավել հաճախ նշվում է $ d $ տառով:

Նշանակում. $ \ Ձախ (((a) _ (n)) \ աջ) $ - առաջընթացն ինքնին, $ d $ - դրա տարբերությունը:

Եվ ընդամենը մի քանի կարևոր նկատողություն: Նախ, միայն կարգուկանոնթվերի հաջորդականություն. նրանց թույլատրվում է կարդալ խստորեն այն հաջորդականությամբ, որով գրված են, և ուրիշ ոչինչ: Դուք չեք կարող վերադասավորել կամ փոխանակել թվերը:

Երկրորդ, հաջորդականությունն ինքնին կարող է լինել վերջավոր կամ անվերջ: Օրինակ, բազմությունը (1; 2; 3) ակնհայտորեն վերջնական թվաբանական առաջընթաց է: Բայց եթե ինչ -որ բան գրում ես ոգով (1; 2; 3; 4; ...) - սա արդեն անվերջ առաջընթաց է: Չորսից հետո էլիպսները, կարծես, ակնարկում են, որ դեռևս բավականին թվեր են ընթանում: Անսահման շատ, օրինակ :)

Նաև կցանկանայի նշել, որ առաջընթացներն ավելանում և նվազում են: Մենք արդեն տեսել ենք աճողները `նույն հավաքածուն (1; 2; 3; 4; ...): Եվ ահա առաջընթացների նվազման օրինակներ.

• 49; 41; 33; 25; 17; ...
• 17,5; 12; 6,5; 1; −4,5; −10; ...
• $ \ sqrt (5); \ \ sqrt (5) -1; \ \ sqrt (5) -2; \ \ sqrt (5) -3; ... $

Լավ, լավ. Այս վերջին օրինակը կարող է չափազանց բարդ թվալ: Բայց մնացածը, կարծում եմ, ձեզ համար պարզ է: Հետևաբար, մենք կներկայացնենք նոր սահմանումներ.

Սահմանում. Թվաբանական առաջընթացը կոչվում է.

1. ավելանում է, եթե յուրաքանչյուր հաջորդ տարր ավելի մեծ է, քան նախորդը.
2. նվազում է, եթե, ընդհակառակը, յուրաքանչյուր հաջորդ տարր ավելի փոքր է, քան նախորդը:

Բացի այդ, կան այսպես կոչված «ստացիոնար» հաջորդականություններ `դրանք բաղկացած են նույն կրկնվող թվից: Օրինակ ՝ (3; 3; 3; ...):

Մնում է միայն մեկ հարց. Ինչպե՞ս տարբերել աճող առաջընթացը նվազողից: Բարեբախտաբար, ամեն ինչ կախված է $ d $ թվի նշանից, այսինքն. տարբերության առաջընթաց.

1. Եթե ​​$ d \ gt 0 $, ապա առաջընթացը մեծանում է.
2. Եթե ​​$ d \ lt 0 $, ապա առաջընթացը ակնհայտորեն նվազում է.
3. Վերջապես, կա դեպք $ d = 0 $ - այս դեպքում ամբողջ առաջընթացը կրճատվում է նույնական թվերի անշարժ հաջորդականության ՝ (1; 1; 1; 1; ...) և այլն:

Փորձենք հաշվարկել $ d $ տարբերությունը վերը նշված երեք նվազող առաջընթացների համար: Դա անելու համար բավական է վերցնել ցանկացած երկու հարակից տարրեր (օրինակ ՝ առաջինը և երկրորդը) և աջից համարից հանել ձախ թիվը: Այն այսպիսի տեսք կունենա.

• 41−49=−8;
• 12−17,5=−5,5;
• $ \ sqrt (5) -1- \ sqrt (5) = - 1 $:

Ինչպես տեսնում եք, երեք դեպքում էլ տարբերությունն իսկապես բացասական է ստացվել: Եվ հիմա, երբ մենք քիչ թե շատ պարզեցինք սահմանումները, ժամանակն է պարզել, թե ինչպես են նկարագրվում առաջընթացները և որոնք են դրանց հատկությունները:

Առաջադիմական անդամներ և պարբերական բանաձև

Քանի որ մեր հաջորդականությունների տարրերը չեն կարող փոխանակվել, դրանք կարող են համարակալվել.

\ [\ ձախ (((a) _ (n)) \ աջ) = \ ձախ \ (((a) _ (1)), \ ((a) _ (2)), ((a) _ (3 )), ... \ ճիշտ \) \]

Այս հավաքածուի առանձին տարրերը կոչվում են առաջընթացի անդամներ: Դրանք նշվում են մի թվով ՝ առաջին տերմին, երկրորդ տերմին և այլն:

Բացի այդ, ինչպես արդեն գիտենք, առաջընթացի հարևան անդամները կապված են բանաձևի հետ.

\ [((ա) _ (n))-((a) _ (n-1)) = d \ Rightarrow ((a) _ (n)) = ((a) _ (n-1)) + d \]

Մի խոսքով, առաջընթացի մեջ $ n $ th տերմինը գտնելու համար հարկավոր է իմանալ $ n-1 $ th տերմինը և $ d $ տարբերությունը: Նման բանաձևը կոչվում է պարբերական, քանի որ նրա օգնությամբ կարող եք գտնել ցանկացած թիվ ՝ իմանալով միայն նախորդը (և իրականում `բոլոր նախորդները): Սա շատ անհարմար է, ուստի կա ավելի բարդ բանաձև, որը նվազեցնում է ցանկացած հաշվարկ առաջին փուլի և տարբերության միջև.

\ [((a) _ (n)) = ((a) _ (1)) + \ ձախ (n-1 \ աջ) d \]

Իհարկե, դուք արդեն հանդիպել եք այս բանաձևին: Նրանք սիրում են այն տալ բոլոր տեսակի տեղեկատու գրքերում և ռեշեբնիկներում: Եվ մաթեմատիկայի վերաբերյալ ցանկացած խելամիտ դասագրքում նա առաջիններից մեկն է:

Այնուամենայնիվ, ես առաջարկում եմ մի փոքր զբաղվել:

Խնդիր թիվ 1: Գրի՛ր $ \ ձախ (((a) _ (n)) \ աջ) $ թվաբանական առաջընթացի առաջին երեք պայմանները, եթե $ ((a) _ (1)) = 8, d = -5 $:

Լուծում: Այսպիսով, մենք գիտենք առաջին տերմինը $ ((a) _ (1)) = 8 $ և առաջընթացի տարբերությունը $ d = -5 $: Եկեք օգտագործենք հենց տրված բանաձևը և փոխարինենք $ n = 1 $, $ n = 2 $ և $ n = 3 $:

\ [\ սկսել (հավասարեցնել) & ((a) _ (n)) = ((a) _ (1)) + \ ձախ (n-1 \ աջ) d; \\ & ((a) _ (1)) = ((a) _ (1)) + \ ձախ (1-1 \ աջ) d = ((a) _ (1)) = 8; \\ & ((a) _ (2)) = ((a) _ (1)) + \ ձախ (2-1 \ աջ) d = ((a) _ (1)) + d = 8-5 = 3; \\ & ((a) _ (3)) = ((a) _ (1)) + \ ձախ (3-1 \ աջ) d = ((a) _ (1)) + 2d = 8-10 = -2. \\ \ վերջ (հավասարեցնել) \]

Պատասխան ՝ (8; 3; −2)

Վերջ! Խնդրում ենք նկատի ունենալ. Մեր առաջընթացը նվազում է:

Իհարկե, $ n = 1 $ չէր կարող փոխարինվել. Առաջին տերմինը մեզ արդեն հայտնի է: Այնուամենայնիվ, մեկը փոխարինելով ՝ մենք համոզվեցինք, որ մեր բանաձևը գործում է նույնիսկ առաջին ժամկետի համար: Այլ դեպքերում, ամեն ինչ հասավ մանրուքի թվաբանության:

Խնդիր թիվ 2: Գրեք թվաբանական առաջընթացի առաջին երեք տերմինները, եթե դրա յոթերորդ տերմինը −40 է, իսկ տասնյոթերորդ տերմինը `−50:

Լուծում: Եկեք գրենք խնդրի վիճակը սովորական տերմիններով.

\ [((a) _ (7)) = - 40; \ quad ((a) _ (17)) = - 50. \]

\ [\ ձախ \ (\ սկսել (հավասարեցնել) & ((ա) _ (7)) = ((ա) _ (1)) + 6 դ \\ & ((ա) _ (17)) = ((ա) _ (1)) + 16d \\ \ վերջ (հավասարեցնել) \ աջ: \]

\ [\ ձախ \ (\ սկսել (հավասարեցնել) & ((ա) _ (1)) + 6d = -40 \\ & ((ա) _ (1)) + 16d = -50 \\ \ վերջ (հավասարեցնել) \ ճիշտ. \]

Ես դրեցի համակարգի նշանը, քանի որ այդ պահանջները պետք է կատարվեն միաժամանակ: Եվ հիմա նշեք, որ եթե առաջինը հանենք երկրորդ հավասարումից (մենք դրա իրավունքն ունենք, քանի որ ունենք համակարգ), մենք ստանում ենք սա.

\ [\ սկսել (հավասարեցնել) & ((a) _ (1)) + 16d- \ ձախ (((a) _ (1)) + 6d \ right) =- 50- \ ձախ (-40 \ աջ); \\ & ((ա) _ (1)) + 16d - ((a) _ (1)) - 6d = -50 + 40; \\ & 10 դ = -10; \\ & դ = -1: \\ \ վերջ (հավասարեցնել) \]

Ահա թե ինչքան հեշտ գտանք առաջընթացի տարբերությունը: Մնում է գտնված թիվը փոխարինել համակարգի ցանկացած հավասարման մեջ: Օրինակ ՝ առաջինում.

\ [\ սկիզբ (մատրիցա) ((ա) _ (1)) + 6d = -40; \ quad d = -1 \\ \ Downarrow \\ ((a) _ (1)) -6 = -40; \\ ((ա) _ (1)) = - 40 + 6 = -34: \\ \ վերջ (մատրիցա) \]

Այժմ, իմանալով առաջին տերմինը և տարբերությունը, մնում է գտնել երկրորդ և երրորդ տերմինները.

\ [\ սկսել (հավասարեցնել) & ((a) _ (2)) = ((a) _ (1)) + d = -34-1 = -35; \\ & ((ա) _ (3)) = ((ա) _ (1)) + 2d = -34-2 = -36: \\ \ վերջ (հավասարեցնել) \]

Պատրաստ է Խնդիրը լուծված է:

Պատասխան ՝ (-34; -35; -36)

Ուշադրություն դարձրեք մեր հայտնաբերած առաջընթացի մի հետաքրքիր հատկության.

\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ ձախ (n -m \ right) \]

Պարզ, բայց շատ օգտակար հատկություն, որը դուք անպայման պետք է իմանաք. Նրա օգնությամբ դուք կարող եք զգալիորեն արագացնել առաջընթացի ընթացքում բազմաթիվ խնդիրների լուծումը: Ահա գլխավոր օրինակը.

Խնդիր թիվ 3: Թվաբանական առաջընթացի հինգերորդ տերմինը 8.4 է, իսկ տասներորդը ՝ 14.4: Գտեք այս առաջընթացի տասնհինգերորդ տերմինը:

Լուծում: Քանի որ $ ((a) _ (5)) = 8.4 $, $ ((a) _ (10)) = 14.4 $, և դուք պետք է գտնեք $ ((a) _ (15)) $, ապա մենք նշում ենք հետևյալը :

\ [\ սկսել (հավասարեցնել) & ((ա) _ (15)) - ((ա) _ (10)) = 5 դ; \\ & ((ա) _ (10)) - ((ա) _ (5)) = 5 դ. \\ \ վերջ (հավասարեցնել) \]

Բայց $ ((a) _ (10)) - ((a) _ (5)) = 14.4-8.4 = 6 $, հետևաբար $ 5d = 6 $, որտեղից մենք ունենք.

\ [\ սկսել (հավասարեցնել) & ((ա) _ (15)) - 14.4 = 6; \\ & ((ա) _ (15)) = 6 + 14.4 = 20.4: \\ \ վերջ (հավասարեցնել) \]

Պատասխան ՝ 20.4

Վերջ! Մեզ պետք չէր հավասարումների որոշ համակարգեր կազմել և հաշվարկել առաջին տերմինը և տարբերությունը. Ամեն ինչ լուծվեց ընդամենը մի քանի տողով:

Այժմ դիտարկենք առաջադրանքների մեկ այլ տեսակ ՝ գտնել առաջընթացի բացասական և դրական անդամներ: Գաղտնիք չէ, որ եթե առաջընթացը մեծանա, մինչդեռ առաջին տերմինը բացասական է, ապա վաղ թե ուշ դրանում կհայտնվեն դրական տերմիններ: Եվ ընդհակառակը. Նվազող առաջընթացի անդամները վաղ թե ուշ բացասական կդառնան:

Միևնույն ժամանակ, միշտ չէ, որ հնարավոր է «ակնթարթորեն» շրջել այս պահը `հաջորդաբար անցնելով տարրերի միջով: Հաճախ խնդիրները ձևավորվում են այնպես, որ առանց բանաձևերն իմանալու հաշվարկները տևեն մի քանի թերթ. Մենք պարզապես քնում էինք, մինչև պատասխանը գտնեինք: Հետեւաբար, մենք կփորձենք ավելի արագ լուծել այդ խնդիրները:

Խնդիր թիվ 4: Քանի՞ բացասական տերմին կա թվաբանական առաջընթացի մեջ -38.5; −35.8; ...?

Լուծում: Այսպիսով, $ ((a) _ (1)) = - 38.5 $, $ ((a) _ (2)) = - 35.8 $, որից մենք անմիջապես գտնում ենք տարբերությունը.

Նշենք, որ տարբերությունը դրական է, ուստի առաջընթացը մեծանում է: Առաջին տերմինը բացասական է, ուստի ինչ -որ պահի մենք իսկապես սայթաքելու ենք դրական թվերի վրա: Հարցը միայն այն է, թե երբ դա տեղի կունենա:

Փորձենք պարզել. Որքա՞ն ժամանակ (այսինքն ՝ մինչև ո՞ր բնական թվին $ n $) պայմանների բացասականությունը պահպանվում է.

\ [\ սկսել (հավասարեցնել) & ((a) _ (n)) \ lt 0 \ Rightarrow ((a) _ (1)) + \ left (n-1 \ right) d \ lt 0; \\ & -38.5+ \ ձախ (n -1 \ աջ) \ cdot 2.7 \ lt 0; \ քառակի \ ձախ | \ cdot 10 \ աջ: \\ & -385 + 27 \ cdot \ ձախ (n -1 \ աջ) \ lt 0; \\ & -385 + 27n -27 \ lt 0; \\ & 27n \ lt 412; \\ & n \ lt 15 \ frac (7) (27) \ Rightarrow ((n) _ (\ max)) = 15: \\ \ վերջ (հավասարեցնել) \]

Վերջին տողը պարզաբանում է պահանջում: Այսպիսով, մենք գիտենք, որ $ n \ lt 15 \ frac (7) (27) $: Մյուս կողմից, մենք կբավարարվենք թվի միայն ամբողջական արժեքներով (ավելին ՝ $ n \ in \ mathbb (N) $), ուստի ամենամեծ թույլատրելի թիվը ճշգրիտ $ n = 15 $ է, և ոչ մի դեպքում 16 է:

Խնդիր թիվ 5: Թվաբանական առաջընթացում $ (() _ (5)) = - 150, (() _ (6)) = - 147 $: Գտեք այս առաջընթացի առաջին դրական տերմինի թիվը:

Դա կլիներ ճիշտ նույն խնդիրը, ինչ նախորդը, բայց մենք չգիտենք $ ((a) _ (1)) $: Բայց հարևան տերմինները հայտնի են ՝ $ ((a) _ (5)) $ և $ ((a) _ (6)) $, այնպես որ մենք կարող ենք հեշտությամբ գտնել առաջընթացի տարբերությունը.

Բացի այդ, մենք կփորձենք հինգերորդ տերմինը արտահայտել առաջինի և տարբերությունը `ըստ ստանդարտ բանաձևի.

\ [\ սկսել (հավասարեցնել) & ((a) _ (n)) = ((a) _ (1)) + \ ձախ (n-1 \ աջ) \ cdot d; \\ & ((ա) _ (5)) = ((ա) _ (1)) + 4d; \\ & -150 = ((ա) _ (1)) + 4 \ cdot 3; \\ & ((ա) _ (1)) = -150-12 = -162: \\ \ վերջ (հավասարեցնել) \]

Այժմ մենք շարունակում ենք նախորդ առաջադրանքի նմանությամբ: Մենք պարզում ենք, թե մեր հաջորդականության որ կետում կլինեն դրական թվեր.

\ [\ սկսել (հավասարեցնել) & ((a) _ (n)) = - 162+ \ ձախ (n -1 \ աջ) \ cdot 3 \ gt 0; \\ & -162 + 3n -3 \ gt 0; \\ & 3n \ gt 165; \\ & n \ gt 55 \ Rightarrow ((n) _ (\ min)) = 56: \\ \ վերջ (հավասարեցնել) \]

Այս անհավասարության ամենափոքր ամբողջական լուծումը 56 -ն է:

Խնդրում ենք նկատի ունենալ.

Այժմ, երբ մենք սովորեցինք, թե ինչպես լուծել պարզ խնդիրները, անցնենք ավելի բարդ խնդիրներին: Բայց նախ, եկեք ուսումնասիրենք թվաբանական առաջընթացների մեկ այլ շատ օգտակար հատկություն, որը հետագայում մեզ կխնայի շատ ժամանակ և անհավասար բջիջներ: :)

Միջին թվաբանական և հավասար նահանջներ

Հաշվի առնենք $ \ ձախ (((a) _ (n)) \ աջ) $ աճող թվաբանական առաջընթացի մի քանի հաջորդական անդամներ: Փորձենք դրանք նշել թվային տողի վրա.

Թվային տողում թվաբանական առաջընթացի անդամներ

Ես հատուկ նշեցի կամայական անդամներ $ ((a) _ (n-3)), ..., ((a) _ (n + 3)) $, ոչ թե որևէ $ ((a) _ (1)), \ ( (ա) _ (2)), \ ((ա) _ (3)) $ և այլն: Քանի որ կանոնը, որի մասին ես հիմա կխոսեմ, նույնն է գործում ցանկացած «հատվածի» դեպքում:

Եվ կանոնը շատ պարզ է: Եկեք հիշենք կրկնության բանաձևը և գրի առնենք այն նշված բոլոր անդամների համար.

\ [\ սկսել (հավասարեցնել) & ((a) _ (n-2)) = ((a) _ (n-3)) + d; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + d; \\ & ((a) _ (n)) = ((a) _ (n-1)) + d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n + 1)) + d; \\ \ վերջ (հավասարեցնել) \]

Այնուամենայնիվ, այս հավասարությունները կարող են այլ կերպ վերաշարադրվել.

\ [\ սկսել (հավասարեցնել) & ((a) _ (n -1)) = ((a) _ (n)) - d; \\ & ((a) _ (n -2)) = ((a) _ (n)) - 2d; \\ & ((a) _ (n -3)) = ((a) _ (n)) - 3d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((ա) _ (n + 3)) = ((ա) _ (n)) + 3d; \\ \ վերջ (հավասարեցնել) \]

Դե, ուրեմն ինչ? Եվ այն, որ $ ((a) _ (n-1)) $ և $ ((a) _ (n + 1)) $ տերմինները գտնվում են $ ((a) _ (n)) $-ից միևնույն հեռավորության վրա: . Եվ այս հեռավորությունը հավասար է $ d $: Նույնը կարելի է ասել $ ((a) _ (n -2)) $ և $ ((a) _ (n + 2)) $ - նրանք նույնպես հեռացված են $ ((a) _ (n) - ից ) $ նույն հեռավորությունը հավասար է $ 2d $: Կարելի է անվերջ շարունակել, բայց իմաստը լավ պատկերված է նկարում:

Պրոգրեսիայի անդամները գտնվում են կենտրոնից նույն հեռավորության վրա

Ի՞նչ է սա նշանակում մեզ համար: Սա նշանակում է, որ դուք կարող եք գտնել $ ((a) _ (n)) $, եթե հարևան թվերը հայտնի են.

\ [((ա) _ (n)) = \ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \]

Մենք հանդես եկանք մի հիանալի հայտարարությամբ. Թվաբանական առաջընթացի յուրաքանչյուր անդամ հավասար է հարևան տերմինների թվաբանական միջինին: Ավելին. Մենք կարող ենք մեր $ ((a) _ (n)) $ - ից ձախ և աջ շեղվել ոչ թե մեկ, այլ $ k $ քայլերով, և այդուհանդերձ բանաձևը ճիշտ կլինի.

\ [((ա) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \]

Նրանք մենք կարող ենք հեշտությամբ գտնել որոշ $ ((a) _ (150)) $, եթե իմանանք $ ((a) _ (100)) $ և $ ((a) _ (200)) $, քանի որ $ ((a) _ (150)) = \ frac (((a) _ (100)) + ((a) _ (200))) (2) $: Առաջին հայացքից կարող է թվալ, որ այս փաստը մեզ ոչ մի օգտակար բան չի տալիս: Այնուամենայնիվ, գործնականում թվաբանական միջինի օգտագործման համար շատ խնդիրներ հատուկ «սրվում են»: Նայել:

Խնդիր թիվ 6: Գտեք $ x $ բոլոր արժեքները, որոնց համար $ -6 ((x) ^ (2)) $, $ x + 1 $ և $ 14 + 4 ((x) ^ (2)) $ թվերը հաջորդական անդամներ են թվաբանական առաջընթացի (ըստ հերթականության):

Լուծում: Քանի որ նշված թվերը առաջընթացի անդամներ են, նրանց համար բավարարվում է թվաբանական միջինի պայմանը. $ X + 1 $ կենտրոնական տարրը կարող է արտահայտվել հարակից տարրերով.

\ [\ սկսել (հավասարեցնել) & x + 1 = \ frac (-6 ((x) ^ (2)) + 14 + 4 ((x) ^ (2))) (2); \\ & x + 1 = \ frac (14-2 ((x) ^ (2))) (2); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (2)) + x-6 = 0: \\ \ վերջ (հավասարեցնել) \]

Արդյունքը դասական քառակուսային հավասարում է: Դրա արմատները ՝ $ x = 2 $ և $ x = -3 $ - ահա պատասխանները:

Պատասխան ՝ −3; 2

Խնդիր թիվ 7: Գտեք $$ արժեքները, որոնց համար $ -1; 4-3; (() ^ (2)) + 1 $ թվերը առաջացնում են թվաբանական առաջընթաց (այդ հերթականությամբ):

Լուծում: Կրկին, մենք արտահայտում ենք միջին տերմինը հարևան տերմինների միջին թվաբանական առումով.

\ [\ սկսել (հավասարեցնել) & 4x-3 = \ frac (x-1 + ((x) ^ (2)) + 1) (2); \\ & 4x-3 = \ frac (((x) ^ (2)) + x) (2); \ quad \ left | \ cdot 2 \ աջ.; \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (2)) - 7x + 6 = 0: \\ \ վերջ (հավասարեցնել) \]

Կրկին քառակուսային հավասարումը: Եվ կրկին երկու արմատ կա ՝ $ x = 6 $ և $ x = 1 $:

Պատասխան ՝ 1; 6

Եթե ​​խնդրի լուծման ընթացքում դուրս եք գալիս դաժան թվերից, կամ լիովին վստահ չեք գտնված պատասխանների ճշգրտությանը, ապա կա մի հրաշալի տեխնիկա, որը թույլ է տալիս ստուգել. Արդյո՞ք մենք խնդիրը ճիշտ լուծեցինք:

Օրինակ, թիվ 6 խնդրում մենք ստացել ենք -3 և 2. պատասխանները: Ինչպե՞ս ստուգել, ​​որ այս պատասխանները ճիշտ են: Եկեք դրանք պարզապես միացնենք և տեսնենք, թե ինչ կլինի: Հիշեցնեմ, որ մենք ունենք երեք թիվ ($ -6 (() ^ (2)) $, $ + 1 $ և $ 14 + 4 (() ^ (2)) $), որոնք պետք է կազմեն թվաբանական առաջընթաց: Փոխարինել $ x = -3 $:

\ [\ սկիզբ (հավասարեցնել) & x = -3 \ Աջ սլաք \\ & -6 ((x) ^ (2)) = -54; \\ & x + 1 = -2; \\ & 14 + 4 ((x) ^ (2)) = 50: \ ավարտ (հավասարեցնել) \]

Ստացված թվերը -54; 2; 50 -ը, որոնք տարբերվում են 52 -ով, անկասկած թվաբանական առաջընթաց է: Նույնը տեղի է ունենում $ x = 2 $ դեպքում.

\ [\ սկսել (հավասարեցնել) & x = 2 \ աջ սլաք \\ & -6 ((x) ^ (2)) = - 24; \\ & x + 1 = 3; \\ & 14 + 4 ((x) ^ (2)) = 30: \ ավարտ (հավասարեցնել) \]

Կրկին առաջընթաց, բայց 27 տարբերությամբ: Այսպիսով, խնդիրը ճիշտ է լուծվում: Interestedանկացողները կարող են ինքնուրույն ստուգել երկրորդ խնդիրը, բայց ես անմիջապես կասեմ. Այնտեղ նույնպես ամեն ինչ ճիշտ է:

Ընդհանրապես, վերջին խնդիրները լուծելիս մենք հանդիպեցինք մեկ այլ հետաքրքիր փաստի, որը նույնպես պետք է հիշել.

Եթե ​​երեք թվերն այնպիսին են, որ երկրորդը առաջինի և վերջինի թվաբանական միջինն է, ապա այդ թվերը կազմում են թվաբանական առաջընթաց:

Ապագայում այս հայտարարության ըմբռնումը թույլ կտա բառացիորեն «կառուցել» անհրաժեշտ առաջընթացները ՝ հիմնվելով խնդրի վիճակի վրա: Բայց նախքան նման «շինարարության» անցնելը, պետք է ուշադրություն դարձնել ևս մեկ փաստի, որն ուղղակիորեն բխում է արդեն դիտարկվածից:

Խմբավորումը և տարրերի գումարը

Կրկին վերադառնանք թվային առանցքին: Եկեք այնտեղ նշենք առաջընթացի մի քանի անդամ, որոնց միջև, հավանաբար: կան շատ այլ անդամներ.

Թվային տողում նշված է 6 տարր

Փորձենք արտահայտել «ձախ պոչը» $ ((a) _ (n)) $ և $ d $, իսկ "աջ պոչը" $ ((a) _ (k)) $ և $ d $ արտահայտություններով: . Շատ պարզ է.

\ [\ սկսել (հավասարեցնել) & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (k -1)) = ((a) _ (k)) - d; \\ & ((a) _ (k -2)) = ((a) _ (k)) - 2 օր: \\ \ վերջ (հավասարեցնել) \]

Այժմ նշեք, որ հետևյալ գումարները հավասար են.

\ [\ սկսել (հավասարեցնել) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & ((ա) _ (n + 1)) + ((a) _ (k -1)) = ((a) _ (n)) + d + ((a) _ (k)) - d = S; \\ & ((ա) _ (n + 2)) + ((a) _ (k -2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = Ս. \ ավարտ (հավասարեցնել) \]

Պարզ ասած, եթե որպես սկիզբ դիտարկենք առաջընթացի երկու տարր, որոնք ընդհանուր առմամբ հավասար են $ S $ որոշակի թվին, ապա մենք սկսում ենք այս տարրերից քայլել հակառակ ուղղություններով (միմյանց նկատմամբ կամ հակառակը ՝ հեռանալու համար) , ապա այն տարրերի գումարները, որոնց վրա մենք սայթաքելու ենք, նույնպես հավասար կլինեն$ S $. Սա առավել հստակ կարելի է պատկերել գրաֆիկորեն.

Հավասար նահանջը տալիս է հավասար գումարներ

Այս փաստի ըմբռնումը թույլ կտա լուծել սկզբունքորեն ավելի բարձր մակարդակի բարդության խնդիրներ, քան նրանք, որոնք մենք վերը դիտարկեցինք: Օրինակ ՝ այդպիսի.

Խնդիր թիվ 8: Որոշեք թվաբանական առաջընթացի տարբերությունը, որի դեպքում առաջին տերմինը 66 է, իսկ երկրորդ և տասներկուերորդ տերմինների արտադրյալը հնարավոր ամենափոքրն է:

Լուծում: Եկեք գրի առնենք այն ամենը, ինչ գիտենք.

\ [\ սկսել (հավասարեցնել) & ((ա) _ (1)) = 66; \\ & դ =? \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ րոպե \ ավարտ (հավասարեցնել) \]

Այսպիսով, մենք չգիտենք $ d $ առաջընթացի տարբերությունը: Իրականում, ամբողջ լուծումը կկառուցվի տարբերության շուրջ, քանի որ $ ((a) _ (2)) \ cdot ((a) _ (12)) $ արտադրանքը կարող է վերաշարադրվել հետևյալ կերպ.

\ [\ սկսել (հավասարեցնել) & ((a) _ (2)) = ((a) _ (1)) + d = 66 + d; \\ & ((ա) _ (12)) = ((ա) _ (1)) + 11d = 66 + 11d; \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ ձախ (66 + d \ right) \ cdot \ left (66 + 11d \ right) = \\ & = 11 \ cdot \ ձախ (d + 66 \ աջ) \ cdot \ ձախ (d + 6 \ աջ): \ ավարտ (հավասարեցնել) \]

Տանկում գտնվողների համար. Երկրորդ փակագծից հանեցի 11 -ի ընդհանուր գործակիցը: Այսպիսով, որոնվող արտադրանքը քառակուսի գործառույթ է ՝ $ d $ փոփոխականի նկատմամբ: Հետևաբար, հաշվի առեք $ f \ left (d \ right) = 11 \ left (d + 66 \ right) \ left (d + 6 \ right) $ ֆունկցիան. Դրա գրաֆիկը պարաբոլա կլինի վերևի ճյուղերով, քանի որ եթե ընդլայնենք փակագծերը, ապա կստանանք.

\ [\ սկսել (հավասարեցնել) & f \ ձախ (d \ աջ) = 11 \ ձախ (((d) ^ (2)) + 66d + 6d + 66 \ cdot 6 \ աջ) = \\ & = 11 (( դ) ^ (2)) + 11 \ cdot 72d + 11 \ cdot 66 \ cdot 6 \ վերջ (հավասարեցնել) \]

Ինչպես տեսնում եք, առաջատար տերմինի գործակիցը 11 է. Սա դրական թիվ է, ուստի մենք իսկապես գործ ունենք պարաբոլայի հետ ՝ ճյուղեր վերև.

քառակուսի ֆունկցիայի գրաֆիկ - պարաբոլա

Խնդրում ենք նկատի ունենալ. Այս պարաբոլան իր գագաթնակետին վերցնում է իր նվազագույն արժեքը $ ((d) _ (0)) $ abscissa- ով: Իհարկե, մենք կարող ենք հաշվարկել այս աբսցիսը ըստ ստանդարտ սխեմայի (կա նաև $ ((d) _ (0)) = (- b) / (2a) \; $ բանաձևը, բայց դա շատ ավելի խելամիտ կլիներ նկատել, որ ցանկալի գագաթը գտնվում է պարաբոլայի առանցքի համաչափության վրա, ուստի $ ((d) _ (0)) $ կետը հավասար հեռավորության վրա է $ f \ ձախ (d \ right) = 0 $ հավասարման արմատներից:

\ [\ սկսել (հավասարեցնել) & f \ ձախ (դ \ աջ) = 0; \\ & 11 \ cdot \ ձախ (d + 66 \ աջ) \ cdot \ ձախ (d + 6 \ աջ) = 0; \\ & ((d) _ (1)) = - 66; \ quad ((d) _ (2)) = - 6: \\ \ վերջ (հավասարեցնել) \]

Ահա թե ինչու ես չէի շտապում բացել փակագծերը. Սկզբնական տեսքով արմատները շատ -շատ հեշտ էր գտնել: Հետևաբար, աբսցիսը հավասար է −66 և −6 թվերի միջին թվաբանականին.

\ [((d) _ (0)) = \ frac (-66-6) (2) =-36 \]

Ի՞նչ է մեզ տալիս հայտնաբերված թիվը: Դրանով պահանջվող արտադրանքը ստանում է ամենափոքր արժեքը (ի դեպ, մենք չենք հաշվել $ ((y) _ (\ min)) $ - սա մեզանից չի պահանջվում): Միևնույն ժամանակ, այս թիվը տարբերությունն է սկզբնական առաջընթացի միջև, այսինքն. գտանք պատասխանը :)

Պատասխան ՝ 36

Խնդիր թիվ 9: $ - \ frac (1) (2) $ և $ - \ frac (1) (6) $ թվերի միջև տեղադրեք երեք թիվ, որպեսզի նրանք տրված թվերի հետ միասին կազմեն թվաբանական առաջընթաց:

Լուծում: Հիմնականում մենք պետք է կազմենք հինգ թվերի հաջորդականություն ՝ առաջին և վերջին թվերն արդեն հայտնի են: Եկեք բաց թողնված թվերը նշենք $ x $, $ y $ և $ z $ փոփոխականներով.

\ [\ ձախ (((a) _ (n)) \ աջ) = \ ձախ \ ( - \ frac (1) (2); x; y; z; - \ frac (1) (6) \ աջ \ ) \]

Նկատի ունեցեք, որ $ y $ թիվը մեր հաջորդականության «միջինն» է. Այն հավասար հեռավորության վրա է և $ x $ և $ z $ թվերից, և $ - \ frac (1) (2) $ և $ - \ թվերից: frac (1) (6) $. Եվ եթե այս պահին մենք չենք կարող $ y $ ստանալ $ x $ և $ z $ թվերից, ապա իրավիճակը տարբեր է առաջընթացի ավարտների դեպքում: Հիշելով թվաբանական միջինը.

Այժմ, իմանալով $ y $, մենք կգտնենք մնացած թվերը: Նկատի ունեցեք, որ $ x $ գտնվում է $ - \ frac (1) (2) $ և նոր գտած $ y = - \ frac (1) (3) $ թվերի միջև: Ահա թե ինչու

Նմանապես պատճառաբանելով ՝ մենք գտնում ենք մնացած թիվը.

Պատրաստ է Մենք գտանք բոլոր երեք թվերը: Եկեք դրանք պատասխանի մեջ գրի առնենք այն հերթականությամբ, որով դրանք պետք է տեղադրվեն սկզբնական թվերի միջև:

Պատասխան ՝ $ - \ frac (5) (12); \ - \ frac (1) (3); \ - \ frac (1) (4) $

Խնդիր թիվ 10: 2 -րդ և 42 -րդ թվերի միջև տեղադրեք մի քանի թվեր, որոնք այս թվերի հետ միասին կազմում են թվաբանական առաջընթաց, եթե գիտեք, որ տեղադրված թվերի առաջին, երկրորդ և վերջինների գումարը 56 է:

Լուծում: Նույնիսկ ավելի բարդ խնդիր, որը, սակայն, լուծվում է նույն սխեմայով, ինչ նախորդները `թվաբանական միջինի միջոցով: Խնդիրն այն է, որ մենք հստակ չգիտենք, թե քանի թիվ պետք է տեղադրել: Հետևաբար, որոշակիության համար ենթադրենք, որ ամեն ինչ մտցնելուց հետո կլինեն ճշգրիտ $ n $ թվեր, որոնցից առաջինը 2 -ն է, իսկ վերջինը `42 -ը: Այս դեպքում ցանկալի թվաբանական առաջընթացը կարող է ներկայացվել հետևյալ կերպ.

\ [\ ձախ (((a) _ (n)) \ աջ) = \ ձախ \ (2; ((a) _ (2)); ((a) _ (3)); ...; (( ա) _ (n-1)); 42 \ աջ \) \]

\ [((ա) _ (2)) + ((ա) _ (3)) + ((ա) _ (n-1)) = 56 \]

Այնուամենայնիվ, նկատի ունեցեք, որ $ ((a) _ (2)) $ և $ ((a) _ (n-1)) $ թվերը ստացվում են եզրերի 2 և 42 թվերից ՝ մեկ քայլով միմյանց նկատմամբ, այսինքն ... հաջորդականության կենտրոն: Սա նշանակում է, որ

\ [((ա) _ (2)) + ((ա) _ (n-1)) = 2 + 42 = 44 \]

Բայց հետո վերը գրված արտահայտությունը կարող է վերաշարադրվել հետևյալ կերպ.

\ [\ սկսել (հավասարեցնել) & ((ա) _ (2)) + ((ա) _ (3)) + ((ա) _ (n-1)) = 56; \\ & \ ձախ (((a) _ (2)) + ((a) _ (n-1)) \ աջ) + ((a) _ (3)) = 56; \\ & 44 + ((ա) _ (3)) = 56; \\ & ((ա) _ (3)) = 56-44 = 12: \\ \ վերջ (հավասարեցնել) \]

Իմանալով $ ((a) _ (3)) $ և $ ((a) _ (1)) $ ՝ մենք կարող ենք հեշտությամբ գտնել առաջընթացի տարբերությունը.

\ [\ սկսել (հավասարեցնել) & ((ա) _ (3)) - ((ա) _ (1)) = 12 - 2 = 10; \\ & ((a) _ (3)) - ((a) _ (1)) = \ ձախ (3-1 \ աջ) \ cdot d = 2d; \\ & 2d = 10 \ Rightarrow d = 5: \\ \ վերջ (հավասարեցնել) \]

Մնում է գտնել մնացած անդամներին.

\ [\ սկսել (հավասարեցնել) & ((ա) _ (1)) = 2; \\ & ((ա) _ (2)) = 2 + 5 = 7; \\ & ((ա) _ (3)) = 12; \\ & ((ա) _ (4)) = 2 + 3 \ cdot 5 = 17; \\ & ((ա) _ (5)) = 2 + 4 \ cdot 5 = 22; \\ & ((ա) _ (6)) = 2 + 5 \ cdot 5 = 27; \\ & ((ա) _ (7)) = 2 + 6 \ cdot 5 = 32; \\ & ((ա) _ (8)) = 2 + 7 \ cdot 5 = 37; \\ & ((ա) _ (9)) = 2 + 8 \ cdot 5 = 42; \\ \ վերջ (հավասարեցնել) \]

Այսպիսով, արդեն 9 -րդ քայլին մենք կհասնենք հաջորդականության ձախ ծայրին `42 թվին: Ընդհանուր առմամբ, անհրաժեշտ էր տեղադրել միայն 7 թիվ: 7; 12; 17; 22; 27; 32; 37.

Պատասխան ՝ 7; 12; 17; 22; 27; 32; 37

Բառային խնդիրներ առաջադիմության հետ

Եզրափակելով, ես կցանկանայի դիտարկել մի քանի համեմատաբար պարզ առաջադրանքներ: Դե, որքան պարզ է. Դպրոցում մաթեմատիկա սովորող և վերը գրվածը չկարդացած աշակերտների մեծ մասի համար այս առաջադրանքները կարող են թիթեղ թվալ: Այնուամենայնիվ, հենց այդպիսի խնդիրներ են հանդիպում մաթեմատիկայի OGE- ում և ՕԳՏԱԳՈՐՈՄԸ, ուստի խորհուրդ եմ տալիս ծանոթանալ դրանց:

Խնդիր թիվ 11: Բրիգադը հունվարին արտադրեց 62 մաս, և յուրաքանչյուր հաջորդ ամսվա ընթացքում այն ​​արտադրեց 14 մաս ավելի, քան նախորդը: Քանի՞ մաս կազմեց թիմը նոյեմբերին:

Լուծում: Ակնհայտ է, որ ըստ ամիսների նախատեսված մասերի քանակը թվաբանական աճող առաջընթաց է ներկայացնելու: Ավելին.

\ [\ սկսել (հավասարեցնել) & ((a) _ (1)) = 62; \ quad d = 14; \\ & ((ա) _ (n)) = 62+ \ ձախ (n-1 \ աջ) \ cdot 14. \\ \ վերջ (հավասարեցնել) \]

Նոյեմբերն է տարվա 11 -րդ ամիսը, ուստի մենք պետք է գտնենք $ ((a) _ (11)) $:

\ [((ա) _ (11)) = 62 + 10 \ cdot 14 = 202 \]

Հետեւաբար, նոյեմբերին կարտադրվի 202 մաս:

Խնդիր թիվ 12: Գրքարտադրման արհեստանոցը հունվարին կապեց 216 գիրք, իսկ յուրաքանչյուր հաջորդ ամիս `4 -ով ավելի, քան նախորդը: Քանի՞ գիրք էր կապված սեմինարին դեկտեմբերին:

Լուծում: Ամեն ինչ նույնն է:

$ \ սկսել (հավասարեցնել) & ((a) _ (1)) = 216; \ quad d = 4; \\ & ((ա) _ (n)) = 216+ \ ձախ (n-1 \ աջ) \ cdot 4. \\ \ վերջ (հավասարեցնել) $

Դեկտեմբերը տարվա վերջին ՝ 12 -րդ ամիսն է, ուստի մենք փնտրում ենք $ ((a) _ (12)) $:

\ [((ա) _ (12)) = 216 + 11 \ cdot 4 = 260 \]

Սա է պատասխանը. Դեկտեմբերին կփակվի 260 գիրք:

Դե, եթե մինչ այժմ կարդացել եք, ես շտապում եմ շնորհավորել ձեզ. Դուք հաջողությամբ անցել եք «երիտասարդ մարտիկների դասընթացը» թվաբանական առաջընթացներում: Դուք կարող եք ապահով կերպով անցնել հաջորդ դասին, որտեղ մենք կուսումնասիրենք առաջընթացի գումարի բանաձևը, ինչպես նաև դրանից կարևոր և շատ օգտակար հետևանքները:

Օրինակ ՝ հաջորդականությունը \ (2 \); \ (5 \); \(ութ\); \ (տասնմեկ \); \ (14 \) ... թվաբանական առաջընթաց է, քանի որ յուրաքանչյուր հաջորդ տարր նախորդից տարբերվում է երեքով (կարելի է ձեռք բերել նախորդից ՝ եռյակ ավելացնելով).

Այս առաջընթացի դեպքում տարբերությունը \ (d \) դրական է (հավասար է \ (3 \)), և, հետևաբար, յուրաքանչյուր հաջորդ տերմին ավելի մեծ է, քան նախորդը: Նման առաջընթացները կոչվում են աճող.

Այնուամենայնիվ, \ (d \) կարող է լինել նաև բացասական: Օրինակ, թվաբանական պրոգրեսիայում \ (16 \); \ (տասը); \ (4 \); \ (- 2 \); \ (- 8 \) ... առաջընթացի տարբերությունը \ (d \) հավասար է մինուս վեցին:

Եվ այս դեպքում յուրաքանչյուր հաջորդ տարր պակաս կլինի նախորդից: Այս առաջընթացները կոչվում են նվազում է.

Թվաբանական առաջընթացի նշում

Առաջընթացը նշվում է լատինատառ փոքր տառով:

Առաջընթացը կազմող թվերը կոչում են այն -ի անդամները(կամ տարրեր):

Դրանք նշվում են նույն տառով, ինչ թվաբանական առաջընթացը, բայց թվային ինդեքսով, որը հավասար է կարգի տարրի թվին:

Օրինակ, թվաբանական առաջընթացը \ (a_n = \ ձախ \ (2; 5; 8; 11; 14 ... \ աջ \) \) բաղկացած է \ (a_1 = 2 \) տարրերից; \ (a_2 = 5 \); \ (a_3 = 8 \) և այլն:

Այլ կերպ ասած, առաջընթացի համար \ (a_n = \ ձախ \ (2; 5; 8; 11; 14 ... \ աջ \) \)

Խնդիրների լուծում թվաբանական առաջընթացի համար

Սկզբունքորեն, վերը նշված տեղեկատվությունն արդեն բավական է թվաբանական առաջընթացի գրեթե ցանկացած խնդիր լուծելու համար (ներառյալ OGE- ում առաջարկվողները):

Օրինակ (OGE): Թվաբանական առաջընթացը որոշվում է \ (b_1 = 7; d = 4 \) պայմաններով: Գտեք \ (b_5 \):
Լուծում.

Պատասխան. \ (b_5 = 23 \)

Օրինակ (OGE): Տրված են թվաբանական առաջընթացի առաջին երեք տերմինները. \ (62; 49; 36 ... \) Գտեք այս առաջընթացի առաջին բացասական տերմինի արժեքը ..
Լուծում.

	Մեզ տրվում են հաջորդականության առաջին տարրերը և գիտենք, որ դա թվաբանական առաջընթաց է: Այսինքն ՝ յուրաքանչյուր տարր հարևան տարրից տարբերվում է նույն թվով: Պարզեք, թե որն է ՝ նախորդը հանելով հաջորդ տարրից ՝ \ (d = 49-62 = -13 \):
	Այժմ մենք կարող ենք վերականգնել մեր առաջընթացը մեզ անհրաժեշտ (առաջին բացասական) տարրի վրա:
	Պատրաստ է: Կարող եք պատասխան գրել:

Պատասխան. \(-3\)

Օրինակ (OGE): Տրված են թվաբանական առաջընթացի մի քանի հաջորդական տարրեր. \ (… 5; x; 10; 12,5 ... \) Գտեք \ (x \) տառով նշված տարրի արժեքը:
Լուծում.

	\ (X \) գտնելու համար մենք պետք է իմանանք, թե հաջորդ տարրը որքանով է տարբերվում նախորդից, այլ կերպ ասած ՝ առաջընթացի տարբերությունը: Եկեք այն գտնենք երկու հայտնի հարևան տարրերից ՝ \ (d = 12.5-10 = 2.5 \):
	Եվ այժմ մենք առանց որևէ խնդրի գտնում ենք ցանկալիը ՝ \ (x = 5 + 2.5 = 7.5 \):
	Պատրաստ է: Կարող եք պատասխան գրել:

Պատասխան. \(7,5\).

Օրինակ (OGE): Թվաբանական առաջընթացը որոշվում է հետևյալ պայմաններով. \ (A_1 = -11 \); \ (a_ (n + 1) = a_n + 5 \) Գտեք այս առաջընթացի առաջին վեց տերմինների գումարը:
Լուծում.

Մենք պետք է գտնենք առաջընթացի առաջին վեց պայմանների գումարը: Բայց մենք չգիտենք դրանց իմաստները, մեզ տրվում է միայն առաջին տարրը: Հետևաբար, առաջին հերթին մենք արժեքներն ենք հաշվարկում ՝ օգտագործելով մեզ տրված տվյալները. \ (n = 1 \); \ (a_ (1 + 1) = a_1 + 5 = -11 + 5 = -6 \) \ (n = 2 \); \ (a_ (2 + 1) = a_2 + 5 = -6 + 5 = -1 \) \ (n = 3 \); \ (a_ (3 + 1) = a_3 + 5 = -1 + 5 = 4 \) Եվ հաշվարկելով մեզ անհրաժեշտ վեց տարրերը, մենք գտնում ենք դրանց գումարը:

\ (S_6 = a_1 + a_2 + a_3 + a_4 + a_5 + a_6 = \) \(=(-11)+(-6)+(-1)+4+9+14=9\)

Գումարը, որը դուք փնտրում եք, գտնվել է:

Պատասխան. \ (S_6 = 9 \):

Օրինակ (OGE): Թվաբանական առաջընթացում \ (a_ (12) = 23 \); \ (a_ (16) = 51 \): Գտեք այս առաջընթացի տարբերությունը:
Լուծում.

Պատասխան. \ (d = 7 \):

Կարևոր թվաբանական առաջընթացի բանաձևեր

Ինչպես տեսնում եք, թվաբանական առաջընթացի բազմաթիվ խնդիրներ կարող են լուծվել պարզապես հասկանալով հիմնականը. Թվաբանական առաջընթացը թվերի շղթա է, և այս շղթայի յուրաքանչյուր հաջորդ տարրը ստացվում է նախորդին նույն թիվը ավելացնելով (տարբերությունը առաջընթացի):

Այնուամենայնիվ, երբեմն լինում են իրավիճակներ, երբ շատ անհարմար է «դեմ առ դեմ» որոշելը: Օրինակ, պատկերացրեք, որ առաջին իսկ օրինակում մենք պետք է գտնենք ոչ թե հինգերորդ տարրը \ (b_5 \), այլ երեք հարյուր ութսունվեցերորդը (b_ (386) \): Ի՞նչ է դա, մենք \ (385 \) անգամ ավելացնում ենք չորս: Կամ պատկերացրեք, որ նախավերջին օրինակում անհրաժեշտ է գտնել առաջին յոթանասուներեք տարրերի գումարը: Ձեզ կտանջեն հաշվել ...

Հետեւաբար, նման դեպքերում նրանք չեն լուծում «դեմ առ դեմ», այլ օգտագործում են թվաբանական առաջընթացի համար ստացված հատուկ բանաձեւեր: Իսկ հիմնականը պրոգրեսիայի n -րդ տերմինի բանաձևն է և առաջին տերմինների գումարի \ (n \) բանաձևը:

Բանաձև \ (n \) - րդ անդամ. \ (A_n = a_1 + (n -1) d \), որտեղ \ (a_1 \) առաջընթացի առաջին տերմինն է.
\ (n \) - որոնվող տարրի համարը.
\ (a_n \) առաջընթացի անդամ է \ (n \) թվով:

Այս բանաձևը թույլ է տալիս մեզ արագ գտնել առնվազն երեք հարյուրերորդ, նույնիսկ միլիոներորդ տարրը ՝ իմանալով միայն առաջինի և առաջընթացի տարբերությունը:

Օրինակ. Թվաբանական առաջընթացը որոշվում է պայմաններով. \ (B_1 = -159 \); \ (d = 8.2 \): Գտեք \ (b_ (246) \):
Լուծում.

Պատասխան. \ (b_ (246) = 1850 \):

Առաջին n տերմինների գումարի բանաձևը ՝ \ (S_n = \ frac (a_1 + a_n) (2) \ cdot n \), որտեղ

\ (a_n \) - վերջին ամփոփված տերմինը;

Օրինակ (OGE): Թվաբանական առաջընթացը որոշվում է \ (a_n = 3,4n-0,6 \) պայմաններով: Գտեք այս առաջընթացի առաջին \ (25 \) անդամների գումարը:
Լուծում.

\ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot 25 \)		Առաջին քսանհինգ տարրերի գումարը հաշվարկելու համար մենք պետք է իմանանք առաջին և քսանհինգ պայմանների արժեքը: Մեր առաջընթացը տրվում է n -րդ տերմինի բանաձևով `կախված նրա թվից (տե՛ս մանրամասները): Եկեք հաշվենք առաջին տարրը ՝ մեկը փոխարինելով \ (n \) -ով:
\ (n = 1; \) \ (a_1 = 3.4 1-0.6 = 2.8 \)		Այժմ մենք գտնում ենք քսանհինգերորդ տերմինը ՝ \ (n \) փոխարեն փոխարինելով քսանհինգով:
\ (n = 25; \) \ (a_ (25) = 3.4 25-0.6 = 84.4 \)		Դե, հիմա մենք կարող ենք հաշվարկել պահանջվող գումարը առանց խնդիրների:
\ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot 25 = \) \ (= \) \ (\ frac (2.8 + 84.4) (2) \) \ (\ cdot 25 = \) \ (1090 \)		Պատասխանը պատրաստ է:

Պատասխան. \ (S_ (25) = 1090 \):

Առաջին պայմանների գումարի \ (n \) համար կարող եք ստանալ մեկ այլ բանաձև. Պարզապես անհրաժեշտ է \ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot 25 \) \ (a_n \) փոխարեն փոխարինեք բանաձևով \ (a_n = a_1 + (n-1) d \): Մենք ստանում ենք.

Առաջին n տերմինների գումարի բանաձևը. \ (S_n = \) \ (\ frac (2a_1 + (n-1) d) (2) \) \ (\ cdot n \), որտեղ

\ (S_n \) - առաջին տարրերի պահանջվող գումարը \ (n \);
\ (a_1 \) - առաջին ամփոփված տերմինը;
\ (d \) - առաջընթացի տարբերություն;
\ (n \) - գումարի տարրերի քանակը:

Օրինակ. Գտեք թվաբանական առաջընթացի առաջին \ (33 \) - նախկին անդամների գումարը. \ (17 \); \ (15.5 \); \ (տասնչորս \)…
Լուծում.

Պատասխան. \ (S_ (33) = - 231 \):

Ավելի բարդ թվաբանական առաջընթացի խնդիրներ

Այժմ դուք ունեք ամբողջ տեղեկատվությունը, որն անհրաժեշտ է գրեթե ցանկացած թվաբանական առաջընթացի խնդիր լուծելու համար: Մենք թեման եզրափակում ենք ՝ հաշվի առնելով խնդիրներ, որոնցում պետք է ոչ միայն բանաձևեր կիրառել, այլև մի փոքր մտածել (մաթեմատիկայում դա կարող է օգտակար լինել)

Օրինակ (OGE): Գտեք առաջընթացի բոլոր բացասական տերմինների գումարը ՝ \ (- 19,3 \); \ (-19 \); \ (- 18.7 \) ...
Լուծում.

\ (S_n = \) \ (\ frac (2a_1 + (n-1) դ) (2) \) \ (\ cdot n \)		Առաջադրանքը շատ նման է նախորդին: Մենք նույնպես սկսում ենք լուծել. Նախ գտնում ենք \ (d \):
\ (d = a_2 -a_1 = -19 - ( - 19.3) = 0.3 \)		Հիմա ես գումարի բանաձևում \ (d \) կփոխարինեի ... և այստեղ մի փոքր նրբերանգ է առաջանում. Մենք չգիտենք \ (n \): Այսինքն, մենք չգիտենք, թե քանի տերմին պետք է ավելացվի: Ինչպե՞ս պարզել: Եկեք մտածենք. Մենք կդադարենք տարրեր ավելացնելուց, երբ հասնենք առաջին դրական տարրին: Այսինքն, դուք պետք է պարզեք այս տարրի թիվը: Ինչպե՞ս: Եկեք գրի առնենք թվաբանական առաջընթացի ցանկացած տարրի հաշվարկման բանաձևը. \ (A_n = a_1 + (n-1) d \) մեր դեպքում:
\ (a_n = a_1 + (n-1) d \)
\ (a_n = -19.3 + (n -1) 0.3 \)		Մեզ անհրաժեշտ է \ (a_n \) զրոյից մեծ լինելու համար: Եկեք պարզենք, թե ինչ \ (n \) դա տեղի կունենա:
\ (- 19.3+ (n-1) 0.3> 0 \)
\ ((n-1) 0.3> 19.3 \) \ (|: 0.3 \)		Անհավասարության երկու կողմերը բաժանում ենք \ (0,3 \) - ով:
\ (n-1> \) \ (\ frac (19,3) (0,3) \)		Տեղափոխեք մինուս մեկը ՝ հիշելով նշաններ փոխելու մասին
\ (n> \) \ (\ frac (19,3) (0,3) \) \ (+ 1 \)		Մենք հաշվարկում ենք ...
\ (n> 65,333 ... \)		... և պարզվում է, որ առաջին դրական տարրը կունենա \ \ (66 \) թիվը: Ըստ այդմ, վերջին բացասականն ունի \ (n = 65 \): Եկեք ստուգենք այն ամեն դեպքում:
\ (n = 65; \) \ (a_ (65) = -19.3+ (65-1) 0.3 = -0.1 \) \ (n = 66; \) \ (a_ (66) = - 19.3+ (66-1) 0.3 = 0.2 \)		Այսպիսով, մենք պետք է ավելացնենք առաջին \ (65 \) տարրերը:
\ (S_ (65) = \) \ (\ frac (2 \ cdot (-19.3) + (65-1) 0.3) (2) \)\ (\ cdot 65 \) \ (S_ (65) = \) \ (( - 38.6 + 19.2) (2) \) \ (\ cdot 65 = -630.5 \)		Պատասխանը պատրաստ է:

Պատասխան. \ (S_ (65) = - 630.5 \):

Օրինակ (OGE): Թվաբանական առաջընթացը որոշվում է պայմաններով. \ (A_1 = -33 \); \ (a_ (n + 1) = a_n + 4 \): Գտեք \ (26 \) th- ից \ (42 \) տարրը ներառյալ գումարը:
Լուծում.

\ (a_1 = -33; \) \ (a_ (n + 1) = a_n + 4 \)	Այս խնդրում անհրաժեշտ է գտնել նաև տարրերի գումարը, բայց ոչ թե առաջինից, այլ \ (26 \) - ից: Նման դեպքի համար մենք բանաձև չունենք: Ինչպե՞ս որոշել: Հեշտ - գումարը \ (26 \) - th- ից \ (42 \) - oh- ից ստանալու համար, նախ պետք է գտնել գումարը \ (1 \) - th- ից \ (42 \) - oh- ից, այնուհետև հանել գումարը սկզբից մինչև \ (25 \) - րդ (տես նկարը):
	Մեր առաջընթացի համար \ (a_1 = -33 \) և տարբերության \ (d = 4 \) (ի վերջո, այն չորսն են, որ մենք ավելացնում ենք նախորդ տարրի վրա ՝ հաջորդը գտնելու համար): Սա իմանալով ՝ մենք գտնում ենք առաջին \ (42 \) - yh տարրերի գումարը:
\ (S_ (42) = \) \ (\ frac (2 \ cdot (-33) + (42-1) 4) (2) \)\ (\ cdot 42 = \) \ (= \) \ (\ frac (-66 + 164) (2) \) \ (\ cdot 42 = 2058 \)	Այժմ առաջին \ (25 \) - ty տարրերի գումարը:
\ (S_ (25) = \) \ (\ frac (2 \ cdot (-33) + (25-1) 4) (2) \)\ (\ cdot 25 = \) \ (= \) \ (\ frac (-66 + 96) (2) \) \ (\ cdot 25 = 375 \)	Ի վերջո, մենք հաշվարկում ենք պատասխանը:
\ (S = S_ (42) -S_ (25) = 2058-375 = 1683 \)

Պատասխան. \ (S = 1683 \):

Թվաբանական առաջընթացի համար կան ևս մի քանի բանաձևեր, որոնք մենք չենք դիտարկել այս հոդվածում `իրենց ցածր գործնական օգտակարության պատճառով: Այնուամենայնիվ, դրանք հեշտությամբ կարող եք գտնել:

Ինչ -որ մեկը զգուշանում է «առաջընթաց» բառից, որպես շատ բարդ տերմին բարձրագույն մաթեմատիկայի ճյուղերից: Մինչդեռ թվաբանական ամենապարզ առաջընթացը տաքսի հաշվիչի աշխատանքն է (որտեղ նրանք դեռ մնում են): Իսկ թվաբանական հաջորդականության էությունը (իսկ մաթեմատիկայում չկա ավելի կարևոր, քան «էությունը հասկանալը») այնքան էլ դժվար չէ ՝ վերլուծելով մի քանի տարրական հասկացություններ:

Մաթեմատիկական թվերի հաջորդականություն

Ընդունված է թվերի շարք անվանել թվային հաջորդականությամբ, որոնցից յուրաքանչյուրն ունի իր համարը:

a 1 - հաջորդականության առաջին անդամը.

իսկ 2 -ը հաջորդականության երկրորդ անդամն է.

իսկ 7 -ը հաջորդականության յոթերորդ անդամն է.

իսկ n- ը հաջորդականության n-րդ անդամն է.

Այնուամենայնիվ, մեզ չի հետաքրքրում թվերի և թվերի կամայական հավաքածու: Մեր ուշադրությունը կենտրոնացած կլինի թվային հաջորդականության վրա, որում n -րդ տերմինի արժեքը կապված է նրա հերթական համարի հետ ՝ կախվածությամբ, որը կարող է հստակ ձևակերպվել մաթեմատիկորեն: Այլ կերպ ասած. N-րդ համարի թվային արժեքը n- ի որոշ գործառույթ է:

a - թվային հաջորդականության անդամի արժեքը.

n- ը դրա սերիական համարն է.

f (n) այն գործառույթն է, որտեղ n թվային հաջորդականության հերթականը փաստարկ է:

Սահմանում

Ընդունված է թվաբանական առաջընթաց անվանել թվային հաջորդականություն, որում յուրաքանչյուր հաջորդ տերմին նույն թվով ավելի մեծ է (պակաս), քան նախորդը: Թվաբանական հաջորդականության 9 -րդ անդամի բանաձևը հետևյալն է.

a n - թվաբանական առաջընթացի ներկա անդամի արժեքը.

a n + 1 - հաջորդ համարի բանաձևը.

d - տարբերություն (որոշակի թիվ):

Հեշտ է որոշել, որ եթե տարբերությունը դրական է (d> 0), ապա դիտարկվող շարքի յուրաքանչյուր հաջորդ տերմինը կլինի ավելի մեծ, քան նախորդը, և նման թվաբանական առաջընթացը կաճի:

Ստորև բերված գծապատկերում հեշտ է տեսնել, թե ինչու է թվերի հաջորդականությունը կոչվում «աճող»:

Այն դեպքերում, երբ տարբերությունը բացասական է (մ<0), каждый последующий член по понятным причинам будет меньше предыдущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убывающей.

Նշված անդամի արժեքը

Երբեմն անհրաժեշտ է որոշել ցանկացած կամայական անդամի արժեքը ՝ թվաբանական առաջընթացի n- ով: Դուք կարող եք դա անել ՝ հաջորդականորեն հաշվարկելով թվաբանական առաջընթացի բոլոր անդամների արժեքները ՝ սկսած առաջինից մինչև ցանկալիը: Այնուամենայնիվ, այս ճանապարհը միշտ չէ, որ ընդունելի է, եթե, օրինակ, անհրաժեշտ է գտնել հինգ հազարերորդ կամ ութ միլիոներորդ անդամի իմաստը: Ավանդական հաշվարկը երկար կտեւի: Այնուամենայնիվ, որոշակի թվաբանական առաջընթացը կարող է ուսումնասիրվել `օգտագործելով հատուկ բանաձևեր: Կա նաև իններորդ տերմինի բանաձև. Թվաբանական առաջընթացի ցանկացած անդամի արժեքը կարող է սահմանվել որպես առաջընթացի առաջին տերմինի գումար `պրոգրեսիայի տարբերությամբ` բազմապատկած փնտրվող տերմինի թվով, նվազած մեկը

Բանաձևը համընդհանուր է ինչպես առաջընթացի մեծացման, այնպես էլ նվազման համար:

Տրված անդամի արժեքը հաշվարկելու օրինակ

Եկեք լուծենք թվաբանական առաջընթացի n -րդ տերմինի արժեքը գտնելու հետևյալ խնդիրը.

Վիճակ. Կա թվաբանական առաջընթաց պարամետրերով.

Հաջորդականության առաջին տերմինը 3 է;

Թվային շարքերի տարբերությունը 1.2 է:

Առաջադրանք. Դուք պետք է գտնեք 214 անդամի արժեքը

Լուծում. Տերմինի արժեքը որոշելու համար մենք օգտագործում ենք բանաձևը.

a (n) = a1 + d (n-1)

Խնդրի վիճակից տվյալները արտահայտության մեջ փոխարինելով ՝ մենք ունենք.

a (214) = a1 + d (n-1)

ա (214) = 3 + 1.2 (214-1) = 258.6

Պատասխան. Հաջորդականության 214 -րդ տերմինը 258.6 է:

Այս հաշվարկի մեթոդի առավելություններն ակնհայտ են. Ամբողջ լուծումը տևում է ոչ ավելի, քան 2 տող:

Տրված անդամների գումարը

Շատ հաճախ տվյալ թվաբանական շարքում պահանջվում է որոշել դրա որոշակի հատվածի արժեքների գումարը: Սա նաև չի պահանջում յուրաքանչյուր տերմինի արժեքների հաշվարկ և այնուհետև ամփոփում: Այս մեթոդը կիրառելի է, եթե գտնվող տերմինների թիվը փոքր է: Այլ դեպքերում ավելի հարմար է օգտագործել հետեւյալ բանաձեւը.

1 -ից n- ի թվաբանական առաջընթացի անդամների գումարը հավասար է առաջին և n -րդ անդամների գումարին ՝ բազմապատկված n անդամի թվով և բաժանված երկուսի: Եթե ​​բանաձևում n -րդ տերմինի արժեքը փոխարինվում է հոդվածի նախորդ պարբերության արտահայտությամբ, մենք ստանում ենք.

Հաշվարկի օրինակ

Օրինակ, եկեք խնդիր լուծենք հետևյալ պայմաններով.

Հաջորդականության առաջին տերմինը զրո է.

Տարբերությունը 0.5 է:

Խնդիրում դուք պետք է որոշեք շարքի անդամների գումարը 56 -ից 101 -ի սահմաններում:

Լուծում: Եկեք օգտագործենք առաջադիմության գումարը որոշելու բանաձևը.

s (n) = (2 ∙ a1 + d ∙ (n-1)) ∙ n / 2

Նախ, մենք որոշում ենք առաջընթացի 101 անդամների արժեքների գումարը ՝ մեր խնդրի պայմանների տվյալները փոխարինելով բանաձևով.

s 101 = (2 ∙ 0 + 0.5 ∙ (101-1)) ∙ 101/2 = 2 525

Ակնհայտ է, որ 56 -րդից 101 -րդ առաջընթացի անդամների գումարը պարզելու համար անհրաժեշտ է S 101 -ից հանել S 55 -ը:

s 55 = (2 ∙ 0 + 0.5 ∙ (55-1)) ∙ 55/2 = 742.5

Այսպիսով, այս օրինակի թվաբանական առաջընթացի գումարը.

s 101 - s 55 = 2,525 - 742,5 = 1,782,5

Թվաբանական առաջընթացի գործնական կիրառման օրինակ

Հոդվածի վերջում վերադառնանք առաջին պարբերությունում տրված թվաբանական հաջորդականության օրինակին ՝ տաքսիմետր (տաքսի մեքենայի հաշվիչ): Եկեք դիտարկենք մի օրինակ:

Տաքսու նստելը (որը ներառում է 3 կմ վազք) արժե 50 ռուբլի: Յուրաքանչյուր հաջորդ կիլոմետր վճարվում է 22 ռուբլի / կմ փոխարժեքով: Travelանապարհորդության հեռավորությունը 30 կմ: Հաշվեք ճանապարհորդության արժեքը:

1. Եկեք հրաժարվենք առաջին 3 կմ -ից, որի գինը ներառված է վայրէջքի գնի մեջ:

30 - 3 = 27 կմ:

2. Հետագա հաշվարկը ոչ այլ ինչ է, քան թվաբանական թվերի շարքի վերլուծություն:

Անդամի համարը `անցած կիլոմետրերի քանակը (հանած առաջին երեքը):

Անդամների արժեքը գումարն է:

Այս խնդրի առաջին տերմինը հավասար կլինի 1 = 50 p- ի:

Տարբերությունը առաջընթացի d = 22 p.

մեզ հետաքրքրող թիվը թվաբանական առաջընթացի (27 + 1) -երորդ տերմինի արժեքն է. 27 -րդ կիլոմետրի վերջի հաշվիչի ընթերցումը 27.999… = 28 կմ է:

a 28 = 50 + 22 ∙ (28 - 1) = 644

Կամայական երկար ժամանակահատվածի համար օրացուցային տվյալների հաշվարկները հիմնված են որոշակի թվային հաջորդականություններ նկարագրող բանաձևերի վրա: Աստղագիտության մեջ ուղեծրի երկարությունը երկրաչափականորեն կախված է երկնային մարմնի հեռավորությունից մինչև լուսատուին: Բացի այդ, տարբեր թվային շարքեր հաջողությամբ օգտագործվում են վիճակագրության և մաթեմատիկայի այլ կիրառական ճյուղերում:

Թվերի հաջորդականության մեկ այլ տեսակ երկրաչափական է

Երկրաչափական առաջընթացը բնութագրվում է փոփոխությունների մեծ թվաբանությամբ: Պատահական չէ, որ քաղաքականության, սոցիոլոգիայի, բժշկության մեջ հաճախ ասում են, որ գործընթացը զարգանում է երկրաչափական կերպով ՝ ցույց տալու այս կամ այն ​​երևույթի տարածման բարձր տեմպը, օրինակ ՝ հիվանդության համաճարակի ժամանակ:

Երկրաչափական թվային շարքի N- րդ տերմինը նախորդից տարբերվում է նրանով, որ այն բազմապատկվում է ինչ -որ հաստատուն թվով. Հայտարարը, օրինակ, առաջին տերմինը 1 է, հայտարարը `համապատասխանաբար, 2, ապա.

n = 1: 1 ∙ 2 = 2

n = 2: 2 ∙ 2 = 4

n = 3: 4 2 = 8

n = 4: 8 ∙ 2 = 16

n = 5: 16 ∙ 2 = 32,

b n - երկրաչափական առաջընթացի ներկա անդամի արժեքը.

b n + 1 - երկրաչափական առաջընթացի հաջորդ տերմինի բանաձևը.

q- ը երկրաչափական առաջընթացի հայտարար է (հաստատուն թիվ):

Եթե ​​թվաբանական առաջընթացի գրաֆիկը ուղիղ գիծ է, ապա երկրաչափականը մի փոքր այլ պատկեր է տալիս.

Ինչպես թվաբանության դեպքում, երկրաչափական առաջընթացն ունի կամայական տերմինի արժեքի բանաձև: Երկրաչափական առաջընթացի ցանկացած n-րդ տերմինը հավասար է առաջին տերմինի արտադրյալին `n- ի հզորության առաջընթացի հայտարարի միջոցով, մեկով կրճատված.

Օրինակ. Մենք ունենք երկրաչափական պրոգրեսիա, որի առաջին տերմինը հավասար է 3 -ի, իսկ առաջադիմության հայտարարը `1.5 -ի: Գտեք առաջադիմության 5 -րդ տերմինը

b 5 = b 1 ∙ q (5-1) = 3 ∙ 1.5 4 = 15.1875

Տվյալ թվով անդամների գումարը հաշվարկվում է նույն ձևով ՝ օգտագործելով հատուկ բանաձև: Երկրաչափական առաջընթացի առաջին n տերմինների գումարը հավասար է առաջընթացի 9 -րդ տերմինի և դրա հայտարարի արտադրյալի և առաջընթացի առաջին տերմինի միջև տարբերությանը, որը բաժանված է հայտարարով `կրճատված մեկով.

Եթե ​​b n- ը փոխարինվի ՝ օգտագործելով վերը նշված բանաձևը, համարվող թվային շարքի առաջին n տերմինների գումարի արժեքը կունենա հետևյալ տեսքը.

Օրինակ. Երկրաչափական առաջընթացը սկսվում է 1 -ին հավասար 1 -ին վերջավորությամբ: Նշանակիչը հավասար է 3 -ի: Գտեք առաջին ութ տերմինների գումարը:

s8 = 1 ∙ (3 8 -1) / (3-1) = 3 280