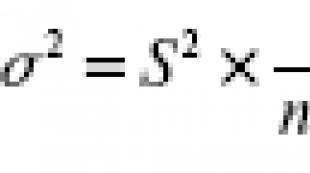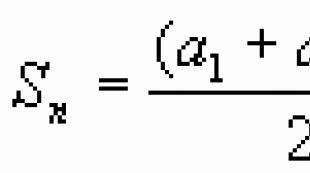Kaardid

Kõik valemid on aritmeetilises progressioonis. Aritmeetiline progressioon. Teine numbrijada tüüp on geomeetriline

Matemaatikal on oma ilu, nagu maalil ja luulel.

Vene teadlane, mehaanik N.E. Žukovski

Aritmeetilise progressi mõistega seotud probleemid on matemaatika sisseastumiseksamitel väga levinud probleemid. Selliste probleemide edukaks lahendamiseks on vaja hästi teada aritmeetilise progressiooni omadusi ja omada teatud oskusi nende rakendamisel.

Meenutame kõigepealt aritmeetilise progressi peamisi omadusi ja esitame olulisemad valemid, selle kontseptsiooniga seotud.

Määratlus. Numbrite jada, kus iga järgnev termin erineb eelmisest sama numbriga, nimetatakse aritmeetiliseks progressiooniks. Pealegi numbernimetatakse progressi erinevuseks.

Aritmeetiliseks progresseerumiseks kehtivad järgmised valemid

, (1)

kus. Valemit (1) nimetatakse aritmeetilise progressiooni üldnimetuse valemiks ja valem (2) on aritmeetilise progressiooni peamine omadus: iga progressioonitermin langeb kokku selle naaberterminite aritmeetilise keskmisega ja.

Pange tähele, et just selle omaduse tõttu nimetatakse vaadeldavat progressi "aritmeetikaks".

Ülaltoodud valemid (1) ja (2) on üldistatud järgmiselt:

(3)

Summa arvutamiseks esimene aritmeetilise progressiooni liikmedtavaliselt rakendatakse valemit

(5) kus ja.

Võttes arvesse valemit (1), siis eeldab valem (5)

Kui tähistame, siis

kus. Kuna valemid (7) ja (8) on vastavate valemite (5) ja (6) üldistus.

Eriti , valem (5) eeldab, mida

Aritmeetilise progressiooni omadus, mis on sõnastatud järgmise teoreemi abil, on enamiku õpilaste jaoks vähetuntud.

Teoreem. Kui siis

Tõestus. Kui siis

Teoreem on tõestatud.

Näiteks , kasutades teoreemi, seda saab näidata

Läheme edasi tüüpiliste probleemide lahendamise näidete kaalumisele teemal "Aritmeetiline progress".

Näide 1. Lase ja. Leia.

Lahendus. Rakendades valemit (6), saame. Kuna ja, siis või.

Näide 2. Olgu see kolm korda rohkem ja jagatuna jagatisega saame 2 ja ülejäänud 8. Määrake ja.

Lahendus. Näite tingimus eeldab võrrandisüsteemi

Kuna ,, ja siis võrrandisüsteemist (10) saame

Selle võrrandisüsteemi lahendus on ja.

Näide 3. Leia, kas ja.

Lahendus. Valemi (5) kohaselt on meil või. Kuid kasutades omadust (9), saame.

Alates ja siis võrdsusest järgneb võrrand või.

Näide 4. Leia, kui.

Lahendus.Valemi (5) järgi on meil

Teoreemi kasutades saab aga kirjutada

Sellest ja valemist (11) saame.

Näide 5. Antud :. Leia.

Lahendus. Sellest ajast. Siiski, seetõttu.

Näide 6. Lase, ja. Leia.

Lahendus. Valemi (9) abil saame. Seega, kui, siis või.

Alates ja, siis siin on meil võrrandisüsteem

Selle lahendamisel saame ja.

Võrrandi loomulik juur on an.

Näide 7. Leia, kas ja.

Lahendus. Kuna valemi (3) järgi on see meil olemas, eeldab probleemlause võrrandisüsteemi

Kui asendate väljendisüsteemi teise võrrandisse, siis saame või.

Ruutvõrrandi juured on ja.

Vaatleme kahte juhtumit.

1. Lase siis. Alates ja siis.

Sel juhul on meil valemi (6) kohaselt olemas

2. Kui, siis ja

Vastus: ja.

Näide 8. On teada, et ja. Leia.

Lahendus. Võttes arvesse valemit (5) ja näite tingimust, kirjutame üles ja.

Seega järgitakse võrrandisüsteemi

Kui korrutame süsteemi esimese võrrandi 2 -ga ja lisame selle siis teisele võrrandile, saame

Valemi (9) kohaselt on meil... Sellega seoses järeldub (12) või.

Alates ja siis.

Vastus:.

Näide 9. Leia, kas ja.

Lahendus. Kuna ja tingimusel, siis või.

Valemist (5) on see teada, mida . Sellest ajast.

Seega siin on meil lineaarvõrrandite süsteem

Seega saame ja. Võttes arvesse valemit (8), kirjutame.

Näide 10. Lahendage võrrand.

Lahendus. Antud võrrandist järeldub, et. Oletame, et ,, ja. Sel juhul .

Vastavalt valemile (1) saate kirjutada või.

Kuna võrrandil (13) on üks sobiv juur.

Näide 11. Leidke maksimaalne väärtus tingimusel, et ja.

Lahendus. Sellest ajast alates on aritmeetiline progress vähenev. Sellega seoses omandab avaldis maksimaalse väärtuse, kui see on progressiooni minimaalse positiivse termini arv.

Kasutame valemit (1) ja fakti, nagu. Siis saame selle või.

Kuna, siis või ... Siiski selles ebavõrdsusessuurim looduslik arv, seega.

Kui väärtused ja asendatakse valemis (6), saame.

Vastus:.

Näide 12. Määrake kõigi kahekohaliste loodusarvude summa, mis jagatuna 6-ga annab ülejäänud 5.

Lahendus. Tähistagem kõigi kahekohaliste loodusarvude hulgaga, s.t. ... Järgnevalt konstrueerime alamhulga, mis koosneb hulga nendest elementidest (numbritest), mis jagatuna 6 -ga annavad ülejäänud 5.

Selle kehtestamine pole keeruline, mida . Ilmselgelt, et komplekti elemendidmoodustavad aritmeetilise progressiooni, milles ja.

Hulga kardinaalsuse (elementide arvu) kindlakstegemiseks eeldame, et. Kuna ja, siis valemist (1) tuleneb või. Võttes arvesse valemit (5), saame.

Ülaltoodud näited probleemide lahendamisest ei saa mingil juhul olla ammendavad. See artikkel on kirjutatud antud teema tüüpiliste probleemide lahendamise kaasaegsete meetodite analüüsi põhjal. Aritmeetilise progresseerumisega seotud probleemide lahendamise meetodite põhjalikumaks uurimiseks on soovitatav tutvuda soovitatud kirjanduse loendiga.

1. Ülesannete kogumine matemaatikas tehnikakõrgkoolide taotlejatele / Toim. M.I. Skanavi. - M.: Rahu ja haridus, 2013 .-- 608 lk.

2. Suprun V.P. Matemaatika gümnasistidele: kooli õppekava täiendavad lõigud. - M.: Lenand / URSS, 2014 .-- 216 lk.

3. Medynsky M.M. Läbida elementaarse matemaatika kursus ülesannetes ja harjutustes. 2. raamat: numbrijadad ja progressioonid. - M.: Edithus, 2015 .-- 208 lk.

Kas teil on veel küsimusi?

Juhendajalt abi saamiseks - registreeruge.

saidil, materjali täieliku või osalise kopeerimisega, on vaja linki allikale.

Õppetüüp: uue materjali õppimine.

Õppetunni eesmärgid:

õpilaste ideede laiendamine ja süvendamine aritmeetilise progressiooni abil lahendatud probleemide kohta; õpilaste otsingutegevuse korraldamine aritmeetilise progressiooni esimese n liikme summa valemi tuletamisel;
oskuste arendamine uute teadmiste iseseisvaks omandamiseks, juba omandatud teadmiste kasutamine püstitatud ülesande saavutamiseks;
soovi ja vajaduse kujunemine saadud fakte üldistada, iseseisvuse kujunemine.

Ülesanded:

üldistada ja süstematiseerida olemasolevaid teadmisi teemal “Aritmeetiline progressioon”;
tuletada valemid aritmeetilise progresseerumise esimese n termini summa arvutamiseks;
õpetada saadud valemite rakendamist erinevate ülesannete lahendamisel;
juhtida õpilaste tähelepanu numbrilise avaldise väärtuse leidmisel toimingute järjekorrale.

Varustus:

kaardid koos ülesannetega rühmas ja paaris töötamiseks;
hindamispaber;
esitlus"Aritmeetiline progress".

I. Baasteadmiste uuendamine.

1. Iseseisev töö paaris.

1. variant:

Määratlege aritmeetiline progressioon. Kirjutage üles korduv valem, mis määratleb aritmeetilise progressiooni. Tere näide aritmeetilisest progressioonist ja näidake selle erinevust.

Teine võimalus:

Kirjutage üles aritmeetilise progressi n -nda liigendi valem. Leidke aritmeetilise progressi 100. liige ( a n}: 2, 5, 8 …
Sel ajal valmistavad kaks õpilast tahvli tagaküljel samadele küsimustele vastused.
Õpilased hindavad partneri tööd tahvli vastu. (Vastuslehed antakse üle).

2. Mänguhetk.

Harjutus 1.

Õpetaja. Olen mõelnud välja mõne aritmeetilise progressi. Lihtsalt küsige minult kaks küsimust, et saaksite pärast vastuseid kiiresti nimetada selle progresseerumise 7. tähtaja. (1, 3, 5, 7, 9, 11, 13, 15 ...)

Õpilaste küsimused.

Mis on progressiooni kuues termin ja mis vahe on?
Mis on progresseerumise kaheksas termin ja mis vahe on?

Kui küsimusi enam ei ole, saab õpetaja neid stimuleerida - d -le „erinevus” (erinevus), st ei tohi küsida, mis vahe on. Võite esitada küsimusi: mis on progresseerumise kuues ja milline on progresseerumise kaheksas liige?

Ülesanne 2.

Tahvlile on kirjutatud 20 numbrit: 1, 4, 7 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58.

Õpetaja seisab seljaga tahvli poole. Õpilased helistavad numbri numbrile ja õpetaja helistab kohe numbrile endale. Selgitage, kuidas ma seda teen?

Õpetaja mäletab n -nda semestri valemit a n = 3n - 2 ja asendades n antud väärtused, leiab vastavad väärtused a n.

II. Haridusprobleemi avaldus.

Teen ettepaneku lahendada iidne probleem, mis pärineb 2. aastatuhandest eKr ja leiti Egiptuse papüürustest.

Ülesanne:"Olgu teile öeldud: jagage kümme mõõdu otra 10 inimese vahel, vahe iga inimese ja tema naabri vahel on 1/8 mõõdust."

Kuidas on see ülesanne seotud aritmeetilise progressiooni teemaga? (Iga järgmine saab 1/8 mõõtmist rohkem, mis tähendab erinevust d = 1/8, 10 inimest, mis tähendab n = 10.)
Mida arvate, mida arv 10 tähendab? (Progressiooni kõigi liikmete summa.)
Mida veel peate teadma, et oleks lihtne ja lihtne jagada otra vastavalt ülesande tingimustele? (Edenemise esimene tähtaeg.)

Õppetunni eesmärk- edusammuliikmete summa sõltuvuse määramine nende arvust, esimesest liikmest ja erinevusest ning kontrollimine, kas iidsetel aegadel oli probleem õigesti lahendatud.

Enne valemi järelduse tegemist vaatame, kuidas muistsed egiptlased probleemi lahendasid.

Ja nad lahendasid selle järgmiselt:

1) 10 mõõdet: 10 = 1 meede - keskmine osakaal;
2) 1 mõõt ∙ = 2 mõõdet - kahekordistunud keskmine jaga.
Kahekordistunud keskmine osa on 5. ja 6. inimese aktsiate summa.
3) 2 mõõdet - 1/8 mõõdet = 1 7/8 mõõdet - kaks korda suurem kui viienda inimese osakaal.
4) 1 7/8: 2 = 5/16 - viienda osa; ja nii edasi, leiate iga eelmise ja järgneva inimese osa.

Saame jada:

III. Lahendus probleemile.

1. Töötamine rühmades

I rühm: Leidke 20 järjestikuse naturaalarvu summa: S 20 = (20 + 1) ∙ 10 = 210.

Üldiselt

II rühm: Leidke looduslike arvude summa vahemikus 1 kuni 100 (Legend of the Little Gauss).

S 100 = (1 + 100) ∙ 50 = 5050

Väljund:

III rühm: Leidke looduslike arvude summa vahemikus 1 kuni 21.

Lahendus: 1 + 21 = 2 + 20 = 3 + 19 = 4 + 18 ...

Väljund:

IV rühm: Leidke looduslike arvude summa vahemikus 1 kuni 101.

Väljund:

Seda meetodit vaadeldavate probleemide lahendamiseks nimetatakse "Gaussi meetodiks".

2. Iga rühm esitab tahvlile lahenduse probleemile.

3. Kavandatud lahenduste üldistamine suvalisele aritmeetilisele progressioonile:

a 1, 2, 3, ..., n-2, n-1, n.
S n = a 1 + a 2 + a 3 + a 4 +… + a n-3 + a n-2 + a n-1 + a n.

Leiame selle summa sarnaselt arutledes:

4. Kas oleme lahendanud ülesande?(Jah.)

IV. Saadud valemite esmane mõistmine ja rakendamine ülesannete lahendamisel.

1. Vana probleemi lahenduse kontrollimine valemi abil.

2. Valemi rakendamine erinevate probleemide lahendamisel.

3. Harjutused valemi rakendamise oskuse kujundamiseks probleemide lahendamisel.

A) nr 613

Antud: ( a n) - aritmeetiline progressioon;

(a n): 1, 2, 3, ..., 1500

Leia: S 1500

Lahendus: , a 1 = 1, 1500 = 1500,

B) Arvestades: ( a n) - aritmeetiline progressioon;
(a n): 1, 2, 3, ...
S n = 210

Leia: n
Lahendus:

V. Iseseisev töö vastastikuse kontrollimisega.

Denis läks tööle kullerina. Esimesel kuul oli tema palk 200 rubla, igal järgneval kuul tõusis see 30 rubla võrra. Kui palju ta aastaga teenis?

Antud: ( a n) - aritmeetiline progressioon;
a 1 = 200, d = 30, n = 12
Leia: S 12
Lahendus:

Vastus: Denis sai aastaga 4380 rubla.

Vi. Kodutööde briifing.

lk 4.3 - õppida valemi tuletamist.
№№ 585, 623 .
Looge ülesanne, mis lahendatakse, kasutades valemit aritmeetilise progressiooni esimese n -liigendi summale.

Vii. Õppetund kokku võttes.

1. Hindamisleht

2. Jätka lauseid

Täna õppetunnis õppisin ...
Õpitud valemid ...
Ma arvan, et …

3. Kas leiate numbrite summa vahemikus 1 kuni 500? Millist meetodit selle probleemi lahendamiseks kasutate?

Bibliograafia.

1. Algebra, 9. klass. Õpik haridusasutustele. Ed. G.V. Dorofejeva. M.: "Haridus", 2009.

Jah, jah: aritmeetiline progress ei ole teie jaoks mänguasi :)

Noh, sõbrad, kui te seda teksti loete, siis sisemine kork-ilmsus ütleb mulle, et te ei tea veel, mis on aritmeetiline progress, kuid te tõesti (ei, niimoodi: NII!) Tahate teada. Seetõttu ei piinata ma teid pikkade sissejuhatustega ja asun otse asja juurde.

Alustame paari näitega. Mõelge mitmele numbrikomplektile:

1; 2; 3; 4; ...
15; 20; 25; 30; ...
$ \ sqrt (2); \ 2 \ sqrt (2); \ 3 \ sqrt (2); ... $

Mis on kõigil neil komplektidel ühist? Esmapilgul mitte midagi. Aga tegelikult on midagi. Nimelt: iga järgmine element erineb eelmisest ühe ja sama numbriga.

Otsustage ise. Esimene komplekt on lihtsalt järjestikused numbrid, iga järgmine on rohkem kui eelmine. Teisel juhul on külgnevate numbrite vahe juba võrdne viiega, kuid see erinevus on endiselt konstantne. Kolmandal juhul juured üldiselt. Kuid $ 2 \ sqrt (2) = \ sqrt (2) + \ sqrt (2) $ ja $ 3 \ sqrt (2) = 2 \ sqrt (2) + \ sqrt (2) $, s.t. ja sel juhul suureneb iga järgmine element lihtsalt $ \ sqrt (2) $ võrra (ja ärge kartke, et see arv on irratsionaalne).

Niisiis: kõiki selliseid järjestusi nimetatakse aritmeetilisteks progressioonideks. Anname range määratluse:

Määratlus. Numbrite jada, milles iga järgmine erineb eelmisest täpselt sama palju, nimetatakse aritmeetiliseks progressiooniks. Seda summat, mille võrra numbrid erinevad, nimetatakse progressiooni erinevuseks ja seda tähistatakse kõige sagedamini tähega $ d $.

Nimetus: $ \ left (((a) _ (n)) \ right) $ - progressioon ise, $ d $ - selle erinevus.

Ja vaid paar olulist märkust. Esiteks, ainult korras numbrite jada: neid on lubatud lugeda rangelt nende kirjutamise järjekorras - ja mitte midagi muud. Te ei saa numbreid ümber paigutada ega vahetada.

Teiseks võib jada ise olla kas piiratud või lõpmatu. Näiteks hulk (1; 2; 3) on ilmselgelt piiratud aritmeetiline progressioon. Aga kui kirjutada midagi vaimus (1; 2; 3; 4; ...) - see on juba lõputu edasiminek. Neljajärgne ellips vihjab justkui sellele, et numbreid on ikka päris palju. Näiteks lõputult palju. :)

Samuti tahaksin märkida, et edusammud suurenevad ja vähenevad. Oleme juba näinud kasvavaid - sama komplekti (1; 2; 3; 4; ...). Ja siin on näited progressiooni vähenemisest:

49; 41; 33; 25; 17; ...
17,5; 12; 6,5; 1; −4,5; −10; ...
$ \ sqrt (5); \ \ sqrt (5) -1; \ \ sqrt (5) -2; \ \ sqrt (5) -3; ... $

Okei, okei: see viimane näide võib tunduda liiga keeruline. Aga ülejäänud, ma arvan, on teile selge. Seetõttu tutvustame uusi määratlusi:

Määratlus. Aritmeetilist progressiooni nimetatakse:

suureneb, kui iga järgmine element on suurem kui eelmine;

väheneb, kui vastupidi, iga järgnev element on väiksem kui eelmine.

Lisaks on olemas nn "statsionaarsed" järjestused - need koosnevad samast korduvast numbrist. Näiteks (3; 3; 3; ...).

Jääb vaid üks küsimus: kuidas eristada suurenevat progresseerumist vähenevast? Õnneks sõltub kõik numbri $ d $ märgist, s.t. erinevuse areng:

Kui $ d \ gt 0 $, siis progresseerumine suureneb;
Kui $ d \ lt 0 $, siis progress väheneb ilmselgelt;
Lõpuks on juhtum $ d = 0 $ - sel juhul taandatakse kogu progressioon identsete numbrite statsionaarseks jadaks: (1; 1; 1; 1; ...) jne.

Proovime arvutada erinevuse $ d $ kolme ülaltoodud kahaneva progressiooni jaoks. Selleks piisab kahe suvalise elemendi (näiteks esimene ja teine) võtmisest ja paremal olevast numbrist lahutamisest. See näeb välja selline:

41−49=−8;
12−17,5=−5,5;
$ \ sqrt (5) -1- \ sqrt (5) = - 1 $.

Nagu näete, osutus vahe kõigil kolmel juhul tõesti negatiivseks. Ja nüüd, kui oleme määratlused enam -vähem selgeks saanud, on aeg välja mõelda, kuidas progressioone kirjeldatakse ja millised on nende omadused.

Edenemise liikmed ja korduv valem

Kuna meie järjestuste elemente ei saa vahetada, saab neid nummerdada:

\ [\ vasak (((a) _ (n)) \ parem) = \ vasak \ (((a) _ (1)), \ ((a) _ (2)), (a) _ (3 )), ... \ õige \) \]

Selle komplekti üksikuid elemente nimetatakse progressiooni liikmeteks. Neid tähistatakse numbriga: esimene, teine ja nii edasi.

Lisaks, nagu me juba teame, on progresseerumise naaberliikmed seotud järgmise valemiga:

\ [((a) _ (n))-((a) _ (n-1)) = d \ Paremnool ((a) _ (n)) = ((a) _ (n-1)) + d \]

Lühidalt öeldes, et leida $ n $ th termin progressioonist, peate teadma $ n-1 $ th terminit ja $ d $ erinevust. Sellist valemit nimetatakse korduvaks, kuna selle abil saate leida mis tahes arvu, teades ainult eelmist (ja tegelikult - kõiki eelnevaid). See on väga ebamugav, seega on olemas keerulisem valem, mis vähendab kõik arvutused esimese tähtajani ja erinevuse:

\ [((a) _ (n)) = ((a) _ (1)) + \ vasak (n-1 \ parem) d \]

Kindlasti olete selle valemiga juba kokku puutunud. Neile meeldib seda anda kõikvõimalikes teatmeteostes ja reshebnikutes. Ja igas mõistlikus matemaatikaõpikus on ta üks esimesi.

Soovitan siiski natuke harjutada.

Probleem number 1. Kirjutage välja aritmeetilise progressiooni kolm esimest terminit $ \ left (((a) _ (n)) \ right) $, kui $ ((a) _ (1)) = 8, d = -5 $.

Lahendus. Niisiis, me teame esimest terminit $ ((a) _ (1)) = 8 $ ja progresseerumise erinevust $ d = -5 $. Kasutame äsja antud valemit ja asendame $ n = 1 $, $ n = 2 $ ja $ n = 3 $:

\ [\ algus (joondamine) & ((a) _ (n)) = ((a) _ (1)) + \ vasak (n-1 \ parem) d; \\ & ((a) _ (1)) = ((a) _ (1)) + \ vasak (1-1 \ parem) d = ((a) _ (1)) = 8; \\ & ((a) _ (2)) = ((a) _ (1)) + \ vasak (2-1 \ parem) d = ((a) _ (1)) + d = 8-5 = 3; \\ & ((a) _ (3)) = ((a) _ (1)) + \ vasak (3-1 \ parem) d = ((a) _ (1)) + 2d = 8-10 = -2. \\ \ lõpp (joondamine) \]

Vastus: (8; 3; −2)

See on kõik! Pange tähele: meie areng väheneb.

Loomulikult ei saanud $ n = 1 $ asendada - esimene termin on meile juba teada. Kuid ühe asendades veendusime, et meie valem töötab isegi esimese ametiaja jooksul. Muudel juhtudel taandus see kõik tühisele aritmeetikale.

Probleem number 2. Kirjutage üles aritmeetilise progressi kolm esimest terminit, kui selle seitsmes liige on –40 ja seitsmeteistkümnes liige on –50.

Lahendus. Kirjutame probleemi seisukorra tavalistele tingimustele:

\ [((a) _ (7)) = - 40; \ quad ((a) _ (17)) = - 50. \]

\ [\ vasakule \ (\ algus (joondamine) & (a) _ (7)) = ((a) _ (1)) + 6d \\ & ((a) _ (17)) = ((a) _ (1)) + 16d \\ \ lõpp (joondamine) \ parem. \]

\ [\ vasakule \ (\ algus (joondamine) & (a) _ (1)) + 6d = -40 \\ & ((a) _ (1)) + 16d = -50 \\ \ lõpp (joondamine) \ õige. \]

Panin süsteemi märgi, sest need nõuded peavad olema täidetud samaaegselt. Ja nüüd pange tähele, et kui lahutame teisest võrrandist esimese (meil on õigus seda teha, kuna meil on süsteem), saame selle:

\ [\ algus (joondamine) & ((a) _ (1)) + 16d- \ vasak ((((a) _ (1)) + 6d \ parem) =- 50- \ vasak (-40 \ parem); \\ & ((a) _ (1)) + 16d - ((a) _ (1)) - 6d = -50 + 40; \\ & 10d = -10; \\ & d = -1. \\ \ lõpp (joondamine) \]

Nii lihtsalt leidsimegi progressi erinevuse! Jääb vaid asendada leitud arv mis tahes süsteemi võrranditega. Näiteks esimeses:

\ [\ start (maatriks) ((a) _ (1)) + 6d = -40; \ quad d = -1 \\ \ Downarrow \\ ((a) _ (1)) -6 = -40; \\ ((a) _ (1)) = - 40 + 6 = -34. \\ \ lõpp (maatriks) \]

Nüüd, teades esimest terminit ja erinevust, jääb üle leida teine ja kolmas termin:

\ [\ algus (joondamine) & ((a) _ (2)) = ((a) _ (1)) + d = -34-1 = -35; \\ & ((a) _ (3)) = ((a) _ (1)) + 2d = -34-2 = -36. \\ \ lõpp (joondamine) \]

Valmis! Probleem on lahendatud.

Vastus: (-34; -35; -36)

Pöörake tähelepanu meie avastatud progresseerumise huvitavale omadusele: kui võtame $ n $ th ja $ m $ th tingimused ja lahutame need üksteisest, siis saame progresseerumise vahe korrutatuna arvuga $ n-m $:

\ [((a) _ (n)) - ((a) _ (m)) = d \ cdot \ vasak (n -m \ parem) \]

Lihtne, kuid väga kasulik omadus, mida peaksite kindlasti teadma - selle abil saate märkimisväärselt kiirendada paljude probleemide lahendamist. Siin on suurepärane näide:

Probleem number 3. Aritmeetilise progressiooni viies liige on 8,4 ja selle kümnes liikmeks on 14,4. Leidke selle progressiooni viieteistkümnes tähtaeg.

Lahendus. Kuna $ ((a) _ (5)) = 8,4 $, $ ((a) _ (10)) = 14,4 $ ja peate leidma $ ((a) _ (15)) $, siis paneme tähele järgmist :

\ [\ algus (joondamine) & ((a) _ (15)) - ((a) _ (10)) = 5d; \\ & ((a) _ (10)) - ((a) _ (5)) = 5d. \\ \ lõpp (joondamine) \]

Kuid tingimusel $ ((a) _ (10)) - ((a) _ (5)) = 14,4-8,4 = 6 dollarit, seega 5 dollarit = 6 dollarit, kust meil on:

\ [\ algus (joondamine) & ((a) _ (15)) - 14,4 = 6; \\ & (a) _ (15)) = 6 + 14,4 = 20,4. \\ \ lõpp (joondamine) \]

Vastus: 20.4

See on kõik! Me ei pidanud koostama mõningaid võrrandisüsteeme ning arvutama esimest terminit ja erinevust - kõik lahendati vaid paari reaga.

Nüüd kaalume teist tüüpi ülesandeid - leida negatiivsed ja positiivsed progressiooni liikmed. Pole saladus, et kui progresseerumine suureneb, samal ajal kui esimene termin on negatiivne, ilmuvad selles varem või hiljem positiivsed terminid. Ja vastupidi: väheneva progressiooni liikmed muutuvad varem või hiljem negatiivseks.

Samas pole kaugeltki alati võimalik seda hetke "pea ees" käperdada, järjestikku elemente läbides. Sageli on probleemid kavandatud nii, et ilma valemeid teadmata võtaksid arvutused mitu lehte - me jääksime vastuse leidmise ajal lihtsalt magama. Seetõttu püüame neid probleeme kiiremini lahendada.

Probleem number 4. Kui palju negatiivseid termineid on aritmeetilises progressioonis -38,5; −35,8; ...?

Lahendus. Niisiis, $ ((a) _ (1)) = - 38,5 $, $ ((a) _ (2)) = - 35,8 $, kust leiame kohe erinevuse:

Pange tähele, et erinevus on positiivne, seega progresseerumine suureneb. Esimene termin on negatiivne, nii et mingil hetkel komistame tõesti positiivsete numbrite otsa. Ainus küsimus on, millal see juhtub.

Proovime välja selgitada: kui kaua (st kuni millise loomuliku arvuni $ n $) säilib terminite negatiivsus:

\ [\ algus (joondamine) & ((a) _ (n)) \ lt 0 \ paremnool ((a) _ (1)) + \ vasak (n-1 \ parem) d \ lt 0; \\ & -38.5+ \ vasak (n -1 \ parem) \ cdot 2.7 \ lt 0; \ quad \ left | \ cdot 10 \ õige. \\ & -385 + 27 \ cdot \ vasak (n -1 \ parem) \ lt 0; \\ & -385 + 27n -27 \ lt 0; \\ & 27n \ lt 412; \\ & n \ lt 15 \ frac (7) (27) \ paremnool ((n) _ (\ max)) = 15. \\ \ lõpp (joondamine) \]

Viimane rida vajab selgitust. Niisiis, me teame, et $ n \ lt 15 \ frac (7) (27) $. Teisest küljest oleme rahul ainult arvu täisarvudega (pealegi: $ n \ in \ mathbb (N) $), seega on suurim lubatud arv täpselt $ n = 15 $ ja mitte mingil juhul 16.

Probleem number 5. Aritmeetilises progresseerumises $ (() _ (5)) = - 150, (() _ (6)) = - 147 $. Leidke selle progressiooni esimese positiivse termini number.

See oleks täpselt sama probleem nagu eelmine, kuid me ei tea $ ((a) _ (1)) $. Kuid naaberterminid on teada: $ ((a) _ (5)) $ ja $ ((a) _ (6)) $, nii et saame hõlpsalt leida progresseerumise erinevuse:

Lisaks püüame väljendada viiendat terminit esimese ja erinevuse järgi vastavalt standardvalemile:

\ [\ algus (joondamine) & ((a) _ (n)) = ((a) _ (1)) + \ vasak (n-1 \ parem) \ cdot d; \\ & ((a) _ (5)) = ((a) _ (1)) + 4d; \\ & -150 = ((a) _ (1)) + 4 \ cdot 3; \\ & ((a) _ (1)) = -150-12 = -162. \\ \ lõpp (joondamine) \]

Nüüd jätkame analoogselt eelmise ülesandega. Saame teada, millises meie järjestuse punktis on positiivsed numbrid:

\ [\ begin (align) & ((a) _ (n)) = - 162+ \ left (n -1 \ right) \ cdot 3 \ gt 0; \\ & -162 + 3n -3 \ gt 0; \\ & 3n \ gt 165; \\ & n \ gt 55 \ Paremnool ((n) _ (\ min)) = 56. \\ \ lõpp (joondamine) \]

Selle ebavõrdsuse väikseim täisarvuline lahendus on 56.

Pange tähele: viimases ülesandes taandati kõik rangeks ebavõrdsuseks, nii et valik $ n = 55 $ meile ei sobi.

Nüüd, kui oleme õppinud lihtsaid probleeme lahendama, liigume edasi keerukamate juurde. Kuid kõigepealt uurime veel ühte aritmeetilise progressiooni väga kasulikku omadust, mis säästab tulevikus palju aega ja ebavõrdseid lahtreid. :)

Aritmeetiline keskmine ja võrdsed taanded

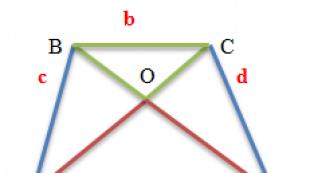
Mõtle kasvavale aritmeetilisele progressioonile mitu järjestikust liiget $ \ left (((a) _ (n)) \ right) $. Proovime need numbrireale märkida:

Aritmeetilise progresseerumise liikmed numbrireal

Ma märkisin konkreetselt suvalisi termineid $ ((a) _ (n-3)), ..., (a) _ (n + 3)) $, mitte ühtegi $ ((a) _ (1)), \ ( (a) _ (2)), \ ((a) _ (3)) $ jne. Sest reegel, millest ma nüüd räägin, töötab sama mis tahes "segmentide" puhul.

Ja reegel on väga lihtne. Pidagem meeles kordusvalemit ja kirjutage see kõigi märgitud liikmete jaoks üles:

\ [\ algus (joondamine) & ((a) _ (n-2)) = ((a) _ (n-3)) + d; \\ & ((a) _ (n-1)) = ((a) _ (n-2)) + d; \\ & ((a) _ (n)) = ((a) _ (n-1)) + d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n + 1)) + d; \\ \ lõpp (joondamine) \]

Neid võrdsusi saab aga teisiti ümber kirjutada:

\ [\ algus (joondamine) & ((a) _ (n -1)) = ((a) _ (n)) - d; \\ & ((a) _ (n -2)) = ((a) _ (n)) - 2d; \\ & ((a) _ (n -3)) = ((a) _ (n)) - 3d; \\ & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (n + 3)) = ((a) _ (n)) + 3d; \\ \ lõpp (joondamine) \]

No mis siis? Ja asjaolu, et terminid $ ((a) _ (n-1)) $ ja $ ((a) _ (n + 1)) $ asuvad $ ((a) _ (n)) $ samal kaugusel . Ja see vahemaa on võrdne $ d $. Sama võib öelda liikmete $ ((a) _ (n -2)) $ ja $ ((a) _ (n + 2)) $ kohta - need eemaldatakse ka $ ((a) _ (n) ) $ sama vahemaa võrdub $ 2d $. Võite jätkata lõputult, kuid tähendust illustreerib pilt hästi.

Progressiooni liikmed asuvad keskusest samal kaugusel

Mida see meie jaoks tähendab? See tähendab, et võite leida $ ((a) _ (n)) $, kui naabernumbrid on teada:

\ [((a) _ (n)) = \ frac (((a) _ (n-1)) + ((a) _ (n + 1))) (2) \]

Saime suurepärase väite: iga aritmeetilise progressiooni liige on võrdne naaberterminite aritmeetilise keskmisega! Veelgi enam: me ei saa kõrvale kalduda oma $ ((a) _ (n)) $ vasakule ja paremale mitte ühe sammu, vaid $ k $ sammu võrra - ja ikkagi on valem õige:

\ [((a) _ (n)) = \ frac (((a) _ (n-k)) + ((a) _ (n + k))) (2) \]

Need. kui teame $ ((a) _ (100)) $ ja $ ((a) _ (200)) $, leiame hõlpsalt mõned $ ((a) _ (150)) $, sest $ ((a) _ $) (150)) = \ frac (((a) _ (100)) + ((a) _ (200))) (2) $. Esmapilgul võib tunduda, et see asjaolu ei anna meile midagi kasulikku. Kuid praktikas on paljud probleemid spetsiaalselt "teritatud" aritmeetilise keskmise kasutamiseks. Vaata:

Probleem number 6. Leidke kõik $ x $ väärtused, mille numbrid $ -6 ((x) ^ (2)) $, $ x + 1 $ ja $ 14 + 4 ((x) ^ (2)) $ on järjestikused liikmed aritmeetilisest progressioonist (järjekorras).

Lahendus. Kuna näidatud numbrid on progresseerumise liikmed, on nende aritmeetilise keskmise tingimus täidetud: keskset elementi $ x + 1 $ saab väljendada külgnevate elementidega:

\ [\ algus (joondamine) & x + 1 = \ frac (-6 ((x) ^ (2)) + 14 + 4 ((x) ^ (2))) (2); \\ & x + 1 = \ frac (14-2 ((x) ^ (2))) (2); \\ & x + 1 = 7 - ((x) ^ (2)); \\ & ((x) ^ (2)) + x-6 = 0. \\ \ lõpp (joondamine) \]

Tulemuseks on klassikaline ruutvõrrand. Selle juured: $ x = 2 $ ja $ x = -3 $ - need on vastused.

Vastus: −3; 2.

Probleem number 7. Leidke väärtused $$, mille numbrid $ -1; 4-3; (() ^ (2)) + 1 $ teevad aritmeetilise progressiooni (selles järjekorras).

Lahendus. Jällegi väljendame keskmist terminit naaberterminite aritmeetilise keskmise järgi:

\ [\ begin (align) & 4x-3 = \ frac (x-1 + ((x) ^ (2)) + 1) (2); \\ & 4x-3 = \ frac ((((x) ^ (2)) + x) (2); \ quad \ left | \ cdot 2 \ õige.; \\ & 8x-6 = ((x) ^ (2)) + x; \\ & ((x) ^ (2)) - 7x + 6 = 0. \\ \ lõpp (joondamine) \]

Jälle ruutvõrrand. Ja jällegi on kaks juurt: $ x = 6 $ ja $ x = 1 $.

Vastus: 1; 6.

Kui probleemi lahendamise käigus saate mõne jõhkra numbri või te ei ole leitud vastuste õigsuses täiesti kindel, siis on olemas suurepärane tehnika, mis võimaldab teil kontrollida: kas me lahendasime probleemi õigesti?

Näiteks ülesandes nr 6 saime vastused -3 ja 2. Kuidas kontrollida, kas need vastused on õiged? Ühendame need lihtsalt vooluvõrku ja vaatame, mis juhtub. Tuletan meelde, et meil on kolm numbrit ($ -6 (() ^ (2)) $, $ + 1 $ ja $ 14 + 4 (() ^ (2)) $), mis peavad moodustama aritmeetilise progressiooni. Asendaja $ x = -3 $:

\ [\ algus (joondamine) & x = -3 \ paremnool \\ & -6 ((x) ^ (2)) = -54; \\ & x + 1 = -2; \\ & 14 + 4 ((x) ^ (2)) = 50. \ end (joondama) \]

Saadud numbrid -54; −2; 50, mis erinevad 52 võrra, on kahtlemata aritmeetiline progressioon. Sama juhtub $ x = 2 $ puhul:

\ [\ algus (joondamine) & x = 2 \ paremnool \\ & -6 ((x) ^ (2)) = - 24; \\ & x + 1 = 3; \\ & 14 + 4 ((x) ^ (2)) = 30. \ end (joondama) \]

Jällegi progressioon, kuid erinevusega 27. Seega on probleem õigesti lahendatud. Huvilised saavad teist probleemi iseseisvalt kontrollida, kuid ütlen kohe: ka seal on kõik õige.

Üldiselt puutusime viimaste probleemide lahendamisel kokku veel ühe huvitava fakti, mida tuleb samuti meeles pidada:

Kui kolm arvu on sellised, et teine on esimese ja viimase aritmeetiline keskmine, siis moodustavad need arvud aritmeetilise progressiooni.

Tulevikus võimaldab selle väite mõistmine meil sõna otseses mõttes "konstrueerida" vajalikke edusamme, lähtudes probleemi seisundist. Aga enne kui sellise "ehitamise" juurde asuda, peaksime tähelepanu pöörama veel ühele asjaolule, mis tuleneb otseselt juba käsitletust.

Elementide rühmitamine ja summa

Läheme jälle tagasi arvtelje juurde. Märgime seal mitmeid progressiooni liikmeid, mille vahel ehk. seal on palju teisi liikmeid:

Numbrireal on märgitud 6 elementi

Proovime väljendada "vasak saba" $ ((a) _ (n)) $ ja $ d $ ning "paremat saba" $ ((a) _ (k)) $ ja $ d $ . See on väga lihtne:

\ [\ algus (joondamine) & ((a) _ (n + 1)) = ((a) _ (n)) + d; \\ & ((a) _ (n + 2)) = ((a) _ (n)) + 2d; \\ & ((a) _ (k -1)) = ((a) _ (k)) - d; \\ & ((a) _ (k -2)) = ((a) _ (k)) - 2d. \\ \ lõpp (joondamine) \]

Pange nüüd tähele, et järgmised summad on võrdsed:

\ [\ algus (joondamine) & ((a) _ (n)) + ((a) _ (k)) = S; \\ & ((a) _ (n + 1)) + ((a) _ (k -1)) = ((a) _ (n)) + d + ((a) _ (k)) - d = S; \\ & ((a) _ (n + 2)) + ((a) _ (k -2)) = ((a) _ (n)) + 2d + ((a) _ (k)) - 2d = S. \ end (joondama) \]

Lihtsamalt öeldes, kui käsitleda algusena kaht progressiooni elementi, mis kokku on võrdsed mõne $ S $ numbriga, ja siis hakkame nendest elementidest vastassuunas liikuma (üksteise poole või vastupidi, et eemalduda) , siis ka nende elementide summad, millele me komistame, on võrdsed$ S $. Seda saab kõige selgemalt kujutada graafiliselt:

Võrdne taane annab võrdsed summad

Selle fakti mõistmine võimaldab meil lahendada põhimõtteliselt kõrgema keerukusega probleeme kui need, mida me eespool käsitlesime. Näiteks sellised:

Probleem number 8. Määrake aritmeetilise progressi erinevus, milles esimene liige on 66 ja teise ja kaheteistkümnenda termini korrutis on väikseim võimalik.

Lahendus. Paneme kirja kõik, mida teame:

\ [\ begin (align) & ((a) _ (1)) = 66; \\ & d =? \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ min. \ end (joondama) \]

Niisiis, me ei tea $ d $ progresseerumise erinevust. Tegelikult ehitatakse kogu lahendus erinevuse ümber, kuna toote $ ((a) _ (2)) \ cdot ((a) _ (12)) $ saab ümber kirjutada järgmiselt:

\ [\ begin (align) & ((a) _ (2)) = ((a) _ (1)) + d = 66 + d; \\ & (a) _ (12)) = ((a) _ (1)) + 11d = 66 + 11d; \\ & ((a) _ (2)) \ cdot ((a) _ (12)) = \ vasak (66 + d \ parem) \ cdot \ vasak (66 + 11 d \ parem) = \\ & = 11 \ cdot \ left (d + 66 \ right) \ cdot \ left (d + 6 \ right). \ end (joondama) \]

Paagis olijatele: võtsin teisest sulust välja ühise teguri 11. Seega on otsitav toode muutuja $ d $ suhtes ruutfunktsioon. Seetõttu kaaluge funktsiooni $ f \ left (d \ right) = 11 \ left (d + 66 \ right) \ left (d + 6 \ right) $ - selle graafik on parabool harudega üles, sest kui laiendame sulgusid, saame:

\ [\ algus (joondamine) & f \ vasak (d \ parem) = 11 \ vasak ((((d) ^) (2)) + 66d + 6d + 66 \ cdot 6 \ parem) = \\ & = 11 ((( d) ^ (2)) + 11 \ cdot 72d + 11 \ cdot 66 \ cdot 6 \ end (joondama) \]

Nagu näete, on juhttermini koefitsient 11 - see on positiivne arv, seega tegeleme tõepoolest parabooliga, millel on oksad üles:

ruutfunktsiooni graafik - parabool
Pange tähele: see parabool võtab oma tipus minimaalse väärtuse abstsissiga $ ((d) _ (0)) $. Muidugi saame selle abstsissi arvutada vastavalt standardsele skeemile (on ka valem $ ((d) _ (0)) = (- b) / (2a) \; $), kuid see oleks palju mõistlikum märgata, et soovitud tipp asub parabooli telje sümmeetrial, seega on punkt $ ((d) _ (0)) $ võrdsel kaugusel juurtest $ f \ left (d \ right) = 0 $:

\ [\ begin (align) & f \ left (d \ right) = 0; \\ & 11 \ cdot \ left (d + 66 \ right) \ cdot \ left (d + 6 \ right) = 0; \\ & ((d) _ (1)) = - 66; \ quad ((d) _ (2)) = - 6. \\ \ lõpp (joondamine) \]

Seetõttu ei kiirustanud ma sulgude avamisega: algsel kujul olid juured väga -väga kergesti leitavad. Seetõttu on abstsiss võrdne numbrite −66 ja −6 aritmeetilise keskmisega:

\ [((d) _ (0)) = \ frac (-66-6) (2) =-36 \]

Mida annab meile avastatud number? Sellega omandab nõutud toode väikseima väärtuse (muide, me pole arvestanud $ ((y) _ (\ min)) $ - me ei vaja seda). Samas on see arv esialgse progresseerumise vahe, s.t. leidsime vastuse. :)

Vastus: −36

Probleem number 9. Sisestage numbrite $ - \ frac (1) (2) $ ja $ - \ frac (1) (6) $ vahele kolm numbrit, nii et need koos antud arvudega moodustaksid aritmeetilise progressiooni.

Lahendus. Põhimõtteliselt peame tegema viiest numbrist koosneva jada, kus esimene ja viimane arv on juba teada. Tähistame puuduvaid numbreid muutujatega $ x $, $ y $ ja $ z $:

\ [\ vasak (((a) _ (n)) \ parem) = \ vasak \ ( - \ frac (1) (2); x; y; z; - \ frac (1) (6) \ parem \ ) \]

Pange tähele, et number $ y $ on meie jada "keskel" - see on võrdsel kaugusel nii arvudest $ x $ ja $ z $ kui ka numbritest $ - \ frac (1) (2) $ ja $ - \ frac (1) (6) $. Ja kui praegu ei saa me numbritelt $ x $ ja $ z $ $ y $, siis progressi lõppedes on olukord teine. Meenutades aritmeetilist keskmist:

Nüüd, teades $ y $, leiame ülejäänud numbrid. Pange tähele, et $ x $ asub äsja leitud numbrite $ - \ frac (1) (2) $ ja $ y = - \ frac (1) (3) $ vahel. Sellepärast

Sarnaselt arutledes leiame allesjäänud arvu:

Valmis! Leidsime kõik kolm numbrit. Kirjutame need vastusesse üles selles järjekorras, kuidas need algnumbrite vahele sisestada.

Vastus: $ - \ frac (5) (12); \ - \ frac (1) (3); \ - \ frac (1) (4) $

Probleem number 10. Sisestage numbrite 2 ja 42 vahele mitu numbrit, mis koos nende arvudega moodustavad aritmeetilise progressiooni, kui teate, et sisestatud numbrite esimese, teise ja viimase summa on 56.

Lahendus. Veelgi keerulisem ülesanne, mis aga lahendatakse sama skeemi järgi nagu eelmisedki - läbi aritmeetilise keskmise. Probleem on selles, et me ei tea täpselt, mitu numbrit sisestada. Seetõttu oletame täpsuse huvides, et pärast kõige sisestamist on täpselt $ n $ numbreid ja esimene neist on 2 ja viimane 42. Sel juhul saab soovitud aritmeetilise progressiooni esitada järgmiselt:

\ [\ vasak (((a) _ (n)) \ parem) = \ vasak \ (2; ((a) _ (2)); ((a) _ (3)); ...; (( a) _ (n-1)); 42 \ paremal \) \]

\ [((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56 \]

Pange aga tähele, et numbrid $ ((a) _ (2)) $ ja $ ((a) _ (n-1)) $ saadakse servadest numbrite 2 ja 42 ühe sammu võrra, st ... jada keskele. See tähendab, et

\ [((a) _ (2)) + ((a) _ (n-1)) = 2 + 42 = 44 \]

Kuid siis saab ülalkirjeldatud väljendi ümber kirjutada järgmiselt:

\ [\ algus (joondamine) & ((a) _ (2)) + ((a) _ (3)) + ((a) _ (n-1)) = 56; \\ & \ vasak (((a) _ (2)) + ((a) _ (n-1)) \ parem) + ((a) _ (3)) = 56; \\ & 44 + ((a) _ (3)) = 56; \\ & (a) _ (3)) = 56-44 = 12. \\ \ lõpp (joondamine) \]

Teades $ ((a) _ (3)) $ ja $ ((a) _ (1)) $, saame hõlpsalt leida progresseerumise erinevuse:

\ [\ algus (joondamine) & ((a) _ (3)) - ((a) _ (1)) = 12 - 2 = 10; \\ & ((a) _ (3)) - ((a) _ (1)) = \ vasak (3-1 \ parem) \ cdot d = 2d; \\ & 2d = 10 \ Paremnool d = 5. \\ \ lõpp (joondamine) \]

Jääb vaid ülejäänud liikmed üles leida:

\ [\ begin (align) & ((a) _ (1)) = 2; \\ & (a) _ (2)) = 2 + 5 = 7; \\ & (a) _ (3)) = 12; \\ & (a) _ (4)) = 2 + 3 \ cdot 5 = 17; \\ & (a) _ (5)) = 2 + 4 \ cdot 5 = 22; \\ & (a) _ (6)) = 2 + 5 \ cdot 5 = 27; \\ & (a) _ (7)) = 2 + 6 \ cdot 5 = 32; \\ & (a) _ (8)) = 2 + 7 \ cdot 5 = 37; \\ & ((a) _ (9)) = 2 + 8 \ cdot 5 = 42; \\ \ lõpp (joondamine) \]

Seega jõuame juba 9. sammul jada vasakusse otsa - arv 42. Kokku oli vaja sisestada ainult 7 numbrit: 7; 12; 17; 22; 27; 32; 37.

Vastus: 7; 12; 17; 22; 27; 32; 37

Sõnaprobleemid edusammudega

Kokkuvõtteks tahaksin kaaluda paari suhteliselt lihtsat ülesannet. Noh, kui lihtne: enamiku õpilaste jaoks, kes õpivad koolis matemaatikat ega ole lugenud eespool kirjutatut, võivad need ülesanded tunduda tina. Sellegipoolest satuvad OGE ja USE matemaatikasse just sellised probleemid, seega soovitan teil nendega tutvuda.

Probleem number 11. Brigaad tootis jaanuaris 62 osa ja igal järgmisel kuul toodeti 14 osa rohkem kui eelmisel. Mitu osa tegi meeskond novembris?

Lahendus. Ilmselt tähistab osade arv, mis on planeeritud kuude kaupa, üha suurenevat aritmeetilist progressi. Enamgi veel:

\ [\ begin (align) & ((a) _ (1)) = 62; \ quad d = 14; \\ & ((a) _ (n)) = 62+ \ vasak (n-1 \ parem) \ cdot 14. \\ \ lõpp (joondamine) \]

November on aasta 11. kuu, seega peame leidma $ ((a) _ (11)) $:

\ [((a) _ (11)) = 62 + 10 \ cdot 14 = 202 \]

Sellest tulenevalt valmistatakse novembris 202 detaili.

Probleem number 12. Raamatuköitmistöökoda köitis jaanuaris 216 raamatut ja igal järgmisel kuul köitis see 4 raamatut rohkem kui eelmine. Mitu raamatut köitis töötuba detsembris?

Lahendus. Kõik on sama:

$ \ begin (align) & (a) _ (1)) = 216; \ quad d = 4; \\ & ((a) _ (n)) = 216+ \ vasak (n-1 \ parem) \ cdot 4. \\ \ lõpp (joondamine) $

Detsember on aasta viimane, 12. kuu, seega otsime $ ((a) _ (12)) $:

\ [((a) _ (12)) = 216 + 11 \ cdot 4 = 260 \]

See on vastus - detsembris köidetakse 260 raamatut.

Noh, kui olete nii kaugele lugenud, kiirustan teid õnnitlema: olete edukalt läbinud "noorte võitlejate kursuse" aritmeetilistes edusammudes. Võite turvaliselt jätkata järgmise õppetunniga, kus uurime progresseerumise summa valemit, samuti selle olulisi ja väga kasulikke tagajärgi.

Näiteks jada \ (2 \); \ (5 \); \ (kaheksa \); \ (üksteist \); \ (14 \) ... on aritmeetiline progressioon, sest iga järgmine element erineb eelmisest kolme võrra (eelmisest saab kolmiku lisamise teel):

Selles progressioonis on erinevus \ (d \) positiivne (võrdne \ (3 \)) ja seetõttu on iga järgmine termin suurem kui eelmine. Selliseid edusamme nimetatakse suureneb.

Kuid \ (d \) võib olla ka negatiivne. Näiteks, aritmeetilises progressioonis \ (16 \); $kümme$; \ (4 \); \ (- 2 \); \ (- 8 \) ... progressiooni erinevus \ (d \) on võrdne miinus kuuega.

Ja sel juhul on iga järgmine element väiksem kui eelmine. Neid edusamme nimetatakse vähenemas.

Aritmeetiline progressiooni märge

Edenemist näitab väike ladina täht.

Progressiooni moodustavad numbrid nimetavad seda liikmed(või elemendid).

Neid tähistatakse sama tähega kui aritmeetiline progress, kuid numbrilise indeksiga, mis on võrdne elemendi arvuga järjekorras.

Näiteks aritmeetiline progress \ (a_n = \ left \ (2; 5; 8; 11; 14 ... \ right \) \) koosneb elementidest \ (a_1 = 2 \); \ (a_2 = 5 \); \ (a_3 = 8 \) ja nii edasi.

Teisisõnu, progressiooni jaoks \ (a_n = \ left \ (2; 5; 8; 11; 14 ... \ right \) \)

Ülesannete lahendamine aritmeetiliseks progressiooniks

Põhimõtteliselt piisab ülaltoodud teabest peaaegu iga aritmeetilise progresseerumise probleemi lahendamiseks (sealhulgas OGE -s pakutavate probleemide lahendamiseks).

Näide (OGE). Aritmeetilist progressi määravad tingimused \ (b_1 = 7; d = 4 \). Otsige üles \ (b_5 \).
Lahendus:

Vastus: \ (b_5 = 23 \)

Näide (OGE). Aritmeetilise progressiooni kolm esimest mõistet on antud: \ (62; 49; 36 ... \) Leidke selle progressiooni esimese negatiivse termini väärtus.
Lahendus:

	Meile on antud jada esimesed elemendid ja me teame, et see on aritmeetiline progressioon. See tähendab, et iga element erineb naaberüksusest sama arvu võrra. Uurige, millist, lahutades järgmisest elemendist eelmise: \ (d = 49-62 = -13 \).
	Nüüd saame taastada oma progressiooni vajaliku (esimese negatiivse) elemendi juurde.
	Valmis. Võite vastuse kirjutada.

Vastus: $-3$

Näide (OGE). Esitatakse mitu järjestikust aritmeetilise progressiooni elementi: \ (… 5; x; 10; 12,5 ... \) Leidke tähega \ (x \) tähistatud elemendi väärtus.
Lahendus:

	Et leida \ (x \), peame teadma, kui palju järgmine element erineb eelmisest, teisisõnu progresseerumise erinevus. Leiame selle kahest teadaolevast naaberelemendist: \ (d = 12,5-10 = 2,5 \).
	Ja nüüd leiame soovitud ilma probleemideta: \ (x = 5 + 2,5 = 7,5 \).
	Valmis. Võite vastuse kirjutada.

Vastus: $7,5$.

Näide (OGE). Aritmeetilist progressi määravad järgmised tingimused: \ (a_1 = -11 \); \ (a_ (n + 1) = a_n + 5 \) Leidke selle progressiooni esimese kuue liikme summa.
Lahendus:

Peame leidma progressiooni kuue esimese astme summa. Kuid me ei tea nende tähendusi, meile antakse ainult esimene element. Seetõttu arvutame kõigepealt väärtused kordamööda, kasutades meile antud:

\ (n = 1 \); \ (a_ (1 + 1) = a_1 + 5 = -11 + 5 = -6 \)
\ (n = 2 \); \ (a_ (2 + 1) = a_2 + 5 = -6 + 5 = -1 \)
\ (n = 3 \); \ (a_ (3 + 1) = a_3 + 5 = -1 + 5 = 4 \)
Ja olles välja arvutanud kuus vajaminevat elementi, leiame nende summa.

\ (S_6 = a_1 + a_2 + a_3 + a_4 + a_5 + a_6 = \)
$=(-11)+(-6)+(-1)+4+9+14=9$

Otsitav summa on leitud.

Vastus: \ (S_6 = 9 \).

Näide (OGE). Aritmeetilises progressioonis \ (a_ (12) = 23 \); \ (a_ (16) = 51 \). Leidke erinevus selle progresseerumise vahel.
Lahendus:

Vastus: \ (d = 7 \).

Olulised aritmeetilise progressi valemid

Nagu näete, saab paljusid aritmeetilisi progresseerumisülesandeid lahendada lihtsalt aru saades põhiasjast - et aritmeetiline progressioon on numbrite ahel ja selle ahela iga järgmine element saadakse samale numbrile eelmisele lisades (erinevus progresseerumisest).

Kuid mõnikord on olukordi, kus on "ebamugav" otsustada. Kujutage näiteks ette, et kõige esimeses näites peame leidma mitte viienda elemendi \ (b_5 \), vaid kolmsada kaheksakümne kuuenda \ (b_ (386) \). Mis see on, lisame (385) korda neli? Või kujutage ette, et eelviimases näites peate leidma esimese seitsmekümne kolme elemendi summa. Teid piinatakse loendama ...

Seetõttu ei lahenda nad sellistel juhtudel "peaga", vaid kasutavad aritmeetiliseks progressiooniks tuletatud spetsiaalseid valemeid. Ja peamised neist on progresseerumise n -nda termini valem ja esimeste liikmete summa \ (n \) valem.

Valem \ (n \) - kolmas liige: \ (a_n = a_1 + (n -1) d \), kus \ (a_1 \) on progresseerumise esimene liige;
\ (n \) - otsitava elemendi number;
\ (a_n \) on progressiooni liige numbriga \ (n \).

See valem võimaldab meil kiiresti leida vähemalt kolmesaja, isegi miljoni elemendi, teades ainult esimest ja progressiooni erinevust.

Näide. Aritmeetilist progressi määravad tingimused: \ (b_1 = -159 \); \ (d = 8,2 \). Leidke \ (b_ (246) \).
Lahendus:

Vastus: \ (b_ (246) = 1850).

Esimese n termini summa valem: \ (S_n = \ frac (a_1 + a_n) (2) \ cdot n \), kus

\ (a_n \) - viimane summeeritud termin;

Näide (OGE). Aritmeetilist progressi määravad tingimused \ (a_n = 3,4n-0,6 \). Leidke selle progressiooni esimeste \ (25 \) liikmete summa.
Lahendus:

\ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot 25 \)		Esimese kahekümne viie elemendi summa arvutamiseks peame teadma esimese ja kahekümne viienda termini väärtust. Meie edenemise annab n -nda liikme valem sõltuvalt selle arvust (vt üksikasju). Arvutame esimese elemendi, asendades ühe elemendiga \ (n \).
\ (n = 1; \) \ (a_1 = 3,4 1-0,6 = 2,8 \)		Nüüd leiame kahekümne viienda termini, asendades \ (n \) asemel kakskümmend viis.
\ (n = 25; \) \ (a_ (25) = 3,4 25-0,6 = 84,4 \)		Noh, nüüd saame vajaliku summa ilma probleemideta välja arvutada.
\ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot 25 = \) \ (= \) \ (\ frac (2,8 + 84,4) (2) \) \ (\ cdot 25 = \) \ (1090 \)		Vastus on valmis.

Vastus: \ (S_ (25) = 1090 \).

Esimeste terminite summa \ (n \) eest saate teise valemi: peate lihtsalt \ (S_ (25) = \) \ (\ frac (a_1 + a_ (25)) (2) \) \ (\ cdot 25 \) asemel \ (a_n \) asendage selle valem \ (a_n = a_1 + (n-1) d \). Saame:

Esimese n termini summa valem: \ (S_n = \) \ (\ frac (2a_1 + (n-1) d) (2) \) \ (\ cdot n \), kus

\ (S_n \) - esimeste elementide nõutav summa \ (n \);
\ (a_1 \) - esimene summeeritud termin;
\ (d \) - progressiooni erinevus;
\ (n \) - objektide arv summas.

Näide. Leidke aritmeetilise progressiooni esimeste \ (33 \) - endiste liikmete summa: \ (17 \); \ (15,5 \); \ (neliteist \)…
Lahendus:

Vastus: \ (S_ (33) = - 231 \).

Keerulisemad aritmeetilised progressiooniprobleemid

Nüüd on teil kogu teave, mida vajate peaaegu iga aritmeetilise progresseerumise probleemi lahendamiseks. Lõpetame teema, kaaludes probleeme, mille puhul peate mitte ainult valemeid rakendama, vaid ka natuke mõtlema (matemaatikas võib see olla kasulik).

Näide (OGE). Leidke progresseerumise kõigi negatiivsete tingimuste summa: \ (- 19,3 \); \ (-19 \); \ (- 18,7 \) ...
Lahendus:

\ (S_n = \) \ (\ frac (2a_1 + (n-1) d) (2) \) \ (\ cdot n \)		Ülesanne on eelmisega väga sarnane. Hakkame lahendama ka: kõigepealt leiame \ (d \).
\ (d = a_2 -a_1 = -19 - ( - 19,3) = 0,3 \)		Nüüd asendaksin summa valemis \ (d \) ... ja siin ilmneb väike nüanss - me ei tea \ (n \). Teisisõnu, me ei tea, kui palju termineid tuleb lisada. Kuidas teada saada? Mõtleme. Me lõpetame elementide lisamise, kui jõuame esimese positiivse elemendini. See tähendab, et peate välja selgitama selle elemendi numbri. Kuidas? Paneme kirja aritmeetilise progressiooni mis tahes elemendi arvutamise valemi: \ (a_n = a_1 + (n-1) d \) meie juhtumi puhul.
\ (a_n = a_1 + (n-1) d \)
\ (a_n = -19,3 + (n -1) 0,3 \)		Peame, et \ (a_n \) oleks suurem kui null. Uurime, mis \ (n \) see juhtub.
\ (- 19,3+ (n-1) 0,3> 0 \)
\ ((n-1) 0,3> 19,3 \) \ (\|: 0,3 \)		Jagame mõlemad ebavõrdsuse pooled \ (0,3 \) -ga.
\ (n-1> \) \ (\ frac (19,3) (0,3) \)		Liigutage miinus üks, pidage meeles märkide muutmist
\ (n> \) \ (\ frac (19,3) (0,3) \) \ (+ 1 \)		Me arvutame ...
\ (n> 65 333 ... \)		... ja selgub, et esimesel positiivsel elemendil on number \ (66 \). Vastavalt sellele on viimasel negatiivil \ (n = 65 \). Vaatame igaks juhuks üle.
\ (n = 65; \) \ (a_ (65) = -19,3+ (65-1) 0,3 = -0,1 \) \ (n = 66; \) \ (a_ (66) = - 19,3+ (66-1) 0,3 = 0,2 \)		Seega peame lisama esimesed \ (65 \) elemendid.
\ (S_ (65) = \) \ (\ frac (2 \ cdot (-19,3) + (65-1) 0,3) (2) \)\ (\ cdot 65 \) \ (S_ (65) = \) \ (( - 38,6 + 19,2) (2) \) \ (\ cdot 65 = -630,5 \)		Vastus on valmis.

Vastus: \ (S_ (65) = - 630,5 \).

Näide (OGE). Aritmeetilist progressi määravad tingimused: \ (a_1 = -33 \); \ (a_ (n + 1) = a_n + 4 \). Leidke summa elemendist \ (26 \) kuni \ (42 \) (kaasa arvatud).
Lahendus:

\ (a_1 = -33; \) \ (a_ (n + 1) = a_n + 4 \)	Selle ülesande puhul peate leidma ka elementide summa, kuid alustades mitte esimesest, vaid \ (26 \) - th. Sellisel juhul pole meil valemit. Kuidas otsustada? Lihtne - saada summa vahemikust \ (26 \) - th kuni \ (42 \) - oh, kõigepealt peate leidma summa vahemikus \ (1 \) - th kuni \ (42 \) - oh ja seejärel lahutama summa sellest kõigepealt kuni \ (25 \) - th (vt pilti).
	Meie edenemise jaoks \ (a_1 = -33 \) ja erinevus \ (d = 4 \) (lõppude lõpuks on see neli, mille lisame eelmisele elemendile järgmise leidmiseks). Seda teades leiame esimeste \ (42 \) - yh elementide summa.
\ (S_ (42) = \) \ (\ frac (2 \ cdot (-33) + (42-1) 4) (2) \)\ (\ cdot 42 = \) \ (= \) \ (\ frac (-66 + 164) (2) \) \ (\ cdot 42 = 2058 \)	Nüüd esimese \ (25 \) - elemendi summa.
\ (S_ (25) = \) \ (\ frac (2 \ cdot (-33) + (25-1) 4) (2) \)\ (\ cdot 25 = \) \ (= \) \ (\ frac (-66 + 96) (2) \) \ (\ cdot 25 = 375 \)	Lõpuks arvutame vastuse.
\ (S = S_ (42) -S_ (25) = 2058-375 = 1683 \)

Vastus: \ (S = 1683).

Aritmeetilise progressi jaoks on veel mitu valemit, mida me selles artiklis nende väikese praktilise kasulikkuse tõttu ei kaalunud. Siiski saate neid hõlpsalt leida.

Keegi on ettevaatlik sõna "progressioon" suhtes, mis on väga keeruline termin kõrgema matemaatika harudest. Vahepeal on lihtsaim aritmeetiline progresseerumine taksomeetri töö (kuhu need endiselt jäävad). Ja mõista aritmeetilise jada olemust (ja matemaatikas pole midagi tähtsamat kui "olemuse mõistmine") pole nii keeruline, olles analüüsinud mitmeid elementaarseid mõisteid.

Matemaatiline numbrijada

Numbrite seeriat on tavaks nimetada numbrilise jada järgi, millest igaühel on oma number.

a 1 - jada esimene liige;

ja 2 on jada teine liige;

ja 7 on jada seitsmes liige;

ja n on jada n -nda liige;

Meid ei huvita aga ükski meelevaldne numbrite ja numbrite kogum. Keskendume oma tähelepanu numbrilisele järjestusele, milles n -nda termini väärtus on seotud selle järgarvuga sõltuvusega, mida saab matemaatiliselt selgelt sõnastada. Teisisõnu: n-nda arvu arvväärtus on n funktsioon.

a - numbrilise jada liikme väärtus;

n on selle seerianumber;

f (n) on funktsioon, mille numbrilise jada järgarv on argument.

Määratlus

Aritmeetilist progressiooni on tavaks nimetada numbriliseks jadaks, milles iga järgnev liige on sama numbriga eelmine suurem (väiksem). Aritmeetilise jada n -nda liikme valem on järgmine:

a n - aritmeetilise progressiooni praeguse liikme väärtus;

a n + 1 - järgmise numbri valem;

d - erinevus (teatud arv).

On lihtne kindlaks teha, et kui erinevus on positiivne (d> 0), siis on vaadeldava seeria iga järgnev termin suurem kui eelmine ja selline aritmeetiline progress suureneb.

Alloleval graafikul on lihtne mõista, miks numbrijada nimetatakse kasvavaks.

Juhul kui erinevus on negatiivne (d<0), каждый последующий член по понятным причинам будет меньше предыдущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убывающей.

Määratud liikme väärtus

Mõnikord on vaja määrata aritmeetilise progresseerumise suvalise liikme a väärtus n. Seda saate teha, arvutades järjestikku kõigi aritmeetilise progressiooni liikmete väärtused, alustades esimesest kuni soovitud. See tee pole aga alati vastuvõetav, kui näiteks on vaja leida viie tuhande või kaheksa miljoni liikme tähendus. Traditsiooniline arvutamine võtab kaua aega. Siiski saab spetsiifilist aritmeetilist progressi uurida konkreetsete valemite abil. Ka n -nda termini jaoks on olemas valem: aritmeetilise progresseerumise mis tahes liikme väärtust saab määratleda kui progresseerumise esimese liikme summat progressiooni erinevusega, korrutatuna otsitava termini arvuga, vähendades üks.

Valem on universaalne nii progresseerumise suurendamiseks kui ka vähendamiseks.

Näide antud liikme väärtuse arvutamiseks

Lahendame järgmise probleemi aritmeetilise progressiooni n -nda termini väärtuse leidmisel.

Seisukord: toimub aritmeetiline progressioon parameetritega:

Järjestuse esimene termin on 3;

Numbriseeria erinevus on 1,2.

Ülesanne: peate leidma 214 liikme väärtuse

Lahendus: antud termini väärtuse määramiseks kasutame valemit:

a (n) = a1 + d (n-1)

Asendades probleemlause andmed avaldisse, on meil järgmine:

a (214) = a1 + d (n-1)

a (214) = 3 + 1,2 (214-1) = 258,6

Vastus: 214. liige järjestuses on 258,6.

Selle arvutusmeetodi eelised on ilmsed - kogu lahendus võtab mitte rohkem kui 2 rida.

Teatud liikmete arvu summa

Väga sageli on antud aritmeetilises reas vaja kindlaks määrata selle teatud segmendi väärtuste summa. See ei nõua ka iga termini väärtuste arvutamist ja seejärel summeerimist. Seda meetodit saab kasutada, kui leiduvate terminite arv on väike. Muudel juhtudel on mugavam kasutada järgmist valemit.

Aritmeetilise progressi liikmete summa 1 -st n -ni on võrdne esimese ja n -nda liikme summaga, korrutatuna liikme n arvuga ja jagatuna kahega. Kui valemis asendatakse n -nda termini väärtus artikli eelmise lõigu avaldisega, saame:

Arvutamise näide

Näiteks lahendame probleemi järgmistel tingimustel.

Jada esimene liige on null;

Erinevus on 0,5.

Ülesandes peate määrama sarja liikmete summa vahemikus 56. kuni 101.

Lahendus. Progressiooni summa määramiseks kasutame valemit:

s (n) = (2 ∙ a1 + d ∙ (n-1)) ∙ n / 2

Esiteks määrame progresseerumise 101 liikme väärtuste summa, asendades andmed meie probleemi tingimuste kohta valemiga:

s 101 = (2 ∙ 0 + 0,5 ∙ (101-1)) ∙ 101/2 = 2525

Ilmselgelt on 56. kohalt 101. liikumise liikmete summa väljaselgitamiseks vaja S 101 -st lahutada S 55.

s 55 = (2 ∙ 0 + 0,5 ∙ (55-1)) ∙ 55/2 = 742,5

Seega selle näite aritmeetilise progressi summa:

s 101 - s 55 = 2525 - 742,5 = 1782,5

Näide aritmeetilise progressiooni praktilisest rakendamisest

Artikli lõpus pöördume tagasi esimeses lõigus toodud aritmeetilise järjestuse näite juurde - taksomeeter (taksosõiduki arvesti). Vaatleme näidet.

Taksosse istumine (mis sisaldab 3 km jooksu) maksab 50 rubla. Iga järgneva kilomeetri eest makstakse 22 rubla / km. Reisi kaugus 30 km. Arvutage reisi maksumus.

1. Loobume esimesed 3 km, mille hind on maandumishinna sees.

30 - 3 = 27 km.

2. Edasine arvutamine pole midagi muud kui aritmeetilise numbriseeria analüüs.

Liikme number - läbitud kilomeetrite arv (miinus kolm esimest).

Liikme väärtus on summa.

Selle ülesande esimene termin on võrdne 1 = 50 p.

Progressiooni erinevus d = 22 p.

meid huvitav arv on aritmeetilise progressi (27 + 1) -nenda termini väärtus - loenduri näit 27. kilomeetri lõpus on 27,999… = 28 km.

a 28 = 50 + 22 ∙ (28 - 1) = 644

Meelevaldselt pika ajavahemiku kalendriandmete arvutused põhinevad teatud arvujärke kirjeldavatel valemitel. Astronoomias sõltub orbiidi pikkus geomeetriliselt taevakeha kaugusest valgusti. Lisaks kasutatakse statistikas ja muudes matemaatika harudes edukalt erinevaid numbrilisi seeriaid.

Teine numbrijada tüüp on geomeetriline

Geomeetrilist progresseerumist iseloomustavad suured muutumiskiirused võrreldes aritmeetikaga. Pole juhus, et poliitikas, sotsioloogias, meditsiinis ütlevad nad sageli, et protsess areneb plahvatuslikult, et näidata nähtuse, näiteks haiguse epideemia ajal suurt levimiskiirust.

Geomeetrilise numbrilise rea N -i liige erineb eelmisest selle poolest, et see korrutatakse mõne konstantse arvuga - nimetaja, näiteks esimene liige on 1, nimetaja vastavalt 2, siis:

n = 1: 1 ∙ 2 = 2

n = 2: 2 ∙ 2 = 4

n = 3: 4 ∙ 2 = 8

n = 4: 8 ∙ 2 = 16

n = 5: 16 ∙ 2 = 32,

b n - geomeetrilise progressiooni praeguse liikme väärtus;

b n + 1 - geomeetrilise progressiooni järgmise termini valem;

q on geomeetrilise progressiooni nimetaja (konstantarv).

Kui aritmeetilise progressi graafik on sirgjooneline, siis geomeetriline joonistab veidi teistsuguse pildi:

Nagu aritmeetika puhul, on ka geomeetrilisel progressioonil suvalise termini väärtuse valem. Mis tahes geomeetrilise progresseerumise n-ndik liige on võrdne esimese astme korrutisega n-astmeks kulgemise nimetaja võrra, vähendatud ühega:

Näide. Meil on geomeetriline progressioon, kus esimene liige on 3 ja progressiooni nimetaja on 1,5. Leidke progresseerumise viies liige

b 5 = b 1 ∙ q (5-1) = 3 ∙ 1,5 4 = 15,1875

Teatud arvu liikmete summa arvutatakse samal viisil spetsiaalse valemi abil. Geomeetrilise progresseerumise esimese n -tähe summa on võrdne progresseerumise n -nda termini ja selle nimetaja ning progressiooni esimese liikme korrutise vahega, jagatuna nimetajaga, mis on vähendatud ühega: