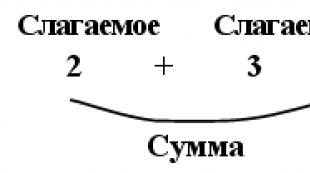
Examples of credible and impossible events. Come up with two reliable, random and impossible events yourself. Some information from combinatorics
An event is the result of a test. What is an event? One ball is taken at random from the urn. Removing the ball from the urn is a test. The appearance of a ball of a certain color is an event. In the theory of probability, an event is understood as something about which, after a certain moment in time, one and only one of two things can be said. Yes, it happened. No, it didn't happen. The possible outcome of an experiment is called an elementary event, and many such outcomes are simply called an event.

Unpredictable events are called random events. An event is called random if, under the same conditions, it may or may not happen. When the die is rolled, a six will be dropped. I have a lottery ticket. After the results of the lottery draw are published, the event of interest to me - winning a thousand rubles, either happens or does not happen. Example.

Two events that can occur simultaneously under these conditions are called joint, and those that cannot occur simultaneously are called incompatible. A coin is thrown. The appearance of the "coat of arms" excludes the appearance of the inscription. The events “a coat of arms appeared” and “an inscription appeared” are incompatible. Example.

An event that always happens is called credible. An event that cannot happen is called impossible. For example, let a ball be taken out of an urn containing only black balls. Then the appearance of the black ball is a certain event; the appearance of a white ball is an impossible event. Examples. Snow will not fall next year. When the die is rolled, a seven will be dropped. These are impossible events. Snow will fall next year. On the roll of the die, a number less than seven will be rolled. Sunrise every day. These are reliable events.

Problem solving For each of the described events, determine what it is: impossible, certain or accidental. 1. Out of 25 students in the class, two celebrate their birthday a) January 30; b) February 30. 2. A literature textbook opens at random and the second word is found on the left page. This word begins: a) with the letter "K"; b) with the letter "b".

3. Today in Sochi the barometer shows normal atmospheric pressure. In this case: a) the water in the saucepan boiled at a temperature of 80 ° C; b) when the temperature dropped to -5 ° C, the water in the puddle froze. 4. Throw two dice: a) the first dice has 3 points, and the second - 5 points; b) the sum of the points dropped on two dice is equal to 1; c) the sum of the points dropped on two dice is 13; d) 3 points were scored on both bones; e) the sum of points on two dice is less than 15. Solving problems

5. You have opened a book on any page and read the first noun that comes across. It turned out that: a) there is a vowel in the spelling of the selected word; b) the spelling of the selected word contains the letter "O"; c) there are no vowels in the spelling of the selected word; d) there is a soft sign in the spelling of the selected word. Solving problems

Probability theory, like any branch of mathematics, operates with a certain range of concepts. Most concepts of the theory of probability are given a definition, but some are taken as primary, not defined, as in geometry a point, a straight line, a plane. The primary concept of the theory of probability is an event. An event is understood as something about which, after a certain moment in time, one and only one of two things can be said:
- · Yes, it happened.
- · No, it did not happen.
For example, I have a lottery ticket. After the results of the lottery draw are published, the event that interests me is that the winning of a thousand rubles either happens or does not happen. Any event occurs as a result of a test (or experience). Test (or experience) refers to the conditions that result in an event. For example, tossing a coin is a test, and the appearance of a "coat of arms" on it is an event. The event is usually designated by capital Latin letters: A, B, C,…. Events in the material world can be divided into three categories - reliable, impossible and accidental.
A credible event is an event that is known in advance to occur. It is denoted by the letter W. So, it is reliable to get no more than six points when throwing an ordinary dice, the appearance of a white ball when removed from an urn containing only white balls, etc.
An impossible event is an event that is known in advance that it will not happen. It is denoted by the letter E. Examples of impossible events are the removal of more than four aces from a regular deck of cards, the appearance of a red ball from an urn containing only white and black balls, etc.
A random event is an event that may or may not occur as a result of a test. Events A and B are called incompatible if the onset of one of them excludes the possibility of the onset of the other. So the appearance of any possible number of points when throwing a dice (event A) is incompatible with the appearance of a different number (event B). An even number of points is inconsistent with an odd number. On the contrary, the loss of even points (event A) and the number of points that is a multiple of three (event B) will not be inconsistent, because the loss of six points means the occurrence of both events A and events B, so that the occurrence of one of them does not exclude the occurrence of the other. You can perform operations with events. The union of two events C = AUB is an event C that occurs if and only if at least one of these events A and B occurs. The intersection of two events D = A ?? B is called an event that occurs if and only when events of both A and B.
The events (phenomena) we observe can be divided into the following three types: reliable, impossible and random.
Credible is called an event that will necessarily occur if a certain set of conditions S is implemented. For example, if a vessel contains water at normal atmospheric pressure and a temperature of 20 °, then the event “water in the vessel is in a liquid state” is reliable. In this example, the set atmospheric pressure and water temperature are the set of conditions S.
Impossible is called an event that will not happen if the set of conditions S is fulfilled. For example, the event "water in the vessel is in a solid state" will certainly not happen if the set of conditions of the previous example is fulfilled.
Random is an event that, when a set of conditions S is fulfilled, can either happen or not. For example, if a coin is thrown, then it can fall so that there will be either a coat of arms or an inscription on top. Therefore, the event “when the coin was thrown, the“ coat of arms ”fell out - random. Each random event, in particular the fall of the "coat of arms", is a consequence of the action of very many random causes (in our example: the force with which the coin is thrown, the shape of the coin, and many others). It is impossible to take into account the influence on the result of all these reasons, since their number is very large and the laws of their action are unknown. Therefore, probability theory does not set itself the task of predicting whether a single event will occur or not - it simply cannot do it.
The situation is different if random events are considered that can be observed many times under the same conditions S, that is, if we are talking about mass homogeneous random events. It turns out that a sufficiently large number of homogeneous random events, regardless of their specific nature, obeys certain laws, namely, probabilistic laws. The establishment of these regularities is dealt with by the theory of probability.
Thus, the subject of probability theory is the study of the probabilistic laws of mass homogeneous random events.
The methods of probability theory are widely used in various branches of natural science and technology. Probability theory also serves to substantiate mathematical and applied statistics.
Types of random events... Events are called inconsistent if the occurrence of one of them excludes the occurrence of other events in the same trial.
Example. A coin is thrown. The appearance of the "coat of arms" excludes the appearance of the inscription. The events “a coat of arms appeared” and “an inscription appeared” are incompatible.
Several events form full group if at least one of them appears as a result of the test. In particular, if the events that form a complete group are pairwise inconsistent, then one and only one of these events will appear as a result of the test. This particular case is of the greatest interest to us, since it is used below.
Example 2. Two cash lottery tickets are purchased. One and only one of the following events will surely happen: "the winnings fell on the first ticket and did not fall on the second", "the winnings did not fall on the first ticket and fell on the second", "the winnings fell on both tickets", "on both tickets, the winnings did not dropped out. " These events form a complete group of pairwise incompatible events.
Example 3. The shooter fired a shot at the target. One of the following two events will surely happen: hit, miss. These two incompatible events form a complete group.
Events are called equally possible if there is reason to believe that none of them is more possible than the other.
Example 4. The appearance of the "coat of arms" and the appearance of an inscription when a coin is tossed are equally possible events. Indeed, it is assumed that the coin is made of a homogeneous material, has a regular cylindrical shape, and the presence of minting does not affect the fallout of one or another side of the coin.
Own is denoted by capital letters of the Latin alphabet: A, B, C, .. A 1, A 2 ..
The only two possible entities that form a complete group are called opposite. If one of the two opposites. events are denoted by A, then others are denoted by A '.
Example 5. Hitting and missing when firing at a target - opposite field. so-i.
The purpose of the lesson:
- Introduce the concept of reliable, impossible and random events.
- To form knowledge and skills to determine the type of events.
- Develop: computational skill; Attention; the ability to analyze, reason, draw conclusions; group work skills.
During the classes
1) Organizational moment.
Interactive exercise: children must solve examples and decipher words, according to the results they are divided into groups (reliable, impossible and random) and determine the topic of the lesson.
1 card.
| 0,5 | 1,6 | 12,6 | 5,2 | 7,5 | 8 | 5,2 | 2,08 | 0,5 | 9,54 | 1,6 |
2 card
| 0,5 | 2,1 | 14,5 | 1,9 | 2,1 | 20,4 | 14 | 1,6 | 5,08 | 8,94 | 14 |
3 card
| 5 | 2,4 | 6,7 | 4,7 | 8,1 | 18 | 40 | 9,54 | 0,78 |
2) Updating the knowledge learned.
Clap game: even number - clap, odd - stand up.
Task: from a given series of numbers 42, 35, 8, 9, 7, 10, 543, 88, 56, 13, 31, 77, ... determine even and odd.
3) Learning a new topic.
You have cubes on your tables. Let's take a closer look at them. What do you see?
Where are dice used? How?
Group work.
Carrying out an experiment.
What predictions can you make when rolling the dice?
First prediction: one of the numbers 1,2,3,4,5 or 6 will be dropped.
An event that will necessarily occur in this experience is called reliable.
Second prediction: number 7 will be dropped.
Do you think the predicted event will come or not?
It's impossible!
An event that cannot occur in a given experience is called impossible.
Third prediction: number 1 will be dropped.
Will this event come?
An event that in a given experience may or may not occur is called random.
4) Consolidation of the studied material.
I. Determine the type of event
-It will snow red tomorrow.
Heavy snow tomorrow.
Tomorrow, even though it is July, it will snow.
Tomorrow, even though it is July, there will be no snow.
Tomorrow it will snow and there will be a blizzard.
II. Add a word to this sentence so that the event becomes impossible.
Kolya got an A in history.
Sasha did not complete a single task on the test.
Oksana Mikhailovna (history teacher) will explain the new topic.
III. Give examples of impossible, accidental and reliable events.
IV. Work according to the textbook (in groups).
Describe the events referred to in the tasks below as plausible, impossible, or random.
No. 959. Petya conceived a natural number. The event is as follows:
a) an even number is conceived;
b) an odd number is conceived;
c) a number is conceived that is neither even nor odd;
d) a number that is odd or even is conceived.
No. 960. You opened this tutorial on any page and chose the first noun that came across. The event is as follows:
a) there is a vowel in the spelling of the selected word;
b) there is a letter “o” in the spelling of the selected word;
c) there are no vowels in the spelling of the selected word;
d) there is a soft sign in the spelling of the selected word.
Solve No. 961, No. 964.
Discussion of the solved tasks.
5) Reflection.
1.What events did you meet in the lesson?
2. Indicate which of the following events is reliable, which is impossible and which is accidental:
a) there will be no summer vacations;
b) the sandwich will fall butter down;
c) the school year will end someday.
6) Homework:
Come up with two reliable, random and impossible events.
Draw a drawing to one of them.
Grade 5. Introduction to Probability (4 hours)
(development of 4 lessons on this topic)
Learning objectives : - introduce the definition of a random, reliable and impossible event;
Lead the first ideas about solving combinatorial problems: using a tree of options and using the rule of multiplication.
Educational purpose: development of the worldview of students.
Developing goal : development of spatial imagination, improvement of the skill of working with a ruler.
Credible, impossible and random events(2h.)
Combinatorial tasks (2h.)
Reliable, impossible and random events.
First lesson
Lesson equipment: dice, coin, backgammon.
Our life is largely made up of accidents. There is such a science "Theory of Probabilities". Using her language, many phenomena and situations can be described.
Even the primitive leader understood that a dozen hunters have a "probability" of hitting a bison with a spear more than one. Therefore, they hunted collectively then.
Such ancient generals as Alexander the Great or Dmitry Donskoy, preparing for battle, relied not only on the valor and skill of warriors, but also on chance.
Many people love mathematics for the eternal truths twice two are always four, the sum of even numbers is even, the area of a rectangle is equal to the product of its adjacent sides, etc. In any problem that you solve, everyone gets the same answer - you just need not make mistakes in the solution.
Real life is not so simple and straightforward. The outcomes of many phenomena cannot be predicted in advance. It is impossible, for example, to say for sure which side the coin tossed up will fall on, when the first snow falls next year, or how many people in the city will want to call in the next hour. Such unpredictable phenomena are called random .
However, the case also has its own laws, which begin to manifest themselves with repeated repetition of random phenomena. If you flip a coin 1000 times, then the "heads" will fall out about half of the time, which cannot be said about two or even ten tosses. "Approximately" does not mean half. This, as a rule, may or may not be so. The law does not state anything for certain at all, but gives a certain degree of certainty that some random event will occur. Such patterns are studied by a special section of mathematics - Probability theory . With its help, it is possible with a greater degree of confidence (but still not certain) to predict both the date of the first snowfall and the number of phone calls.
Probability theory is inextricably linked to our daily life. This gives us a wonderful opportunity to establish many probabilistic laws empirically, repeating random experiments many times. The materials for these experiments will most often be an ordinary coin, a dice, a set of dominoes, backgammon, roulette, or even a deck of cards. Each of these items is somehow related to games. The fact is that the case appears here in the most frequent form. And the first probabilistic problems were associated with assessing the chances of players to win.
Modern probability theory has moved away from gambling, but its props are still the simplest and most reliable source of chance. After practicing with the roulette wheel and the dice, you will learn how to calculate the probability of random events in real life situations, which will allow you to assess your chances of success, test hypotheses, and make optimal decisions not only in games and lotteries.
When solving probabilistic problems, be very careful, try to justify every step you take, for no other area of mathematics contains so many paradoxes. Like probability theory. And perhaps the main explanation for this is her connection with the real world in which we live.
Many games use a dice with a different number of dots on each face from 1 to 6. The player throws a dice, looks at how many dots have dropped out (on the face that is on top), and makes the corresponding number of moves: 1,2,3 , 4,5, or 6. Throwing a die can be considered an experience, experiment, test, and the result obtained is an event. People are usually very interested in guessing the onset of an event, predicting its outcome. What predictions can they make when they roll the dice? First prediction: one of the numbers 1, 2, 3, 4, 5 will drop out, or 6. Do you think the predicted event will come or not? Of course, it will definitely come. An event that will necessarily occur in this experience is called reliable event.
Second prediction : number 7 will drop out. Do you think the predicted event will come or not? Of course it won't, it's just impossible. An event that cannot occur in a given experience is called impossible event.
Third prediction : number 1 will drop out. What do you think, the predicted event will come or not? We are not in a position to answer this question with complete confidence, since the predicted event may or may not occur. An event that in a given experience may or may not occur is called a random event.
Exercise : Describe the events referred to in the tasks below. How reliable, impossible, or accidental.
We flip a coin. The coat of arms appeared. (random)
The hunter shot the wolf and hit it. (random)
The schoolboy goes for a walk every evening. While walking on Monday, he met three acquaintances. (random)
Let's mentally carry out the following experiment: turn the glass of water upside down. If this experiment is carried out not in space, but at home or in the classroom, then the water will pour out. (reliable)
Three shots were fired at the target. " There were five hits "(Impossible)
We throw the stone up. The stone remains suspended in the air. (impossible)
We rearrange the letters of the word "antagonism" at random. The word "anachroism" will turn out. (impossible)
№959. Petya conceived a natural number. The event is as follows:
a) an even number is conceived; (random) b) an odd number is conceived; (random)
c) a number is conceived that is neither even nor odd; (impossible)
d) a number that is odd or even is conceived. (reliable)
№ 961. Petya and Tolya compare their birthdays. The event is as follows:
a) their birthdays do not match; (random) b) their birthdays are the same; (random)
d) the birthdays of both fall on the holidays - New Year (January 1) and the Independence Day of Russia (June 12). (random)
№ 962. When playing backgammon, two dice are used. The number of moves that a participant in the game makes is determined by adding the numbers on the two dropped edges of the dice, and if a "double" falls out (1 + 1.2 + 2.3 + 3.4 + 4.5 + 5.6 + 6), then the number of moves is doubled. You roll the dice and figure out how many moves you have to make. The event is as follows:
a) you must make one move; b) you must make 7 moves;
c) you must make 24 moves; d) you must make 13 moves.
a) - impossible (1 move can be made if the combination 1 + 0 falls out, but there is no number 0 on the dice).
b) - random (if 1 + 6 or 2 + 5 falls out).
c) - random (if the combination is 6 +6).
d) - the impossible (there are no combinations of numbers from 1 to 6, the sum of which is 13; this number cannot be obtained even when the "double" appears, since it is odd).
Test yourself. (math dictation)
1) Indicate which of the following events are impossible, which are reliable, which are random:
The football match "Spartak" - "Dynamo" will end in a draw. (random)
You will win by participating in the win-win lottery (verified)
Snow will fall at midnight and the sun will shine in 24 hours. (impossible)
Tomorrow there will be a math test. (random)
You will be elected President of the United States. (impossible)
You will be elected President of Russia. (random)
2) You bought a TV set in a store, for which the manufacturer gives a two-year warranty. Which of the following events are impossible, which are random, which are reliable:
The TV won't break down for a year. (random)
The TV won't break down in two years. (random)
Within two years, you will not have to pay to repair your TV. (reliable)
The TV will break down in the third year. (random)
3) The bus, which carries 15 passengers, will have to make 10 stops. Which of the following events are impossible, which are random, which are reliable:
All passengers will get off the bus at different stops. (impossible)
All passengers will disembark at one stop. (random)
At every stop, at least someone will get out. (random)
There will be a stop where no one gets off. (random)
An even number of passengers will leave at all stops. (impossible)
An odd number of passengers will leave at all stops. (impossible)
Homework : p. 53 №960, 963, 965 (think of two reliable, random and impossible events yourself).
Second lesson.
Examination homework... (orally)
a) Explain what a certain, random and impossible event is.
b) Indicate which of the following events is reliable, which is impossible, which is accidental:
There will be no summer vacations. (impossible)
The sandwich will fall butter down. (random)
The school year will end someday. (reliable)
They'll ask me in class tomorrow. (random)
I will meet a black cat today. (random)
№ 960. You have opened this tutorial on any page and selected the first noun that comes across. The event is as follows:
a) there is a vowel in the spelling of the selected word. ((reliable)
b) there is a letter "o" in the spelling of the selected word. (random)
c) there are no vowels in the spelling of the selected word. (impossible)
d) there is a soft sign in the spelling of the selected word. (random)
№ 963. You are playing backgammon again. Describe the following event:
a) the player must make no more than two moves. (impossible - with the combination of the smallest numbers 1 + 1, the player makes 4 moves; the combination 1 + 2 gives 3 moves; all other combinations give more than 3 moves)
b) the player must make more than two moves. (reliable - any combination gives 3 or more moves)
c) the player must make no more than 24 moves. (reliable - the combination of the highest numbers 6 + 6 gives 24 moves, and all the rest - less than 24 moves)
d) the player must make a two-digit number of moves. (random - for example, the combination 2 + 3 gives a single-digit number of moves: 5, and the fall of two fours - a two-digit number of moves)
2. Solving problems.
№ 964. The bag contains 10 balls: 3 blue, 3 white and 4 red. Describe the following event:
a) 4 balls were taken out of the bag, and they are all blue; (impossible)
b) 4 balls were taken out of the bag, and they are all red; (random)
c) 4 balls were taken out of the bag, and they all turned out to be of a different color; (impossible)
d) 4 balls were taken out of the bag, and there was no black ball among them. (reliable)
Objective 1. The box contains 10 red, 1 green and 2 blue pens. Two items are taken out of the box at random. Which of the following events are impossible, which are random, which are reliable:
a) two red handles are taken out (random)
b) two green handles are taken out; (impossible)
c) two blue handles are taken out; (random)
d) handles of two different colors are taken out; (random)
e) two handles are removed; (reliable)
f) two pencils are taken out. (impossible)
Objective 2. Winnie the Pooh, Piglet and all - all - all sit down at the round table to celebrate their birthday. How many of all - all - of all the event “Winnie the Pooh and Piglet will be sitting next to each other” is reliable, and how many is it random?
(if all - all - all are only 1, then the event is reliable, if more than 1, then it is random).
Objective 3. Among the 100 charity lottery tickets, 20 are winning How many tickets do you need to buy to make the "you win nothing" event impossible?
Task 4. There are 10 boys and 20 girls in the class. Which of the following events are impossible for such a class, which are accidental, which are reliable
There are two people in the class who were born in different months. (random)
There are two people in the class who were born in the same month. (reliable)
There are two boys in the class who were born in the same month. (random)
There are two girls in the class who were born in the same month. (reliable)
All the boys were born in different months. (reliable)
All girls were born in different months. (random)
There is a boy and a girl born in the same month. (random)
There is a boy and a girl who were born in different months. (random)
Task 5. The box contains 3 red, 3 yellow, 3 green balls. We take out 4 balls at random. Consider the event “Among the balls taken out there will be balls of exactly M colors”. For each M from 1 to 4, determine which event is impossible, reliable or accidental, and fill in the table:
Independent work.
Ioption
a) your friend's birthday number is less than 32;
c) tomorrow there will be a test in mathematics;
d) Next year, the first snow in Moscow will fall on Sunday.
Throw the dice. Describe the event:
a) the cube, having fallen, will stand on the edge;
b) one of the numbers will be dropped: 1, 2, 3, 4, 5, 6;
c) the number 6 will be dropped;
d) a multiple of 7 will be dropped.
The box contains 3 red, 3 yellow and 3 green balls. Describe the event:
a) all removed balls of the same color;
b) all removed balls of different colors;
c) among the balls taken out there are balls of different colors;
c) among the balls taken out there is a red, yellow and green ball.
IIoption
Describe the event in question as certain, impossible or accidental:
a) a sandwich that has fallen off the table will fall butter down on the floor;
b) in Moscow at midnight it will snow, and in 24 hours the sun will shine;
c) you win by participating in the win-win lottery;
d) next year, in May, the first spring thunder will be heard.
All two-digit numbers are written on the cards. One card is chosen at random. Describe the event:
a) there was zero on the card;
b) the card has a number that is a multiple of 5;
c) the card has a number that is a multiple of 100;
d) the card has a number greater than 9 and less than 100.
The box contains 10 red, 1 green and 2 blue pens. Two items are taken out of the box at random. Describe the event:
a) two blue handles are taken out;
b) two red handles are taken out;
c) two green handles are taken out;
d) the green and black handles are taken out.
Homework: 1). Come up with two reliable, random and impossible events.
2). Task . The box contains 3 red, 3 yellow, 3 green balls. Take out N balls at random. Consider the event “among the balls taken out there will be balls of exactly three colors”. For each N from 1 to 9, determine which event is impossible, certain or accidental, and fill in the table:
Combinatorial problems.
First lesson
Homework check. (orally)
a) we check the problems that the students came up with.
b) an additional task.
I am reading an excerpt from V. Levshin's book "Three days in Dwarf".
“At first, to the sounds of a smooth waltz, the numbers formed a group: 1+ 3 + 4 + 2 = 10. Then the young skaters began to swap places, forming more and more new groups: 2 + 3 + 4 + 1 = 10
3 + 1 + 2 + 4 = 10
4 + 1 + 3 + 2 = 10
1 + 4 + 2 + 3 = 10, etc.
This continued until the skaters returned to their original position. "
How many times have they swapped places?
Today in the lesson we will learn how to solve such problems. They're called combinatorial.
3. Learning new material.
Objective 1. how many two-digit numbers can be made up of the numbers 1, 2, 3?
Solution: 11, 12, 13
31, 32, 33. There are 9 numbers in total.
When solving this problem, we carried out an enumeration of all possible options, or, as they usually say in these cases. All possible combinations. Therefore, such tasks are called combinatorial. You have to calculate possible (or impossible) options in life quite often, so it is useful to get acquainted with combinatorial problems.
№ 967. Several countries decided to use symbols for their national flag in the form of three horizontal stripes of the same width in different colors - white, blue, red. How many countries can use such symbols, provided that each country has its own flag?
Solution. Let's assume the first stripe is white. Then the second stripe can be blue or red, and the third stripe, respectively, red or blue. It turned out two options: white, blue, red or white, red, blue.
Now let the first stripe be blue, then again we get two options: white, red, blue or blue, red, white.
Let the first stripe be red, then there are two more options: red, white, blue or red, blue, white.
There are 6 possible options in total. This flag can be used by 6 countries.
So, in solving this problem, we were looking for a way to enumerate the possible options. In many cases, it turns out to be useful a technique for constructing a picture - an enumeration scheme. This is, firstly, clearly, Secondly, allows us to take everything into account, not to miss anything.
This scheme is also called the tree of possible options.


Front page
Second lane
Third lane
The resulting combination
№ 968. How many two-digit numbers can be made from the digits 1, 2, 4, 6, 8?
Solution. For the two-digit numbers of interest to us, any of the given digits can be in the first place, except 0. If we put the number 2 in the first place, then any of the given digits can be in the second place. There will be five two-digit numbers: 2., 22, 24, 26, 28. Similarly, there will be five two-digit numbers with the first digit 4, five two-digit numbers with the first digit 6, and five two-digit numbers with the first digit 8.
Answer: there will be 20 numbers in total.
Let's build a tree of possible options for solving this problem.
Double figures
First digit
Second digit
Received numbers

20, 22, 24, 26, 28, 60, 62, 64, 66, 68,
40, 42, 44, 46, 48, 80, 82, 84, 86, 88.
By building a tree of options, solve the following problems.
№ 971. The leadership of a country decided to make its state flag like this: a circle of a different color is placed on a one-color rectangular background in one of the corners. It was decided to choose from three colors: red, yellow, green. How many variants of such a flag
exists? The figure shows some of the possible options.




Answer: 24 options.
№ 973. a) How many three-digit numbers can be made from the digits 1,3, 5,? (27 numbers)
b) How many three-digit numbers can be made from the digits 1,3, 5, provided that the numbers should not be repeated? (6 numbers)
№ 979. Modern pentathletes for two days participate in competitions in five sports: show jumping, fencing, swimming, shooting, and running.
a) How many options are there for the order of the types of competition? (120 options)
b) How many options are there for the order of passing the types of competition, if it is known that the last type should be running? (24 options)
c) How many options are there for the order of passing the types of competition, if it is known that the last type should be running, and the first - show jumping? (6 options)
№ 981. Two urns contain five balls each in five different colors: white, blue, red, yellow, green. One ball is removed from each urn at the same time.
a) how many different combinations of balls taken out are there (combinations like "white - red" and "red - white" are considered the same)?
(15 combinations)
b) How many combinations are there in which the removed balls are of the same color?
(5 combinations)
c) how many combinations are there in which the removed balls are of different colors?
(15 - 5 = 10 combinations)
Homework: p. 54, no. 969, 972, to come up with a combinatorial problem ourselves.
№ 969. Several countries decided to use symbols for their national flag in the form of three vertical stripes of the same width in different colors: green, black, yellow. How many countries can use such symbols, provided that each country has its own flag?
№ 972. a) How many two-digit numbers can be made from the numbers 1, 3, 5, 7, 9?
b) How many two-digit numbers can be made from the numbers 1, 3, 5, 7, 9, provided that the numbers should not be repeated?
Second lesson
Homework check. a) No. 969 and No. 972a) and No. 972b) - build a tree of possible options on the board.
b) verbally check the compiled tasks.
Solving problems.
So, before that, you and I learned how to solve combinatorial problems using a tree of options. Is this a good way? Probably yes, but very cumbersome. Let's try to solve home problem no. 972 in a different way. Who can guess how this can be done?
Answer: for each of the five colors of the T-shirts, there are 4 colors of the panties. Total: 4 * 5 = 20 options.
№ 980. The urns have five balls each in five different colors: white, blue, red, yellow, green. One ball is removed from each urn at the same time. Describe the following event as certain, accidental, or impossible:
a) removed balls of different colors; (random)
b) taken out balls of the same color; (random)
c) black and white balls are taken out; (impossible)
d) two balls were taken out, both of which were painted in one of the following colors: white, blue, red, yellow, green. (reliable)
№ 982. A group of tourists is planning to carry out a hike along the Antonovo - Borisovo - Vlasovo - Gribovo route. From Antonovo to Borisovo you can raft down the river or walk. From Borisovo to Vlasovo you can walk or ride bicycles. From Vlasovo to Gribovo you can swim along the river, ride bicycles or walk. How many hiking options can tourists choose? How many hiking options can tourists choose, provided they have to use bicycles on at least one of the sections of the route?
(12 route options, 8 of them using bicycles)
Independent work.
Option 1
a) How many three-digit numbers can be made from digits: 0, 1, 3, 5, 7?
b) How many three-digit numbers can be made from digits: 0, 1, 3, 5, 7, provided that the numbers should not be repeated?
Athos, Porthos and Aramis have only a sword, a dagger and a pistol.
a) How many ways can the musketeers be armed?
b) How many weapon options are there if Aramis should wield a sword?
c) How many options are there for weapons, if Aramis should own a sword, and Porthos should own a pistol?
To the crow somewhere God sent a piece of cheese, as well as feta cheese, sausage, white and black bread. A crow perched on a spruce, got ready to have breakfast, but wondered: how many ways can you make sandwiches from these products?
Option 2
a) How many three-digit numbers can be made from digits: 0, 2, 4, 6, 8?
b) How many three-digit numbers can be made from digits: 0, 2, 4, 6, 8, provided that the digits should not be repeated?
Count Monte Cristo decided to present Princess Gaide with earrings, a necklace and a bracelet. Each piece of jewelry must contain one type of gem: diamonds, rubies or garnets.
a) How many options are there for combining gemstone jewelry?
b) How many jewelry options are there if the earrings are supposed to be diamond?
c) How many jewelry options are there, if the earrings are to be diamond and the bracelet is garnet?
For breakfast, you can choose a bun, sandwich or gingerbread with coffee or kefir. How many breakfast options can you compose?
Homework : No. 974, 975. (by compiling a tree of variants and using the rule of multiplication)
№ 974 . a) How many three-digit numbers can be made from the digits 0, 2, 4?
b) How many three-digit numbers can be made from the digits 0, 2, 4, provided that the numbers should not be repeated?
№ 975 . a) How many three-digit numbers can be made from the digits 1.3, 5.7?
b) How many three-digit numbers can be made from the digits 1.3, 5.7 provided. That numbers shouldn't be repeated?
Problem numbers are taken from the tutorial
"Mathematics-5", I.I. Zubareva, A.G. Mordkovich, 2004.