التحليل الرياضي.

ورشة عمل.

لطلبة الجامعة في التخصص:

"إدارة الدولة والبلديات"

ت. بافلوفا

كولباشيفو 2008

الفصل 1. مقدمة في التحليل

1.1 وظائف. الخصائص العامة

1.2 نظرية الحدود

1.3 استمرارية الوظيفة

2.1 تعريف المشتق

2.4 استكشاف الوظائف

2.4.1 خطة دراسة الوظائف الكاملة

2.4.2 أمثلة دراسة الوظيفة

2.4.3. أكبر وأصغر قيمة لدالة في مقطع

2.5 قاعدة L'Hôpital

3.1 تكامل غير محدد

3.1.1 التعاريف والخصائص

3.1.2 جدول التكاملات

3.1.3 طرق التكامل الأساسية

3.2 التكامل المحدد

3.2.2 طرق حساب التكامل المحدد

الفصل 4. وظائف من عدة متغيرات

4.1 مفاهيم أساسية

4.2 حدود واستمرارية وظائف عدة متغيرات

4.3.3 التفاضل الكلي وتطبيقه على الحسابات التقريبية

الفصل 5. طرق التحسين الكلاسيكية

6.1 وظيفة المنفعة.

6.2 خطوط اللامبالاة

6.3 مجموعة الميزانية

واجبات منزلية

1.1 وظائف. الخصائص العامة

يتم تحديد دالة عددية في المجموعة D من الأرقام الحقيقية إذا كانت كل قيمة من قيمة المتغير مرتبطة ببعض القيمة الحقيقية المحددة جيدًا للمتغير y ، حيث D هو مجال الوظيفة.

التمثيل التحليلي للوظيفة:

صراحة:

بشكل ضمني:؛

في شكل حدودي:

صيغ مختلفة في مجال التعريف:

الخصائص.

دالة زوجية:. على سبيل المثال ، الوظيفة زوجية ، منذ ذلك الحين ...

وظيفة غريبة: ... على سبيل المثال ، الوظيفة غريبة ، منذ ذلك الحين ...

الوظيفة الدورية: ، حيث T هي فترة الدالة. على سبيل المثال ، الدوال المثلثية.

دالة رتيبة. إذا كان لأي مجال من مجالات التعريف - الوظيفة تتزايد ، - تتناقص. على سبيل المثال - زيادة و - تناقص.

وظيفة محدودة. إذا كان هناك رقم M من هذا القبيل. على سبيل المثال ، وظائف و ، منذ ذلك الحين .

مثال 1. ابحث عن مجال تعريف الوظائف.

+ 2 – 3 +

1.2 نظرية الحدود

التعريف 1... حد الدالة عند هو رقم ب ، إذا كان لأي (- رقم موجب صغير بشكل تعسفي) يمكن للمرء أن يجد مثل هذه القيمة للوسيطة ، بدءًا من استيفاء عدم المساواة.

تعيين:.

التعريف 2... نهاية دالة عند هي رقم ب إذا كان لأي رقم (رقم موجب صغير بشكل تعسفي) عدد موجب بحيث تحافظ المتباينة على جميع قيم x التي تحقق المتباينة.

تعيين:.

التعريف 3.تسمى الوظيفة متناهية الصغر من أجل أو ، إذا أو.

الخصائص.

1. المجموع الجبري لعدد محدود من الكميات متناهية الصغر هو كمية متناهية الصغر.

2. ناتج كمية صغيرة بشكل لا نهائي من خلال دالة محددة (ثابت ، كمية أخرى صغيرة بشكل لانهائي) هو كمية صغيرة بلا حدود.

3. حاصل قسمة كمية صغيرة بشكل لا نهائي على دالة حدها غير صفري هو كمية صغيرة بشكل لا نهائي.

التعريف 4.تسمى الوظيفة كبيرة بشكل لا نهائي عند ، إذا.

الخصائص.

1. منتج كمية كبيرة بشكل لا نهائي بواسطة دالة ، حدها غير صفري ، هو كمية كبيرة بشكل لا نهائي.

2. مجموع القيمة اللانهائية والدالة المقيدة هي قيمة كبيرة بشكل لا نهائي.

3. حاصل قسمة كمية كبيرة بشكل لا نهائي على دالة لها حد هو كمية كبيرة بشكل لا نهائي.

نظرية.(العلاقة بين كمية صغيرة لا متناهية وكمية كبيرة بلا حدود.) إذا كانت الوظيفة متناهية الصغر عند () ، فإن الوظيفة تكون كمية كبيرة بشكل لا نهائي عند (). وعلى العكس من ذلك ، إذا كانت الوظيفة كبيرة بشكل لا نهائي عند () ، فإن الوظيفة تكون صغيرة بشكل لا نهائي عند ().

الحد من النظريات.

1. لا يمكن أن تحتوي الوظيفة على أكثر من حد واحد.

2. حد المجموع الجبري لعدة دوال يساوي المجموع الجبري لحدود هذه الدوال:

3. حد حاصل ضرب عدة دوال يساوي حاصل ضرب حدود هذه الدوال:

4. حد الدرجة يساوي درجة الحد:

5. حد خارج القسمة يساوي حاصل قسمة النهايات إذا كان حد القاسم موجودًا:

.

6. الحد الأول لافت للنظر.

عواقب:

7. الحد الملحوظ الثاني:

عواقب:

القيم المتناهية الصغر المكافئة لـ:

حساب الحدود.

عند حساب الحدود ، يتم استخدام النظريات الأساسية حول الحدود وخصائص الوظائف المستمرة والقواعد الناشئة عن هذه النظريات والخصائص.

المادة 1.لإيجاد النهاية عند نقطة دالة متصلة عند هذه النقطة ، من الضروري استبدال قيمتها النهائية في الدالة تحت علامة النهاية بدلاً من الوسيطة x.

مثال 2. بحث

القاعدة 2.إذا ، عند إيجاد نهاية الكسر ، إذا كانت نهاية المقام تساوي صفرًا ، وكانت نهاية البسط غير صفرية ، فإن نهاية هذه الدالة تكون.

مثال 3. البحث

المادة 3.إذا ، عند إيجاد نهاية الكسر ، إذا كانت نهاية المقام متساوية ، ونهاية البسط مختلفة عن الصفر ، فإن نهاية هذه الدالة تساوي صفرًا.

مثال 4. بحث

في كثير من الأحيان ، يؤدي استبدال قيمة حدية لوسيطة إلى تعبيرات غير محددة مثل

.

يُطلق على العثور على حد الوظيفة في هذه الحالات الكشف عن عدم اليقين. للكشف عن عدم اليقين ، من الضروري تحويل هذا التعبير قبل الذهاب إلى الحد الأقصى. يتم استخدام تقنيات مختلفة للكشف عن أوجه عدم اليقين.

المادة 4... يتم الكشف عن عدم اليقين في النوع من خلال تحويل دالة التسامي ، وبالتالي ، من أجل تحديد عامل في البسط والمقام ، يكون حده صفرًا ، وبعد تقليل الكسر بواسطته ، ابحث عن حد حاصل القسمة. للقيام بذلك ، يتم إما ضرب البسط والمقام أو ضربهما في التعبيرات المرتبطة بالبسط والمقام.

القاعدة 5.إذا كان تعبير التسامي يحتوي على وظائف مثلثية ، فسيتم استخدام الحد الملحوظ الأول لفضح عدم اليقين في الأنواع.

.

القاعدة 6... للكشف عن عدم اليقين في النموذج عند ، يجب قسمة بسط ومقام كسر الحد الفرعي على أعلى درجة من الوسيطة ثم يجب إيجاد حد حاصل القسمة.

النتائج المحتملة:

1) الحد المطلوب يساوي نسبة المعامِلات في أعلى قوى من وسيطة البسط والمقام ، إذا كانت هاتان الدرجات متماثلتين ؛

2) الحد يساوي ما لا نهاية إذا كانت درجة وسيطة البسط أعلى من درجة وسيطة المقام ؛

3) الحد هو صفر إذا كانت درجة وسيطة البسط أقل من درجة وسيطة المقام.

أ)

حيث

الدرجات متساوية ، مما يعني أن الحد يساوي نسبة المعاملات عند الدرجات الأعلى ، أي ...

ب)

درجة البسط ، المقام ، 1 ، ما يعني أن النهاية هي

الخامس)

درجة البسط هي 1 ، درجة المقام ، إذن النهاية هي 0.

المادة 7... للكشف عن عدم اليقين في النموذج ، يجب ضرب بسط ومقام كسر الحد الفرعي بالتعبير المترافق.

المثال 10.

المادة 8... يتم استخدام حد رائع ثانٍ ونتائجه للكشف عن عدم اليقين من النوع.

يمكن إثبات ذلك

المثال 11.

المثال 12.

المثال 13.

القاعدة 9... عند الكشف عن أوجه عدم اليقين ، التي تحتوي وظيفتها اللاشعورية على متناهية الصغر ، من الضروري استبدال حدود هذه اللانهايات. على حدود العناصر المتناهية الصغر المكافئة لها.

المثال 14.

المثال 15.

القاعدة 10. قاعدة L'Hôpital (انظر 2.6).

1.3 استمرارية الوظيفة

تكون الوظيفة متصلة عند نقطة ما إذا كان حد الوظيفة كما الوسيطة يميل إلى a ، وموجود ويساوي قيمة الوظيفة في هذه المرحلة.

الشروط المكافئة:

1. ;

3.

تصنيف نقطة الانهيار:

كسر من النوع الأول

يمكن التخلص منها - توجد حدود أحادية الجانب ومتساوية ؛

فادح (قفزة) - الحدود من جانب واحد ليست متساوية ؛

انقطاع من النوع الثاني: لا يوجد حد للدالة عند نقطة ما.

مثال 16. حدد طبيعة انقطاع الوظيفة عند نقطة أو إثبات استمرارية الوظيفة في هذه المرحلة.

لأن الوظيفة لم يتم تعريفها ، لذلك فهي ليست متصلة في هذه المرحلة. لأن وفي المقابل ، ، إذن هي نقطة الانقطاع القابل للإزالة من النوع الأول.

ب)

بالمقارنة مع المهمة (أ) ، يتم تمديد الوظيفة عند نقطة بحيث ، لذلك ، هذه الوظيفة مستمرة في هذه المرحلة.

عندما لا يتم تعريف الوظيفة ؛

.

لأن أحد الحدود من جانب واحد لانهائي ، فهو إذن نقطة كسر من النوع الثاني.

الفصل 2. حساب التفاضل

2.1 تعريف المشتق

تعريف مشتق

إن أو مشتق دالة معينة هو حد نسبة زيادة الدالة إلى زيادة الوسيطة المقابلة عندما تميل زيادة الوسيطة إلى الصفر:

أو .

المعنى الميكانيكي للمشتق هو معدل تغير الوظيفة. المعنى الهندسي للمشتق هو ظل زاوية ميل المماس للرسم البياني للدالة:

2.2 القواعد الأساسية للتفاضل

اسم	دور	المشتق
الضرب بعامل ثابت
مجموع جبري من وظيفتين
نتاج وظيفتين
وظيفتان خاصتان
وظيفة معقدة

مشتقات الوظائف الابتدائية الأساسية

P / p No.	اسم وظيفة	الوظيفة ومشتقاتها
1	ثابت
2	وظيفة الطاقة حالات خاصة
3	دالة أسية حالة خاصة
4	دالة لوغاريتمية حالة خاصة
5	الدوال المثلثية
6	يعكس حساب المثاثات

ب)

2.3 المشتقات عالية الرتبة

مشتق من الدرجة الثانية لدالة

مشتق الوظيفة من الدرجة الثانية:

المثال 18.

أ) أوجد مشتق الوظيفة من الدرجة الثانية.

المحلول. دعونا نوجد أولًا مشتق من الدرجة الأولى .

لنأخذ مشتق من الدرجة الأولى.

مثال 19. أوجد مشتق من الدرجة الثالثة للدالة.

2.4 استكشاف الوظائف

2.4.1 التخطيط لدراسة وظيفية كاملة:

خطة دراسة الوظائف الكاملة:

1. البحث الأولي:

أوجد مجال ومدى القيم ؛

اكتشف الخصائص العامة: التكافؤ (الغرابة) ، الدورية ؛

أوجد نقاط التقاطع مع محاور الإحداثيات ؛

تحديد مناطق الثبات.

2. الخطوط المقاربة:

ابحث عن الخطوط المقاربة العمودية إذا ؛

البحث عن الخطوط المقاربة المائلة:.

إذا كان أي رقم ، إذن - خطوط مقاربة أفقية.

3. البحث باستخدام:

العثور على النقاط الحرجة ، هؤلاء. النقاط التي أو لا توجد ؛

حدد فترات الزيادة ، تلك. الفواصل الزمنية ، والوظائف المتناقصة - ؛

تحديد الحد الأقصى: النقاط التي يتم من خلالها تغيير العلامة من "+" إلى "-" ، هي الحد الأقصى للنقاط ، من "-" إلى "+" - الحد الأدنى.

4. البحث باستخدام:

البحث عن النقاط التي أو لا توجد ؛

ابحث عن مناطق التحدب ، أي. الفترات التي تكون فيها التقعرات ؛

أوجد نقاط الانعطاف ، أي. نقاط عند المرور من خلالها علامة التغييرات.

1. يتم رسم العناصر الفردية للدراسة على الرسم البياني تدريجيًا ، كما تم العثور عليها.

2. إذا كانت هناك صعوبات في بناء الرسم البياني للوظيفة ، فإن قيم الوظيفة موجودة في بعض النقاط الإضافية.

3. الغرض من الدراسة هو وصف طبيعة سلوك الوظيفة. لذلك ، لا يتم إنشاء رسم بياني دقيق ، ولكن يتم تحديد تقريبه ، حيث يتم تحديد العناصر الموجودة (القيم القصوى ، ونقاط الانقلاب ، والخطوط المقاربة ، وما إلى ذلك) بوضوح.

4. ليس من الضروري التقيد الصارم بالخطة المذكورة أعلاه ؛ من المهم عدم إغفال العناصر المميزة لسلوك الوظيفة.

2.4.2 أمثلة للدراسة الوظيفية:

1)

2) الوظيفة فردية:

.

3) الخطوط المقاربة.

- الخطوط المقاربة العمودية ، لأن

خط مقارب مائل.

5)

- نقطة الأنحراف.

2) الوظيفة فردية:

3) الخطوط المقاربة: لا توجد خطوط مقاربة عمودية.

يميل:

- خطوط مقاربة مائلة

4) - تزداد الوظيفة.

- نقطة الأنحراف.

رسم تخطيطي لهذه الوظيفة:

2) الوظيفة العامة

3) الخطوط المقاربة

- لا توجد خطوط مقاربة مائلة

- خط مقارب أفقي عند

- نقطة الأنحراف

رسم تخطيطي لهذه الوظيفة:

2) الخطوط المقاربة.

- خط مقارب عمودي ، لأن

- لا توجد خطوط مقاربة مائلة

، - خط مقارب أفقي

رسم تخطيطي لهذه الوظيفة:

2) الخطوط المقاربة

- الخط المقارب العمودي عند ، منذ ذلك الحين

- لا توجد خطوط مقاربة مائلة

، - خط مقارب أفقي

3) - تقل الوظيفة في كل فترة من الفترات.

رسم تخطيطي لهذه الوظيفة:

للعثور على أكبر وأصغر قيمة لدالة في مقطع ما ، يمكنك استخدام الرسم التخطيطي:

1. أوجد مشتق الوظيفة.

2. أوجد النقاط الحرجة للوظيفة ، والتي عندها أو غير موجودة.

3. أوجد قيمة الوظيفة في النقاط الحرجة التي تنتمي إلى مقطع معين وفي نهاياته واختر الأكبر والأصغر منها.

مثال. أوجد أصغر وأكبر قيمة للدالة في مقطع معين.

25. ما بين أثنين

2) - النقاط الحرجة

26. بين.

المشتق غير موجود في ، لكن 1 لا ينتمي إلى هذه الفترة الزمنية. تتناقص الدالة في الفترة الزمنية ، مما يعني أنه لا توجد قيمة أكبر ، ولكن توجد أصغر قيمة.

2.5 قاعدة L'Hôpital

نظرية. حد النسبة بين وظيفتين متناهيتين في الصغر أو كبيرتين بشكل لانهائي يساوي حد نسبة مشتقاتهما (محدودة أو لانهائية) ، إذا كانت الأخيرة موجودة بالمعنى المشار إليه.

أولئك. عند الكشف عن أوجه عدم اليقين من النوع أو يمكنك استخدام الصيغة:

.

27.

الفصل 3. حساب التكامل

3.1 تكامل غير محدد

3.1.1 التعاريف والخصائص

التعريف 1. الوظيفة تسمى المشتقة العكسية لـ if.

التعريف 2. التكامل غير المحدد للدالة f (x) هو مجموعة كل المشتقات العكسية لهذه الوظيفة.

تعيين: ، حيث c هو ثابت تعسفي.

خصائص متكاملة غير محددة

1. مشتق من التكامل غير المحدد:

2. تفاضل التكامل غير المحدد:

3. تكامل غير محدد للتفاضل:

4. تكامل غير محدد لمجموع (فرق) وظيفتين:

5. تحريك عامل ثابت إلى ما وراء علامة التكامل غير المحدود:

3.1.2 جدول التكاملات

. 1.3 طرق التكامل الأساسية

1. استخدام خصائص التكامل غير المحدد.

المثال 29.

2. إحضار تحت العلامة التفاضلية.

المثال 30.

3. طريقة الاستبدال المتغير:

أ) الاستبدال في التكامل

أين - وظيفة يسهل تكاملها عن الوظيفة الأصلية ؛ - وظيفة معكوسة للدالة ؛ هي المشتق العكسي للوظيفة.

المثال 31.

ب) الاستبدال في جزء لا يتجزأ من النموذج:

المثال 32.

المثال 33.

4. طريقة التكامل بالأجزاء:

المثال 34.

المثال 35.

دعونا نأخذ التكامل بشكل منفصل

دعنا نعود إلى التكامل:

3.2 التكامل المحدد

3.2.1 مفهوم التكامل المحدد وخصائصه

تعريف.دعنا نعطي دالة مستمرة في بعض الفترات. دعونا نبني الرسم البياني الخاص بها.

الشكل الذي يحده أعلاه منحنى ، إلى اليسار واليمين بخطوط مستقيمة ومن الأسفل بقطعة من محور الإحداثية بين النقطتين أ و ب ، يسمى شبه منحني منحني.

S - منطقة - شبه منحني منحني.

اقسم الفاصل الزمني بالنقاط واحصل على:

مجموع لا يتجزأ:

تعريف. التكامل المحدد هو نهاية المجموع المتكامل.

خصائص متكاملة محددة:

1. يمكن إخراج العامل الثابت من علامة التكامل:

2. تكامل الجمع الجبري لوظيفتين يساوي المجموع الجبري لتكاملات هذه الدوال:

3. إذا تم تقسيم جزء التكامل إلى أجزاء ، فإن التكامل على المقطع بأكمله يساوي مجموع التكاملات لكل جزء من الأجزاء التي نشأت ، أي ، لأي أ ، ب ، ج:

4. إذا كان على جزء ، ثم

5. حدود التكامل يمكن أن تكون متبادلة ، بينما علامة التكامل تتغير:

6.

7. التكامل عند النقطة يساوي 0:

8.

9. ("about mean") اجعل y = f (x) دالة قابلة للتكامل في. ثم ، حيث f (c) هي متوسط ​​قيمة f (x) على:

10. صيغة نيوتن ليبنيز

,

حيث F (x) هي المشتق العكسي لـ f (x).

3.2.2 طرق حساب التكامل المحدد.

1. التكامل المباشر

المثال 35.

أ)

ب)

الخامس)

ه)

2. تغيير المتغيرات تحت علامة التكامل المحددة .

المثال 36.

2. التكامل بالأجزاء في تكامل محدد .

المثال 37.

أ)

ب)

ه)

3.2.3 تطبيقات لا يتجزأ محدد

صفة مميزة	نوع الوظيفة	معادلة
	في الإحداثيات الديكارتية
منطقة القطاع المنحني	في الإحداثيات القطبية
منطقة شبه منحنية منحنية	في شكل حدودي
طول القوس	في الإحداثيات الديكارتية
طول القوس	في الإحداثيات القطبية
طول القوس	في شكل حدودي
حجم الجسم دوران	في الإحداثيات الديكارتية
حجم الجسم مع عرضي معين مقطع عرضي

مثال 38. احسب مساحة شكل محدد بخطوط: و .

المحلول:لنجد نقاط تقاطع الرسوم البيانية لهذه الدوال. للقيام بذلك ، نساوي الدوال ونحل المعادلة

لذلك ، نقاط التقاطع و.

نحسب مساحة الشكل باستخدام الصيغة

.

في حالتنا هذه

الجواب: المساحة تساوي (الوحدات المربعة).

4.1 مفاهيم أساسية

تعريف. إذا تم ، وفقًا لبعض القواعد ، تعيين قيمة واحدة أو أكثر من المتغير z لكل زوج من الأرقام المستقلة من مجموعة معينة ، فإن المتغير z يسمى دالة من متغيرين.

تعريف. مجال الوظيفة z هو مجموعة الأزواج التي توجد لها الوظيفة z.

مجال دالة من متغيرين هو مجموعة من النقاط على المستوى الإحداثي Oxy. يُطلق على الإحداثي z اسم التطبيق ، ثم تُصوَّر الوظيفة نفسها على أنها جزء من السطح في الفضاء E 3. على سبيل المثال:

مثال 39. أوجد مجال الوظيفة.

أ)

التعبير الموجود على الجانب الأيمن له معنى فقط لـ. هذا يعني أن مجال هذه الوظيفة هو مجموعة من جميع النقاط الموجودة داخل وعلى حدود دائرة نصف قطرها R المتمركزة في الأصل.

مجال هذه الوظيفة هو جميع نقاط المستوى ، باستثناء نقاط الخطوط المستقيمة ، أي تنسيق المحاور.

تعريف. خطوط مستوى الوظيفة هي مجموعة من المنحنيات على مستوى الإحداثيات الموصوفة بواسطة معادلات النموذج.

مثال 40. أوجد خطوط مستوى الوظيفة .

المحلول. خطوط المستوى لوظيفة معينة هي مجموعة من المنحنيات في المستوى الموصوف بواسطة المعادلة

تصف المعادلة الأخيرة عائلة من الدوائر المتمركزة عند النقطة O 1 (1 ، 1) من نصف القطر. يصبح سطح الدوران (المكافئ المكافئ) الموصوف بواسطة هذه الوظيفة "أكثر انحدارًا" أثناء تحركه بعيدًا عن المحور ، والذي يتم الحصول عليه من خلال المعادلات x = 1 ، y = 1. (الشكل 4)

4.2 حدود واستمرارية وظائف عدة متغيرات.

1. الحدود.

تعريف. يُطلق على الرقم أ حد الوظيفة حيث تميل النقطة إلى نقطة ما ، إذا كان هناك رقم لكل رقم صغير بشكل تعسفي بحيث يكون الشرط صحيحًا لأي نقطة ، والشرط ... يكتبون: .

مثال 41. أوجد الحدود:

أولئك. يعتمد الحد على ، وبالتالي ، فهو غير موجود.

2. الاستمرارية.

تعريف. دع النقطة تنتمي إلى مجال تعريف الوظيفة. ثم تسمى الوظيفة المستمرة عند نقطة إذا

(1)

علاوة على ذلك ، تميل هذه النقطة إلى النقطة بطريقة عشوائية.

إذا لم يتم استيفاء الشرط (1) في أي وقت ، فإن هذه النقطة تسمى نقطة انقطاع الوظيفة. يمكن أن يكون هذا في الحالات التالية:

1) لم يتم تحديد الوظيفة عند هذه النقطة.

2) لا يوجد حد.

3) هذا الحد موجود ولكنه غير متساوي.

مثال 42. حدد ما إذا كانت الدالة المعطاة متصلة عند النقطة ، إذا.

فهمت ومن ثم ، فإن هذه الوظيفة مستمرة عند هذه النقطة.

يعتمد الحد على k ، أي لم يكن موجودًا في نقطة معينة ، مما يعني أن الوظيفة لها انقطاع في هذه المرحلة.

4.3 مشتقات وتفاضلات وظائف متعددة المتغيرات

4.3.1 المشتقات الجزئية من الدرجة الأولى

المشتق الجزئي للدالة فيما يتعلق بالوسيطة x هو المشتق العادي لدالة لمتغير واحد x لقيمة ثابتة للمتغير y ويشار إليه:

المشتق الجزئي للدالة فيما يتعلق بالوسيطة y هو المشتق العادي لدالة لمتغير واحد y عند قيمة ثابتة للمتغير x ويشار إليه:

مثال 43. أوجد المشتقات الجزئية للدوال.

4.3.2 المشتقات الجزئية من الدرجة الثانية

المشتقات الجزئية من الدرجة الثانية هي مشتقات جزئية للمشتقات الجزئية من الدرجة الأولى. لدالة ذات متغيرين من النموذج ، أربعة أنواع من المشتقات الجزئية من الدرجة الثانية ممكنة:

تسمى المشتقات الجزئية من الدرجة الثانية ، والتي يتم فيها إجراء التفاضل فيما يتعلق بالمتغيرات المختلفة ، بالمشتقات المختلطة. المشتقات المختلطة من الرتبة الثانية لدالة قابلة للاشتقاق مرتين متساوية.

مثال 44. أوجد المشتقات الجزئية من الرتبة الثانية.

4.3.3 التفاضل الكلي وتطبيقه على الحسابات التقريبية.

تعريف. يمكن إيجاد تفاضل الرتبة الأولى لدالة لمتغيرين في الصيغة

.

مثال 45. أوجد الفرق الكلي لوظيفة ما.

المحلول. لنجد المشتقات الجزئية:

.

بالنسبة للزيادات الصغيرة في الوسيطتين x و y ، تكتسب الدالة زيادة تساوي تقريبًا dz ، أي ...

صيغة إيجاد القيمة التقريبية لدالة ما عند نقطة ما ، إذا كانت قيمتها الدقيقة معروفة عند نقطة ما:

مثال 46. بحث .

المحلول. يترك ،

ثم نستخدم الصيغة

إجابه. .

مثال 47. احسب تقريبًا.

المحلول. دعنا نفكر في وظيفة. لدينا

مثال 48. احسب تقريبًا.

المحلول. ضع في اعتبارك الوظيفة ... نحن نحصل:

إجابه. .

4.3.4 تمايز الوظيفة الضمني

تعريف. تسمى الوظيفة ضمنية إذا تم تقديمها بواسطة معادلة غير قابلة للحل فيما يتعلق بـ z.

تم العثور على المشتقات الجزئية لهذه الوظيفة من خلال الصيغ:

مثال 49. أوجد المشتقات الجزئية للدالة z المعطاة بالمعادلة .

المحلول.

تعريف. تسمى الوظيفة ضمنية إذا تم تقديمها بواسطة معادلة غير قابلة للحل فيما يتعلق بـ y.

تم العثور على مشتق هذه الوظيفة من خلال الصيغة:

.

مثال 50. أوجد مشتقات هذه الوظائف.

5.1 الطرف المحلي لدالة من عدة متغيرات

تعريف 1. وظيفة لها حد أقصى عند نقطة ما إذا

التعريف 2. الوظيفة لها حد أدنى عند نقطة ما إذا لجميع النقاط قريبة بدرجة كافية من النقطة ومختلفة عنها.

شرط ضروري لأقصى حد. إذا وصلت الدالة إلى حد أقصى عند نقطة ما ، فإن المشتقات الجزئية للدالة تختفي أو لا توجد في هذه المرحلة.

تسمى النقاط التي تختفي فيها المشتقات الجزئية أو لا توجد حرجة.

علامة كافية على الحد الأقصى. دع الوظيفة يتم تحديدها في بعض المناطق المجاورة للنقطة الحرجة ولها مشتقات جزئية مستمرة من الدرجة الثانية في هذه المرحلة

1) له حد أقصى محلي عند النقطة ، إذا و ؛

2) لديه حد أدنى محلي عند النقطة ، إذا و ؛

3) ليس له حد أقصى محلي عند النقطة إذا ؛

مخطط دراسة الحد الأقصى لدالة متغيرين.

1. أوجد المشتقات الجزئية للدالة: و.

2. حل جملة المعادلات وإيجاد النقاط الحرجة للدالة.

3. أوجد المشتقات الجزئية من الرتبة الثانية ، واحسب قيمها عند النقاط الحرجة ، وباستخدام الشرط الكافي ، توصل إلى استنتاج حول وجود القيم القصوى.

4. أوجد القيمة القصوى للدالة.

مثال 51. أوجد القيمة القصوى لدالة .

1) أوجد المشتقات الجزئية.

2) حل جملة المعادلات

4) أوجد المشتقات الجزئية من الرتبة الثانية وقيمها عند النقاط الحرجة :. في هذه المرحلة نحصل على:

وبالتالي ، لا يوجد حد أقصى عند هذه النقطة. في هذه المرحلة نحصل على:

ومن ثم ، عند هذه النقطة يوجد حد أدنى.

5.2 الحد الأقصى العالمي (أعلى وأدنى قيمة للدالة)

يتم تحقيق أكبر وأصغر قيم لدالة متعددة المتغيرات ، المستمرة على مجموعة مغلقة ، إما عند النقاط القصوى أو على حدود المجموعة.

مخطط إيجاد القيم الأعلى والأدنى.

1) ابحث عن النقاط الحرجة الموجودة داخل المنطقة ، واحسب قيمة الوظيفة في هذه النقاط.

2) اكتشف الوظيفة على حدود المنطقة ؛ إذا كانت الحدود تتكون من عدة خطوط مختلفة ، فيجب إجراء الدراسة لكل موقع على حدة.

3) قارن القيم التي تم الحصول عليها للدالة واختر الأكبر والأصغر.

مثال 52. أوجد أكبر وأصغر قيم دالة في مستطيل.

المحلول. 1) أوجد النقاط الحرجة للدالة ، لهذا نجد المشتقات الجزئية: ، ونحل نظام المعادلات:

استقبلت النقطة الحرجة A. النقطة الناتجة تقع داخل المنطقة المحددة ،

تتكون حدود المنطقة من أربعة أجزاء: و. ابحث عن أكبر وأصغر قيمة للدالة في كل جزء.

4) قارن النتائج التي تم الحصول عليها وتجد ذلك في النقاط .

الفصل 6. نموذج اختيار المستهلك

سنفترض أن هناك سلعًا مختلفة. ثم سيتم الإشارة إلى مجموعة معينة من السلع بواسطة متجه الأبعاد n ، أين هي كمية المنتج من الدرجة الأولى. تسمى مجموعة كل مجموعات السلع X بالمساحة.

يتميز اختيار المستهلك الفردي بعلاقة التفضيل: يُعتقد أن المستهلك يمكنه أن يقول عن أي مجموعتين ، وهو أمر مرغوب فيه أكثر ، أو لا يرى الفرق بينهما. تعتبر علاقة التفضيل متعدية: إذا كانت المجموعة مفضلة على مجموعة ، وكانت المجموعة مفضلة على المجموعة ، فإن المجموعة تكون أفضل من المجموعة. سنفترض أن سلوك المستهلك موصوف بالكامل من خلال بديهية المستهلك الفردي: كل مستهلك فردي يتخذ قرارًا بشأن الاستهلاك والمشتريات وما إلى ذلك ، بناءً على نظام التفضيلات الخاص به.

6.1 وظيفة المنفعة

في مجموعة مجموعات المستهلكين X ، يتم تحديد الوظيفة ، والتي تساوي قيمتها في مجموعة المستهلك تقدير المستهلك للفرد لهذه المجموعة. تسمى الوظيفة وظيفة فائدة المستهلك أو وظيفة تفضيل المستهلك. أولئك. كل مستهلك له وظيفة المنفعة الخاصة به. ولكن يمكن تقسيم المجموعة الكاملة من المستهلكين إلى فئات معينة من المستهلكين (حسب العمر ، وحالة الملكية ، وما إلى ذلك) ويمكن تخصيص بعض وظائف المنفعة المتوسطة لكل فئة ، ربما.

وبالتالي ، فإن الوظيفة هي تقدير المستهلك أو مستوى إشباع احتياجات الفرد عند شراء مجموعة معينة. إذا كانت المجموعة أفضل من مجموعة لفرد معين ، إذن.

خصائص وظيفة المنفعة.

1.

تسمى المشتقات الجزئية الأولى لوظيفة المنفعة بالمرافق الهامشية للمنتجات. ويترتب على هذه الخاصية أن الزيادة في استهلاك منتج واحد بينما يظل استهلاك المنتجات الأخرى دون تغيير يؤدي إلى زيادة في تقييم المستهلك. المتجه هو انحدار الوظيفة ، فهو يوضح اتجاه النمو الأكبر للوظيفة. بالنسبة للدالة ، فإن تدرجها هو متجه للمرافق الهامشية للمنتجات.

2.

أولئك. المنفعة الحدية لأي سلعة تتناقص مع زيادة الاستهلاك.

3.

أولئك. تزداد المنفعة الحدية لكل منتج مع زيادة كمية المنتج الآخر.

بعض أنواع وظائف المرافق.

1) الكلاسيكية الجديدة:.

2) من الدرجة الثانية: حيث تكون المصفوفة سلبية محددة و ل .

3) الوظيفة اللوغاريتمية:.

6.2 خطوط اللامبالاة

في المشكلات والنماذج التطبيقية لاختيار المستهلك ، غالبًا ما يتم استخدام حالة معينة لمجموعة من سلعتين ، أي عندما تعتمد وظيفة المنفعة على متغيرين. خط اللامبالاة هو خط يربط بين مجموعات المستهلكين التي لها نفس المستوى من إشباع احتياجات الفرد. في جوهرها ، خطوط اللامبالاة هي خطوط مستوى الوظيفة. معادلات خط اللامبالاة: .

الخصائص الأساسية لخطوط اللامبالاة.

1. خطوط اللامبالاة ، المقابلة لمستويات مختلفة من إشباع الحاجات ، لا تلمس ولا تتقاطع.

2. انخفاض خطوط اللامبالاة.

3. خطوط اللامبالاة محدبة إلى أسفل.

تشير الخاصية 2 إلى مساواة تقريبية مهمة.

توضح هذه النسبة مقدار زيادة (نقص) الفرد في استهلاك المنتج الثاني مع تقليل (زيادة) استهلاك المنتج الأول بوحدة واحدة دون تغيير مستوى إشباع احتياجاته. تسمى النسبة معدل استبدال المنتج الأول بالثاني ، وتسمى القيمة المعدل الهامشي لاستبدال المنتج الأول بالثاني.

مثال 53. إذا كانت المنفعة الحدية للسلعة الأولى هي 6 ، والثانية - 2 ، فمع انخفاض استهلاك السلعة الأولى بمقدار وحدة واحدة ، من الضروري زيادة استهلاك السلعة الثانية بمقدار 3 وحدات باستخدام نفس المستوى من إشباع الاحتياجات.

6.3 مجموعة الميزانية

يترك - ناقلات أسعار مجموعة من المنتجات n ؛ ط - دخل الفرد الذي يرغب في إنفاقه على شراء مجموعة من المنتجات. تسمى مجموعة مجموعات السلع التي لا تكلف أكثر من أنا بأسعار معينة مجموعة الميزانية B. علاوة على ذلك ، فإن مجموعة مجموعات السلع التي تكلف I تسمى الحد G لمجموعة الميزانية B. المجموعة B محدودة بالحد G والقيود الطبيعية.

يتم وصف مجموعة الميزانية من خلال نظام من عدم المساواة:

بالنسبة لمجموعة من سلعتين ، فإن مجموعة الميزانية B (الشكل 1) هي مثلث في نظام الإحداثيات ، يحده محاور الإحداثيات وخط مستقيم.

6.4 نظرية طلب المستهلك

في نظرية الاستهلاك ، يُفترض أن المستهلك يسعى دائمًا إلى تعظيم منفعته وأن القيد الوحيد بالنسبة له هو الدخل المحدود الأول ، والذي يمكنه إنفاقه على شراء مجموعة من السلع. بشكل عام ، تتم صياغة مشكلة اختيار المستهلك (مشكلة السلوك العقلاني للمستهلك في السوق) على النحو التالي: العثور على مجموعة المستهلك ، والتي تزيد من وظيفة فائدتها لقيود ميزانية معينة. النموذج الرياضي لهذه المشكلة:

في حالة مجموعة من منتجين:

هندسيًا ، يكون حل هذه المشكلة هو نقطة الاتصال بين حدود مجموعة الميزانية G وخط اللامبالاة.

يتم تقليل حل هذه المشكلة إلى حل نظام المعادلات:

(1)

الحل لهذا النظام هو الحل لمشكلة اختيار المستهلك.

يسمى حل مشكلة اختيار المستهلك بنقطة الطلب. تعتمد نقطة الطلب هذه على الأسعار والدخل I. وهذا هو. نقطة الطلب هي دالة الطلب. في المقابل ، فإن دالة الطلب عبارة عن مجموعة من وظائف n ، كل منها يعتمد على الوسيطة:

تسمى هذه الوظائف وظائف الطلب للسلع المقابلة.

مثال 54. لمجموعة من سلعتين في السوق ، الأسعار المعروفة لهما والدخل 1 ، أوجد دوال الطلب إذا كانت دالة المنفعة لها الشكل .

المحلول. دعونا نفرق بين وظيفة المنفعة:

.

استبدل التعبيرات التي تم الحصول عليها في (1) واحصل على نظام المعادلات:

في هذه الحالة ، ستكون مصاريف كل منتج نصف دخل المستهلك ، ومبلغ المنتج المشتراة يساوي المبلغ المصروف عليه مقسومًا على سعر المنتج.

مثال 55. دع وظيفة المنفعة للبضائع الأولى ، والثانية ،

سعر المنتج الأول ، سعر المنتج الثاني. دخل . كم يجب أن يشتري المستهلكون لزيادة المنفعة؟

المحلول. دعونا نجد مشتقات وظائف المنفعة ، ونستبدلها في النظام (1) ونحلها:

هذه المجموعة من السلع هي الأمثل للمستهلك من حيث تعظيم المنفعة.

يجب إجراء الاختبار وفقًا للخيار المحدد بواسطة الرقم الأخير من رقم دفتر التسجيل في دفتر ملاحظات منفصل. يجب أن تحتوي كل مشكلة على شرط ، وحل مفصل وخاتمة.

1. مقدمة في التفاضل والتكامل

المهمة 1. ابحث عن مجال الوظيفة.

5.

المشكلة 2. أوجد حدود الوظائف.

.

المهمة 3. ابحث عن نقاط توقف الوظيفة وحدد نوعها.

1. 2. 3.

الفصل 2. حساب تفاضلي لدالة متغير واحد

المهمة 4. ابحث عن مشتقات هذه الوظائف.

1.a) ؛ ب) ج) ص = ؛

د) ص = س 6 + + + 5 ؛ هـ) ص = x tg x + ln sin x + e 3x ؛

و) ص = 2 س - أركسين س.

2.a) ؛ ب) ص = ؛ ج) ص = ؛ د) ص = س 2 - + 3 ؛ هـ) ص = ج جتا ؛ و) ص =.

3.a) y = lnx ؛ ب) ص = ؛ ج) y = ln ؛

4. أ) ص = ؛ ب) ص = (ه 5 س - 1) 6 ؛ ج) ص = ؛ د) ص = ؛ هـ) ص = س 8 ++ + 5 ؛ و) ص = 3 س - أركسين س.

5. أ) ص = 2 س 3 - + ه س ؛ ب) ص = ؛ ج) ص = ؛

د) ص = ؛ ه) ص = 2 كوس ؛ و) ص =.

6.أ) ص = lnx ؛ ب) ص = ؛ ج) y = ln ؛

د) ص = ؛ هـ) ص = س 7 + + 1 ؛ و) ص = 2.

7.a) ؛ ب) ص = ؛ ج) ص = ؛ د) ص = x 2 + xsinx + ؛ هـ) ص = ج جتا ؛ و) ص =.

8. أ) ص = ؛ ب) ص = (3 × - 4) 6 ؛ ج) ص = سينتج ؛

د) ص = 3 س 4 - - 9+ 9 ؛ ه) ص = ؛

و) ص = س 2 + أركسين س - س.

9.a) ؛ ب) ؛ ج) ص = ؛ د) ص = 5 خطيئة 3 س ؛ هـ) ص = × 3 - - 6+ 3 ؛ و) ص = 4 × 4 + ن.

10.a) ب) ص = ؛ ج) ص = (3 × - 4) 6 ؛ د) ص = ؛ هـ) ص = س 2 - س ؛ و) ص = الخطيئة 3 س + 2.

المهمة 5. تحقق من الوظيفة وقم ببناء الرسم البياني الخاص بها.

1. أ) ب) ج).

2. (أ) ب) الخامس) .

3. (أ) ب) الخامس) .

4. ب) الخامس)

5. (أ) ب) الخامس) .

6. (أ) ب) الخامس) .

7. أ) ب) ج).

8. أ) ب) ج).

9. أ) ب) ج).

10. أ) ب) الخامس) .

المهمة 6. ابحث عن أكبر وأصغر قيمة للدالة في مقطع معين.

1. .

3. .

6. .

8. .

9. .

10. .

الفصل 3. حساب التكامل

المشكلة 7. أوجد تكاملات غير محددة.

1.a) ب)؛

2.a) ؛ ب) ج) د).

4. ز)

5.a) ؛ ب)؛ الخامس) ؛ ز).

6.أ) ؛ ب)؛ الخامس)؛ ز)

7.a) ؛ ب) ؛ الخامس) ؛ ز)

8.a) ؛ ب)؛ الخامس) ؛ ز).

9. أ) ؛ ب) ج) ؛ ز).

10.a) ب) الخامس) ؛ ز).

مشكلة 8. احسب التكاملات المحددة.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

المشكلة 9. أوجد تكاملات غير صحيحة أو أثبت أنها متباعدة.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

مشكلة 10. أوجد مساحة المنطقة التي تحدها المنحنيات

1. .2. .

5. 6.

7. , .8..

10. , .

الفصل الرابع: حساب تفاضل لدالة من عدة متغيرات.

المهمة 11. ابحث عن مجال الوظيفة (تظهر في الرسم).

المشكلة 12. تحقق من استمرارية الوظيفة لـ

المشكلة 13. أوجد مشتق دالة معرفة ضمنيًا.

المشكلة 14. احسب تقريبا

1.a) ؛ ب) ؛ الخامس)

2.a) ؛ ب)؛ الخامس) .

3.a) ؛ ب) ؛ الخامس) .

4 ا) ؛ ب) ؛ الخامس) .

5. أ) ؛ ب) ؛ الخامس) .

6. أ) ؛ ب)؛ الخامس) .

7. أ) ؛ ب) ؛ الخامس) .

8.a) ؛ ب) ؛ الخامس)

9. أ) ؛ ب)؛ الخامس) .

10. أ) ؛ ب) ؛ الخامس)

المشكلة 15. تحقق من وظيفة القيم القصوى.

7. .

8. .

9. .

10. .

المشكلة 16. أوجد أكبر وأصغر قيمة للدالة في منطقة مغلقة معينة.

1. في المستطيل

2.

3. في المستطيل

4. في المنطقة التي يحدها القطع المكافئ

والإحداثي.

5.square

6- في مثلث يحده محاور الإحداثيات وخط مستقيم

7- في مثلث يحده محاور الإحداثيات وخط مستقيم

8. في مثلث يحده محاور الإحداثيات وخط مستقيم

9. في المنطقة التي يحدها القطع المكافئ

والإحداثي.

10. في المنطقة التي يحدها القطع المكافئ

والإحداثي.

الرئيسية

1. إم. كراسوس ، ب. تشوبرينوف. أساسيات الرياضيات وتطبيقاتها في التربية الاقتصادية: كتاب مدرسي. - الطبعة الرابعة ، ISP. - م: ديلو ، 2003.

2. إم. كراسوس ، ب. تشوبرينوف. الرياضيات للتخصصات الاقتصادية: كتاب مدرسي. - الطبعة الرابعة ، ISP. - م: ديلو ، 2003.

3. إم. كراسوس ، ب. تشوبرينوف. الرياضيات لدرجة البكالوريوس في الاقتصاد. كتاب مدرسي. - الطبعة الرابعة ، ISP. - م: ديلو ، 2005.

4. الرياضيات العليا للاقتصاديين. كتاب مدرسي للجامعات / N.Sh. كريمر ، ب. بوتكو ، إ. تريشين ، م. فريدمان. إد. الأستاذ. ان. كريمر - الطبعة الثانية ، منقح. و أضف. - م: الوحدة ، 2003.

5. كريمر إن ش ، بوتكو بكالوريوس ، تريشين إم ، فريدمان إم إن الرياضيات العليا للتخصصات الاقتصادية. الكتاب المدرسي وورشة العمل (الجزءان الأول والثاني) / إد. الأستاذ. ان. كريمر - الطبعة الثانية ، منقح. و أضف. - م: التعليم العالي 2007. - 893 ص. - (أصول العلوم)

6. Danko P.E.، Popov A.G.، Kozhevnikova T.Ya. الرياضيات العليا في التمارين والمشاكل. م. المدرسة الثانوية. 1999.

إضافي

1. I.I. بافرين ، في. البحارة. الرياضيات العليا. "مركز فلادوس للنشر الإنساني" ، 2002.

2. أ. زايتسيف. الرياضيات العليا. "المدرسة الثانوية" ، 1998.

3. أ. سولودوفنيكوف ، ف. بابايتسيف ، أ. برايلوف ، آي جي. شاندرا. الرياضيات في الاقتصاد / قسمين /. م. المالية والإحصاء. 1999.

للطلاب الطبية ، طب الأطفال ، طب الأسنان

وكليات الطب الوقائي

للعمل في المختبر

"المفاهيم الأساسية للتحليل الرياضي"

1 - الإثبات العلمي والمنهجي للموضوع:

المفاهيم المشتقة والتفاضلية هي أحد المفاهيم الأساسية للتحليل الرياضي. حساب المشتقات ضروري عند حل العديد من المسائل في الفيزياء والرياضيات (إيجاد السرعة ، التسارع ، الضغط ، إلخ). يتم تحديد أهمية مفهوم المشتق ، على وجه الخصوص ، من خلال حقيقة أن مشتق الوظيفة يميز معدل تغيير هذه الوظيفة عندما تتغير حجتها.

يتيح استخدام التفاضل إجراء حسابات تقريبية ، وكذلك تقدير الأخطاء.

تشكل طرق إيجاد المشتقات وتفاضلات الوظائف وتطبيقها المشكلة الرئيسية لحساب التفاضل. تنشأ الحاجة إلى مفهوم المشتق فيما يتعلق بصياغة مشكلة حساب سرعة الحركة وإيجاد زاوية المماس للمنحنى. المسألة العكسية ممكنة أيضًا: حدد المسافة التي تقطعها السرعة ، وأوجد الدالة المقابلة بظل منحدر الظل. تؤدي هذه المسألة العكسية إلى مفهوم التكامل غير المحدد.

يُستخدم مفهوم التكامل المحدد في عدد من المشكلات العملية ، لا سيما في مسائل حساب مساحات الأشكال المستوية ، وحساب العمل الذي تقوم به قوة متغيرة ، وإيجاد متوسط ​​قيمة دالة.

في الوصف الرياضي للعمليات والظواهر الفيزيائية والكيميائية والبيولوجية المختلفة ، غالبًا ما تستخدم المعادلات التي لا تحتوي فقط على الكميات قيد الدراسة ، ولكن أيضًا مشتقاتها من أوامر مختلفة من هذه الكميات. على سبيل المثال ، وفقًا لأبسط نسخة من قانون تكاثر البكتيريا ، يتناسب معدل التكاثر مع عدد البكتيريا في وقت معين. إذا تم الإشارة إلى هذه الكمية بواسطة N (t) ، فوفقًا للمعنى المادي للمشتق ، يكون معدل تكاثر البكتيريا مشتقًا من N (t) ، وعلى أساس القانون أعلاه ، يمكننا كتابة النسبة N "(t) = k ∙ N ، حيث k> 0 - معامل التناسب المعادلة الناتجة ليست جبرية ، لأنها لا تحتوي فقط على الوظيفة غير المعروفة N (t) ، ولكن أيضًا مشتقها من الدرجة الأولى.

2. نظرية موجزة:

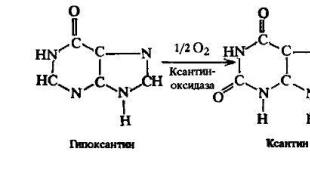
1. مشاكل تؤدي إلى مفهوم المشتق

1. مشكلة إيجاد السرعة v لنقطة مادية... دع بعض النقاط المادية تؤدي حركة مستقيمة. في لحظة من الزمن ر 1 النقطة في الموضع م 1. في لحظة من الزمن ر 2 حامل م 2 . دعونا نشير إلى الفاصل الزمني م 1 م 2 بجانب ΔS; ر 2 - ت 1 = Δt... تسمى القيمة متوسط ​​سرعة الحركة. لإيجاد السرعة اللحظية لنقطة في موضع ما م 1 من الضروري Δtتميل إلى الصفر. رياضيا ، هذا يعني ذلك

, (1)

وبالتالي ، للعثور على السرعة اللحظية لنقطة مادية ، من الضروري حساب حد نسبة الزيادة في الوظيفة ΔSلزيادة الحجة Δt شريطة أن Δt → 0.

2. مشكلة إيجاد زاوية ميل المماس لمنحنى دالة.

رسم بياني 1

ضع في اعتبارك الرسم البياني لبعض الوظائف ص = و (س).ما هي زاوية الميل
ظل عند النقطة م 1 ؟ في هذه النقطة م 1 ارسم ظلًا للرسم البياني للدالة. حدد نقطة عشوائية على الرسم البياني م 2 وارسم القاطع. تميل نحو المحور أوهبزاوية α 1 ... يعتبر Δ م 1 م 2 أ:

, (2)

إذا كانت النقطة م 1 الإصلاح والنقطة م 2 تقترب من م 1 ، ثم القاطع م 1 م 2 ستنتقل إلى المماس للرسم البياني للدالة عند النقطة م 1 ويمكنك أن تكتب:

, (3)

وبالتالي ، من الضروري حساب حد نسبة زيادة الدالة إلى زيادة الوسيطة إذا كانت زيادة الوسيطة تميل إلى الصفر.

حد نسبة الزيادة Δy للدالة y = f (x) إلى زيادة الوسيطة Δx عند نقطة معينة x 0 نظرًا لأن Δx يميل إلى الصفر ، يسمى مشتق الوظيفة عند نقطة معينة.

تدوين مشتق: ص "، و" (خ) ، ... حسب التعريف

, (4)

حيث Δx = x 2 -x 1 هي زيادة الوسيطة (الفرق بين قيمتين متتاليتين للوسيطة) ، Δy = y 2 -y 1 هي زيادة الدالة (الفرق بين القيم للدالة المقابلة لقيم الوسيطة هذه).

يُطلق على إيجاد مشتق دالة معينة اسمها التفاضل... يتم تنفيذ التمايز بين الوظائف الأولية الرئيسية وفقًا للصيغ الجاهزة (انظر الجدول) ، وكذلك باستخدام قواعد:

مشتق من مجموع جبري الدوال تساوي مجموع مشتقات هذه الدوال:

(ش+ υ )"= ش" + υ "

2. مشتق حاصل ضرب وظيفتين يساوي مجموع حاصل ضرب الدالة الثانية بمشتق الدالة الأولى ومشتق الدالة الأولى من مشتق الثانية:

(ش ∙υ ) "= u"υ + شυ "

3. مشتق من حاصل القسمة من دالتين يساوي كسرًا ، بسطه هو الفرق بين حاصل ضرب المقام بمشتق البسط والبسط بمشتق المقام ، والمقام هو مربع المقام:

المعنى المادي للمشتق. تشير المقارنة بين (4) و (1) إلى أن السرعة اللحظية للحركة المستقيمة لنقطة مادية تساوي مشتق اعتماد إحداثياتها على الوقت.

المعنى العام لمشتق الوظيفة هو أنه يميزها معدل (سرعة) تغيير الوظيفةلتغيير حجة معينة. يتم التعبير أيضًا عن سرعة العمليات الفيزيائية والكيميائية وغيرها ، على سبيل المثال ، معدل تبريد الجسم ، ومعدل التفاعل الكيميائي ، ومعدل تكاثر البكتيريا ، وما إلى ذلك ، باستخدام أحد المشتقات.

المعنى الهندسي للمشتق.يسمى حجم ظل زاوية ميل الظل المرسوم على الرسم البياني للوظيفة في الرياضيات منحدر الظل.

يكون ميل المماس للرسم البياني للدالة القابلة للاشتقاق عند نقطة ما مساويًا عدديًا لمشتق الدالة عند هذه النقطة.

هذا البيان يسمى المعنى الهندسي للمشتق.

محتوى المقال

التحليل الرياضي،فرع من فروع الرياضيات يوفر طرقًا للدراسة الكمية لعمليات التغيير المختلفة ؛ يتعامل مع دراسة معدل التغيير (حساب التفاضل) وتحديد أطوال المنحنيات ، ومساحات وأحجام الأشكال المقيدة بخطوط منحنية وأسطح (حساب التفاضل والتكامل). بالنسبة لمشاكل التحليل الرياضي ، من المميز أن يرتبط حلها بمفهوم الحد.

بدأ التحليل الرياضي في عام 1665 من قبل إ. نيوتن و (حوالي 1675) بشكل مستقل بواسطة G. (1601-1665) ، جيه واليس (1616-1703) وإي بارو (1630-1677).

لجعل العرض أكثر حيوية ، سنلجأ إلى لغة الرسوم البيانية. لذلك ، قد يجد القارئ أنه من المفيد إلقاء نظرة على مقالة الهندسة التحليلية قبل قراءة هذا المقال.

حساب التفاضل

الظل.

في التين. يوضح الشكل 1 جزءًا من المنحنى ذ = 2x – x 2 ، المبرمة بين x= –1 و x= 3. تبدو الأجزاء الصغيرة بشكل كافٍ من هذا المنحنى مستقيمة. بمعنى آخر ، إذا صهي نقطة اعتباطية لهذا المنحنى ، إذًا هناك بعض الخط المستقيم الذي يمر عبر هذه النقطة ويكون تقريبًا للمنحنى في منطقة صغيرة من النقطة ص، وكلما كان الحي أصغر ، كان التقريب أفضل. يسمى هذا الخط المستقيم ظل المنحنى عند النقطة ص... تتمثل المهمة الرئيسية لحساب التفاضل في بناء طريقة عامة تسمح لك بإيجاد اتجاه المماس في أي نقطة على المنحنى حيث يوجد المماس. ليس من الصعب تخيل منحنى به كسر حاد (الشكل 2). إذا ص- الجزء العلوي من هذا الفاصل ، ثم يمكنك بناء خط مستقيم تقريبي PT 1 - على يمين النقطة صوخط تقريبي آخر RT 2 - على يسار النقطة ص... لكن لا يوجد خط مستقيم واحد يمر بنقطة ص، والتي اقتربت بشكل جيد من المنحنى بالقرب من النقطة صإلى اليمين وإلى اليسار على حد سواء ، ومن هنا المماس عند النقطة صغير موجود.

في التين. 1 ظل منمن خلال الأصل ا= (0،0). ميل هذا الخط هو 2 ، أي عندما يتغير الإحداثي بمقدار 1 ، يزيد الإحداثي بمقدار 2. إذا xو ذ- إحداثيات نقطة تعسفية على من، ثم الابتعاد عن اعلى مسافة Xوحدات على اليمين ، نبتعد عنها اعلى 2 ذوحدات تصل. لذلك، ذ/x= 2 أو ذ = 2x... هذه هي معادلة الظل منإلى المنحنى ذ = 2x – x 2 عند النقطة ا.

من الضروري الآن شرح السبب من مجموعة الخطوط التي تمر عبر النقطة ا، كان هذا هو الخط المستقيم الذي تم اختياره من... ما الفرق بين الخط المستقيم الذي ميله 2 والخطوط المستقيمة الأخرى؟ هناك إجابة واحدة بسيطة ، ونجد صعوبة في مقاومة إغراء استخدام تشبيه الظل بالدائرة: الظل منتشترك في نقطة واحدة فقط مع المنحنى ، في حين أن أي خط مستقيم غير عمودي يمر عبر هذه النقطة ا، يتقاطع مع المنحنى مرتين. يمكن التحقق من هذا على النحو التالي.

منذ التعبير ذ = 2x – x 2 يمكن الحصول عليها بالطرح X 2 من ذ = 2x(معادلات الخط المستقيم من) ثم القيم ذهناك معرفة أقل للرسم البياني ذلخط مستقيم في جميع النقاط ، باستثناء نقطة x= 0. لذلك ، فإن الرسم البياني موجود في كل مكان ، باستثناء النقطة اتقع أدناه من، وهذا الخط والرسم البياني لهما نقطة واحدة مشتركة. علاوة على ذلك ، إذا ذ = مكس- معادلة خط مستقيم آخر يمر بنقطة ا، فمن المؤكد أن هناك نقطتي تقاطع. هل حقا، مكس = 2x – x 2 ليس فقط ل x= 0 ، ولكن أيضًا لـ x = 2 – م... وفقط عندما م= 2 تتطابق نقطتا التقاطع. في التين. 3 يظهر الحال عندما مأقل من 2 ، لذلك على يمين اهناك نقطة تقاطع ثانية.

ماذا من- الخط المستقيم الوحيد غير الرأسي الذي يمر عبر نقطة اووجود نقطة واحدة مشتركة مع الرسم البياني ، وليست أهم خصائصه. في الواقع ، إذا انتقلنا إلى الرسوم البيانية الأخرى ، فسوف يتضح قريبًا أن خاصية الظل التي لاحظناها في الحالة العامة لم تتحقق. على سبيل المثال ، من التين. 4 يمكن ملاحظة أنه بالقرب من النقطة (1،1) الرسم البياني للمنحنى ذ = x 3 تقترب جيدًا بخط مستقيم RT، والتي ، مع ذلك ، لديها أكثر من نقطة واحدة مشتركة معها. ومع ذلك ، نود النظر RTمماس هذا الرسم البياني عند النقطة ص... لذلك ، من الضروري إيجاد طريقة أخرى لتمييز الظل عن تلك التي خدمتنا جيدًا في المثال الأول.

افترض ذلك من خلال النقطة اونقطة اعتباطية س = (ح,ك) على الرسم البياني للمنحنى ذ = 2x – x 2 (الشكل 5) يرسم خط مستقيم (يسمى قاطع). التعويض في معادلة المنحنى بالقيم x = حو ذ = ك، حصلنا على ذلك ك = 2ح – ح 2 ، إذن ، ميل القاطع هو

مع صغير جدا حالمعنى مقريبة من 2. علاوة على ذلك ، اختيار حقريبة بما يكفي من 0 يمكننا القيام به متقترب بشكل تعسفي من 2. يمكننا أن نقول ذلك م"يميل إلى الحد" يساوي 2 عندما حيميل إلى الصفر ، أو أيا كان الحد ميساوي 2 ل حتميل إلى الصفر. هذا مكتوب بشكل رمزي على النحو التالي:

ثم المماس للرسم البياني عند هذه النقطة ايُعرَّف بأنه خط مستقيم يمر عبر نقطة ابميل يساوي هذا الحد. هذا التعريف للظل قابل للتطبيق بشكل عام.

دعنا نظهر مزايا هذا الأسلوب بمثال آخر: أوجد ميل المماس للرسم البياني للمنحنى ذ = 2x – x 2 في نقطة تعسفية ص = (x,ذ) ، ولا نقصر أنفسنا على أبسط حالة عندما ص = (0,0).

يترك س = (x + ح, ذ + ك) - النقطة الثانية على الرسم البياني ، وتقع على مسافة حعلى يمين ص(الشكل 6). مطلوب للعثور على المنحدر ك/حقاطع PQ... نقطة سعلى مسافة

فوق المحور X.

عند توسيع الأقواس نجد:

طرح من هذه المعادلة ذ = 2x – x 2 ، نجد المسافة العمودية من النقطة صالى حد، الى درجة س:

لذلك ، المنحدر مقاطع PQمساوي ل

الآن هذا حيميل إلى الصفر ، ميميل إلى 2 - 2 x؛ سنأخذ القيمة الأخيرة على أنها ميل المماس PT... (سيتم الحصول على نفس النتيجة إذا حيأخذ القيم السالبة ، والتي تتوافق مع اختيار النقطة سعلى يسار ص.) لاحظ أن من أجل x= 0 النتيجة هي نفسها السابقة.

التعبير 2 - 2 xيسمى مشتق 2 x – x 2. في الأيام الخوالي ، كان المشتق يُطلق عليه أيضًا "النسبة التفاضلية" و "المعامل التفاضلي". إذا كان التعبير 2 x – x 2 عين F(x)، بمعنى آخر.

ثم يمكن الإشارة إلى المشتق

من أجل معرفة ميل المماس للرسم البياني للدالة ذ = F(x) في مرحلة ما ، يجب استبداله بـ Fў ( x) القيمة المقابلة لهذه النقطة X... لذا فإن المنحدر Fў (0) = 2 من أجل X = 0, Fў (0) = 0 من أجل X= 1 و Fў (2) = –2 من أجل X = 2.

يتم الإشارة إلى المشتق أيضًا فيў , دى/DX, د س صو دو.

حقيقة المنحنى ذ = 2x – x 2 بالقرب من نقطة معينة لا يمكن تمييزها عمليًا عن الظل عند هذه النقطة ، مما يسمح لنا بالحديث عن منحدر المماس على أنه "منحدر منحنى" عند نقطة التماس. وبالتالي ، يمكننا التأكيد على أن ميل المنحنى قيد الدراسة له ميل 2 عند النقطة (0،0). ويمكن أيضًا القول أنه عند x= 0 معدل التغيير ذنسبيا xيساوي 2. عند النقطة (2،0) ، يكون ميل المماس (والمنحنى) هو -2. (تعني علامة الطرح أن مثل xعامل ذينخفض.) عند النقطة (1،1) ، يكون الظل أفقيًا. نقول المنحنى ذ = 2x – x 2 له قيمة ثابتة في هذه المرحلة.

مرتفعات ومنخفظات.

لقد أظهرنا للتو أن المنحنى F(x) = 2x – x 2 ثابت عند النقطة (1،1). لأن Fў ( x) = 2 – 2x = 2(1 – x) ، فمن الواضح أن ل xأقل من 1، Fў ( x) موجبة ، وبالتالي ذيزيد؛ في x، كبير 1 Fў ( x) سلبي ، وبالتالي ذالنقصان. وهكذا ، بالقرب من النقطة (1،1) المشار إليها في الشكل. 6 حرف م، المعنى فيينمو إلى حد ما م، ثابت عند النقطة موينخفض ​​بعد النقطة م... هذه النقطة تسمى "الحد الأقصى" لأن القيمة فيعند هذه النقطة يتجاوز أي من قيمه في حي صغير بما فيه الكفاية. وبالمثل ، يتم تعريف "الحد الأدنى" على أنه نقطة بالقرب منها جميع القيم ذيفوق العدد فيفي هذه المرحلة بالذات. قد يحدث ذلك أيضًا على الرغم من أن مشتق F(x) في مرحلة ما وتختفي ، لا تتغير علامتها في محيط هذه النقطة. هذه النقطة ، التي ليست حدًا أقصى ولا حدًا أدنى ، تسمى نقطة انعطاف.

كمثال ، دعونا نجد النقطة الثابتة للمنحنى

مشتق هذه الوظيفة

ويختفي عند x = 0, X= 1 و X= –1 ؛ أولئك. عند النقاط (0،0) ، (1 ، –2 / 15) و (-1 ، 2/15). إذا Xأقل بقليل من -1 ، إذن Fў ( x) سلبي إذا Xأكثر بقليل من -1 ، إذن Fў ( x) إيجابية. لذلك ، فإن النقطة (–1 ، 2/15) هي الحد الأقصى. وبالمثل ، يمكن إظهار أن النقطة (1 ، –2/15) هي الحد الأدنى. لكن المشتق Fў ( x) سالبة قبل وبعد النقطة (0،0). لذلك ، (0،0) هي نقطة الانعطاف.

الدراسة التي أجريت لشكل المنحنى وكذلك حقيقة تقاطع المنحنى مع المحور Xفي F(x) = 0 (على سبيل المثال ، من أجل X= 0 أو) تتيح لك تمثيل الرسم البياني تقريبًا كما هو موضح في الشكل. 7.

بشكل عام ، إذا استبعدنا الحالات غير العادية (المنحنيات التي تحتوي على مقاطع خط مستقيم أو عدد لا حصر له من الانحناءات) ، فهناك أربعة خيارات للموضع النسبي للمنحنى والظل بالقرب من نقطة الظل ص. (سم... أرز. 8 حيث يكون للماس ميل موجب.)

1) على جانبي النقطة صيقع المنحنى فوق الظل (الشكل 8 ، أ). في هذه الحالة يقولون أن المنحنى عند النقطة صمحدب لأسفل أو مقعر.

2) على جانبي النقطة صيقع المنحنى أسفل الظل (الشكل 8 ، ب). في هذه الحالة ، يقال إن المنحنى محدب لأعلى أو محدب ببساطة.

3) و 4) يقع المنحنى فوق المماس على جانب واحد من النقطة صوأدناه - من ناحية أخرى. في هذه الحالة ص- نقطة الأنحراف.

مقارنة القيم Fў ( x) على جانبي صبقيمته عند هذه النقطة ص، فمن الممكن تحديد أي من هذه الحالات الأربع يجب التعامل معها في مشكلة معينة.

التطبيقات.

كل ما سبق يجد تطبيقات مهمة في مختلف المجالات. على سبيل المثال ، إذا تم إلقاء الجسم رأسيًا لأعلى بسرعة ابتدائية 200 قدم في الثانية ، فإن الارتفاع سالتي سيتم تحديد موقعهم من خلالها رستكون الثواني مقارنة بنقطة البداية

نجد أنه يتصرف بنفس الطريقة كما في الأمثلة التي درسناها

هذه القيمة تتلاشى عند ج. المشتق Fў ( x) موجب حتى قيمة c وسالب بعد هذا الوقت. لذلك، سيزداد إلى ، ثم يصبح ثابتًا ، ثم ينقص. هذا وصف عام لحركة الجسد إلى الأعلى. ومنه نعرف متى يصل الجسم إلى أعلى نقطة له. علاوة على ذلك ، استبدال ر= 25/4 بوصة F(ر) ، نحصل على 625 قدمًا ، وهو الحد الأقصى للرفع. في هذه المهمة Fў ( ر) له معنى فيزيائي. يوضح هذا المشتق السرعة التي يتحرك بها الجسم في هذه اللحظة ر.

دعونا ننظر الآن في نوع آخر من التطبيقات (الشكل 9). يلزم عمل صندوق بقاع مربع من ورقة من الورق المقوى بمساحة 75 سم 2. ما هو حجم هذا الصندوق حتى يصل إلى الحجم الأقصى؟ إذا X- جانب قاعدة الصندوق و ح- ارتفاعه ، ثم حجم الصندوق الخامس = x 2 ح، ومساحة السطح 75 = x 2 + 4xh... تحويل المعادلة ، نحصل على:

مستمدة من الخامستبين أنها متساوية

ويختفي عند X= 5. ثم

و الخامس= 125/2. الرسم البياني للوظيفة الخامس = (75x – x 3) / 4 في الشكل. 10 (القيم السالبة Xتم حذفه لأنه ليس له معنى مادي في هذه المشكلة).

المشتقات.

من المهام المهمة لحساب التفاضل التفاضل إنشاء طرق تتيح لك العثور على المشتقات بسرعة وسهولة. على سبيل المثال ، من السهل حساب ذلك

(مشتق الثابت هو بالطبع صفر.) ليس من الصعب استنتاج القاعدة العامة:

أين ن- أي عدد صحيح أو كسر. على سبيل المثال،

(يوضح هذا المثال مدى فائدة الأسس الكسرية.)

فيما يلي بعض أهم الصيغ:

وهناك أيضًا القواعد التالية: 1) إذا كانت كل وظيفة من هاتين الوظيفتين ز(x) و F(x) لها مشتقات ، ثم مشتق مجموعها يساوي مجموع مشتقات هذه الوظائف ، ومشتق الفرق يساوي فرق المشتقات ، أي

2) مشتق من حاصل ضرب وظيفتين يحسب بالصيغة:

3) مشتق نسبة الوظيفتين له الشكل

4) مشتق دالة مضروبة في ثابت يساوي ثابتًا مضروبًا في مشتق هذه الدالة ، أي

غالبًا ما يحدث أنه يجب حساب قيم الوظيفة على مراحل. على سبيل المثال ، لحساب الخطيئة x 2 ، نحتاج أولاً إلى إيجاد ش = x 2 ، ثم احسب جيب الرقم ش... نجد مشتقًا من هذه الوظائف المعقدة باستخدام ما يسمى ب "قاعدة السلسلة":

في مثالنا F(ش) = الخطيئة ش, Fў ( ش) = كوس ش، بالتالي،

تسمح هذه القواعد وغيرها من القواعد المماثلة لكتابة مشتقات العديد من الوظائف على الفور.

التقريبات الخطية.

إن حقيقة أنه ، بمعرفة المشتق ، يمكننا في كثير من الحالات استبدال التمثيل البياني للدالة بالقرب من نقطة معينة من مماسها عند هذه النقطة ، فهي ذات أهمية كبيرة ، حيث يسهل التعامل مع الخطوط المستقيمة.

تجد هذه الفكرة تطبيقًا مباشرًا في حساب القيم التقريبية للوظائف. على سبيل المثال ، من الصعب حساب القيمة عندما x= 1.033. لكن يمكنك الاستفادة من حقيقة أن الرقم 1.033 قريب من 1 وذاك. قريب x= 1 يمكننا استبدال الرسم البياني لمنحنى الظل دون ارتكاب أي خطأ جسيم. منحدر هذا الظل يساوي قيمة المشتق ( x 1/3) ў = (1/3) x–2/3 عند x = 1 ، أي 1/3. نظرًا لأن النقطة (1،1) تقع على المنحنى وميل المماس للمنحنى عند هذه النقطة هو 1/3 ، فإن معادلة الظل لها الشكل

على هذا الخط عند X = 1,033

القيمة الناتجة ذيجب أن تكون قريبة جدًا من القيمة الحقيقية ذ؛ وبالفعل ، إنها فقط 0.00012 أكثر من الحقيقة. في التحليل الرياضي ، تم تطوير طرق لتحسين دقة هذا النوع من التقريب الخطي. تضمن هذه الطرق موثوقية حساباتنا التقريبية.

الإجراء الموصوف للتو يقترح تدوينًا مفيدًا. يترك ص- النقطة المقابلة على الرسم البياني للوظيفة Fعامل Xودع الوظيفة F(x) قابل للتفاضل. استبدل الرسم البياني للمنحنى بالقرب من النقطة صمماسة لها ، مرسومة في هذه المرحلة. إذا Xتغير بالمبلغ ح، ثم سيتغير إحداثيات الظل حسب القيمة حح F ў ( x). إذا حصغير جدًا ، فإن القيمة الأخيرة هي تقريب جيد للتغيير الحقيقي في الإحداثي ذالرسومات. إذا بدلا من حسنكتب الرمز DX(هذا ليس منتجًا!) ، ولكنه تغيير في الإحداثي ذدل دى، ثم نحصل دى = F ў ( x)DX، أو دى/DX = F ў ( x) (سم... أرز. أحد عشر). لذلك ، بدلا من دىأو F ў ( x) غالبًا ما يستخدم الرمز للإشارة إلى مشتق دى/DX... تعتمد ملاءمة هذا الترميز بشكل أساسي على المظهر الصريح لقاعدة السلسلة (تمايز دالة معقدة) ؛ في الترميز الجديد ، تبدو هذه الصيغة كما يلي:

حيث يعني ذلك ضمنيًا فييعتمد على ش، أ شبدوره يعتمد على X.

الحجم دىيسمى التفاضلية في؛ في الحقيقة هذا يعتمد على اثنينالمتغيرات وهي: from Xوالزيادات DX... عند الزيادة DXحجم صغير جدا دىيقترب من التغيير المقابل في القيمة ذ... لكن لنفترض أن الزيادة DXقليل ، لا حاجة.

دالة مشتقة ذ = F(x) أشرنا إليه F ў ( x) أو دى/DX... من الممكن غالبًا أخذ مشتق من المشتق. النتيجة تسمى المشتق الثاني من F (x) والمشار إليها F ўў ( x) أو د 2 ذ/DX 2. على سبيل المثال ، إذا F(x) = x 3 – 3x 2 ، إذن F ў ( x) = 3x 2 – 6xو F ўў ( x) = 6x- 6. تُستخدم تسميات مماثلة للمشتقات ذات الرتبة الأعلى. ومع ذلك ، لتجنب عدد كبير من الشرطات (مساوية لترتيب المشتق) ، يمكن كتابة المشتق الرابع (على سبيل المثال) كـ F (4) (x) والمشتق ن-الترتيب كـ F (ن) (x).

يمكن إثبات أن المنحنى عند نقطة ما يكون محدبًا لأسفل إذا كان المشتق الثاني موجبًا ومحدبًا لأعلى إذا كان المشتق الثاني سالبًا.

إذا كان للدالة مشتق ثانٍ ، فإن التغير في الكمية ذالمقابلة للزيادة DXعامل X، يمكن حسابها تقريبًا بواسطة الصيغة

هذا التقريب أفضل بشكل عام من التقريب الذي قدمه التفاضل Fў ( x)DX... إنه يتوافق مع استبدال جزء من المنحنى بمكافئ بدلاً من خط مستقيم.

إذا كانت الوظيفة F(x) هناك مشتقات من أوامر أعلى إذن

الباقي هو

أين x- عدد بين xو x + DX... تسمى النتيجة أعلاه بصيغة تايلور المتبقية. إذا F(x) له مشتقات لجميع الطلبات ، ثم عادة ص ن® 0 من أجل ن ® Ґ .

حساب متكامل

مربعات.

عند دراسة مناطق الأشكال المستوية المنحنية ، يتم الكشف عن جوانب جديدة للتحليل الرياضي. حتى الإغريق القدماء حاولوا حل مثل هذه المشاكل ، الذين كان تحديد مساحة الدائرة ، على سبيل المثال ، من أصعب المهام. حقق أرخميدس نجاحًا كبيرًا في حل هذه المشكلة ، حيث تمكن أيضًا من العثور على منطقة قطعة مكافئ (الشكل 12). بمساعدة التفكير المعقد للغاية ، أثبت أرخميدس أن مساحة المقطع المكافئ تساوي 2/3 من مساحة المستطيل الموصوف ، وبالتالي في هذه الحالة تساوي (2/3) (16) = 32/3. كما سنرى لاحقًا ، يمكن الحصول على هذه النتيجة بسهولة من خلال طرق التحليل الرياضي.

حل أسلاف نيوتن ولايبنيز ، ولا سيما كبلر وكافالييري ، مشكلة حساب مناطق الأشكال المنحنية باستخدام طريقة يصعب وصفها بالمنطقية ، ولكنها كانت مثمرة للغاية. عندما جمعت واليس في عام 1655 بين طرق كبلر وكافاليري وطرق ديكارت (الهندسة التحليلية) واستخدمت الجبر حديث الولادة ، تم إعداد مرحلة ظهور نيوتن تمامًا.

قسم واليس الشكل ، المطلوب حساب مساحته ، إلى شرائح ضيقة جدًا ، كل منها كان يعتبر تقريبًا مستطيلًا. ثم جمع مساحات المستطيلات التقريبية ، وفي أبسط الحالات ، حصل على القيمة التي يتجه إليها مجموع مساحات المستطيلات عندما يميل عدد الخطوط إلى اللانهاية. في التين. يوضح الشكل 13 مستطيلات تقابل بعض الانقسامات إلى شرائح من المنطقة الواقعة أسفل المنحنى ذ = x 2 .

النظرية الرئيسية.

جعل الاكتشاف العظيم لنيوتن ولايبنيز من الممكن استبعاد العملية الشاقة المتمثلة في تجاوز الحد الأقصى لمجموع المناطق. تم ذلك بفضل نظرة جديدة لمفهوم المربع. النقطة المهمة هي أننا يجب أن نتخيل المنطقة الواقعة أسفل المنحنى كما تم إنشاؤها بواسطة الإحداثي يتحرك من اليسار إلى اليمين ونسأل عن مدى سرعة المنطقة التي اكتسحتها الإحداثيات. سنحصل على مفتاح إجابة هذا السؤال إذا أخذنا في الاعتبار حالتين خاصتين تُعرف المنطقة فيهما مسبقًا.

لنبدأ بالمساحة الموجودة أسفل الرسم البياني للدالة الخطية ذ = 1 + xلأنه في هذه الحالة يمكن حساب المنطقة باستخدام الهندسة الأولية.

يترك أ(x) هو جزء المستوى المحصور بين الخط المستقيم ذ = 1 + xوشريحة اوك(الشكل 14). عند القيادة QPالمنطقة الصحيحة أ(x) يزيد. كيف الصيام؟ ليس من الصعب الإجابة عن هذا السؤال ، لأننا نعلم أن مساحة شبه المنحرف تساوي حاصل ضرب ارتفاعها بنصف مجموع قاعدتها. لذلك،

معدل تغيير المنطقة أ(x) بواسطة مشتقها

نحن نرى ذلك أў ( x) يتزامن مع الإحداثي فينقاط ص... هل هذه صدفة؟ دعنا نحاول التحقق من القطع المكافئ الموضح في الشكل. 15. مربع أ (x) تحت القطع المكافئ في = X 2 في النطاق من 0 إلى Xمساوي ل أ(x) = (1 / 3)(x)(x 2) = x 3/3. يتم تحديد معدل التغيير في هذه المنطقة من خلال التعبير

الذي يتطابق تمامًا مع الإحداثي فينقطة متحركة ص.

إذا افترضنا أن هذه القاعدة يتم الوفاء بها بشكل عام بهذه الطريقة

هو معدل تغير المنطقة الواقعة تحت الرسم البياني للوظيفة ذ = F(x) ، ثم يمكن استخدام هذا في الحسابات وغيرها من المجالات. في الواقع ، النسبة أў ( x) = F(x) يعبر عن نظرية أساسية ، والتي يمكن صياغتها على النحو التالي: المشتق ، أو معدل تغير المنطقة كدالة لـ X، تساوي قيمة الوظيفة F (x) عند النقطة X.

على سبيل المثال ، لإيجاد المنطقة تحت الرسم البياني للدالة ذ = x 3 من 0 إلى X(الشكل 16) وضعنا

الجواب المحتمل هو:

منذ مشتق X 4/4 يساوي حقًا X 3. علاوة على ذلك، أ(x) يساوي صفرًا من أجل X= 0 ، كما ينبغي أن يكون إذا أ(x) هي بالفعل منطقة.

يثبت التحليل الرياضي أن إجابة أخرى إلى جانب التعبير أعلاه عن أ(x)، غير موجود. دعنا نظهر أن هذا البيان معقول باستخدام الاستدلال الاستدلالي (غير الصارم) التالي. افترض أن هناك حلًا ثانيًا الخامس(x). إذا أ(x) و الخامس(x) "ابدأ" في وقت واحد من الصفر عند القيمة X= 0 وتتغير كل الوقت بنفس المعدل ، ثم قيمها بلا قيمة Xلا يمكن أن تصبح مختلفة. يجب أن يكونوا هم نفس الشيء في كل مكان ؛ لذلك ، هناك حل واحد فقط.

كيف يمكن تبرير النسبة؟ أў ( x) = F(x) على العموم؟ لا يمكن الإجابة على هذا السؤال إلا من خلال دراسة معدل تغير المنطقة كدالة لـ Xعلى العموم. يترك م- أصغر قيمة للدالة F (x) في النطاق من Xقبل ( x + ح)، أ م- أكبر قيمة لهذه الوظيفة في نفس الفترة الزمنية. ثم زيادة المساحة على الانتقال من Xل ( x + ح) بين منطقتي مستطيلين (الشكل 17). أساس كلا المستطيلين متساويان ح... المستطيل الأصغر له ارتفاع موالمنطقة مأكبر على التوالي مو م... على قطعة أرض مقابل X(الشكل 18) يمكن ملاحظة أنه عندما تتغير الإحداثيّة بمقدار ح، قيمة الإحداثي (أي المنطقة) تزداد بالمقدار المحصور بينهما مو م... المنحدر القاطع في هذا الرسم البياني يقع بين مو م... ماذا يحدث عندما حيميل إلى الصفر؟ إذا كان الرسم البياني للدالة ذ = F(x) مستمر (أي لا يحتوي على انقطاعات) إذن م، و متميل إلى F(x). لذلك ، المنحدر أў ( x) قطعة أرض كدالة Xمساوي ل F(x). كان على المرء أن يأتي بالضبط إلى مثل هذا الاستنتاج.

اقترح لايبنيز للمنطقة الواقعة تحت المنحنى ذ = F(x) من 0 إلى أتعيين

مع اتباع نهج صارم ، يجب تعريف هذا التكامل المزعوم على أنه حد لمبالغ معينة بطريقة واليس. بالنظر إلى النتيجة أعلاه ، من الواضح أن هذا التكامل محسوب بشرط أن نتمكن من إيجاد مثل هذه الوظيفة أ(x) ، والتي تختفي عند X= 0 ولها مشتق أў ( x) يساوي F (x). عادة ما يسمى العثور على مثل هذه الوظيفة التكامل ، على الرغم من أنه سيكون من الأنسب تسمية هذه العملية بمضاد التمايز ، مما يعني أنها ، بمعنى ما ، معكوس للتفاضل. في حالة كثيرة الحدود ، يكون التكامل واضحًا. على سبيل المثال ، إذا

التي يسهل التحقق منها عن طريق التفاضل أ(x).

لحساب المنطقة أ 1 تحت المنحنى ذ = 1 + x + x 2/2 ، بين الإحداثيين 0 و 1 ، نكتب ببساطة

والاستعاضة عنها X= 1 ، نحصل عليه أ 1 = 1 + 1/2 + 1/6 = 5/3. مربع أ(x) من 0 إلى 2 يساوي أ 2 = 2 + 4/2 + 8/6 = 16/3. كما يتضح من الشكل. 19 ، المنطقة الواقعة بين الإحداثيين 1 و 2 هي أ 2 – أ 1 = 11/3. عادة ما يتم كتابتها على أنها جزء لا يتجزأ

أحجام.

يجعل التفكير المماثل من السهل بشكل مدهش حساب أحجام أجسام الثورة. دعونا نوضح ذلك بمثال حساب حجم الكرة ، وهي مشكلة كلاسيكية أخرى تمكن الإغريق القدماء ، باستخدام الأساليب المعروفة لديهم ، من حلها بصعوبة كبيرة.

قم بتدوير جزء المستوى المحاط بربع دائرة نصف قطرها صبزاوية 360 درجة حول المحور X... نتيجة لذلك ، نحصل على نصف كرة (الشكل 20) ، نشير إلى حجمه الخامس(x). مطلوب لتحديد المعدل الذي يتم عنده الخامس(x) مع زيادة x... الانتقال من Xل X + ح، فمن السهل التحقق من أن زيادة الحجم أقل من الحجم ص(ص 2 – x 2)حنصف قطر الاسطوانة الدائرية والارتفاع ح، وأكثر من الحجم ص[ص 2 – (x + ح) 2 ]حنصف قطر الاسطوانة والارتفاع ح... لذلك ، على الرسم البياني للدالة الخامس(x) منحدر القاطع بين ص(ص 2 – x 2 و ص[ص 2 – (x + ح) 2]. متى حيميل إلى الصفر ، ويميل المنحدر إلى

في x = صنحن نحصل

لحجم نصف الكرة ، وبالتالي 4 ص ص 3/3 لحجم الكرة بأكملها.

تتيح لك طريقة مماثلة العثور على أطوال المنحنيات ومناطق الأسطح المنحنية. على سبيل المثال ، إذا أ(x) - طول القوس العلاقات العامةفي التين. 21 ، ثم مهمتنا هي الحساب أў( x). على مستوى الكشف عن مجريات الأمور ، نستخدم خدعة تسمح لنا بعدم اللجوء إلى الممر المعتاد إلى الحد الأقصى ، وهو أمر ضروري لإثبات النتيجة بدقة. افترض أن معدل تغير الوظيفة أ(x) عند النقطة صهي نفسها لو تم استبدال المنحنى بظلها PTفي هذه النقطة ص... لكن من التين. يمكن رؤية 21 مباشرة عند الخطو حعلى يمين أو يسار النقطة Xعلى امتداد RTالمعنى أ(x) تغيير الى

لذلك ، معدل تغير الوظيفة أ(x) يكون

للعثور على الوظيفة نفسها أ(x) ، من الضروري فقط دمج التعبير على الجانب الأيمن من المساواة. اتضح أن معظم الوظائف يصعب دمجها. لذلك ، يشكل تطوير طرق حساب التفاضل والتكامل جزءًا كبيرًا من التحليل الرياضي.

المشتقات العكسية.

كل دالة مشتقها يساوي دالة معينة F(x) ، يسمى المشتق العكسي (أو البدائي) لـ F(x). على سبيل المثال، X 3/3 المشتق العكسي للدالة X 2 ، منذ ( x 3/3) ў = x 2. بالطبع X 3/3 ليس المشتق العكسي الوحيد للدالة X 2 منذ ذلك الحين x 3 /3 + جهو أيضًا مشتق لـ X 2 لأي ثابت مع... ومع ذلك ، في ما يلي سوف نتفق على حذف هذه الثوابت المضافة. على العموم

أين نهو عدد صحيح موجب ، منذ ( x ن + 1/(ن+ 1)) ў = x ن... العلاقة (1) تحمل معنى أكثر عمومية إذا ناستبدل بأي رقم منطقي كباستثناء -1.

دالة مشتقة تعسفية لوظيفة معينة F(x) عادةً ما يُطلق عليه التكامل غير المحدود لـ F(x) وتدل على أنها

على سبيل المثال ، منذ (sin x) ў = كوس x، الصيغة صحيحة

في كثير من الحالات ، عندما تكون هناك صيغة لتكامل غير محدد لدالة معينة ، يمكن العثور عليها في العديد من الجداول المنشورة على نطاق واسع للتكاملات غير المحددة. تكاملات الدوال الأولية جدولية (تشمل القوى ، اللوغاريتمات ، الوظيفة الأسية ، الدوال المثلثية ، الدوال المثلثية العكسية ، بالإضافة إلى مجموعاتها المحدودة التي تم الحصول عليها باستخدام عمليات الجمع والطرح والضرب والقسمة). باستخدام التكاملات الجدولية ، يمكنك حساب تكاملات وظائف أكثر تعقيدًا. هناك طرق عديدة لحساب التكاملات غير المحددة ؛ الأكثر شيوعًا هو طريقة الاستبدال أو الاستبدال المتغير. يتكون من حقيقة أننا إذا أردنا استبدال التكامل غير المحدد (2) xعلى بعض الوظائف التفاضلية x = ز(ش) ، حتى لا يتغير التكامل ، فمن الضروري xوحل محله زў ( ش)دو... وبعبارة أخرى ، المساواة

(استبدال 2 x = شومن أين 2 DX = دو).

إليك طريقة تكامل أخرى - طريقة التكامل بالأجزاء. يعتمد على الصيغة المعروفة بالفعل

بعد دمج الجانبين الأيمن والأيسر ، ومراعاة ذلك

تسمى هذه الصيغة معادلة التكامل بالأجزاء.

مثال 2. مطلوب منها أن تجد. منذ كوس x= (الخطيئة x) ў ، يمكننا كتابة ذلك

من (5) وضع ش = xو الخامس= الخطيئة x، نحن نحصل

ومنذ ذلك الحين (–cos x) ў = الخطيئة xنجد ذلك و

يجب التأكيد على أننا قصرنا أنفسنا على مقدمة موجزة جدًا لموضوع واسع للغاية ، حيث تراكمت العديد من التقنيات الذكية.

وظائف متغيرين.

بسبب المنحنى ذ = F(x) لقد نظرنا في مهمتين.

1) أوجد ميل المماس للمنحنى عند نقطة معينة. يتم حل هذه المشكلة عن طريق حساب قيمة المشتق Fў ( x) في النقطة المحددة.

2) ابحث عن المنطقة الواقعة أسفل المنحنى فوق جزء المحور Xتحدها خطوط عمودية X = أو X = ب... يتم حل هذه المشكلة عن طريق حساب تكامل محدد.

كل من هذه المشاكل لها نظير في حالة السطح ض = F(x,ذ).

1) أوجد المستوى المماس للسطح عند نقطة معينة.

2) ابحث عن الحجم أسفل السطح فوق جزء المستوى هويحدها منحنى مع، ومن الجانب - عمودي على المستوى س صيمر عبر نقاط منحنى الحدود مع (سم... أرز. 22).

توضح الأمثلة التالية كيف يتم إنجاز هذه المهام.

مثال 4. أوجد المستوى المماس للسطح

عند النقطة (0،0،2).

يتم تعريف المستوى إذا تم إعطاء خطين متقاطعين فيهما. أحد هذه الخطوط ( ل 1) نركب الطائرة xz (في= 0) ، والثاني ( ل 2) - في الطائرة yz (x = 0) (سم... أرز. 23).

بادئ ذي بدء ، إذا في= 0 إذن ض = F(x,0) = 2 – 2x – 3x 2. المشتق فيما يتعلق Xالتي يرمز إليها Fў x(x,0) = –2 – 6x، في X= 0 له قيمة –2. مستقيم ل 1 معطى بواسطة المعادلات ض = 2 – 2x, في= 0 - مماس ل مع 1 ، خطوط تقاطع السطح مع المستوي في= 0. وبالمثل ، إذا X= 0 إذن F(0,ذ) = 2 – ذ – ذ 2 ، والمشتق فيما يتعلق فيلديه الشكل

لأن Fў ذ(0،0) = -1 ، منحنى مع 2 - خط تقاطع السطح مع المستوي yz- له ظل ل 2 معطى بواسطة المعادلات ض = 2 – ذ, X= 0. يحتوي مستوى الظل المطلوب على كلا الخطوط المستقيمة ل 1 و ل 2 ويكتب بواسطة المعادلة

هذه هي معادلة المستوى. بالإضافة إلى ذلك ، نحصل على خطوط مستقيمة ل 1 و ل 2 ، الإعداد ، على التوالي ، في= 0 و X = 0.

يمكن التحقق من حقيقة أن المعادلة (7) تحدد حقًا المستوى المماس على المستوى التجريبي إذا لاحظنا أن هذه المعادلة تحتوي على شروط من الدرجة الأولى مدرجة في المعادلة (6) ، وأنه يمكن تمثيل شروط الدرجة الثانية في شكل -. لأن هذا التعبير سالب لجميع القيم Xو في، بجانب X = في= 0 ، يقع السطح (6) في كل مكان أسفل المستوى (7) ، باستثناء النقطة ص= (0،0،0). يمكننا القول أن السطح (6) محدب لأعلى عند النقطة ص.

مثال 5. أوجد المستوى المماس للسطح ض = F(x,ذ) = x 2 – ذ 2 في الأصل 0.

على السطح في= 0 لدينا: ض = F(x,0) = x 2 و Fў x(x,0) = 2x... على ال مع 1 ، خطوط التقاطع ، ض = x 2. في هذه النقطة االمنحدر Fў x(0،0) = 0. على متن الطائرة X= 0 لدينا: ض = F(0,ذ) = –ذ 2 و Fў ذ(0,ذ) = –2ذ... على ال مع 2 ، خطوط التقاطع ، ض = –ذ 2. في هذه النقطة امنحدر منحنى مع 2 يساوي Fў ذ(0،0) = 0. منذ الظل إلى مع 1 و مع 2 محاور Xو في، المستوى المماس الذي يحتوي عليها هو المستوى ض = 0.

ومع ذلك ، بالقرب من الأصل ، فإن سطحنا ليس على جانب واحد من المستوى المماس. في الواقع ، المنحنى مع 1 في كل مكان ، باستثناء النقطة 0 ، تقع فوق مستوى الظل والمنحنى مع 2 - على التوالي تحتها. يتقاطع السطح مع المستوى المماس ض= 0 في خطوط مستقيمة في = Xو في = –X... ويقال أن مثل هذا السطح به نقطة سرج عند نقطة الأصل (الشكل 24).

المشتقات الجزئية.

في الأمثلة السابقة ، استخدمنا مشتقات من F (x,ذ) تشغيل Xوبواسطة في... دعونا ننظر الآن في هذه المشتقات بشكل عام. إذا كانت لدينا دالة لمتغيرين ، على سبيل المثال ، F(x,ذ) = x 2 – س ص، ثم يمكننا تحديد اثنين من "مشتقاتها الجزئية" في كل نقطة ، واحدة عن طريق تمييز الوظيفة فيما يتعلق Xوتحديد في، عن طريق التفريق فيما يتعلق فيوتحديد X... يشار إلى أول هذه المشتقات كـ Fў x(x,ذ) أو ¶ F/¶ x؛ الثانية - كيف Fو ў ذ... إذا كان كلا المشتقات المختلطة (بواسطة Xو في، تشغيل فيو X) متصلة ، ثم ¶ 2 F/¶ x¶ ذ= ¶ 2 F/¶ ذ¶ x؛ في مثالنا ¶ 2 F/¶ x¶ ذ= ¶ 2 F/¶ ذ¶ x = –1.

اشتقاق جزئي Fў x(x,ذ) يشير إلى معدل تغيير الوظيفة Fعند نقطة ( x,ذ) في اتجاه الزيادة X، أ Fў ذ(x,ذ) هو معدل تغير الوظيفة Fاتجاه تصاعدي في... معدل تغيير الوظيفة Fعند نقطة ( X,في) في اتجاه خط مستقيم يصنع زاوية فمع الاتجاه الإيجابي للمحور X، يسمى مشتق الوظيفة Fقريب؛ قيمتها عبارة عن مجموعة من مشتقين جزئيين للدالة تكاد تكون f في المستوى المماس مساوية (للصغير DXو دى) التغيير الحقيقي ضظاهريًا ، لكن حساب التفاضل عادة ما يكون أسهل.

الصيغة التي درسناها بالفعل من طريقة التغيير المتغير ، والمعروفة باسم مشتق دالة معقدة أو قاعدة سلسلة ، في الحالة أحادية البعد عندما فييعتمد على X، أ Xيعتمد على ر، بالشكل:

بالنسبة إلى دوال متغيرين ، فإن الصيغة المماثلة هي:

من السهل تعميم مفاهيم وتسميات التمايز الجزئي على أبعاد أعلى. على وجه الخصوص ، إذا تم إعطاء السطح ضمنيًا بواسطة المعادلة F(x,ذ,ض) = 0 ، يمكن إعطاء معادلة المستوى المماس للسطح شكلاً أكثر تناسقًا: معادلة مستوى الظل عند النقطة ( س (س 2/4)] ، ثم يتم دمجها X 0 إلى 1. النتيجة النهائية هي 3/4.

يمكن أيضًا تفسير الصيغة (10) على أنها ما يسمى بالتكامل المزدوج ، أي كحد لمجموع أحجام "الخلايا" الأولية. كل خلية لها قاعدة D xد ذوارتفاع يساوي ارتفاع السطح فوق نقطة ما من القاعدة المستطيلة ( سم... أرز. 26). يمكن إثبات أن كلا وجهتي النظر في الصيغة (10) متكافئتان. تستخدم التكاملات المزدوجة لإيجاد مراكز الجاذبية والعديد من اللحظات الموجودة في الميكانيكا.

إثبات أكثر صرامة للجهاز الرياضي.

حتى الآن ، قدمنا ​​مفاهيم وطرق حساب التفاضل والتكامل على مستوى حدسي ولم نتردد في اللجوء إلى الأشكال الهندسية. يبقى لنا أن نفكر بإيجاز في الأساليب الأكثر صرامة التي ظهرت في القرنين التاسع عشر والعشرين.

في بداية القرن التاسع عشر ، عندما انتهى عصر الهجوم والهجوم على "إنشاء التحليل الرياضي" ، برزت أسئلة تبريرها إلى الواجهة. في أعمال أبيل وكوشي وعدد من علماء الرياضيات البارزين الآخرين ، تم تحديد مفاهيم "الحد" و "الوظيفة المستمرة" و "السلسلة المتقاربة" بدقة. كان هذا ضروريًا من أجل تحقيق ترتيب منطقي لأساس التحليل الرياضي من أجل جعله أداة بحث موثوقة. أصبحت الحاجة إلى تبرير شامل أكثر وضوحًا بعد اكتشاف Weierstrass في عام 1872 لوظائف مستمرة في كل مكان ، ولكن لا توجد وظائف قابلة للتفاضل في أي مكان (الرسم البياني لمثل هذه الوظائف له فاصل عند كل نقطة). تركت هذه النتيجة انطباعًا غامرًا لدى علماء الرياضيات ، حيث تناقضت بوضوح مع حدسهم الهندسي. من الأمثلة الأكثر وضوحا على عدم موثوقية الحدس الهندسي هو المنحنى المستمر الذي أنشأه D. Peano ، والذي يملأ مربعًا معينًا تمامًا ، أي يمر بجميع نقاطه. أدت هذه الاكتشافات وغيرها إلى ظهور برنامج "الحساب" للرياضيات ، أي جعلها أكثر موثوقية من خلال إثبات جميع المفاهيم الرياضية باستخدام مفهوم العدد. كان للامتناع شبه المتشدد عن الوضوح في الأعمال على أسس الرياضيات تبريره التاريخي.

وفقًا للشرائع الحديثة للصرامة المنطقية ، من غير المقبول التحدث عن المنطقة الواقعة تحت المنحنى. ذ = F(x) وفوق مقطع المحور X، حتى F- وظيفة مستمرة ، دون تحديد المعنى الدقيق لمصطلح "المنطقة" أولاً وعدم إثبات أن المنطقة المحددة بهذه الطريقة موجودة بالفعل. تم حل هذه المشكلة بنجاح في عام 1854 من قبل ب. ريمان ، الذي قدم تعريفًا دقيقًا لمفهوم التكامل المحدد. منذ ذلك الحين ، كانت فكرة التلخيص وراء فكرة التكامل المحدد موضوع العديد من الدراسات العميقة والتعميمات. نتيجة لذلك ، من الممكن اليوم إعطاء معنى لتكامل محدد ، حتى لو كان التكامل غير متصل في كل مكان. أدت مفاهيم التكامل الجديدة ، التي ساهم في إنشائها أ. ليبيج (1875-1941) وغيره من علماء الرياضيات مساهمة كبيرة ، إلى زيادة قوة وجمال التحليل الرياضي الحديث.

لن يكون من المناسب الخوض في تفاصيل كل هذه المفاهيم وغيرها. سنقتصر فقط على تقديم تعريفات صارمة للحد والتكامل المحدد.

في الختام ، دعنا نقول أن التحليل الرياضي ، باعتباره أداة قيّمة للغاية في يد عالم ومهندس ، يجذب حتى اليوم انتباه علماء الرياضيات كمصدر للأفكار المثمرة. في الوقت نفسه ، يبدو أن التطور الحديث يشير إلى أن التحليل الرياضي يتم امتصاصه بشكل متزايد من قبل هذا السائد في القرن العشرين. فروع الرياضيات مثل الجبر المجرد والطوبولوجيا.

من المستحيل تمامًا حل المشكلات الفيزيائية أو الأمثلة في الرياضيات دون معرفة المشتق وطرق حسابه. المشتق من أهم مفاهيم التحليل الرياضي. قررنا تكريس مقال اليوم لهذا الموضوع الأساسي. ما هو المشتق ، ما هو معناه الفيزيائي والهندسي ، كيف نحسب مشتق دالة؟ يمكن دمج كل هذه الأسئلة في سؤال واحد: كيف نفهم المشتق؟

المعنى الهندسي والمادي للمشتق

يجب ألا تكون هناك وظيفة و (خ) تعطى في بعض الفترات (أ ، ب) ... النقاط х و х0 تنتمي إلى هذا الفاصل الزمني. عندما تتغير x ، تتغير الوظيفة نفسها. تغيير الحجة - الفرق بين قيمها x-x0 ... هذا الاختلاف مكتوب كـ دلتا س ويسمى زيادة الوسيطة. التغيير أو الزيادة في دالة هو الفرق في قيم الدالة عند نقطتين. تعريف مشتق:

مشتق دالة عند نقطة ما هو حد نسبة زيادة الدالة عند نقطة معينة إلى زيادة الوسيطة عندما تميل الأخيرة إلى الصفر.

خلاف ذلك ، يمكن كتابتها على النحو التالي:

ما الهدف من إيجاد مثل هذا الحد؟ وإليك ما يلي:

مشتق الوظيفة عند نقطة ما يساوي ظل الزاوية بين محور OX وظل الرسم البياني للوظيفة عند هذه النقطة.

المعنى المادي للمشتق: مشتق المسار فيما يتعلق بالوقت يساوي سرعة الحركة المستقيمة.

في الواقع ، منذ أوقات الدراسة ، يعلم الجميع أن السرعة مسار خاص. س = و (ر) و الوقت ر ... متوسط ​​السرعة خلال فترة زمنية:

لمعرفة سرعة الحركة في وقت واحد t0 تحتاج إلى حساب الحد:

القاعدة الأولى: إخراج ثابت

يمكن نقل الثابت خارج علامة المشتق. علاوة على ذلك ، يجب أن يتم ذلك. عند حل الأمثلة في الرياضيات ، خذ كقاعدة - إذا كان بإمكانك تبسيط التعبير ، فتأكد من التبسيط .

مثال. دعنا نحسب المشتق:

القاعدة الثانية: مشتق مجموع الوظائف

مشتق مجموع وظيفتين يساوي مجموع مشتقات هاتين الدالتين. وينطبق الشيء نفسه على مشتق فرق الوظائف.

لن نعطي دليلًا على هذه النظرية ، بل سننظر في مثال عملي.

أوجد مشتق دالة:

القاعدة الثالثة: مشتق من حاصل ضرب التوابع

يتم حساب مشتق منتج وظيفتين قابلتين للتفاضل بواسطة الصيغة:

مثال: أوجد مشتق دالة:

المحلول:

من المهم أن نقول هنا عن حساب مشتقات الوظائف المعقدة. مشتق دالة معقدة يساوي منتج مشتق هذه الدالة فيما يتعلق بالحجة الوسيطة بمشتق الوسيطة فيما يتعلق بالمتغير المستقل.

في المثال أعلاه ، نلتقي بالتعبير:

في هذه الحالة ، الوسيطة الوسيطة هي 8x أس الخامس. من أجل حساب مشتق مثل هذا التعبير ، نحسب أولاً مشتق الوظيفة الخارجية فيما يتعلق بالوسيطة الوسيطة ، ثم نضرب في مشتق الوسيطة المباشرة فيما يتعلق بالمتغير المستقل.

القاعدة الرابعة: مشتق خارج القسمة لوظيفتين

صيغة لتحديد مشتق حاصل قسمة وظيفتين:

حاولنا إخباركم عن مشتقات الدمى من الصفر. هذا الموضوع ليس بالبساطة التي يبدو عليها ، لذا كن حذرًا: غالبًا ما تكون هناك عيوب في الأمثلة ، لذا كن حذرًا عند حساب المشتقات.

لأي سؤال حول هذا الموضوع وموضوعات أخرى ، يمكنك الاتصال بخدمة الطلاب. في وقت قصير ، سنساعدك في حل أصعب اختبار والتعامل مع المهام ، حتى لو لم تكن قد قمت بحساب المشتقات من قبل.

حيث قمنا بتحليل أبسط المشتقات ، وكذلك تعرفنا على قواعد التفاضل وبعض التقنيات لإيجاد المشتقات. وبالتالي ، إذا لم تكن مهتمًا كثيرًا بمشتقات الدوال ، أو لم تكن بعض نقاط هذه المقالة واضحة تمامًا ، فاقرأ الدرس أعلاه أولاً. من فضلك ، استمع إلى الحالة المزاجية الجادة - المواد ليست بالأمر السهل ، لكنني سأظل أحاول تقديمها بطريقة بسيطة ويمكن الوصول إليها.

من الناحية العملية ، عليك التعامل مع مشتق دالة معقدة في كثير من الأحيان ، بل أقول ، دائمًا تقريبًا ، عندما يتم تكليفك بمهام لإيجاد المشتقات.

ننظر في الجدول إلى القاعدة (رقم 5) لتمييز دالة معقدة:

فهم. بادئ ذي بدء ، دعنا ننتبه إلى التسجيل. هنا لدينا وظيفتان - علاوة على ذلك ، الوظيفة ، بالمعنى المجازي ، مضمنة في الوظيفة. تسمى الوظيفة من هذا النوع (عندما تتداخل إحدى الوظائف في أخرى) بالدالة المعقدة.

سأقوم باستدعاء الوظيفة وظيفة خارجيةوالوظيفة - وظيفة داخلية (أو متداخلة).

! هذه التعريفات ليست نظرية ولا ينبغي أن تظهر في التصميم النهائي للتخصيصات. أنا أستخدم التعبيرات غير الرسمية "وظيفة خارجية" ، وظيفة "داخلية" فقط لتسهيل فهم المواد.

لتوضيح الموقف ، ضع في اعتبارك:

مثال 1

أوجد مشتق دالة

تحت شرط الجيب ، ليس لدينا فقط الحرف "X" ، ولكن تعبير عدد صحيح ، لذلك لن يكون من الممكن إيجاد المشتق مباشرة من الجدول. نلاحظ أيضًا أنه من المستحيل تطبيق القواعد الأربعة الأولى هنا ، ويبدو أن هناك اختلافًا ، لكن الحقيقة هي أنه لا يمكنك "تمزيق" شرط:

في هذا المثال ، من توضيحاتي ، من الواضح بشكل حدسي أن الوظيفة هي وظيفة معقدة ، وأن كثير الحدود هو وظيفة داخلية (تداخل) ، ووظيفة خارجية.

الخطوة الأولى، والتي يجب إجراؤها عند إيجاد مشتق دالة معقدة ، هو هذا معرفة أي وظيفة داخلية وأيها خارجية.

في حالة الأمثلة البسيطة ، يبدو من الواضح أن كثيرة الحدود متداخلة تحت الجيب. لكن ماذا لو كان كل شيء غير واضح؟ كيف تحدد بالضبط الوظيفة الخارجية وأيها داخلية؟ للقيام بذلك ، أقترح استخدام التقنية التالية ، والتي يمكن إجراؤها عقليًا أو في مسودة.

تخيل أننا بحاجة إلى حساب قيمة التعبير في الآلة الحاسبة (بدلاً من واحد ، يمكن أن يكون هناك أي رقم).

ماذا سنحسب أولا؟ أولاسوف تحتاج إلى القيام بالإجراء التالي: وبالتالي فإن كثير الحدود سيكون وظيفة داخلية:

ثانياسوف تحتاج إلى العثور عليها ، لذا فإن الجيب سيكون وظيفة خارجية:

بعد نحن اكتشفمع الوظائف الداخلية والخارجية ، حان الوقت لتطبيق قاعدة التمايز لوظيفة معقدة .

نبدأ في اتخاذ القرار. من الدرس كيف أجد المشتق؟نتذكر أن تصميم حل أي مشتق يبدأ دائمًا على هذا النحو - نضع التعبير بين قوسين ونضع حدًا في أعلى اليمين:

أولاأوجد مشتق الوظيفة الخارجية (الجيب) ، وانظر إلى جدول مشتقات الدوال الأولية ولاحظ ذلك. جميع الصيغ الجدولية قابلة للتطبيق حتى إذا تم استبدال "x" بتعبير معقد، في هذه الحالة:

لاحظ أن الوظيفة الداخلية لم يتغير ، نحن لا نتطرق إليه.

حسنًا ، من الواضح أن

نتيجة تطبيق الصيغة في التصميم النهائي يبدو كالتالي:

عادة ما يتم وضع عامل ثابت في بداية التعبير:

إذا كان هناك أي لبس ، فاكتب الحل واقرأ التفسيرات مرة أخرى.

مثال 2

أوجد مشتق دالة

مثال 3

أوجد مشتق دالة

كالعادة ، نكتب:

لنكتشف أين لدينا وظيفة خارجية ، وأين لدينا وظيفة داخلية. للقيام بذلك ، حاول (عقليًا أو في مسودة) لحساب قيمة التعبير في. ما الذي يجب عمله اولا؟ بادئ ذي بدء ، تحتاج إلى حساب ما تساوي القاعدة: مما يعني أن كثير الحدود هو الوظيفة الداخلية:

وعندها فقط يتم تنفيذ الأس ، وبالتالي ، فإن وظيفة الطاقة هي وظيفة خارجية:

حسب الصيغة ، أولا تحتاج إلى إيجاد مشتق الوظيفة الخارجية ، في هذه الحالة ، الدرجة. نحن نبحث عن الصيغة المطلوبة في الجدول:. نكرر مرة أخرى: أي صيغة جدولية صالحة ليس فقط لـ "x" ، ولكن أيضًا للتعبير المعقد... وبالتالي ، نتيجة تطبيق قاعدة تفاضل دالة معقدة التالي:

أؤكد مرة أخرى أنه عندما نأخذ مشتق الوظيفة الخارجية ، فإن الوظيفة الداخلية لا تتغير بالنسبة لنا:

يبقى الآن العثور على مشتق بسيط جدًا للدالة الداخلية و "مشط" النتيجة قليلاً:

مثال 4

أوجد مشتق دالة

هذا مثال لحل مستقل (الإجابة في نهاية البرنامج التعليمي).

لتوطيد فهم مشتق دالة معقدة ، سأقدم مثالًا بدون تعليقات ، أحاول اكتشافه بنفسك ، وتكهن أين هو الخارجي وأين الوظيفة الداخلية ، لماذا تم حل المهام بهذه الطريقة؟

مثال 5

أ) أوجد مشتق الوظيفة

ب) أوجد مشتق الوظيفة

مثال 6

أوجد مشتق دالة

هنا لدينا جذر ، ولتمييز الجذر ، يجب تمثيله كدرجة. وبالتالي ، نأتي بالدالة أولاً إلى شكل مناسب للتمايز:

عند تحليل الوظيفة ، توصلنا إلى استنتاج مفاده أن مجموع المصطلحات الثلاثة هو وظيفة داخلية ، وأن الأس دالة خارجية. نطبق قاعدة اشتقاق دالة معقدة :

يتم تمثيل الدرجة مرة أخرى على أنها جذرية (جذر) ، وبالنسبة لمشتق الوظيفة الداخلية ، نطبق قاعدة بسيطة لتمييز المجموع:

مستعد. يمكنك أيضًا إحضار التعبير إلى مقام موحد بين قوسين وكتابة كل شيء في كسر واحد. جميل بالطبع ، ولكن عندما يتم الحصول على مشتقات طويلة مرهقة ، فمن الأفضل عدم القيام بذلك (من السهل الخلط ، وارتكاب خطأ غير ضروري ، وسيكون من غير المناسب للمعلم التحقق).

مثال 7

أوجد مشتق دالة

هذا مثال لحل مستقل (الإجابة في نهاية البرنامج التعليمي).

من المثير للاهتمام أن نلاحظ أنه في بعض الأحيان ، بدلاً من قاعدة اشتقاق دالة معقدة ، يمكن للمرء استخدام القاعدة لاشتقاق حاصل القسمة ، لكن مثل هذا الحل سيبدو غير عادي باعتباره تحريفًا. هذا مثال نموذجي:

المثال 8

أوجد مشتق دالة

هنا يمكنك استخدام القاعدة لاشتقاق حاصل القسمة ، ولكن من الأكثر ربحية العثور على المشتق من خلال قاعدة اشتقاق دالة معقدة:

نحضر دالة الاشتقاق - نحرك الطرح خارج علامة المشتق ، ونرفع جيب التمام إلى البسط:

جيب التمام هو دالة داخلية ، الأُس دالة خارجية.
نحن نستخدم حكمنا :

أوجد مشتق الوظيفة الداخلية ، وأعد ضبط جيب التمام لأسفل:

مستعد. في المثال المدروس ، من المهم عدم الخلط بين العلامات. بالمناسبة ، حاول حلها بالقاعدة ، يجب أن تتطابق الإجابات.

المثال 9

أوجد مشتق دالة

هذا مثال لحل مستقل (الإجابة في نهاية البرنامج التعليمي).

حتى الآن ، نظرنا في الحالات التي كان لدينا فيها مرفق واحد فقط في وظيفة معقدة. في المهام العملية ، يمكنك غالبًا العثور على مشتقات ، حيث ، مثل الدمى المتداخلة ، واحدة داخل الأخرى ، 3 أو حتى 4-5 وظائف متداخلة في وقت واحد.

المثال 10

أوجد مشتق دالة

دعونا نفهم مرفقات هذه الوظيفة. محاولة تقييم التعبير باستخدام قيمة الاختبار. كيف نعتمد على الآلة الحاسبة؟

تحتاج أولاً إلى البحث ، مما يعني أن القوس هو أعمق تداخل:

ثم يجب أن يكون قوس جيب الزاوية هذا تربيعًا:

وأخيرًا ، ارفع الرقم 7 إلى القوة:

أي في هذا المثال لدينا ثلاث وظائف مختلفة ومرفقان ، في حين أن الوظيفة الأعمق هي القوس ، والدالة الخارجية هي الدالة الأسية.

نبدأ في الحل

حسب القاعدة أولا عليك أن تأخذ مشتق الدالة الخارجية. ننظر إلى جدول المشتقات ونجد مشتق الدالة الأسية: الاختلاف الوحيد هو أنه بدلاً من "x" لدينا تعبير مركب ، والذي لا ينفي صحة هذه الصيغة. إذن ، نتيجة تطبيق قاعدة اشتقاق دالة معقدة التالي.