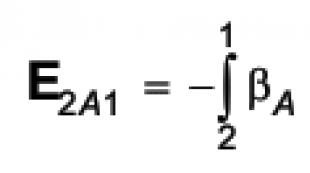Imtihonga hali ko'p vaqt borligini his qilyapsizmi? Bu oymi? Ikki? Yil? Amaliyot shuni ko'rsatadiki, agar talaba imtihonga oldindan tayyorgarlik ko'rishni boshlasa, uni eng yaxshi tarzda engadi. Yagona davlat imtihonida maktab o'quvchilari va bo'lajak abituriyentlarning eng yuqori ball olish yo'lida to'sqinlik qiladigan juda ko'p qiyin vazifalar mavjud. Siz bu to'siqlarni engib o'tishni o'rganishingiz kerak va bundan tashqari, buni qilish qiyin emas. Chiptalardan turli xil vazifalar bilan ishlash tamoyilini tushunishingiz kerak. Keyin yangilari bilan hech qanday muammo bo'lmaydi.

Bir qarashda logarifmlar nihoyatda murakkab ko'rinadi, ammo batafsil tahlil bilan vaziyat ancha soddalashadi. Agar siz Yagona davlat imtihonini eng yuqori ball bilan topshirmoqchi bo'lsangiz, ushbu maqolada biz nima qilishni taklif qilayotgan ushbu tushunchani tushunishingiz kerak.

Birinchidan, ushbu ta'riflarni ajratamiz. Logarifm (log) nima? Bu belgilangan raqamni olish uchun bazani ko'tarish kerak bo'lgan quvvatning ko'rsatkichidir. Agar aniq bo'lmasa, oddiy misolni ko'rib chiqaylik.

Bunday holda, 4 raqamini olish uchun pastki qismdagi tayanch ikkinchi kuchga ko'tarilishi kerak.

Endi ikkinchi kontseptsiyani ko'rib chiqaylik. Funksiyaning istalgan shakldagi hosilasi funksiyaning berilgan nuqtadagi o‘zgarishini tavsiflovchi tushunchadir. Biroq, bu maktab o'quv dasturi va agar siz ushbu tushunchalar bilan alohida muammolarga duch kelsangiz, mavzuni takrorlashga arziydi.

Logarifmning hosilasi

Ushbu mavzu bo'yicha Yagona davlat imtihon topshiriqlarida siz misol sifatida bir nechta topshiriqlarni berishingiz mumkin. Boshlash uchun, eng oddiy logarifmik lotin. Quyidagi funksiyaning hosilasini topish kerak.

Biz keyingi hosilani topishimiz kerak

Maxsus formula mavjud.

Bu holda x=u, log3x=v. Funktsiyamizdagi qiymatlarni formulaga almashtiramiz.

X ning hosilasi birga teng bo'ladi. Logarifm biroz qiyinroq. Ammo qadriyatlarni shunchaki almashtirsangiz, printsipni tushunasiz. Eslatib o'tamiz, lg x ning hosilasi o'nlik logarifmning hosilasi, ln x ning hosilasi esa natural logarifmning hosilasidir (e asosida).

Endi olingan qiymatlarni formulaga ulang. O'zingiz sinab ko'ring, keyin javobni tekshiramiz.

Ba'zilar uchun bu erda qanday muammo bo'lishi mumkin? Biz natural logarifm tushunchasini kiritdik. Keling, bu haqda gaplashaylik va shu bilan birga u bilan muammolarni qanday hal qilishni aniqlaymiz. Ayniqsa, uning ishlash tamoyilini tushunganingizda, siz hech qanday murakkab narsani ko'rmaysiz. Siz ko'nikishingiz kerak, chunki u ko'pincha matematikada qo'llaniladi (bundan ham ko'proq oliy o'quv yurtlarida).

Natural logarifmning hosilasi

Uning asosida u logarifmning e asosiga hosilasidir (bu irratsional son, taxminan 2,7). Aslida, ln juda oddiy, shuning uchun u ko'pincha matematikada umuman qo'llaniladi. Aslida, u bilan muammoni hal qilish ham muammo bo'lmaydi. Shuni esda tutish kerakki, tabiiy logarifmning e asosiga hosilasi x ga bo'lingan birga teng bo'ladi. Quyidagi misolning yechimi eng aniq bo'ladi.

Keling, uni ikkita oddiydan tashkil topgan murakkab funktsiya sifatida tasavvur qilaylik.

Buning uchun konvertatsiya qilish kifoya

Biz u ning x ga nisbatan hosilasini qidiramiz

Keling, ikkinchisini davom ettiramiz

Murakkab funktsiyaning hosilasini u=nx o'rniga qo'yish orqali yechish usulidan foydalanamiz.

Oxiri nima bo'ldi?

Keling, ushbu misolda n nimani anglatishini eslaylik? Bu natural logarifmda x ning oldida paydo bo'lishi mumkin bo'lgan har qanday raqam. Javob unga bog'liq emasligini tushunish muhimdir. O'zingiz xohlagan narsani almashtiring, javob hali ham 1/x bo'ladi.

Ko'rib turganingizdek, bu erda hech qanday murakkab narsa yo'q, siz ushbu mavzu bo'yicha muammolarni tez va samarali hal qilish tamoyilini tushunishingiz kerak. Endi siz nazariyani bilasiz, uni amalda qo'llash kifoya. Muammolarni hal qilish tamoyilini uzoq vaqt davomida eslab qolish uchun ularni hal qilishni mashq qiling. Maktabni tugatgandan keyin sizga bu bilim kerak bo'lmasligi mumkin, ammo imtihonda u har qachongidan ham dolzarb bo'ladi. Omad sizga!

Logarifmik hosila yordamida hosilalarni hisoblashga misollar keltirilgan.

Tarkib

Shuningdek qarang: Natural logarifmning xossalari

Yechim usuli

Mayli
(1)
x o'zgaruvchining differentsiallanuvchi funktsiyasidir. Birinchidan, biz uni y ijobiy qiymatlarni qabul qiladigan x qiymatlari to'plamida ko'rib chiqamiz: . Quyida biz olingan barcha natijalar ning salbiy qiymatlari uchun ham amal qilishini ko'rsatamiz.

Ayrim hollarda (1) funksiyaning hosilasini topish uchun uni oldindan logarifm qilish qulay.
,
va keyin hosilani hisoblang. Keyin kompleks funktsiyani differentsiallash qoidasiga ko'ra,
.
Bu yerdan
(2) .

Funksiya logarifmining hosilasi logarifmik hosila deyiladi:
.

y = funksiyaning logarifmik hosilasi f(x) bu funksiyaning natural logarifmining hosilasi: (ln f(x))'.

Salbiy y qiymatlari holati

Endi o'zgaruvchi ham ijobiy, ham salbiy qiymatlarni qabul qilishi mumkin bo'lgan holatni ko'rib chiqing. Bunday holda, modulning logarifmini oling va uning hosilasini toping:
.
Bu yerdan
(3) .
Ya'ni, umumiy holatda, siz funktsiya modulining logarifmining hosilasini topishingiz kerak.

(2) va (3) ni solishtirsak, bizda:
.
Ya'ni, logarifmik hosilani hisoblashning rasmiy natijasi modulni olganimiz yoki yo'qligimizga bog'liq emas. Shuning uchun, logarifmik hosilani hisoblashda biz funktsiyaning qanday belgisi borligi haqida tashvishlanishimiz shart emas.

Bu holat kompleks sonlar yordamida aniqlanishi mumkin. X ning ba'zi qiymatlari uchun manfiy bo'lsin: . Agar biz faqat haqiqiy sonlarni hisobga olsak, u holda funktsiya aniqlanmagan. Ammo, agar biz kompleks sonlarni hisobga olsak, biz quyidagilarni olamiz:
.
Ya'ni, funktsiyalar va murakkab konstanta bilan farqlanadi:
.
Doimiyning hosilasi nolga teng bo'lgani uchun
.

Logarifmik hosilaning xossasi

Bunday mulohazadan shunday xulosa kelib chiqadi funktsiyani ixtiyoriy doimiyga ko'paytirsangiz logarifmik hosila o'zgarmaydi :
.
Haqiqatan ham, foydalanish logarifmning xossalari, formulalar hosila summasi Va doimiyning hosilasi, bizda ... bor:

.

Logarifmik hosilaning qo'llanilishi

Dastlabki funktsiya daraja yoki ko'rsatkichli funktsiyalar mahsulotidan iborat bo'lgan hollarda logarifmik hosiladan foydalanish qulay. Bunda logarifm amali funksiyalar ko‘paytmasini ularning yig‘indisiga aylantiradi. Bu lotinni hisoblashni soddalashtiradi.

1-misol

Funktsiyaning hosilasini toping:
.

Keling, asl funktsiyani logarifm qilamiz:
.

X o'zgaruvchisiga nisbatan farqlaylik.
Sanoat jadvalida biz quyidagilarni topamiz:
.
Biz murakkab funksiyalarni differentsiallash qoidasini qo'llaymiz.
;
;
;
;
(A1.1) .
Quyidagiga ko'paytiring:

.

Shunday qilib, biz logarifmik hosilani topdik:
.
Bu yerdan biz asl funktsiyaning hosilasini topamiz:
.

Eslatma

Agar biz faqat haqiqiy raqamlardan foydalanmoqchi bo'lsak, u holda biz asl funktsiya modulining logarifmini olishimiz kerak:
.
Keyin
;
.
Va biz formulani oldik (A1.1). Shuning uchun natija o'zgarmadi.

2-misol

Logarifmik hosiladan foydalanib, funktsiyaning hosilasini toping
.

Keling, logarifmlarni olaylik:
(A2.1) .
X o'zgaruvchisiga qarab farqlang:
;
;

;
;
;
.

Quyidagiga ko'paytiring:
.
Bu yerdan logarifmik hosilani olamiz:
.

Asl funktsiyaning hosilasi:
.

Eslatma

Bu yerda asl funksiya manfiy emas: . da aniqlanadi. Agar logarifmni argumentning salbiy qiymatlari uchun aniqlash mumkin deb hisoblamasak, formula (A2.1) quyidagicha yozilishi kerak:
.
Chunki

Va
,
bu yakuniy natijaga ta'sir qilmaydi.

3-misol

Hosilini toping
.

Biz logarifmik hosila yordamida differentsiatsiya qilamiz. Shuni hisobga olgan holda logarifmni olaylik:
(A3.1) .

Farqlash orqali biz logarifmik hosilani olamiz.
;
;
;
(A3.2) .

O'shandan beri

.

Eslatma

Keling, argumentning manfiy qiymatlari uchun logarifm aniqlanishi mumkin degan taxminsiz hisob-kitoblarni amalga oshiraylik. Buning uchun asl funktsiya modulining logarifmini oling:
.
Keyin (A3.1) o'rniga bizda:
;

.
(A3.2) bilan solishtirsak, natija o'zgarmaganligini ko'ramiz.

Shuningdek qarang:

Murakkab hosilalar. Logarifmik hosila.
Kuch-ko'rsatkichli funktsiyaning hosilasi

Biz farqlash texnikamizni yaxshilashda davom etamiz. Ushbu darsda biz o'tgan materialni birlashtiramiz, yanada murakkab hosilalarni ko'rib chiqamiz, shuningdek, hosila topishning yangi usullari va usullari, xususan, logarifmik hosila bilan tanishamiz.

Tayyorgarlik darajasi past bo'lgan o'quvchilar maqolaga murojaat qilishlari kerak hosilani qanday topish mumkin? Yechimlarga misollar, bu sizning mahoratingizni deyarli noldan oshirishga imkon beradi. Keyinchalik, sahifani diqqat bilan o'rganishingiz kerak Murakkab funktsiyaning hosilasi, tushunish va hal qilish Hammasi men keltirgan misollar. Ushbu dars mantiqan uchinchisi bo'lib, uni o'zlashtirganingizdan so'ng siz juda murakkab funktsiyalarni ishonchli tarzda ajratasiz. “Yana qayerda? Bu yetarli!”, chunki barcha misollar va yechimlar haqiqiy sinovlardan olingan va amaliyotda tez-tez uchrab turadi.

Keling, takrorlashdan boshlaylik. Darsda Murakkab funktsiyaning hosilasi Biz batafsil sharhlar bilan bir qator misollarni ko'rib chiqdik. Differensial hisoblash va matematik tahlilning boshqa sohalarini o'rganish jarayonida siz tez-tez farqlashingiz kerak bo'ladi va misollarni batafsil tavsiflash har doim ham qulay emas (va har doim ham kerak emas). Shuning uchun biz hosilalarni og'zaki ravishda topishni mashq qilamiz. Buning uchun eng mos "nomzodlar" eng oddiy murakkab funktsiyalarning hosilalaridir, masalan:

Murakkab funktsiyalarni differentsiallash qoidasiga ko'ra :

Kelajakda boshqa matan mavzularini o'rganishda bunday batafsil yozuv ko'pincha talab qilinmaydi, talaba avtopilotda bunday lotinlarni qanday topishni biladi deb taxmin qilinadi. Tasavvur qilaylik, ertalab soat 3 da telefon jiringladi va yoqimli ovoz: "Ikki X ning tangensi nima?" Buning ortidan deyarli bir zumda va muloyim javob bo'lishi kerak: .

Birinchi misol darhol mustaqil yechim uchun mo'ljallangan bo'ladi.

1-misol

Quyidagi hosilalarni og‘zaki, bir harakatda toping, masalan: . Vazifani bajarish uchun siz faqat foydalanishingiz kerak elementar funksiyalarning hosilalari jadvali(agar siz buni hali eslamagan bo'lsangiz). Agar sizda biron bir qiyinchilik bo'lsa, darsni qayta o'qishni maslahat beraman Murakkab funktsiyaning hosilasi.

, , ,
, , ,
, , ,

, , ,

, , ,

, , ,

, ,

Dars oxirida javoblar

Murakkab hosilalar

Dastlabki artilleriya tayyorgarligidan so'ng, 3-4-5 funktsiyalarni o'rnatish misollari kamroq qo'rqinchli bo'ladi. Quyidagi ikkita misol ba'zilar uchun murakkab bo'lib tuyulishi mumkin, ammo agar siz ularni tushunsangiz (kimdir azoblanadi), differensial hisoblashda qolgan deyarli hamma narsa bolalarning haziliga o'xshaydi.

2-misol

Funktsiyaning hosilasini toping

Yuqorida aytib o'tilganidek, murakkab funktsiyaning hosilasini topishda, birinchi navbatda, kerak To'g'ri Investitsiyalaringizni TUSHUNING. Shubhalar mavjud bo'lsa, men sizga foydali texnikani eslataman: biz, masalan, "x" ning eksperimental qiymatini olamiz va (aqliy yoki qoralamada) bu qiymatni "dahshatli ifoda" ga almashtirishga harakat qilamiz.

1) Avval biz ifodani hisoblashimiz kerak, ya'ni yig'indi eng chuqur joylashuvdir.

2) Keyin logarifmni hisoblashingiz kerak:

4) Keyin kosinusni kubga aylantiring:

5) Beshinchi bosqichda farq:

6) Va nihoyat, eng tashqi funktsiya kvadrat ildizdir:

Murakkab funktsiyani farqlash formulasi teskari tartibda, eng tashqi funktsiyadan eng ichkigacha qo'llaniladi. Biz qaror qilamiz:

Hech qanday xatolik yo'qdek ...

(1) Kvadrat ildizning hosilasini oling.

(2) Biz qoida yordamida farqning hosilasini olamiz

(3) Uchlik hosilasi nolga teng. Ikkinchi muddatda biz darajaning hosilasini olamiz (kub).

(4) Kosinusning hosilasini oling.

(5) Logarifmning hosilasini oling.

(6) Va nihoyat, biz eng chuqur joylashtirishning hosilasini olamiz.

Bu juda qiyin tuyulishi mumkin, ammo bu eng shafqatsiz misol emas. Misol uchun, Kuznetsovning kollektsiyasini oling va tahlil qilingan lotinning barcha go'zalligi va soddaligini qadrlaysiz. Men shuni payqadimki, ular talaba murakkab funktsiyaning hosilasini qanday topishni tushunadimi yoki tushunmaydimi yoki yo'qligini tekshirish uchun imtihonda shunga o'xshash narsani berishni yaxshi ko'radilar.

Quyidagi misol siz o'zingiz hal qilishingiz mumkin.

3-misol

Funktsiyaning hosilasini toping

Maslahat: Avval chiziqlilik qoidalari va mahsulotni farqlash qoidasini qo'llaymiz

To'liq yechim va javob dars oxirida.

Kichikroq va chiroyliroq narsaga o'tish vaqti keldi.
Misol uchun ikkita emas, balki uchta funktsiyaning mahsulotini ko'rsatish odatiy hol emas. Uch omil mahsulotining hosilasi qanday topiladi?

4-misol

Funktsiyaning hosilasini toping

Avval qaraymiz, uchta funktsiyaning mahsulotini ikkita funktsiyaning mahsulotiga aylantirish mumkinmi? Misol uchun, agar mahsulotda ikkita polinom bo'lsa, biz qavslarni ochishimiz mumkin. Ammo ko'rib chiqilayotgan misolda barcha funktsiyalar boshqacha: daraja, ko'rsatkich va logarifm.

Bunday hollarda kerak ketma-ket mahsulotni farqlash qoidasini qo'llang ikki marta

Ayyorlik shundan iboratki, "y" bilan biz ikkita funktsiyaning mahsulotini belgilaymiz: va "ve" bilan logarifmni belgilaymiz: . Nima uchun buni qilish mumkin? Haqiqatan ham – bu ikki omilning mahsuli emas va qoida ishlamaydi?! Hech qanday murakkab narsa yo'q:

Endi qoidani ikkinchi marta qo'llash qoladi qavsga:

Siz ham buralib, qavs ichidan biror narsani qo'yishingiz mumkin, ammo bu holda javobni aynan shu shaklda qoldirgan ma'qul - tekshirish osonroq bo'ladi.

Ko'rib chiqilgan misolni ikkinchi usulda hal qilish mumkin:

Ikkala yechim ham mutlaqo ekvivalentdir.

5-misol

Funktsiyaning hosilasini toping

Bu mustaqil yechim uchun misol, namunada u birinchi usul yordamida hal qilinadi.

Keling, kasrlar bilan o'xshash misollarni ko'rib chiqaylik.

6-misol

Funktsiyaning hosilasini toping

Bu yerga bir necha usul bilan borishingiz mumkin:

Yoki shunday:

Lekin birinchi navbatda qismni differentsiallash qoidasidan foydalansak, yechim yanada ixchamroq yoziladi , butun hisoblagich uchun:

Asos sifatida, misol hal qilinadi va agar u shunday qoldirilsa, bu xato bo'lmaydi. Ammo vaqtingiz bo'lsa, javobni soddalashtirish mumkinligini bilish uchun har doim qoralamani tekshirish tavsiya etiladi? Numeratorning ifodasini umumiy maxrajga kamaytiramiz va keling, uch qavatli fraksiyadan xalos bo'laylik:

Qo'shimcha soddalashtirishlarning kamchiligi shundaki, hosilani topishda emas, balki maktabdagi oddiy o'zgarishlar paytida xato qilish xavfi mavjud. Boshqa tomondan, o'qituvchilar ko'pincha topshiriqni rad etadilar va lotinni "yodiga keltirishni" so'rashadi.

O'zingiz hal qilish uchun oddiyroq misol:

7-misol

Funktsiyaning hosilasini toping

Biz hosilani topish usullarini o'zlashtirishni davom ettirmoqdamiz va endi farqlash uchun "dahshatli" logarifm taklif qilingan odatiy holatni ko'rib chiqamiz.

8-misol

Funktsiyaning hosilasini toping

Bu erda siz murakkab funktsiyani farqlash qoidasidan foydalanib, uzoq yo'lni bosib o'tishingiz mumkin:

Ammo birinchi qadam sizni darhol tushkunlikka soladi - siz kasr kuchidan yoqimsiz hosila olishingiz kerak, keyin esa kasrdan.

Shunung uchun oldin"Murakkab" logarifmning hosilasini qanday olish kerak, u birinchi navbatda taniqli maktab xususiyatlaridan foydalangan holda soddalashtiriladi:

! Agar qo'lingizda mashq daftaringiz bo'lsa, ushbu formulalarni to'g'ridan-to'g'ri u erga ko'chiring. Agar sizda daftar bo'lmasa, ularni qog'ozga ko'chiring, chunki darsning qolgan misollari ushbu formulalar atrofida aylanadi.

Yechimning o'zi shunday yozilishi mumkin:

Funktsiyani o'zgartiramiz:

Hosilini topish:

Funktsiyani oldindan konvertatsiya qilishning o'zi yechimni ancha soddalashtirdi. Shunday qilib, farqlash uchun shunga o'xshash logarifm taklif qilinganda, uni har doim "buzish" tavsiya etiladi.

Va endi siz o'zingiz hal qilishingiz uchun bir nechta oddiy misollar:

9-misol

Funktsiyaning hosilasini toping

10-misol

Funktsiyaning hosilasini toping

Barcha o'zgarishlar va javoblar dars oxirida.

Logarifmik hosila

Agar logarifmlarning hosilasi shunday shirin musiqa bo'lsa, unda savol tug'iladi: ba'zi hollarda logarifmni sun'iy ravishda tashkil qilish mumkinmi? Mumkin! Va hatto zarur.

11-misol

Funktsiyaning hosilasini toping

Biz yaqinda shunga o'xshash misollarni ko'rib chiqdik. Nima qilish kerak? Ketma-ket ko'rsatkichni farqlash qoidasini, keyin esa mahsulotning differentsiallash qoidasini qo'llashingiz mumkin. Ushbu usulning nochorligi shundaki, siz uch qavatli katta qismga ega bo'lasiz, bu bilan siz umuman shug'ullanishni xohlamaysiz.

Ammo nazariya va amaliyotda logarifmik hosila kabi ajoyib narsa bor. Logarifmlarni sun'iy ravishda ikkala tomonga "osish" orqali tashkil qilish mumkin:

Eslatma : chunki funktsiya salbiy qiymatlarni qabul qilishi mumkin, keyin, odatda, modullardan foydalanishingiz kerak: , bu farqlanish natijasida yo'qoladi. Biroq, joriy dizayn ham qabul qilinadi, bu erda sukut bo'yicha u hisobga olinadi murakkab ma'nolari. Ammo agar qat'iy bo'lsa, unda ikkala holatda ham buni oldindan belgilash kerak.

Endi siz o'ng tomonning logarifmini iloji boricha "parchalashingiz" kerak (ko'zlaringiz oldida formulalar?). Men bu jarayonni batafsil tasvirlab beraman:

Keling, farqlashdan boshlaylik.
Biz ikkala qismni asosiy ostida yakunlaymiz:

O'ng tomonning hosilasi juda oddiy, men bunga izoh bermayman, chunki agar siz ushbu matnni o'qiyotgan bo'lsangiz, uni ishonchli tarzda boshqarishingiz kerak.

Chap tomon haqida nima deyish mumkin?

Chap tomonda biz bor murakkab funktsiya. Men savolni oldindan ko'raman: "Nega, logarifm ostida bitta "Y" harfi bormi?"

Gap shundaki, bu "bir harfli o'yin" - O'ZI FUNKSIYA(agar u juda aniq bo'lmasa, bevosita ko'rsatilgan funktsiyaning hosilasi maqolasiga qarang). Demak, logarifm tashqi funktsiya, “y” esa ichki funktsiyadir. Va biz murakkab funktsiyani farqlash uchun qoidadan foydalanamiz :

Chap tomonda, go'yo sehr bilan, bizda lotin bor. Keyinchalik, mutanosiblik qoidasiga ko'ra, biz "y" ni chap tomonning maxrajidan o'ng tomonning yuqori qismiga o'tkazamiz:

Keling, differensiatsiya paytida qanday "o'yinchi" funksiyasi haqida gapirganimizni eslaylik? Keling, shartni ko'rib chiqaylik:

Yakuniy javob:

12-misol

Funktsiyaning hosilasini toping

Bu siz o'zingiz hal qilishingiz uchun misoldir. Ushbu turdagi namunaning namunaviy dizayni dars oxirida.

Logarifmik hosiladan foydalanib, 4-7-sonli misollarning har qandayini hal qilish mumkin edi, boshqa narsa shundaki, u erda funktsiyalar oddiyroq va, ehtimol, logarifmik hosiladan foydalanish unchalik oqlanmagan.

Kuch-ko'rsatkichli funktsiyaning hosilasi

Biz bu funktsiyani hali ko'rib chiqmadik. Quvvat-eksponensial funktsiya bu uchun funktsiyadir daraja ham, asos ham "x" ga bog'liq. Har qanday darslikda yoki ma'ruzada sizga beriladigan klassik misol:

Kuch-eksponensial funksiyaning hosilasi qanday topiladi?

Hozirgina muhokama qilingan texnikadan foydalanish kerak - logarifmik lotin. Biz logarifmlarni ikkala tomonga osib qo'yamiz:

Qoida tariqasida, o'ng tomonda daraja logarifm ostidan chiqariladi:

Natijada, o'ng tomonda biz standart formula bo'yicha farqlanadigan ikkita funktsiya mahsulotiga egamiz. .

Biz hosilani topamiz, buning uchun ikkala qismni ham chiziqlar ostiga qo'yamiz:

Keyingi harakatlar oddiy:

Nihoyat:

Agar biron bir konvertatsiya to'liq aniq bo'lmasa, iltimos, 11-misolning tushuntirishlarini diqqat bilan qayta o'qing.

Amaliy topshiriqlarda kuch-eksponensial funktsiya har doim ko'rib chiqilgan ma'ruza misolidan ko'ra murakkabroq bo'ladi.

13-misol

Funktsiyaning hosilasini toping

Biz logarifmik hosiladan foydalanamiz.

O'ng tomonda bizda doimiy va ikkita omil ko'paytmasi bor - "x" va "logarifm x logarifmi" (boshqa logarifm logarifm ostida joylashgan). Farqlashda, biz eslayotganimizdek, konstantani darhol hosila belgisidan chiqarib tashlagan ma'qul, to'sqinlik qilmasligi uchun; va, albatta, biz tanish qoidani qo'llaymiz :

Eksponensial daraja funksiyalarini yoki noqulay kasr ifodalarini farqlashda logarifmik hosiladan foydalanish qulay. Ushbu maqolada biz batafsil echimlar bilan uni qo'llash misollarini ko'rib chiqamiz.

Keyingi taqdimot hosilalar jadvalidan foydalanish qobiliyatini, differentsiatsiya qoidalarini va murakkab funktsiyaning hosilasi formulasini bilishni o'z ichiga oladi.

Logarifmik hosila uchun formulani hosil qilish.

Birinchidan, logarifmlarni e asosiga olamiz, logarifmning xossalaridan foydalangan holda funktsiya shaklini soddalashtiramiz, so'ngra aniq belgilangan funktsiyaning hosilasini topamiz:

Masalan, ko‘rsatkichli daraja funksiyasi x ning x darajali hosilasi topilsin.

Logarifmlarni qabul qilish . Logarifmning xususiyatlariga ko'ra. Tenglikning ikkala tomonini farqlash natijaga olib keladi:

Javob: .

Xuddi shu misolni logarifmik hosiladan foydalanmasdan yechish mumkin. Siz ba'zi o'zgarishlarni amalga oshirishingiz va eksponensial quvvat funktsiyasini farqlashdan murakkab funktsiyaning hosilasini topishga o'tishingiz mumkin:

Misol.

Funktsiyaning hosilasini toping .

Yechim.

Ushbu misolda funktsiya kasr bo'lib, uning hosilasini differensiallash qoidalaridan foydalanib topish mumkin. Ammo iboraning noqulayligi tufayli bu ko'plab o'zgarishlarni talab qiladi. Bunday hollarda logarifmik hosila formulasidan foydalanish maqsadga muvofiqdir . Nega? Endi tushunasiz.

Avval topib olaylik. O'zgartirishlarda biz logarifmning xususiyatlaridan foydalanamiz (kasrning logarifmi logarifmalar ayirmasiga teng, mahsulotning logarifmi esa logarifmalar yig'indisiga teng va logarifm belgisi ostidagi ifoda darajasi bo'lishi mumkin) logarifm oldidagi koeffitsient sifatida olinadi):

Ushbu o'zgarishlar bizni juda oddiy iboraga olib keldi, uning hosilasini topish oson:

Olingan natijani logarifmik hosila formulasiga almashtiramiz va javobni olamiz:

Materialni birlashtirish uchun biz batafsil tushuntirishlarsiz yana bir nechta misol keltiramiz.

Misol.

Ko‘rsatkichli daraja funksiyasining hosilasini toping

Natural logarifm va logarifmning hosilasi uchun formulalarni isbotlash va hosil qilish a asosi. ln 2x, ln 3x va ln nx hosilalarini hisoblash misollari. n-tartibli logarifm hosilasi formulasini matematik induksiya usuli yordamida isbotlash.

Tarkib

Shuningdek qarang: Logarifm - xossalar, formulalar, grafik
Natural logarifm - xossalar, formulalar, grafik

Tabiiy logarifm va logarifmning hosilalari uchun formulalar hosil qilish.

X ning natural logarifmining hosilasi x ga bo'lingan birga teng:
(1) (ln x)' =.

a asosining logarifm hosilasi x o‘zgaruvchiga bo‘linib a ning natural logarifmiga ko‘paytirilgan birga teng:
(2) (log a x)' =.

Isbot

Birga teng bo'lmagan ijobiy son bo'lsin. X o'zgaruvchisiga bog'liq funktsiyani ko'rib chiqing, bu bazaning logarifmi:
.
Bu funktsiya da belgilangan. Uning x o‘zgaruvchisiga nisbatan hosilasi topilsin. Ta'rifga ko'ra, lotin quyidagi chegara hisoblanadi:
(3) .

Keling, ushbu ifodani ma'lum matematik xususiyatlar va qoidalarga qisqartirish uchun aylantiramiz. Buning uchun biz quyidagi faktlarni bilishimiz kerak:
A) Logarifmning xossalari. Bizga quyidagi formulalar kerak bo'ladi:
(4) ;
(5) ;
(6) ;
B) Logarifmning uzluksizligi va uzluksiz funksiya uchun limitlar xossasi:
(7) .
Bu erda chegarasi bo'lgan funksiya va bu chegara ijobiydir.
IN) Ikkinchi ajoyib chegaraning ma'nosi:
(8) .

Keling, ushbu faktlarni o'z chegaramizga qo'llaylik. Avval algebraik ifodani o'zgartiramiz
.
Buning uchun (4) va (5) xossalarni qo'llaymiz.

.

Keling, (7) xususiyatni va ikkinchi ajoyib chegarani (8) ishlatamiz:
.

Va nihoyat, biz mulkni qo'llaymiz (6):
.
Logarifmdan asosga e chaqirdi tabiiy logarifm. U quyidagicha belgilanadi:
.
Keyin;
.

Shunday qilib, logarifmning hosilasi uchun formula (2) ni oldik.

Natural logarifmning hosilasi

Biz yana bir bor logarifm hosilasi formulasini a asosiga yozamiz:
.
Bu formula natural logarifm uchun eng oddiy shaklga ega, buning uchun , . Keyin
(1) .

Ushbu soddaligi tufayli tabiiy logarifm matematik tahlilda va matematikaning differentsial hisob bilan bog'liq boshqa sohalarida juda keng qo'llaniladi. Boshqa asoslar bilan logarifmik funksiyalar (6) xossasi yordamida natural logarifm bilan ifodalanishi mumkin:
.

Logarifmning asosga nisbatan hosilasini (1) formuladan topish mumkin, agar siz doimiyni differentsiatsiya belgisidan chiqarsangiz:
.

Logarifmning hosilasini isbotlashning boshqa usullari

Bu erda biz eksponensial hosilaning formulasini bilamiz deb taxmin qilamiz:
(9) .
Keyin, logarifm ko'rsatkichning teskari funktsiyasi ekanligini hisobga olsak, natural logarifmaning hosilasi formulasini chiqarishimiz mumkin.

Natural logarifm hosilasi formulasini isbotlaylik, teskari funktsiyaning hosilasi uchun formulani qo'llash:
.
Bizning holatimizda. Natural logarifmga teskari funktsiya eksponensial hisoblanadi:
.
Uning hosilasi (9) formula bilan aniqlanadi. O'zgaruvchilar har qanday harf bilan belgilanishi mumkin. (9) formuladagi x o'zgaruvchisini y bilan almashtiring:
.
O'shandan beri
.
Keyin
.
Formula isbotlangan.

Endi biz natural logarifm hosilasi formulasini foydalanib isbotlaymiz murakkab funktsiyalarni farqlash qoidalari. va funktsiyalari bir-biriga teskari bo'lgani uchun
.
Bu tenglamani x o‘zgaruvchisiga nisbatan farqlaylik:
(10) .
x ning hosilasi birga teng:
.
Biz murakkab funktsiyalarni differentsiallash qoidasini qo'llaymiz:
.
Bu yerga . (10) ni almashtiramiz:
.
Bu yerdan
.

Misol

ning hosilalarini toping ln 2x, ln 3x Va lnnx.

Asl funktsiyalar shunga o'xshash shaklga ega. Shuning uchun biz funktsiyaning hosilasini topamiz y = log nx. Keyin n = 2 va n = 3 ni almashtiramiz. Shunday qilib, hosilalarining formulalarini olamiz ln 2x Va ln 3x .

Shunday qilib, biz funktsiyaning hosilasini qidiramiz
y = log nx .
Keling, ushbu funktsiyani ikkita funktsiyadan iborat murakkab funktsiya sifatida tasavvur qilaylik:
1) O'zgaruvchiga bog'liq funksiyalar: ;
2) O'zgaruvchiga bog'liq funksiyalar: .
Keyin asl funktsiya quyidagi funktsiyalardan iborat bo'ladi:
.

Funktsiyaning x o'zgaruvchiga nisbatan hosilasi topilsin:
.
Funktsiyaning o'zgaruvchiga nisbatan hosilasi topilsin:
.
Kompleks funktsiyaning hosilasi uchun formulani qo'llaymiz.
.
Mana biz uni o'rnatdik.

Shunday qilib, biz topdik:
(11) .
Biz hosila n ga bog'liq emasligini ko'ramiz. Agar mahsulotning logarifmi uchun formuladan foydalanib, asl funktsiyani o'zgartirsak, bu natija tabiiydir:
.
- bu doimiy. Uning hosilasi nolga teng. Keyin, yig'indini farqlash qoidasiga ko'ra, bizda:
.

; ; .

X modulining logarifmining hosilasi

Keling, yana bir muhim funktsiyaning hosilasi - x modulining natural logarifmini topamiz:
(12) .

Keling, ishni ko'rib chiqaylik. Keyin funktsiya quyidagicha ko'rinadi:
.
Uning hosilasi (1) formula bilan aniqlanadi:
.

Endi ishni ko'rib chiqaylik. Keyin funktsiya quyidagicha ko'rinadi:
,
Qayerda.
Lekin biz yuqoridagi misolda bu funksiyaning hosilasini ham topdik. U n ga bog'liq emas va ga teng
.
Keyin
.

Biz ushbu ikki holatni bitta formulaga birlashtiramiz:
.

Shunga ko'ra, logarifm a ga asoslanishi uchun bizda quyidagilar mavjud:
.

Natural logarifmning yuqori tartibli hosilalari

Funktsiyani ko'rib chiqing
.
Biz uning birinchi tartibli hosilasini topdik:
(13) .

Ikkinchi tartibli hosilani topamiz:
.
Uchinchi tartibli hosilani topamiz:
.
To'rtinchi tartibli hosilani topamiz:
.

n-tartibli hosila quyidagi shaklga ega ekanligini ko'rishingiz mumkin:
(14) .
Keling, buni matematik induksiya bilan isbotlaylik.

Isbot

n = 1 qiymatini (14) formulaga almashtiramiz:
.
dan beri, keyin n = bo'lganda 1 , formula (14) amal qiladi.

Faraz qilaylik, (14) formula n = k uchun qanoatlansin. Bu formulaning n = k uchun haqiqiyligini bildirishini isbotlaylik + 1 .

Darhaqiqat, n = k uchun bizda:
.
X o'zgaruvchisiga qarab farqlang:

.
Shunday qilib, biz oldik:
.
Bu formula n = k + uchun formula (14) bilan mos keladi 1 . Shunday qilib, (14) formula n = k uchun o'rinli degan farazdan (14) formula n = k + uchun o'rinli degan xulosaga keladi. 1 .

Demak, n-tartibli hosila uchun (14) formula har qanday n uchun amal qiladi.

A asosi uchun logarifmning yuqori tartibli hosilalari

Logarifmning n-tartibli hosilasini a ga asos qilib olish uchun uni natural logarifm bilan ifodalash kerak:
.
(14) formuladan foydalanib, n-chi hosilani topamiz:
.

Shuningdek qarang: