Matematik tahlil.

Seminar.

Mutaxassislik bo'yicha universitet talabalari uchun:

"Davlat va shahar ma'muriyati"

T.Z. Pavlova

Kolpashevo 2008 yil

1-bob. Tahlilga kirish

1.1 Funktsiyalar. Umumiy xususiyatlar

1.2 Limitlar nazariyasi

1.3 Funksiyaning uzluksizligi

2.1 Hosila tushunchasi

2.4 Funktsiyalarni o'rganish

2.4.1 To'liq funktsiyani o'rganish rejasi

2.4.2 Funktsiyalarni o'rganishga misollar

2.4.3. Segmentdagi funksiyaning eng katta va eng kichik qiymati

2.5 L'Hopital qoidasi

3.1 Noaniq integral

3.1.1 Ta'riflar va xususiyatlar

3.1.2 Integrallar jadvali

3.1.3 Integratsiyaning asosiy usullari

3.2 Aniq integral

3.2.2 Aniq integralni hisoblash usullari

4-bob. Bir nechta o'zgaruvchilarning funktsiyalari

4.1 Asosiy tushunchalar

4.2 Bir necha o'zgaruvchili funksiyalarning chegaralari va uzluksizligi

4.3.3 Umumiy differensial va uning taxminiy hisob-kitoblarga qo'llanilishi

5-bob. Klassik optimallashtirish usullari

6.1 Utility funksiyasi.

6.2 Befarqlik chiziqlari

6.3 Byudjet to'plami

Uyga topshiriqlar

1.1 Funktsiyalar. Umumiy xususiyatlar

Agar o'zgaruvchining har bir qiymati y o'zgaruvchining qandaydir aniq belgilangan haqiqiy qiymati bilan bog'langan bo'lsa, D - funktsiya sohasi bo'lgan haqiqiy sonlar to'plamida raqamli funktsiya aniqlanadi.

Funktsiyaning analitik ko'rinishi:

aniq:;

bilvosita:;

parametrik shaklda:

ta'rif sohasidagi turli formulalar:

Xususiyatlari.

Juft funktsiya:. Masalan, funktsiya juft, chunki ...

G'alati funktsiya: ... Masalan, funktsiya g'alati, chunki ...

Davriy funktsiya: , bu yerda T - funksiyaning davri,. Masalan, trigonometrik funktsiyalar.

Monotonik funktsiya. Ta'rif sohalaridan birortasi uchun - funktsiya ortib bormoqda, - kamaymoqda. Masalan, - ortib, - kamayuvchi.

Cheklangan funksiya. Agar shunday M raqami bo'lsa. Masalan, funktsiyalar va, beri .

1-misol. Funksiyalarni aniqlash sohasini toping.

+ 2 – 3 +

1.2 Limitlar nazariyasi

Ta'rif 1... Funktsiya chegarasi b soni bo'lsa, har qanday (- ixtiyoriy kichik musbat son) uchun argumentning shunday qiymatini topish mumkin, undan boshlab tengsizlik qondiriladi.

Belgilanishi:.

Ta'rif 2... Funktsiyaning chegarasi b soni bo'lsa, agar birontasi uchun (ixtiyoriy ravishda kichik musbat son bo'lsa) musbat son mavjud bo'lsa, unda tengsizlikni qondiruvchi x ning barcha qiymatlari uchun tengsizlik amal qiladi.

Belgilanishi:.

Ta'rif 3. Funktsiya yoki uchun cheksiz kichik deb ataladi, agar yoki.

Xususiyatlari.

1. Chekli sonli cheksiz kichik miqdorlarning algebraik yig‘indisi cheksiz kichik miqdordir.

2. Cheklangan funksiya (doimiy, boshqa cheksiz kichik miqdor) bo‘yicha cheksiz kichik miqdorning ko‘paytmasi cheksiz kichik miqdordir.

3. Chegarasi nolga teng bo‘lmagan funksiyaga cheksiz kichik miqdorni bo‘lish qismi cheksiz kichik miqdordir.

Ta'rif 4. Funktsiya cheksiz katta da deyiladi, agar.

Xususiyatlari.

1. Chegarasi nolga teng bo‘lmagan funksiya bo‘yicha cheksiz katta miqdorning ko‘paytmasi cheksiz katta miqdordir.

2. Cheksiz katta qiymat va chegaralangan funksiya yig‘indisi cheksiz katta qiymatdir.

3. Cheksiz katta miqdorni chegarasi bo‘lgan funksiyaga bo‘lish qismi cheksiz katta miqdordir.

Teorema.(Cheksiz kichik miqdor va cheksiz katta miqdor o'rtasidagi munosabat.) Agar funktsiya () da cheksiz kichik bo'lsa, u holda funksiya () da cheksiz katta miqdor bo'ladi. Va aksincha, agar funktsiya () da cheksiz katta bo'lsa, u holda funktsiya () da cheksiz kichik bo'ladi.

Limit teoremalari.

1. Funksiyaning bir nechta chegarasi bo‘lishi mumkin emas.

2. Bir nechta funksiyalarning algebraik yig‘indisining chegarasi bu funksiyalar chegaralarining algebraik yig‘indisiga teng:

3. Bir nechta funksiyalar ko‘paytmasining chegarasi ushbu funksiyalar chegaralarining ko‘paytmasiga teng:

4. Darajaning chegarasi chegaraning darajasiga teng:

5. Agar bo'linuvchi chegara mavjud bo'lsa, bo'linish chegarasi chegaralar qismiga teng:

.

6. Birinchi diqqatga sazovor chegara.

Oqibatlari:

7. Ikkinchi ajoyib chegara:

Oqibatlari:

Ekvivalent cheksiz kichik qiymatlar uchun:

Limitlarni hisoblash.

Limitlarni hisoblashda chegaralar haqidagi asosiy teoremalardan, uzluksiz funksiyalarning xossalaridan, shu teorema va xossalardan kelib chiqadigan qoidalardan foydalaniladi.

1-qoida. Funksiyaning shu nuqtada uzluksiz bo‘lgan nuqtasidagi chegarani topish uchun funksiyadagi chegara belgisi ostidagi x argumenti o‘rniga uning chegara qiymatini qo‘yish kerak.

2-misol. Toping

2-qoida. Agar kasr chegarasini topishda maxrajning chegarasi nolga teng bo'lsa va pay chegarasi nolga teng bo'lsa, bunday funktsiyaning chegarasi.

Misol 3. Toping

3-qoida. Agar kasr chegarasini topishda maxraj chegarasi teng bo'lsa va pay chegarasi noldan farq qilsa, bunday funktsiyaning chegarasi nolga teng bo'ladi.

4-misol. Toping

Ko'pincha argument uchun chegara qiymatini almashtirish kabi aniqlanmagan iboralarga olib keladi

.

Bunday hollarda funksiya chegarasini topish noaniqlikni ochish deyiladi. Noaniqlikni oshkor qilish uchun chegaraga o'tishdan oldin ushbu ifodani o'zgartirish kerak. Noaniqliklarni oshkor qilish uchun turli usullar qo'llaniladi.

4-qoida... Turning noaniqligi sublimit funktsiyasini o'zgartirish orqali aniqlanadi, shuning uchun son va maxrajda chegarasi nolga teng bo'lgan koeffitsientni tanlash va kasrni u bilan kamaytirib, qism chegarasini topish uchun. Buning uchun sanoq va maxraj ko‘paytiriladi yoki son va maxrajga bog‘langan ifodalar bilan ko‘paytiriladi.

5-qoida. Agar sublimit ifodasi trigonometrik funktsiyalarni o'z ichiga olgan bo'lsa, unda birinchi ajoyib chegara turning noaniqligini fosh qilish uchun ishlatiladi.

.

6-qoida... At shaklining noaniqligini aniqlash uchun pastki chegara kasrning sonini va maxrajini argumentning eng yuqori darajasiga bo'lish kerak, so'ngra qism chegarasini topish kerak.

Mumkin natijalar:

1) kerakli chegara, agar bu darajalar bir xil bo'lsa, hisoblagich va maxraj argumentining eng yuqori darajalaridagi koeffitsientlar nisbatiga teng;

2) sonning argumenti darajasi maxrajning argumenti darajasidan yuqori bo'lsa, chegara cheksizlikka teng;

3) agar hisoblovchining argumenti darajasi maxraj argumentining darajasidan past bo'lsa, chegara nolga teng.

a)

beri

Darajalar teng, ya'ni chegara yuqori darajalarda koeffitsientlar nisbatiga teng, ya'ni. ...

b)

Numeratorning darajasi, maxraji 1 ga teng, bu chegara ekanligini bildiradi

v)

Numeratorning darajasi 1 ga, maxrajning darajasi esa 0 ga teng.

7-qoida... Shaklning noaniqligini aniqlash uchun pastki chegara kasrning sonini va maxrajini konjugat ifodaga ko'paytirish kerak.

10-misol.

8-qoida... Ikkinchi ajoyib chegara va uning oqibatlari turlarning noaniqligini ochish uchun ishlatiladi.

Buni isbotlash mumkin

11-misol.

12-misol.

13-misol.

9-qoida... Subliminal funktsiyasi cheksiz kichiklikni o'z ichiga olgan noaniqliklarni ochib berganda, bu cheksizlarning chegaralarini almashtirish kerak. ularga ekvivalent cheksiz kichik elementlar chegarasida.

14-misol.

15-misol.

10-qoida. L'Hôpital qoidasi (2.6-bandga qarang).

1.3 Funksiyaning uzluksizligi

Argument sifatida funktsiya chegarasi a ga moyil bo'lsa, mavjud bo'lsa va shu nuqtadagi funktsiya qiymatiga teng bo'lsa, funktsiya nuqtada uzluksizdir.

Ekvivalent shartlar:

1. ;

3.

Buzilish nuqtasi tasnifi:

birinchi turdagi tanaffus

Bir martalik - bir tomonlama chegaralar mavjud va tengdir;

Fatal (sakrash) - bir tomonlama chegaralar teng emas;

ikkinchi turdagi uzilish: nuqtada funksiya chegarasi mavjud emas.

16-misol. Funksiyaning nuqtadagi uzilish tabiatini aniqlang yoki shu nuqtadagi funksiyaning uzluksizligini isbotlang.

chunki funktsiya aniqlanmagan, shuning uchun bu nuqtada u uzluksiz emas. Chunki va shunga mos ravishda, , keyin birinchi turdagi olinadigan uzilish nuqtasi.

b)

vazifa (a) bilan solishtirganda, funktsiya shunday bir nuqtada kengaytirilgan , shuning uchun bu funktsiya shu nuqtada uzluksizdir.

Funktsiya aniqlanmaganda;

.

Chunki bir tomonlama chegaralardan biri cheksiz bo'lsa, u ikkinchi turdagi sinish nuqtasidir.

2-bob. Differensial hisoblash

2.1 Hosila tushunchasi

Hosila ta'rifi

Berilgan funktsiyaning hosilasi yoki argument o'sishi nolga moyil bo'lganda, funktsiya o'sishining mos keladigan argument o'sishiga nisbati chegarasi:

Yoki .

Hosilning mexanik ma’nosi funksiyaning o‘zgarish tezligidir. Hosilning geometrik ma'nosi - bu funksiya grafigiga teginish burchagining tangensi:

2.2 Differensiallashning asosiy qoidalari

Ism	Funktsiya	Hosil
Doimiy koeffitsientga ko'paytirish
Ikki funktsiyaning algebraik yig'indisi
Ikki funktsiyaning mahsuloti
Shaxsiy ikkita funktsiya
Murakkab funktsiya

Asosiy elementar funksiyalarning hosilalari

P / p raqami.	Funktsiya nomi	Funksiya va uning hosilasi
1	doimiy
2	quvvat funktsiyasi maxsus holatlar
3	eksponensial funktsiya maxsus holat
4	logarifmik funktsiya maxsus holat
5	trigonometrik funktsiyalar
6	teskari trigonometrik

b)

2.3 Yuqori tartibli hosilalar

Funktsiyaning ikkinchi tartibli hosilasi

Funktsiyaning ikkinchi tartibli hosilasi:

18-misol.

a) funksiyaning ikkinchi tartibli hosilasini toping.

Yechim. Avval birinchi tartibli hosilani topamiz .

Birinchi tartibli hosilaning hosilasini olaylik.

19-misol. Funksiyaning uchinchi tartibli hosilasini toping.

2.4 Funktsiyalarni o'rganish

2.4.1 Funktsiyani to'liq o'rganish rejasi:

To'liq funktsiyani o'rganish rejasi:

1. Boshlang'ich tadqiqot:

Domen va qiymatlar oralig'ini toping;

Umumiy xususiyatlarni aniqlang: paritet (g'alatilik), davriylik;

Koordinata o'qlari bilan kesishish nuqtalarini toping;

Doimiylik sohalarini aniqlang.

2. Asimptotalar:

Vertikal asimptotalarni toping, agar;

Qiya asimptotalarni toping:.

Agar biron bir raqam bo'lsa, u holda - gorizontal asimptotlar.

3. Tadqiqotdan foydalanish:

Kritik nuqtalarni toping, ular. mavjud yoki mavjud bo'lmagan nuqtalar;

O'sish oraliqlarini aniqlang, ular. intervallar, qaysi va kamayuvchi funktsiyalari -;

Ekstremani aniqlang: u o'tganda "+" dan "-" belgisini o'zgartiradigan nuqtalar maksimal nuqtalar, "-" dan "+" gacha - minimal.

4. Tadqiqotdan foydalanish:

Qaysi yoki mavjud bo'lmagan nuqtalarni toping;

Qavariqlik joylarini toping, ya'ni. konkavlar bo'lgan intervallarni;

Burilish nuqtalarini toping, ya'ni. o'tishda belgi o'zgargan nuqtalar.

1. Tadqiqotning alohida elementlari topilganidek, asta-sekin grafikda chiziladi.

2. Agar funktsiya grafigini qurishda qiyinchiliklar yuzaga kelsa, u holda funktsiyaning qiymatlari ba'zi qo'shimcha nuqtalarda topiladi.

3. Tadqiqotning maqsadi - funktsiyaning xatti-harakatining xarakterini tavsiflash. Shuning uchun aniq grafik tuzilmaydi, balki topilgan elementlar (ekstrema, burilish nuqtalari, asimptotlar va boshqalar) aniq ko'rsatilgan uning yaqinlashishi.

4. Yuqoridagi rejaga qat'iy rioya qilish shart emas; funktsiya xatti-harakatlarining xarakterli elementlarini e'tibordan chetda qoldirmaslik kerak.

2.4.2 Funktsiyani o'rganishga misollar:

1)

2) Funktsiya g'alati:

.

3) Asimptotalar.

- vertikal asimptotlar, chunki

Egri asimptota.

5)

- burilish nuqtasi.

2) Funktsiya g'alati:

3) Asimptotalar: Vertikal asimptotlar yo'q.

Egiluvchan:

- qiya asimptotlar

4) - funksiya kuchayadi.

- burilish nuqtasi.

Ushbu funktsiyaning sxematik diagrammasi:

2) Umumiy funksiya

3) Asimptotalar

- qiya asimptotlar yo'q

- gorizontal asimptota da

- burilish nuqtasi

Ushbu funktsiyaning sxematik diagrammasi:

2) Asimptotalar.

- vertikal asimptota, chunki

- qiya asimptotlar yo'q

, - gorizontal asimptota

Ushbu funktsiyaning sxematik diagrammasi:

2) Asimptotalar

- vertikal asimptota da, beri

- qiya asimptotlar yo'q

, - gorizontal asimptota

3) - intervallarning har birida funktsiya kamayadi.

Ushbu funktsiyaning sxematik diagrammasi:

Segmentdagi funksiyaning eng katta va eng kichik qiymatini topish uchun diagrammadan foydalanishingiz mumkin:

1. Funktsiyaning hosilasini toping.

2. Funksiyaning mavjud yoki mavjud bo‘lmagan kritik nuqtalarini toping.

3. Funksiyaning berilgan segmentga va uning uchlariga tegishli kritik nuqtalardagi qiymatini toping va ulardan eng kattasini va eng kichigini tanlang.

Misol. Berilgan segmentdagi funksiyaning eng kichik va eng katta qiymatini toping.

25. orasida

2) - tanqidiy nuqtalar

26. orasida.

Hosilda mavjud emas, lekin 1 bu intervalga tegishli emas. Funktsiya intervalda kamayadi, ya'ni eng katta qiymat yo'q, lekin eng kichik qiymat mavjud.

2.5 L'Hopital qoidasi

Teorema. Ikki cheksiz kichik yoki cheksiz katta funktsiyalarning nisbati chegarasi, agar ikkinchisi ko'rsatilgan ma'noda mavjud bo'lsa, ularning hosilalari nisbati chegarasiga (cheklangan yoki cheksiz) tengdir.

Bular. turdagi noaniqliklarni oshkor qilganda yoki quyidagi formuladan foydalanishingiz mumkin:

.

27.

3-bob. Integral hisob

3.1 Noaniq integral

3.1.1 Ta'riflar va xususiyatlar

Ta'rif 1. Funktsiya if uchun antiderivativ deyiladi.

Ta'rif 2. f (x) funksiyaning noaniq integrali bu funksiya uchun barcha anti hosilalar yig'indisidir.

Belgilash: , bu yerda c ixtiyoriy doimiydir.

Noaniq integral xossalari

1. Noaniq integralning hosilasi:

2. Noaniq integralning differensiali:

3. Differensialning noaniq integrali:

4. Ikki funktsiya yig'indisining (farqining) noaniq integrali:

5. O‘zgarmas ko‘paytmani noaniq integral belgisidan tashqariga ko‘chirish:

3.1.2 Integrallar jadvali

.1.3 Integrasiyaning asosiy usullari

1. Noaniq integralning xossalaridan foydalanish.

29-misol.

2. Differensial belgi ostida olib kelish.

30-misol.

3. O'zgaruvchan almashtirish usuli:

a) integralda almashtirish

qayerda - asl funktsiyadan ko'ra integrallash osonroq bo'lgan funksiya; - funksiyaga teskari funksiya; funksiyaning anti hosilasi hisoblanadi.

31-misol.

b) shaklning integraliga almashtirish:

32-misol.

33-misol.

4. Qismlar bo'yicha integratsiya usuli:

34-misol.

35-misol.

Keling, integralni alohida olaylik

Keling, integralimizga qaytaylik:

3.2 Aniq integral

3.2.1 Aniq integral tushunchasi va uning xossalari

Ta'rif. Uzluksiz funksiya qandaydir intervalda berilgan bo'lsin. Keling, uning grafigini tuzamiz.

Yuqoridan egri chiziq bilan, chapdan va o'ngdan to'g'ri chiziqlar bilan va pastdan a va b nuqtalar orasidagi abscissa o'qi segmenti bilan chegaralangan figuraga egri chiziqli trapesiya deyiladi.

S - maydon - kavisli trapezoid.

Intervalni nuqta bilan ajrating va quyidagilarni oling:

Integral yig'indisi:

Ta'rif. Aniq integral - bu integral yig'indining chegarasi.

Aniq integral xossalar:

1. O‘zgarmas koeffitsientni integral belgisidan chiqarish mumkin:

2. Ikki funktsiyaning algebraik yig‘indisining integrali bu funksiyalar integrallarining algebraik yig‘indisiga teng:

3. Agar integrallash segmenti qismlarga bo’linsa, butun segment bo’yicha integral yuzaga kelgan qismlarning har biri uchun integrallar yig’indisiga teng bo’ladi, ya’ni. har qanday a, b, c uchun:

4. Agar segmentda bo'lsa, u holda

5. Integral chegaralari o'zaro almashinishi mumkin, bunda integral belgisi o'zgaradi:

6.

7. Nuqtadagi integral 0 ga teng:

8.

9. (“o‘rtacha haqida”) y = f (x) integrallanuvchi funksiya bo‘lsin. Keyin , bu erda, f (c) f (x) ning o'rtacha qiymati:

10. Nyuton-Leybnits formulasi

,

Bu erda F (x) f (x) ga qarshi hosiladir.

3.2.2 Aniq integralni hisoblash usullari.

1. To'g'ridan-to'g'ri integratsiya

35-misol.

a)

b)

v)

e)

2. Aniq integral belgisi ostidagi o‘zgaruvchilarning o‘zgarishi .

36-misol.

2. Aniq integraldagi qismlar bo'yicha integrallash .

37-misol.

a)

b)

e)

3.2.3 Aniq integralning qo'llanilishi

Xarakterli	Funktsiya turi	Formula
	Dekart koordinatalarida
kavisli sektor maydoni	qutb koordinatalarida
kavisli trapezoid maydoni	parametrik shaklda
yoy uzunligi	Dekart koordinatalarida
yoy uzunligi	qutb koordinatalarida
yoy uzunligi	parametrik shaklda
tana hajmi aylanish	Dekart koordinatalarida
berilgan ko'ndalang bilan tana hajmi ko'ndalang kesim

38-misol. Chiziqlar bilan chegaralangan shaklning maydonini hisoblang: va .

Yechim: Bu funksiyalar grafiklarining kesishish nuqtalarini topamiz. Buning uchun funksiyalarni tenglashtiramiz va tenglamani yechamiz

Shunday qilib, kesishish nuqtalari va.

Formuladan foydalanib, rasmning maydonini topamiz

.

Bizning holatda

Javob: maydoni teng (kvadrat birlik).

4.1 Asosiy tushunchalar

Ta'rif. Agar biron bir qoidaga ko'ra, z o'zgaruvchisining bir yoki bir nechta qiymati ma'lum bir to'plamdan har bir mustaqil sonlar juftligiga tayinlangan bo'lsa, u holda z o'zgaruvchisi ikkita o'zgaruvchining funktsiyasi deb ataladi.

Ta'rif. z funksiyaning sohasi z funksiyasi mavjud bo‘lgan juftliklar to‘plamidir.

Ikki oʻzgaruvchili funksiyaning sohasi Oxy koordinata tekisligidagi nuqtalar toʻplamidir. Z-koordinata ilova deb ataladi, so'ngra funksiyaning o'zi E 3 fazoda qandaydir sirt sifatida tasvirlanadi. Masalan:

39-misol. Funksiya sohasini toping.

a)

O'ng tarafdagi ifoda faqat uchun ma'nolidir. Bu shuni anglatadiki, bu funktsiyaning sohasi koordinatali R radiusli doiraning ichida va chegarasida joylashgan barcha nuqtalarning yig'indisidir.

Ushbu funktsiyaning sohasi tekislikning barcha nuqtalari, to'g'ri chiziqlar nuqtalaridan tashqari, ya'ni. koordinata o'qlari.

Ta'rif. Funksiya darajasidagi chiziqlar - bu koordinatalar tekisligidagi egri chiziqlar turkumi.

40-misol. Funksiya darajasidagi chiziqlarni toping .

Yechim. Berilgan funksiyaning darajali chiziqlari tenglama bilan tasvirlangan tekislikdagi egri chiziqlar oilasidir

Oxirgi tenglama radiusning O 1 (1, 1) nuqtasida markazlashgan doiralar oilasini tasvirlaydi. Bu funksiya bilan tasvirlangan inqilob yuzasi (paraboloid) x = 1, y = 1 tenglamalar bilan berilgan o'qdan uzoqlashganda "tikroq" bo'ladi. (4-rasm).

4.2 Bir necha o'zgaruvchili funksiyalarning chegaralari va uzluksizligi.

1. Limitlar.

Ta'rif. A soni funktsiyaning chegarasi deyiladi, chunki nuqta nuqtaga intiladi, agar har bir ixtiyoriy kichik son uchun har qanday nuqta uchun shart to'g'ri bo'ladigan son mavjud bo'lsa va shart ... Ular yozadilar: .

41-misol. Chegaralarni toping:

bular. chegara bog'liq va, shuning uchun, u mavjud emas.

2. Davomiylik.

Ta'rif. Nuqta funksiyaning aniqlanish sohasiga tegishli bo'lsin. U holda funktsiya agar nuqtada uzluksiz deb ataladi

(1)

bundan tashqari, nuqta o'zboshimchalik bilan nuqtaga intiladi.

Agar biror nuqtada (1) shart bajarilmasa, u holda bu nuqta funksiyaning uzilish nuqtasi deyiladi. Bu quyidagi hollarda bo'lishi mumkin:

1) Funktsiya nuqtada aniqlanmagan.

2) Hech qanday cheklov yo'q.

3) Bu chegara mavjud, lekin u teng emas.

42-misol. Berilgan funksiya nuqtada uzluksiz ekanligini aniqlang, agar.

Tushundim demak, bu funksiya nuqtada uzluksizdir.

chegarasi k ga bog'liq, ya'ni. u berilgan nuqtada mavjud emas, demak, funksiya shu nuqtada uzilishga ega.

4.3 Bir necha o‘zgaruvchili funksiyalarning hosilalari va differentsiallari

4.3.1 Birinchi tartibning qisman hosilalari

Funksiyaning x argumentiga nisbatan qisman hosilasi y o‘zgaruvchining o‘zgarmas qiymati uchun bitta x o‘zgaruvchining funksiyasining oddiy hosilasi bo‘lib, quyidagicha belgilanadi:

Funksiyaning y argumentiga nisbatan qisman hosilasi x o‘zgaruvchining o‘zgarmas qiymatida bitta y o‘zgaruvchining funksiyasining oddiy hosilasi bo‘lib, quyidagicha belgilanadi:

43-misol. Funksiyalarning qisman hosilalarini toping.

4.3.2 Ikkinchi tartibli qisman hosilalar

Ikkinchi tartibli qisman hosilalar birinchi tartibli qisman hosilalarning qisman hosilalaridir. Shaklning ikkita o'zgaruvchisi funktsiyasi uchun to'rt turdagi ikkinchi tartibli qisman hosilalar mumkin:

Turli oʻzgaruvchilarga nisbatan differensiatsiya qilinadigan ikkinchi tartibli qisman hosilalar aralash hosilalar deyiladi. Ikki marta differentsiallanuvchi funksiyaning ikkinchi tartibli aralash hosilalari teng.

44-misol. Ikkinchi tartibli qisman hosilalarni toping.

4.3.3 Umumiy differensial va uning taxminiy hisob-kitoblarga qo'llanilishi.

Ta'rif. Ikki o‘zgaruvchili funksiyaning birinchi tartibli differensialligi formula bo‘yicha topiladi

.

45-misol. Funksiyaning umumiy differentsialini toping.

Yechim. Keling, qisman hosilalarni topamiz:

.

X va y argumentlarining kichik o'sishi uchun funktsiya taxminan dz ga teng o'sishni oladi, ya'ni. ...

Funktsiyaning nuqtadagi taxminiy qiymatini topish formulasi, agar uning nuqtadagi aniq qiymati ma'lum bo'lsa:

46-misol. Toping .

Yechim. Keling,

Keyin formuladan foydalanamiz

Javob. .

Misol 47. Taxminan hisoblang.

Yechim. Funktsiyani ko'rib chiqaylik. Bizda ... bor

Misol 48. Taxminan hisoblang.

Yechim. Funktsiyani ko'rib chiqing ... Biz olamiz:

Javob. .

4.3.4 Implisit funktsiyani farqlash

Ta'rif. Agar funktsiya z ga nisbatan yechilmaydigan tenglama bilan berilgan bo'lsa, u yopiq deyiladi.

Bunday funktsiyaning qisman hosilalari quyidagi formulalar bilan topiladi:

49-misol. Tenglama orqali berilgan z funksiyaning qisman hosilalarini toping .

Yechim.

Ta'rif. Agar funktsiya y ga nisbatan yechilmaydigan tenglama bilan berilgan bo'lsa, u yopiq deyiladi.

Bunday funktsiyaning hosilasi quyidagi formula bo'yicha topiladi:

.

50-misol. Bu funksiyalarning hosilalarini toping.

5.1 Bir necha o‘zgaruvchili funksiyaning mahalliy ekstremumlari

Ta'rif 1. Funktsiya agar nuqtada maksimalga ega

Ta'rif 2. Funksiya if nuqtada minimalga ega nuqtaga etarlicha yaqin va undan farq qiladigan barcha nuqtalar uchun.

Ekstremum uchun zaruriy shart. Agar funksiya biror nuqtada ekstremumga yetsa, funksiyaning qisman hosilalari yo‘qoladi yoki bu nuqtada mavjud bo‘lmaydi.

Qisman hosilalarning yo'q bo'lib ketadigan yoki mavjud bo'lmagan nuqtalari kritik deyiladi.

Ekstremumning etarli belgisi. Funktsiya kritik nuqtaning qaysidir qo'shnisida aniqlansin va shu nuqtada uzluksiz ikkinchi tartibli qisman hosilalarga ega bo'lsin.

1) nuqtada mahalliy maksimalga ega, agar va;

2) nuqtada mahalliy minimumga ega, agar va;

3) agar nuqtada mahalliy ekstremumga ega bo'lmasa;

Ikki o'zgaruvchili funktsiyaning ekstremumini o'rganish sxemasi.

1. Funksiyaning qisman hosilalarini toping: va.

2. Tenglamalar sistemasini yeching va funksiyaning kritik nuqtalarini toping.

3. Ikkinchi tartibli qisman hosilalarni toping, ularning kritik nuqtalardagi qiymatlarini hisoblang va etarli shartdan foydalanib, ekstremallarning mavjudligi haqida xulosa chiqaring.

4. Funksiyaning ekstremal qismini toping.

51-misol. Funksiyaning ekstremumlarini toping .

1) qisman hosilalarni toping.

2) Tenglamalar sistemasini yeching

4) Ikkinchi tartibli qisman hosilalarni va ularning kritik nuqtalardagi qiymatlarini toping:. Shu nuqtada biz quyidagilarni olamiz:

demak, nuqtada ekstremum yo'q. Shu nuqtada biz quyidagilarni olamiz:

demak, nuqtada minimal bo'ladi.

5.2 Global ekstremum (funktsiyaning eng yuqori va eng past qiymati)

Ba'zi bir yopiq to'plamda uzluksiz bo'lgan bir nechta o'zgaruvchilardan iborat funktsiyaning eng katta va eng kichik qiymatlariga ekstremum nuqtalarda yoki to'plam chegarasida erishiladi.

Eng yuqori va eng past qiymatlarni topish sxemasi.

1) Mintaqada yotgan kritik nuqtalarni toping, ushbu nuqtalarda funksiyaning qiymatini hisoblang.

2) maydon chegarasidagi funksiyani o‘rganing; agar chegara bir nechta turli chiziqlardan iborat bo'lsa, u holda tadqiqot har bir sayt uchun alohida amalga oshirilishi kerak.

3) funksiyaning olingan qiymatlarini solishtiring va eng katta va eng kichikni tanlang.

52-misol. To'rtburchakdagi eng katta va eng kichik funksiya qiymatlarini toping.

Yechim. 1) Funktsiyaning kritik nuqtalarini toping, buning uchun qisman hosilalarni topamiz: va tenglamalar tizimini yeching:

A kritik nuqta olindi. Olingan nuqta belgilangan maydon ichida joylashgan,

Hudud chegarasi to'rt segmentdan iborat: va. Har bir segmentdagi funksiyaning eng katta va eng kichik qiymatini toping.

4) Olingan natijalarni solishtiring va uni nuqtalarda toping .

6-bob. Iste'molchi tanlovi modeli

Biz n xil tovar bor deb taxmin qilamiz. Keyin ma'lum tovarlar to'plami n o'lchovli vektor bilan belgilanadi , bu yerda i-chi mahsulotning miqdori. X tovarning barcha to'plamlari to'plami fazo deb ataladi.

Yakka tartibdagi iste'molchining tanlovi afzallik munosabatlari bilan tavsiflanadi: iste'molchi istalgan ikkita to'plam haqida aytishi mumkin, deb ishoniladi, bu ko'proq ma'qulroq yoki u ular orasidagi farqni ko'rmaydi. Afzallik munosabati o'tishli: agar to'plam to'plamdan afzal bo'lsa va to'plam to'plamdan afzal bo'lsa, to'plam to'plamdan afzalroqdir. Biz iste'molchining xulq-atvori individual iste'molchining aksiomasi bilan to'liq tavsiflangan deb taxmin qilamiz: har bir individual iste'molchi o'zining afzalliklari tizimidan kelib chiqqan holda iste'mol qilish, xarid qilish va hokazolar haqida qaror qabul qiladi.

6.1 Utility funksiyasi

X iste'molchi to'plamlari to'plamida funktsiya aniqlanadi , iste'molchi to'plamidagi qiymati iste'molchining ushbu to'plam uchun jismoniy shaxsning taxminiga teng. Funktsiya iste'molchining foydali funktsiyasi yoki iste'molchining afzal ko'rish funktsiyasi deb ataladi. Bular. har bir iste'molchi o'zining foydali funktsiyasiga ega. Lekin iste'molchilarning butun to'plamini ma'lum iste'molchilar sinflariga (yoshi, mulkiy holati va boshqalar bo'yicha) bo'lish mumkin va har bir sinfga ba'zi, ehtimol, o'rtacha foydalilik funktsiyasi tayinlanishi mumkin.

Shunday qilib, funktsiya iste'molchi bahosi yoki ma'lum bir to'plamni sotib olayotganda shaxsning ehtiyojlarini qondirish darajasidir. Agar ma'lum bir shaxs uchun to'plam afzalroq bo'lsa, u holda.

Utility funksiyasi xususiyatlari.

1.

Foydalilik funksiyasining birinchi qisman hosilalari mahsulotlarning marjinal foydaliliklari deb ataladi. Bu xususiyatdan kelib chiqadiki, bir mahsulot iste'molining ko'payishi, boshqa mahsulotlarning iste'moli o'zgarishsiz qolishi iste'molchi bahosining oshishiga olib keladi. Vektor funktsiyaning gradienti bo'lib, u funktsiyaning eng katta o'sish yo'nalishini ko'rsatadi. Funktsiya uchun uning gradienti mahsulotlarning marjinal foydalilik vektoridir.

2.

Bular. har qanday tovarning marjinal foydaliligi iste'molning oshishi bilan kamayadi.

3.

Bular. har bir mahsulotning marjinal foydaliligi boshqa mahsulot miqdori ortib boradi.

Foydali funksiyalarning ayrim turlari.

1) Neoklassik:.

2) Kvadrat: bu erda matritsa manfiy aniq va uchun .

3) Logarifmik funksiya:.

6.2 Befarqlik chiziqlari

Amaliy muammolar va iste'molchi tanlash modellarida ko'pincha ikkita tovar to'plamining alohida holati qo'llaniladi, ya'ni. foydali funksiya ikkita o'zgaruvchiga bog'liq bo'lganda. Befarqlik chizig'i - bu shaxsning ehtiyojlarini qondirish darajasi bir xil bo'lgan iste'molchilar to'plamini bog'laydigan chiziq. Aslini olganda, befarqlik chiziqlari funksiya darajasining chiziqlaridir. Befarq chiziq tenglamalari: .

Befarqlik chiziqlarining asosiy xossalari.

1. Ehtiyojlarni qondirishning turli darajalariga mos keladigan befarqlik chiziqlari tegmaydi va kesishmaydi.

2. Befarqlik chiziqlari kamayadi.

3. Befarqlik chiziqlari pastga qarab qavariq.

2-xususiyat muhim taxminiy tenglikni nazarda tutadi.

Bu nisbat shaxs ikkinchi mahsulot iste'molini qanchalik ko'paytirishi (kamaytirishi) kerakligini ko'rsatadi, shu bilan birga birinchi mahsulot iste'molini bir birlikka kamaytirsa (ko'paytirsa), uning ehtiyojlarini qondirish darajasini o'zgartirmasdan. Nisbat birinchi mahsulotning ikkinchisiga almashinish tezligi, qiymat esa birinchi mahsulotning ikkinchisiga almashinish tezligi deb ataladi.

53-misol. Agar birinchi tovarning marjinal foydaliligi 6, ikkinchisi esa 2 bo'lsa, birinchi tovar iste'moli bir birlikka kamayishi bilan ikkinchi tovar iste'molini 3 birlikka oshirish kerak. ehtiyojlarni qondirishning bir xil darajasi.

6.3 Byudjet to'plami

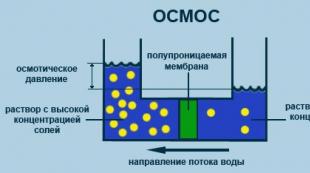
Mayli - n ta mahsulot to'plami uchun narxlar vektori; I - jismoniy shaxsning mahsulot to'plamini sotib olishga sarflashga tayyor bo'lgan daromadi. Berilgan narxlarda qiymati I dan oshmaydigan tovarlar to'plami B byudjet to'plami deb ataladi. Bundan tashqari, I bo'lgan tovarlar to'plami B byudjet to'plamining G chegarasi deb ataladi. B to'plami G chegarasi va tabiiy cheklovlar bilan chegaralangan.

Byudjet to'plami tengsizliklar tizimi bilan tavsiflanadi:

Ikkita tovar to'plami uchun byudjet to'plami B (1-rasm) koordinata o'qlari va to'g'ri chiziq bilan chegaralangan koordinatalar tizimidagi uchburchakdir.

6.4 Iste'molchi talabi nazariyasi

Iste'mol nazariyasida iste'molchi har doim o'z foydaliligini maksimal darajada oshirishga intiladi va u uchun yagona cheklov - bu tovarlar to'plamini sotib olishga sarflashi mumkin bo'lgan cheklangan daromad I. Umuman olganda, iste'molchini tanlash muammosi (bozorda iste'molchining oqilona xatti-harakati muammosi) quyidagicha tuzilgan: iste'molchi to'plamini toping. , bu berilgan byudjet cheklovi uchun foydalilik funksiyasini maksimal darajada oshiradi. Ushbu muammoning matematik modeli:

Ikkita mahsulot to'plami bo'lsa:

Geometrik jihatdan bu muammoni hal qilish G byudjet to'plamining chegarasi va befarqlik chizig'i o'rtasidagi aloqa nuqtasidir.

Ushbu muammoning yechimi tenglamalar tizimini echishga qisqartiriladi:

(1)

Ushbu tizimning yechimi iste'molchi tanlash muammosini hal qilishdir.

Iste'molchi tanlash muammosini hal qilish talab nuqtasi deb ataladi. Bu talab nuqtasi narxlar va daromadga bog'liq I. Ya'ni. talab nuqtasi talabning funktsiyasidir. O'z navbatida, talab funktsiyasi n ta funktsiya to'plami bo'lib, ularning har biri argumentga bog'liq:

Bu funksiyalar tegishli tovarlarning talab funksiyalari deyiladi.

54-misol. Bozordagi ikkita tovar to‘plami, ular uchun ma’lum narxlar va I daromadlari uchun, agar foydalilik funksiyasi ko‘rinishga ega bo‘lsa, talab funksiyalarini toping. .

Yechim. Foydali funksiyani farqlaylik:

.

Olingan ifodalarni (1) o'rniga qo'ying va tenglamalar tizimini oling:

Bunda har bir mahsulot uchun sarflangan mablag‘ iste’molchi daromadining yarmini tashkil etadi va sotib olingan mahsulot miqdori unga sarflangan summaga teng bo‘lib, mahsulot narxiga bo‘linadi.

55-misol. Foydalilik birinchi yaxshilik uchun, ikkinchisi,

birinchi mahsulotning narxi, ikkinchisining narxi. Daromad. Foydalilikni oshirish uchun iste'molchi qancha sotib olishi kerak?

Yechim. Foydali funksiyalarning hosilalarini topamiz, ularni (1) tizimga almashtiramiz va uni yechamiz:

Ushbu tovarlar to'plami iste'molchi uchun foydalilikni maksimal darajada oshirish nuqtai nazaridan maqbuldir.

Sinov alohida daftarda ro'yxatga olish kitobi raqamining oxirgi raqami bilan tanlangan variantga muvofiq amalga oshirilishi kerak. Har bir muammo shart, batafsil yechim va xulosani o'z ichiga olishi kerak.

1. Hisoblash faniga kirish

Topshiriq 1. Funksiyaning aniqlanish sohasini toping.

5.

Masala 2. Funksiyalarning chegaralarini toping.

.

3-topshiriq. Funksiyaning uzilish nuqtalarini toping va ularning turini aniqlang.

1. 2. 3.

2-bob. Bitta o‘zgaruvchili funksiyaning differentsial hisobi

4-topshiriq. Bu funksiyalarning hosilalarini toping.

1.a); b) c) y =;

d) y = x 6 + + + 5; e) y = x tg x + ln sin x + e 3x;

f) y = 2 x - arksin x.

2.a) ; b) y =; c) y =; d) y = x 2 - + 3; e) y = e cos; f) y =.

3.a) y = lnx; b) y =; c) y = ln;

4. a) y =; b) y = (e 5 x - 1) 6; c) y =; d) y =; e) y = x 8 ++ + 5; f) y = 3 x - arksin x.

5.a) y = 2x 3 - + e x; b) y =; c) y =;

d) y =; e) y = 2 cos; f) y =.

6.a) y = lnx; b) y =; c) y = ln;

d) y =; e) y = x 7 + + 1; f) y = 2.

7.a) ; b) y =; c) y =; d) y = x 2 + xsinx +; e) y = e cos; f) y =.

8. a) y =; b) y = (3 x - 4) 6; c) y = sintg;

d) y = 3x 4 - - 9+ 9; e) y =;

f) y = x 2 + arcsin x - x.

9.a); b) ; c) y =; d) y = 5 sin 3 x; e) y = x 3 - - 6+ 3; f) y = 4x 4 + ln.

10.a) b) y =; c) y = (3 x - 4) 6; d) y =; e) y = x 2 - x; f) y = e sin 3 x + 2.

5-topshiriq. Funktsiyani o'rganing va uning grafigini tuzing.

1. a) b) c).

2.a) b) v) .

3.a) b) v) .

4.b) v)

5.a) b) v) .

6.a) b) v) .

7. a) b) c).

8. a) b) c).

9.a) b) c).

10. a) b) v) .

6-topshiriq. Berilgan segmentdagi funksiyaning eng katta va eng kichik qiymatini toping.

1. .

3. .

6. .

8. .

9. .

10. .

3-bob. Integral hisob

Masala 7. Noaniq integrallarni toping.

1.a) b);

2.a) ; b) c) d).

4. G)

5.a) ; b); v) ; G).

6.a) ; b); v); G)

7.a) ; b) ; v) ; G)

8.a) ; b); v) ; G) .

9.a) ; b) c); G).

10.a) b) v) ; G) .

Masala 8. Aniq integrallarni hisoblang.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

Masala 9. Noto'g'ri integrallarni toping yoki ularning ajralib turishini isbotlang.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Masala 10. Egri chiziqlar bilan chegaralangan maydon maydonini toping

1. .2. .

5. 6.

7. , .8..

10. , .

4-bob. Bir necha o‘zgaruvchili funksiyaning differentsial hisobi.

11-topshiriq. Funksiya sohasini toping (chizmada ko'rsating).

Masala 12. uchun funksiyaning uzluksizligini o‘rganing

Masala 13. Aniq aniqlangan funksiyaning hosilasini toping.

Masala 14. Taxminan hisoblang

1.a); b) ; v)

2.a) ; b); v) .

3.a) ; b) ; v) .

4.a) ; b) ; v) .

5. a); b) ; v) .

6. a); b); v) .

7. a); b) ; v) .

8.a); b) ; v)

9.a) ; b); v) .

10. a); b) ; v)

Masala 15. Ekstrema uchun funktsiyani o'rganing.

7. .

8. .

9. .

10. .

Masala 16. Berilgan yopiq sohadagi funksiyaning eng katta va eng kichik qiymatini toping.

1.to'rtburchakda

2.

3. to'rtburchakda

4.parabola bilan chegaralangan mintaqada

Va abscissa.

5.kvadrat

6.koordinata o‘qlari va to‘g‘ri chiziq bilan chegaralangan uchburchakda

7.koordinata o'qlari va to'g'ri chiziq bilan chegaralangan uchburchakda

8. koordinata o'qlari va to'g'ri chiziq bilan chegaralangan uchburchakda

9.parabola bilan chegaralangan mintaqada

Va abscissa.

10.parabola bilan chegaralangan mintaqada

Va abscissa.

Asosiy

1. M.S. Krassus, B.P. Chuprynov. Matematika asoslari va uning iqtisodiy ta’limda qo‘llanilishi: Darslik. - 4-nashr, ISP. - M .: Delo, 2003 yil.

2. M.S. Krassus, B.P. Chuprynov. Iqtisodiy mutaxassisliklar uchun matematika: Darslik. - 4-nashr, ISP. - M .: Delo, 2003 yil.

3. M.S. Krassus, B.P. Chuprynov. Iqtisodiyot bakalavriat darajasi uchun matematika. Darslik. - 4-nashr, ISP. - M .: Delo, 2005 yil.

4. Iqtisodchilar uchun oliy matematika. Universitetlar uchun darslik / N.Sh. Kremer, B.A. Putko, I.M. Trishin, M.N. Fridman; Ed. prof. N.Sh. Kremer, - 2-nashr, Qayta ko'rib chiqilgan. va qo'shing. - M: BIRLIK, 2003 yil.

5. Kremer N.Sh, Putko BA, Trishin IM, Fridman M.N. Iqtisodiy mutaxassisliklar uchun oliy matematika. Darslik va seminar (I va II qismlar) / Ed. prof. N.Sh. Kremer, - 2-nashr, Qayta ko'rib chiqilgan. va qo'shing. - M: Oliy ta'lim, 2007. - 893p. - (Fan asoslari)

6. Danko P.E., Popov A.G., Kozhevnikova T.Ya. Mashqlar va masalalarda oliy matematika. M. oʻrta maktab. 1999 yil.

Qo'shimcha

1. I.I. Bavrin, V.L. Dengizchilar. Oliy matematika. "Vlados gumanitar nashriyot markazi", 2002 yil.

2. I.A. Zaitsev. Oliy matematika. "O'rta maktab", 1998 yil.

3. A.S. Solodovnikov, V.A. Babaytsev, A.V. Brailov, I.G. Shandra. Iqtisodiyotda matematika /ikki qismda/. M. Moliya va statistika. 1999 yil.

talabalar uchun tibbiy, pediatriya, stomatologiya

va tibbiyot profilaktika fakultetlari

laboratoriya ishlariga

“Matematik analizning asosiy tushunchalari”

1. Mavzuning ilmiy-uslubiy asoslanishi:

Hosila va differensial tushunchalar matematik analizning asosiy tushunchalaridan biridir. Hosilalarni hisoblash fizika va matematikadan ko‘plab masalalarni yechishda (tezlik, tezlanish, bosim va boshqalarni topish) zarur. Hosila tushunchasining ahamiyati, xususan, funktsiyaning hosilasi uning argumenti o'zgarganda ushbu funktsiyaning o'zgarish tezligini tavsiflashi bilan belgilanadi.

Differensialdan foydalanish taxminiy hisob-kitoblarni amalga oshirish, shuningdek, xatolarni baholash imkonini beradi.

Funktsiyalarning hosilalari va differentsiallarini topish usullari va ularni qo'llash differensial hisoblashning asosiy muammosini tashkil qiladi. Hosila tushunchasiga ehtiyoj harakat tezligini hisoblash va egri chiziqqa teginish burchagini topish masalasini shakllantirish bilan bog'liq holda paydo bo'ladi. Teskari masala ham mumkin: tezlik bo'yicha bosib o'tilgan masofani aniqlang va teginish qiyalik tangensi bilan mos keladigan funktsiyani toping. Bu teskari masala noaniq integral tushunchasiga olib keladi.

Aniq integral tushunchasi bir qator amaliy masalalarda, xususan, tekis figuralarning maydonlarini hisoblash, oʻzgaruvchan kuch bajargan ishni hisoblash, funksiyaning oʻrtacha qiymatini topish masalalarida qoʻllaniladi.

Turli fizik, kimyoviy, biologik jarayonlar va hodisalarni matematik tavsiflashda ko'pincha o'rganilayotgan miqdorlarni emas, balki ularning bu miqdorlarning turli tartibli hosilalarini ham o'z ichiga olgan tenglamalar qo'llaniladi. Masalan, bakteriyalarning ko'payishi qonunining eng oddiy versiyasiga ko'ra, ko'payish tezligi ma'lum bir vaqtda bakteriyalar soniga mutanosibdir. Agar bu miqdor N (t) bilan belgilansa, hosilaning fizik ma'nosiga muvofiq bakteriyalarning ko'payish tezligi N (t) ning hosilasi bo'lib, yuqoridagi qonun asosida quyidagicha yozishimiz mumkin. nisbat N "(t) = k ∙ N, bu erda k> 0 - proportsionallik koeffitsienti Olingan tenglama algebraik emas, chunki u nafaqat noma'lum N (t) funktsiyasini, balki uning birinchi tartibli hosilasini ham o'z ichiga oladi.

2. Qisqacha nazariya:

1. Hosila tushunchasiga olib keladigan masalalar

1. Moddiy nuqtaning v tezligini topish masalasi... Ba'zi bir moddiy nuqta to'g'ri chiziqli harakat qilsin. Bir lahzada t 1 nuqta pozitsiyada M 1. Bir lahzada t 2 homilador M 2 . Intervalni belgilaylik M 1 , M 2 bo'ylab D.S; t 2 - t 1 = Dt... Qiymat harakatning o'rtacha tezligi deb ataladi. Bir joydagi nuqtaning oniy tezligini topish uchun M 1 zarur Dt nolga moyil. Matematik jihatdan bu shuni anglatadi

, (1)

Shunday qilib, moddiy nuqtaning oniy tezligini topish uchun funktsiyaning o'sish nisbati chegarasini hisoblash kerak. D.S argumentning ortishiga Dt sharti bilan Dt → 0.

2. Funksiya grafigiga teginish burchagini topish masalasi.

1-rasm

Ba'zi funktsiyaning grafigini ko'rib chiqing y = f (x). Nishab burchagi qanday
nuqtadagi tangens M 1 ? Shu nuqtada M 1 funksiya grafigiga tangens chizing. Grafikdagi ixtiyoriy nuqtani tanlang M 2 va sekant chizish. U eksa tomon egilgan OH burchak ostida α 1 ... O'ylab ko'ring DM 1 M 2 A:

, (2)

Agar nuqta M 1 tuzating va ishora qiling M 2 ga yaqinroq harakatlaning M 1 , keyin sekant M 1 M 2 nuqtadagi funksiya grafigining tangensiga o‘tadi M 1 va siz yozishingiz mumkin:

, (3)

Shunday qilib, agar argument o'sishi nolga moyil bo'lsa, funktsiya o'sishining argument o'sishiga nisbati chegarasini hisoblash kerak.

y = f (x) funktsiyaning Dy o'sishning ma'lum x nuqtadagi Dx argumentining o'sishiga nisbati chegarasi. 0 chunki Dx nolga intiladi, funksiyaning berilgan nuqtadagi hosilasi deyiladi.

Hosila belgisi: y ", f" (x), ... Ta'rifi bo'yicha

, (4)

Bu erda Dx = x 2 -x 1 - argumentning o'sishi (argumentning ikkita keyingi etarlicha yaqin qiymatlari orasidagi farq), Dy = y 2 -y 1 - funktsiyaning o'sishi (qiymatlar orasidagi farq ​argumentning ushbu qiymatlariga mos keladigan funktsiya).

Berilgan funksiyaning hosilasini topish uning deyiladi farqlash... Asosiy elementar funktsiyalarni farqlash tayyor formulalar bo'yicha amalga oshiriladi (jadvalga qarang), shuningdek, qoidalar:

Algebraik yig‘indining hosilasi funktsiyalari ushbu funktsiyalarning hosilalari yig'indisiga teng:

(u+ υ )"= u" + υ "

2. Ikki funktsiya hosilasining hosilasi ikkinchi funktsiyaning birinchi va birinchi funktsiyaning ikkinchi hosilasining hosilasi yig'indisiga teng:

(u ∙υ ) "= u"υ + uυ "

3. Bo‘lakning hosilasi Ikki funktsiyaning soni kasrga teng bo'lib, uning ayirmasi maxrajning hosilasi bilan maxrajning hosilasiga ko'paytirilishi va maxrajning kvadrati bo'ladi:

Hosilning fizik ma'nosi. (4) va (1) ni taqqoslash shuni ko'rsatadiki, moddiy nuqtaning to'g'ri chiziqli harakatining oniy tezligi uning koordinatasining vaqtga bog'liqligi hosilasiga tengdir.

Funksiya hosilasining umumiy ma’nosi uning xarakterlashidir funksiya o'zgarishi tezligi (tezligi). berilgan argument o'zgarishi uchun. Jismoniy, kimyoviy va boshqa jarayonlarning tezligi, masalan, tananing sovish tezligi, kimyoviy reaktsiya tezligi, bakteriyalarning ko'payish tezligi va boshqalar ham hosila yordamida ifodalanadi.

Hosilning geometrik ma'nosi. Funksiya grafigiga chizilgan tangensning moyillik burchagi tangensining kattaligi matematikada deyiladi. tangensning qiyaligi.

Differensiallanuvchi funksiya grafigiga bir nuqtadagi tangensning qiyaligi son jihatdan bu nuqtadagi funksiya hosilasiga teng.

Ushbu bayonot deyiladi hosilaning geometrik ma'nosi.

Maqolaning mazmuni

MATEMATIK TAHLIL, turli xil oʻzgarishlar jarayonlarini miqdoriy oʻrganish usullarini taʼminlovchi matematikaning boʻlimi; oʻzgarish tezligini (differensial hisob) oʻrganish va egri konturlar va sirtlar bilan chegaralangan egri chiziqlar uzunliklari, figuralarning maydonlari va hajmlarini aniqlash (integral hisob) bilan shugʻullanadi. Matematik tahlil masalalari uchun ularning yechimi chegara tushunchasi bilan bog'liqligi xarakterlidir.

Matematik tahlil 1665 yilda I. Nyuton va (taxminan 1675 yil) mustaqil ravishda G. Leybnits tomonidan boshlangan, garchi muhim tayyorgarlik ishlarini I. Kepler (1571–1630), F. Kavalyeri (1598–1647), P. Ferma olib borishgan. (1601-1665), J. Uollis (1616-1703) va I. Barrou (1630-1677).

Taqdimotni yanada jonli qilish uchun biz grafiklar tiliga murojaat qilamiz. Shuning uchun, o'quvchi ushbu maqolani o'qishdan oldin ANALİTİK GEOMETRIYA maqolasini ko'rib chiqishni foydali deb topishi mumkin.

DIFFERENTSIAL HISOB

Tangentlar.

Shaklda. 1 egri chiziqning bir qismini ko'rsatadi y = 2x – x 2, o'rtasida tuzilgan x= –1 va x= 3. Ushbu egri chiziqning etarlicha kichik segmentlari to'g'ri ko'rinadi. Boshqacha qilib aytganda, agar R Bu egri chiziqning ixtiyoriy nuqtasi bo'lsa, u holda bu nuqtadan o'tadigan va nuqtaning kichik qo'shnisida egri chiziqning yaqinlashuvi bo'lgan qandaydir to'g'ri chiziq bor. R, va mahalla qanchalik kichik bo'lsa, yaqinlik shunchalik yaxshi bo'ladi. Bunday to'g'ri chiziq nuqtadagi egri chiziqqa tegish deyiladi R... Differensial hisoblashning asosiy vazifasi tangens mavjud bo'lgan egri chiziqning istalgan nuqtasida teginish yo'nalishini topishga imkon beradigan umumiy usulni qurishdir. O'tkir tanaffus bilan egri chiziqni tasavvur qilish qiyin emas (2-rasm). Agar R- bunday tanaffusning tepasi, keyin siz yaqinlashuvchi to'g'ri chiziqni qurishingiz mumkin PT 1 - nuqtaning o'ng tomonida R va yana bir taxminiy chiziq RT 2 - nuqtadan chapga R... Lekin nuqtadan o'tadigan yagona to'g'ri chiziq yo'q R, bu nuqta yaqinidagi egri chiziqqa teng darajada yaxshi yaqinlashdi P ham o'ngga, ham chapga, shuning uchun nuqtadagi tangens P mavjud emas.

Shaklda. 1 tangens FROM kelib chiqishi orqali chizilgan O= (0,0). Ushbu chiziqning qiyaligi 2 ga teng, ya'ni. abscissa 1 ga o'zgarganda ordinata 2 ga ortadi. Agar x va y- ixtiyoriy nuqtaning koordinatalari FROM, keyin, dan uzoqlashish O masofada X o'ngga birliklar, biz uzoqlashamiz O 2 da y birlik yuqoriga. Demak, y/x= 2 yoki y = 2x... Bu tangens tenglama FROM egri chiziqqa y = 2x – x 2 nuqtada O.

Endi nuqtadan o'tadigan chiziqlar to'plamidan nima uchun ekanligini tushuntirish kerak O, bu to'g'ri chiziq tanlangan edi FROM... Qiyaligi 2 ga teng bo‘lgan to‘g‘ri chiziqning boshqa to‘g‘ri chiziqlardan farqi nimada? Bitta oddiy javob bor va biz aylanaga teginishning o'xshashligini ishlatish vasvasasiga qarshi turish qiyin. FROM egri chiziq bilan faqat bitta umumiy nuqtaga ega, shu bilan birga nuqtadan o'tadigan har qanday vertikal bo'lmagan to'g'ri chiziq O, egri chiziqni ikki marta kesib o'tadi. Buni quyidagicha tekshirish mumkin.

Ifodasi beri y = 2x – x 2 ni ayirish orqali olish mumkin X 2 dan y = 2x(to'g'ri chiziq tenglamalari FROM), keyin qiymatlar y grafik uchun kamroq bilim bor y nuqtadan tashqari barcha nuqtalarda to'g'ri chiziq uchun x= 0. Demak, grafik nuqtadan tashqari hamma joyda O quyida joylashgan FROM, va bu chiziq va grafik faqat bitta umumiy nuqtaga ega. Bundan tashqari, agar y = mx- nuqtadan o'tuvchi boshqa to'g'ri chiziq tenglamasi O, keyin ikkita kesishish nuqtasi bo'lishi aniq. Haqiqatan ham, mx = 2x – x 2 nafaqat uchun x= 0, balki uchun ham x = 2 – m... Va faqat qachon m= 2 ikkala kesishish nuqtasi mos keladi. Shaklda. 3 qachon holatni ko'rsatadi m 2 dan kam, shuning uchun o'ng tomonda O ikkinchi kesishish nuqtasi mavjud.

Nima FROM- nuqtadan o'tadigan yagona vertikal bo'lmagan to'g'ri chiziq O va grafik bilan faqat bitta umumiy nuqtaga ega, uning eng muhim xususiyati emas. Haqiqatan ham, agar boshqa grafiklarga murojaat qilsak, umumiy holatda biz qayd etgan tangensning xossasi bajarilmaganligi tez orada ma'lum bo'ladi. Masalan, rasmdan. 4 (1,1) nuqtaga yaqin egri chiziq grafigini ko'rish mumkin y = x 3 to'g'ri chiziq bilan yaxshi yaqinlashtirilgan RT, ammo u bilan bir nechta umumiy nuqtaga ega. Biroq, biz ko'rib chiqmoqchimiz RT nuqtadagi ushbu grafikga teginish R... Shuning uchun, birinchi misolda bizga juda yaxshi xizmat qilganidan ko'ra, tangensni ta'kidlashning boshqa usulini topish kerak.

Aytaylik, bu nuqta orqali O va ixtiyoriy nuqta Q = (h,k) egri chiziq grafigida y = 2x – x 2 (5-rasm) to'g'ri chiziq (sekant deb ataladi) chizilgan. Egri chiziq tenglamasiga qiymatlarni qo'yish x = h va y = k, biz buni tushunamiz k = 2h – h 2, demak, sekantning qiyaligi

Juda kichik bilan h ma'nosi m yaqin 2. Bundan tashqari, tanlash h 0 ga yaqin biz qila olamiz m ixtiyoriy ravishda 2 ga yaqin. Buni aytishimiz mumkin m Qachon 2 ga teng "chegaraga intiladi" h nolga yoki chegaradan qat'i nazar m uchun 2 ga teng h nolga moyil. Bu ramziy ma'noda quyidagicha yoziladi:

Keyin nuqtadagi grafaga teginish O nuqtadan oʻtuvchi toʻgʻri chiziq sifatida aniqlanadi O, bu chegaraga teng qiyalik bilan. Tangensning bu ta'rifi odatda qo'llaniladi.

Keling, ushbu yondashuvning afzalliklarini boshqa misol bilan ko'rsatamiz: egri chiziq grafigiga teginishning qiyaligini toping. y = 2x – x 2 ixtiyoriy nuqtada P = (x,y), o'zimizni eng oddiy holat bilan cheklamagan holda P = (0,0).

Mayli Q = (x + h, y + k) - diagrammadagi ikkinchi nuqta, masofada joylashgan h ning o'ng tomoniga R(6-rasm). Nishabni topish talab qilinadi k/h sekant PQ... Nuqta Q masofada joylashgan

eksa ustida X.

Qavslarni kengaytirib, biz quyidagilarni topamiz:

Bu tenglamadan ayirish y = 2x – x 2, nuqtadan vertikal masofani topamiz R nuqtaga Q:

Shuning uchun, qiyalik m sekant PQ ga teng

Endi bu h nolga intiladi, m 2-2 ga intiladi x; biz oxirgi qiymatni tangensning qiyaligi sifatida olamiz PT... (Agar shunday bo'lsa ham xuddi shunday natija olinadi h nuqtani tanlashga mos keladigan salbiy qiymatlarni oladi Q ning chap tomonida P.) Buning uchun e'tibor bering x= 0 natija oldingi bilan bir xil.

Ifoda 2 - 2 x 2 ning hosilasi deyiladi x – x 2. Qadimgi kunlarda hosila "differensial nisbat" va "differensial koeffitsient" deb ham atalgan. Agar ifoda 2 x – x 2 belgilang f(x), ya'ni.

keyin hosila belgilanishi mumkin

Funksiya grafigiga teginish qiyaligini bilish uchun y = f(x) qaysidir nuqtada almashtirilishi kerak fў ( x) ushbu nuqtaga mos keladigan qiymat X... Shunday qilib, qiyalik f o (0) = 2 uchun X = 0, f o (0) = 0 uchun X= 1 va f o (2) = -2 uchun X = 2.

hosila ham belgilanadi daў , dy/dx, D x y va Du.

Egri chiziq ekanligi y = 2x – x Berilgan nuqta yaqinidagi 2 bu nuqtada uning tangensidan deyarli farqlanmaydi, teginish nuqtasida "egri chiziqning qiyaligi" sifatida tangensning qiyaligi haqida gapirishga imkon beradi. Shunday qilib, ko'rib chiqilayotgan egri chiziqning qiyaligi (0,0) nuqtada 2 ga teng qiyalikka ega ekanligini ta'kidlashimiz mumkin. x= 0 o'zgarish tezligi y nisbatan x 2. (2,0) nuqtada tangens (va egri chiziq) qiyaligi –2 ga teng. (Minus belgisi shuni anglatadiki x o'zgaruvchan y kamayadi.) (1,1) nuqtada tangens gorizontal. Biz egri chiziqni aytamiz y = 2x – x 2 bu nuqtada statsionar qiymatga ega.

Yuqori va past darajalar.

Biz hozirgina egri chiziqni ko'rsatdik f(x) = 2x – x 2 (1,1) nuqtada harakatsiz. Chunki fў ( x) = 2 – 2x = 2(1 – x), uchun bu aniq x 1 dan kam, fў ( x) ijobiy, shuning uchun y ortadi; da x, katta 1, fў ( x) salbiy, shuning uchun y kamayadi. Shunday qilib, rasmda ko'rsatilgan (1,1) nuqtaga yaqin joyda. 6 harf M, ma'nosi da nuqtagacha o'sadi M, nuqtada statsionar M va nuqtadan keyin kamayadi M... Bu nuqta "maksimal" deb ataladi, chunki qiymat da bu nuqtada uning etarlicha kichik mahallasida uning har qanday qiymatlaridan oshib ketadi. Xuddi shunday, "minimal" ham barcha qiymatlari yaqin bo'lgan nuqta sifatida belgilanadi y ko'p da aynan shu nuqtada. ning hosilasi bo'lsa ham shunday bo'lishi mumkin f(x) bir nuqtada va yo'qoladi, bu nuqtaga yaqin joyda uning belgisi o'zgarmaydi. Maksimal ham, minimal ham bo'lmagan bunday nuqtaga burilish nuqtasi deyiladi.

Misol tariqasida egri chiziqning statsionar nuqtasini topamiz

Bu funktsiyaning hosilasi

va da g'oyib bo'ladi x = 0, X= 1 va X= –1; bular. (0,0), (1, –2/15) va (–1, 2/15) nuqtalarda. Agar X-1 dan bir oz kamroq, keyin fў ( x) salbiy; agar X-1 dan bir oz ko'proq, keyin fў ( x) ijobiy. Shuning uchun nuqta (-1, 2/15) maksimal hisoblanadi. Xuddi shunday, nuqta (1, –2/15) minimal ekanligini ko'rsatish mumkin. Ammo hosila fў ( x) (0,0) nuqtadan oldin ham, keyin ham manfiy. Shuning uchun (0,0) burilish nuqtasidir.

O'tkazilgan o'rganish egri chiziqning shaklini, shuningdek, egri o'qni kesib o'tishini aniqladi. X da f(x) = 0 (ya'ni, uchun X= 0 yoki) uning grafigini taxminan rasmda ko'rsatilganidek ko'rsatishga imkon beradi. 7.

Umuman olganda, agar biz noodatiy holatlarni (to'g'ri chiziq segmentlarini yoki cheksiz sonli egilishlarni o'z ichiga olgan egri chiziqlar) istisno qilsak, egri chiziqning nisbiy pozitsiyasi va teginish nuqtasi yaqinidagi tangens uchun to'rtta variant mavjud. R. (Sm... guruch. 8 bu erda tangens musbat qiyalikka ega.)

1) Nuqtaning har ikki tomonida R egri chiziq tangens ustida joylashgan (8-rasm, a). Bunday holda, ular nuqtada egri deb aytishadi R qavariq pastga yoki botiq.

2) Nuqtaning har ikki tomonida R egri chiziq tangens ostida joylashgan (8-rasm, b). Bunday holda, egri chiziq yuqoriga qarab qavariq yoki oddiygina qavariq deyiladi.

3) va 4) Egri chiziq nuqtaning bir tomonida teginish ustida joylashgan R va pastda - boshqa tomonda. Ushbu holatda R- burilish nuqtasi.

Qiymatlarni solishtirish fў ( x) ikkala tomonida R nuqtadagi qiymati bilan R, ma'lum bir muammoda ushbu to'rtta holatdan qaysi biri bilan shug'ullanish kerakligini aniqlash mumkin.

Ilovalar.

Yuqoridagilarning barchasi turli sohalarda muhim ilovalarni topadi. Misol uchun, agar tana sekundiga 200 fut boshlang'ich tezlikda vertikal yuqoriga tashlangan bo'lsa, u holda balandlik s ular orqali joylashgan bo'ladi t boshlanish nuqtasiga nisbatan soniya bo'ladi

Biz ko'rib chiqqan misollardagi kabi harakat qilib, topamiz

bu qiymat c da yo'qoladi. Hosil fў ( x) c qiymatiga qadar musbat va bu vaqtdan keyin manfiy. Demak, s gacha ortadi, so‘ngra statsionar bo‘ladi, keyin esa kamayadi. Bu yuqoriga tashlangan tananing harakatining umumiy tavsifi. Undan biz tananing qachon eng yuqori nuqtasiga yetganini bilamiz. Bundan tashqari, almashtirish t= 25/4 dyuym f(t), biz 625 futni olamiz, maksimal ko'tarilish. Bu vazifada fў ( t) jismoniy ma'noga ega. Ushbu lotin tananing vaqt momentida harakat qilish tezligini ko'rsatadi t.

Keling, boshqa turdagi arizalarni ko'rib chiqaylik (9-rasm). Maydoni 75 sm 2 bo'lgan karton varag'idan to'rtburchak taglikli quti yasash kerak. Maksimal hajmga ega bo'lishi uchun bu quti qanchalik katta bo'lishi kerak? Agar X- qutining poydevorining yon tomoni va h- uning balandligi, keyin qutining hajmi V = x 2 h, va sirt maydoni 75 = ga teng x 2 + 4xh... Tenglamani o'zgartirib, biz quyidagilarni olamiz:

dan olingan V teng bo'lib chiqadi

va da g'oyib bo'ladi X= 5. Keyin

va V= 125/2. Funktsiya grafigi V = (75x – x 3) / 4 rasmda ko'rsatilgan. 10 (salbiy qiymatlar X Ushbu muammoda jismoniy ma'no yo'qligi sababli chiqarib tashlangan).

Hosila hosilalari.

Differensial hisoblashning muhim vazifasi hosilalarni tez va qulay topish imkonini beruvchi usullarni yaratishdir. Masalan, buni hisoblash oson

(Doimiy miqdorning hosilasi, albatta, nolga teng.) Umumiy qoidani chiqarish qiyin emas:

qayerda n- har qanday butun yoki kasr. Masalan,

(Ushbu misol kasr ko'rsatkichlarining qanchalik foydali ekanligini ko'rsatadi.)

Bu erda eng muhim formulalardan ba'zilari:

Shuningdek, quyidagi qoidalar mavjud: 1) agar ikkala funktsiyaning har biri g(x) va f(x) hosilalari bor, u holda ularning yigʻindisining hosilasi bu funksiyalarning hosilalari yigʻindisiga, ayirma hosilasi esa hosilalarning ayirmasiga teng boʻladi, yaʼni.

2) ikkita funktsiya hosilasining hosilasi quyidagi formula bo'yicha hisoblanadi:

3) ikki funksiya nisbatining hosilasi shaklga ega

4) funktsiyaning doimiyga ko'paytirilgan hosilasi doimiyning ushbu funktsiyaning hosilasiga ko'paytirilganga teng, ya'ni.

Ko'pincha funktsiyaning qiymatlarini bosqichma-bosqich hisoblash kerak bo'ladi. Masalan, gunohni hisoblash uchun x 2, biz birinchi navbatda topishimiz kerak u = x 2 va keyin sonning sinusini hisoblang u... Biz shunday murakkab funksiyalarning hosilasini "zanjir qoidasi" yordamida topamiz:

Bizning misolimizda f(u) = gunoh u, fў ( u) = cos u, shuning uchun,

Ushbu va boshqa shunga o'xshash qoidalar ko'p funktsiyalarning hosilalarini darhol yozishga imkon beradi.

Chiziqli yaqinlashishlar.

Hosilni bilgan holda, biz ko'p hollarda funksiya grafigini shu nuqtada uning tangensining qaysidir nuqtasiga yaqin joyda o'zgartirishimiz mumkinligi katta ahamiyatga ega, chunki to'g'ri chiziqlar bilan ishlash osonroq.

Ushbu g'oya funktsiyalarning taxminiy qiymatlarini hisoblashda bevosita qo'llanilishini topadi. Masalan, qachon qiymatni hisoblash juda qiyin x= 1,033. Lekin siz 1.033 raqamining 1 ga yaqinligidan va undan foydalanishingiz mumkin. Yopish x= 1 tangens egri chizig'ining grafigini jiddiy xatoga yo'l qo'ymasdan almashtira olamiz. Bunday tangensning qiyaligi hosilaning qiymatiga teng ( x 1/3) o = (1/3) x-2/3 da x = 1, ya'ni 1/3. (1,1) nuqta egri chiziqda yotganligi va bu nuqtada egri chiziqqa tangensning qiyaligi 1/3 bo'lgani uchun tangens tenglamasi ko'rinishga ega bo'ladi.

Ushbu qatorda X = 1,033

Olingan qiymat y haqiqiy qiymatga juda yaqin bo'lishi kerak y; va, albatta, bu haqiqatdan atigi 0,00012 ga ko'p. Matematik tahlilda bunday chiziqli yaqinlashishning aniqligini oshirish usullari ishlab chiqilgan. Ushbu usullar bizning taxminiy hisob-kitoblarimizning ishonchliligini ta'minlaydi.

Yuqorida tavsiflangan protsedura foydali belgini taklif qiladi. Mayli P- funksiya grafigiga mos keladigan nuqta f o'zgaruvchan X va funksiyaga ruxsat bering f(x) farqlanadi. Nuqta yaqinidagi egri chiziq grafigini almashtiring R unga teginish, shu nuqtada chizilgan. Agar X miqdori bo'yicha o'zgartirish h, u holda tangensning ordinatasi qiymatga o'zgaradi h H f ў ( x). Agar h juda kichik bo'lsa, oxirgi qiymat ordinataning haqiqiy o'zgarishiga yaxshi yaqinlikdir y grafika. Agar o'rniga h belgisini yozamiz dx(bu mahsulot emas!), lekin ordinataning o'zgarishi y bildirmoq dy, keyin olamiz dy = f ў ( x)dx, yoki dy/dx = f ў ( x) (sm... guruch. o'n bir). Shuning uchun, o'rniga Dy yoki f ў ( x) belgi ko'pincha hosilani belgilash uchun ishlatiladi dy/dx... Ushbu belgining qulayligi, asosan, zanjir qoidasining aniq ko'rinishiga bog'liq (murakkab funktsiyani farqlash); yangi yozuvda ushbu formula quyidagicha ko'rinadi:

qaerda bu nazarda tutilgan da ga bog'liq u, a u o'z navbatida bog'liqdir X.

Kattaligi dy differensial deb ataladi da; aslida bunga bog'liq ikki o'zgaruvchilar, ya'ni: dan X va o'sishlar dx... Qachon o'sish dx juda kichik, kattalik dy qiymatning mos keladigan o'zgarishiga yaqin y... Lekin o'sish, deb taxmin qilish uchun dx oz, kerak emas.

Hosila funksiyasi y = f(x) belgiladik f ў ( x) yoki dy/dx... Ko'pincha hosilaning hosilasini olish mumkin. Natijada ning ikkinchi hosilasi deyiladi f (x) va belgilangan f ўў ( x) yoki d 2 y/dx 2. Masalan, agar f(x) = x 3 – 3x 2, keyin f ў ( x) = 3x 2 – 6x va f ўў ( x) = 6x- 6. Shu kabi belgilar yuqori tartibli hosilalar uchun qo'llaniladi. Biroq, ko'p sonli chiziqchalardan qochish uchun (hosilning tartibiga teng), to'rtinchi hosila (masalan,) quyidagicha yozilishi mumkin. f (4) (x) va hosila n-chi tartib sifatida f (n) (x).

Agar ikkinchi hosila musbat bo'lsa, nuqtadagi egri chiziq pastga qavariq, ikkinchi hosila manfiy bo'lsa yuqoriga qavariq ekanligini ko'rsatish mumkin.

Agar funktsiya ikkinchi hosilaga ega bo'lsa, u holda miqdorning o'zgarishi y o'sishga mos keladi dx o'zgaruvchan X, formula bo'yicha taxminan hisoblash mumkin

Bu yaqinlik odatda differentsial tomonidan berilganidan yaxshiroq fў ( x)dx... Egri chiziqning bir qismini to'g'ri chiziq bilan emas, balki parabola bilan almashtirishga mos keladi.

Agar funktsiya f(x) undan yuqori tartibli hosilalar mavjud

Qolganlari esa

qayerda x- orasida bir nechta raqam x va x + dx... Yuqoridagi natija qoldiq Teylor formulasi deb ataladi. Agar f(x) barcha tartiblarning hosilalariga ega, keyin odatda R n® 0 uchun n ® Ґ .

INTEGRAL HISOB

Kvadratchalar.

Egri chiziqli tekislik figuralari sohalarini o'rganishda matematik tahlilning yangi qirralari ochiladi. Hatto qadimgi yunonlar ham bunday muammolarni hal qilishga harakat qilishgan, ular uchun, masalan, aylana maydonini aniqlash eng qiyin vazifalardan biri edi. Arximed bu muammoni hal qilishda katta muvaffaqiyatga erishdi, u ham parabolik segmentning maydonini topishga muvaffaq bo'ldi (12-rasm). Juda murakkab mulohazalar yordamida Arximed parabolik segmentning maydoni tasvirlangan to'rtburchaklar maydonining 2/3 qismini tashkil etishini va shuning uchun bu holda (2/3) (16) ga teng ekanligini isbotladi. = 32/3. Keyinchalik ko'rib chiqamiz, bu natijani matematik tahlil usullari bilan osongina olish mumkin.

Nyuton va Leybnitsning o'tmishdoshlari, asosan Kepler va Kavalyeri egri chiziqli figuralarning maydonlarini hisoblash muammosini mantiqiy deb atash qiyin bo'lgan, ammo juda samarali bo'lgan usul yordamida hal qildilar. Uollis 1655 yilda Kepler va Kavaleri usullarini Dekart (analitik geometriya) usullari bilan birlashtirib, yangi tug'ilgan algebrani qo'llaganida, Nyutonning paydo bo'lishi uchun sahna to'liq tayyor bo'ldi.

Uollis maydonini hisoblash kerak bo'lgan raqamni juda tor chiziqlarga ajratdi, ularning har biri taxminan to'rtburchaklar hisoblanadi. Keyin u yaqinlashuvchi to'rtburchaklar maydonlarini qo'shdi va eng oddiy hollarda, chiziqlar soni cheksizlikka moyil bo'lganda, to'rtburchaklar maydonlarining yig'indisi moyil bo'lgan qiymatni oldi. Shaklda. 13-rasmda egri chiziq ostidagi maydonning chiziqlariga bo'linishiga mos keladigan to'rtburchaklar ko'rsatilgan y = x 2 .

Asosiy teorema.

Nyuton va Leybnitsning buyuk kashfiyoti maydonlar yig'indisi chegarasiga o'tishning mashaqqatli jarayonini istisno qilishga imkon berdi. Bu kvadrat tushunchasiga yangi qarash tufayli amalga oshirildi. Gap shundaki, biz ordinataning chapdan o'ngga siljishi natijasida hosil bo'lgan egri chiziq ostidagi maydonni tasavvur qilishimiz va ordinatalar tomonidan supurib tashlangan maydon qanchalik tez o'zgarishini so'rashimiz kerak. Agar hudud oldindan ma'lum bo'lgan ikkita maxsus holatni ko'rib chiqsak, bu savolga javob kalitini olamiz.

Chiziqli funksiya grafigi ostidagi maydondan boshlaylik y = 1 + x chunki bu holda maydonni elementar geometriya yordamida hisoblash mumkin.

Mayli A(x) tekislikning toʻgʻri chiziq orasiga oʻralgan qismi y = 1 + x va segment OQ(14-rasm). Haydash paytida QP to'g'ri maydon A(x) ortadi. Qanchalik tez? Bu savolga javob berish qiyin emas, chunki biz bilamizki, trapezoidning maydoni uning balandligining asoslarining yarmi yig'indisiga teng. Demak,

Hududni o'zgartirish tezligi A(x) hosilasi bilan aniqlanadi

Biz buni ko'ramiz Aў ( x) ordinata bilan mos keladi da ball R... Bu tasodifmi? Keling, rasmda ko'rsatilgan parabolani tekshirishga harakat qilaylik. 15. Kvadrat A (x) parabola ostida da = X 0 dan 2 gacha X ga teng A(x) = (1 / 3)(x)(x 2) = x 3/3. Bu maydonning o'zgarish tezligi ifoda bilan aniqlanadi

bu ordinataga to'liq mos keladi da harakatlanuvchi nuqta R.

Agar bu qoida odatda shunday bajarilgan deb hisoblasak

funktsiya grafigi ostidagi maydonning o'zgarish tezligi y = f(x), keyin bu hisob-kitoblar va boshqa sohalar uchun ishlatilishi mumkin. Aslida, nisbat Aў ( x) = f(x) fundamental teoremani ifodalaydi, uni quyidagicha shakllantirish mumkin: hosila yoki maydonning funktsiya sifatida o'zgarish tezligi. X, funksiya qiymatiga teng f (x) nuqtada X.

Masalan, funksiya grafigi ostidagi maydonni topish y = x 0 dan 3 gacha X(16-rasm), biz qo'ydik

Mumkin javob:

ning hosilasidan boshlab X 4/4 haqiqatan ham teng X 3. Bundan tashqari, A(x) uchun nolga teng X= 0, agar bo'lishi kerak bo'lsa A(x) haqiqatan ham hududdir.

Matematik tahlil yuqoridagi ifodadan tashqari yana bir javob ekanligini isbotlaydi A(x), mavjud emas. Keling, quyidagi evristik (qat'iy bo'lmagan) mulohazalardan foydalanib, bu gapning asosli ekanligini ko'rsataylik. Aytaylik, ikkinchi yechim bor V(x). Agar A(x) va V(x) Nol qiymatdan bir vaqtning o'zida "Boshlash" X= 0 va har doim bir xil tezlikda o'zgaradi, keyin ularning qiymatlari no X boshqacha bo‘la olmaydi. Ular hamma joyda bir xil bo'lishi kerak; shuning uchun faqat bitta yechim bor.

Qanday qilib nisbatni oqlash mumkin? Aў ( x) = f(x) umuman? Bu savolga faqat funktsiya sifatida maydonning o'zgarish tezligini o'rganish orqali javob berish mumkin X umuman. Mayli m- funksiyaning eng kichik qiymati f (x) oralig'ida X oldin ( x + h), a M- bu funksiyaning bir xil intervaldagi eng katta qiymati. Shundan so'ng, maydonning o'sishi X Kimga ( x + h) ikkita to'rtburchakning maydonlari orasiga o'ralgan bo'lishi kerak (17-rasm). Ikkala to'rtburchakning asoslari teng h... Kichikroq to'rtburchak balandlikka ega m va maydon mh, mos ravishda kattaroq, M va Mh... Hududga qarshi uchastkada X(18-rasm) abscissa tomonidan o'zgarganda ko'rish mumkin h, ordinataning qiymati (ya'ni, maydon) orasiga kiritilgan miqdorga oshiriladi. mh va Mh... Ushbu grafikdagi sekant qiyaligi orasida m va M... qachon nima bo'ladi h nolga intiladi? Agar funktsiyaning grafigi y = f(x) uzluksiz (ya'ni uzilishlarni o'z ichiga olmaydi), keyin M, va m moyil f(x). Shuning uchun, qiyalik Aў ( x) funksiyasi sifatida maydon uchastkasi X ga teng f(x). Aynan shunday xulosaga kelish kerak edi.

Leybnits egri chiziq ostidagi maydonni taklif qildi y = f(x) 0 dan a belgilash

Qattiq yondashuv bilan, bu aniq integral deb atalmish Vallis usulida ma'lum summalarning chegarasi sifatida belgilanishi kerak. Yuqoridagi natijani hisobga olsak, bunday funktsiyani topishimiz sharti bilan bu integral hisoblanganligi aniq A(x), da yo'qoladi X= 0 va hosilasi bor Aў ( x) ga teng f (x). Bunday funktsiyani topish odatda integratsiya deb ataladi, garchi bu operatsiyani antidifferentsiatsiya deb atash to'g'riroq bo'ladi, ya'ni u ma'lum ma'noda differensiatsiyaga teskari. Ko'phadli bo'lsa, integratsiya oddiy. Masalan, agar

farqlash orqali tekshirish oson A(x).

Hududni hisoblash uchun A 1 egri chiziq ostida y = 1 + x + x 2/2, 0 va 1 ordinatalari orasiga qo'yilgan, biz shunchaki yozamiz

va almashtirish X= 1, biz olamiz A 1 = 1 + 1/2 + 1/6 = 5/3. Kvadrat A(x) 0 dan 2 ga teng A 2 = 2 + 4/2 + 8/6 = 16/3. Shakldan ko'rinib turibdiki. 19, 1 va 2 ordinatalar orasidagi maydon A 2 – A 1 = 11/3. Odatda aniq integral sifatida yoziladi

Jildlar.

Shunga o'xshash fikrlash inqilob jismlarining hajmlarini hisoblashni hayratlanarli darajada osonlashtiradi. Keling, buni to'p hajmini hisoblash misolida ko'rsataylik, qadimgi yunonlar o'zlariga ma'lum bo'lgan usullardan foydalanib, juda qiyinchilik bilan hal qilishga muvaffaq bo'lgan yana bir klassik muammo.

Radius doirasining to'rtdan bir qismi ichida o'ralgan tekislikning qismini aylantiring r, eksa atrofida 360 ° burchak ostida X... Natijada, biz yarim sharni olamiz (20-rasm), uning hajmini biz belgilaymiz V(x). Buning tezligini aniqlash kerak V(x) ortishi bilan x... dan harakatlanish X Kimga X + h, tovush o'sishi ovoz balandligidan kamroq ekanligini tekshirish oson p(r 2 – x 2)h dumaloq silindr radiusi va balandligi h, va hajmdan ko'proq p[r 2 – (x + h) 2 ]h silindr radiusi va balandligi h... Shuning uchun funksiya grafigida V(x) sekantning qiyaligi orasida p(r 2 – x 2) va p[r 2 – (x + h) 2]. Qachon h nolga intiladi, nishab intiladi

Da x = r olamiz

yarim sharning hajmi uchun va shuning uchun 4 p r Butun to'pning hajmi uchun 3/3.

Shunga o'xshash usul sizga egri chiziqlar uzunligini va kavisli sirtlarning maydonlarini topishga imkon beradi. Masalan, agar a(x) - yoy uzunligi PR rasmda. 21, keyin bizning vazifamiz hisoblashdir aў( x). Evristik darajada biz natijani qat'iy isbotlash uchun zarur bo'lgan chegaraga odatiy o'tishga murojaat qilmaslikka imkon beradigan hiyla ishlatamiz. Faraz qilaylik, funksiyaning o'zgarish tezligi a(x) nuqtada R egri chiziq tangensi bilan almashtirilsa, xuddi shunday bo'ladi PT nuqtada P... Lekin anjirdan. 21 ni qadam bosayotganda to'g'ridan-to'g'ri ko'rish mumkin h nuqtadan o'ngga yoki chapga X birga RT ma'nosi a(x) ga o'zgaradi

Shuning uchun funktsiyaning o'zgarish tezligi a(x) hisoblanadi

Funktsiyaning o'zini topish uchun a(x), faqat tenglikning o'ng tomonidagi ifodani birlashtirish kerak. Ma'lum bo'lishicha, aksariyat funktsiyalarni birlashtirish qiyin. Shuning uchun integral hisoblash usullarini ishlab chiqish matematik tahlilning katta qismini tashkil qiladi.

Antiderivativlar.

Hosilasi berilgan funktsiyaga teng bo'lgan har bir funktsiya f(x), uchun antiderivativ (yoki ibtidoiy) deyiladi f(x). Masalan, X 3/3 funksiya uchun antiderivativ hisoblanadi X 2, beri ( x 3/3) o = x 2. Albatta X 3/3 funktsiyaning yagona antiderivativi emas X 2 yildan beri x 3 /3 + C ning hosilasi hamdir X Har qanday doimiy uchun 2 BILAN... Biroq, keyingi ishlarda biz bunday qo'shimcha konstantalarni olib tashlashga rozi bo'lamiz. Umuman

qayerda n musbat butun son, chunki ( x n + 1/(n+ 1)) o = x n... Munosabat (1) agar umumiyroq ma'noda amal qiladi n istalgan ratsional son bilan almashtiring k-1 dan tashqari.

Berilgan funksiya uchun ixtiyoriy antiderivativ funktsiya f(x) odatda ning noaniq integrali deb ataladi f(x) va uni sifatida belgilang

Masalan, beri (gunoh x) o = cos x, formula haqiqiydir

Ko'pgina hollarda, berilgan funktsiyaning noaniq integrali uchun formula mavjud bo'lganda, uni noaniq integrallarning ko'plab keng nashr etilgan jadvallarida topish mumkin. Elementar funksiyalarning integrallari jadval shaklida (bularga darajalar, logarifmlar, ko‘rsatkichli funksiyalar, trigonometrik funksiyalar, teskari trigonometrik funksiyalar, shuningdek, qo‘shish, ayirish, ko‘paytirish va bo‘lish amallari yordamida olingan ularning chekli birikmalari kiradi). Jadvalli integrallardan foydalanib, murakkabroq funksiyalarning integrallarini hisoblashingiz mumkin. Noaniq integrallarni hisoblashning ko'plab usullari mavjud; ularning eng keng tarqalgani o'zgaruvchan almashtirish yoki almashtirish usulidir. Bu shundan iboratki, agar biz noaniq integralni (2) almashtirmoqchi bo'lsak. x ba'zi bir differentsiallanadigan funksiya haqida x = g(u), integral o'zgarmasligi uchun kerak x bilan almashtirildi gў ( u)du... Boshqacha aytganda, tenglik

(almashtirish 2 x = u, qaerdan 2 dx = du).

Bu erda yana bir integratsiya usuli - qismlar bo'yicha integratsiya usuli. U allaqachon ma'lum bo'lgan formulaga asoslanadi

Chap va o'ng tomonlarni birlashtirib, buni hisobga olgan holda

Bu formula qismlar bo'yicha integrallash formulasi deb ataladi.

Misol 2. Topish talab qilinadi. Chunki cos x= (gunoh x) o, buni yozishimiz mumkin

(5) dan boshlab, sozlash u = x va v= gunoh x, olamiz

Va beri (-cos x) o = gunoh x biz buni topamiz va

Shuni ta'kidlash kerakki, biz juda ko'p aqlli texnikalar to'plangan juda keng mavzuga juda qisqacha kirish bilan cheklandik.

Ikki o'zgaruvchining funksiyalari.

Egrilik tufayli y = f(x) biz ikkita vazifani ko'rib chiqdik.

1) Berilgan nuqtadagi egri chiziqqa tangensning qiyaligini toping. Bu masala hosilaning qiymatini hisoblash yo'li bilan hal qilinadi fў ( x) belgilangan nuqtada.

2) o'q segmenti ustidagi egri chiziq ostidagi maydonni toping X vertikal chiziqlar bilan chegaralangan X = a va X = b... Bu masala aniq integralni hisoblash yo'li bilan hal qilinadi.

Ushbu muammolarning har biri sirt holatida analogga ega z = f(x,y).

1) Berilgan nuqtada sirtga teguvchi tekislikni toping.

2) Tekislik qismi ustidagi sirt ostidagi hajmni toping hu egri chiziq bilan chegaralangan BILAN, va yon tomondan - tekislikka perpendikulyarlar xy chegaraviy egri chiziqning nuqtalaridan o'tuvchi BILAN (sm... guruch. 22).

Quyidagi misollar bu vazifalar qanday bajarilishini ko'rsatadi.

Misol 4. Sirtga teguvchi tekislikni toping

nuqtada (0,0,2).

Agar tekislikda yotgan ikkita kesishuvchi chiziq berilgan bo'lsa, tekislik aniqlanadi. Ushbu qatorlardan biri ( l 1) biz samolyotga tushamiz xz (da= 0), ikkinchisi ( l 2) - samolyotda yz (x = 0) (sm... guruch. 23).

Avvalo, agar da= 0, keyin z = f(x,0) = 2 – 2x – 3x 2. ga nisbatan hosila X bilan belgilanadi fў x(x,0) = –2 – 6x, da X= 0 qiymati –2 ga teng. Streyt l 1 tenglamalar bilan berilgan z = 2 – 2x, da= 0 - teginish BILAN 1, sirtning tekislik bilan kesishish chiziqlari da= 0. Xuddi shunday, agar X= 0, keyin f(0,y) = 2 – y – y 2-ga nisbatan hosila da shaklga ega

Chunki fў y(0,0) = –1, egri chiziq BILAN 2 - sirtning tekislik bilan kesishish chizig'i yz- tangensga ega l 2 tenglamalar bilan berilgan z = 2 – y, X= 0. Kerakli tangens tekislik ikkala to'g'ri chiziqni o'z ichiga oladi l 1 va l 2 va tenglama bilan yoziladi

Bu tekislikning tenglamasi. Bundan tashqari, biz to'g'ri chiziqlarga ega bo'lamiz l 1 va l 2, mos ravishda sozlash, da= 0 va X = 0.

Tenglama (7) haqiqatan ham tangens tekislikni aniqlaganligini evristik darajada tekshirish mumkin, agar bu tenglama (6) tenglamaga kiritilgan birinchi tartibli hadlarni o'z ichiga olganligini va ikkinchi darajali hadlar quyidagi shaklda ifodalanishi mumkinligini sezsak. shakl -. Chunki bu ifoda barcha qiymatlar uchun salbiy X va da, Bundan tashqari X = da= 0, sirt (6) nuqtadan tashqari (7) tekislik ostida hamma joyda yotadi R= (0,0,0). Aytishimiz mumkinki, sirt (6) nuqtada yuqoriga qarab qavariq R.

Misol 5. Sirtga teguvchi tekislikni toping z = f(x,y) = x 2 – y 2 boshida 0.

Sirtda da= 0 bizda: z = f(x,0) = x 2 va fў x(x,0) = 2x... Ustida BILAN 1, kesishish chiziqlari, z = x 2. Shu nuqtada O qiyaligi fў x(0,0) = 0. Samolyotda X= 0 bizda: z = f(0,y) = –y 2 va fў y(0,y) = –2y... Ustida BILAN 2, kesishish chiziqlari, z = –y 2. Shu nuqtada O egri chiziqning qiyaligi BILAN 2 teng fў y(0,0) = 0. ga teglar ekan BILAN 1 va BILAN 2 - o'qlar X va da, ularni o'z ichiga olgan tangens tekislik tekislikdir z = 0.

Biroq, kelib chiqishi yaqinida bizning sirtimiz teginish tekisligining bir tomonida emas. Haqiqatan ham, egri chiziq BILAN 1 hamma joyda, 0 nuqtadan tashqari, tangens tekislik va egri chiziq ustida joylashgan BILAN 2 - mos ravishda uning ostida. Sirt tangens tekislik bilan kesishadi z to'g'ri chiziqlarda = 0 da = X va da = –X... Bunday sirtning boshida egar nuqtasi bor deb aytiladi (24-rasm).

Qisman hosilalar.

Oldingi misollarda biz lotinlardan foydalanganmiz f (x,y) yoqilgan X va tomonidan da... Keling, bunday hosilalarni umumiyroq ko'rib chiqaylik. Agar bizda ikkita o'zgaruvchining funktsiyasi bo'lsa, masalan, F(x,y) = x 2 – xy, keyin biz har bir nuqtada uning ikkita "qisman hosilalari" ni aniqlashimiz mumkin, biri funktsiyani ga nisbatan farqlash orqali. X va tuzatish da ga nisbatan farqlash orqali ikkinchisi da va tuzatish X... Bu hosilalarning birinchisi sifatida belgilanadi fў x(x,y) yoki ¶ f/¶ x; ikkinchisi - qanday qilib f f o y... Agar ikkala aralash hosila bo'lsa (by X va da, yoqilgan da va X) uzluksiz, keyin ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x; bizning misolimizda ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x = –1.

Qisman hosila fў x(x,y) funksiyaning o‘zgarish tezligini ko‘rsatadi f nuqtada ( x,y) oshirish yo'nalishida X, a fў y(x,y) Funktsiyaning o'zgarish tezligi f ko'tarilish yo'nalishi da... Funktsiyani o'zgartirish tezligi f nuqtada ( X,da) burchak hosil qiluvchi to‘g‘ri chiziq yo‘nalishida q o'qning ijobiy yo'nalishi bilan X, funksiyaning hosilasi deyiladi f tomon; uning qiymati funksiyaning ikkita qisman hosilasining birikmasidir tangens tekisligida f deyarli teng (kichik dx va dy) haqiqiy o'zgarish z sirtda, lekin differentsialni hisoblash odatda osonroq.

Murakkab funktsiya yoki zanjir qoidasining hosilasi sifatida tanilgan o'zgaruvchan o'zgartirish usulidan biz allaqachon ko'rib chiqqan formula, bir o'lchovli holatda da ga bog'liq X, a X ga bog'liq t, shaklga ega:

Ikki o'zgaruvchining funktsiyalari uchun o'xshash formula:

Qisman farqlash tushunchalari va belgilarini yuqori o'lchamlarga umumlashtirish oson. Xususan, agar sirt tenglama bilan bevosita berilgan bo'lsa f(x,y,z) = 0, sirtga teginish tekisligi tenglamasini yanada simmetrik ko'rinishda berish mumkin: nuqtadagi teginish tekislik tenglamasi ( x (x 2/4)], keyin u ustidan integrallanadi X 0 dan 1. Yakuniy natija 3/4.

Formula (10) qo'sh integral deb ataladigan narsa sifatida ham talqin qilinishi mumkin, ya'ni. elementar "hujayralar" hajmlari yig'indisining chegarasi sifatida. Har bir bunday hujayra D asosiga ega x D y va to'rtburchak asosning biron bir nuqtasi ustidagi sirt balandligiga teng balandlik ( sm... guruch. 26). (10) formula bo'yicha ikkala nuqtai nazar ham ekvivalent ekanligini ko'rsatish mumkin. Ikki tomonlama integrallar og'irlik markazlarini va mexanikada topilgan ko'p sonli momentlarni topish uchun ishlatiladi.

Matematik apparatni yanada qat'iy asoslash.

Hozirgacha biz intuitiv darajada hisoblash tushunchalari va usullarini taqdim etdik va geometrik shakllarga murojaat qilishdan tortinmadik. 19-20-asrlarda paydo bo'lgan yanada qat'iy usullarni qisqacha ko'rib chiqish biz uchun qoladi.

19-asrning boshlarida "matematik tahlilni yaratish"da hujum va hujum davri tugagach, uni asoslash masalalari birinchi o'ringa chiqdi. Abel, Koshi va boshqa bir qator taniqli matematiklarning asarlarida “chegara”, “uzluksiz funksiya”, “yaqinlashuvchi qatorlar” tushunchalariga aniq ta’rif berilgan. Bu matematik tahlilni ishonchli tadqiqot vositasiga aylantirish uchun asosga mantiqiy tartibni keltirish uchun zarur edi. To'liq asoslash zarurati 1872 yilda Weiershtrass tomonidan hamma joyda uzluksiz, lekin hech qanday joyda differentsiallanmaydigan funktsiyalarni kashf qilgandan keyin yanada aniqroq bo'ldi (bunday funktsiyalar grafigi har bir nuqtada tanaffusga ega). Bu natija matematiklarda katta taassurot qoldirdi, chunki bu ularning geometrik sezgilariga aniq zid edi. Geometrik sezgi ishonchsizligining yanada yorqin misoli D. Peano tomonidan qurilgan doimiy egri chiziq bo'lib, u ma'lum bir kvadratni to'liq to'ldiradi, ya'ni. uning barcha nuqtalaridan o'tadi. Bu va boshqa kashfiyotlar matematikaning "arifmetizatsiyasi" dasturini yaratdi, ya'ni. son tushunchasidan foydalangan holda barcha matematik tushunchalarni asoslash orqali uni yanada ishonchli qilish. Matematika asoslari bo'yicha ishlarda aniqlikdan deyarli puritanlikdan voz kechish o'zining tarixiy asosiga ega edi.

Mantiqiy qat'iylikning zamonaviy qonunlariga ko'ra, egri chiziq ostidagi maydon haqida gapirishga yo'l qo'yib bo'lmaydi. y = f(x) va o'q segmenti ustida X, Agarda f- birinchi navbatda "hudud" atamasining aniq ma'nosini aniqlamasdan va shu tarzda aniqlangan maydon haqiqatan ham mavjudligini aniqlamasdan, uzluksiz funktsiya. Bu muammoni 1854-yilda B.Riman muvaffaqiyatli hal etib, aniq integral tushunchasiga aniq ta’rif berdi. O'shandan beri aniq integral tushunchasi orqasida yig'indilash g'oyasi ko'plab chuqur tadqiqotlar va umumlashmalarning mavzusi bo'ldi. Natijada, bugungi kunda integral hamma joyda uzilishli bo'lsa ham, aniq integralga ma'no berish mumkin. Integrasiyaning yangi kontseptsiyalari, ularning yaratilishida A.Lebesg (1875–1941) va boshqa matematiklar katta hissa qo'shdilar, zamonaviy matematik tahlilning kuchi va go'zalligini oshirdilar.

Bu va boshqa tushunchalarning barchasiga batafsil to'xtalib o'tish o'rinli bo'lmaydi. Biz faqat chegara va aniq integralning qat'iy ta'riflarini berish bilan cheklanamiz.

Xulosa o‘rnida aytamizki, matematik tahlil olim va muhandis qo‘lidagi nihoyatda qimmatli vosita bo‘lib, bugungi kunda ham samarali g‘oyalar manbai sifatida matematiklar e’tiborini tortmoqda. Shu bilan birga, zamonaviy rivojlanish 20-asrda matematik tahlil bunday dominant tomonidan tobora ko'proq o'zlashtirilayotganini ko'rsatmoqda. mavhum algebra va topologiya kabi matematikaning tarmoqlari.

Hosila va uni hisoblash usullarini bilmasdan turib, matematikada fizik masalalar yoki misollarni yechish mutlaqo mumkin emas. Hosila matematik tahlilning eng muhim tushunchalaridan biridir. Biz bugungi maqolani ushbu asosiy mavzuga bag'ishlashga qaror qildik. Hosila nima, uning fizik va geometrik ma'nosi nima, funktsiyaning hosilasi qanday hisoblanadi? Bu savollarning barchasini bittaga birlashtirish mumkin: lotinni qanday tushunish kerak?

Hosilning geometrik va fizik ma'nosi

Funktsiya bo'lsin f (x) ma'lum bir intervalda berilgan (a, b) ... X va x0 nuqtalari shu intervalga tegishli. X o'zgarganda, funktsiyaning o'zi o'zgaradi. Argumentni o'zgartirish - uning qiymatlari orasidagi farq x-x0 ... Bu farq quyidagicha yoziladi delta x va argument ortishi deyiladi. Funktsiyaning o'zgarishi yoki ortishi - bu funktsiya qiymatlarining ikki nuqtadagi farqi. Hosila ta'rifi:

Funktsiyaning nuqtadagi hosilasi - bu funksiyaning ma'lum nuqtadagi o'sishining argumentning o'sishiga nisbati chegarasi, bu nolga moyil bo'lganda.

Aks holda, u quyidagicha yozilishi mumkin:

Bunday chegarani topishning nima keragi bor? Va mana nima:

nuqtadagi funksiyaning hosilasi OX o‘qi orasidagi burchak tangensiga va shu nuqtadagi funksiya grafigiga teginishga teng.

Hosilning jismoniy ma'nosi: yo'lning vaqtga nisbatan hosilasi to'g'ri chiziqli harakat tezligiga teng.

Darhaqiqat, maktab davridan beri hamma tezlikni shaxsiy yo'l ekanligini biladi. x = f (t) va vaqt t ... Vaqt oralig'idagi o'rtacha tezlik:

Bir vaqtning o'zida harakat tezligini aniqlash uchun t0 limitni hisoblashingiz kerak:

Birinchi qoida: doimiyni chiqaring

Doimiy hosila belgisidan tashqariga ko'chirilishi mumkin. Bundan tashqari, buni qilish kerak. Matematikadan misollarni echishda, qoida tariqasida, oling - ifodani soddalashtira olsangiz, soddalashtirishga ishonch hosil qiling .

Misol. Keling, hosilani hisoblaylik:

Ikkinchi qoida: funktsiyalar yig'indisining hosilasi

Ikki funktsiya yig'indisining hosilasi bu funksiyalarning hosilalari yig'indisiga teng. Xuddi shu narsa funksiyalar farqining hosilasi uchun ham amal qiladi.

Biz bu teoremaning isbotini keltirmaymiz, balki amaliy misolni ko'rib chiqamiz.

Funktsiyaning hosilasini toping:

Uchinchi qoida: funksiyalar mahsulotining hosilasi

Ikki differentsiallanuvchi funktsiyaning hosilasi quyidagi formula bo'yicha hisoblanadi:

Misol: funktsiyaning hosilasini toping:

Yechim:

Bu erda murakkab funktsiyalarning hosilalarini hisoblash haqida gapirish muhimdir. Murakkab funktsiyaning hosilasi ushbu funktsiyaning oraliq argumentga nisbatan hosilasi mustaqil o'zgaruvchiga nisbatan oraliq argumentning hosilasi bilan teng.

Yuqoridagi misolda biz quyidagi iborani uchratamiz:

Bunday holda, oraliq argument beshinchi darajaga 8x. Bunday ifodaning hosilasini hisoblash uchun avval tashqi funktsiyaning oraliq argumentga nisbatan hosilasini hisoblab chiqamiz, so'ngra mustaqil o'zgaruvchiga nisbatan bevosita oraliq argumentning hosilasiga ko'paytiramiz.

To'rtinchi qoida: ikkita funktsiyaning qism hosilasi

Ikki funktsiyaning bo'linmasining hosilasini aniqlash formulasi:

Biz sizga noldan dummies uchun derivativlar haqida aytib berishga harakat qildik. Bu mavzu ko'rinadigan darajada oddiy emas, shuning uchun ogohlantiring: misollarda ko'pincha tuzoqlar mavjud, shuning uchun lotinlarni hisoblashda ehtiyot bo'ling.

Ushbu va boshqa mavzular bo'yicha har qanday savol uchun siz talabalar xizmatiga murojaat qilishingiz mumkin. Qisqa vaqt ichida biz sizga eng qiyin testni hal qilishda yordam beramiz va siz ilgari hech qachon lotinlarni hisoblash bilan shug'ullanmagan bo'lsangiz ham, vazifalarni hal qilamiz.

Unda biz eng oddiy hosilalarni tahlil qildik, shuningdek, differentsiallash qoidalari va hosilalarni topishning ba'zi usullari bilan tanishdik. Shunday qilib, agar siz funktsiyalarning hosilalari bilan unchalik tanish bo'lmasangiz yoki ushbu maqolaning ba'zi fikrlari to'liq tushunarli bo'lmasa, avval yuqoridagi darsni o'qing. Iltimos, jiddiy kayfiyatni sozlang - material oson emas, lekin baribir uni oddiy va tushunarli tarzda taqdim etishga harakat qilaman.

Amalda murakkab funksiyaning hosilasi bilan juda tez-tez shug‘ullanishga to‘g‘ri keladi, hattoki, hosilalarni topish bo‘yicha topshiriqlar berilganda ham, deyarli har doim aytaman.

Murakkab funktsiyani differensiallash uchun qoida (№ 5) jadvaliga qaraymiz:

Tushunish. Avvalo, yozuvga e'tibor beraylik. Bu erda biz ikkita funktsiyaga egamiz - va bundan tashqari, funktsiya, majoziy ma'noda, funktsiyaga kiritilgan. Bunday turdagi funktsiya (bir funktsiya boshqasining ichiga joylashtirilganda) murakkab funktsiya deyiladi.

Men funktsiyani chaqiraman tashqi funktsiya va funksiya - ichki (yoki o'rnatilgan) funktsiya.

! Ushbu ta'riflar nazariy emas va topshiriqlarning yakuniy dizaynida ko'rinmasligi kerak. Men "tashqi funktsiya", "ichki" funktsiya norasmiy iboralarni faqat materialni tushunishingizni osonlashtirish uchun ishlataman.

Vaziyatga aniqlik kiritish uchun quyidagilarni ko'rib chiqing:

1-misol

Funktsiyaning hosilasini toping

Sinus ostida bizda nafaqat "X" harfi, balki butun son ifodasi mavjud, shuning uchun jadvaldan hosilani darhol topish mumkin bo'lmaydi. Bundan tashqari, biz bu erda birinchi to'rtta qoidani qo'llashning iloji yo'qligini ko'ramiz, farq borga o'xshaydi, lekin haqiqat shundaki, siz sinusni "ajratib" olmaysiz:

Ushbu misolda, mening tushuntirishlarimdan ko'rinib turibdiki, funktsiya murakkab funktsiya, polinom esa ichki funktsiya (uyalash) va tashqi funktsiyadir.

Birinchi qadam, murakkab funktsiyaning hosilasini topishda bajarilishi kerak bo'lgan, bu qaysi funktsiya ichki va qaysi tashqi ekanligini aniqlang.

Oddiy misollarda, ko'phad sinus ostida joylashganligi aniq ko'rinadi. Ammo hamma narsa aniq bo'lmasa-chi? Qaysi funktsiya tashqi va qaysi ichki ekanligini qanday aniqlash mumkin? Buning uchun men aqliy yoki qoralama ustida bajarilishi mumkin bo'lgan quyidagi texnikadan foydalanishni taklif qilaman.

Tasavvur qiling-a, biz kalkulyatorda ifoda qiymatini hisoblashimiz kerak (bitta o'rniga har qanday raqam bo'lishi mumkin).

Avval nimani hisoblaymiz? Birinchidan siz quyidagi amalni bajarishingiz kerak bo'ladi:, shuning uchun polinom ichki funktsiya bo'ladi:

Ikkinchidan topilishi kerak, shuning uchun sinus tashqi funktsiya bo'ladi:

Bizdan keyin Tushundim ichki va tashqi funktsiyalar bilan, murakkab funktsiyani differentsiallash qoidasini qo'llash vaqti keldi .

Biz qaror qabul qilishni boshlaymiz. Darsdan lotinni qanday topsam bo'ladi? biz har qanday hosila eritmasining dizayni har doim shunday boshlanishini eslaymiz - biz ifodani qavs ichiga olamiz va yuqori o'ng tomonga chiziq qo'yamiz:

Birinchidan tashqi funktsiyaning (sinus) hosilasini toping, elementar funksiyalarning hosilalari jadvaliga qarang va bunga e'tibor bering. Barcha jadval formulalari "x" murakkab ifoda bilan almashtirilsa ham amal qiladi, Ushbu holatda:

E'tibor bering, ichki funktsiya o'zgarmagan, biz unga tegmaymiz.

Xo'sh, bu juda aniq

Formulani qo'llash natijasi Yakuniy dizaynda u quyidagicha ko'rinadi:

Doimiy omil odatda ifoda boshida qo'yiladi:

Agar chalkashlik bo'lsa, yechimni yozib oling va tushuntirishlarni qayta o'qing.

2-misol

Funktsiyaning hosilasini toping

3-misol

Funktsiyaning hosilasini toping

Har doimgidek, biz yozamiz:

Keling, qaerda tashqi funktsiyamiz borligini va qaerda ichki funksiyamiz borligini aniqlaylik. Buni amalga oshirish uchun (aqliy yoki qoralama ustida) ifoda qiymatini hisoblashga harakat qiling. Avval nima qilish kerak? Avvalo, asos nimaga teng ekanligini hisoblashingiz kerak: bu polinom ichki funktsiya ekanligini anglatadi:

Va shundan keyingina eksponentsiya bajariladi, shuning uchun quvvat funktsiyasi tashqi funktsiyadir:

Formulaga ko'ra , birinchi navbatda tashqi funktsiyaning hosilasini, bu holda darajani topishingiz kerak. Biz jadvalda kerakli formulani qidiramiz:. Yana takrorlaymiz: har qanday jadval formulasi nafaqat "x" uchun, balki murakkab ifoda uchun ham amal qiladi... Shunday qilib, murakkab funktsiyani differentsiallash qoidasini qo'llash natijasi Keyingi:

Yana bir bor ta'kidlaymanki, biz tashqi funktsiyaning hosilasini olganimizda, biz uchun ichki funktsiya o'zgarmaydi:

Endi ichki funktsiyaning juda oddiy hosilasini topish va natijani biroz "tarash" qoladi:

4-misol

Funktsiyaning hosilasini toping

Bu mustaqil yechim uchun misol (qo'llanma oxirida javob).

Murakkab funktsiyaning hosilasi haqidagi tushunchani mustahkamlash uchun men izohlarsiz misol keltiraman, uni o'zingiz aniqlashga harakat qiling, tashqi va ichki funksiya qayerda ekanligini taxmin qiling, nima uchun vazifalar bu tarzda hal qilindi?

5-misol

a) funksiyaning hosilasini toping

b) funksiyaning hosilasini toping

6-misol

Funktsiyaning hosilasini toping

Bu erda bizda ildiz bor va ildizni farqlash uchun u daraja sifatida ifodalanishi kerak. Shunday qilib, avval biz funktsiyani farqlash uchun mos shaklga keltiramiz:

Funksiyani tahlil qilib, biz uchta hadning yig'indisi ichki funktsiya, ko'rsatkich esa tashqi funktsiya degan xulosaga kelamiz. Kompleks funktsiyani differentsiallash qoidasini qo'llaymiz :

Daraja yana radikal (ildiz) sifatida ifodalanadi va ichki funktsiyaning hosilasi uchun biz yig'indini farqlash uchun oddiy qoidani qo'llaymiz:

Tayyor. Bundan tashqari, ifodani qavs ichida umumiy maxrajga olib kelishingiz va hamma narsani bitta kasrga yozishingiz mumkin. Albatta, yaxshi, lekin og'ir uzun lotinlar olinganda, buni qilmaslik yaxshiroqdir (buni chalkashtirib yuborish, keraksiz xatoga yo'l qo'yish oson va o'qituvchiga tekshirish noqulay bo'ladi).

7-misol

Funktsiyaning hosilasini toping

Bu mustaqil yechim uchun misol (qo'llanma oxirida javob).

Shunisi qiziqki, ba'zida murakkab funktsiyani farqlash qoidasi o'rniga, qismni farqlash qoidasidan foydalanish mumkin. , lekin bunday yechim buzuqlik kabi g'ayrioddiy ko'rinadi. Mana odatiy misol:

8-misol

Funktsiyaning hosilasini toping

Bu erda siz qismni farqlash uchun qoidadan foydalanishingiz mumkin , lekin hosilani murakkab funktsiyani differentsiallash qoidasi orqali topish ancha foydalidir:

Biz funktsiyani farqlash uchun tayyorlaymiz - biz minusni hosila belgisidan tashqariga o'tkazamiz va kosinusni hisoblagichga ko'taramiz:

Kosinus - ichki funktsiya, ko'rsatkich - tashqi funktsiya.
Biz qoidamizdan foydalanamiz :

Ichki funktsiyaning hosilasini toping, kosinusni pastga qaytaring:

Tayyor. Ko'rib chiqilgan misolda, belgilarda chalkashmaslik kerak. Aytgancha, uni qoida bilan hal qilishga harakat qiling , javoblar mos kelishi kerak.

9-misol

Funktsiyaning hosilasini toping

Bu mustaqil yechim uchun misol (qo'llanma oxirida javob).

Hozirgacha biz murakkab funksiyada faqat bitta qo‘shimchaga ega bo‘lgan holatlarni ko‘rib chiqdik. Amaliy topshiriqlarda siz ko'pincha lotinlarni topishingiz mumkin, bu erda, xuddi qo'g'irchoqlar kabi, bir vaqtning o'zida 3 yoki hatto 4-5 funktsiya bir-birining ichiga joylashtirilgan.

10-misol

Funktsiyaning hosilasini toping

Keling, ushbu funktsiyaning qo'shimchalarini tushunaylik. Sinov qiymatidan foydalanib ifodani baholashga urinish. Kalkulyatorga qanday ishonishimiz mumkin?

Avval siz topishingiz kerak, ya'ni arksine eng chuqur uyasi:

Keyin birning bu yoyi kvadrati bo'lishi kerak:

Va nihoyat, 7 ni kuchga ko'taring:

Ya'ni, bu misolda bizda uch xil funktsiya va ikkita qo'shimcha mavjud, eng ichki funktsiya arksinus, eng tashqi funktsiya esa eksponensial funktsiyadir.

Biz hal qilishni boshlaymiz

Qoidaga ko'ra avval siz tashqi funktsiyaning hosilasini olishingiz kerak. Biz hosilalar jadvalini ko'rib chiqamiz va ko'rsatkichli funktsiyaning hosilasini topamiz: Yagona farq shundaki, "x" o'rniga bizda murakkab ifoda mavjud bo'lib, bu formulaning haqiqiyligini inkor etmaydi. Demak, murakkab funktsiyani differentsiallash qoidasini qo'llash natijasi Keyingi.