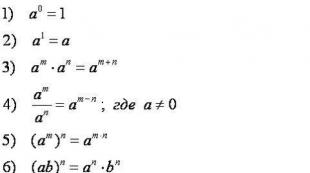A b kubad. Kubmontering Var kommer förkortade multiplikationsformler ifrån?
Exponentiering är en operation som är nära relaterad till multiplikation; denna operation är resultatet av multipel multiplikation av ett tal i sig. Låt oss representera med formeln: a1 * a2 * ... * an = an.
Till exempel a = 2, n = 3: 2 * 2 * 2 = 2 ^ 3 = 8.
I allmänhet används exponentiering ofta i olika formler i matematik och fysik. Denna funktion har ett mer vetenskapligt syfte än de fyra huvudsakliga: Addition, Subtraktion, Multiplication, Division.
Att höja ett nummer till en makt
Att höja ett tal till makten är inte en svår operation. Det är relaterat till multiplikation som förhållandet mellan multiplikation och addition. Notation an är en kort notation av det n: e antalet siffror "a" multiplicerat med varandra.
Överväg exponentiering med de enklaste exemplen och gå vidare till komplexa.
Till exempel 42,42 = 4 * 4 = 16. Fyra kvadrat (andra kraft) är lika med sexton. Om du inte förstår multiplikation 4 * 4, läs sedan vår artikel om multiplikation.
Låt oss titta på ett annat exempel: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125 ... Fem kubade (i den tredje kraften) är lika med hundra tjugofem.
Ett annat exempel: 9 ^ 3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729 ... Nio kuber motsvarar sju hundra tjugonio.
Exponentieringsformler
För att höja till en makt måste du komma ihåg och känna till formlerna nedan. Det finns inget som är naturligt i detta, det viktigaste är att förstå kärnan och då kommer de inte bara att komma ihåg utan verkar också lätta.

Exponentiering av en monomial
Vad är en monomial? Detta är produkten av siffror och variabler i valfri mängd. Till exempel är två en monomial. Och den här artikeln handlar om att höja makten hos sådana monomialer.
Med hjälp av exponentieringsformlerna blir det inte svårt att beräkna exponentieringen av ett monomium.
Till exempel, (3x ^ 2y ^ 3) ^ 2 = 3 ^ 2 * x ^ 2 * 2 * y ^ (3 * 2) = 9x ^ 4y ^ 6; Om du höjer en monomial till en makt, höjs varje sammansatt monomial till en makt.
Om du höjer en variabel som redan har en grad multipliceras graderna. Till exempel (x ^ 2) ^ 3 = x ^ (2 * 3) = x ^ 6;
Negativ exponentiering
En negativ kraft är det omvända. Vad är ett ömsesidigt? Varje nummer X kommer att vara inverterat 1 / X. Det vill säga X-1 = 1 / X. Detta är kärnan i den negativa graden.
Tänk på ett exempel (3Y) ^ - 3:
(3Y) ^ - 3 = 1 / (27Y ^ 3).
Varför är det så? Eftersom det finns ett minus i graden överför vi helt enkelt detta uttryck till nämnaren och höjer det sedan till tredje graden. Är det inte?
Fraktionerad exponentiering
Låt oss börja överväga problemet med ett specifikt exempel. 43/2. Vad betyder 3/2 grad? 3 - täljare, betyder att höja ett tal (i detta fall 4) till en kub. Siffran 2 är nämnaren, det är extraktionen av nummerets andra rot (i detta fall 4).
Sedan får vi kvadratroten 43 = 2 ^ 3 = 8. Svar: 8.
Så, nämnaren för bråkgraden kan vara antingen 3 eller 4 och till oändligt valfritt tal, och detta nummer bestämmer graden av kvadratroten som extraheras från ett givet nummer. Naturligtvis kan nämnaren inte vara noll.
Exponentiering
Om roten höjs till en kraft som är lika med rotens kraft, blir svaret ett radikalt uttryck. Till exempel (√x) 2 = x. Och så i alla fall, jämställdheten mellan graden av roten och graden av rotering.
Om (√x) ^ 4. Sedan (√x) ^ 4 = x ^ 2. För att kontrollera lösningen, låt oss översätta uttrycket till ett uttryck med en fraktionerad kraft. Eftersom roten är kvadratisk är nämnaren 2. Och om roten höjs till den fjärde kraften är täljaren 4. Vi får 4/2 = 2. Svar: x = 2.
I vilket fall som helst är det bästa alternativet att helt enkelt konvertera uttrycket till ett fraktionerat kraftuttryck. Om fraktionen inte avbryts kommer svaret att vara, förutsatt att roten till det angivna numret inte är markerad.
Exponentiering av ett komplext tal
Vad är ett komplext tal? Ett komplext tal är ett uttryck med formeln a + b * i; a, b - reella tal. i är det tal som, när det är kvadrat, ger numret -1.
Låt oss titta på ett exempel. (2 + 3i) ^ 2.
(2 + 3i) ^ 2 = 22 +2 * 2 * 3i + (3i) ^ 2 = 4 + 12i ^ -9 = -5 + 12i.
Gå på kursen "Påskynda verbal räkning, INTE mental aritmetik" för att lära dig hur man snabbt och korrekt lägger till, subtraherar, multiplicerar, delar, kvadrerar och till och med rotar. På 30 dagar lär du dig att använda lätta knep för att förenkla aritmetiska operationer. Varje lektion har nya tekniker, tydliga exempel och hjälpsamma uppgifter.
Exponentiering online
Med vår miniräknare kan du beräkna exponentieringen av ett tal:
Exponentiering betyg 7
Exponentiering startas först i sjunde klass.
Exponentiering är en operation som är nära relaterad till multiplikation; denna operation är resultatet av multipel multiplikation av ett tal i sig. Låt oss representera med formeln: a1 * a2 * ... * an = an.
Till exempel, a = 2, n = 3: 2 * 2 * 2 = 2 ^ 3 = 8.
Exempel på lösning:

Exponentiering presentation
Avläggande av examenpresentation för sjunde klassare. Presentationen kan klargöra några av de förvirrande punkterna, men förmodligen kommer det inte att finnas sådana ögonblick tack vare vår artikel.
Resultat
Vi har bara täckt toppen av isberget för att förstå matematik bättre - anmäl dig till vår kurs: Påskynda verbal räkning - INTE mental aritmetik.
Från kursen kommer du inte bara att lära dig dussintals tekniker för förenklad och snabb multiplikation, addition, multiplikation, division, procentberäkning, utan också träna dem i speciella uppgifter och pedagogiska spel! Verbal räkning kräver också mycket uppmärksamhet och koncentration, som tränas aktivt när man löser intressanta problem.
Matematiska uttryck (formler) förkortad multiplikation(kvadraten av summan och skillnaden, kuben av summan och skillnaden, skillnaden mellan kvadraterna, summan och skillnaden mellan kuberna) är extremt oersättliga i många områden med exakt vetenskap. Dessa 7 symboliska notationer är oersättliga för att förenkla uttryck, lösa ekvationer, multiplicera polynom, avbryta fraktioner, lösa integraler och mycket mer. Det betyder att det kommer att vara mycket användbart att förstå hur de erhålls, vad de är för, och viktigast av allt, hur man kommer ihåg dem och sedan tillämpar dem. Sedan ansöker förkortade multiplikationsformler i praktiken är det svåraste att se vad som är x och vad har du. Uppenbarligen finns det inga begränsningar för a och b nej, vilket betyder att det kan vara några numeriska eller bokstavliga uttryck.
Och så är de:
Den första x 2 - vid 2 = (x - y) (x + y).Att beräkna skillnad i rutor två uttryck måste multipliceras med skillnaderna mellan dessa uttryck och deras summor.
Den andra (x + y) 2 = x 2 + 2xy + y 2... Att hitta kvadraten på summan två uttryck måste du lägga till den dubbla produkten från det första uttrycket till det andra plus kvadraten för det andra uttrycket till det första uttryckets kvadrat.
Tredje (x - y) 2 = x 2 - 2xy + y 2... Att beräkna kvadratisk skillnad två uttryck, måste du subtrahera den dubbla produkten från det första uttrycket med det andra plus kvadraten för det andra uttrycket från det första uttryckets kvadrat.
Fjärde (x + y) 3 = x 3 + 3x 2 y + 3x 2 + y 3. Att beräkna kubsumma två uttryck, måste du lägga till kuben i det första uttrycket trippelprodukten av kvadraten för det första uttrycket med det andra plus tredubbla produkten av det första uttrycket med kvadraten av det andra plus kuben i det andra uttrycket.
Femte (x - y) 3 = x 3 - 3x 2 y + 3x 2 - vid 3... Att beräkna skillnadskub av två uttryck, är det nödvändigt att subtrahera trippelprodukten från fyrkanten av det första uttrycket från kuben av det första uttrycket med det andra plus det tredubbla produkten av det första uttrycket med det andra uttrycket minus kuben i det andra uttrycket .
Sjätte x 3 + vid 3 = (x + y) (x 2 - xy + y 2) Att beräkna summan av kuber två uttryck, måste du multiplicera summan av det första och andra uttrycket med den ofullständiga kvadraten av skillnaden mellan dessa uttryck.
Sjunde x 3 - vid 3 = (x - y) (x 2 + xy + y 2) Att utföra en beräkning skillnadskuber två uttryck måste skillnaden mellan det första och andra uttrycket multipliceras med den ofullständiga kvadraten av summan av dessa uttryck.
Det är inte svårt att komma ihåg att alla formler används för att utföra beräkningar och i motsatt riktning (från höger till vänster).
Förekomsten av dessa regelbundenheter upptäcktes för cirka 4 tusen år sedan. De användes allmänt av invånarna i forntida Babylon och Egypten. Men i dessa tider uttrycktes de verbalt eller geometriskt och använde inte bokstäver i beräkningarna.
Låt oss analysera summa kvadratisk bevis(a + b) 2 = a 2 + 2ab + b 2.
Den första detta matematiskt mönster bevisat av den antika grekiska forskaren Euclid, som arbetade i Alexandria under III-talet f.Kr., använde han för detta en geometrisk metod för att bevisa formeln, eftersom forskarna i antika Grekland inte använde bokstäver för att beteckna siffror. De använde i stor utsträckning inte "a 2" utan "en kvadrat på ett segment a", inte "ab", utan "en rektangel innesluten mellan segmenten a och b".
I föregående lektion räknade vi ut factoring. Vi behärskade två metoder: att ta den gemensamma faktorn ur parentes och gruppera. I denna handledning är nästa kraftfulla sätt: förkortade multiplikationsformler... Kort sagt - FSU.
Förkortade multiplikationsformler (kvadrat av summan och skillnaden, kuben av summan och skillnaden, skillnaden i kvadrater, summan och skillnaden mellan kuber) är väsentliga i alla grenar av matematiken. De används för att förenkla uttryck, lösa ekvationer, multiplicera polynom, avbryta fraktioner, lösa integraler etc. etc. Kort sagt, det finns all anledning att hantera dem. Förstå varifrån de kommer, varför de behövs, hur man kommer ihåg dem och hur man tillämpar dem.
Förståelse?)
Var kommer förkortade multiplikationsformler ifrån?
Likhet 6 och 7 är inte skrivna på ett mycket välbekant sätt. Som om tvärtom. Detta är avsiktligt.) All jämlikhet fungerar både från vänster till höger och från höger till vänster. I en sådan post är det tydligare var FSO kommer ifrån.
De kommer från multiplikation.) Till exempel:
(a + b) 2 = (a + b) (a + b) = a 2 + ab + ba + b 2 = a 2 + 2ab + b 2
Det är det, inga vetenskapliga knep. Vi multiplicerar bara parenteserna och ger liknande. Så det visar sig alla förkortade multiplikationsformler. Förkortad multiplikation beror på att det i själva formlerna inte finns någon multiplikation av parenteser och en gjutning av liknande. Förkortat.) Resultatet ges omedelbart.
FSO behöver veta det av hjärtat. Utan de första tre kan du inte drömma om en tre, utan resten - om en fyra och en fem.)
Varför behöver vi förkortade formler för multiplikation?
Det finns två skäl att lära sig, till och med att memorera dessa formler. Den första är att ett färdigt svar på maskinen kraftigt minskar antalet fel. Men det här är inte huvudorsaken. Men den andra ...
Om du gillar den här webbplatsen ...
Förresten, jag har ett par intressanta platser till dig.)
Du kan öva på att lösa exempel och ta reda på din nivå. Omedelbar valideringstestning. Lärande - med intresse!)
du kan bekanta dig med funktioner och derivat.
Formler eller regler för förkortad multiplikation används i aritmetik, eller snarare i algebra, för en snabbare process för att beräkna stora algebraiska uttryck. Formlerna själva är härledda från reglerna som finns i algebra för att multiplicera flera polynomer.
Användningen av dessa formler ger en ganska snabb lösning på olika matematiska problem och hjälper också till att förenkla uttryck. Reglerna för algebraiska transformationer gör att du kan utföra vissa manipulationer med uttryck, varefter du kan få uttrycket på vänster sida av jämställdheten på höger sida, eller omvandla höger sida av jämlikheten (för att få uttrycket på vänster sida efter likhetstecknet).
Det är bekvämt att känna till de formler som används för förkortad multiplikation med minne, eftersom de ofta används för att lösa problem och ekvationer. Nedan visas de viktigaste formlerna i listan och deras namn.
Summa i kvadrat
För att beräkna kvadraten på summan måste du hitta summan som består av kvadraten för den första termen, två gånger produkten av den första termen med den andra och kvadraten för den andra. Som uttryck skrivs denna regel enligt följande: (a + c) ² = a² + 2ac + c².
Skillnad i kvadrat
För att beräkna kvadraten av skillnaden måste du beräkna summan som består av kvadraten för det första numret, två gånger produkten av det första numret med det andra (taget med motsatt tecken) och kvadraten för det andra numret. I form av ett uttryck ser denna regel ut så här: (a - c) ² = a² - 2ac + c².
Skillnad mellan rutor
Formeln för skillnaden mellan två nummer i kvadrat är lika med produkten av summan av dessa siffror med deras skillnad. I form av ett uttryck ser denna regel ut så här: a² - c² = (a + c) · (a - c).
Sum kub
För att beräkna kuben av summan av två termer är det nödvändigt att beräkna summan som består av kuben av den första termen, den tredubbla produkten av kvadraten av den första termen och den andra, trippelprodukten från den första termen och den andra kvadrat, liksom kuben av den andra termen. I form av ett uttryck ser denna regel ut så här: (a + c) ³ = a³ + 3a²c + 3ac² + c³.

Summan av kuber
Enligt formeln likställs den med produkten av summan av dessa termer med deras ofullständiga kvadrat av skillnaden. I form av ett uttryck ser denna regel ut så här: a³ + c³ = (a + c) · (a² - ac + c²).
Exempel. Det är nödvändigt att beräkna volymen på en figur som bildas genom att lägga till två kuber. Endast storlekarna på deras sidor är kända.
Om sidovärdena är små är beräkningarna enkla.
Om sidornas längder uttrycks i besvärliga siffror är det i detta fall lättare att tillämpa formeln "Summa av kuber", vilket i hög grad förenklar beräkningarna.

Skillnadskub
Uttrycket för den kubiska skillnaden är som följer: som summan av den tredje termens tredje kraft, tredubblar den negativa produkten av kvadraten för den första termen med den andra, tredubblar produkten av den första termen med kvadraten av den andra och den andra termens negativa kub. I form av ett matematiskt uttryck ser skillnadens kub ut så här: (a - c) ³ = a³ - 3a²c + 3ac² - c³.

Skillnad mellan kuber
Formeln för skillnaden i kuber skiljer sig från summan av kuber i endast ett tecken. Således är skillnaden mellan kuberna en formel som är lika med produkten av skillnaden mellan dessa tal med deras ofullständiga kvadrat av summan. I formen ser skillnaden på kuber ut så här: a 3 - c 3 = (a - c) (a 2 + ac + c 2).
Exempel. Det är nödvändigt att beräkna volymen på figuren som kommer att finnas kvar efter att den gula volymetriska siffran har subtraherats från volymen på den blå kuben, som också är en kub. Endast storleken på sidan av den lilla och stora kuben är känd.
Om sidovärdena är små är beräkningarna ganska enkla. Och om sidornas längder uttrycks i betydande antal, är det värt att använda en formel med titeln "Skillnadskuber" (eller "Skillnadskub"), vilket i hög grad förenklar beräkningarna.
Tre faktorer, som var och en är lika med x. (\ displaystyle x.) Denna aritmetiska operation kallas "kubering", dess resultat betecknas x 3 (\ displaystyle x ^ (3)):
x 3 = x ⋅ x ⋅ x (\ displaystyle x ^ (3) = x \ cdot x \ cdot x)För kubering är den omvända operationen kubrotxtraktion. Tredje gradens geometriska namn " kub»Beror på det faktum att forntida matematiker ansåg värdena på kuber som kubiknummer, en speciell typ av lockiga nummer (se nedan), eftersom kuben för numret x (\ displaystyle x)är lika med volymen på en kub med en kantlängd lika med x (\ displaystyle x).
Sekvens av kuber
, , , , , 125, 216, 343, 512, 729, , 1331, , 2197, 2744, 3375, 4096, 4913, 5832, 6859, 8000, 9261, 10648, 12167, 13824, 15625, 17576, 19683, 21952, 24389, 27000, 29791, 32768, 35937, 39304, 42875, 46656, 50653, 54872, 59319, 64000, 68921, 74088, 79507, 85184, 91125, 97736, 103823, 110592, 117649, 125000, 132651, 140608, 148877, 157464, 166375, 175616, 185193, 195112, 205379, 216000, 226981, 238328…Summan av kuber först n (\ displaystyle n) positiva naturliga tal beräknas med formeln:
∑ i = 1 ni 3 = 1 3 + 2 3 + 3 3 + ... + n 3 = (n (n + 1) 2) 2 (\ displaystyle \ sum _ (i = 1) ^ (n) i ^ (3 ) = 1 ^ (3) + 2 ^ (3) + 3 ^ (3) + \ ldots + n ^ (3) = \ left ((\ frac (n (n + 1)) (2)) \ höger) ^ (2))Formelderivation
Formeln för summan av kuber kan härledas med multiplikationstabellen och formeln för summan av en aritmetisk progression. Med tanke på två multiplikationstabeller 5 × 5 som en illustration av metoden kommer vi att utföra resonemanget för tabeller av storlek n × n.
|
|
Summan av siffrorna i det k-th (k = 1,2, ...) valda området i den första tabellen:
k 2 + 2 k ∑ l = 1 k - 1 l = k 2 + 2 kk (k - 1) 2 = k 3 (\ displaystyle k ^ (2) + 2k \ sum _ (l = 1) ^ (k- 1) l = k ^ (2) + 2k (\ frac (k (k-1)) (2)) = k ^ (3))Och summan av siffrorna i det k-th (k = 1,2, ...) valda området i den andra tabellen, som representerar en aritmetisk progression:
k ∑ l = 1 n l = k n (n + 1) 2 (\ displaystyle k \ sum _ (l = 1) ^ (n) l = k (\ frac (n (n + 1)) (2)))Sammanfattning över alla utvalda områden i den första tabellen får vi samma antal som att summera över alla utvalda områden i den andra tabellen:
∑ k = 1 nk 3 = ∑ k = 1 nkn (n + 1) 2 = n (n + 1) 2 ∑ k = 1 nk = (n (n + 1) 2) 2 (\ displaystyle \ sum _ (k = 1) ^ (n) k ^ (3) = \ sum _ (k = 1) ^ (n) k (\ frac (n (n + 1)) (2)) = (\ frac (n (n + 1)) (2)) \ sum _ (k = 1) ^ (n) k = \ vänster ((\ frac (n (n + 1)) (2)) \ höger) ^ (2))Vissa fastigheter
- I decimalnotation kan en kub sluta med vilken siffra som helst (i motsats till en kvadrat)
- I decimalnotation kan de sista två siffrorna i kuben vara 00, 01, 03, 04, 07, 08, 09, 11, 12, 13, 16, 17, 19, 21, 23, 24, 25, 27, 28 , 29, 31, 32, 33, 36, 37, 39, 41, 43, 44, 47, 48, 49, 51, 52, 53, 56, 57, 59, 61, 63, 64, 67, 68, 69 , 71, 72, 73, 75, 76, 77, 79, 81, 83, 84, 87, 88, 89, 91, 92, 93, 96, 97, 99. Beroendet av den näst sista kubsiffran på den sista kan representeras i följande tabell:
Kuber som lockiga siffror
"Kubiskt nummer" Q n = n 3 (\ displaystyle Q_ (n) = n ^ (3)) historiskt betraktad som ett slags rumsliga lockiga nummer. Det kan representeras som skillnaden mellan kvadraterna i på varandra följande triangulära tal T n (\ displaystyle T_ (n)):
Q n = (T n) 2 - (T n - 1) 2, n ⩾ 2 (\ displaystyle Q_ (n) = (T_ (n)) ^ (2) - (T_ (n-1)) ^ (2 ), n \ geqslant 2) Q 1 + Q 2 + Q 3 + ⋯ + Q n = (T n) 2 (\ displaystyle Q_ (1) + Q_ (2) + Q_ (3) + \ dots + Q_ (n) = (T_ (n) ) ^ (2))Skillnaden mellan två intilliggande kubiska siffror är det centrerade hexagonala talet.
Uttryck av ett kubiskt tal i termer av tetraeder Π n (3) (\ displaystyle \ Pi _ (n) ^ ((3))).