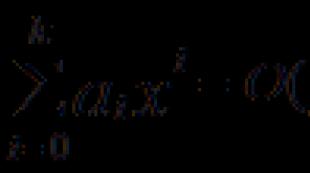återkommande metoder. Allmänna och särskilda lösningar av återkommande relationer Beräkna bestämningsfaktorerna för ordningen n med metoden för återkommande relationer
Med en stor mängd observationsdata Xändliga metoder för att lösa sannolikhetsekvationen leder till betydande beräkningssvårigheter förknippade med behovet av att komma ihåg ett stort antal initiala data och mellanliggande resultat av beräkningar. I detta avseende är återkommande metoder av särskilt intresse, där den maximala sannolikhetsuppskattningen beräknas i steg med gradvis ökande noggrannhet, varje steg är associerat med att erhålla nya observationsdata, och den återkommande proceduren är konstruerad på ett sådant sätt att den lagras i minne så lite data som möjligt från de föregående stegen. En ytterligare och mycket betydande fördel ur praktisk synvinkel av rekursiva metoder är beredskapen att utfärda ett resultat vid vilket mellanliggande steg som helst.
Detta gör det ändamålsenligt att använda återkommande metoder även i de fall där det är möjligt att få en exakt lösning av den maximala sannolikhetsekvationen med en finit metod, och gör dem ännu mer värdefulla när det är omöjligt att hitta ett exakt analytiskt uttryck för att uppskatta det maximala sannolikhet.
Låt uppsättningen observationsdata vara en sekvens för beskrivningen av vilken vi introducerar vektorn. (Som alltid kan var och en av dess komponenter i sin tur vara en vektor, ett segment av en slumpmässig process, etc.). Låt vara sannolikhetsfunktionen, och
dess logaritm. Den senare kan alltid representeras som
Logsannolikheten för observationsdatauppsättningen utan det sista värdet, och
Logaritmen för den villkorade sannolikhetstätheten för värdet för givna värden på och .
Representation (7.5.16) för sannolikhetsfunktionens logaritm är grunden för att erhålla en återkommande procedur för att beräkna den maximala sannolikhetsuppskattningen. Låt oss överväga det vanliga fallet. I detta fall kan maximal sannolikhetsuppskattning hittas som en lösning på ekvationen
som skiljer sig från (7.1.6) endast genom att införa index p y logaritm för sannolikhetsfunktionen.
Låt oss beteckna lösningen av denna ekvation genom att på så sätt betona att denna uppskattning erhölls från totalen av observationsdata. På liknande sätt, låt oss beteckna med lösningen av ekvationen den maximala sannolikhetsuppskattningen som erhålls från datamängden.
Ekvation (7.5.19) kan skrivas om med hänsyn till (7.5.16) i följande form:
Låt oss expandera den vänstra sidan av (7.5.20) till en Taylor-serie i närheten av punkten . Vart i
(7.5.22)
Gradientvektorn för funktionen vid punkten ; term försvinner på grund av det faktum att , är lösningen av sannolikhetsekvationen för föregående (P - 1:e steget:
Den symmetriska matrisen av andraderivatorna av logaritmen av sannolikhetsfunktionen vid punkten , taget med motsatt tecken, de oskrivna termerna för expansionen har en kvadratisk och högre ordning av litenhet med avseende på skillnaden . Om vi försummar dessa senare får vi följande ungefärliga lösning av ekvationen för maximal sannolikhet:
var är den omvända matrisen.
Denna lösning presenteras i form av en återfallsrelation som bestämmer nästa värde av skattningen genom uppskattningen i föregående steg och korrigeringen , beroende av tillgängliga observationsdata direkt och genom tidigare utvärdering. Korrigeringen bildas som produkten av gradienten av logaritmen av den villkorade sannolikhetstätheten för det nyligen erhållna värdet X n vid den punkt som är lika med den tidigare uppskattningen, på viktmatrisen . Den senare bestäms av uttryck (7.5.23) och beror också på uppskattningen vid föregående steg, och dess beroende av nya observationsdata bestäms helt av formen av logaritmen för den villkorliga sannolikhetstätheten .
Relationsformen (7.5.24) är mycket lik (7.5.8), som implementerar ett iterativt sätt att beräkna maximal sannolikhetsuppskattning med Newtons metod. Men i själva verket skiljer de sig väsentligt från varandra. I (7.5.8) bestäms korrigeringen till det tidigare värdet av uppskattningen av storleken på gradienten av logaritmen för hela sannolikhetsfunktionen, som alltid beror på alla tillgängliga observationsdata , vilket kräver att man memorerar hela populationen. I enlighet med (7.5.24) bestäms korrigeringen till av gradientens storlek, som, på grund av egenskaperna hos den villkorade sannolikhetstätheten, faktiskt bara beror på de värden () som är i ett starkt statistiskt samband med X n. Denna skillnad är en konsekvens av det speciella valet av den tidigare approximationen som den maximala sannolikhetsuppskattningen som hittats från uppsättningen observationsdata reducerad med ett värde , och är särskilt uttalad för oberoende värden på (). I det sista fallet
på grund av vilket det bara beror på och X n , och gradienten är endast från det tidigare värdet av uppskattningen och det nyligen erhållna P-Övervakningsdatasteg. För att oberoende värden ska kunna bilda en vektor är det därför inte nödvändigt att lagra någon annan information från föregående steg, förutom värdet av uppskattningen.
På liknande sätt, i fallet med en Markov-sekvens av observationsdata, det vill säga när
vektorn beror endast på , nuvarande och ett tidigare värde . I det här fallet, för beräkningen, är det nödvändigt att komma ihåg från föregående steg, förutom värdet , endast värdet , men inte hela uppsättningen observationsdata, som i det iterativa förfarandet. I allmänhet kan beräkningen kräva att ett större antal tidigare värden lagras (), men på grund av behovet av att endast ta hänsyn till de värden som är statistiskt beroende av , är detta antal nästan alltid mindre än den totala volymen av observationsdatauppsättningen. Så om en vektor beskriver en tidssekvens, så bestäms antalet memorerade medlemmar av denna sekvens av tiden för dess korrelation, och deras relativa andel minskar omvänt proportionellt n, som i fallet med oberoende värderingar.
Låt oss nu betrakta strukturen av viktmatrisen, inkluderad i den återkommande relationen (7.5.24). Enligt definitionen (7.5.23), på grund av termens närvaro, beror det i allmänhet på alla värden även för oberoende värden på , vilket berövar återfallsrelationen (7.5.24) fördelarna förknippade med en möjlig minskning av mängden lagrad data från föregående steg. Det finns flera sätt att approximera matrisen , som avhjälper denna brist.
Den första av dem är baserad på en mer konsekvent användning av det grundläggande antagandet om en liten skillnad mellan två på varandra följande värden av uppskattningen och , som är grunden för att erhålla återfallsrelationen (7.5.24). Detta gör det möjligt för oss att erhålla en liknande återfallsrelation för viktmatrisen. Med användning av litenheten från (7.5.23) har vi faktiskt
Genom att introducera notationen
från (7.5.24) och (7.5.25) får vi ett system av återkommande relationer för vektorn och viktmatrisen
Detta system, tillsammans med de initiala värdena, bestämmer fullständigt värdet av uppskattningen vid vilket steg som helst, vilket kräver att var och en av dem endast beräknar gradienten och matrisen för andraderivator av logaritmen för den villkorade sannolikhetstätheten för det aktuella observerade värdet . De initiala värdena väljs med hänsyn till tillgängliga a priori-data om möjliga värden och ändringsintervallet för parametrarna, och i avsaknad av dessa data anses de vara noll (,).
För oberoende värden beskriver systemet med återkommande relationer (7.5.27) uppenbarligen en flerdimensionell (dimensioner) Markov slumpmässig process, vars komponent konvergerar till det sanna värdet av parametern och komponenten konvergerar till Fishers informationsmatris (7.3. 8), där är det sanna värdet av den uppskattade parametern och ökar på obestämd tid som P. System (7.5.27) har liknande konvergensegenskaper under mer allmänna förhållanden om sekvensen är ergodisk.
Den andra av de nämnda metoderna bygger på att ersätta matrisen av andraderivator av logaritmen för sannolikhetsfunktionen med dess matematiska förväntan - Fisher-informationsmatrisen, som, med hänsyn till (7.5.16), kan skrivas som:
där liknande (7.5.26)
Genom att ersätta matrisen i (7.5.24) med matrisen får vi den återkommande relationen
för den ungefärliga beräkningen av de maximala sannolikhetsuppskattningarna föreslagna av Sakrison (i originalet för oberoende identiskt fördelade , när och . Denna upprepningsrelation är enklare än systemet (7.5.27), eftersom den optimala viktmatrisen ersätts av dess matematiska förväntan och tillgängliga observationsdata krävs inte för att hitta den, förutom de som är koncentrerade till värdet av skattningen. Samtidigt är det uppenbart att en sådan ersättning innebär ett behov av att uppfylla ett ytterligare krav jämfört med (7.5. 27) att matrisen av andraderivator ligger nära dess matematiska förväntan.
Om sannolikhetstäthetsfördelningen och matrisen ändras från steg till steg, kan det krävas för många beräkningar för att hitta varje steg direkt. Samtidigt, på grund av en ytterligare minskning av resultatens noggrannhet, som bestäms av olikheten noll av små skillnader, kan man fortsätta till återkommande beräkning av det ungefärliga värdet av matrisen . För att återgå till föregående notation för detta ungefärliga värde får vi ett annat system av återkommande relationer
Matematisk förväntan på matrisen (Fisher informationsmatris för en observation), tagen vid punkten . Detta system skiljer sig från (7.5.27) genom att det andra av återfallsrelationerna (7.5.31) inte direkt involverar observationsdata.
Något av systemen för återkommande relationer som betraktas ovan är helt exakt om funktionen beror kvadratiskt på , och dessutom matrisen av andraderivator inte beror på . I själva verket motsvarar detta fallet med oberoende normalfördelade (inte nödvändigtvis lika) värden med en okänd matematisk förväntan, som är den uppskattade parametern.
Systemet med återfallsrelationer (7.5.24) ger den exakta lösningen av ekvationen för maximal sannolikhet under mycket bredare förhållanden med det enda kravet att funktionen beror kvadratiskt på . I detta fall är beroendet av godtyckligt, vilket motsvarar en bred klass av populationssannolikhetsfördelningar med både oberoende och beroende värden.
Tillsammans med de övervägda generella metoderna finns det ett antal metoder för att välja en matris av viktkoefficienter i återfallsrelationen (7.5.24), anpassade till vissa specifika restriktioner. Det enklaste av dessa är valet i form av en diagonal matris, så att , ( jagär identitetsmatrisen), där är en minskande sekvens av numeriska koefficienter, vald oberoende av sannolikhetsfunktionens egenskaper på samma sätt som i Robins-Monroes stokastiska approximationsprocedur, som kommer att diskuteras i följande kapitel.
Det bör noteras att alla iterativa eller återkommande förfaranden för att hitta maximala sannolikhetsuppskattningar i allmänhet är ungefärliga. Generellt sett måste därför konsekvens, asymptotisk effektivitet och asymptotisk normalitet bevisas på nytt för de uppskattningar som erhålls som ett resultat av tillämpningen av dessa procedurer. För iterativa procedurer garanteras de nödvändiga egenskaperna hos uppskattningar av det faktum att sådana procedurer i princip, med ett lämpligt antal iterationer, ger en lösning på sannolikhetsekvationen med vilken som helst förutbestämd noggrannhet. För återkommande procedurer som (7.5.27), (7.5.30), (7.5.31) och andra finns det speciella bevis. Samtidigt, utöver kravet på regelbundenhet, ställs några ytterligare krav:
På beteendet hos funktionen (7.2.2) för olika värden på ||, för att med den återkommande proceduren uppnå det globala maximumet för denna funktion vid den punkt som motsvarar parameterns sanna värde;
Genom en tillväxtordning för de andra momenten av derivatorna av logaritmen av sannolikhetsfunktionen för stora modulovärden på . Dessa krav är en följd av mer allmänna villkor för konvergens till en punkt av alla eller delar av komponenterna i en Markov slumpmässig process, till vilken ett eller annat återkommande förfarande leder.
Sammanfattningsvis noterar vi också att i fallet när det finns en exakt lösning av ekvationen för maximal sannolikhet kan den nästan alltid representeras i en rekursiv form. Vi ger två enkla heterogena exempel. Alltså en elementär uppskattning av den okända matematiska förväntan av en normal slumpvariabel i aggregatet n dess urvalsvärden i form av ett aritmetiskt medelvärde
är den maximala sannolikhetsuppskattningen och kan representeras i den rekursiva formen:
vilket är det enklaste specialfallet (7.5.30) för
Ett annat exempel är den oregelbundna maximala sannolikhetsuppskattningen för parametern - bredden på den rektangulära fördelningen - från (7.4.2), som också kan bestämmas av återfallsrelationen
med initialt skick. Denna upprepningsrelation är av en annan typ: dess högra sida kan inte representeras som summan av den tidigare uppskattningen och en liten korrigering, vilket är en konsekvens av oegentligheten i detta exempel; det har dock alla fördelarna med det rekursiva tillvägagångssättet: det kräver att bara ett nummer kommer ihåg från föregående steg - uppskattningen - och det minskar drastiskt uppräkningen till en jämförelse istället för att jämföra alla värden.
De givna exemplen illustrerar fördelarna med rekursiva metoder även i de fall då ekvationen för maximal sannolikhet tillåter en exakt lösning, eftersom enkelheten i den analytiska representationen av resultatet inte är identisk med den beräkningsmässiga enkelheten att erhålla det.
7.5.3. Övergång till kontinuerlig tid. Differentialekvationer för uppskattningar av maximal sannolikhet
Låt oss nu överväga ett specialfall där tillgängliga observationsdata X beskrivs inte av en uppsättning provpunkter , men representerar ett segment av genomförandet av någon process , beroende på parametrarna , angivna på intervallet , dessutom kan längden på detta intervall öka under observation (tid tär variabel).
För en statistisk beskrivning av observationsdata, i detta fall, introduceras sannolikhetsförhållandet funktionell, vilket är gränsen vid , max för förhållandet mellan sannolikhetstätheten för uppsättningen värden vid ett godtyckligt givet värde till en liknande sannolikhet densitet vid något fast värde, och i vissa fall, när den medger representationen, var är en slumpmässig process, oberoende av, till sannolikhetstätheten för uppsättningen värden förutsatt att . Användningen av sannolikhetskvotsfunktionen gör det möjligt att eliminera de formella svårigheterna med att bestämma sannolikhetstätheten som uppstår vid övergången till kontinuerlig tid.
Logaritmen för den funktionella sannolikhetsförhållandet kan representeras som
var är någon process funktionell på intervallet. I vissa fall urartar den funktionella till en funktion som bara beror på värdet av . Så om
där är en känd funktion av tid och parametrar, och är en delta-korrelerad slumpmässig process ("vitt" brus) med spektral densitet N o välj sedan sannolikhetsfördelningens sannolikhetsförhållande som nämnare X kl, kommer vi att ha
Låt - den maximala sannolikhetsuppskattningen av parametern, byggd på implementeringen av processen på intervallet, det vill säga lösningen av ekvationen för maximal sannolikhet
Att differentiera den vänstra sidan av denna ekvation med avseende på tid får vi
Introduktion av notationen
och lösa ekvationen (7.5.42) med avseende på , får vi differentialekvationen för maximal sannolikhetsuppskattning
Matrisen bestäms i sin tur enligt (7.5.37) av differentialekvationen
Precis som i det diskreta fallet kan matrisen i (7.5.45), (7.5.47) ersättas med dess matematiska förväntan - Fisher-informationsmatrisen med värdet och differentialekvationen (7.5.46) för viktmatrisen - enligt ekvationen
där, i likhet med det diskreta fallet
Matematisk förväntan på matrisen av andraderivator.
Uppsättningen differentialekvationer (7.5.45), (7.5.46) eller (7.5.45), (7.5.48), tillsammans med de initiala villkoren, angående valet av vilket allt som sägs för det diskreta fallet förblir giltigt, helt och hållet bestämmer den maximala sannolikhetsuppskattningen för någon tidpunkt. Denna uppsättning kan simuleras med hjälp av lämpliga, generellt sett, icke-linjära analoga enheter eller, med lämplig tidssampling, lösas av en dator. Sammanfattningsvis noterar vi en av modifikationerna av dessa ekvationer, vilket gör det möjligt att undvika behovet av att invertera matrisen.
Introduktion av notationen
, var jag
och differentiera förhållandet med avseende på tid , var jagär identitetsmatrisen får vi med hjälp av (7.5.46) en differentialekvation som direkt bestämmer matrisen:
(och på liknande sätt när det ersätts av ), vilket tillsammans med ekvation (7.5.45)
bestämmer poängen , utan att kräva matrisinversion. I detta fall sker en övergång från den enklaste linjära differentialekvationen (7.5.46) till en icke-linjär med avseende på differentialekvationen (7.5.51) av typen Riccati.
Kombinatoriska beräkningar på finita mängder
Introduktion till kombinatorik
Ämnet för teorin om kombinatoriska algoritmer, ofta kallade kombinatoriska beräkningar, är beräkningar på diskreta matematiska strukturer. I denna teori ägnas mycket uppmärksamhet åt den algoritmiska metoden för att lösa problem med diskret matematik, optimering av uppräkning av alternativ och minskning av antalet övervägda lösningar.
Området kombinatoriska algoritmer inkluderar uppgifter som kräver att man räknar (uppskattar) antalet element i en ändlig mängd eller listar dessa element i en speciell ordning (Bilaga B). I det här fallet används förfarandet för att välja element med retur och dess varianter i stor utsträckning.
Det finns två typer av räkneproblem. I det enkla fallet ges en specifik uppsättning och den krävs bestämma det exakta antalet element i honom. I det allmänna fallet finns det en familj av uppsättningar definierade av någon parameter, och uppsättningens kardinalitet definieras som en funktion av parametern. Samtidigt är det ofta en tillräcklig uppskattning av funktionsordningen och ibland behöver man bara bedömning av dess tillväxttakt. Till exempel, om kraften hos den uppsättning som övervägs växer exponentiellt i någon parameter, kan detta vara tillräckligt för att överge den föreslagna metoden för att studera problemet utan att gå in på olika detaljer. För denna mer allmänna typ av problem tillämpas procedurerna för asymptotiska expansioner, återfallsrelationer och genererande funktioner.
Asymptotika
En asymptot är en speciell linje (oftast en rät linje), som är gränsen för den aktuella kurvan.
Asymptotik är konsten att uppskatta och jämföra tillväxthastigheter för funktioner. Det säger de kl X®¥-funktionen "beter sig som X", eller "ökar i samma takt som X", och kl X®0 "beter sig som 1/ x". De säger att "logga x på x®0 och alla e>0 beter sig som x e, och vad n®¥ växer inte snabbare än n logga n". Sådana oprecisa men intuitivt tydliga uttalanden är användbara för att jämföra funktioner på samma sätt som relationerna<, £ и = при сравнивании чисел.
Låt oss definiera tre huvudsakliga asymptotiska samband.
Definition 1. Fungera f(x) är ekvivalent med g(x) kl X® x0, om och endast om =1.
I det här fallet sägs funktionen vara f(x) är asymptotiskt lika med funktionen g(x) eller vad f(x) växer i samma takt som g(x).
Definition 2. f(x)=o( g(x)) kl x® x0, om och endast om =0.
Det säger de kl x® x 0 f(x) växer långsammare än g(x), eller vad f(x) "det finns o-small" från g(x).
Definition 3 . f(x)=O( g(x)) kl x® x0, om och endast om det finns en konstant C så att sup =C.
I det här fallet säger de det f(x) växer inte snabbare än g(x), eller vad som helst x® x 0 f(x) "det finns ett stort O" från g(x).
Förhållande f(x)=g(x)+o(h(x)) kl x®¥ betyder det f(x)-g(x)=o(h(x)). Liknande f(x)=g(x)+O(h(x)) betyder att f(x)-g(x)=O(h(x)).
Uttrycken O( ) och o( ) kan också användas i olikheter. Till exempel ojämlikhet x+o(x) £2 x på x®0 betyder det för alla funktioner f(x) Så att f(x)=o(x), kl x®¥ x+f(x) £2 x för alla tillräckligt stora värden X.
Låt oss presentera några användbara asymptotiska likheter.
Polynomet är asymptotiskt lika med dess högsta term:
 på x®¥; (4.1)
på x®¥; (4.1)
 på x®¥; (4.2)
på x®¥; (4.2)
 på x®¥ och ett k¹0. (4.3)
på x®¥ och ett k¹0. (4.3)
Summorna av potenser av heltal uppfyller förhållandet:
på n®¥. (4.4)
Därför har vi i synnerhet n®¥
I ett mer allmänt fall, när n®¥ och för vilket heltal som helst k³0
 ; (4.6)
; (4.6)
 . (4.7)
. (4.7)
Återkommande relationer
Låt oss illustrera begreppet återfallsrelationer med det klassiska problemet som Fibonacci ställde och studerade omkring 1200.
Fibonacci satte sitt problem i form av en berättelse om tillväxttakten för en population av kaniner under följande antaganden. Allt börjar med ett par kaniner. Varje kaninpar blir fertilt (fertilt) efter en månad, varefter varje par föder ett nytt kaninpar varje månad. Kaniner dör aldrig och deras fortplantning slutar aldrig. Låta F n- antalet kaninpar i populationen efter n månader och låt denna befolkning bestå av N n kullpar och O n”gamla” par, d.v.s. F n = N n + O n. Följande händelser kommer alltså att inträffa under nästa månad:
Gammal befolkning i ( n+1)-th momentet kommer att öka med antalet födslar vid tillfället n, dvs. O n+1 = O n + N n= F n;
Varje gammal vid en tidpunkt n paret producerar vid tidpunkten ( n+1) ett par avkommor, d.v.s. Nn+1= C n.
Följande månad upprepas detta mönster:
O n+2 = O n+1+ Nn+1= Fn+1,
Nn+2=O n+1;
genom att kombinera dessa likheter får vi Fibonacci-återfallsrelationen:
O n+2 + Nn+2=Fn+1 + O n+1,
Fn+2 = Fn+1 + F n. (4.8)
Valet av initiala villkor för Fibonacci-sekvensen är inte viktigt; de väsentliga egenskaperna för denna sekvens bestäms av den återkommande relationen (4.8). Brukar tro F0=0, F1=1 (ibland F0=F1=1).
Återkommande relationen (4.8) är ett specialfall av homogena linjära återfallsrelationer med konstanta koefficienter:
x n = a 1 x n-1 + a 2 x n-2 +...a k x n-k , (4,9)
där koefficienter ett i inte är beroende av n och x 1, x2, …, x k anses givna.
Det finns en generell metod för att lösa (det vill säga att hitta x n som en funktion n) linjära återkommande relationer med konstanta koefficienter. Låt oss betrakta denna metod med hjälp av relation (4.8) som ett exempel. Vi hittar en lösning i formuläret
F n=crn (4.10)
med permanent Med och r. Genom att ersätta detta uttryck med (4.8), får vi
cr + 2 = crn+ 1 + crn,
crn(rn-r-1)=0. (4.11)
Det betyder att F n=crnär en lösning om antingen Med=0, eller r= 0 (och därmed Fn =0 för alla n), och även (och det här är ett mer intressant fall) if r 2 - r -1=0, och konstanten Med slumpmässig. Sedan från (4.11) följer det
r= eller r = . (4.12)
Siffran "1,618" är känt som det "gyllene" förhållandet, eftersom man sedan urminnes tider har trott att en triangel (rektangel) med sidorna 1 har de mest tilltalande proportionerna.
Summan av två lösningar till ett homogent linjärt recidiv är uppenbarligen också en lösning, och man kan faktiskt visa att den allmänna lösningen av Fibonacci-sekvensen är
F n= ![]() , (4.13)
, (4.13)
var är konstanterna Med och Med' bestäms av de initiala förhållandena. Genom att sätta F 0 =0 och F 1 =1 får vi följande linjära ekvationssystem:
 , (4.14)
, (4.14)
vars lösning ger
c = -c" = . (4.15)
Linjära återkommande relationer med konstanta koefficienter. Grundläggande definitioner och exempel på återfallsrelationer Ofta kan lösningen av ett kombinatoriskt problem reduceras till lösningen av liknande problem av mindre dimension med hjälp av någon relation som kallas recurrence från det latinska ordet recurrere - att återvända. Lösningen av ett komplext problem kan alltså erhållas genom att successivt hitta en lösning på lättare problem och sedan räkna om enligt återkommande relationer för att hitta en lösning på ett svårt problem. Återkommande förhållandet av...
Dela arbete på sociala nätverk
Om detta verk inte passar dig finns en lista med liknande verk längst ner på sidan. Du kan också använda sökknappen
Aranov Viktor Pavlovich Diskret matematik. Avsnitt 2. Komponenter i kombinatorik.
Föreläsning 5
Föreläsningar 5. METOD FÖR ÅTERKOMMANDE RELATIONER
Föreläsningsplan:
- Grundläggande definitioner och exempel på återkommande relationer.
- Linjära återkommande relationer med konstanta koefficienter. Formel
Binet.
- Grundläggande definitioner och exempel på återfallsrelationer
Ofta kan lösningen av ett kombinatoriskt problem reduceras till lösningen av liknande problem av lägre dimension genom att använda någon relation som kallas floden R hyra (från det latinska ordetåterkommande - lämna tillbaka). Således kan en lösning på ett komplext problem erhållas genom att sekventiellt hitta en lösning på lättare problem, och vidare, n e beräkna genom återkommande relationer, hitta en lösning på ett svårt problem.
Återkommande förhållandet av -th ordningenmellan element i en talföljd kallas en formel för formen
(1)
Privat beslutåterkommande relation är vilken som helst efterföljare b relation som gör relation (1) till en identitet. Relation (1) im e det finns oändligt många specifika lösningar, eftersom de första elementen är sekventiella O sti kan ställas in godtyckligt. Till exempel är sekvensen sid e återkommande förhållande O lösningar, eftersom identiteten håller.
Lösningen av -th order recurrence relationen kallas vanligt, om det är för en beror på godtyckliga konstanter, och genom att välja dessa konstanter kan vi väl men få någon lösning på detta förhållande. Till exempel för kvoterna och inte
(2)
den allmänna lösningen skulle vara
. (3)
Det är faktiskt lätt att kontrollera att sekvens (3) förvandlar relation (2) till en identitet. Därför är det bara nödvändigt att visa att varje lösning av relation (2) kan väl men representerar i formen (3). Men varje lösning på detta förhållande är unikt bestämt. T med värderingar och. Därför måste vi bevisa att för alla siffror och det finns m a vilka värderingar och vad
Eftersom detta system har en lösning för alla värden av och, så är lösning (3) verkligen en generell lösning av relation (2).
Exempel 1 . Fibonacci-siffror.År 1202, den berömda italienska matematikern Le O nardo från Pisa, som är mer känd under sitt smeknamn Fibonacci ( Fib o nacci - förkortat filius Bonacci , d.v.s. Bonaccis son), skrevs en bok " Liber abacci "(" Bok och ha om kulramen"). Den här boken har kommit till oss i sin andra version, som går tillbaka till 1228. Låt oss överväga ett av de många problem som ges i den här boken.
Ett par kaniner ger en gång i månaden en avkomma till två kaniner (hona och hane) osv. och än nyfödda kaniner, två månader efter födseln, redan får avkomma. Hur många kaniner kommer att dyka upp e res år, om det i början av året fanns ett par kaniner?
Av tillståndet för problemet följer att det om en månad kommer att finnas två par kaniner. Två månader senare jag är endast det första kaninparet kommer att ge avkomma, och du kommer att få 3 par. A om ytterligare en månad kommer både det ursprungliga kaninparet och det kaninpar som dök upp för två månader sedan att ge avkomma. Därför blir det 5 par kaniner totalt osv.
Beteckna med antalet kaninpar efter månader från början av r O Ja. Sedan om månader kommer det att finnas dessa par och så många fler nyfödda par. O ansikten, hur många det var i slutet av den e månaden, det vill säga fler par. Det finns alltså r e nuvarande förhållandet
. (4)
Sedan hittar vi sekventiellt: etc. Dessa siffror utgör sekvensen
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,…,
kallad nära Fibonacci och dess medlemmar - Fibonacci-siffror. De har ett antal underbara egenskaper. Fibonacci-tal är relaterade till följande kombinator men en svår uppgift.
Hitta antalet binära ord av längd där inga två 1:or följer med d rad.
Låt oss kalla dessa ord korrekt och ange deras nummer med . Låt oss dela upp mängden av dessa vanliga ord i två klasser: ord som slutar på noll och ord som slutar på ett. Låt oss beteckna antalet ord i dessa klasser och T ansvarig. Enligt tilläggsregeln
(5)
Uppenbarligen, för ett ord som slutar på noll, bildar de första tecknen ett regelbundet ord med längd, eller med andra ord, det finns en bijektion mellan uppsättningen av regelbundna ord som slutar på noll och uppsättningen av regelbundna ord, det vill säga.
Om ett ord med giltig längd slutar på ett, måste det föregående tecknet i det ordet vara noll, och de första tecknen måste bilda ett ord med giltig längd. Liksom i det föregående fallet har vi återigen en bijektion mellan mängden reguljära ord med längd som slutar på ett och mängden regelbundna längdord. Därmed. . Från formel (5) får vi den rekursiva relationen Handla om
. (6)
För att använda återfallsrelationen är det nödvändigt för denna beräkning Med förändring av alla tidigare värden. Till exempel om vi behöver veta antalet regler b ord med 10 tecken, så kan den hittas genom att sekventiellt fylla i följande tabell b ansikte:
bord 1
De två första värdena hittas direkt (-ord 0 och 1; - ord 000, 010, 101), och resten - med formel (6).
Exempel 2 Problemet med att placera parenteser i ett uttryck med en icke-associativ bin drift. Låt "" beteckna någon binär operation. Tänk in s uttryck där en symbol betecknar någon binär icke-association a aktiv drift. Hur många olika sätt att ordna parentes finns det i detta s raz e nii?
Ett exempel på en icke-associativ operation är vektorprodukten. Ett annat exempel är den vanliga additionen och multiplikationen som utförs på en dator. In med och att representationen av varje nummer i datorns minne begränsas av en viss n antal siffror, vid varje operation uppstår ett fel och m Det förväntade resultatet av dessa fel beror på arrangemanget av parenteser. Låt - maskin noll . Det betyder att. Sedan medan.
Låt oss beteckna antalet möjliga sätt att ordna parenteser med. Sedan
Vi kallar verksamheten villkorligt för en produkt. För ett godtyckligt delar vi upp alla sätt att ordna parenteser i klasser, inklusive i den -th klassen sätten som a chala, produkten av den första och sista operanden beräknas med ett visst avstånd a nya parenteser, och sedan beräknas deras produkt:
(7)
var.
Per definition är antalet sätt att ordna parenteser för att beräkna de första operanderna lika, det sista - . Enligt produktregeln, antalet arrangemang O sida för uttryck (4) är lika. Enligt tilläggsregeln
, (8)
Till exempel, .
- Linjära återfallsrelationer med konstanta koefficienter
Låt funktionen i relation (1) vara en linje th noah
, (9)
var finns några siffror. Sådana förhållanden kallas linjära förhållanden lösningar av -e ordningen med konstanta koefficienter.
Låt oss först undersöka andra ordningens relationer i detalj och sedan gå vidare till o b aktuellt tillfälle. Vid , från formel (9) får vi
, . (10)
Lösningen av dessa relationer är baserad på följande lätt bevisade påståenden e niyakh.
Lemma 1. Låta vara en lösning av relation (10), och vara vilket tal som helst. Då är också sekvensen löst och ät detta förhållande.
Lemma 2. Låt och vara lösningar av O lösningar (10). Sedan är sekvensen också jag är är en lösning på detta förhållande.
Dessa två enkla lemman leder till följande viktiga slutsats. skopa P förekomsten av alla möjliga sekvenser med vilooperationer R Dinatisk addition och multiplikation med en skalär bildar ett vektorrum. skopa P antal sekvenser som är lösningar av relation (10) representerar med O bekämpa ett delrum av det utrymmet. Det omslutande utrymmet av alla möjliga O sekvenser är oändligt dimensionella, men underrummet av lösningar av en linjär återkommande T relationen har en ändlig dimension som är lika med ekvationens ordning och inte.
Lemma 3. Dimensionen på lösningsutrymmet för den återkommande relationen (10) är lika med två.
Av Lemma 3 följer att för att bestämma alla lösningar av ekvation (12) är det nödvändigt att hitta två linjärt oberoende lösningar. Alla andra lösningar kommer att vara b är en linjär kombination av dessa grundläggande lösningar.
Betrakta första ordningens återkommande relation
, (11)
var är en konstant.
Om, så från (11) har vi
, (12)
det vill säga lösningen på en första ordningens rekursiv ekvation är en geometrisk progression.
Vi kommer att leta efter lösningen av andra ordningens återfallsrelation också i formen (12). Sedan, genom att ersätta (12) med (9), får vi
. (13)
För =0 har vi en nolllösning, som inte är av intresse. Med tanke på att vi delar det sista förhållandet med:
(14)
Således är den geometriska progressionen (12) en lösning på återfallsrelationen (10) om nämnaren för progressionen är roten till andragradsekvationen e nyja (14). Denna ekvation kallaskarakteristisk ekvationför återkommande coo t bär (9).
Konstruktionen av grundläggande lösningar beror på rötterna och den karakteristiska ekvationen (14).
- (). I det här fallet har vi två lösningar och som l och okänd sims. För att verifiera detta visar vi det från formeln
(15)
genom ett lämpligt val av konstanter kan vilken lösning som helst av relationen (10) erhållas. Överväg en godtycklig lösning. Vi väljer konstanter och så att för och:
(16)
Linjär systemdeterminant (16)
därför har systemet en unik lösning, vilket innebär att formel (15) är ett allmänt р e förhållande (10).
- . I fallet med multipla rötter har den karakteristiska ekvationen (13) formen eller. Sedan, och för relation (10) sid O får vi en ekvation som ger två grundläggande lösningar och. Den allmänna lösningen representeras som
. (17)
I fallet med den e ordningens relationen (9) sker påståenden liknande de som anses för 2:a ordningens ekvationer.
- Mängden av alla lösningar av ekvation (9) är ett delrum i pr O utrymmet för alla sekvenser.
- Dimensionen på detta utrymme är lika, det vill säga varje lösning bestäms unikt av dess första värden.
- För att bestämma grunden för underrummet av lösningar, en egenskap e ekvation
. (18)
Polynom
(19)
kallad karakteristiskt polynomrekursiv relation (9).
- Om den karakteristiska ekvationen har olika rötter, så har den allmänna lösningen av den återkommande relationen (9) formen
. (20)
För givna initiala värden för lösningen är konstanterna n a gå ut ur systemet
- Om är roten till den karakteristiska multiplicitetsekvationen, så har relation (9) följande lösningar
Låt den karakteristiska ekvationen (18) ha rötter: ,..., multipliciteter med O ansvarsfullt, ... dessutom. Sedan den karakteristiska uppsättningen O termen och den allmänna lösningen av relation (9) representeras som
Exempel 3 . Binet formel . Låt oss sätta uppgiften att erhålla en formel i explicit form för h och satt Fibonacci. För att göra detta hittar vi en lösning på återfallsrelationen (4) under förutsättning att. Vi sammanställer den karakteristiska ekvationen, hittar dess rötter och får en generell lösning. Konstanter och definitioner e lim från de ursprungliga villkoren: . Då heller
, (21)
var är det gyllene snittet. Formel (21) kallas Binets formel . Vart i. Av Binets formel följer det.
Andra relaterade verk som kan intressera dig.vshm> |
|||
| 3792. | Rationaliteten hos nyckeltal i företagets tillgång | 113,83 KB | |
| Balansräkningen är den huvudsakliga formen för finansiella rapporter. Det kännetecknar organisationens egendom och finansiella ställning vid rapporteringsdatumet. Balansräkningen återspeglar saldot på alla redovisningskonton på rapportdagen. Dessa indikatorer ges i balansräkningen i en viss grupp. | |||
| 8407. | konstant metod | 17,82 kB | |
| En objektmetod sägs ha egenskapen oföränderlighet (konstans) om objektets tillstånd inte ändras efter dess utförande. Om du inte kontrollerar oföränderlighetsegenskapen, kommer dess tillhandahållande helt och hållet att bero på skickligheten hos programmerare. Om den oföränderliga metoden ger främmande effekter under exekvering, kan resultatet bli det mest oväntade, och det är mycket svårt att felsöka och underhålla sådan kod. | |||
| 13457. | Fasplansmetod | 892,42 KB | |
| Fasplanmetoden tillämpades först på studien av olinjära system av den franske forskaren Henri Poincaré. Den största fördelen med denna metod är noggrannheten och synligheten för analysen av rörelserna i ett olinjärt system. Metoden är kvalitativ | |||
| 2243. | MÖJLIGA ANVISNINGAR METOD | 113,98 KB | |
| Tanken med metoden för möjliga MRI-riktningar är att det vid varje på varandra följande punkt finns en nedstigningsriktning så att förflyttning av en punkt längs denna riktning för ett visst avstånd inte bryter mot begränsningarna för problemet. En riktning som bestäms av en vektor kallas en möjlig riktning vid en punkt om en tillräckligt liten rörelse från i riktningen inte tar punkten utanför det tillåtna området m. Uppenbarligen, om är en intern punkt i mängden, då vilken riktning som helst vid denna punkt är möjlig. Möjlig... | |||
| 12947. | HARMONISK LINEARISERINGSMETOD | 338,05 kB | |
| När vi vänder oss direkt till övervägandet av den harmoniska linjäriseringsmetoden kommer vi att anta att det olinjära systemet som studeras reduceras till den form som visas i. Ett icke-linjärt element kan ha vilken egenskap som helst så länge det är integrerbart utan diskontinuiteter av det andra slaget. Transformationen av denna variabel för ett exempel med ett icke-linjärt element med en dödzon visas i fig. | |||
| 2248. | Grafisk metod för att lösa LLP | 219,13 KB | |
| Punkter som ligger inom och på gränsen till detta område är giltiga plan. Alla punkter i segmentet AB är nämligen de optimala planerna för problemet på vilka det maximala värdet av den linjära formen uppnås. Metod för förbättring av sekventiell plan Metoden bygger på en ordnad uppräkning av hörnpunkterna i uppsättningen av problemplaner i riktning mot att öka eller minska den linjära formen och innehåller tre väsentliga punkter. Först specificeras metoden för att beräkna baslinjen. | |||
| 7113. | Harmonisk linjäriseringsmetod | 536.48KB | |
| Metod för harmonisk linjärisering Eftersom denna metod är ungefärlig, kommer de erhållna resultaten att ligga nära sanningen endast om vissa antaganden är uppfyllda: Ett icke-linjärt system bör endast innehålla en icke-linjäritet; Den linjära delen av systemet bör vara ett lågpassfilter som dämpar de högre övertonerna som förekommer i gränscykeln; Metoden är endast tillämplig på autonoma system. Vi studerar systemets fria rörelse, det vill säga rörelsen under initiala förhållanden som inte är noll i frånvaro av yttre påverkan.... | |||
| 10649. | Index analysmetod | 121,13 KB | |
| individuella index. Allmänna aggregerade index. Genomsnittligt konverterade index. Index för variabel och konstant sammansättning av strukturella förändringar. | |||
| 12914. | Minsta kvadratiska metod | 308,27 KB | |
| Låt oss från teoretiska överväganden veta det. Därför kan vi säga att vår uppgift är att dra en rak linje på bästa möjliga sätt. Vi kommer att anta att hela felet ligger i. Vi kommer att välja de önskade koefficienterna från övervägandena så att den slumpmässiga additionen är den minsta. | |||
| 9514. | Redovisningsmetod | 1002,23 KB | |
| Redovisning rahunki att їх pobudova. Vіn sladєtsya z ett antal elementіv golovnі z yakikh: dokumentation; lager; rahunki; delpost; bedömning; beräkning; balans; sundhet. Rahunki redovisning erkänd för utseendet av närvaron av tillgångar och skulder. Redovisning rahunki att їх pobudova. | |||
ÅTERKOMMANDE RELATIONER
ÅTERKOMMANDE RELATIONER
(av lat. recur-rens, släktfall recurrentis - återvändande) - f-s av samma typ, som förbinder en viss följd efter varandra (detta kan vara en talföljd, f-tioner etc. ). Beroende på arten av de objekt som är kopplade till R. med., kan dessa relationer vara algebraiska, funktionella, differentiella, integrala, etc.
Naib. välkänd klass av R. s. är återkommande funktioner för specialfunktioner. Ja, för cylindriska funktioner Z m (x)P. Med. ser ut som
De tillåter genom funktion Z m0 (x) hitta funktioner Z m (x)på T= T 0 b 1, T 0 b 2 etc. eller till exempel enligt funktioners värden ![]() vid något tillfälle X 0 . 0 hitta (i numeriska beräkningar) värdet av någon av funktionerna
vid något tillfälle X 0 . 0 hitta (i numeriska beräkningar) värdet av någon av funktionerna
På samma punkt (här m 0 - valfritt reellt tal).
Dr. en viktig klass av R. s. ge många metoder för successiva approximationer (jfr. iterationsmetod); här är metoderna teorins störningar.
Inom kvantmekaniken finns det ytterligare en typ av R. s., som förbinder vektorer i Hilbert-tillståndsutrymmet. Till exempel, stationära harmonier, oscillatorer parametriseras av icke-negativa heltal. Motsvarande vektorer, betecknade med , där n- hel, med olika n kan erhållas från varandra genom att skapa operatörer ett + och förstörelse a:

Dessa samband kan lösas genom att uttrycka vilken vektor som helst i termer av (det lägsta energitillståndet, h = 0):
![]()
En generalisering av denna konstruktion är representationen andra kvantiseringen i kvantstatistik. mekanik och kvantfältteori (se Fock Plats).
Ett typiskt exempel på R. s. i statistiken mekanik - ekvationer för partiella fördelningsfunktioner som bildar Bogolyubov-kedjan (se. Bogolyubov ekvationer); kunskap om sådana f-tioner gör att du kan hitta alla termodynamiska. systemegenskaper.
Inom kvantfältteori dynamisk. ingår till exempel i Greens funktioner. För deras beräkning, olika approximationer, oftast - beräkningar av störningsteori. Ett alternativt tillvägagångssätt bygger på integrodifferentiell Dysons ekvationer, vilka är R. s.: ekvationen för tvåpunktsgröns funktion innehåller en fyrapunkts etta, etc. Liksom Bogolyubovs ekvation kan detta system endast lösas genom att "bryta" kedjan (platsen för "avbrottet" väljs vanligtvis utifrån fysiska överväganden och bestämmer resultatet ).
En annan typ av R. s. i kvantfältteori - Horden av identiteter i teorier kalibreringsfält. Dessa identiteter representerar också en kedja av integrodifferentiella relationer som förbinder Greens funktioner med dec. antalet yttre linjer, p är en konsekvens av teorins måttinvarians. De spelar en avgörande roll för att kontrollera kalibreringssymmetrin under proceduren renormalisering.
Slutligen är sig själv också en återkommande procedur: vid varje steg (i varje efterföljande loop) motvillkor, erhålls från beräkningen av diagram med färre slingor (för mer information, se R operation).A. M. Malokostov.
Fysisk uppslagsverk. I 5 volymer. - M.: Sovjetiskt uppslagsverk. Chefredaktör A. M. Prokhorov. 1988 .
Se vad "ÅTERKOMMANDE RELATIONER" är i andra ordböcker:
återkommande relationer- - [L.G. Sumenko. Engelsk rysk ordbok för informationsteknologi. M .: GP TsNIIS, 2003.] Ämnen informationsteknologi i allmänhet EN återkommande relationer ... Teknisk översättarhandbok
- (Weber-funktioner) det allmänna namnet för specialfunktioner som är lösningar av differentialekvationer som erhålls genom att tillämpa metoden för separation av variabler för ekvationer av matematisk fysik, såsom Laplace-ekvationen, ekvationen ... ... Wikipedia
Eller så är Josefusrimmet ett välkänt matematiskt problem med historiska övertoner. Uppgiften är baserad på legenden att avdelningen av Josephus Flavius, som försvarade staden Yodfat, inte ville kapitulera till de överlägsna styrkorna från romarna som blockerade grottan. ... ... Wikipedia
Pafnuty Lvovich Chebyshev Inom matematiken kallas en oändlig sekvens av verkliga polynom en sekvens av ortogonala polynom ... Wikipedia
Denna artikel föreslås raderas. En förklaring av skälen och en motsvarande diskussion finns på Wikipedia-sidan: Ska raderas / 22 november 2012. Medan diskussionsprocessen ... Wikipedia
Padovan-sekvensen är en heltalssekvens P(n) med initiala värden och en linjär återfallsrelation. De första värdena av P(n) är 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265 ... Wikipedia
Hermitpolynom av en viss form är en sekvens av polynom i en reell variabel. Hermitpolynom uppstår i sannolikhetsteori, i kombinatorik och fysik. Dessa polynom är uppkallade efter Charles Hermite. Innehåll 1 ... ... Wikipedia
- (Bessel-funktioner) lösningar Zv(z) i Bessel-ekvationen där parametern (index) v är ett godtyckligt reellt eller komplext tal. I applikationer möter man ofta en ekvation som beror på fyra parametrar: lösningarna som uttrycks i termer av C... Fysisk uppslagsverk
Metod för att lösa ett system av linjär algebraisk. ekvationerna A x= b med en hermitisk icke-singular matris A. Bland direkta metoder är den mest effektiv när den implementeras på en dator. Metodens beräkningsschema är i allmänhet baserat på den hermitiska faktoriseringen ... ... Matematisk uppslagsverk
Modifierade Bessel-funktioner är Bessel-funktioner av ett rent imaginärt argument. Om vi ersätter med i Bessel differentialekvation kommer den att ha formen Denna ekvation kallas den modifierade Bessel-ekvationen ... Wikipedia
Återfallsrelationen har beställa k , om det tillåter uttryck av f(n+k) i termer av f(n), f(n+1), …, f(n+k-1).
Exempel.
f(n+2)=f(n)f(n+1)-3f2(n+1)+1 är en andra ordningens återkommande relation.
f(n+3)=6f(n)f(n+2)+f(n+1) är en återkommande relation av tredje ordningen.
Om en k-te ordningens upprepningsrelation ges, så kan oändligt många sekvenser uppfylla den, eftersom de första k elementen i sekvensen kan ställas in godtyckligt - det finns inga relationer mellan dem. Men om de första k termerna är givna, är alla andra element unikt bestämda.
Med hjälp av upprepningsrelationen och de initiala termerna kan man skriva ut termerna för sekvensen en efter en, och förr eller senare kommer vi att få någon av dess medlemmar. Men om du bara behöver känna till en specifik medlem av sekvensen, är det inte rationellt att beräkna alla tidigare. I det här fallet är det bekvämare att ha en formel för att beräkna den n:e termen.
Lösningen av återfallsrelationen vilken sekvens som helst för vilken den givna relationen gäller identiskt kallas.
Exempel. Sekvensen 2, 4, 8, …, 2 n är lösningen för relationen f(n+2)=3∙f(n+1) – 2∙f(n).
Bevis. Den vanliga termen för sekvensen är f(n)=2 n . Så f(n+2)= 2 n+2, f(n+1)= 2n+1 . För vilket n som helst gäller identiteten 2 n+2 =3∙2 n+1 – 2∙2 n. Därför, när sekvensen 2 n ersätts med formeln f(n+2)=3f(n+1) – 2f(n), uppfylls relationen identiskt. Därför är 2 n lösningen av det angivna sambandet.
Lösning av återfallsrelationen k:te ordningen kallas allmän, om det beror på k godtyckliga konstanter α 1 , α 2 , … α k och genom att välja dessa konstanter, kan vilken lösning som helst av detta samband erhållas.
Exempel. Upprepningsrelationen ges: f(n+2)=5f(n+1)-6f(n). Låt oss bevisa att dess allmänna lösning har formen: f(n)= α 2 n + β3 n .
1. Först bevisar vi att sekvensen f(n)=α 2 n + β3 n är en lösning på återfallsrelationen. Ersätt denna sekvens i återfallsrelationen.
f(n)= α 2 n + β 3 n, så f(n+1)= (α 2 n+1 + β 3 n +1), f(n+2)= α 2 n+2 + β 3 n+2, då
5f(n+1)-6f(n)=5∙(α 2 n+1 + β 3 n +1)-6∙(α 2 n + β 3 n)= α (5 2 n+1 –6 2 n)+ β (5 3 n +1 –6 3 n)= =α2 n ∙(10–6)+ β 3 n ∙(15 – 6)= α 2 n+2 + β 3 n +2 = f( n+2).
Återkommande relationen gäller, därför är α 2 n + β 3 n lösningen på detta återkommande förhållande.
2. Låt oss bevisa att vilken lösning som helst av relationen f(n+2)=5f(n+1)–6f(n) kan skrivas som f(n)= α 2 n + β 3 n . Men varje lösning av andra ordningens återfallsrelation bestäms unikt av värdena för de två första termerna i sekvensen. Därför räcker det att visa att för alla a=f(1) och b=f(2) finns α och β så att 2 α +3 β =a och 4 α +9 β =b. Det är lätt att se att ekvationssystemet har en lösning för alla värden på a och b.
Således är f(n)= α 2 n + β 3 n den allmänna lösningen av det återkommande sambandet f(n+2)=5f(n+1)–6f(n).
Linjära återfallsrelationer med konstanta koefficienter
Det finns inga generella regler för att lösa återkommande relationer, men det finns en ofta förekommande klass av återkommande relationer för vilka en algoritm för att lösa dem är känd. Dessa är linjära återkommande relationer med konstanta koefficienter, d.v.s. typförhållanden:
f(n+k)=c1f(n+k-1)+c2f(n+k-2)+...+c kf(n).
Låt oss hitta lösningen för den allmänna linjära återfallsrelationen med konstanta koefficienter av första ordningen.
En linjär återfallsrelation med konstanta koefficienter av första ordningen har formen: f(n+1)=c f(n).
Låt f(1)=a, sedan f(2)=c∙f(1)=c∙a, f(3)=c∙f(2)=c 2 ∙a, liknande f(4)=c 3 ∙a och så vidare, notera att f(n)=cn -1 ∙f(1).
Låt oss bevisa att sekvensen c n -1 ∙f(1) är lösningen av första ordningens återfallsrelation. f(n)=cn-1 ∙f(1), så f(n+1)=cnf(1). Genom att ersätta detta uttryck i relationen får vi identiteten c n f(1)=с∙ c n -1 ∙f(1).
Låt oss nu överväga mer i detalj linjära återfallsrelationer med konstanta koefficienter av andra ordningen , det vill säga formens relationer
f(n+2)=Ci∙f(n+1)+C2∙f(n). (*).
Observera att alla överväganden gäller även för högre ordningsrelationer.
Lösningsegenskaper:
1) Om sekvensen x n är en lösning (*), så är sekvensen a∙x n också en lösning.
Bevis.
x n är en lösning till (*), därför x n +2 =C 1 x n +1 + C 2 x n . Vi multiplicerar båda sidor av jämställdheten med a. Vi får a∙x n +2 =a∙(С 1 ∙x n +1 +С 2 ∙x n)= С 1 ∙a∙x n +1 +С 2 ∙a∙x n . Det betyder att ax n är lösningen (*).
2) Om sekvenserna x n och y n är lösningar (*), så är sekvensen x n + y n också en lösning.
Bevis.
x n och y n är lösningar, så följande identiteter gäller:
x n +2 \u003d C 1 x n +1 + C 2 x n.
yn+2 =C1yn+1+C2yn.
Låt oss lägga till de två likheterna term för term:
xn +2 +yn +2 =С 1 ∙xn +1 +С 2 ∙xn + С 1 ∙yn +1 +С 2 ∙yn = С 1 ∙(xn +1 + yn +1)+С 2 ∙(xn +yn). Det betyder att x n +y n är lösningen på (*).
3) Om r 1 är en lösning till andragradsekvationen r 2 =С 1 r+С 2, så är sekvensen (r 1) n lösningen till relationen (*).
r 1 är lösningen av andragradsekvationen r 2 =C 1 r+C 2 , så (r 1) 2 =C 1 r 1 + C 2 . Låt oss multiplicera båda sidor av likheten med (r 1) n . Skaffa sig
r 1 2 r 1 n \u003d (C 1 r 1 + C 2) r n.
r 1 n +2 \u003d C 1 r 1 n +1 + C 2 r 1 n.
Det betyder att sekvensen (r 1) n är lösningen till (*).
Av dessa fastigheter följer lösning sätt linjära återfallsrelationer med konstanta koefficienter av andra ordningen:
1. Komponera den karakteristiska (kvadratiska) ekvationen r 2 =C 1 r+C 2 . Låt oss hitta dess rötter r 1, r 2. Om rötterna är olika så är den allmänna lösningen f(n)= ar 1 n +βr 2 n .
2. Hitta koefficienterna a och β. Låt f(0)=a, f(1)=b. Ekvationssystem
har en lösning för alla a och b. Dessa lösningar är
![]()
Uppgift . Låt oss hitta en formel för den gemensamma termen för Fibonacci-sekvensen.
Lösning .
Den karakteristiska ekvationen har formen x 2 \u003d x + 1 eller x 2 -x-1 \u003d 0, dess rötter är tal, vilket betyder att den allmänna lösningen har formen f (n) \u003d  . Som det är lätt att se, av initialvillkoren f(0)=0, f(1)=1 följer att a=-b=1/Ö5, och följaktligen har den allmänna lösningen av Fibonacci-sekvensen formen :
. Som det är lätt att se, av initialvillkoren f(0)=0, f(1)=1 följer att a=-b=1/Ö5, och följaktligen har den allmänna lösningen av Fibonacci-sekvensen formen :
 .
.
Överraskande nog tar detta uttryck heltalsvärden för alla naturliga värden av n.