kartice

Kakšen je znak pravokotnosti dveh ravnin? Predavanje iz matematike na temo "znak pravokotnosti dveh ravnin." Ko sta ravnini pravokotni

Če ena od dveh ravnin poteka skozi premico, pravokotno na drugo ravnino, sta dani ravnini pravokotni () (slika 28)

α – ravnina, V– premica, ki je pravokotna nanjo, β – ravnina, ki poteka skozi premico V, In z– premica, po kateri se sekata ravnini α in β.

Posledica.Če je ravnina pravokotna na presečišče dveh danih ravnin, potem je pravokotna na vsako od teh ravnin

Problem 1. Dokaži, da lahko skozi katero koli točko na premici v prostoru potegnemo dve različni premici, pravokotni nanjo.

Dokaz:

Po aksiomu jaz obstaja točka, ki ni na črti A. Po izreku 2.1 skozi točko IN in neposredno A lahko narišemo ravnino α. (Slika 29) Po izreku 2.3 skozi točko A v ravnini α lahko narišemo premico A. Po aksiomu C 1 obstaja točka Z, ki ne pripada α. Po izreku 15.1 skozi točko Z in neposredno A lahko narišemo ravnino β. V ravnini β lahko po izreku 2.3 skozi točko a narišemo premico z A. Po konstrukciji imata premici b in c samo eno skupno točko A in obe sta pravokotni

Naloga 2. Zgornja konca dveh navpično stoječih stebrov, ki sta med seboj oddaljena 3,4 m, sta povezana s prečko. Višina enega stebra je 5,8 m, drugega pa 3,9 m. Poiščite dolžino prečke.

AC= 5,8 m, ВD= 3,9 m, AB- ? (slika 30)

AE = AC – CE = AC – BD= 5,8 – 3,9 = 1,9 (m)

Po Pitagorovem izreku iz ∆ AEV dobimo:

AB 2 = AE 2 + EB 2 = AE 2 + CD 2 = ( 1,9) 2 + (3,4) 2 = 15,17 (m2)

AB= = 3,9 (m)

Naloge

Tarča. Naučite se analizirati v najpreprostejših primerih medsebojni dogovor objektov v prostoru, uporablja planimetrična dejstva in metode pri reševanju stereometričnih problemov.

1. Dokaži, da lahko skozi katero koli točko premice v prostoru potegneš premico pravokotno nanjo.

2. Premice AB, AC in AD so v parih pravokotne. Poišči segment CD, če:

1) AB = 3 cm , sonce= 7 cm, AD= 1,5 cm;

2) VD= 9 cm, AD= 5 cm, sonce= 16 cm;

3) AB = b, BC = a, AD = d;

4) ВD = с, ВС = а, АD = d

3. Točka A je oddaljena a z vrhov enakostranični trikotnik s stranjo A. Poiščite razdaljo od točke A do ravnine trikotnika.

4. Dokaži, da če je premica vzporedna z ravnino, so vse njene točke enako oddaljene od ravnine.

5. Telefonska žica dolžine 15 m je napeta od telefonskega stebra, kjer je pritrjena na višini 8 m od površine tal, do hiše, kjer je pritrjena na višini 20 m. Poiščite razdaljo med hišo in stebrom, ob predpostavki, da žica ne povesi.

6. Iz točke na ravnino sta narisani dve nagnjeni nagibi, enaki 10 cm in 17 cm, razlika v projekcijah teh nagnjenih je 9 cm, poišči projekciji nagnjenih.

7. Iz točke na ravnino narišemo dve nagnjeni, od katerih je ena za 26 cm večja od druge. Nagnjeni projekciji sta 12 cm in 40 cm Poišči nagnjeni.

8. Iz točke na ravnino narišemo dve nagnjeni premici. Poišči dolžini poševnic, če sta v razmerju 1:2 in sta projekciji poševnic 1 cm in 7 cm.

9. Iz točke na ravnino sta narisani dve nagnjeni pobočji, enaki 23 cm in 33 cm.

razdalja od te točke do ravnine, če so nagnjene projekcije v razmerju 2:3.

10. Poiščite razdaljo od sredine odseka AB do ravnine, ki tega odseka ne seka, če sta razdalji od točk a in B do ravnine: 1) 3,2 cm in 5,3 cm;7,4 cm in 6,1 cm; 3) a in c.

11. Reši prejšnjo nalogo pod pogojem, da odsek AB seka ravnino.

12. Odsek dolg 1 m seka ravnino, njegova konca sta od ravnine oddaljena 0,5 m in 0,3 m. Poiščite dolžino projekcije odseka na ravnino.

13. Iz točk A in B spustimo navpičnici na ravnino. Poišči razdaljo med točkama A in B, če sta navpičnici 3 m in 2 m, razdalja med njunima osnovama je 2,4 m in odsek AB ne seka ravnine.

14. Iz točk A in B, ki ležita v dveh pravokotnih ravninah, spustimo navpičnici AC in BD na presečišče ravnin. Poišči dolžino odseka AB, če: 1) AC = 6 m, BD = 7 m, CD = 6 m; 2) AC = 3 m, ВD = 4 m, CD = 12 m; 3) AD = 4 m, BC = 7 m, CD = 1 m; 4) AD = BC = 5 m, CD = 1 m; 4) AC = a, BD = b, CD = c; 5) AD = a, BC = b, CD = c.

15. Iz oglišč A in B enakostraničnega trikotnika ABC vrnemo navpičnici AA 1 in BB 1 na ravnino trikotnika. Poiščite razdaljo od oglišča C do sredine segmenta A 1 B 1, če je AB = 2 m, CA 1 = 3 m, CB 1 = 7 m in segment A 1 B 1 ne seka ravnine trikotnika

16. Iz oglišč A in B ostrih kotov pravokotnega trikotnika ABC stojita navpičnici AA 1 in BB 1 na ravnino trikotnika. Poiščite razdaljo od oglišča C do sredine odseka A 1 B 1, če je A 1 C = 4 m, AA 1 = 3 m, CB 1 = 6 m, BB 1 = 2 m in se odsek A 1 B 1 ne seka ravnina trikotnika.

Koncept pravokotnih ravnin

Ko se dve ravnini sekata, dobimo $4$ diedrske kote. Dva kota sta enaka $\varphi $, druga dva pa $(180)^0-\varphi $.

Definicija 1

Kot med ravninama je najmanjši od diedrskih kotov, ki jih tvorita ti ravnini.

Definicija 2

Dve sekajoči se ravnini imenujemo pravokotni, če je kot med tema ravninama $90^\circ$ (slika 1).

Slika 1. Pravokotne ravnine

Znak pravokotnosti dveh ravnin

1. izrek

Če je premica ravnine pravokotna na drugo ravnino, potem sta ti ravnini pravokotni druga na drugo.

Dokaz.

Naj imava ravnini $\alpha $ in $\beta $, ki se sekata po premici $AC$. Naj bo premica $AB$, ki leži v ravnini $\alpha $, pravokotna na ravnino $\beta $ (slika 2).

Slika 2.

Ker je premica $AB$ pravokotna na ravnino $\beta$, je pravokotna tudi na premico $AC$. Dodatno narišimo premico $AD$ v ravnini $\beta$, pravokotno na premico $AC$.

Ugotovimo, da je kot $BAD$ linearni kot diedričnega kota, ki je enak $90^\circ$. To pomeni, da je po definiciji 1 kot med ravninama $90^\circ$, kar pomeni, da sta ravnini pravokotni.

Izrek je dokazan.

Iz tega izreka izhaja naslednji izrek.

2. izrek

Če je ravnina pravokotna na premico, po kateri se sekata drugi ravnini, potem je pravokotna tudi na ti ravnini.

Dokaz.

Naj imamo dve ravnini $\alpha $ in $\beta $, ki se sekata vzdolž premice $c$. Ravnina $\gamma $ je pravokotna na premico $c$ (slika 3)

Slika 3.

Ker premica $c$ pripada ravnini $\alpha $ in je ravnina $\gamma $ pravokotna na premico $c$, potem sta po izreku 1 ravnini $\alpha $ in $\gamma $ pravokotni.

Ker premica $c$ pripada ravnini $\beta $ in je ravnina $\gamma $ pravokotna na premico $c$, potem sta po izreku 1 ravnini $\beta $ in $\gamma $ pravokotni.

Izrek je dokazan.

Za vsakega od teh izrekov veljajo tudi obratne trditve.

Vzorčne težave

Primer 1

Naj nam je dan pravokoten paralelopiped $ABCDA_1B_1C_1D_1$. Poiščite vse pare pravokotnih ravnin (slika 5).

Slika 4.

rešitev.

Po definiciji pravokotnega paralelopipeda in pravokotnih ravnin vidimo naslednjih osem parov ravnin, pravokotnih druga na drugo: $(ABB_1)$ in $(ADD_1)$, $(ABB_1)$ in $(A_1B_1C_1)$, $( ABB_1)$ in $(BCC_1) $, $(ABB_1)$ in $(ABC)$, $(DCC_1)$ in $(ADD_1)$, $(DCC_1)$ in $(A_1B_1C_1)$, $(DCC_1) $ in $(BCC_1)$, $(DCC_1)$ in $(ABC)$.

Primer 2

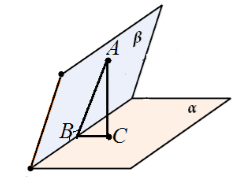
Naj imava dve med seboj pravokotni ravnini. Iz točke na eni ravnini je potegnjena navpičnica na drugo ravnino. Dokaži, da ta premica leži v dani ravnini.

Dokaz.

Naj imamo dani pravokotni ravnini $\alpha $ in $\beta $, ki se sekata vzdolž premice $c$. Iz točke $A$ ravnine $\beta $ je narisana pravokotnica $AC$ na ravnino $\alpha $. Predpostavimo, da $AC$ ne leži v ravnini $\beta$ (slika 6).

Slika 5.

Razmislite o trikotniku $ABC$. Je pravokotnik s pravim kotom $ACB$. Zato je $\kotnik ABC\ne (90)^0$.

Po drugi strani pa je $\angle ABC$ linearni kot diedričnega kota, ki ga tvorita ti ravnini. To pomeni, da diedrski kot, ki ga tvorita ti ravnini, ni enak 90 stopinj. Ugotovimo, da kot med ravninama ni enak $90^\circ$. Protislovje. Zato $AC$ leži v ravnini $\beta$.

Konstrukcija dveh med seboj pravokotnih ravnin. Kot je znano, ravnine so pravokotne, če je premica, ki pripada eni ravnini, pravokotna na drugo ravnino. Zato lahko ravnino, pravokotno na dano, narišemo skozi premico, pravokotno na dano ravnino, ali pravokotno na premico, ki leži v dani ravnini.

Prikazano na sl. 4.12 ravnini (ravnina trikotnika ABC in ravnina P) sta medsebojno pravokotni, saj je ravnina P pravokotna na premico A1, ki leži v ravnini trikotnika. Projekcija ravnine P, ki poteka skozi premico s projekcijami m 2 n 2, m 1 n 1 in je pravokotna na ravnino, določeno s projekcijami a 2 b 2 c 2, a 1 b 1 c 1 trikotnika, je prikazana v sl. 4.12.

Konstrukcija: 1. Narišite glavne črte ravnine, C1 - vodoravno, C2 - čelno.

2. Skozi poljubno točko E (ki je zunaj trikotnika ABC) narišimo premico EF, pravokotno na glavne črte ravnine (c 2 f 2 je pravokotna na c 2 2 2 in c 1 f 1 je pravokotna na 1 1 1).

3. Skozi točko N narišemo poljubno premico EM, ki se seka z EF, dobimo ravnino P, ki jo določata dve sekajoči se premici (EM X EF).

Torej je ravnina P(ME X EF) pravokotna na ravnino Q(trikotnik ABC).

Upoštevati je treba, da pri medsebojno pravokotnih ravninah v splošnem položaju njihove istoimenske sledi nikoli niso pravokotne. Če pa je ena od danih ravnin (ali obe) splošna ravnina, potem medsebojna pravokotnost na diagramu enega para njunih sledi kaže na pravokotnost ravnin v prostoru.

18) Premico presečišča dveh ravnin lahko določimo z njunima skupnima točkama. Če želite to narediti, določite presečišče poljubnih dveh ravnin ene ravnine z drugo ravnino ali presečišče ravnine na vsaki ravnini z drugo ravnino.

Zaporedje gradnje:

Presek dveh ravnin najdemo tako, da pri reševanju uporabimo pomožne sečne ravnine. Običajno so izbrane projekcijske ravnine (pogosto vodoravne ali čelne)

Izberimo poljubno sekantno pomožno horizontalno ravnino Ф1, ki seka dani ravnini po premicah (12 in 34), ki se (na p1 sekata v točki k)

Druga sekantna vodoravna ravnina seka dane ravnine tudi po horizontalah, te pa se sekajo v točki E

Premica KE je presečišče danih ravnin.

Razmislimo o rešitvi tega problema na ravni risbi.

1. stopnja rešitve Za konstrukcijo točke M uporabimo vodoravno projicirajočo ravnino - posrednico ("), ki oklepa stranico AB trikotnika ABC.

2. stopnja rešitve Konstruiramo presečišče (na risbi je določeno s točkama 1 in 2) vmesne ravnine (") in ravnine DEK.

3. stopnja rešitve Poiščite točko M presečišča premice 1 - 2 s premico AB.

Ena točka M želenega presečišča je bila najdena.

Za konstrukcijo točke N uporabimo vodoravno projicirajočo ravnino  ("), ki oklepa stranico AC trikotnika ABC.

Konstrukcije so podobne prejšnjim.

Določanje vidljivosti na ravnini H se opravi z vodoravno konkurenčnima točkama 4 in 8

Točka 4 se nahaja nad točko 8 (4" in 8"), tako da na ravnini H del trikotnika DEK, ki se nahaja proti točki 4, pokriva del trikotnika ABC, ki se nahaja od presečišča proti točki 8. S pomočjo določen je par čelno konkurenčnih točk 6 in 7 vidljivosti na ravnini V.

Presek dveh čelno štrlečih ravnin (?)

Presek dveh vodoravno štrlečih ravnin (?)

19) Rez je podoba predmeta, ki je mentalno razčlenjena z eno ali več ravninami, medtem ko se mentalna disekcija predmeta nanaša samo na ta rez in ne pomeni spremembe drugih podob istega predmeta. Razdelek prikazuje kaj se nahaja v rezalni ravnini in kaj za njo.

Glede na število sekantnih ravnin je odsek razdeljen na:

Enostavno (z eno rezalno ravnino)

Kompleks (z več rezalnimi ravninami)

Glede na položaj rezalne ravnine glede na vodoravno projekcijsko ravnino so odseki razdeljeni na:

HORIZONTALNO – rezalna ravnina je vzporedna z vodoravno projekcijsko ravnino

NAVPIČNO - rezalna ravnina je pravokotna na vodoravno projekcijsko ravnino

POŠEVNO - rezalna ravnina je posredni kot z vodoravno ravnino =) NAVPIČNI prerez se imenuje čelniče je rezalna ravnina vzporedna s čelno ravnino projekcij. IN profilče je rezalna ravnina vzporedna s profilno ravnino projekcij.

KOMPLEKSNI rezi so VZDOLŽNI, če so rezalne ravnine usmerjene po dolžini ali višini predmeta. IN PREČNO, ČE so sečne ravnine usmerjene PRAVOKOTNO na dolžino ali višino predmeta.

KORAK – če sta sečni ravnini med seboj vzporedni

Zlomljeno – če se sekalne ravnine med seboj sekajo.

LOKALNI rezi služijo razkrivanju notranje strukture predmeta na ločenem omejenem mestu. LOKALNI IZREZ je v pogledu poudarjen s polno, valovito, tanko črto.

Oznaka rezov - Položaj rezalne ravnine je označen z odprto presečno črto. Začetna in končna poteza črte odseka ne sme sekati obrisa ustrezne slike. Na začetno in končno potezo je treba postaviti puščice, ki označujejo smer pogleda, in sicer na razdalji 2...3 mm od zunanjega konca poteze.

ZA ZLOŽEN REZ se poteze odprte prerezne črte narišejo tudi na pregibih prerezne črte.

BLIZU puščic, ki označujejo smer pogleda, so na zunanji strani vogala velike črke ruske abecede. Oznake črk so dodeljene po abecednem vrstnem redu brez ponovitev ali izpustov.

Sam rez mora biti označen z napisom kot A-A

Če sekantna ravnina sovpada z ravnino simetrije predmeta in je prerez narejen na mestu ustreznega pogleda v projekcijski povezavi, potem za vodoravne, čelne in profilne odseke ni treba označiti položaja sekante. ploskev in rez ni opremljen z napisom.

Če konturna črta predmeta sovpada s simetrijsko osjo, je meja med pogledom in prerezom označena z valovito črto, ki je narisana tako, da se ohrani slika roba.

Ta lekcija bo pomagala tistim, ki želijo razumeti temo "Znak pravokotnosti dveh ravnin." Na začetku bomo ponovili definicijo diedrskega in linearnega kota. Nato bomo razmislili, katere ravnine imenujemo pravokotne, in dokazali znak pravokotnosti dveh ravnin.

Tema: Pravokotnost premic in ravnin

Lekcija: Znak pravokotnosti dveh ravnin

Opredelitev. Diedrski kot je lik, ki ga tvorita dve polravnini, ki ne pripadata isti ravnini, in njuna skupna premica a (a je rob).

riž. 1

Oglejmo si dve polravnini α in β (slika 1). Njihova skupna meja je l. Ta slika se imenuje diedrski kot. Dve sekajoči se ravnini tvorita štiri diedrske kote s skupnim robom.

Diedrski kot se meri z njegovim linearnim kotom. Izberemo poljubno točko na skupnem robu l diedrskega kota. V polravninah α in β iz te točke potegnemo navpičnici a in b na premico l in dobimo linearni kot diedrskega kota.

Premici a in b tvorita štiri kote, enake φ, 180° - φ, φ, 180° - φ. Spomnimo se, da je kot med ravnimi črtami najmanjši od teh kotov.

Opredelitev. Kot med ravninama je najmanjši od diedrskih kotov, ki jih tvorita ti ravnini. φ je kot med ravninama α in β, če

Opredelitev. Dve sekajoči se ravnini imenujemo pravokotni (medsebojno pravokotni), če je kot med njima 90°.

riž. 2

Na robu l izberemo poljubno točko M (slika 2). Na rob l v ravnini α narišimo dve pravokotni premici MA = a in MB = b v ravnini β. Dobili smo kot AMB. Kot AMB je linearni kot diedrskega kota. Če je kot AMB 90°, se ravnini α in β imenujeta pravokotni.

Premica b je po konstrukciji pravokotna na premico l. Premica b je pravokotna na premico a, saj je kot med ravninama α in β 90°. Ugotovimo, da je premica b pravokotna na dve sekajoči se premici a in l iz ravnine α. To pomeni, da je premica b pravokotna na ravnino α.

Podobno lahko dokažemo, da je premica a pravokotna na ravnino β. Premica a je po konstrukciji pravokotna na premico l. Premica a je pravokotna na premico b, saj je kot med ravninama α in β 90°. Ugotovimo, da je premica a pravokotna na dve sekajoči se premici b in l iz ravnine β. To pomeni, da je premica a pravokotna na ravnino β.

Če ena od dveh ravnin poteka skozi premico, pravokotno na drugo ravnino, sta ravnini pravokotni.

Dokaži:

riž. 3

Dokaz:

Naj se ravnini α in β sekata vzdolž premice AC (slika 3). Če želite dokazati, da sta ravnini medsebojno pravokotni, morate med njima sestaviti linearni kot in pokazati, da je ta kot 90°.

Premica AB je pravokotna na ravnino β in torej na premico AC, ki leži v ravnini β.

Narišimo premico AD pravokotno na premico AC v ravnini β. Potem je BAD linearni kot diedričnega kota.

Premica AB je pravokotna na ravnino β in torej na premico AD, ki leži v ravnini β. To pomeni, da je linearni kot BAD 90°. To pomeni, da sta ravnini α in β pravokotni, kar je bilo potrebno tudi dokazati.

Ravnina, pravokotna na premico, po kateri se sekata dve dani ravnini, je pravokotna na vsako od teh ravnin (slika 4).

Dokaži: