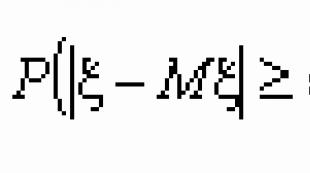Санамсаргүй үзэгдлүүдийг судлах практик нь бие даасан ажиглалтын үр дүн, тэр ч байтугай ижил нөхцөлд хийгдсэн ажиглалтын үр дүн эрс ялгаатай байж болох ч хангалттай олон тооны ажиглалтын дундаж үр дүн нь тогтвортой, сул хамааралтай болохыг харуулж байна. бие даасан ажиглалтын үр дүн.

Санамсаргүй үзэгдлийн энэхүү гайхалтай шинж чанарын онолын үндэс нь юм их тооны хууль. "Их тооны хууль" гэсэн нэр нь олон тооны санамсаргүй үзэгдлийн дундаж үр дүнгийн тогтвортой байдлыг тогтоож, энэ тогтвортой байдлын шалтгааныг тайлбарладаг бүлэг теоремуудыг нэгтгэдэг.

Их тооны хуулийн хамгийн энгийн хэлбэр бөгөөд энэ хэсгийн түүхэн дэх анхны теорем нь юм Бернуллигийн теорем, хэрэв аливаа үйл явдлын магадлал бүх туршилтанд ижил байвал туршилтын тоо нэмэгдэх тусам үйл явдлын давтамж нь тухайн үйл явдлын магадлал руу чиглэж, санамсаргүй байхаа болино гэж заасан.

Пуассоны теорем нь хэд хэдэн бие даасан туршилтын явцад үйл явдлын давтамж нь түүний магадлалын арифметик дундаж руу чиглэж, санамсаргүй байхаа болино гэж заасан.

Магадлалын онолын хязгаарын теорем, теорем Мойвр-Лапласүйл явдлын давтамжийн тогтвортой байдлын мөн чанарыг тайлбарлах. Энэ мөн чанар нь туршилтын тоог хязгааргүй нэмэгдүүлэх (хэрэв үйл явдлын магадлал бүх туршилтанд ижил байвал) үйл явдлын тохиолдлын тоог хязгаарлах хуваарилалтад оршдог. хэвийн тархалт.

Төвийн хязгаарын теорем нь өргөн тархсан байдлыг тайлбарладаг ердийн хуульхуваарилалт. Хязгаарлагдмал дисперстэй олон тооны бие даасан санамсаргүй хэмжигдэхүүнүүдийг нэмсний үр дүнд санамсаргүй хэмжигдэхүүн үүсэх бүрд энэхүү санамсаргүй хэмжигдэхүүний тархалтын хууль практикт нийцдэг гэж теорем заасан байдаг. хэвийнхуулиар.

Доор өгөгдсөн теорем нь " Их тооны хууль"Тодорхой, нэлээд ерөнхий нөхцөлд санамсаргүй хэмжигдэхүүнүүдийн тоо нэмэгдэхийн хэрээр тэдгээрийн арифметик дундаж нь математикийн хүлээлтийн арифметик дундаж руу чиглэж, санамсаргүй байхаа болино гэж заасан.

Ляпуновын теорем нь өргөн тархсаныг тайлбарладаг ердийн хуультархалт ба үүсэх механизмыг тайлбарлана. Тус теорем нь нийлбэрийн дисперстэй харьцуулахад дисперс нь бага байдаг олон тооны бие даасан санамсаргүй хэмжигдэхүүнүүдийг нэмсний үр дүнд санамсаргүй хэмжигдэхүүн үүсэх бүрт энэхүү санамсаргүй хэмжигдэхүүний тархалтын хууль өөрчлөгддөг гэдгийг хэлэх боломжийг бидэнд олгодог. практик дээр байх болно хэвийнхуулиар. Санамсаргүй хэмжигдэхүүнүүд нь үргэлж хязгааргүй олон шалтгаанаар үүсгэгддэг бөгөөд ихэнхдээ тэдгээрийн аль нь ч санамсаргүй хэмжигдэхүүний дисперстэй дүйцэхүйц тархалтгүй байдаг тул практикт тохиолддог ихэнх санамсаргүй хэмжигдэхүүнүүд нь ердийн тархалтын хуульд захирагддаг.

Олон тооны хуулийн чанарын болон тоон мэдэгдлүүд дээр үндэслэсэн болно Чебышевын тэгш бус байдал. Энэ нь санамсаргүй хэмжигдэхүүний утгын математикийн хүлээлтээс хазайх нь тодорхой заасан тооноос их байх магадлалын дээд хязгаарыг тодорхойлдог. Чебышевын тэгш бус байдал нь үйл явдлын магадлалын тооцоог өгдөг нь гайхалтай юм тархалт нь тодорхойгүй санамсаргүй хэмжигдэхүүний хувьд зөвхөн математикийн хүлээлт ба дисперс нь мэдэгддэг.

Чебышевын тэгш бус байдал.Хэрэв санамсаргүй хэмжигдэхүүн x нь дисперстэй бол ямар ч e > 0-ийн хувьд дараахь тэгш бус байдал үүснэ. , Хаана М x ба Д x - x санамсаргүй хэмжигдэхүүний математик хүлээлт ба дисперс.

Бернуллигийн теорем. m n нь n Бернулли туршилтын амжилтын тоо, p нь бие даасан туршилтын амжилтын магадлал гэж үзье. Тэгвэл ямар ч e > 0 бол энэ нь үнэн юм .

Төвийн хязгаарын теорем.Хэрэв санамсаргүй хэмжигдэхүүнүүд x 1 , x 2 , …, x n , … нь хосоороо бие даасан, ижил тархалттай, хязгаарлагдмал дисперстэй бол n ®-ийн хувьд x (- ,)-д жигд байна.

Амжилттай борлуулагчдын нууц юу вэ? Хэрэв та аль ч компанид хамгийн сайн борлуулагчдыг ажиглавал тэд нэг нийтлэг зүйлтэй болохыг анзаарах болно. Тэд тус бүр нь амжилт муутай борлуулагчдаас илүү олон хүнтэй уулзаж, олон илтгэл тавьдаг. Эдгээр хүмүүс борлуулалт бол тооны тоглоом гэдгийг ойлгодог бөгөөд олон хүнд бүтээгдэхүүн, үйлчилгээнийхээ талаар ярих тусам тэд илүү олон хэлэлцээрийг хаах болно - энэ бол бүх зүйл. Хэрэв тэд зөвхөн "Тийм" гэж хэлэх цөөхөн хүмүүстэй төдийгүй тэдний саналыг тийм ч их сонирхдоггүй хүмүүстэй харилцаж байвал дундаж хэмжүүрийн хууль тэдний талд ажиллах болно гэдгийг тэд ойлгодог.

Таны орлого борлуулалтын тооноос хамаарна, гэхдээ тэр үед таны хийсэн илтгэлийн тоотой шууд пропорциональ байх болно. Дундаж хэмжүүрийн хуулийг ойлгож, дадлагажуулснаар шинэ бизнес эхлүүлэх, шинэ салбарт ажиллахтай холбоотой түгшүүр багасаж эхэлнэ. Үүний үр дүнд хяналт, мөнгө олох чадварт итгэх итгэл нэмэгдэж эхэлнэ. Хэрэв та зүгээр л танилцуулга хийж, энэ явцад ур чадвараа дээшлүүлбэл хэлэлцээрүүд гарах болно.

Хэлэлцээрийн тоог бодохын оронд илтгэлүүдийн тоог сайн бодоорой. Өглөө босоод, орой гэртээ ирээд бараагаа хэн авах бол гэж гайхаад байх нь утгагүй. Үүний оронд өдөрт хэдэн удаа дуудлага хийхээ төлөвлөх нь дээр. Тэгээд дараа нь юу ч байсан хамаагүй - эдгээр бүх дуудлагыг хий! Энэ арга нь таны ажлыг хөнгөвчлөх болно - учир нь энэ нь энгийн бөгөөд тодорхой зорилго юм. Хэрэв та тодорхой, хүрч болох зорилготой гэдгээ мэдэж байвал төлөвлөсөн тооны дуудлага хийхэд хялбар байх болно. Хэрэв та энэ үйл явцын туршид "тийм" гэж хэд хэдэн удаа сонсвол хамаагүй дээр!

Хэрэв "үгүй" гэж үзвэл үдэш та чадах бүхнээ шударгаар хийсэн гэдгээ мэдэрч, өдөрт хичнээн их мөнгө олсон, хэдэн хамтрагчтай болсон тухай бодолд шаналахгүй.

Танай компани эсвэл бизнест дунджаар нэг борлуулагч дөрвөн илтгэл тутамд нэг хэлцлийг хаадаг гэж бодъё. Одоо та тавцангаас карт зурж байна гэж төсөөлөөд үз дээ. Хүрз, очир алмааз, дугуй гэсэн гурван хослолын карт бүр нь бүтээгдэхүүн, үйлчилгээ, боломжоо мэргэжлийн түвшинд танилцуулах үзүүлэн юм. Та чадах чинээгээрээ сайн хийдэг ч гэрээгээ хаадаггүй. Зүрхний карт бүр нь мөнгө авах эсвэл шинэ хамтрагч олж авах боломжийг олгодог хэлцэл юм.

Ийм нөхцөлд та тавцангаас аль болох олон карт зурахыг хүсэхгүй байна уу? Зүрхний карт сугалах бүртээ танд мөнгө төлж, шинэ хамтрагч санал болгохын зэрэгцээ хүссэн хэмжээгээрээ карт зурахыг санал болгож байна гэж бодъё. Та урам зоригтойгоор карт зурж эхлэх бөгөөд таны гаргасан карт ямар тохирохыг бараг анзаарах болно.

Тавин хоёр картын тавцанд арван гурван зүрх байдаг гэдгийг та мэднэ. Хоёр тавцан дээр хорин зургаан зүрхний карт гэх мэт. Хүз, очир алмааз, дугуй зурахдаа сэтгэл дундуур байх уу? Мэдээж үгүй! Ийм "мисс" бүр таныг юунд ойртуулдаг гэж та бодох болно? Зүрхний карт руу!

Гэхдээ та юу мэдэх вэ? Танд аль хэдийн ийм санал ирсэн. Та хүссэн хэмжээгээрээ олж, амьдралдаа зурахыг хүссэн олон зүрх сэтгэлийг татах онцгой байр суурьтай байна. Хэрэв та зүгээр л "хөзөр зурж", ур чадвараа дээшлүүлж, бага зэрэг хүрз, очир алмааз, дугуйг тэвчвэл та маш сайн худалдагч болж, амжилтанд хүрэх болно.

Борлуулалтыг маш хөгжилтэй болгодог нэг зүйл бол та тавцангаа холих бүрт картууд өөр өөр холилдсон байдаг. Заримдаа бүх зүрх сэтгэл тавцангийн эхэнд дуусдаг бөгөөд азтай цувралын дараа (бид хэзээ ч алдахгүй юм шиг санагдаж байвал) өөр хувцасны урт эгнээ биднийг хүлээж байдаг. Мөн бусад үед эхний зүрхэнд хүрэхийн тулд та эцэс төгсгөлгүй олон тооны хүрз, дугуй, алмаазыг туулах хэрэгтэй болно. Заримдаа янз бүрийн костюмтай картууд дарааллаар нь харагдана. Гэхдээ ямар ч тохиолдолд тавин хоёр картын тавцан бүрт ямар нэгэн дарааллаар үргэлж арван гурван зүрх байдаг. Картуудаа олох хүртлээ зүгээр л сугалж ав.

Хэнээс: Лейля,  

Олон тооны тухай үгс нь тестийн тоог хэлдэг - санамсаргүй хэмжигдэхүүний олон тооны утгууд эсвэл олон тооны санамсаргүй хэмжигдэхүүний хуримтлагдах нөлөөг авч үздэг. Энэ хуулийн мөн чанар нь дараах байдалтай байна: нэг туршилтаар бие даасан санамсаргүй хэмжигдэхүүн ямар утгыг авахыг урьдчилан таамаглах боломжгүй боловч олон тооны бие даасан санамсаргүй хэмжигдэхүүний үйл ажиллагааны нийт үр дүн нь санамсаргүй шинж чанараа алдаж, . бараг найдвартай урьдчилан таамаглах (өөрөөр хэлбэл өндөр магадлалтай). Жишээлбэл, нэг зоос ямар замаар буухыг таамаглах боломжгүй юм. Гэсэн хэдий ч, хэрэв та 2 тонн зоос шидсэн бол бид маш их итгэлтэйгээр төрийн сүлдээ унасан зоосны жин 1 тоннтой тэнцэнэ гэж хэлж болно.

Их тооны хууль нь үндсэндээ Чебышевын тэгш бус байдал гэж нэрлэгддэг бөгөөд энэ нь санамсаргүй хэмжигдэхүүн нь дундаж утгаас өгөгдсөн утгаас илүүгүй зөрүүтэй утгыг хүлээн авах магадлалыг нэг тестээр тооцдог.

Чебышевын тэгш бус байдал. Болъё X- дурын санамсаргүй хэмжигдэхүүн; a=M(X) , А Д(X) - түүний хэлбэлзэл. Дараа нь

Жишээ. Машиныг асаасан ханцуйны диаметрийн нэрлэсэн (жишээ нь шаардлагатай) утга нь тэнцүү байна. 5мм, мөн тархалт байхгүй болсон 0.01 (энэ нь машины нарийвчлалын хүлцэл юм). Нэг бутыг үйлдвэрлэх явцад түүний диаметр нь нэрлэсэн хэмжээнээс бага байх магадлалыг тооцоол. 0.5 мм .

Шийдэл. r.v. X– үйлдвэрлэсэн бутны диаметр. Нөхцөл байдлын дагуу түүний математик хүлээлт нь нэрлэсэн диаметртэй тэнцүү байна (хэрэв машины тохиргоонд системчилсэн гэмтэл байхгүй бол): a=M(X)=5 , болон тархалт Д(X)≤0.01. Чебышевын тэгш бус байдлыг ашиглах нь ε = 0.5, бид авах:

Тиймээс ийм хазайлтын магадлал нэлээд өндөр байгаа тул нэг хэсгийг үйлдвэрлэхэд диаметрийн нэрлэсэн хэмжээнээс хазайх нь бараг тодорхой байна гэж бид дүгнэж болно. 0.5 мм .

Үүний утгаараа стандарт хазайлт σ онцлогтой дундажсанамсаргүй хэмжигдэхүүний төвөөс хазайлт (өөрөөр хэлбэл математикийн хүлээлтээс). Учир нь энэ дундажхазайлт, дараа нь туршилтын явцад их хэмжээний (o-г онцолсон) хазайлт боломжтой. Практикт хэр их хазайлт хийх боломжтой вэ? Хэвийн тархалттай санамсаргүй хэмжигдэхүүнийг судлахдаа бид "гурван сигма" дүрмийг гаргасан: хэвийн тархалттай санамсаргүй хэмжигдэхүүн. X нэг тестээр-аас бараг дунджаас хазайдаггүй 3σ, Хаана σ= σ(X)– r.v-ийн стандарт хазайлт. X. Бид тэгш бус байдлыг олж авсан баримтаас энэ дүрмийг гаргаж авсан

.

Одоо гарах магадлалыг тооцоолъё дур зоргоороосанамсаргүй хувьсагч Xдунджаас стандарт хазайлтаас гурав дахин ихгүй зөрүүтэй утгыг хүлээн авна. Чебышевын тэгш бус байдлыг ашиглах нь ε = 3σмөн үүнийг өгсөн Д(Х)= σ 2 , бид авах:

.

Тиймээс, ерөнхийдөөБид санамсаргүй хэмжигдэхүүний дундажаас гурван стандарт хазайлтаас илүүгүй хазайх магадлалыг тоогоор нь тооцоолж болно. 0.89 , харин хэвийн тархалтын хувьд үүнийг магадлалаар баталгаажуулж болно 0.997 .

Чебышевын тэгш бус байдлыг бие даасан адил тархсан санамсаргүй хэмжигдэхүүнүүдийн системд нэгтгэж болно.

Чебышевын ерөнхий тэгш бус байдал. Хэрэв бие даасан санамсаргүй хэмжигдэхүүн X 1 , X 2 , … , X n М(X би )= аболон зөрүү Д(X би )= Д, Тэр

At n=1 Энэхүү тэгш бус байдал нь дээр дурдсан Чебышевын тэгш бус байдал болж хувирдаг.

Харгалзах асуудлыг шийдвэрлэхэд бие даасан ач холбогдолтой Чебышевын тэгш бус байдлыг Чебышевын теорем гэж нэрлэдэгийг батлахад ашигладаг. Бид эхлээд энэ теоремын мөн чанарын тухай ярьж, дараа нь түүний албан ёсны томъёоллыг өгнө.

Болъё X 1 , X 2 , … , X n– математикийн хүлээлт бүхий олон тооны бие даасан санамсаргүй хэмжигдэхүүн М(X 1 )=а 1 , … , М(X n )=а n. Туршилтын үр дүнд тус бүр нь дунджаас хол утгыг (жишээлбэл, математикийн хүлээлт) авч чаддаг боловч санамсаргүй хэмжигдэхүүн юм.
, тэдгээрийн арифметик дундажтай тэнцүү байх нь тогтмол тоотой ойролцоо утгыг авах магадлалтай
(энэ нь бүх математикийн хүлээлтийн дундаж юм). Энэ нь дараах гэсэн үг юм. Туршилтын үр дүнд бие даасан санамсаргүй хэмжигдэхүүнүүдийг авч үзье X 1 , X 2 , … , X n(тэдгээрийн ихэнх нь байдаг!) дагуу үнэ цэнийг авсан X 1 , X 2 , … , X nтус тус. Дараа нь эдгээр утгууд нь харгалзах санамсаргүй хэмжигдэхүүний дундаж утгуудаас хол байж болох юм бол тэдгээрийн дундаж утга
тоотой ойролцоо байх магадлалтай
. Тиймээс олон тооны санамсаргүй хэмжигдэхүүний арифметик дундаж нь санамсаргүй шинж чанараа аль хэдийн алдаж, маш нарийвчлалтай урьдчилан таамаглах боломжтой байдаг. Үүнийг утгын санамсаргүй хазайлтаар тайлбарлаж болно X би-аас а биөөр өөр шинж тэмдэгтэй байж болох тул нийтдээ эдгээр хазайлтыг нөхөх магадлалтай.

Терема Чебышев (их тооны хуульЧебышев хэлбэрээр). Болъё X 1 , X 2 , … , X n … – дисперсүүд нь ижил тоогоор хязгаарлагддаг, хос бие даасан санамсаргүй хэмжигдэхүүнүүдийн дараалал. Тэгвэл ε тоог хичнээн бага авсан ч тэгш бус байх магадлал

Хэрэв тоо нь хүссэнээр нэгтэй ойролцоо байх болно nхангалттай том санамсаргүй хэмжигдэхүүн авах. Албан ёсоор энэ нь теоремийн нөхцөлд гэсэн үг юм

Энэ төрлийн нийлэлтийг магадлалаар нийлэх гэж нэрлэдэг бөгөөд дараах байдлаар тэмдэглэнэ.

Тиймээс Чебышевын теоремд хэрэв хангалттай олон тооны бие даасан санамсаргүй хэмжигдэхүүн байгаа бол нэг тестийн арифметик дундаж нь тэдний математик хүлээлтийн дундажтай ойролцоо утгыг бараг найдвартай авна гэж хэлдэг.

Ихэнх тохиолдолд Чебышевын теоремыг санамсаргүй хэмжигдэхүүнтэй нөхцөлд ашигладаг X 1 , X 2 , … , X n … ижил тархалттай (өөрөөр хэлбэл ижил тархалтын хууль эсвэл ижил магадлалын нягт). Үнэн хэрэгтээ энэ нь зүгээр л нэг санамсаргүй хэмжигдэхүүний олон тооны жишээ юм.

Үр дагавар(чебышевын ерөнхий тэгш бус байдал). Хэрэв бие даасан санамсаргүй хэмжигдэхүүн X 1 , X 2 , … , X n … Математикийн хүлээлттэй ижил тархалттай байна М(X би )= аболон зөрүү Д(X би )= Д, Тэр

, өөрөөр хэлбэл
.

Нотлох баримт нь Чебышевын ерөнхий тэгш бус байдлын хязгаарт шилжих замаар гарч ирдэг n→∞ .

Дээр бичсэн тэгшитгэлүүд нь тухайн хэмжигдэхүүний утгыг баталгаажуулахгүй гэдгийг дахин тэмдэглэе
тэмүүлдэг Ацагт n→∞. Энэ хэмжигдэхүүн нь санамсаргүй хэмжигдэхүүн хэвээр байгаа бөгөөд түүний бие даасан утга нь үүнээс нэлээд хол байж болно А. Гэхдээ ийм магадлал (хол А) нэмэгдэж буй үнэ цэнэ n 0-д хүрэх хандлагатай байна.

Сэтгэгдэл. Үр дүнгийн дүгнэлт нь бие даасан санамсаргүй хэмжигдэхүүн байх үед илүү ерөнхий тохиолдолд бас хүчинтэй байх нь ойлгомжтой. X 1 , X 2 , … , X n … өөр өөр тархалттай, гэхдээ ижил математикийн хүлээлт (тэнцүү А) болон хамтран хязгаарлагдмал зөрүү. Энэ нь эдгээр хэмжилтийг өөр өөр хэрэглүүрээр хийсэн байсан ч тодорхой хэмжигдэхүүнийг хэмжих нарийвчлалыг урьдчилан таамаглах боломжийг олгодог.

Хэмжигдэхүүнийг хэмжихдээ энэ үр дүнгийн хэрэглээг илүү нарийвчлан авч үзье. Зарим төхөөрөмж ашиглацгаая nижил хэмжигдэхүүний хэмжигдэхүүн, жинхэнэ утга нь тэнцүү байна Амөн бид мэдэхгүй. Ийм хэмжилтийн үр дүн X 1 , X 2 , … , X nбие биенээсээ эрс ялгаатай байж болно (мөн жинхэнэ утгаас А) янз бүрийн санамсаргүй хүчин зүйлээс (даралтын өөрчлөлт, температур, санамсаргүй чичиргээ гэх мэт). r.v-г авч үзье. X– хэмжигдэхүүнийг нэг удаа хэмжих багажийн заалт, түүнчлэн r.v-ийн багц. X 1 , X 2 , … , X n– эхний, хоёр дахь, ..., сүүлчийн хэмжилтийн үед багажийн уншилт. Тиймээс тоо хэмжээ тус бүр X 1 , X 2 , … , X n s.v-ийн ганцхан тохиолдол бий. X, тиймээс тэд бүгд r.v-тэй ижил тархалттай байна. X. Хэмжилтийн үр дүн нь бие биенээсээ хамаардаггүй тул r.v. X 1 , X 2 , … , X nбие даасан гэж үзэж болно. Хэрэв төхөөрөмж системчилсэн алдаа гаргадаггүй бол (жишээлбэл, хуваарь дээрх тэг нь "унтраагүй", пүрш нь сунадаггүй гэх мэт) бол математикийн хүлээлт гэж бид үзэж болно. M(X) = a, Тиймээс М(X 1 ) = ... = M(X n ) = a. Тиймээс дээрх үр дүнгийн нөхцөлүүд хангагдсан тул тоо хэмжээний ойролцоо утгатай болно. Абид санамсаргүй хэмжигдэхүүний "бодит байдлыг" авч болно
бидний туршилтанд (цуврал явуулахаас бүрдсэн nхэмжилт), жишээлбэл.

.

Олон тооны хэмжилт хийснээр энэ томъёог ашиглан тооцооллын сайн нарийвчлал нь бараг тодорхой юм. Энэ нь олон тооны хэмжилтийн үед тэдгээрийн арифметик дундаж нь хэмжсэн утгын жинхэнэ утгаас бараг ялгаагүй гэсэн практик зарчмын үндэслэл юм.

Математикийн статистикт өргөн хэрэглэгддэг "түүвэрлэлтийн" арга нь санамсаргүй хэмжигдэхүүний харьцангуй бага түүврээс объектив шинж чанарыг хүлээн зөвшөөрөгдөх нарийвчлалтайгаар олж авах боломжийг олгодог олон тооны хууль дээр суурилдаг. Гэхдээ энэ талаар дараагийн хэсэгт хэлэлцэх болно.

Жишээ. Тодорхой хэмжигдэхүүнийг системчилсэн гажуудал үүсгэдэггүй хэмжих төхөөрөмж дээр хэмждэг Анэг удаа (хүлээн авсан үнэ цэнэ X 1 ), дараа нь өөр 99 удаа (авсан утгууд X 2 , … , X 100 ). Жинхэнэ хэмжилтийн утгын хувьд АЭхний хэмжилтийн үр дүнг эхлээд авна
, дараа нь бүх хэмжилтийн арифметик дундаж
. Төхөөрөмжийн хэмжилтийн нарийвчлал нь хэмжилтийн стандарт хазайлт σ нь 1-ээс ихгүй байна (иймээс хэлбэлзэл Д=σ 2 мөн 1-ээс хэтрэхгүй). Хэмжилтийн арга бүрийн хувьд хэмжилтийн алдаа 2-оос хэтрэхгүй байх магадлалыг тооцоол.

Шийдэл. r.v. X– нэг хэмжилтийн багажийн уншилт. Дараа нь нөхцөлөөр M(X)=a. Асуултанд хариулахын тулд бид Чебышевын ерөнхий тэгш бус байдлыг ашигладаг

ε цагт =2 эхлээд n=1 тэгээд дараа нь n=100 . Эхний тохиолдолд бид авдаг
, хоёрдугаарт. Тиймээс хоёр дахь тохиолдол нь хэмжилтийн нарийвчлалыг баталгаажуулдаг бол эхнийх нь энэ утгаараа ихээхэн эргэлзээ төрүүлдэг.

Дээрх мэдэгдлүүдийг Бернулли схемд үүссэн санамсаргүй хэмжигдэхүүнүүдэд хэрэглэцгээе. Энэ схемийн мөн чанарыг эргэн санацгаая. Үүнийг үйлдвэрлэе n бие даасан туршилтууд, тус бүр нь зарим үйл явдлыг агуулдаг Аижил магадлалтай гарч ирж болно Р, А q=1–р(энэ нь эсрэг үйл явдлын магадлал юм - тохиолдохгүй байгаа үйл явдал А) . Хэдэн тоо гаргая nийм туршилтууд. Санамсаргүй хэмжигдэхүүнүүдийг авч үзье: X 1 - үйл явдлын тохиолдлын тоо АВ 1 -р тест, ..., X n- үйл явдлын тохиолдлын тоо АВ n--р шалгалт. Бүгд орсон s.v. утгыг авч болно 0 эсвэл 1 (үйл явдал Атестэнд харагдах эсвэл харагдахгүй байж болно), мөн утга 1 нөхцөлийн дагуу туршилт бүрт магадлалаар хүлээн зөвшөөрөгддөг х(үйл явдал болох магадлал Атуршилт бүрт), мөн үнэ цэнэ 0 магадлалаар q= 1 – х. Тиймээс эдгээр хэмжигдэхүүнүүд ижил хуваарилалтын хуультай байна:

X 1

X n

Тиймээс эдгээр хэмжигдэхүүний дундаж утга ба тэдгээрийн хэлбэлзэл нь мөн адил байна: М(X 1 )=0 ∙ q+1 ∙ p= p, …, M(X n )= х ; Д(X 1 )=(0 2 ∙ q+1 2 ∙ х)− х 2 = х∙(1− х)= х ∙ q, … , Д(X n )= х ∙ q. Эдгээр утгыг Чебышевын ерөнхий тэгш бус байдалд орлуулснаар бид олж авна

.

r.v гэдэг нь тодорхой байна. X=X 1 +…+X nнь үйл явдлын тохиолдлын тоо юм Абүгдээрээ nтестүүд (тэдний хэлснээр - "амжилтын тоо" nтуршилтууд). Хийсэн зүйлээ оруул nтуршилтын үйл явдал А-д гарч ирэв к тэднээс. Дараа нь өмнөх тэгш бус байдлыг дараах байдлаар бичиж болно

.

Гэхдээ хэмжээ
, үйл явдлын тохиолдлын тооны харьцаатай тэнцүү байна АВ nбие даасан туршилтыг нийт туршилтын тоонд харьцуулсан үйл явдлын давтамж гэж нэрлэдэг байсан АВ nтуршилтууд. Тиймээс тэгш бус байдал бий

.

Одоо хязгаар руу эргэж байна n→∞, бид олж авна
, өөрөөр хэлбэл
(магадлалаар). Энэ нь Бернулли хэлбэрийн их тооны хуулийн агуулгыг бүрдүүлдэг. Үүнээс үзэхэд хангалттай олон тооны туршилтууд байдаг nхарьцангуй давтамжийн дур мэдэн жижиг хазайлт
түүний магадлалаас үйл явдал Р- бараг найдвартай үйл явдлууд, том хазайлтууд - бараг боломжгүй. Харьцангуй давтамжийн ийм тогтвортой байдлын талаархи дүгнэлт (бид үүнийг өмнө нь ярьж байсан туршилтынбаримт) нь үйл явдлын магадлалын тухай өмнө нь танилцуулсан статистик тодорхойлолтыг эргэн тойронд нь үйл явдлын харьцангуй давтамж хэлбэлздэг тоо гэж зөвтгөдөг.

Энэ илэрхийлэл гэж үзвэл х∙ q= х∙(1− х)= х− х 2 өөрчлөлтийн интервалаас хэтрэхгүй
(энэ сегмент дээрх энэ функцийн хамгийн бага утгыг олох замаар үүнийг шалгахад хялбар байдаг), дээрх тэгш бус байдлаас
үүнийг авахад амархан

,

холбогдох асуудлыг шийдвэрлэхэд ашигладаг (тэдгээрийн аль нэгийг доор өгөв).

Жишээ. Зоосыг 1000 удаа шидэв. Сүлд харагдах харьцангуй давтамжийн магадлалаас хазайх нь 0.1-ээс бага байх магадлалыг тооцоол.

Шийдэл. Тэгш бус байдлыг хэрэглэх
цагт х= q=1/2 , n=1000 , ε=0.1, бид хүлээн авах болно.

Жишээ. Өмнөх жишээний нөхцөлд тоо гарах магадлалыг тооцоол кунасан эмблемүүд нь дараах хооронд байх болно 400 өмнө 600 .

Шийдэл. Нөхцөл байдал 400< к<600 гэсэн үг 400/1000< к/ n<600/1000 , өөрөөр хэлбэл 0.4< В n (А)<0.6 эсвэл
. Өмнөх жишээнээс харахад ийм үйл явдлын магадлал багагүй байна 0.975 .

Жишээ. Зарим үйл явдлын магадлалыг тооцоолох АҮйл явдал болох 1000 туршилт хийсэн А 300 удаа гарч ирэв. Харьцангуй давтамж (300/1000 = 0.3-тай тэнцүү) бодит магадлалаас хол байх магадлалыг тооцоол. Р 0.1-ээс ихгүй байна.

Шийдэл. Дээрх тэгш бус байдлыг ашиглах
n=1000, ε=0.1-ийн хувьд бид .

Том, олон янзын материал дээр илрүүлсэн санамсаргүй үйл явдлын давтамжийг тогтворжуулах үзэгдэл нь эхэндээ ямар ч үндэслэлгүй бөгөөд цэвэр эмпирик баримт гэж үздэг байв. Энэ чиглэлийн онолын анхны үр дүн нь 1713 онд хэвлэгдсэн алдарт Бернулли теорем бөгөөд их тооны хуулиудын үндэс суурийг тавьсан юм.

Агуулгын хувьд Бернуллигийн теорем нь хязгаарын теорем, өөрөөр хэлбэл олон тооны ажиглалт бүхий магадлалын параметрүүдэд юу тохиолдохыг хэлдэг асимптот утгын мэдэгдэл юм. Энэ төрлийн орчин үеийн олон тооны мэдэгдлийн өвөг дээдэс нь яг Бернуллигийн теорем юм.

Өнөөдөр олон тооны математикийн хууль нь олон тооны бодит үйл явцын ерөнхий шинж чанарын тусгал юм.

Манай зууны хамгийн агуу математикчдын нэг А.Н. Колмогоров энэхүү хуулийг хэрэглэх шавхагдашгүй боломжуудтай нийцүүлэн, их тооны хуулийг хамгийн өргөн цар хүрээтэй болгохыг хүсч байсан тул түүний мөн чанарыг дараах байдлаар томъёолжээ: Их тооны хууль "Олон тооны санамсаргүй хүчин зүйлийн нийлбэр нөлөөгөөр бараг тохиолдлын хамааралгүй үр дүнд хүргэдэг ерөнхий зарчим."

Тиймээс их тооны хууль нь хоёр тайлбартай байдаг. Нэг нь математик, тодорхой математик загвар, томъёолол, онолтой холбоотой, хоёр дахь нь илүү ерөнхий бөгөөд энэ хүрээнээс давж гардаг. Хоёрдахь тайлбар нь практикт ихэвчлэн ажиглагддаг олон тооны далд эсвэл харагдахуйц үйл ажиллагааны хүчин зүйлүүдийн цаана ийм тасралтгүй байдал байхгүй, илүү их эсвэл бага чиглэсэн үйл ажиллагаа үүсэх үзэгдэлтэй холбоотой юм. Хоёрдахь тайлбартай холбоотой жишээ бол чөлөөт зах зээл дээр үнэ тогтоох, тодорхой асуудлаар олон нийтийн санаа бодлыг бий болгох явдал юм.

Олон тооны хуулийн энэхүү ерөнхий тайлбарыг тэмдэглэсний дараа энэ хуулийн тусгай математик томъёололд хандъя.

Дээр хэлсэнчлэн магадлалын онолын хувьд хамгийн эхний бөгөөд хамгийн чухал нь Бернуллигийн теорем юм. Эргэн тойрон дахь ертөнцийн хамгийн чухал хуулиудын нэгийг тусгасан энэхүү математик баримтын агуулга нь дараах байдалтай байна.

Нөхцөл нь туршилтаас тест хүртэл байнга хуулбарлагддаг, хамааралгүй (өөрөөр хэлбэл бие даасан) тестүүдийн дарааллыг авч үзье. Туршилт бүрийн үр дүн нь бидний сонирхсон үйл явдлын харагдах байдал эсвэл тохиолдохгүй байх явдал юм А.

Энэхүү процедурыг (Бернуллигийн схем) олон практик талбарт ердийн зүйл гэж үзэж болох нь ойлгомжтой: нярай хүүхдийн дараалалд "хөвгүүн - охин", өдөр тутмын цаг уурын ажиглалт ("бороо орсон - тийм биш"), үйлдвэрлэсэн бүтээгдэхүүний урсгалыг хянах ( "хэвийн - гэмтэлтэй") гэх мэт.

Үйл явдал тохиолдох давтамж Ацагт Птуршилтууд ( t A -

үйл явдлын давтамж АВ Птестүүд) өсөлттэй байна Птүүний үнэ цэнийг тогтворжуулах хандлага нь эмпирик баримт юм.

Бернуллигийн теорем.Дурын жижиг эерэг тоог сонгоё e Дараа нь

Бернуллигийн тодорхой математик загварт (Бернулли схемд) тогтоосон математик баримтыг давтамжийн тогтвортой байдлын эмпирик тогтсон зүй тогтолтой андуурч болохгүй гэдгийг бид онцолж байна. Бернулли зөвхөн (9.1) томъёог дурьдахад сэтгэл хангалуун бус байсан ч практикийн хэрэгцээг харгалзан энэ томъёонд байгаа тэгш бус байдлын үнэлгээг өгсөн. Бид энэ тайлбарыг доор авч үзэх болно.

Бернуллигийн олон тооны хууль нь түүнийг боловсронгуй болгохыг эрэлхийлсэн олон тооны математикчдын судалгааны сэдэв байсаар ирсэн. Эдгээр сайжруулалтын нэгийг Английн математикч Мойвр олж авсан бөгөөд одоогоор Мойвр-Лапласын теорем гэж нэрлэгддэг. Бернулли схемд нормчлогдсон хэмжигдэхүүний дарааллыг авч үзье.

Мойврын интеграл теорем - Лаплас.Дурын хоёр тоог сонгоцгооё X (Тэгээд x 2.Энэ тохиолдолд x, x 7, дараа нь at П -» °°

Хэрэв (9.3) томъёоны баруун талд хувьсагч х ххязгааргүй байх хандлагатай бол зөвхөн x 2-оос хамаарч үүссэн хязгаар нь (энэ тохиолдолд 2-р индексийг устгаж болно) хуваарилалтын функц байх болно, үүнийг гэж нэрлэдэг. стандарт хэвийн тархалт,эсвэл Гауссын хууль.

(9.3) томъёоны баруун тал нь y =-тэй тэнцүү байна F(x 2) - F(x x). F(x 2)-> 1 цагт x 2-> °° ба F(x,) -> x at 0, -> Хангалттай том сонголттой учраас

X] > 0 ба X]n нь үнэмлэхүй утгаараа хангалттай том бол бид дараах тэгш бус байдлыг олж авна.

Томъёо (9.2)-ыг харгалзан бид практик найдвартай тооцоог гаргаж чадна.

Хэрэв итгэлийн түвшин y = 0.95 (өөрөөр хэлбэл алдааны магадлал 0.05) хэн нэгэнд хангалтгүй мэт санагдаж байвал та дээр дурдсан гурван сигма дүрмийг ашиглан "аюулгүй тоглож" бага зэрэг илүү өргөн итгэлийн интервал байгуулж болно:

Энэ интервал нь маш өндөр итгэлийн түвшинтэй тохирч байна y = 0.997 (хэвийн хуваарилалтын хүснэгтийг үзнэ үү).

Зоос шидэхтэй холбоотой жишээг авч үзье. Бид зоос шидье n = 100 удаа. Энэ нь давтамжтай байж болох уу Рмагадлалаас тэс өөр байх болно Р= 0.5 (зоосыг тэгш хэмтэй гэж үзвэл), жишээлбэл, тэгтэй тэнцүү байх уу? Үүний тулд төрийн сүлд нэг удаа ч гэсэн унахгүй байх шаардлагатай. Ийм үйл явдал онолын хувьд боломжтой, гэхдээ бид ижил төстэй магадлалыг аль хэдийн тооцоолсон; энэ үйл явдлын хувьд энэ нь тэнцүү байх болно. Энэ үнэ цэнэ

маш жижиг, түүний дараалал нь аравтын бутархайн дараа 30 тэгтэй тоо юм. Ийм магадлал бүхий үйл явдлыг бараг боломжгүй гэж үзэж болно. Олон тооны туршилтын үед магадлалаас ямар давтамжийн хазайлт бараг боломжтой вэ? Мойвр-Лаплас теоремыг ашиглан бид энэ асуултанд дараах байдлаар хариулна: магадлалаар цагт= 0.95 сүлд давтамж Ритгэлийн интервалд тохирно:

Хэрэв 0.05 алдаа бага биш юм шиг санагдаж байвал та туршилтын тоог нэмэгдүүлэх хэрэгтэй (зоос шидэх). Өсөх үед Питгэлийн интервалын өргөн багасна (харамсалтай нь бидний хүссэн шиг хурдан биш, харин урвуу пропорциональ байна. -Jn).Жишээлбэл, хэзээ П= 10,000 бид үүнийг ойлгодог Ритгэх магадлал бүхий итгэлийн интервалд оршдог цагт= 0.95: 0.5 ±0.01.

Тиймээс бид давтамжийг магадлалд ойртуулах асуудлыг тоон утгаараа ойлгосон.

Одоо түүний давтамж дээр үндэслэн үйл явдлын магадлалыг олж, энэ ойролцооллын алдааг тооцоолъё.

Олон тооны туршилтуудыг хийцгээе П(зоос шидэх), үйл явдлын давтамжийг ол Амөн бид түүний магадлалыг тооцоолохыг хүсч байна Р.

Их тооны хуулиас Пдараах нь:

Одоо ойролцоо тэгш байдлын (9.7) практик боломжит алдааг тооцоолъё. Үүнийг хийхийн тулд бид тэгш бус байдлыг (9.5) дараах хэлбэрээр ашиглана.

Олох Р By Рбид тэгш бус байдлыг (9.8) шийдэх хэрэгтэй, үүний тулд бид үүнийг квадрат болгож, харгалзах квадрат тэгшитгэлийг шийдэх хэрэгтэй. Үүний үр дүнд бид:

Хаана

Тооцооллын хувьд Р By Р(9.8) томъёонд байж болно. Рбаруун талд нь солино Рэсвэл (9.10), (9.11) томъёонд гэж үзнэ

Дараа нь бид:

Оруул П= 400 туршилтын давтамжийн утгыг олж авсан Р= 0.25, дараа нь y = 0.95 итгэлийн түвшинтэй бол бид дараахь зүйлийг олно.

Хэрэв бид магадлалыг илүү нарийвчлалтай, жишээ нь 0.01-ээс ихгүй алдаатай мэдэх шаардлагатай бол яах вэ? Үүний тулд туршилтын тоог нэмэгдүүлэх шаардлагатай.

(9.12) томъёонд магадлалыг тооцвол Р= 0.25, бид алдааны утгыг өгөгдсөн утгатай 0.01-тэй тэнцүүлж, тэгшитгэлийг олж авна. P:

Энэ тэгшитгэлийг шийдэж, бид олж авна n~ 7500.

Одоо өөр нэг асуултыг авч үзье: туршилтаар олж авсан магадлалаас давтамжийн хазайлтыг санамсаргүй шалтгаанаар тайлбарлаж болох уу, эсвэл энэ хазайлт нь магадлал бидний хүлээж байсан шиг биш гэдгийг харуулж байна уу? Өөрөөр хэлбэл, туршлага нь хүлээн зөвшөөрөгдсөн статистик таамаглалыг баталж байна уу, эсвэл эсрэгээр үүнийг үгүйсгэхийг шаарддаг уу?

Жишээлбэл, зоос шидээрэй П= 800 удаа, бид сүлдний харагдах давтамжийг авдаг Р= 0.52. Бид зоос тэгш хэмтэй биш гэж сэжиглэж байсан. Энэ хардлага үндэслэлтэй юу? Энэ асуултад хариулахын тулд бид зоос нь тэгш хэмтэй гэсэн таамаглалыг үндэслэнэ (p = 0.5). Итгэлийн интервалыг олцгооё (итгэлтэй магадлалаар цагт= 0.95) сүлд харагдах давтамж. Хэрэв туршилтаар олж авсан үнэ цэнэ Р= 0.52 энэ интервалд таарч байна - бүх зүйл хэвийн, зоосны тэгш хэмийн талаархи хүлээн зөвшөөрөгдсөн таамаглал нь туршилтын өгөгдөлтэй зөрчилддөггүй. Формула (9.12) at Р= 0.5 нь 0.5 ± 0.035 интервалыг өгдөг; хүлээн авсан үнэ цэнэ p = 0.52 нь энэ интервалд таарч байгаа бөгөөд энэ нь зоосыг тэгш бус байдлын сэжигээс "цэвэрлэх" шаардлагатай гэсэн үг юм.

Санамсаргүй үзэгдлүүдэд ажиглагдсан математикийн хүлээлтээс янз бүрийн хазайлт нь санамсаргүй эсвэл "чухал" эсэхийг дүгнэхэд ижил төстэй аргуудыг ашигладаг. Жишээлбэл, савласан барааны цөөн хэдэн дээжээс тураал нь санамсаргүй байдлаар илэрсэн үү, эсвэл энэ нь үйлчлүүлэгчдийг системтэйгээр хуурч байгааг илтгэж байна уу? Шинэ эм хэрэглэж байгаа өвчтөнүүдийн эдгэрэлтийн хувь тохиолдлоор нэмэгдсэн үү, эсвэл энэ нь эмийн нөлөөгөөр үү?

Ердийн хууль нь магадлалын онол болон түүний практик хэрэглээнд онцгой үүрэг гүйцэтгэдэг. Санамсаргүй хэмжигдэхүүн буюу Бернулли схем дэх зарим үйл явдлын тохиолдлын тоо гэдгийг бид дээр дурдсан. П-» °° нь ердийн хууль руу буурсан байна. Гэсэн хэдий ч илүү ерөнхий үр дүн бий.

Төвийн хязгаарын теорем.Олон тооны бие даасан (эсвэл сул хамааралтай) санамсаргүй хэмжигдэхүүнүүдийн нийлбэр, тэдгээрийн дисперсийн дарааллаар бие биентэйгээ харьцуулах боломжтой бөгөөд нэр томъёоны тархалтын хууль ямар байснаас үл хамааран ердийн хуулийн дагуу хуваарилагдана. Дээрх мэдэгдэл нь төвлөрсөн хязгаарын онолын чанарын бүдүүлэг томъёолол юм. Энэ теорем нь олон хэлбэртэй бөгөөд санамсаргүй хэмжигдэхүүнүүдийн нийлбэрийг гишүүний тоо ихсэх замаар "нормаци" болгохын тулд хангах ёстой нөхцлөөр бие биенээсээ ялгаатай.

Хэвийн тархалтын нягт Dx)-ийг дараах томъёогоор илэрхийлнэ.

Хаана А -санамсаргүй хэмжигдэхүүний математик хүлээлт X с= V7) нь түүний стандарт хазайлт юм.

(x 1? x 2) интервалд х орох магадлалыг тооцоолохын тулд интегралыг ашиглана:

Нягт (9.13) дахь интеграл (9.14) нь үндсэн функцээр илэрхийлэгдээгүй ("аваагүй") тул (9.14) тооцоолохдоо стандарт хэвийн тархалтын интеграл тархалтын функцийн хүснэгтийг ашигладаг. a = 0, a = 1 (ийм хүснэгтүүд нь магадлалын онолын сурах бичигт байдаг):

(10.15) тэгшитгэлийг ашиглан (9.14) магадлалыг дараах томъёогоор илэрхийлнэ.

Жишээ. Санамсаргүй хэмжигдэхүүн болох магадлалыг ол X,параметртэй хэвийн тархалттай байх А, a нь математикийн хүлээлтийн модулиасаа 3-аас ихгүй зөрүүтэй байна.

Томъёо (9.16) ба ердийн хуулийн тархалтын функцийн хүснэгтийг ашиглан бид дараахь зүйлийг олж авна.

Жишээ. 700 бие даасан туршилт бүрт үйл явдал Атогтмол магадлалтайгаар тохиолддог Р= 0.35. Үйл явдал болох магадлалыг ол Атохиолдох болно:

• 1) яг 270 удаа;
• 2) 270-аас бага, 230-аас дээш удаа;
• 3) 270-аас дээш удаа.

Математикийн хүлээлтийг олох А = гэх мэтба стандарт хазайлт:

санамсаргүй хэмжигдэхүүн - үйл явдлын тохиолдлын тоо Х:

Төвлөрсөн ба хэвийн утгыг олох X:

Хэвийн тархалтын нягтын хүснэгтээс бид олдог f(x):

Одоо олъё R w (x,> 270) = P 700 (270 F(1.98) = = 1 - 0.97615 = 0.02385.

Олон тооны асуудлыг судлах ноцтой алхамыг 1867 онд П.Л.Чебышев хийсэн. Тэрээр бие даасан санамсаргүй хэмжигдэхүүнүүдээс математикийн хүлээлт, дисперс байхаас өөр юу ч шаарддаггүй маш ерөнхий тохиолдлыг авч үзсэн.

Чебышевын тэгш бус байдал.Дурын жижиг эерэг тооны e хувьд дараах тэгш бус байдал үүснэ.

Чебышевын теорем.Хэрэв x x, x 2, ..., x p -хос бие даасан санамсаргүй хэмжигдэхүүнүүд бөгөөд тус бүр нь математикийн хүлээлттэй байдаг E(Xj) = ciболон хэлбэлзэл D(x,) =), мөн ялгаа нь жигд хязгаарлагдмал, өөрөөр хэлбэл. 1,2 ..., дараа нь дурын жижиг эерэг тооны хувьд ддараах хамаарал байна:

Үр дагавар. Хэрэв a,= aio, -o 2 , би= 1.2 ..., тэгвэл

Даалгавар. Магадлал нь түүнээс багагүй байхын тулд зоосыг хэдэн удаа шидэх ёстой вэ? у - 0.997, Төрийн сүлд унах давтамж (0.499; 0.501) интервалд байх болно гэж маргаж болох уу?

Зоосыг тэгш хэмтэй гэж үзье. p - q - 0.5. Санамсаргүй хэмжигдэхүүнд (9.19) томъёонд Чебышевын теоремыг хэрэглэцгээе X-төрийн сүлдний харагдах давтамж Пзоос шидэх. Үүнийг бид аль хэдийн дээр харуулсан X = X x + X 2 + ... +X„,Хаана X t -Хэрэв зоос толгой бол 1, сүүл бол 0 утгыг авдаг санамсаргүй хэмжигдэхүүн. Тэгэхээр:

Магадлалын тэмдгийн дор заасан үйл явдлын эсрэг үйл явдлын тэгш бус байдлыг (9.19) бичье.

Манай тохиолдолд [e = 0.001, cj 2 = /?-p)]t нь төрийн сүлдний тохиолдлын тоо юм. Пшидэх. Эдгээр хэмжигдэхүүнийг сүүлчийн тэгш бус байдалд орлуулж, асуудлын нөхцлийн дагуу тэгш бус байдлыг хангах ёстойг харгалзан бид дараахь зүйлийг олж авна.

Өгөгдсөн жишээ нь санамсаргүй хэмжигдэхүүний тодорхой хазайлтын магадлалыг тооцоолохын тулд Чебышевын тэгш бус байдлыг ашиглах боломжийг харуулж байна (мөн эдгээр магадлалыг тооцоолохтой холбоотой энэ жишээ гэх мэт асуудлууд). Чебышевын тэгш бус байдлын давуу тал нь санамсаргүй хэмжигдэхүүний тархалтын хуулиудын мэдлэг шаарддаггүй явдал юм. Мэдээжийн хэрэг, хэрэв ийм хууль мэдэгдэж байгаа бол Чебышевын тэгш бус байдал нь хэтэрхий бүдүүлэг тооцоог өгдөг.

Үүнтэй ижил жишээг харцгаая, гэхдээ зоос шидэх нь Бернуллигийн схемийн онцгой тохиолдол юм. Амжилтын тоо (жишээнд - Төрийн сүлдний тоо) нь хоёртын хуулийг дагаж мөрддөг бөгөөд том хэмжээтэй байдаг. ПЭнэ хуулийг Мойвр-Лапласын интеграл теоремоос шалтгаалан математикийн хүлээлттэй ердийн хуулиар төлөөлж болно. a = pr = n? 0.5 ба стандарт хазайлттай a = yfnpq - 25=0.5л/л. Санамсаргүй хэмжигдэхүүн - Төрийн сүлд унах давтамж нь математикийн хүлээлт = 0.5 ба стандарт хазайлттай байна.

Дараа нь бидэнд байна:

Сүүлийн тэгш бус байдлаас бид дараахь зүйлийг олж авна.

Ердийн хуваарилалтын хүснэгтээс бид дараахь зүйлийг олно.

Ердийн ойролцоо тооцоолол нь төрийн сүлдний магадлалыг тооцоолоход өгөгдсөн алдааг өгдөг зоос шидсэн тоог өгдөг бөгөөд энэ нь Чебышевын тэгш бус байдлыг ашиглан олж авсан тооцоотой харьцуулахад 37 дахин бага байна (гэхдээ Чебышевын тэгш бус байдал нь үүнийг хийх боломжтой болгодог. судалж буй санамсаргүй хэмжигдэхүүний тархалтын хуулийн талаар мэдээлэл байхгүй тохиолдолд ижил төстэй тооцоолол).

Одоо (9.16) томъёог ашиглан шийдэгдсэн хэрэглээний асуудлыг авч үзье.

Өрсөлдөөний асуудал. Өрсөлдөгч хоёр төмөр замын компани Москва, Санкт-Петербургийн хооронд нэг галт тэрэг явдаг. Эдгээр галт тэрэгнүүд ойролцоогоор адилхан тоноглогдсон бөгөөд ойролцоогоор ижил цагт хөдөлж, ирдэг. Ингэж жүжиглэе П= 1000 зорчигч бие даан, санамсаргүй байдлаар галт тэргээ сонгодог тул зорчигчдын галт тэрэг сонгох математик загвар болгон бид Бернулли схемийг ашигладаг. Псорилт, амжилтанд хүрэх магадлал Р= 0.5. Тус компани галт тэргэнд хэдэн суудал өгөхөө шийдэх ёстой бөгөөд энэ нь хоорондоо зөрчилддөг хоёр нөхцөлийг харгалзан үзэх ёстой: нэг талаас та хоосон суудалтай байхыг хүсэхгүй байгаа, нөгөө талаас та хүмүүсийн сэтгэл ханамжгүй байхыг хүсэхгүй байна. суудал дутагдалтай (дараагийн удаа тэд өрсөлдөгч компаниудыг илүүд үзэх болно). Мэдээжийн хэрэг, үүнийг галт тэргэнд өгч болно П= 1000 газар, гэхдээ дараа нь хоосон газар байх нь тодорхой. Санамсаргүй хэмжигдэхүүн - галт тэрэгний зорчигчдын тоо - Мойврын интеграл онолыг ашиглан батлагдсан математик загварын хүрээнд - Лаплас математикийн хүлээлттэй ердийн хуулийг дагаж мөрддөг. a = pr = p/2 ба дисперс a 2 = npq = p/4дараалсан. -аас их байх магадлал сЗорчигчийг дараахь харьцаагаар тодорхойлно.

Эрсдлийн түвшинг тогтоох А, өөрөөр хэлбэл илүү их зүйл ирэх магадлал сзорчигчид:

Эндээс:

Хэрэв АЭнэ нь ердийн хуулийн тархалтын функцийн хүснэгтээс олдсон сүүлчийн тэгшитгэлийн эрсдэлийн үндэс бөгөөд бид дараахь зүйлийг олж авна.

Хэрэв, жишээ нь, П = 1000, А= 0.01 (эрсдлийн энэ түвшин нь газрын тоо с 100 тохиолдлын 99 тохиолдолд хангалттай байх болно), дараа нь x a ~ 2.33 ба s = 537 газар. Түүнээс гадна, хэрэв хоёр компани ижил түвшний эрсдэлийг хүлээн зөвшөөрвөл А= 0.01, тэгвэл хоёр галт тэрэг нийт 1074 хүний ​​суудалтай, 74 нь хоосон байна. Үүний нэгэн адил нийт тохиолдлын 80%-д 514 суудал, 1000 тохиолдлын 999-д 549 суудал хангалттай байхаар тооцоолж болно.

Өрсөлдөгч үйлчилгээний бусад асуудлуудад ижил төстэй асуудлууд хамаарна. Жишээлбэл, хэрэв Ткино театрууд ч үүний төлөө өрсөлддөг Пүзэгчид, тэгвэл хүлээж авах ёстой Р= -. Бид авдаг,

суудлын тоо хэд вэ скино театрт дараахь харьцаагаар тодорхойлогддог.

Хоосон зайны нийт тоо дараахтай тэнцүү байна.

Учир нь А = 0,01, П= 1000 ба Т= 2, 3, 4 бол энэ тооны утга нь ойролцоогоор 74, 126, 147-той тэнцүү байна.

Өөр нэг жишээг харцгаая. Галт тэрэг бүрдэх болтугай P - 100 вагон. Машин бүрийн жин нь математикийн хүлээлттэй санамсаргүй хэмжигдэхүүн юм А - 65 тонн ба дундаж квадрат хүлээлт o = 9 тонн.Зүтгүүрийн жин 6600 тонноос хэтрэхгүй бол галт тэрэг тээвэрлэх боломжтой; Үгүй бол та хоёр дахь зүтгүүрийг холбох хэрэгтэй. Та үүнийг хийх шаардлагагүй байх магадлалыг олох хэрэгтэй.

бие даасан автомашины жин: , ижил математикийн хүлээлттэй А - 65 ба ижил зөрүү d- o 2 = 81. Математикийн хүлээлтийн дүрмээр: E(x) - 100 * 65 = 6500. Вариацийг нэмэх дүрмийн дагуу: D(х) = 100 x 81 = 8100. Үндэсийг гаргаж авснаар стандарт хазайлтыг олно. Нэг зүтгүүр галт тэрэг татахын тулд галт тэрэгний жин нь байх ёстой Xхязгаарлагдмал болж хувирсан, өөрөөр хэлбэл интервал дотор унасан (0; 6600). Санамсаргүй хэмжигдэхүүн x - 100 гишүүний нийлбэр - хэвийн тархалттай гэж үзэж болно. (9.16) томъёог ашиглан бид дараахь зүйлийг олж авна.

Үүнээс үзэхэд зүтгүүр нь ойролцоогоор 0.864 магадлал бүхий галт тэргийг "даах" болно. Одоо галт тэрэгний вагоны тоог хоёроор цөөрүүлье, өөрөөр хэлбэл ав П= 98. Одоо зүтгүүр галт тэргийг "даах" магадлалыг тооцоолохдоо бид 0.99 гэсэн дарааллын утгыг, өөрөөр хэлбэл бараг тодорхой үйл явдлыг олж авна, гэхдээ үүний тулд зөвхөн хоёр вагоныг зайлуулах шаардлагатай байсан.

Тиймээс, хэрэв бид олон тооны санамсаргүй хэмжигдэхүүний нийлбэртэй харьцаж байгаа бол ердийн хуулийг ашиглаж болно. Мэдээжийн хэрэг, эндээс асуулт гарч ирнэ: нийлбэрийн тархалтын хууль аль хэдийн "нормчилогдсон" байхын тулд хичнээн санамсаргүй хэмжигдэхүүнийг нэмэх шаардлагатай вэ? Энэ нь нэр томьёоны тархалтын хууль ямар байхаас хамаарна. Маш олон тооны нэр томьёотой л хэвийн байдал үүсдэг тийм нарийн хуулиуд байдаг. Гэхдээ эдгээр хуулиудыг математикчид зохион бүтээсэн бөгөөд байгаль нь дүрмээр бол санаатайгаар ийм бэрхшээл үүсгэдэггүй. Ер нь практик дээр ердийн хуулийг ашиглахын тулд тав, зургаан нэр томъёо хангалттай байдаг.

Ижил тархсан санамсаргүй хэмжигдэхүүний нийлбэрийн тархалтын хуулийг "нормальчлах" хурдыг (0, 1) интервал дээр жигд тархалттай санамсаргүй хэмжигдэхүүнүүдийн жишээгээр дүрсэлж болно. Ийм тархалтын муруй нь тэгш өнцөгт хэлбэртэй бөгөөд энэ нь ердийн хуультай төстэй байхаа больсон. Ийм хоёр бие даасан хувьсагчийг нэмье - бид Симпсоны хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүнийг олж авах бөгөөд график дүрслэл нь тэгш өнцөгт гурвалжин хэлбэртэй байдаг. Энэ нь бас энгийн хууль мэт харагдахгүй байгаа ч илүү дээр юм. Хэрэв та ийм жигд тархсан санамсаргүй хэмжигдэхүүнийг 3-ыг нэмбэл энгийн муруйтай маш төстэй параболын гурван сегментээс бүрдсэн муруй болно. Хэрэв та ийм зургаан санамсаргүй хэмжигдэхүүнийг нэмбэл хэвийн хэмжээнээс ялгаатай муруй гарч ирнэ. Энэ нь ердийн тархалттай санамсаргүй хэмжигдэхүүнийг олж авах өргөн хэрэглэгддэг аргын үндэс суурь бөгөөд орчин үеийн бүх компьютерууд жигд тархсан (0, 1) санамсаргүй тоонуудын мэдрэгчээр тоноглогдсон байдаг.

Үүнийг шалгах нэг практик арга болгон дараах аргыг ашиглахыг зөвлөж байна. Бид түвшинтэй үйл явдлын давтамжийн итгэлийн интервалыг байгуулдаг цагтГурван сигма дүрмийн дагуу = 0.997:

хэрэв түүний хоёр төгсгөл нь хэрчмээс (0, 1) цааш гарахгүй бол ердийн хуулийг ашиглаж болно. Хэрэв итгэлцлийн интервалын аль нэг хил нь сегментээс гадуур байвал (0, 1) хэвийн хуулийг ашиглах боломжгүй. Гэсэн хэдий ч, зарим тохиолдолд санамсаргүй тохиолдлын давтамжийн хоёртын хууль, хэрэв энэ нь ердийн зүйл рүү чиглээгүй бол өөр хууль руу чиглэж болно.

Олон хэрэглээнд Бернулли схемийг санамсаргүй туршилтын математик загвар болгон ашигладаг бөгөөд туршилтын тоо Птом, санамсаргүй үйл явдал нэлээд ховор тохиолддог, i.e. Р = гэх мэтжижиг биш, гэхдээ бас их биш (O -5-20 мужид хэлбэлздэг). Энэ тохиолдолд хязгаарлалтын хамаарал нь:

Баруун талд байгаа магадлалын тархалтыг Пуассоны хууль гэж нэрлэдэг тул (9.20) томъёог хоёр гишүүний хуулийн Пуассоны ойролцоо тооцоолол гэж нэрлэдэг. Пуассоны тархалтыг ховор тохиолдлын магадлалын тархалт гэж нэрлэдэг, учир нь энэ нь хязгаарыг хангасан үед тохиолддог. П -»°°, Р-»0, гэхдээ X = pr oo.

Жишээ. Төрсөн өдрүүд. магадлал хэд вэ R t (k) 500 хүнтэй нийгэмд руухүмүүс шинэ жилийн өдөр төрсөн үү? Хэрэв эдгээр 500 хүнийг санамсаргүй байдлаар сонгосон бол амжилтанд хүрэх магадлал бүхий Бернуллигийн схемийг ашиглаж болно. P = 1/365. Дараа нь

Төрөл бүрийн магадлалын тооцоолол руудараах утгыг өгнө. RU = 0,3484...; R 2 = 0,2388...; R 3 = 0,1089...; P 4 = 0,0372...; R 5 = 0,0101...; R 6= 0.0023... Пуассоны томьёог ашиглан харгалзах ойролцоо тоо X = 500 1/365 = 1,37

дараах утгыг өгнө. Ru = 0,3481...; R 2 = 0,2385...; P ъ = 0,1089; R 4 = 0,0373...; P 5 = 0,0102...; P 6 = 0.0023... Бүх алдаа зөвхөн дөрөв дэх аравтын бутархайд байна.

Пуассоны ховор тохиолдлын хуулийг ашиглаж болох нөхцөл байдлын жишээ энд байна.

Утасны станц дээр буруу холболт үүсэх магадлал бага байдаг R,ихэвчлэн Р~0.005. Дараа нь Пуассоны томъёо нь өгөгдсөн нийт холболтын тооны буруу холболтын магадлалыг олох боломжийг олгодог. n~Хэзээ 1000 X = pr =1000 0,005 = 5.

Талхыг жигнэх үед зуурмаг дээр үзэм нэмнэ. Хутгасны улмаас үзэмтэй боовны давтамж нь Пуассоны хуваарилалтын дагуу ойролцоогоор байх ёстой R p (k, X),Хаана X-зуурмаг дахь үзэмний нягтрал.

Цацраг идэвхит бодис нь π тоосонцор ялгаруулдаг. Цаг хугацааны явцад d-бөөмсийн тоо хүрэх үйл явдал төгөгдсөн орон зай нь тогтмол утгыг авдаг руу,Пуассоны хуулийг дагаж мөрддөг.

Рентген туяанд өртөх үед өөрчлөгдсөн хромосомтой амьд эсийн тоо Пуассоны тархалтыг дагаж мөрддөг.

Тиймээс олон тооны хуулиуд нь санамсаргүй туршилтын анхан шатны үр дүнгийн үл мэдэгдэх магадлалыг тооцоолохтой холбоотой математик статистикийн асуудлыг шийдвэрлэх боломжийг олгодог. Энэхүү мэдлэгийн ачаар бид магадлалын онолын аргуудыг практик ач холбогдолтой, хэрэгцээтэй болгодог. Олон тооны хуулиуд нь үл мэдэгдэх энгийн магадлалын талаархи мэдээллийг өөр хэлбэрээр олж авах асуудлыг шийдвэрлэх боломжийг олгодог - статистик таамаглалыг шалгах хэлбэрээр.

Статистикийн таамаглалыг шалгах асуудлыг шийдвэрлэх томъёолол, магадлалын механизмыг илүү нарийвчлан авч үзье.

Их тооны хуульМагадлалын онолд тогтмол тархалтаас хангалттай том хязгаарлагдмал түүврийн эмпирик дундаж (арифметик дундаж) нь энэ тархалтын онолын дундажтай (математикийн хүлээлт) ойролцоо байна гэж заасан. Конвергенцийн төрлөөс хамааран нийлэх магадлалын хувьд их тооны сул хууль, бараг хаа сайгүй нийлдэг их тооны хүчтэй хуулийг хооронд нь ялгадаг.

Үргэлж хязгаарлагдмал тооны туршилтууд байдаг бөгөөд тэдгээр нь урьдчилсан магадлалаар бага байдаг 1 зарим үйл явдлын харьцангуй давтамж нь түүний магадлалаас аль болох бага ялгаатай байх болно.

Олон тооны хуулийн ерөнхий утга нь: олон тооны ижил, бие даасан санамсаргүй хүчин зүйлсийн хамтарсан үйл ажиллагаа нь хязгаарт тохиолдлоос хамаардаггүй үр дүнд хүргэдэг.

Хязгаарлагдмал түүврийн шинжилгээнд үндэслэн магадлалыг тооцоолох аргууд нь энэ шинж чанарт суурилдаг. Үүний тод жишээ бол сонгогчдын түүвэр судалгаанд үндэслэн сонгуулийн үр дүнгийн таамаглал юм.

Нэвтэрхий толь бичиг YouTube

1 / 5

✪ Их тооны хууль

✪ 07 - Магадлалын онол. Их тооны хууль

✪ 42 Их тооны хууль

✪ 1 - Чебышевын олон тооны хууль

✪ 11-р анги, 25-р хичээл, Гауссын муруй. Их тооны хууль

Хадмал орчуулга

Математик болон магадлалын онолын хамгийн зөн совингийн хууль болох их тооны хуулийг авч үзье. Мөн энэ нь маш олон зүйлд хамаатай учраас заримдаа хэрэглэж, буруугаар ойлгодог. Эхлээд үүнийг үнэн зөвөөр нь тодорхойлж өгье, дараа нь бид зөн совингийн талаар ярилцъя. Санамсаргүй хэмжигдэхүүнийг авч үзье, жишээ нь X. Бид түүний математик хүлээлт эсвэл популяцийн дундаж утгыг мэддэг гэж бодъё. Хэрэв бид санамсаргүй хэмжигдэхүүний n-р тооны ажиглалтын жишээг аваад тэдгээр бүх ажиглалтын дунджийг авбал... Нэг хувьсагчийг авч үзье гэж Их тоонуудын тухай хуульд энгийнээр заасан байдаг. Үүнийг X гэж нэрлэе. Энэ нь бидний санамсаргүй хэмжигдэхүүний ажиглалтын n дахь тооны арифметик дундаж юм. Энд миний анхны ажиглалт байна. Би туршилтыг нэг удаа хийгээд энэ ажиглалтыг хийчихээд, дараа нь дахин хийж, энэ ажиглалтыг хийж, дахин хийж үүнийг олж авдаг. Би энэ туршилтыг n дэх удаагаа хийж, дараа нь ажиглалтын тоонд хуваана. Энд миний жишээ дундаж байна. Миний хийсэн бүх ажиглалтын дундажийг энд харуулав. Том тоонуудын хууль нь миний түүврийн дундаж нь санамсаргүй хэмжигдэхүүний хүлээгдэж буй утгад ойртоно гэж бидэнд хэлдэг. Эсвэл миний түүврийн дундаж нь хязгааргүй рүү чиглэсэн n-р хэмжигдэхүүний дунджид ойртох болно гэж би бас бичиж болно. Би "ойролцоо" ба "нийцэх" хоёрын хооронд тодорхой ялгаа гаргахгүй, гэхдээ би эндээс нэлээд том түүвэр авбал нийт хүн амын хүлээгдэж буй утгыг авна гэдгийг та бүхэн зөн совингоор ойлгоно гэж найдаж байна. Хэрэв би олон жишээн дээр хангалттай тест хийвэл эцэст нь туршилтууд нь хүлээгдэж буй үнэ цэнэ, магадлал болон тэр бүх жаазыг харгалзан үзэхэд миний хүлээж буй утгыг өгөх болно гэдгийг та нарын ихэнх нь зөн совингоор ойлгож байгаа гэж бодож байна. Гэхдээ яагаад ийм зүйл болдог нь ихэвчлэн ойлгомжгүй байдаг гэж би бодож байна. Яагаад ийм байдгийг тайлбарлахаасаа өмнө тодорхой жишээ хэлье. Их тооны тухай хууль бидэнд ингэж хэлдэг... Бид санамсаргүй хэмжигдэхүүнтэй X байна гэж бодъё. Энэ нь шударга зоос 100 шидэхэд толгойн тоотой тэнцүү байна. Юуны өмнө бид энэ санамсаргүй хэмжигдэхүүний математик хүлээлтийг мэддэг. Энэ нь зоос шидэлтийн тоо буюу туршилтын тоог аливаа туршилтын амжилтын магадлалаар үржүүлсэн тоо юм. Тэгэхээр энэ нь 50-тай тэнцүү байна. Өөрөөр хэлбэл, олон тооны хуулинд хэрэв бид дээж авбал, эсвэл би эдгээр туршилтуудыг дундажлавал би авна гэсэн үг юм. .. Би анх удаа тест хийхдээ 100 удаа зоос шиднэ, эсвэл зуун зоостой хайрцгийг аваад сэгсэрнэ, тэгээд хэдэн толгой авснаа тоолоод 55 гэсэн тоог авна. X1 байх болно. Дараа нь би хайрцгийг дахин сэгсэрч, 65-ын тоог авна. Дараа нь би 45-ыг авна. Тэгээд би үүнийг n олон удаа хийж, дараа нь туршилтын тоонд хуваана. Их тооны хууль нь n хязгааргүйд ойртох тусам энэ дундаж (миний бүх ажиглалтын дундаж) 50-д ойртох болно гэдгийг бидэнд хэлдэг. Одоо би яагаад ийм зүйл болдог талаар бага зэрэг ярихыг хүсч байна. Хэрэв 100 туршилтын дараа миний үр дүн дунджаас дээгүүр байвал магадлалын хуулийн дагуу зөрүүг нөхөхийн тулд би илүү их эсвэл цөөн тооны толгой авах ёстой гэж олон хүмүүс үздэг. Энэ нь яг ийм зүйл болохгүй. Үүнийг ихэвчлэн "мөрийтэй тоглоомчдын төөрөгдөл" гэж нэрлэдэг. Би танд ялгааг харуулъя. Би дараах жишээг ашиглах болно. Би график зуръя. Өнгийг нь өөрчилье. Энэ бол n, миний x тэнхлэг бол n. Энэ бол миний хийх тестийн тоо юм. Миний Y тэнхлэг нь түүврийн дундаж болно. Энэхүү дурын хувьсагчийн математикийн хүлээлт 50 гэдгийг бид мэднэ. Би зуръя. Энэ бол 50. Өөрийнхөө жишээ рүү буцъя. Хэрэв n бол... Эхний шалгалтын үеэр би 55 авсан, энэ бол миний дундаж. Надад зөвхөн нэг өгөгдөл оруулах цэг байна. Тэгээд хоёр шалгалтын дараа би 65 авдаг. Тэгэхээр миний дундаж 65+55-ыг 2-т хуваасан байна. Энэ нь 60. Тэгээд миний дундаж бага зэрэг өссөн. Дараа нь би 45 авсан нь миний арифметик дундажийг дахин бууруулсан. Би 45-р зураглал хийхгүй. Одоо би энэ бүгдийг дундажлах хэрэгтэй. 45+65 хэдтэй тэнцүү вэ? Би цэгийг илэрхийлэхийн тулд энэ утгыг тооцоолъё. Энэ нь 165-ыг 3-т хуваана. Энэ нь 53. Үгүй, 55. Тэгэхээр дундаж нь 55 болж буурна. Бид эдгээр туршилтуудыг үргэлжлүүлж болно. Бид гурван туршилт хийж, дундаж оноо авсны дараа олон хүмүүс магадлалын бурхад биднийг ирээдүйд цөөн толгойтой болгох болно, дараагийн хэдэн туршилтууд дунджийг бууруулахын тулд бага оноотой байх болно гэж олон хүмүүс боддог. Гэхдээ энэ нь үргэлж тийм байдаггүй. Ирээдүйд магадлал үргэлж ижил хэвээр байна. Би толгойгоо авах 50% магадлал үргэлж байх болно. Энэ нь би эхэндээ бодож байснаас илүү тодорхой тооны толгойтой болж, дараа нь гэнэт сүүлтэй болох ёстой гэсэн үг биш юм. Энэ бол мөрийтэй тоглоомчдын төөрөгдөл юм. Хэзээ нэгэн цагт та пропорциональ бус олон тооны толгойтой болж эхэлнэ гэсэн үг биш юм. Энэ нь бүхэлдээ үнэн биш юм. Энэ нь хамаагүй гэдгийг их тооны хууль бидэнд хэлдэг. Тодорхой хязгаарлагдмал тооны шалгалтын дараа таны дундаж... Үүний магадлал нэлээд бага, гэхдээ, гэсэн хэдий ч... Таны дундаж энэ оноо - 70 хүрсэн гэж бодъё. Та "Хөөх, бид хүлээгдэж буй үнэ цэнээсээ холдчихлоо" гэж бодож байна. Гэхдээ олон тооны тухай хуульд бид хичнээн шинжилгээ хийх нь хамаагүй гэсэн. Бидний өмнө эцэс төгсгөлгүй олон сорилт байсаар байна. Энэхүү хязгааргүй тооны туршилтын математикийн хүлээлт, ялангуяа ийм нөхцөл байдалд дараах байдалтай байна. Та ямар нэгэн том утгыг илэрхийлдэг хязгаарлагдмал тоо дээр ирэхэд түүнтэй нийлэх хязгааргүй тоо дахин хүлээгдэж буй утга руу хүргэнэ. Энэ нь мэдээжийн хэрэг маш сул тайлбар боловч их тооны хууль үүнийг бидэнд хэлдэг. Энэ нь чухал юм. Олон толгой авчихвал яаж ийгээд нөхөхийн тулд сүүл авах магадлал нэмэгдэнэ гэж хэлэхгүй. Хязгааргүй тооны сорилт үлдсэн л бол хязгааргүй тооны туршилтын үр дүн ямар байх нь хамаагүй гэдгийг энэ хууль бидэнд хэлж байна. Хэрэв та эдгээрийг хангалттай хийвэл дахин хүлээгдэж буй үнэ цэнэдээ хүрэх болно. Энэ бол чухал цэг юм. Үүний тухай бодож үз. Гэхдээ үүнийг өдөр бүр сугалаа, казиногийн хувьд практикт ашигладаггүй, гэхдээ хангалттай туршилт хийвэл бид үүнийг тооцоолж чадна ... бид нормоос ноцтой хазайх магадлал хэд вэ? Харин казино, хонжворт хонжворт сугалаа өдөр бүр ажилладаг, хэрэв та хангалттай хүнээ, аяндаа, богино хугацаанд, бага хэмжээний түүврээр авбал хэдэн хүн жекпот хожно гэсэн зарчмаар ажилладаг. Гэвч удаан хугацааны туршид казино таныг тоглохыг урьсан тоглоомуудын параметрүүдээс шалтгаалан үргэлж хожих болно. Энэ бол зөн совингийн магадлалын чухал зарчим юм. Хэдийгээр заримдаа үүнийг санамсаргүй хэмжигдэхүүнээр албан ёсоор тайлбарлавал энэ бүхэн бага зэрэг ойлгомжгүй мэт санагддаг. Энэ бүх хуульд түүвэр их байх тусмаа тэдгээр түүврийн арифметик дундаж нь жинхэнэ дундаж руу чиглэнэ гэж заасан байдаг. Илүү тодорхой болгохын тулд таны түүврийн арифметик дундаж нь санамсаргүй хэмжигдэхүүний математикийн хүлээлттэй нийлнэ. Тэгээд л болоо. Дараагийн видеогоор уулзацгаая!

Их тооны сул хууль

Их тооны сул хуулийг 1713 онд баталсан Якоб Бернуллигийн нэрээр Бернуллийн теорем гэж бас нэрлэдэг.

Ижил тархсан ба хамааралгүй санамсаргүй хэмжигдэхүүнүүдийн хязгааргүй дараалал (дараалсан тоолол) байг. Энэ нь тэдний ковариац юм c o v (X i , X j) = 0 , ∀ i ≠ j (\displaystyle \mathrm (cov) (X_(i),X_(j))=0,\;\forall i\not =j). Let . Эхний түүврийн дундажаар тэмдэглэе n (\displaystyle n)гишүүд:

.

Дараа нь X ¯ n → P μ (\ displaystyle (\bar (X))_(n)\to ^(\!\!\!\!\!\!\mathbb (P) )\mu ).

Энэ нь аливаа эерэг зүйлийн хувьд ε (\displaystyle \varepsilon)

lim n → ∞ Pr (| X ¯ n − μ |< ε) = 1. {\displaystyle \lim _{n\to \infty }\Pr \!\left(\,|{\bar {X}}_{n}-\mu |<\varepsilon \,\right)=1.}

Их тооны тухай хуулийг чангатгасан

Бие даасан ижил тархсан санамсаргүй хэмжигдэхүүнүүдийн хязгааргүй дараалал байг ( X i ) i = 1 ∞ (\displaystyle \(X_(i)\)_(i=1)^(\infty )), нэг магадлалын орон зайд тодорхойлогдсон (Ω , F , P) (\displaystyle (\Омега,(\маткал (F)),\mathbb (P))). Болъё E X i = μ , ∀ i ∈ N (\displaystyle \mathbb (E) X_(i)=\mu ,\;\forall i\in \mathbb (N) ). -ээр тэмдэглэе X ¯ n (\displaystyle (\бар (X))_(n))эхний дундаж жишээ n (\displaystyle n)гишүүд:

X ¯ n = 1 n ∑ i = 1 n X i , n ∈ N (\displaystyle (\bar (X))_(n)=(\frac (1)(n))\нийлбэр \limits _(i=) 1)^(n)X_(i),\;n\-д \mathbb (N) ).

Дараа нь X ¯ n → μ (\displaystyle (\bar (X))_(n)\to \mu )бараг үргэлж.

Pr (lim n → ∞ X ¯ n = μ) = 1. (\displaystyle \Pr \!\left(\lim _(n\to \infty )(\bar (X))_(n)=\mu \ баруун) = 1.) .

Математикийн аливаа хуулийн нэгэн адил их тооны хуулийг бодит ертөнцөд зөвхөн тодорхой хэмжээний нарийвчлалтайгаар биелүүлэх боломжтой тодорхой таамаглалын дагуу л хэрэглэж болно. Жишээлбэл, дараалсан туршилтын нөхцөлийг хязгааргүй, үнэмлэхүй нарийвчлалтайгаар хадгалах боломжгүй байдаг. Нэмж дурдахад, их тооны хууль зөвхөн ярьдаг магадлалгүйматематикийн хүлээлтээс дундаж утгын мэдэгдэхүйц хазайлт.