Sužinokite, kurią tiesę apibrėžia lygtis. Tiesės lygties apibrėžimas, tiesės plokštumoje pavyzdžiai. paralelizmo sąlyga

Svarbiausia analitinės geometrijos samprata yra tiesės lygtis plokštumoje.

Apibrėžimas. Tiesės (kreivės) lygtis plokštumoje Oxy yra lygtis, kurią tenkina koordinatės x Ir y kiekvienas tam tikros tiesės taškas ir jų netenkina bet kurio taško, esančio ne šioje tiesėje, koordinatės (1 pav.).

Apskritai linijos lygtis gali būti parašyta kaip F(x,y)=0 arba y=f(x).

Pavyzdys. Raskite taškų aibės, vienodais atstumais nuo taškų, lygtį A(-4;2), B(-2;-6).

Sprendimas. Jeigu M(x;y) yra savavališkas norimos linijos taškas (2 pav.), tada turime AM = BM arba

Po transformacijų gauname

Akivaizdu, kad tai yra tiesės lygtis M.D.– statmena atkurta nuo atkarpos vidurio AB.

Iš visų lėktuve esančių linijų ta, kuri yra ypač svarbi tiesi linija. Tai tiesinės funkcijos grafikas, naudojamas dažniausiai praktikoje sutinkamuose tiesiniuose ekonominiuose ir matematiniuose modeliuose.

Skirtingi tiesių lygčių tipai:

1) su nuolydžiu k ir pradine ordinate b:

y = kx + b,

kur yra kampas tarp tiesės ir teigiamos ašies krypties OI(3 pav.).

Ypatingi atvejai:

- eina tiesi linija kilmės(4 pav.):

– bisektorius pirmas ir trečias, antras ir ketvirtas koordinačių kampai:

y=+x, y=-x;

– tiesus lygiagrečiai OX ašiai ir ji pati OX ašis(5 pav.):

y=b, y=0;

– tiesus lygiagrečiai OY ašiai ir ji pati OY ašis(6 pav.):

x=a, x=0;

2) pravažiuojant nurodyta kryptimi (su nuolydžiu) k per duotą tašką (7 pav.) :

.

Jei pateiktoje lygtyje k yra savavališkas skaičius, tada lygtis nustato tiesių linijų krūva, einantis per tašką išskyrus ašiai lygiagrečią tiesę Oy.

PavyzdysA(3,-2):

a) kampu ašies atžvilgiu OI;

b) lygiagrečiai ašiai OY.

Sprendimas.

A) , y-(-2) = -1 (x-3) arba y=-x+1;

b) x=3.

3) einant per du duotus taškus (8 pav.) :

.

Pavyzdys. Parašykite tiesės, einančios per taškus, lygtį A(-5,4), B(3,-2).

Sprendimas. ,

4) linijos lygtis atkarpose (9 pav.):

Kur a, b – segmentai, atitinkamai nupjauti ant ašių Jautis Ir Oy.

Pavyzdys. Parašykite tiesės, einančios per tašką, lygtį A(2,-1), jei ši tiesi linija nutrūksta nuo teigiamos pusašies Oy dvigubai ilgesnė atkarpa nei nuo teigiamos pusašies Jautis(10 pav.).

Sprendimas. Pagal sąlygą b=2a, Tada. Pakeiskime taško koordinates A(2,-1):

Kur a = 1,5.

Galiausiai gauname:

Arba y=-2x+3.

5) bendroji tiesės lygtis:

Ax+By+C=0,

Kur a Ir b tuo pačiu metu nėra lygūs nuliui.

Kai kurios svarbios tiesių linijų charakteristikos :

1) atstumas d nuo taško iki tiesės:

.

2) kampas tarp tiesių ir atitinkamai:

Ir .

3) lygiagrečių linijų sąlyga:

arba .

4) linijų statmenumo sąlyga:

arba .

1 pavyzdys. Parašykite dviejų tiesių, einančių per tašką, lygtį A(5.1), iš kurių viena lygiagreti linijai 3x+2y-7=0, o kita yra statmena tai pačiai linijai. Raskite atstumą tarp lygiagrečių linijų.

Sprendimas. 11 pav.

1) lygiagrečios tiesės Ax+By+C=0 lygtis:

iš paralelizmo sąlygos;

imant proporcingumo koeficientą, lygų 1, gauname A = 3, B = 2;

Tai. 3x+2y+C=0;

prasmė SU rasime pakeitę koordinates t. A(5,1),

3*5+2*1+С=0, kur C=-17;

lygiagrečios tiesės lygtis 3x+2y-17=0.

2) statmenos tiesės lygtis iš statmenumo sąlygos turės formą 2x-3y+C=0;

pakeičiant koordinates t. A(5.1), mes gauname 2*5-3*1+С=0, kur C=-7;

statmenos tiesės lygtis 2x-3y-7=0.

3) atstumas tarp lygiagrečių tiesių galima rasti kaip atstumą nuo t. A(5.1) duotas tiesiogiai 3x+2y-7=0:

.

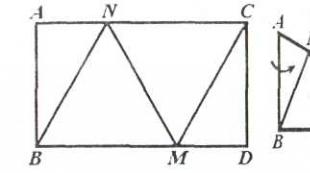
2 pavyzdys. Pateikiamos trikampio kraštinių lygtys:

3x-4y+24=0 (AB), 4x+3y+32=0 (BC), 2x-y-4=0 (AC).

Parašykite kampo bisektoriaus lygtį ABC.

Sprendimas. Pirmiausia randame viršūnės koordinates IN trikampis:

,

kur x = -8, y = 0, tie. V(-8,0)(12 pav.) .

Pagal bisektoriaus savybę atstumas nuo kiekvieno taško M(x,y), Bisektoriai BDį šonus AB Ir Saulė yra lygūs, t.y.

,

Gauname dvi lygtis

x+7y+8=0, 7x-y+56=0.

Pagal 12 paveikslą norimos tiesės kampinis koeficientas yra neigiamas (kampas su Oi bukas), todėl pirmoji lygtis mums tinka x+7y+8=0 arba y = -1/7x-8/7.

Panagrinėkime formos santykį F(x, y)=0, jungiantis kintamieji x Ir adresu. Mes vadinsime lygybe (1) lygtis su dviem kintamaisiais x, y, jei ši lygybė galioja ne visoms skaičių poroms X Ir adresu. Lygčių pavyzdžiai: 2x + 3y = 0, x 2 + y 2 – 25 = 0,

sin x + sin y – 1 = 0.

Jei (1) yra teisingas visoms skaičių poroms x ir y, tada jis vadinamas tapatybę. Tapatybių pavyzdžiai: (x + y) 2 - x 2 - 2xy - y 2 = 0, (x + y) (x - y) - x 2 + y 2 = 0.

Mes vadinsime (1) lygtį taškų aibės lygtis (x; y), jei šią lygtį tenkina koordinatės X Ir adresu bet kurį aibės tašką ir jų netenkina nė vieno šiai aibei nepriklausančio taško koordinatės.

Svarbi analitinės geometrijos sąvoka yra tiesės lygties sąvoka. Tegu plokštumoje duota stačiakampė koordinačių sistema ir tam tikra tiesė α.

Apibrėžimas. Lygtis (1) vadinama tiesine lygtimi α (sukurtoje koordinačių sistemoje), jei šią lygtį tenkina koordinatės X Ir adresu bet kuris taškas, esantis ant linijos α , ir netenkina jokio taško, esančio ne šioje tiesėje, koordinačių.

Jei (1) yra tiesės lygtis α, tada mes pasakysime, kad lygtis (1) apibrėžia (rinkinius) linija α.

Linija α gali būti nustatytas ne tik pagal formos lygtį (1), bet ir pagal formos lygtį

F (P, φ) = 0 kuriose yra polinės koordinatės.

• tiesės lygtis su kampiniu koeficientu;

Tegu yra tiesi linija, o ne statmena ašiai OI. Paskambinkime pasvirimo kampas duota tiesi linija į ašį OI kampas α , į kurią reikia pasukti ašį OI kad teigiama kryptis sutaptų su viena iš tiesės krypčių. Tiesios linijos polinkio kampo liestinė su ašimi OI paskambino nuolydisši eilutė ir žymima raide KAM.

	K=tg α
		(1)

Išveskime šios tiesės lygtį, jei ją žinome KAM ir segmento vertę OB, kurią jis nupjauna ašyje OU.

(2)

y=kx+b

Pažymėkime pagal M"lėktuvo taškas (x; y). Jei pieštume tiesiai BN Ir N.M., lygiagrečiai ašims, tada r BNM – stačiakampio formos. T. MC C BM <=>, kai reikšmės N.M. Ir BN patenkinti sąlygą: . Bet NM=CM-CN=CM-OB=y-b, BN=x=> atsižvelgdami į (1), gauname, kad taškas M(x;y)Cšioje linijoje<=>, kai jo koordinatės tenkina lygtį: =>

(2) lygtis vadinama tiesės lygtis su kampiniu koeficientu. Jeigu K=0, tada tiesi linija yra lygiagreti ašiai OI o jo lygtis yra y = b.

• tiesės, einančios per du taškus, lygtis;

(4)

Tegul du taškai M 1 (x 1; y 1) Ir M2 (x 2; y 2). Paėmimas (3) taške M(x;y) už nugaros M 2 (x 2; y 2), mes gauname y 2 -y 1 =k(x 2 - x 1). Apibrėžimas k iš paskutinės lygybės ir pakeisdami ją į (3) lygtį, gauname norimą tiesės lygtį: . Tai lygtis, jei y 1 ≠ y 2, gali būti parašytas taip:

Jeigu y 1 = y 2, tada norimos linijos lygtis turi formą y = y 1. Šiuo atveju tiesi linija yra lygiagreti ašiai OI. Jeigu x 1 = x 2, tada tiesi linija, einanti per taškus M 1 Ir M 2, lygiagrečiai ašiai OU, jos lygtis turi formą x = x 1.

• tiesės, einančios per tam tikrą tašką tam tikru nuolydžiu, lygtis;

(3)

Аx + Вy + С = 0

Teorema. Stačiakampėje koordinačių sistemoje Oho bet kuri tiesi linija nurodoma pirmojo laipsnio lygtimi:

ir, atvirkščiai, (5) lygtis savavališkiems koeficientams A, B, C (A Ir B ≠ 0 vienu metu) apibrėžia tam tikrą tiesę stačiakampėje koordinačių sistemoje Oho.

Įrodymas.

Pirma, įrodykime pirmąjį teiginį. Jei linija nėra statmena Oi, tada jis nustatomas pagal pirmojo laipsnio lygtį: y = kx + b, t.y. (5) formos lygtis, kur

A = k, B = -1 Ir C = b. Jei linija statmena Oi, tada visi jo taškai turi tą pačią abscisę, lygią reikšmei α segmentas, nupjautas tiesia linija ašyje Oi.

Šios linijos lygtis turi formą x = α, tie. taip pat yra (5) formos pirmojo laipsnio lygtis, kur A = 1, B = 0, C = - α. Tai patvirtina pirmąjį teiginį.

Įrodykime priešingą teiginį. Tegu pateikta (5) lygtis ir bent vienas iš koeficientų A Ir B ≠ 0.

Jeigu B ≠ 0, tada (5) gali būti parašytas forma . Butas , gauname lygtį y = kx + b, t.y. (2) formos lygtis, apibrėžianti tiesę.

Jeigu B = 0, Tai A ≠ 0 ir (5) turi formą . Žymima pagal α, mes gauname

x = α, t.y. tiesės lygtis statmena Oh.

Vadinamos tiesės, apibrėžtos stačiakampėje koordinačių sistemoje pirmojo laipsnio lygtimi pirmosios eilės.

Formos lygtis Ax + Wu + C = 0 yra nepilnas, t.y. Kai kurie koeficientai yra lygūs nuliui.

1) C = 0; Ah + Wu = 0 ir apibrėžia tiesę, einančią per pradžią.

2) B = 0 (A ≠ 0); lygtis Ax + C = 0 OU.

3) A = 0 (B ≠ 0); Wu + C = 0 ir apibrėžia lygiagrečią tiesę Oi.

Lygtis (6) vadinama tiesės lygtimi „atkarpomis“. Skaičiai A Ir b yra atkarpų, kurias tiesi linija nukerta koordinačių ašyse, reikšmės. Ši lygties forma yra patogi geometrinė konstrukcija tiesiai.

• normalioji tiesės lygtis;

Аx + Вy + С = 0 yra bendroji tam tikros tiesės lygtis ir (5) x cos α + y sin α – p = 0(7)

jos normalioji lygtis.

Kadangi (5) ir (7) lygtys apibrėžia tą pačią tiesę, tada ( A 1x + B 1y + C 1 = 0 Ir

A 2x + B 2y + C 2 = 0 => ) šių lygčių koeficientai yra proporcingi. Tai reiškia, kad padauginę visus (5) lygties narius iš tam tikro koeficiento M, gauname lygtį MA x + MV y + MS = 0, sutampa su (7) lygtimi, t.y.

MA = cos α, MB = sin α, MC = - P(8)

Norėdami rasti koeficientą M, sugretiname pirmąsias dvi lygybes ir pridedame:

M 2 (A 2 + B 2) = cos 2 α + sin 2 α = 1

(9)

apibrėžia kreivę plokštumoje. Terminų grupė vadinama kvadratine forma, – linijinė forma. Jei kvadratinėje formoje yra tik kintamųjų kvadratai, tai ši forma vadinama kanonine, o ortonormalaus pagrindo, kuriame kvadratinė forma turi kanoninę formą, vektoriai vadinami pagrindinėmis kvadratinės formos ašimis.
Matrica vadinama kvadratinės formos matrica. Čia a 1 2 = a 2 1. Norint sumažinti matricą B iki įstrižainės formos, reikia paimti šios matricos savuosius vektorius, tada , kur λ 1 ir λ 2 yra matricos B savosios reikšmės.
Matricos B savųjų vektorių pagrindu kvadratinė forma turės kanoninę formą: λ 1 x 2 1 +λ 2 y 2 1 .
Ši operacija atitinka koordinačių ašių sukimąsi. Tada koordinačių kilmė perkeliama, taip atsikratant linijinės formos.
Antrosios eilės kreivės kanoninė forma: λ 1 x 2 2 +λ 2 y 2 2 =a ir:
a) jei λ 1 >0; λ 2 >0 yra elipsė, ypač kai λ 1 =λ 2 tai yra apskritimas;
b) jei λ 1 >0, λ 2<0 (λ 1 <0, λ 2 >0) turime hiperbolę;
c) jei λ 1 =0 arba λ 2 =0, tai kreivė yra parabolė ir pasukus koordinačių ašis turi formą λ 1 x 2 1 =ax 1 +by 1 +c (čia λ 2 =0). Papildydami pilną kvadratą, gauname: λ 1 x 2 2 =b 1 y 2.

Pavyzdys. Kreivės 3x 2 +10xy+3y 2 -2x-14y-13=0 lygtis pateikta koordinačių sistemoje (0,i,j), kur i =(1,0) ir j =(0,1) .
1. Nustatykite kreivės tipą.
2. Išveskite lygtį į kanoninę formą ir sukurkite kreivę pradinėje koordinačių sistemoje.
3. Raskite atitinkamas koordinačių transformacijas.

Sprendimas. Kvadratinę formą B=3x 2 +10xy+3y 2 perkeliame į pagrindines ašis, tai yra į kanoninę formą. Šios kvadratinės formos matrica yra . Mes randame šios matricos savąsias reikšmes ir savuosius vektorius:

Charakteristinė lygtis:
; λ 1 =-2, λ 2 =8. Kvadratinės formos tipas: .
Pradinė lygtis apibrėžia hiperbolę.
Atkreipkite dėmesį, kad kvadratinės formos forma yra dviprasmiška. Galima rašyti 8x 1 2 -2y 1 2 , bet kreivės tipas išlieka tas pats – hiperbolė.
Randame pagrindines kvadratinės formos ašis, tai yra, matricos B savuosius vektorius. .
Savasis vektorius, atitinkantis skaičių λ=-2, kai x 1 =1: x 1 =(1,-1).
Kaip vienetinį savąjį vektorių imame vektorių , kur yra vektoriaus ilgis x 1 .
Iš sistemos randamos antrojo savojo vektoriaus koordinatės, atitinkančios antrąją savąją reikšmę λ=8
.
1, j 1).
Pagal 4.3.3 punkto (5) formules. Pereikime prie naujo pagrindo:
arba

; . (*)

Išraiškas x ir y įvedame į pradinę lygtį ir po transformacijų gauname: .
Ištisų kvadratų pasirinkimas: .
Atliekame lygiagretų koordinačių ašių vertimą į naują pradžią: , .
Jei įvesime šiuos ryšius į (*) ir išspręstume šias lygybes x 2 ir y 2, gautume: , . Koordinačių sistemoje (0*, i 1, j 1) ši lygtis turi tokią formą: .
Kreivei sudaryti senoje koordinačių sistemoje sudarome naują: ašis x 2 =0 senojoje koordinačių sistemoje nurodoma lygtimi x-y-3=0, o ašis y 2 =0 – lygtimi x+ y-1 = 0. Naujos koordinačių sistemos 0 * (2,-1) pradžia yra šių tiesių susikirtimo taškas.
Norėdami supaprastinti suvokimą, grafiko sudarymo procesą padalinsime į 2 etapus:
1. Perėjimas į koordinačių sistemą, kurios ašys x 2 =0, y 2 =0, senojoje koordinačių sistemoje nurodytos atitinkamai lygtimis x-y-3=0 ir x+y-1=0.

2. Funkcijos grafiko sudarymas gautoje koordinačių sistemoje.

Galutinė grafiko versija atrodo taip (žr. Sprendimas: Atsisiųskite sprendimą

Pratimas. Nustatykite, kad kiekviena iš šių lygčių apibrėžia elipsę, ir suraskite jos centro C koordinates, pusašį, ekscentriškumą, krypties lygtis. Brėžinyje nupieškite elipsę, nurodydami simetrijos ašis, židinius ir kryptis.
Sprendimas.

§ 9. Tiesės lygties samprata.

Linijos apibrėžimas naudojant lygtį

F formos lygybė (x, y) = 0 vadinama lygtimi iš dviejų kintamųjų x, y, jei tai teisinga ne visoms skaičių poroms x, y. Jie sako du skaičius x = x 0 , y=y 0, tenkina kokią nors formos lygtį F(x, y) = 0, jei pakeičiant šiuos skaičius vietoj kintamųjų X Ir adresu lygtyje jos kairioji pusė išnyksta.

Tam tikros linijos lygtis (nurodytoje koordinačių sistemoje) yra lygtis su dviem kintamaisiais, kurią tenkina kiekvieno šioje tiesėje esančio taško koordinatės, o ne kiekvieno joje esančio taško koordinatės.

Toliau vietoj posakio „pateikta tiesės lygtis F(x, y) = 0" dažnai sakysime trumpai: duota eilutė F (x, y) = 0.

Jei pateiktos dviejų eilučių lygtys F(x, y) = 0 Ir Ф(x, y) = Q, tada bendras sistemos sprendimas

Pateikiami visi jų susikirtimo taškai. Tiksliau, kiekviena skaičių pora, kuri yra jungtinis šios sistemos sprendimas, nustato vieną iš susikirtimo taškų.

1)X 2 +y 2 = 8, x-y = 0;

2) X 2 +y 2 -16x+4adresu+18 = 0, x + y= 0;

3) X 2 +y 2 -2x+4adresu -3 = 0, X 2 + y 2 = 25;

4) X 2 +y 2 -8x+10у+40 = 0, X 2 + y 2 = 4.

163. Taškai pateikiami polinių koordinačių sistemoje

Nustatykite, kurie iš šių taškų yra tiesėje, apibrėžtoje lygtimi polinėmis koordinatėmis  = 2 cos , o kurios ne. Kurią tiesę lemia ši lygtis? (Nupieškite ant piešinio :)

164. Tiesėje, apibrėžtoje lygtimi  =
, Raskite taškus, kurių poliariniai kampai yra lygūs šiems skaičiams: a) ,b) - ,c) 0, d) . Kurią tiesę apibrėžia ši lygtis?

(Sukurkite jį ant piešinio.)

165. Tiesėje, apibrėžtoje lygtimi  =
, raskite taškus, kurių poliariniai spinduliai lygūs šiems skaičiams: a) 1, b) 2, c)
. Kurią tiesę apibrėžia ši lygtis? (Sukurkite jį ant piešinio.)

166. Nustatykite, kurios tiesės yra nustatytos polinėse koordinatėse šiomis lygtimis (sukonstruokite jas brėžinyje):

1)  = 5; 2)  = ; 3)  = ; 4)  cos  = 2; 5)  sin  = 1;

6)  = 6 cos ; 7)  = 10 sin ; 8) nuodėmė  =

Apsvarstykite funkciją, pateiktą pagal formulę (lygtį)

Ši funkcija, taigi ir (11) lygtis, atitinka tiksliai apibrėžtą tiesę plokštumoje, kuri yra šios funkcijos grafikas (žr. 20 pav.). Iš funkcijos grafiko apibrėžimo matyti, kad šią tiesę sudaro tie ir tik tie plokštumos taškai, kurių koordinatės tenkina (11) lygtį.

Leisk tai dabar

Tiesė, kuri yra šios funkcijos grafikas, susideda iš tų ir tik tų plokštumos taškų, kurių koordinatės tenkina (12) lygtį. Tai reiškia, kad jei taškas yra nurodytoje tiesėje, tada jo koordinatės atitinka (12) lygtį. Jei taškas nėra šioje tiesėje, tai jo koordinatės netenkina (12) lygties.

(12) lygtis išspręsta y atžvilgiu. Apsvarstykite lygtį, kurioje yra x ir y ir kuri nėra išspręsta y, pavyzdžiui, lygtis

Parodykime, kad ši lygtis plokštumoje taip pat atitinka tiesę, būtent apskritimą, kurio centras yra ištakoje, o spindulys lygus 2. Perrašykime lygtį į formą

Jo kairioji pusė yra taško atstumo nuo pradžios kvadratas (žr. § 2, 2 pastraipą, 3 formulę). Iš lygybės (14) išplaukia, kad šio atstumo kvadratas yra lygus 4.

Tai reiškia, kad bet kuris taškas, kurio koordinatės atitinka (14) lygtį, taigi ir (13) lygtį, yra 2 atstumu nuo pradžios.

Geometrinė tokių taškų vieta yra apskritimas, kurio centras yra pradžioje ir spindulys 2. Šis apskritimas bus tiesė, atitinkanti (13) lygtį. Bet kurio jo taško koordinatės akivaizdžiai atitinka (13) lygtį. Jei taškas yra ne ant apskritimo, kurį radome, tada jo atstumo nuo pradžios kvadratas bus arba didesnis, arba mažesnis už 4, o tai reiškia, kad tokio taško koordinatės netenkina (13) lygties.

Dabar bendruoju atveju duokime lygtį

kurio kairėje pusėje yra išraiška, kurioje yra x ir y.

Apibrėžimas. Tiesė, apibrėžta (15) lygtimi, yra geometrinis taškų lokusas plokštumoje, kurių koordinatės tenkina šią lygtį.

Tai reiškia, kad jei tiesė L yra nustatyta lygtimi, tai bet kurio taško L koordinatės tenkina šią lygtį, tačiau bet kurio plokštumos taško, esančio už L ribų, koordinatės netenkina (15) lygties.

Lygtis (15) vadinama tiesine lygtimi

komentuoti. Nereikėtų manyti, kad bet kokia lygtis lemia kokią nors tiesę. Pavyzdžiui, lygtis neapibrėžia jokios linijos. Tiesą sakant, bet kurioms tikrosioms ir y reikšmėms kairioji šios lygties pusė yra teigiama, o dešinioji lygi nuliui, todėl šios lygties negalima patenkinti bet kurio plokštumos taško koordinatėmis.

Tiesę plokštumoje galima apibrėžti ne tik lygtimi, turinčia Dekarto koordinates, bet ir lygtimi poliarinėse koordinates. Tiesė, apibrėžta lygtimi polinėmis koordinatėmis, yra geometrinis taškų lokusas plokštumoje, kurių polinės koordinatės tenkina šią lygtį.

1 pavyzdys. Sukurkite Archimedo spiralę ties .

Sprendimas. Padarykime lentelę su kai kuriomis polinio kampo reikšmėmis ir atitinkamomis polinio spindulio reikšmėmis.

Poliarinėje koordinačių sistemoje sukonstruojame tašką, kuris akivaizdžiai sutampa su ašigaliu; tada, nubrėždami ašį kampu į poliarinę ašį, šioje ašyje sukonstruojame tašką su teigiama koordinate, po kurio panašiai statome taškus su teigiamomis polinio kampo ir poliarinio spindulio reikšmėmis (šių taškų ašys yra nenurodyta 30 pav.).

Sujungę taškus, gauname vieną kreivės atšaką, parodytą fig. 30 su paryškinta linija. Keičiant nuo 0 iki šios kreivės atšaka susideda iš begalinio skaičiaus posūkių.