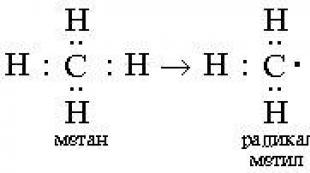វិធីសាស្រ្តអភិវឌ្ឍន៍

មុខងារ Möbius ។ រូបមន្តបញ្ច្រាសMöbius បន្ទះ Mobius - ការរកឃើញដ៏អស្ចារ្យ "វេទមន្ត" នៃបន្ទះ Mobius

គ្រឹះស្ថានអប់រំថវិកាក្រុង អនុវិទ្យាល័យ ដែលមានការសិក្សាស៊ីជម្រៅលើបុគ្គល

ធាតុជាមួយ។ Terbuny

បន្ទះ Mobius

បញ្ចប់ដោយ: Chepurina Anna Vitalievna,

សិស្សថ្នាក់ទី 10

ក្បាល៖ Kirikova M.A.

គ្រូគណិតវិទ្យាទីមួយ

ប្រភេទគុណវុឌ្ឍិ

ភូមិ Terbuny

ឆ្នាំ 2015

សេចក្តីផ្តើម…………………………………………………………………..................៣

ប្រវត្តិ …………………………………………………… ៤

បន្ទះ Möbius - ការចាប់ផ្តើមនៃវិទ្យាសាស្រ្តថ្មីនៃ topology ..................................... 5

ការបង្កើតបន្ទះ Mobius ………………………………… ៦

ការពិសោធន៍ជាមួយបន្ទះ Mobius ........................................... ………………….៩

លក្ខណៈសម្បត្តិ Topological នៃបន្ទះMöbius ……………………..11

ទ្រឹស្តីបទនៅលើបន្ទះMöbius……………………………………….១២

ល្បិចជាមួយបន្ទះ Mobius …………………………………………………… ១៥

ការអនុវត្តបន្ទះMöbius……………………………………..១៦

សេចក្តីសន្និដ្ឋាន ................................................... ........................................២៣

បញ្ជីអក្សរសិល្ប៍ដែលបានប្រើ........................................... ............ .២៥

ការដាក់ពាក្យ

សេចក្តីផ្តើម

សព្វថ្ងៃនេះវាមានសារៈសំខាន់ណាស់ក្នុងការសិក្សាអំពីលក្ខណៈសម្បត្តិផ្សេងៗនិងការអនុវត្តមិនស្តង់ដារនៃតួលេខមិនធម្មតា។

តើអ្នកធ្លាប់លឺពីបន្ទះMöbiusទេ? តើវាត្រូវបានបង្កើតឡើងដោយរបៀបណា ដែលវាទាក់ទងនឹងគណិតវិទ្យា និងកន្លែងដែលវាត្រូវបានគេប្រើក្នុងជីវិត។

ខណៈពេលដែលកំពុងធ្វើការងារនេះ ខ្ញុំបានសន្និដ្ឋានថា ទោះបីជាបន្ទះMöbiusត្រូវបានរកឃើញត្រឡប់មកវិញនៅក្នុងសតវត្សទី 19 ក៏ដោយក៏វាពាក់ព័ន្ធទាំងនៅក្នុងសតវត្សទី 20 និង 20 ។ លក្ខណៈសម្បត្តិដ៏អស្ចារ្យនៃបន្ទះMöbiusត្រូវបាន និងប្រើប្រាស់ក្នុងការចម្អិនអាហារ បច្ចេកវិទ្យា រូបវិទ្យា គំនូរ ស្ថាបត្យកម្ម និងក្នុងការរចនាគ្រឿងអលង្ការ និងគ្រឿងអលង្ការសំលៀកបំពាក់។ គាត់បានបំផុសគំនិតច្នៃប្រឌិតរបស់អ្នកនិពន្ធ និងសិល្បករជាច្រើន។

ចំណាប់អារម្មណ៍លើបន្ទះMöbiusមិនទាន់រលត់រហូតមកដល់សព្វថ្ងៃនេះទេ។ នៅទីក្រុងមូស្គូ ក្នុងខែកញ្ញា ឆ្នាំ២០០៦ មហោស្រពគណិតវិទ្យាសិល្បៈបានប្រព្រឹត្តទៅ។ សុន្ទរកថារបស់សាស្រ្តាចារ្យមកពីទីក្រុងតូក្យូត្រូវបានទទួលដោយជោគជ័យដ៏អស្ចារ្យ។

ខ្ញុំចាប់អារម្មណ៍ និងចាប់អារម្មណ៍យ៉ាងខ្លាំងចំពោះប្រធានបទនេះ។ ខ្ញុំបានសិក្សាអក្សរសិល្ប៍ បន្ទាប់មកបង្កើតបន្ទះ Mobius ដោយខ្លួនឯង ហើយបន្ទាប់មកធ្វើការស្រាវជ្រាវ ធ្វើការពិសោធន៍ សិក្សាពីលក្ខណៈសម្បត្តិវេទមន្ត និងអស្ចារ្យរបស់វា។

បន្ទះ Möbius គឺជាបន្ទះក្រដាសដែលមានចុងម្ខាងបត់ពាក់កណ្តាលវេន (ឧទាហរណ៍ 180 ដឺក្រេ) ហើយស្អិតជាប់នឹងចុងម្ខាងទៀត។ មនុស្សរាប់លាននាក់នៅគ្រប់ផ្នែកទាំងអស់នៃពិភពលោកមិនទាំងដឹងថាពួកគេប្រើបន្ទះMöbiusជារៀងរាល់ថ្ងៃ។

គោលដៅ ៖ ប្រាប់ និងបង្ហាញមិត្តរួមថ្នាក់របស់អ្នកថា ខ្សែបូដែលមើលទៅហាក់ដូចជាសាមញ្ញ ប្រែទៅជា

ពាក់កណ្តាលវេនជាមួយនឹងការបញ្ចប់ស្អិតជាប់, អាចមានច្រើន។

ការភ្ញាក់ផ្អើល។

កម្មវត្ថុនៃការសិក្សា៖ បន្ទះ Möbius ។

ភារកិច្ច: កំណត់ប្រភព និងអក្សរសិល្ប៍លើប្រធានបទនេះ ហើយវិភាគពួកវា។

ស្គាល់ប្រវត្តិនៃបន្ទះ Mobius;

រៀនពីរបៀបធ្វើបន្ទះ Mobius;

សិក្សាលក្ខណៈសម្បត្តិផ្សេងៗនៃបន្ទះMöbius;

នៅពេលធ្វើការលើប្រធានបទ ខ្ញុំបានប្រើចំណុចខាងក្រោម វិធីសាស្រ្ត: ការវិភាគ, សំយោគ,

ការសង្កេត ការពិសោធន៍ ការប្រៀបធៀប និងការស្ទង់មតិសង្គមវិទ្យា។

ជំពូក ខ្ញុំ

"បន្ទះ Möbius - ការចាប់ផ្តើមនៃវិទ្យាសាស្រ្តថ្មី"

1. 1. ប្រវត្តិប្រវត្តិសាស្ត្រ

បន្ទះ Möbius ដ៏អាថ៌កំបាំង និងល្បីល្បាញត្រូវបានបង្កើតនៅឆ្នាំ 1858 ដោយម៉ាស៊ីនវាស់ធរណីមាត្រអាល្លឺម៉ង់សីហា Ferdinand Mobius . ពួកគេនិយាយថា Mobius ត្រូវបានជួយឱ្យបើក "ស្លឹក" របស់គាត់ដោយអ្នកបំរើម្នាក់ដែលបានដេរចុងបញ្ចប់នៃខ្សែបូវែងមិនត្រឹមត្រូវ។ គាត់បានរង់ចាំប្រាំពីរឆ្នាំសម្រាប់ការងាររបស់គាត់ត្រូវបានពិនិត្យឡើងវិញ ហើយដោយមិនរង់ចាំ គាត់បានបោះពុម្ពលទ្ធផលរបស់វា។

ក្នុងពេលជាមួយគ្នាជាមួយ Möbius សិស្សម្នាក់ទៀតរបស់ K. F. Gauss បានបង្កើតស្លឹកនេះ -ការចុះបញ្ជី Johann Benedict, សាស្រ្តាចារ្យនៅសាកលវិទ្យាល័យ Göttingen ។ គាត់បានបោះពុម្ពការងាររបស់គាត់បីឆ្នាំជាង Mobius ក្នុងឆ្នាំ 1862 ។ A. F. Mobius កើតនៅទីក្រុង Schulpforte ។ សម្រាប់ពេលខ្លះ ក្រោមការដឹកនាំរបស់ K. Gauss គាត់បានសិក្សាផ្នែកតារាសាស្ត្រ។ គាត់បានចាប់ផ្តើមធ្វើការសង្កេតតារាសាស្ត្រឯករាជ្យនៅឯ Pleisenburg Observatory ក្នុងឆ្នាំ 1818 ។ បានក្លាយជានាយករបស់ខ្លួន។ នៅសម័យនោះ គណិតវិទ្យាមិនត្រូវបានគាំទ្រទេ ហើយតារាសាស្ត្របានផ្តល់ប្រាក់គ្រប់គ្រាន់មិនឱ្យគិតអំពីពួកគេ ហើយទុកពេលសម្រាប់គំនិតផ្ទាល់ខ្លួន។ ក្លាយជាសាស្រ្តាចារ្យនៅសាកលវិទ្យាល័យ Leipzig ក្នុងឆ្នាំ 1816 លោក Möbius បានណែនាំជាលើកដំបូងនូវធរណីមាត្រទស្សន៍ទាយ ប្រព័ន្ធកូអរដោនេ និងវិធីសាស្រ្តវិភាគនៃការស្រាវជ្រាវ។ បានបង្កើតអត្ថិភាពនៃផ្ទៃម្ខាង (បន្ទះMöbius) polyhedra ដែល "ច្បាប់នៃគែម" មិនត្រូវបានអនុវត្ត និងដែលមិនមានបរិមាណ។ Möbius គឺជាស្ថាបនិកម្នាក់នៃទ្រឹស្ដីនៃការបំប្លែងធរណីមាត្រ ក៏ដូចជាទ្រឹស្តីបទ។ គាត់ទទួលបានលទ្ធផលសំខាន់ៗនៅក្នុងទ្រឹស្តីលេខ (មុខងារ Möbius) ហើយបានក្លាយជាធរណីមាត្រឈានមុខគេនៃពេលវេលារបស់គាត់។

១.២. បន្ទះ Möbius - ការចាប់ផ្តើមនៃវិទ្យាសាស្រ្តថ្មីនៃ topology

ចាប់ពីពេលដែលគណិតវិទូជនជាតិអាឡឺម៉ង់ A. F. Möbius បានរកឃើញអត្ថិភាពនៃសន្លឹកក្រដាសមួយចំហៀងដ៏អស្ចារ្យ សាខាថ្មីទាំងមូលនៃគណិតវិទ្យាបានចាប់ផ្តើមអភិវឌ្ឍ ដែលហៅថា topology ។ ពាក្យ "topology" អាចត្រូវបានកំណត់គុណលក្ខណៈពីរផ្នែកនៃគណិតវិទ្យា។ តូប៉ូឡូញមួយ ដែលជាស្ថាបនិកនៃនោះគឺ Poincaré ត្រូវបានគេហៅថា combinatorial អស់រយៈពេលជាយូរមកហើយ។ អ្នកផ្សេងទៀតដែលមានដើមកំណើតជាអ្នកវិទ្យាសាស្ត្រអាឡឺម៉ង់ Georg Cantor ត្រូវបានគេដាក់ឈ្មោះទូទៅឬទ្រឹស្តីកំណត់។

Combinatorial topology គឺជាសាខានៃធរណីមាត្រ។ "ធរណីមាត្រ" គឺជាពាក្យក្រិកដែលបកប្រែជាភាសារុស្សីមានន័យថា "ការវាស់វែងដី" ("ភូមិសាស្ត្រ" មានន័យថាផែនដីនៅក្នុងភាសាក្រិចនិង "ម៉ែត្រ" មានន័យថាវាស់) សិក្សាលក្ខណៈសម្បត្តិនៃតួលេខ។ ដូចវិទ្យាសាស្ត្រណាមួយដែរធរណីមាត្រត្រូវបានបែងចែកទៅជាផ្នែក។

1. Planimetry (ពាក្យឡាតាំង "planum" - ផ្ទៃ + ធរណីមាត្រ) ផ្នែកនៃធរណីមាត្រដែលសិក្សាពីលក្ខណៈសម្បត្តិនៃតួលេខនៅលើយន្តហោះ (ត្រីកោណ ការ៉េ រង្វង់ រង្វង់។ល។)

2. ស្តេរ៉េអូមេទ្រី (ភាសាក្រិច "ស្តេរ៉េអូ" - លំហ + ធរណីមាត្រ) - ផ្នែកនៃធរណីមាត្រដែលសិក្សាពីលក្ខណៈសម្បត្តិនៃតួលេខក្នុងលំហ (ស្វ៊ែរ គូប ប៉ារ៉ាឡែលភីប។ល។)

H. Topology (ភាសាក្រិច "topos" - កន្លែង, ដី + តក្កវិជ្ជា) គឺជាផ្នែក "ក្មេងបំផុត" នៃធរណីមាត្រទំនើប ដែលសិក្សាពីលក្ខណៈសម្បត្តិនៃតួលេខបែបនេះ ដែលមិនផ្លាស់ប្តូរ ប្រសិនបើពួកវាពត់ លាតសន្ធឹង បង្រួម ប៉ុន្តែមិនស្អិតជាប់។ ហើយកុំហែក ពោលគឺកុំប្តូរពេលខូច។ ឧទាហរណ៏នៃវត្ថុ topological គឺ: អក្សរ I និង H, ប៉េងប៉ោងវែងស្តើង។

Combinatorial topology សិក្សាពីលក្ខណៈសម្បត្តិនៃតួលេខធរណីមាត្រដែលនៅតែមិនផ្លាស់ប្តូរក្រោមការគូសផែនទីពីមួយទៅមួយ និងបន្ត។ អស់រយៈពេលជាយូរមកហើយ topology ត្រូវបានគេយល់ថាជាវិទ្យាសាស្ត្រដែលនៅឆ្ងាយពីជីវិតដែលមានគោលបំណងត្រឹមតែ "លើកតម្កើងចិត្តមនុស្ស" ។ ប៉ុន្តែនៅក្នុងសម័យរបស់យើង វាបានក្លាយទៅជាច្បាស់ថាវាទាក់ទងដោយផ្ទាល់ទៅនឹងការពន្យល់អំពីរចនាសម្ព័ន្ធនៃសកលលោក។

ទ្រឹស្ដីទូទៅគឺនៅជាប់នឹងទ្រឹស្តីកំណត់ ហើយស្ថិតនៅមូលដ្ឋាននៃគណិតវិទ្យា។ នេះគឺជាទ្រឹស្តី axiomatic ដែលត្រូវបានរចនាឡើងដើម្បីស្វែងយល់ពីគោលគំនិតដូចជា "ដែនកំណត់" "ការបញ្ចូលគ្នា" "ការបន្ត" ជាដើម។ មូលដ្ឋានគ្រឹះនៃ axiomatics នៃលំហ topological ត្រូវបានដាក់ដោយ Felix Hausdorff និងបញ្ចប់ដោយគណិតវិទូជនជាតិរុស្សី Pavel Sergeevich Alexandrov ។

១.៣. របៀបធ្វើបន្ទះMöbius

● បន្ទះ Möbius គឺជាផ្នែកមួយនៃ (ការភ្ញាក់ផ្អើលគណិតវិទ្យា) ដើម្បីធ្វើបន្ទះMöbius យកបន្ទះចតុកោណ ABស៊ីឌីបង្វិលវា 180 ដឺក្រេហើយកាវបិទភាគីទល់មុខ AB និងស៊ីឌី, i.e. ដូច្នេះពិន្ទុ A ហើយនឹងស្របគ្នា។គនិងចំណុច ឃនិង V.

សូមមើល adj ។ ដប់មួយ

● រូបរាងនិងទំហំនៃបន្ទះក្រដាស សម្រាប់បន្ទះMöbius។

បន្ទះគួរតែតូចចង្អៀត និងវែង ដែលមានប្រវែងធំបំផុតដែលអាចធ្វើទៅបានទៅសមាមាត្រទទឹង។ អ្នកមិនអាចធ្វើបន្ទះMöbiusពីសន្លឹកក្រដាសការ៉េបានទេ។ នេះជាការពិត ប៉ុន្តែវាមិនគួរត្រូវបានប៉ាន់ស្មានថាការរឹតបន្តឹងទំហំមានសារៈសំខាន់នៅពេលដែលក្រដាសមិនត្រូវបានអនុញ្ញាតឱ្យជ្រួញ។ ប្រសិនបើការគៀបក្រដាសមិនត្រូវបានហាមឃាត់ទេនោះ បន្ទះMöbiusអាចត្រូវបានស្អិតជាប់មិនត្រឹមតែពីការ៉េប៉ុណ្ណោះទេប៉ុន្តែពីចតុកោណនៃទំហំណាមួយ - ផ្នែកដែលស្អិតជាប់អាចមានប្រវែងវែងជាងបន្ទះដែលមិនស្អិតជាប់។

●ផ្ទៃអភិវឌ្ឍន៍.

ដោយសារតម្រូវការមិនជ្រីវជ្រួញលើក្រដាសគឺសំខាន់ សូមមើលអត្ថន័យគណិតវិទ្យារបស់វា?

វាងាយស្រួលយល់ថា ការហាមប្រាមប្រឆាំងនឹងក្រដាស់គ្រេចមានកម្រិតយ៉ាងសំខាន់

សមត្ថភាពក្នុងការរៀបចំសន្លឹកក្រដាស។ ជាឧទាហរណ៍ ក្រដាសមួយសន្លឹកអាចរមៀលចូលទៅក្នុងបំពង់ ឬបត់ជាពាក់កណ្តាលដោយមិនបត់ ប៉ុន្តែមិនអាចបត់ជាបួនបានទេ។ អ្នកអាចធ្វើកោណពីសន្លឹកក្រដាសដោយមិនធ្វើឱ្យខូចវា ប៉ុន្តែអ្នកមិនអាចបង្កើតរាងជារង្វង់ ឬសូម្បីតែបំណែករបស់វាបានទេ៖ ចុចសន្លឹកក្រដាសទល់នឹងផែនដី ហើយផ្នត់នឹងច្បាស់ជាលេចឡើង។ ដូចដែលអ្នកអាចឃើញ សន្លឹកក្រដាសមួយមិនអាចមានរូបរាងណាមួយឡើយ។ សូមមើល adj ។ ២.

ផ្ទៃដែលអាចធ្វើពីក្រដាស់មួយសន្លឹកដោយពត់វាដោយមិនបុក ត្រូវបានគេហៅថាផ្ទៃដែលអាចអភិវឌ្ឍបានដោយគណិតវិទូ។ នៅក្នុងគណិតវិទ្យា ផ្ទៃដែលអាចអភិវឌ្ឍបានត្រូវបានកំណត់ខុសគ្នា៖ នៅក្នុងភាសា metamathematical មិនមានពាក្យ "paper", "crumple", "make" ទេ។ មានទ្រឹស្ដីទាំងមូលនៃផ្ទៃដែលអាចអភិវឌ្ឍបាន ក្នុងចំណោមសមិទ្ធិផលដែលជាចម្លើយដែលពេញចិត្តចំពោះសំណួរនៃអ្វីដែលពួកគេអាចជា; គណិតវិទូហៅការចាត់ថ្នាក់នេះថា "ការចាត់ថ្នាក់" (ចម្លើយជារបស់ Leonardo Euler)។ អនុញ្ញាតឱ្យយើងបង្ហាញតែលក្ខណៈសម្បត្តិមួយចំនួននៃផ្ទៃដែលអាចអភិវឌ្ឍបានដែលជាការពិតពិសោធន៍។

សូមមើល adj ។ ៣

1. តាមរយៈចំនុច A នីមួយៗនៃផ្ទៃដែលអាចអភិវឌ្ឍបាន ដែលមិនស្ថិតនៅលើព្រំប្រទល់របស់វា មានផ្នែកមួយដែលស្ថិតនៅលើផ្ទៃដែលមិនបញ្ចប់ត្រឹម A. ម្យ៉ាងវិញទៀត ទៅកាន់ចំនុចនីមួយៗលើផ្ទៃដែលអាចអភិវឌ្ឍបាន (កោង ប៉ុន្តែមិនកំទេច សន្លឹកក្រដាស) ម្ជុលប៉ាក់អាចត្រូវបានភ្ជាប់ដូច្នេះវានៅជាប់នឹងផ្ទៃសម្រាប់វិសាលភាពមួយចំនួននៅលើផ្នែកទាំងពីរនៃចំណុចដែលបានយក។ ផ្នែកបែបនេះត្រូវបានគេហៅថា generatrix នៃផ្ទៃ (អនុញ្ញាតឱ្យយើងយល់ស្របថាឈ្មោះនេះអនុវត្តតែចំពោះផ្នែកនៃប្រវែងអតិបរមាដែលស្ថិតនៅលើផ្ទៃទាំងស្រុង ពោលគឺចំពោះផ្នែកដែលមិនមាននៅក្នុងផ្នែកធំជាមួយនឹងទ្រព្យសម្បត្តិនេះ)។

2. ប្រសិនបើម៉ាស៊ីនភ្លើងពីរផ្សេងគ្នាឆ្លងកាត់ចំណុច A ដែលមិនស្ថិតនៅលើព្រំប្រទល់នៃផ្ទៃមួយ ហើយ A មិនមែនជាចុងបញ្ចប់នៃពួកវាទាំងពីរទេ នោះដុំតូចមួយគ្រប់គ្រាន់នៃផ្ទៃជុំវិញ A គឺរាបស្មើ។ ក្នុងករណីនេះយើងនឹងហៅចំណុច A ផ្ទះល្វែង។

3. ប្រសិនបើចំនុច A ដែលមិនស្ថិតនៅលើព្រំប្រទល់នៃផ្ទៃ គឺជាចុងបញ្ចប់នៃម៉ាស៊ីនភ្លើងមួយចំនួន និយាយថាក បន្ទាប់មកសង្កាត់នៃចំណុច A ត្រូវបានរៀបចំដូចនេះ៖ តាមរយៈចំណុច A មាន generatrix តែមួយគត់ដែលមិនបញ្ចប់នៅទីនោះ។ខ . generatrix នេះបែងចែកផ្ទៃជាពីរផ្នែក។ នៅផ្នែកម្ខាងទៀតនៃ generatrixខ ដែល generatrix មានទីតាំងនៅក ទៅកាន់ម៉ាស៊ីនភ្លើង ខ បំណែកផ្ទះល្វែងមួយនៅជាប់គ្នានៅម្ខាងទៀត។ខ តាមអំពើចិត្តពីចំណុច A មានចំណុចមិនរាបស្មើ។ ក្នុងស្ថានភាពនេះ យើងនឹងហៅចំណុច A ពាក់កណ្តាលផ្ទះល្វែង។

យើងសង្កត់ធ្ងន់ថា ប្រសិនបើចំនុចមួយនៅលើផ្ទៃមួយមិនមានព្រំដែន ឬរាបស្មើទេ នោះមាន generatrix តែមួយឆ្លងកាត់វា ហើយចុងបញ្ចប់នៃ generatrix នេះស្ថិតនៅលើព្រំដែននៃផ្ទៃ។

●ឧទាហរណ៍៖ ក្រដាសមួយសន្លឹកដែលរមៀលចូលទៅក្នុងស៊ីឡាំង ឬកោណ មិនមានចំណុចសំប៉ែត (ឬពាក់កណ្តាលផ្ទះល្វែង) ទេ។ សម្រាប់ស៊ីឡាំងមួយ ម៉ាស៊ីនបង្កើតបង្កើតជាក្រុមគ្រួសារនៃផ្នែកប៉ារ៉ាឡែលមួយ សម្រាប់កោណ ពួកគេបង្កើតជាក្រុមនៃចម្រៀកដែលចេញមកពីចំណុចមួយ។ ការរៀបចំស្មុគស្មាញបន្ថែមទៀតនៃ generatrices គឺអាចធ្វើទៅបាន។

សូមមើល adj ។ ៤.

ឧទាហរណ៍ ម៉ាស៊ីនភ្លើង និងចំណុចសំប៉ែតនៃផ្ទៃដែលកំពុងអភិវឌ្ឍន៍ត្រូវបានបង្ហាញក្នុងរូប (ដែលផ្ទៃត្រូវបានលាតចូលទៅក្នុងក្រដាសរាបស្មើ): បន្ទាត់ស្តើងគឺជាម៉ាស៊ីនភ្លើង ហើយតំបន់ដែលមានស្រមោលមានចំណុចរាបស្មើ។

ចំនុចដែលស្ថិតនៅលើព្រំប្រទល់នៃតំបន់នៃចំនុចផ្ទះល្វែង គឺជាចំណុចព្រំដែនសម្រាប់ផ្ទៃទាំងមូល ឬពាក់កណ្តាលផ្ទះល្វែង។ ប្រសិនបើផ្ទៃមួយត្រូវបានធ្វើពីពហុកោណក្រដាស (និយាយ ចតុកោណកែង) នោះចំនុចនៃប្លង់បង្កើតជាពហុកោណប្លង់មួយ ឬច្រើន ពហុកោណទាំងនេះនីមួយៗមានចំនុចកំពូលស្ថិតនៅលើព្រំប្រទល់នៃផ្ទៃ និងភាគីទាំងសងខាងនៅលើព្រំដែន ឬមាន នៃចំណុចពាក់កណ្តាលប្លង់។

ជំពូក 2

២.១. ការពិសោធន៍ជាមួយបន្ទះ Mobius

យើងម្នាក់ៗមានគំនិតវិចារណញាណនៃអ្វីដែលជា "ផ្ទៃ" ។ ផ្ទៃនៃសន្លឹកក្រដាស ផ្ទៃជញ្ជាំងនៃថ្នាក់រៀន ផ្ទៃនៃពិភពលោកត្រូវបានគេស្គាល់គ្រប់គ្នា។ តើអាចមានអ្វីអាថ៌កំបាំងក្នុងគំនិតធម្មតាបែបនេះទេ? បាទ ប្រហែលជាឧទាហរណ៍មួយគឺបន្ទះMöbius។ ដើម្បីសិក្សាពីលក្ខណៈសម្បត្តិរបស់វា ខ្ញុំបានធ្វើការពិសោធន៍ជាច្រើន (បែងចែកវាជាពីរក្រុម) ដោយខ្លួនឯង។

ខ្ញុំ ក្រុមនៃការពិសោធន៍

ការពិសោធន៍លេខ 1. យើងត្រូវបានគេទម្លាប់ធ្វើការកត់សំគាល់លើការពិតដែលថានៅផ្ទៃណាមួយពីណា

យើងកំពុងដោះស្រាយ (សន្លឹកក្រដាស កង់ ឬបំពង់បាល់ទះ) -

ភាគីទាំងពីរ។

ខ្ញុំចាប់ផ្ដើមគូរបន្ទះ Mobius ដោយមិនបានបង្វែរវាចេញទេ។

លទ្ធផល . បន្ទះ Möbius ត្រូវបានលាបពណ៌ទាំងស្រុង។

«បើអ្នកណាសម្រេចចិត្តពណ៌តែម្ខាង

ផ្ទៃនៃបន្ទះMöbius អនុញ្ញាតឱ្យគាត់ជ្រមុជវាភ្លាមៗនៅក្នុងធុងថ្នាំលាប" - សរសេរ Richard Courant និង Herbert Robins យ៉ាងល្អឥតខ្ចោះ

សៀវភៅ "តើគណិតវិទ្យាជាអ្វី?"

បទពិសោធន៍លេខ 2 ។ ខ្ញុំបានបង្កើតសត្វពីងពាង និងរុយចេញពីក្រដាស ហើយបានផ្ញើវា “សម្រាប់ដើរ” ជុំវិញ

ចិញ្ចៀនធម្មតា ប៉ុន្តែហាមមិនឱ្យពួកគេឆ្លងព្រំដែន។

លទ្ធផល។ សត្វពីងពាងមិនអាចហោះហើរបានទេ។

ការពិសោធន៍លេខ 3. ខ្ញុំបានបញ្ជូនសត្វពីងពាងទាំងនេះ ហើយហោះហើរតែតាមបន្ទះ Mobius ប៉ុណ្ណោះ។ និង

ហាមមិនឲ្យវារឆ្លងព្រំដែន។

លទ្ធផល។សត្វរុយដ៏កំសត់នឹងត្រូវស៊ីប្រសិនបើសត្វពីងពាងកំពុងរត់

លឿនជាងមុន!

បទពិសោធន៍លេខ 4 ។ ខ្ញុំបានបង្កើតបុរសតូចម្នាក់ចេញពីក្រដាស ហើយបញ្ជូនគាត់ឱ្យធ្វើដំណើរតាមបន្ទះ Mobius ។

លទ្ធផល។ បុរសតូចនឹងត្រលប់ទៅចំណុចនៃការចាកចេញ ដែលជាកន្លែងដែលគាត់នឹងជួបរូបភាពកញ្ចក់របស់គាត់។

IIក្រុមពិសោធន៍

ទាក់ទងនឹងការកាត់បន្ទះMöbius លទ្ធផលត្រូវបានរាយក្នុងតារាង

បទពិសោធន៍

ការពិពណ៌នាអំពីបទពិសោធន៍

លទ្ធផល

ខ្ញុំកាត់ចិញ្ចៀនសាមញ្ញមួយតាមបណ្តោយចុះកណ្តាល។

ខ្ញុំបានចិញ្ចៀនធម្មតាពីរដែលមានប្រវែងដូចគ្នា ទទឹងពីរដងដែលមានស៊ុមពីរ។

បន្ទះMöbiusត្រូវបានកាត់តាមប្រវែងនៅកណ្តាល។

ខ្ញុំបានទទួលចិញ្ចៀន១វង់ ដែលប្រវែងវែងជាង២ដង ទទឹងតូចជាង២ដង បត់១ជុំពេញមួយវង់ ។

ទទឹងបន្ទះMöbius

កាត់ប្រវែង 5 សង់ទីម៉ែត្រនៅចម្ងាយ 1 សង់ទីម៉ែត្រពីគែម។

ខ្ញុំបានទទួលចិញ្ចៀនពីរដែលភ្ជាប់គ្នាទៅវិញទៅមក៖ 1) បន្ទះ Mobius - ប្រវែង = ប្រវែងនៃដើមមួយទទឹង 3 សង់ទីម៉ែត្រ; 2) ទទឹង 1cm, ប្រវែងពីរដងនៃដើម, twisted ពីរវេនពេញលេញ, ជាមួយនឹងព្រំដែនពីរ។

ទទឹងបន្ទះMöbius

កាត់ប្រវែង 5 សង់ទីម៉ែត្រនៅចម្ងាយ 2 សង់ទីម៉ែត្រពីគែម។

ខ្ញុំបានទទួលចិញ្ចៀនពីរដែលភ្ជាប់គ្នាទៅវិញទៅមក៖ 1) ចិញ្ចៀនគឺជាបន្ទះMöbius ទទឹង 1 សង់ទីម៉ែត្រប្រវែង = ប្រវែងនៃដើមមួយ; 2) ចិញ្ចៀន - ទទឹង 2 សង់ទីម៉ែត្រ, ពីរដងវែងដូចដើមមួយ, បង្វិលដោយពីរវេនពេញលេញ, ជាមួយនឹងព្រំដែនពីរ។

បន្ទះMöbius ទទឹង 5cm កាត់ប្រវែងនៅចម្ងាយ 3cm ពីគែម។

ខ្ញុំទទួលបានចិញ្ចៀនពីរដែលភ្ជាប់គ្នាទៅវិញទៅមក៖ 1) ចិញ្ចៀនគឺជាបន្ទះMöbiusដែលមានទទឹង

1 សង់ទីម៉ែត្រនៃប្រវែងដូចគ្នា; 2) ចិញ្ចៀន - ទទឹង 2 សង់ទីម៉ែត្រ, ប្រវែងរបស់វាគឺពីរដងនៃដើម, បង្វិលពីរដងពេញ។

លទ្ធផលនៃការស្ទង់មតិសង្គមវិទ្យាជាមួយសិស្សថ្នាក់ទី 10 ។

សំណួរ

បាទ

ទេ

តើអ្នកបានលឺទេ?

1. តើអ្នកដឹងថាអ្វីជា topology ទេ?

2. តើអ្នកដឹងថាបន្ទះ Mobius ជាអ្វីទេ?

3. តើអ្នកដឹងទេ? លក្ខណៈសម្បត្តិនៃបន្ទះ Mobius?

មានតែ 5% នៃសិស្សថ្នាក់ទី 10 ដែលដឹងថាអ្វីជា topology ។ 30% នៃសិស្សដឹងថាបន្ទះ Mobius គឺជាអ្វី។ 20% បានឮអំពីវា។ 50% មិនមានគំនិតអំពីបន្ទះ Mobius ទេ។ 25% នៃសិស្សដឹងពីលក្ខណៈសម្បត្តិរបស់បន្ទះនេះ 10% បានឮអំពីពួកគេ 65% មិនដឹងអ្វីទាំងអស់អំពីលក្ខណៈសម្បត្តិរបស់បន្ទះMöbius។

2.2.Topological properties នៃបន្ទះMöbius

ដោយផ្អែកលើលទ្ធផលនៃការពិសោធន៍ យើងអាចបង្កើតលក្ខណៈសម្បត្តិ topological ខាងក្រោមនៃបន្ទះMöbius ដែលទាក់ទងទៅនឹងការភ្ញាក់ផ្អើលគណិតវិទ្យា។

ភាពម្ខាងគឺជាទ្រព្យសម្បត្តិ topological នៃបន្ទះMöbius លក្ខណៈរបស់វាតែប៉ុណ្ណោះ។

ការបន្ត - នៅលើបន្ទះMöbiusចំណុចណាមួយអាចត្រូវបានតភ្ជាប់

ជាមួយនឹងចំណុចផ្សេងទៀត។ មិនមានការសម្រាកទេ - ការបន្តពេញលេញ។

តាមទស្សនៈ topological រង្វង់មួយមិនអាចបែងចែកចេញពីការ៉េ

ព្រោះវាងាយនឹងបំប្លែងគ្នាទៅជាមួយដោយមិនបែកបាក់

ការបន្ត។

ការតភ្ជាប់ - ការកាត់ពីរនឹងត្រូវបានទាមទារដើម្បីកាត់បន្ថយចិញ្ចៀនពាក់កណ្តាល។ ចំពោះបន្ទះ Möbius ចំនួននៃការតភ្ជាប់ត្រូវបានជំនួសអាស្រ័យលើការផ្លាស់ប្តូរនៃចំនួនវេននៃកាសែត: ប្រសិនបើវេនមួយត្រូវបានភ្ជាប់ទ្វេដងប្រសិនបើពីរវេនត្រូវបានភ្ជាប់យ៉ាងសាមញ្ញប្រសិនបើបីវេនត្រូវបានភ្ជាប់ទ្វេដង។ ចែកការ៉េជាពីរផ្នែក យើងត្រូវការកាត់តែមួយប៉ុណ្ណោះ។ ការតភ្ជាប់ជាធម្មតាត្រូវបានវាយតម្លៃដោយលេខ Betti ឬពេលខ្លះលក្ខណៈអយល័រត្រូវបានប្រើ។

4. ការតំរង់ទិសគឺជាទ្រព្យសម្បត្តិដែលអវត្តមាននៅក្នុងបន្ទះMöbius។ ដូច្នេះ ប្រសិនបើមនុស្សម្នាក់អាចធ្វើដំណើរតាមបណ្តោយផ្លូវកោងទាំងអស់នៃបន្ទះ Mobius នោះគាត់នឹងត្រលប់ទៅចំណុចចាប់ផ្តើមវិញ ប៉ុន្តែនឹងប្រែទៅជារូបភាពកញ្ចក់របស់គាត់។

5. “លេខពណ៌” គឺជាចំនួនអតិបរមានៃផ្ទៃដែលអាចគូសលើផ្ទៃមួយ ដើម្បីឱ្យពួកវានីមួយៗមានព្រំប្រទល់រួមជាមួយនឹងផ្នែកផ្សេងទៀត។ ចំនួន chromatic នៃបន្ទះ Möbius គឺប្រាំមួយ។

6. ទ្រឹស្តីបទនៅលើបន្ទះMöbius

ទ្រឹស្តីបទ 1: λ ≥ π/2

ដោយសារតែភាពស្មុគស្មាញនៃភស្តុតាង ខ្ញុំមិនចាត់ទុកវានៅក្នុងការងាររបស់ខ្ញុំទេ។

ទ្រឹស្តីបទ 2: λ ≤ √3

ទ្រឹស្តីបទនេះគឺសាមញ្ញជាងកំណែមុន៖ ដើម្បីបញ្ជាក់វាគ្រប់គ្រាន់ដើម្បីពន្យល់ពីរបៀបកាវបិទបន្ទះMöbiusពីបន្ទះដែលមានប្រវែងធំជាង√3។ ចូរយើងសន្មត់ថាប្រវែងរបស់វាគឺពិតប្រាកដ √3 ។ បន្ទាប់មកអ្នកអាចដាក់ត្រីកោណធម្មតាពីរនៅលើបន្ទះនេះ។ ចូរបត់បន្ទះនៅតាមជ្រុងនៃត្រីកោណទាំងនេះ ដោយឆ្លាស់គ្នាក្នុងទិសបត់។ គែម AB និង CD នៃបន្ទះនឹងតម្រឹម ហើយចំនុច A នឹងតម្រឹមជាមួយចំនុច D ហើយចំនុច B ដែលមានចំនុច C )

នៅក្នុងការសាងសង់នេះច្បាប់ចម្បងត្រូវបានរំលោភបំពាន - កុំធ្វើឱ្យក្រដាសជ្រួញ។ ប៉ុន្តែវាងាយស្រួលក្នុងការយល់ថាប្រសិនបើប្រវែងនៃបន្ទះគឺយ៉ាងហោចណាស់លើសពី √3 នោះការបំបែកនៅតាមបណ្តោយ generatrix អាចត្រូវបានជំនួសដោយការពត់កោងដែលត្រូវបានអនុវត្តនៅក្នុងផ្នែកតូចចង្អៀត។ សរុបមក យើងមិនខ្លាចការបត់ត្រង់តាមផ្នែកត្រង់ទេ៖ វាអាចត្រូវបានជំនួសដោយពត់ជិតវា។ (ការបត់ក្រដាសមិនអាចកែបានកើតឡើងនៅពេលដែលបន្ទាត់បត់ពីរប្រសព្វគ្នា ពោលគឺនៅពេលដែលសន្លឹកត្រូវបានបត់ដូចជាកន្សែងដៃ - អ្វីទាំងអស់នេះត្រូវបានគេដឹងដោយយើងពីបទពិសោធន៍ប្រចាំថ្ងៃ។ ) រចនាសម្ព័នរបស់វាអាចត្រូវបានស្រមៃដូចខាងក្រោម: ត្រីកោណធម្មតាចំនួនបី ABC, A"B"C", A"B"C" ស្ថិតនៅស្របគ្នាទៅវិញទៅមក ចំនុចដែលត្រូវគ្នាគឺនៅពីលើចំនុចដែលត្រូវគ្នា; ផ្នែក AB និង A "B", B" C" និង B "C", C "A" និង CA ត្រូវបានតភ្ជាប់ដោយ jumpers ។ បន្ទាត់ gluing រត់តាមបណ្តោយមធ្យមនៃត្រីកោណមួយ។

ហេតុអ្វីបានជាយើងមិនអាចរកឃើញ λ កាន់តែត្រឹមត្រូវ?

ទាល់តែដោះស្រាយបានទើបពិបាកនិយាយថា ហេតុអ្វីមិនបានដោះស្រាយ។ ទោះជាយ៉ាងណាក៏ដោយ ជួនកាលនៅក្នុងបញ្ហាផ្សេងៗដែលមិនទាន់ដោះស្រាយ វាអាចធ្វើទៅបានដើម្បីតាមដានការលំបាកទូទៅ ដើម្បីសម្គាល់ ដូច្នេះដើម្បីនិយាយ កន្លែងពិបាកៗនៅលើផែនទីគណិតវិទ្យា ដែលជួនកាលធ្វើឱ្យវាអាចទស្សន៍ទាយជោគជ័យ ឬបរាជ័យក្នុងការដោះស្រាយបញ្ហាជាក់លាក់ណាមួយ។

ទ្រឹស្តីបទ 3. បន្ទះMöbiusដែលមានចំនុចប្រសព្វដោយខ្លួនឯងអាចត្រូវបានស្អិតជាប់គ្នាពីបន្ទះដែលមានប្រវែងណាមួយធំជាងπ/2។

វាត្រូវបានធ្វើដូចនេះ។ ចូរយកលេខសេសធំល្មម ហើយសង់ n-gon ធម្មតាដែលមានចារឹកក្នុងរង្វង់អង្កត់ផ្ចិត 1។ ពិចារណាបន្ថែម ត្រីកោណ n ដែលមានកណ្តាលរង្វង់ ដែលនីមួយៗត្រូវបានកំណត់ដោយចំហៀង និងអង្កត់ទ្រូងពីរនៃ n- ហ្គុន (n=7) ។ ត្រីកោណទាំងនេះគ្របដណ្តប់ n-gon របស់យើង កន្លែងខ្លះរបស់វាច្រើនដង។ ឥឡូវនេះ ចូរយើងអនុវត្តត្រីកោណ n ទាំងនេះទៅគ្នាទៅវិញទៅមក បន្ទាប់ពីនោះយើងកាត់ពាក់កណ្តាលនៃត្រីកោណខាងឆ្វេងបំផុតតាមបណ្តោយមធ្យមវែង ហើយអនុវត្តវាទៅត្រីកោណខាងស្តាំបំផុត។ លទ្ធផលគឺជាបន្ទះចតុកោណដែលមានសមាមាត្រនៃប្រវែងទៅទទឹងធំជាង π/2 និងទំនោរទៅ π/2 ជា n ទំនោរទៅ ∞ (ទទឹងនៃបន្ទះមានទំនោរទៅ 1 និងប្រវែងទៅ π/2) ។ បត់បន្ទះនេះជាប់គ្នាតាមបន្ទាត់ទាំងអស់ដែលបានគូសនៅលើវា ឆ្លាស់គ្នាទិសដៅបត់។ ផ្នែក AB និង CD ស្ទើរតែស្របគ្នា - វានឹងមានស្រទាប់ក្រដាសបត់ពីរបីស្រទាប់រវាងពួកវា។ នៅក្នុង "ស្ទើរតែតម្រឹម" ចំណុច A នឹងតម្រឹមជាមួយ D ហើយចំនុច B នឹងតម្រឹមជាមួយ C ដូច្នេះប្រសិនបើយើងអាច "ឆ្លងកាត់កាសែត" និងកាវបិទ |AB| ជាមួយ |CD| បន្ទាប់មកលទ្ធផលនឹងជាបន្ទះMöbius។ ប្រសិនបើអ្នកយកខ្សែអាត់យូរជាងនេះបន្តិច អ្នកអាចជៀសវាងការបត់ដូចដែលយើងបានធ្វើនៅក្នុងភស្តុតាងនៃទ្រឹស្តីបទ 2។ យើងបានទទួលបន្ទះMöbius ដែលគែមត្រូវបានបំបែកដោយស្រទាប់ជាច្រើននៃក្រដាស សូមមើលឧបសម្ព័ន្ធ 1.3 ។ ប៉ុន្តែសូមត្រលប់ទៅបន្ទះMöbiusវិញ។ ទ្រឹស្តីបទទី 1 ដូចដែលយើងបានឃើញជាក់ស្តែងអនុវត្តចំពោះក្រុមដែលប្រសព្វដោយខ្លួនឯង។ វាមិនទំនងថាលក្ខខណ្ឌគ្មានការប្រសព្វដោយខ្លួនឯងនឹងមិនមានឥទ្ធិពលលើ λ; ទោះយ៉ាងណាក៏ដោយ វាមិនអាចយកឥទ្ធិពលនេះទៅក្នុងគណនីបានទេ ដោយសារគណិតវិទ្យាមិនមានមធ្យោបាយបច្ចេកទេសគ្រប់គ្រាន់ដើម្បីសិក្សាផ្នែកប្រសព្វដោយខ្លួនឯងក្នុងលំហបីវិមាត្រ។ ផ្ទុយទៅវិញ វាទំនងជាថាទ្រឹស្តីបទ 2 មិនអាចកែលម្អបានទេ។ បន្ទាប់ពីបានទាំងអស់ ការកែលម្អវាមានន័យថានឹងមកជាមួយនឹងការរចនាកាសែតថ្មីមួយ។ បទពិសោធន៍បង្ហាញថា សំណង់ដ៏ល្អប្រសើរគឺសាមញ្ញ និងចុះសម្រុងគ្នា ដែលជាការស្ថាបនាពីភស្តុតាងនៃទ្រឹស្តីបទទី 2។ វាជាធម្មជាតិដែលសន្មត់ថា ប្រសិនបើសំណង់ល្អបំផុតមានមែននោះ វានឹងត្រូវបានរកឃើញ - បន្ទាប់ពីច្រើនឆ្នាំមកនេះ!

នេះជាមូលហេតុដែលយើងអាចរំពឹងថា λ = √3 ។

ល្បិចឆ្នូត Moebius

បញ្ហានៃការចងខ្សែ

តើធ្វើដូចម្តេចដើម្បីចង knot នៅក្នុងកន្សែងមួយដោយមិនអនុញ្ញាតឱ្យទៅចុងរបស់វា? វាអាចត្រូវបានធ្វើដូចនេះ។ ដាក់កន្សែងនៅលើតុ។ ហុចដៃរបស់អ្នកលើទ្រូងរបស់អ្នក។ ដោយបន្តកាន់ពួកគេនៅក្នុងទីតាំងនេះ ពត់លើតុ ហើយយកក្រមាមួយចុងដោយដៃនីមួយៗជាវេន។ បន្ទាប់ពីដៃត្រូវបានលាតសន្ធឹងដាច់ពីគ្នា ស្នាមដេរនឹងបង្កើតដោយស្វ័យប្រវត្តិនៅកណ្តាលក្រម៉ា ដោយប្រើវាក្យស័ព្ទ topological យើងអាចនិយាយបានថាដៃរបស់អ្នកមើល រាងកាយ និងកន្សែងរបស់គាត់បង្កើតជាខ្សែកោងបិទជិតក្នុងទម្រង់ជា "ស្លឹកបី" ។ ពេលលាតដៃ ចំណងផ្លាស់ទីពីដៃទៅក្រមាប៉ុណ្ណោះ។

ចងក្រមាដោយដៃម្ខាង ដោយមិនឲ្យចុងក្រមាចេញពីដៃឡើយ។ ចម្លើយចំពោះល្បែងផ្គុំរូបនេះអាចរកឃើញនៅក្នុងសៀវភៅ “អច្ឆរិយៈ និងអាថ៌កំបាំង” ដោយ M. Gardner ។

តាមទស្សនៈ topological អាវកាក់អាចត្រូវបានចាត់ទុកថាជាផ្ទៃពីរដែលមានគែមមិនជាប់គ្នាចំនួនបី ដែលនីមួយៗគឺជាខ្សែកោងបិទធម្មតា។ អាវកាក់ដែលមានប៊ូតុងគឺជាផ្ទៃពីរដែលមានគែមបួន។

រង្វិលជុំអាថ៌កំបាំង។

អ្នកមើលដែលពាក់អាវកាក់មានរង្វិលជុំដាក់លើដៃរបស់គាត់ ហើយបន្ទាប់មកត្រូវបានស្នើឱ្យដាក់មេដៃក្នុងហោប៉ៅខាងក្រោមនៃអាវកាក់។ ឥឡូវនេះអ្នកអាចអញ្ជើញអ្នកដែលមានវត្តមានឱ្យដករង្វិលជុំចេញពីដៃរបស់អ្នកដោយមិនចាំបាច់ដកម្រាមដៃរបស់អ្នកចេញពីហោប៉ៅអាវកាក់របស់អ្នក។ ដំណោះស្រាយគឺដូចនេះ៖ រង្វិលជុំត្រូវទាញចូលទៅក្នុងរន្ធអាវកាក់សម្រាប់ដៃអាវ បោះពីលើក្បាលអ្នកមើល ទាញចេញតាមរន្ធទីពីរសម្រាប់ដៃអាវ ហើយផ្លាស់ទីនៅក្រោមដៃទីពីរ។ ជាលទ្ធផលនៃសកម្មភាពទាំងនេះរង្វិលជុំនឹងស្ថិតនៅក្រោមអាវកាក់ដែលព័ទ្ធជុំវិញទ្រូង។ បន្ទាបវារហូតទាល់តែវាលេចចេញពីក្រោមអាវកាក់ ហើយបន្ទាប់មកឱ្យវាធ្លាក់ដល់ឥដ្ឋ។

បង្វែរអាវកាក់ខាងក្នុងចេញដោយមិនយកវាចេញពីមនុស្ស។

ម្ចាស់អាវកាក់ត្រូវដាក់ម្រាមដៃនៅខាងក្រោយខ្នង។ អ្នកដែលនៅជុំវិញអ្នកគួរដោះអាវកាក់ចេញពីខាងក្នុងចេញដោយមិនបាច់ចែកដៃម្ចាស់។ ដើម្បីបង្ហាញពីបទពិសោធន៍នេះ វាចាំបាច់ក្នុងការដោះអាវកាក់ចេញ ហើយទាញវាពីលើដៃនៅពីក្រោយខ្នងរបស់អ្នកពាក់។ អាវកាក់នឹងរសាត់ទៅតាមអាកាស ប៉ុន្តែប្រាកដណាស់ វានឹងមិនរលត់ឡើយ ព្រោះដៃត្រូវបានតោង។ ឥឡូវអ្នកត្រូវយកអាវកាក់ខាងឆ្វេង ហើយព្យាយាមកុំឱ្យអាវកាក់ជ្រីវជ្រួញ រុញវាឱ្យឆ្ងាយតាមដែលអាចធ្វើទៅបានទៅក្នុងរន្ធដៃស្តាំ។ បន្ទាប់មកយក armhole ខាងស្តាំហើយបញ្ចូលវាទៅក្នុង armhole ដូចគ្នានិងក្នុងទិសដៅដូចគ្នា។ អ្វីដែលនៅសល់គឺតម្រង់អាវកាក់ឱ្យត្រង់ ហើយទាញវាទៅលើម្ចាស់។ អាវកាក់នឹងត្រូវបើកនៅខាងក្នុង។ យើងអនុវត្តល្បិចនេះ ហើយថតជាមួយមិត្តរួមថ្នាក់របស់យើង។ វាមាននៅក្នុងបទបង្ហាញ "Mobius Strip" ។

២.៣. ការអនុវត្តបន្ទះMöbius

∞ នៅច្រកចូលសារមន្ទីរប្រវត្តិសាស្ត្រ និងបច្ចេកវិទ្យាក្នុងទីក្រុងវ៉ាស៊ីនតោន ខ្សែបូដែកបានបង្វិលពាក់កណ្តាលវេនយឺតៗនៅលើជើងទម្រ។ នៅឆ្នាំ 1967 នៅពេលដែលសមាជគណិតវិទ្យាអន្តរជាតិបានធ្វើឡើងនៅប្រទេសប្រេស៊ីល អ្នករៀបចំរបស់ខ្លួនបានចេញត្រារំលឹកមួយនៅក្នុងនិកាយនៃ centavos ប្រាំ។ វាពណ៌នាបន្ទះMöbius។ ទាំងវិមាននេះមានកម្ពស់ជាងពីរម៉ែត្រ និងត្រាដ៏តូច គឺជាវិមានដ៏ពិសេសរបស់គណិតវិទូ និងតារាវិទូអាល្លឺម៉ង់ August Ferdinand Möbius។

សូមមើលឧបសម្ព័ន្ធទី 5 ។

សេវាកម្មប៉ាតង់បានចុះបញ្ជីការច្នៃប្រឌិតជាច្រើនដោយផ្អែកលើផ្ទៃម្ខាងដូចគ្នា។

∞ បន្ទះ Möbius ត្រូវបានប្រើនៅក្នុងការច្នៃប្រឌិតជាច្រើនដែលត្រូវបានបំផុសគំនិតដោយការសិក្សាយ៉ាងប្រុងប្រយ័ត្នអំពីលក្ខណៈសម្បត្តិនៃផ្ទៃម្ខាង។ បន្ទះខ្សែក្រវាត់ conveyor ដែលផលិតក្នុងទម្រង់ជាបន្ទះMöbius អនុញ្ញាតឱ្យវាដំណើរការបានយូរជាងពីរដង ពីព្រោះផ្ទៃទាំងមូលនៃសន្លឹកមានភាពស្មើគ្នា។ នៅឆ្នាំ 1923 ប៉ាតង់មួយត្រូវបានចេញឱ្យអ្នកបង្កើត Lee de Force ដែលបានស្នើឱ្យថតសំឡេងនៅលើខ្សែភាពយន្តដោយមិនផ្លាស់ប្តូរ reels ទាំងសងខាងក្នុងពេលតែមួយ។ កាសែតសម្រាប់ថតខ្សែអាត់ត្រូវបានបង្កើតឡើង ដែលខ្សែអាត់ត្រូវបានបង្វិល និងស្អិតជាប់ជារង្វង់ ដែលធ្វើឱ្យវាអាចកត់ត្រា ឬអានព័ត៌មានពីភាគីទាំងពីរក្នុងពេលតែមួយ ដែលបង្កើនសមត្ថភាពរបស់កាសែតទ្វេដង និងតាមពេលវេលានៃការចាក់។ នៅក្នុងម៉ាស៊ីនបោះពុម្ព dot matrix ខ្សែបូទឹកថ្នាំមានរាងដូចបន្ទះMöbius ដើម្បីបង្កើនអាយុកាលធ្នើ។ នេះផ្តល់នូវការសន្សំដ៏សំខាន់។ បន្ទះ Möbius ត្រូវបានប្រើក្នុងការជិះកង់ និងបំពង់បាល់ទះ។

∞ ថ្មីៗនេះពួកគេបានរកឃើញការប្រើប្រាស់មួយផ្សេងទៀតសម្រាប់វា - វាបានចាប់ផ្តើមដើរតួជានិទាឃរដូវមានតែនិទាឃរដូវពិសេសប៉ុណ្ណោះ។ ដូចដែលអ្នកបានដឹងហើយថា និទាឃរដូវដែលសាកថ្មឆេះក្នុងទិសដៅផ្ទុយ។ បន្ទះ Mobius ផ្ទុយនឹងច្បាប់ទាំងអស់មិនផ្លាស់ប្តូរទិសដៅនៃប្រតិបត្តិការដូចជាយន្តការដែលមានទីតាំងស្ថេរភាពពីរ។ និទាឃរដូវបែបនេះអាចមានតម្លៃមិនអាចកាត់ថ្លៃបាននៅក្នុងប្រដាប់ប្រដាក្មេងលេង - វាមិនអាចបង្វិលដូចធម្មតាបានទេ - ប្រភេទម៉ាស៊ីនចលនាជារៀងរហូត។

សូមមើល adj ។ ៦.

∞ នៅឆ្នាំ 1971 អ្នកបង្កើតមកពី Urals P.N. Chesnokov ។ បានអនុវត្តតម្រងក្នុងទម្រង់ជាបន្ទះ Mobius ។

∞ ស្លឹក Mobius ត្រូវបានគេប្រើក្នុងការធ្វើម្ហូបដើម្បីបង្កើតរូបរាងគួរឱ្យចាប់អារម្មណ៍ និងគួរឱ្យចាប់អារម្មណ៍សម្រាប់នំនំកែកឃឺ និងឈើជក់។ ហើយក៏នៅក្នុងការផលិតឧបករណ៍សម្រាប់រៀបចំនិងតុបតែងចានផ្សេងៗ រចនាសម្ព័ន្ធថាមពល (ម៉ាស៊ីនកូរ) ។

សូមមើល adj ។ ៧.

∞ ដោយមានជំនួយពីបន្ទះMöbius ស្នាដៃទាំងមូលត្រូវបានបង្កើតឡើង។

បន្ទះ Möbius បានបម្រើជាការបំផុសគំនិតសម្រាប់រូបចម្លាក់ និងសិល្បៈក្រាហ្វិក។ Escher គឺជាវិចិត្រករម្នាក់ដែលចូលចិត្តវាជាពិសេស ហើយបានឧទ្ទិសអក្សរសិល្ប៍ជាច្រើនរបស់គាត់ចំពោះវត្ថុគណិតវិទ្យានេះ។ រឿងដ៏ល្បីល្បាញមួយបង្ហាញស្រមោចវារលើផ្ទៃនៃបន្ទះMöbius។

សូមមើលឧបសម្ព័ន្ធទី ៩ ។

∞ បន្ទះ Möbius ក៏លេចឡើងជាទៀងទាត់នៅក្នុងរឿងប្រឌិតបែបវិទ្យាសាស្ត្រ ដូចជានៅក្នុងរឿងរបស់ Arthur C. Clarke "The Wall of Darkness" ជាដើម។ ពេលខ្លះរឿងប្រឌិតបែបវិទ្យាសាស្ត្រណែនាំថាចក្រវាឡរបស់យើងអាចជាប្រភេទនៃបន្ទះMöbiusទូទៅ។ នៅក្នុងរឿងរបស់អ្នកនិពន្ធ A.J. Deitch រថភ្លើងក្រោមដីរបស់បូស្តុនកំពុងសាងសង់ខ្សែថ្មី ដែលផ្លូវនេះមានភាពច្របូកច្របល់រហូតដល់វាប្រែទៅជាបន្ទះ Mobius បន្ទាប់ពីនោះរថភ្លើងចាប់ផ្តើមបាត់នៅលើខ្សែនេះ។

∞ មានសម្មតិកម្មមួយដែលថាវង់ DNA ខ្លួនវាក៏ជាបំណែកនៃបន្ទះ Mobius ដែរ ហើយនោះគឺជាហេតុផលតែមួយគត់ដែលហេតុអ្វីបានជាលេខកូដហ្សែនពិបាកបកស្រាយ និងយល់ឃើញណាស់។ លើសពីនេះទៅទៀតរចនាសម្ព័ន្ធបែបនេះពន្យល់យ៉ាងត្រឹមត្រូវអំពីហេតុផលសម្រាប់ការចាប់ផ្តើមនៃការស្លាប់ជីវសាស្រ្ត: វង់បិទដោយខ្លួនឯងហើយការបំផ្លិចបំផ្លាញខ្លួនឯងកើតឡើង។

ឧបសម្ព័ន្ធ 10 ។

∞ បន្ទះ Möbius មិនត្រឹមតែចូលចិត្តដោយគណិតវិទូប៉ុណ្ណោះទេ ប៉ុន្តែថែមទាំងដោយអ្នកលេងប៉ាហីផងដែរ។

អស់រយៈពេលជាង 100 ឆ្នាំមកហើយ បន្ទះMöbius ត្រូវបានប្រើដើម្បីអនុវត្តល្បិចវេទមន្ត និងការកម្សាន្តផ្សេងៗ។ លក្ខណៈសម្បត្តិដ៏អស្ចារ្យនៃស្លឹកត្រូវបានបង្ហាញសូម្បីតែនៅក្នុងសៀកដែលខ្សែបូភ្លឺបានស្អិតជាប់គ្នាក្នុងទម្រង់ជាបន្ទះMöbiusត្រូវបានព្យួរ។ បុរសលេងប៉ាហីបានដុតបារីមួយ ហើយចុងបញ្ចប់ដែលឆេះបានប៉ះខ្សែកណ្តាលនៃខ្សែបូនីមួយៗ ដែលធ្វើពីប៉ូតាស្យូមនីត្រាត។ ផ្លូវដ៏ក្ដៅគគុកបានប្រែក្លាយខ្សែបូទីមួយទៅជាខ្សែវែងមួយ ហើយទីពីរទៅជាខ្សែបូពីរ ខ្សែមួយចូលទៅក្នុងមួយទៀត។ (ក្នុងករណីនេះបុរសលេងប៉ាហីបានកាត់បន្ទះ Mobius មិននៅកណ្តាលទេប៉ុន្តែនៅចម្ងាយមួយភាគបីនៃទទឹងរបស់វា) ។

∞ អ្នករូបវិទ្យាអះអាងថា ច្បាប់អុបទិកទាំងអស់គឺផ្អែកលើលក្ខណៈសម្បត្តិរបស់បន្ទះ Mobius ជាពិសេសការឆ្លុះកញ្ចក់គឺជាប្រភេទនៃការផ្ទេរពេលវេលា ក្នុងរយៈពេលខ្លី និងយូរអង្វែងរាប់រយវិនាទី ដោយសារយើងឃើញនៅពីមុខយើង។ នោះជាការត្រឹមត្រូវ កញ្ចក់របស់យើងទ្វេដង។

∞មានសម្មតិកម្មមួយដែលថាចក្រវាឡរបស់យើងទំនងជាត្រូវបានបិទនៅក្នុងបន្ទះ Mobius ដូចគ្នានេះបើយោងតាមទ្រឹស្ដីនៃទំនាក់ទំនង ម៉ាស់កាន់តែច្រើន ភាពកោងនៃលំហកាន់តែធំ។ ទ្រឹស្ដីនេះបញ្ជាក់យ៉ាងពេញលេញនូវការសន្មត់ថា យានអវកាសដែលហោះហើរត្រង់គ្រប់ពេល អាចត្រឡប់ទៅចំណុចចាប់ផ្តើមវិញ នេះបញ្ជាក់អំពីភាពគ្មានដែនកំណត់ និងរយៈពេលនៃចក្រវាឡ។

សូមមើល adj ។ ដប់មួយ

∞ ចំណាប់អារម្មណ៍លើបន្ទះMöbiusមិនទាន់រលត់រហូតមកដល់សព្វថ្ងៃនេះទេ។ មហោស្រពគណិតវិទ្យាសិល្បៈបានធ្វើឡើងនៅទីក្រុងមូស្គូក្នុងខែកញ្ញាឆ្នាំ 2006 ។ សុន្ទរកថារបស់សាស្រ្តាចារ្យមកពីទីក្រុងតូក្យូ Jin Akiyama ត្រូវបានទទួលដោយជោគជ័យដ៏អស្ចារ្យ។ ការសម្តែងរបស់គាត់គឺនឹកឃើញដល់ការបង្ហាញរបស់អ្នកបំភាន់ដែលមានកន្លែងសម្រាប់បន្ទះMöbius (ធ្វើការជាមួយក្រដាស "Möbius strip និងការកែប្រែរបស់វា")។

កីឡា

ឧបករណ៍ពង្រីកដោយដៃ "Robur"

សូមមើល adj ។ ១២.

មួយនៃរបស់ដែលចូលចិត្តរបស់គ្រូអប់រំកាយសាលាទាំងអស់ ដែលយោងទៅតាមពួកគេ។នៅក្នុងពាក្យផ្ទាល់ខ្លួនរបស់គាត់ "កុំហ្វឹកហាត់សាច់ដុំដៃតែប៉ុណ្ណោះនិងសាច់ដុំខួរក្បាល។ "Carpal expander ពីស្ទូឌីយោ Artemy Lebedev ធ្វើម្តងទៀតនូវរូបរាងនៃបន្ទះMöbius។ មធ្យោបាយដោះស្រាយដ៏ល្អសម្រាប់បំបាត់ភាពតានតឹង ការគិតគ្មានដែនកំណត់ និងគ្រាន់តែជាវិធីមានប្រយោជន៍ក្នុងការរក្សាដៃរបស់អ្នកឱ្យរវល់។

ទឹកអប់

ទឹកអប់ Bugatti

សូមមើល adj ។ ១៣

ក្រុមហ៊ុនរថយន្តម៉ាក Bugattiបានចាប់ផ្តើមផលិតមិនត្រឹមតែរថយន្តដែលមានតម្លៃថ្លៃប៉ុណ្ណោះទេ (ម៉ូដែលវីរុនមានតម្លៃ 1.3 លានអឺរ៉ូ) ប៉ុន្តែក៏មាន... ទឹកអប់ផងដែរ។ ដបនីមួយៗធ្វើពីគ្រីស្តាល់ និងស្រោបដោយមាសពិត ត្រូវបានរចនាឡើងក្នុងទម្រង់ជាបន្ទះMöbius មិនធម្មតាដែលមានតែមួយចំហៀង។ តម្លៃទឹកអប់រថយន្តម៉ាក Bugattiគឺ 3500 អឺរ៉ូ ។

ទឹកអប់ Loewe Quzas, Quizas, Quizas

សូមមើល adj ។ ១៤.

នៅរដូវស្លឹកឈើជ្រុះឆ្នាំ 2011 កំណែពណ៌ក្រហមនៃក្លិនក្រអូបត្រូវបានចេញផ្សាយដែលដបត្រូវបានរុំដោយបន្ទះ Mobius ដែលជានិមិត្តសញ្ញានៃវដ្តនៃតណ្ហានៅក្នុងធម្មជាតិ។ ភាពសម្បូរបែបនៃសមាសភាពរួមមានភាពស្រស់នៃក្រូចអាស៊ី ប៊ឺហ្កាម៉ុត បឺរីក្រហម បន្តដោយបេះដូងផ្កានៃផ្កាម៉ាណូលីយ៉ា ផ្កាសេរី និងផ្កាពណ៌ទឹកក្រូច ហើយបញ្ចប់ដោយផ្លូវត្រេកត្រអាលនៃឈើខៀវ មាស amber និង vetiver ។

ទឹកអប់ UFO Limited Edition, Kenzo

សូមមើល adj ។ ១៥.

បទបង្ហាញអំពីក្លិនក្រអូបខេនហ្សូបានធ្វើឡើងក្នុងឆ្នាំ ២០០៩ នៅឯការតាំងពិពណ៌ឡើងវិញនៃស្នាដៃរបស់ Ron Arad (រ៉ុនអារ៉ាដ) នៅមជ្ឈមណ្ឌល Pompidou ក្នុងទីក្រុងប៉ារីស។ វាគឺជាវិចិត្រករ និងស្ថាបត្យករម្នាក់នេះ ដែលបានបង្កើតឡើងជាមួយនឹងការរចនាលោហធាតុនៃដបក្នុងទម្រង់ជាបន្ទះ Mobius ។ វាត្រូវបានរចនាឡើងដើម្បីឱ្យសមនឹងបាតដៃរបស់អ្នក។មិនស្គាល់អត្តសញ្ញាណក្លិនក្រអូបវត្ថុឬ "វត្ថុក្រអូបដែលមិនស្គាល់អត្តសញ្ញាណ" ត្រូវបានកំណត់ត្រឹមតែ 180 ដុំប៉ុណ្ណោះ ហើយលក់រាយក្នុងតម្លៃ 188 ដុល្លារ។

គ្រឿងសង្ហារឹម

តារាង Mobius

សូមមើល adj ។ ១៦

តុមួយដែលមានផ្ទៃមួយដែលអ្នកអាចឈរ អង្គុយ និងដេកបានយ៉ាងស្រួល។

ធ្នើសៀវភៅ Infinity

សូមមើល adj ។ ១៧.

អ្នករចនា Job Kelevius បានបំបែកផ្សិតនៅពេលដែលគាត់បានរចនាប្រអប់សៀវភៅ Infinity របស់គាត់។ ដោយប្រើគំនិតគណិតវិទ្យានៃ Lemniscate និងអ្វីមួយដែលស្រដៀងទៅនឹងបន្ទះMöbius អ្នករចនាបានបញ្ចូលគំនិតរូបវន្តនៃភាពគ្មានទីបញ្ចប់នៅក្នុង Infinity Shelf ។ នេះមានន័យថា ប្រសិនបើអ្នកបានអានសៀវភៅទាំងអស់នៅលើធ្នើនេះ សូមពិចារណាថាអ្នកបានយល់ពីអក្សរសិល្ប៍គ្មានដែនកំណត់ទាំងមូល។

សាឡុង Mobius

សូមមើល adj ។ ១៨.

កើតនៅក្រោមបាវចនា "កៅអីទ្វេ - ភាពរីករាយទ្វេដង" កៅអីសាឡុងម៉ូប៊ីយូសទ្វេដងកៅអីបង្កើតឡើងដោយអ្នករចនាហ្គាអ៊ីតាន់វ៉ាន់ដឺវីយឺរមកពីប្រទេសបែលហ្សិក និងនាំមកនូវចក្ខុវិស័យថ្មីនៃគ្រឿងសង្ហារឹមសម្រាប់អ្នកស្រឡាញ់។

ឡូហ្គោស

និមិត្តសញ្ញាក្រុមហ៊ុន Woolmark

សូមមើល adj ។ ១៩.

និមិត្តសញ្ញានេះត្រូវបានបង្កើតឡើងក្នុងឆ្នាំ 1964 ជាលទ្ធផលនៃការប្រកួតប្រជែងការរចនា។ សមាជិកគណៈវិនិច្ឆ័យហ្វ្រង់កូហ្គ្រីននីមិនអាចទប់ទល់បាន និងបានផ្តល់កំណែរបស់គាត់ដោយលាក់ខ្លួនក្រោមឈ្មោះក្លែងក្លាយហ្វ្រង់សស្កូសេរ៉ាគ្លីយ៉ូ. និមិត្តសញ្ញានេះប្រហាក់ប្រហែលនឹងបន្ទះ Mobius និងជានិមិត្តសញ្ញានៃភាពអស់កល្បនិងភាពបត់បែនរបស់ក្រុមហ៊ុន។

និមិត្តសញ្ញាកែច្នៃឡើងវិញ

សូមមើល adj ។ ២០.

និមិត្តសញ្ញាអន្តរជាតិសម្រាប់ការកែច្នៃឡើងវិញគឺបន្ទះMöbius។ការកែច្នៃឡើងវិញ (លក្ខខណ្ឌផ្សេងទៀត៖ ការកែឆ្នៃកាកសំណល់,ការកែច្នៃឡើងវិញ និង ការកែច្នៃឡើងវិញ)- ប្រើប្រាស់ឡើងវិញ ឬត្រឡប់ចូលទៅក្នុងចរាចរកាកសំណល់ឧស្សាហកម្ម ឬសម្រាម។ ទូទៅបំផុតគឺអនុវិទ្យាល័យ, ទីបីនិងធ. e. ការកែឆ្នៃលើមាត្រដ្ឋានមួយ ឬសម្ភារៈផ្សេងទៀតដូចជា កញ្ចក់ ក្រដាស អាលុយមីញ៉ូម ជ័រកៅស៊ូ ដែក ក្រណាត់ និងប្រភេទផ្សេងៗនៃប្លាស្ទិក។ កាកសំណល់កសិកម្មសរីរាង្គ និងក្នុងគ្រួសារក៏ត្រូវបានប្រើប្រាស់ក្នុងវិស័យកសិកម្មតាំងពីបុរាណកាលមកម្ល៉េះ។

និមិត្តសញ្ញាគណិតវិទ្យា

សូមមើល adj ។ ២១.

បន្ទះ Möbius ត្រូវបានគេចាត់ទុកថាជានិមិត្តរូបនៃគណិតវិទ្យាសម័យទំនើប ព្រោះវាជាអ្នកដែលផ្តល់កម្លាំងចិត្តដល់ការស្រាវជ្រាវគណិតវិទ្យាថ្មី។

សម្លៀកបំពាក់ និងស្បែកជើង

ស្បែកជើង

សូមមើល adj ។ ២២.

បង្កើតឡើងក្នុងឆ្នាំ 2003 ដោយស្ថាបត្យករ Ram Di Koolhaase និងអ្នកផលិតស្បែកជើង Galahad ClarkUnitedអាក្រាតមានជំនាញក្នុងការផលិតស្បែកជើងអ្នករចនាប្រកបដោយភាពច្នៃប្រឌិត។ ការអភិវឌ្ឍន៍ជោគជ័យបំផុតមួយរបស់ក្រុមហ៊ុនគឺស្បែកជើងម៉ូប៊ីស ត្រូវបានដាក់ឈ្មោះតាមធរណីមាត្រ August Möbius និងគំនិតរបស់គាត់អំពីផ្ទៃម្ខាង។ គំនិតនៃស្បែកជើងគឺនេះ: ស្បែកខាងលើនៃស្បែកជើងនិងតែមួយគត់គឺជាខ្សែបូតែមួយ, រមួលនៅក្នុងវិធីជាក់លាក់មួយ។

កន្សែង Mobius

សូមមើល adj ។ ២៣.

អ្វីដែលគួរឱ្យចាប់អារម្មណ៍មួយគឺកន្សែង Möbius ដែលលេចឡើងនៅក្នុងទូខោអាវនៃសតវត្សទី 21 ។ អ្នកអាចធ្វើក្រមាMöbiusដោយខ្លួនឯងដោយចងចុងក្រមា ហើយបង្វិលវាមួយវេន។

គំនូរ

ផ្ទាំងគំនូរ

សូមមើល adj ។ ២៤.

បន្ទះ Möbius ទំនើបត្រូវបានលាបពណ៌លើជញ្ជាំងក្នុងទីក្រុង Prague សាធារណរដ្ឋឆែក។   យានជំនិះពីរប្រភេទធ្វើចលនាតាមខ្សែអាត់៖ រថក្រោះ និងឧបករណ៍សាងសង់ផ្លូវ និមិត្តសញ្ញានៃអរិយធម៌ទំនើប៖ បំផ្លាញ-សាងសង់-បំផ្លាញ-សាងសង់..

ស្ថាបត្យកម្ម

អគារបណ្ណាល័យ

សូមមើល adj ។ ២៥.

គម្រោងសាងសង់បណ្ណាល័យក្នុងទម្រង់ជាបន្ទះ Mobius នៅកាហ្សាក់ស្ថានបច្ចុប្បន្នកំពុងត្រូវបានពិចារណា។

ខ្សែកោងនៃអាគារបង្កើតបានជាបន្ទះMöbius ដូច្នេះចន្លោះខាងក្នុងហូរចូលទៅក្នុងខាងក្រៅ និងច្រាសមកវិញ។ តាមរបៀបស្រដៀងគ្នា ជញ្ជាំងបំប្លែងទៅជាដំបូល ហើយដំបូលប្រែទៅជាជញ្ជាំងវិញ។ ពន្លឺធម្មជាតិចូលទៅក្នុងច្រករបៀងខាងក្នុងតាមរយៈការបើកធរណីមាត្រនៅក្នុងសែលខាងក្រៅ បង្កើតឱ្យមានចន្លោះភ្លឺច្បាស់ល្អសម្រាប់ការអាន។

កន្លែងទាក់ទាញ

សូមមើល adj ។ ២៦.

ការជិះរទេះរុញមានរូបរាងស្រដៀងនឹងបន្ទះ Mobius ។ នៅទីក្រុងមូស្គូ មានរទេះរុញបញ្ច្រាសដ៏ធំបំផុតរបស់ពិភពលោក ដែលមនុស្សម្នាក់អង្គុយលើកៅអីព្យួរ ហើយជើងរបស់គាត់នៅលើអាកាស។ ល្បឿន - 81 គីឡូម៉ែត្រ / ម៉ោង, កម្ពស់ 30 ម៉ែត្រ។ កម្ពស់បើប្រៀបធៀបទៅនឹង analogues បរទេសគឺតូចប៉ុន្តែវាច្រើនជាងការទូទាត់ជាមួយនឹងភាពសម្បូរបែបនៃវង់ចិញ្ចៀននិងរង្វិលជុំ។

ខ្សែភាពយន្ត

សូមមើល adj ។ ២៧.

នៅឆ្នាំ 1923 ប៉ាតង់មួយត្រូវបានចេញឱ្យអ្នកបង្កើត Lee de Force ដែលបានស្នើសុំការថតសំឡេងនៅលើខ្សែភាពយន្តដោយមិនផ្លាស់ប្តូរ reels ពីភាគីទាំងពីរក្នុងពេលតែមួយ។

កាសែត

សូមមើល adj ។ ២៨.

កាសែតត្រូវបានបង្កើតឡើងសម្រាប់ឧបករណ៍ថតសំឡេង ដែលកាសែតត្រូវបានបង្វិល និងស្អិតជាប់ជារង្វង់ ដែលធ្វើឱ្យវាអាចកត់ត្រា ឬអានព័ត៌មានពីភាគីទាំងពីរក្នុងពេលតែមួយ ដែលបង្កើនសមត្ថភាពរបស់កាសែត និងតាមពេលវេលានៃការចាក់។

រថយន្ត Toyota MOB

សូមមើល adj ។ ២៩.

បន្ទះMöbiusត្រូវបានរចនាឡើងដោយអ្នករចនាជនជាតិអេស្ប៉ាញ Jorge Marti Vidal ហើយរួមបញ្ចូលគ្នានូវភាពស្រស់ស្អាត និងអាថ៌កំបាំងនៃបន្ទះMöbius។ រូបរាងរាងកាយតែមួយគត់ផ្តល់ឱ្យរថយន្តប្រណាំងជាមួយនឹងឌីណាមិកល្អ។

ម៉ាស៊ីនបោះពុម្ពម៉ាទ្រីស

សូមមើល adj ។ សាមសិប

នៅក្នុងម៉ាស៊ីនបោះពុម្ពម៉ាទ្រីសជាច្រើន ខ្សែបូទឹកថ្នាំក៏មានទម្រង់ជាបន្ទះ Mobius ដើម្បីបង្កើនធនធានរបស់វា។

ឧបករណ៍ទប់ទល់ Möbius

សូមមើល adj ។ ៣១.

នេះជាធាតុអេឡិចត្រូនិកដែលទើបបង្កើតថ្មីដែលមិនមានអាំងឌុចទ័ររបស់វាទេ។

ខ្សែក្រវ៉ាត់ខ្សាច់

សូមមើល adj ។ ៣២.

នៅឆ្នាំ 1969 អ្នកបង្កើតសូវៀត Gubaidullin បានស្នើសុំខ្សែក្រវ៉ាត់ខ្សាច់គ្មានទីបញ្ចប់ក្នុងទម្រង់ជាបន្ទះMöbius។

សេចក្តីសន្និដ្ឋាន

បន្ទះ Möbius គឺជាផ្ទៃម្ខាងដំបូងដែលអ្នកវិទ្យាសាស្ត្របានរកឃើញ។ ក្រោយមក គណិតវិទូបានរកឃើញស៊េរីទាំងមូលនៃផ្ទៃម្ខាង។ ប៉ុន្តែ

មួយនេះ ជាដំបូងបង្អស់ ដែលបានចាក់គ្រឹះសម្រាប់ទិសដៅទាំងមូលនៅក្នុងធរណីមាត្រ បន្តទាក់ទាញចំណាប់អារម្មណ៍របស់អ្នកវិទ្យាសាស្ត្រ អ្នកច្នៃប្រឌិត សិល្បករ និងសិស្សរបស់យើង។ ខ្ញុំចាប់អារម្មណ៍យ៉ាងខ្លាំងចំពោះលក្ខណៈសម្បត្តិបើកចំហនៃបន្ទះMöbius:

បន្ទះ Mobius មានគែមមួយចំហៀង

បន្ទះ Möbius គឺជាវត្ថុ topological ។ ដូចរូប topological ណាមួយដែរ វាមិនផ្លាស់ប្តូរលក្ខណៈសម្បត្តិរបស់វាទេ រហូតដល់វាត្រូវបានកាត់ រហែក ឬបំណែកនីមួយៗរបស់វាត្រូវបានស្អិតជាប់ជាមួយគ្នា។

គែមមួយ និងផ្នែកម្ខាងនៃបន្ទះ Mobius មិនទាក់ទងទៅនឹងទីតាំងរបស់វានៅក្នុងលំហទេ ហើយក៏មិនទាក់ទងទៅនឹងគោលគំនិតនៃចម្ងាយដែរ។

បន្ទះ Möbius រកឃើញកម្មវិធីជាច្រើនក្នុងការចម្អិនអាហារ បច្ចេកវិទ្យា រូបវិទ្យា គំនូរ ស្ថាបត្យកម្ម ការរចនាគ្រឿងអលង្ការ និងការសិក្សាអំពីលក្ខណៈសម្បត្តិនៃសកលលោក។ គាត់បានបំផុសគំនិតច្នៃប្រឌិតរបស់អ្នកនិពន្ធ និងសិល្បករជាច្រើន។

μ( ន) ត្រូវបានកំណត់សម្រាប់លេខធម្មជាតិទាំងអស់។ ននិងយកតម្លៃអាស្រ័យលើធម្មជាតិនៃការពង្រីកចំនួន នចំពោះកត្តាសាមញ្ញ៖

μ( ន) = 1 ប្រសិនបើ នមិនមានការេ (ឧ. គ្មានលេខបឋមត្រូវបានបែងចែកដោយការេ) និងការបំបែក នចំនួនគូនៃកត្តា;
μ( ន) = − 1 ប្រសិនបើ នដោយឥតគិតថ្លៃពីការេនិងការរលួយ នទៅជាកត្តាចម្បងមានកត្តាចំនួនសេស។
μ( ន) = 0 ប្រសិនបើ នមិនទំនេរពីការ៉េ។

តាមនិយមន័យ យើងក៏សន្មត់ថា μ(1) = 1។

លក្ខណៈសម្បត្តិ និងកម្មវិធី

អនុគមន៍ Möbius គឺពហុគុណ៖ សម្រាប់លេខ coprime ណាមួយ។ កនិង ខរក្សាសមភាព μ( កខ) = μ( ក)μ( ខ) .

ផលបូកនៃតម្លៃនៃអនុគមន៍ Möbius លើផ្នែកទាំងអស់នៃចំនួនគត់ នមិនស្មើនឹងមួយ គឺស្មើនឹងសូន្យ

រចនាប័ទ្ម = "ទទឹងអតិបរមា៖ ៩៨%; កម្ពស់៖ ស្វ័យប្រវត្តិ; ទទឹង៖ ស្វ័យប្រវត្តិ;" src="/pictures/wiki/files/49/1bee8d0f6bd91176912a8cedc63e174b.png" border="0">

ពីទីនេះ ជាពិសេស វាធ្វើតាមថា សម្រាប់សំណុំកំណត់មិនទទេណាមួយ ចំនួននៃសំណុំរងផ្សេងៗគ្នាដែលមានចំនួនសេសនៃធាតុគឺស្មើនឹងចំនួននៃសំណុំរងផ្សេងៗគ្នាដែលមានចំនួនគូនៃធាតុ - ការពិតដែលត្រូវបានប្រើនៅក្នុង ភស្តុតាង។

អនុគមន៍ Möbius គឺទាក់ទងទៅនឹងមុខងារ Mertens ដោយទំនាក់ទំនង

នៅក្នុងវេនមុខងារ Mertens ត្រូវបានទាក់ទងយ៉ាងជិតស្និទ្ធទៅនឹងបញ្ហានៃសូន្យនៃមុខងារ Riemann zeta សូមមើលអត្ថបទ សម្មតិកម្ម Mertens ។

បញ្ច្រាស Mobius

រូបមន្តបញ្ច្រាសMöbiusដំបូង

សម្រាប់មុខងារនព្វន្ធ fនិង g ,

g(ន) =	∑	f(ឃ)
	ឃ \| ន

ពេលនោះហើយតែពេលណា

រូបមន្តបញ្ច្រាសMöbiusទីពីរ

សម្រាប់មុខងារដែលមានតម្លៃពិតប្រាកដ f(x) និង g(x) បានកំណត់នៅ,

ពេលនោះហើយតែពេលណា

នៅទីនេះចំនួនទឹកប្រាក់ត្រូវបានបកប្រែជា .

មូលនិធិវិគីមេឌា។ ឆ្នាំ ២០១០។

សូមមើលអ្វីដែល "មុខងារ Mobius" មាននៅក្នុងវចនានុក្រមផ្សេងទៀត៖

អនុគមន៍ Möbius μ(n) គឺជាអនុគមន៍លេខនព្វន្ធដែលប្រើក្នុងទ្រឹស្ដីលេខ និងបន្សំ ដែលដាក់ឈ្មោះតាមគណិតវិទូជនជាតិអាឡឺម៉ង់ Möbius ដែលបានពិចារណាវាជាលើកដំបូងក្នុងឆ្នាំ 1831។ ខ្លឹមសារ 1 និយមន័យ 2 លក្ខណៈសម្បត្តិ និងកម្មវិធី ... វិគីភីឌា

ប្រភេទនៃការបំប្លែងលើប្លង់ស្មុគ្រស្មាញ (ប្រផេះ) និងលំហ Riemann (ខ្មៅ) ខ្លឹមសារ ១ និយមន័យ ២ លក្ខណៈសម្បត្តិពិជគណិត ... វិគីភីឌា

អនុគមន៍លីនេអ៊ែរប្រភាគគឺជាមុខងារនៃទម្រង់ដែល z = (z1,...,zn) គឺជាអថេរស្មុគស្មាញ ឬពិតប្រាកដ ai,b,ci,d គឺជាមេគុណស្មុគស្មាញ ឬពិតប្រាកដ។ ជាញឹកញាប់ពាក្យ "អនុគមន៍លីនេអ៊ែរប្រភាគ" ត្រូវបានប្រើសម្រាប់ករណីពិសេសនៃការបំប្លែងរបស់វា ... ... វិគីភីឌា

ស៊េរី Möbius គឺជាស៊េរីមុខងារនៃទម្រង់ ស៊េរីនេះត្រូវបានសិក្សាដោយ Möbius ដែលបានរកឃើញរូបមន្តបញ្ច្រាសសម្រាប់ស៊េរីនេះ៖ ដែល μ(s) គឺជាអនុគមន៍ Möbius ... Wikipedia

វិធីសាស្រ្តនៃការស្រាវជ្រាវវេជ្ជសាស្រ្ត- ខ្ញុំ។ គោលការណ៍ទូទៅនៃការស្រាវជ្រាវវេជ្ជសាស្រ្ត។ ការរីកចម្រើន និងស៊ីជម្រៅនៃចំណេះដឹងរបស់យើង ឧបករណ៍បច្ចេកទេសកាន់តែច្រើនឡើងៗរបស់គ្លីនិក ដោយផ្អែកលើការប្រើប្រាស់សមិទ្ធិផលចុងក្រោយបំផុតនៃរូបវិទ្យា គីមីវិទ្យា និងបច្ចេកវិទ្យា ភាពស្មុគស្មាញដែលពាក់ព័ន្ធនៃវិធីសាស្រ្ត ...... សព្វវចនាធិប្បាយវេជ្ជសាស្ត្រដ៏អស្ចារ្យ

ស្ថានភាពរោគសាស្ត្រដែលវិវឌ្ឍន៍អំឡុងពេលសម្រាលកូនហើយត្រូវបានកំណត់លក្ខណៈដោយការខូចខាតជាលិកានិងសរីរាង្គរបស់កុមារដែលអមដំណើរជាក្បួនដោយភាពមិនប្រក្រតីនៃមុខងាររបស់ពួកគេ។ កត្តាដែលនាំឲ្យមានការវិវឌ្ឍន៍របស់ R. ដែលគេហៅថាមិនត្រឹមត្រូវ ...... សព្វវចនាធិប្បាយវេជ្ជសាស្ត្រ

លេម៉ា។

ភស្តុតាង. សេចក្តីថ្លែងការណ៍គឺជាក់ស្តែង។ អនុញ្ញាតឱ្យនិងជាការពង្រីក Canonical នៃចំនួន . បន្ទាប់មក ដោយគិតគូរថា ការបែងចែកមានទម្រង់ កន្លែងណា , ,…, ; , យើងទទួលបាន

ដោយសារតែ

ទ្រឹស្តីបទ។ (រូបមន្តបញ្ច្រាសMöbiusបន្ថែម.) អនុញ្ញាតឱ្យ និងជាមុខងារនៃអាគុយម៉ង់ធម្មជាតិ។ បន្ទាប់មកប្រសិនបើ

ភស្តុតាង. យើងមាន

អនុញ្ញាតឱ្យ។ បន្ទាប់មកថេរមួយរត់តាមរយៈតម្លៃទាំងអស់នៃការចែកលេខ . នេះមានន័យថាសញ្ញាបូកសរុបនៅក្នុងផលបូកពីរដងចុងក្រោយអាចបញ្ច្រាស់បាន i.e.

ឥឡូវនេះបានផ្តល់ថា

យើងទទួលបាន

មានទម្រង់មួយផ្សេងទៀតនៃទ្រឹស្តីបទដែលបានបញ្ជាក់៖

ទ្រឹស្តីបទ. (រូបមន្តច្រាសពហុគុណMöbius.) អនុញ្ញាតឱ្យ

ដែលជាកន្លែងដែលនិមិត្តសញ្ញាតំណាងឱ្យផលិតផលដែលបានពង្រីកទៅផ្នែកទាំងអស់នៃលេខ។

ភស្តុតាង:

ឧទាហរណ៍នៃការប្រើប្រាស់រូបមន្តបញ្ច្រាសMöbius:

បញ្ហានៅលើចំនួននៃលំដាប់ចិញ្ចៀន។ សូមមើល: Hall M. Combinatorics ។ M.: Mir, , §។

ចំនួនពហុនាមដែលមិនអាចកាត់ថ្លៃបាននៃសញ្ញាបត្រដែលបានផ្តល់ឱ្យលើវាលកំណត់នៃធាតុ។ សូមមើល៖ Berlekamp E. ទ្រឹស្តីសរសេរកូដពិជគណិត។ - M.: Mir, 1970, Ch ។ ៣.

Glukhov M. M., Elizarov V. P., Nechaev A. A. ពិជគណិត។ នៅក្នុង t. M.: Helios, . T. , §។

សម្រាប់ការសិក្សាដោយខ្លួនឯង។:

ការដាក់បញ្ច្រាស Möbius នៅលើសំណុំដែលបានបញ្ជាដោយផ្នែក។ គោលការណ៍នៃការរាប់បញ្ចូល-ដកចេញជាករណីពិសេសនៃរូបមន្តបញ្ច្រាសMöbius។ សូមមើល: Hall M. Combinatorics ។ M.: Mir, , § ; Bender E., Goldman J. លើកម្មវិធីនៃការបញ្ច្រាសMöbiusក្នុងការវិភាគបន្សំ។ នៅក្នុងសៀវភៅ៖ បញ្ហាបូកសរុបនៃការវិភាគរួម។ M.: Mir, 1971. S. - ។

ការប្រៀបធៀបសម្រាប់បន្សំលេខ

សូមឱ្យជាលេខសំខាន់។

លេម៉ា។

ភស្តុតាង. នៅពេលដែលលេខភាគក្នុងរូបមន្ត

ផលវិបាក។

ភស្តុតាង.

លេម៉ា។សូមឱ្យ , , , ជាចំនួនគត់មិនអវិជ្ជមាន ហើយអនុញ្ញាតឱ្យ , . បន្ទាប់មក

ភស្តុតាង. យើងមាន

នៅម្ខាងទៀត,

ការប្រៀបធៀបមេគុណនៅដឺក្រេដូចគ្នាយើងទទួលបានលទ្ធផលដែលត្រូវការ។ ∎

- តំណាងនៃចំនួនគត់មិនអវិជ្ជមាន និង រ៉ាឌីក។ (នេះគឺជាចំនួនគត់ដែល , )។ នៅលើសំណុំនៃចំនួនគត់មិនអវិជ្ជមាន យើងកំណត់ទំនាក់ទំនងលំដាប់ដោយផ្នែក (ទំនាក់ទំនង អាទិភាព) សន្មតថាប្រសិនបើនិងប្រសិនបើ

ទ្រឹស្តីបទរបស់ Lucas ( ).

ភស្តុតាង. នេះបើតាមការលើកឡើងរបស់លោកលើកមុន។

កន្លែងណា, ។ អនុវត្តឡេម៉ាម្តងហើយម្តងទៀតក្នុងចំនួនដងសមស្រប យើងទទួលបានលទ្ធផលចាំបាច់។ ∎

មតិយោបល់។ទ្រឹស្តីបទមិនពិតសម្រាប់អ្នកដែលមិនសំខាន់។ ឧទាហរណ៍ (មើល Berlekamp ទំ។ )

ផលវិបាក.

II . រចនាសម្ព័ន្ធពិជគណិត

II. ១. កំណត់ជាមួយប្រតិបត្តិការគោលពីរ។ ក្រុម, ក្រុមពាក់កណ្តាល, monooids

ប្រតិបត្តិការពិជគណិតគោលពីរ(ឬ ច្បាប់នៃសមាសភាព) នៅលើសំណុំមិនទទេ សហៅថាផែនទី : ការផ្គូផ្គងធាតុគូទៅនឹងធាតុដែលបានកំណត់ដោយឡែក។ ប្រតិបត្តិការជាច្រើនអាចត្រូវបានបញ្ជាក់នៅលើសំណុំមួយ។ (ជាឧទាហរណ៍ ប្រសិនបើជាឧទាហរណ៍ នោះចំនួននៃវិធីគឺស្មើនឹង កន្លែងណាជាចំនួនធាតុនៅក្នុង .) ប្រសិនបើអ្នកចង់បន្លិចមួយក្នុងចំណោមពួកវា ឧទាហរណ៍ សរសេរ , . វត្ថុបែបនេះត្រូវបានគេហៅថា ពិជគណិតគោលពីរ, ឬ ជាក្រុម. ជំនួសឱ្យ ពួកវាតែងតែសរសេរ ហើយប្រតិបត្តិការខ្លួនឯងត្រូវបានតំណាងដោយនិមិត្តសញ្ញាមួយចំនួន ( , , , ល។ ) ។

មតិយោបល់។រួមជាមួយនឹងប្រតិបត្តិការគោលពីរ ប្រតិបត្តិការ -ary ទូទៅត្រូវបានពិចារណា (unary at, ternary at ។ល។)។ រចនាសម្ព័ន្ធពិជគណិត (ប្រព័ន្ធ) ដែលភ្ជាប់ជាមួយពួកគេបង្កើតជាប្រធានបទនៃការស្រាវជ្រាវនៃអ្វីដែលគេហៅថា។ ពិជគណិតសកល។

ប្រតិបត្តិការគោលពីរនៅលើសំណុំមួយត្រូវបានគេហៅថា សមាគម, ប្រសិនបើ

, សម្រាប់ណាមួយ , , .

groupoid ដែលមានប្រតិបត្តិការសហការត្រូវបានគេហៅថា ក្រុមពាក់កណ្តាល.

ឧទាហរណ៍នៃ groupoid ដែលមិនពាក់ព័ន្ធ។នៅលើសំណុំយើងកំណត់ប្រតិបត្តិការជា . ប្រតិបត្តិការគឺមិនពាក់ព័ន្ធ៖ ប៉ុន្តែ .

ទ្រឹស្តីបទ។ប្រសិនបើប្រតិបត្តិការគោលពីរនៅលើសំណុំមួយគឺជាប់ទាក់ទងគ្នា នោះតម្លៃនៃកន្សោមមិនអាស្រ័យលើការដាក់វង់ក្រចកនៅក្នុងវាទេ។

ភស្តុតាង។ជាមួយ ឬសេចក្តីថ្លែងការណ៍គឺជាក់ស្តែង។ សម្រាប់វាគឺគ្រប់គ្រាន់ដើម្បីបង្ហាញ, ប្រើ induction, នោះ។

សម្រាប់ណាមួយ, ។ ដោយសម្មតិកម្មនៃការបញ្ចូល ការដាក់តង្កៀបនៅក្នុង

មិនសំខាន់; ជាពិសេស, ។

បើអញ្ចឹង។

បើអញ្ចឹង

ផ្នែកខាងស្តាំនៃសមភាពដែលកំពុងត្រូវបានបញ្ជាក់ (1) ក៏ត្រូវបានកាត់បន្ថយទៅជាទម្រង់ដូចគ្នា។ ∎

ធាតុត្រូវបានគេហៅថា អព្យាក្រឹតទាក់ទងនឹងប្រតិបត្តិការប្រសិនបើ

សម្រាប់នរណាម្នាក់។

ក្រុមពាក់កណ្តាលដែលមានធាតុត្រូវបានគេហៅថា ម៉ូណូអ៊ីដ(ឬ ក្រុមពាក់កណ្តាលដែលមានអត្តសញ្ញាណ) និងបញ្ជាក់ , , .

ក្រុមពាក់កណ្តាល (ក្រុម) អាចមានធាតុអព្យាក្រឹតបំផុតមួយ៖ ប្រសិនបើ

នោះគឺជាធាតុអព្យាក្រឹត

groupoid (ក្រុមពាក់កណ្តាល) ត្រូវបានគេហៅថា ក្រុមរង (ក្រុមរង) groupoid (ក្រុមពាក់កណ្តាល), , ប្រសិនបើ

និងសម្រាប់ណាមួយ, ។

ក្នុងករណីនេះពួកគេនិយាយថាសំណុំរង បានបិទនៅក្រោមប្រតិបត្តិការ. Monoid ត្រូវបានគេហៅថា submonoid monoid , , , ប្រសិនបើ និង .

ធាតុនៃម៉ូណូអ៊ីតត្រូវបានគេហៅថា អាចបញ្ច្រាស់បាន។ប្រសិនបើមានធាតុបែបនេះ (ច្បាស់ណាស់ យើងនឹងដាក់បញ្ច្រាស)។ ប្រសិនបើធាតុមានទ្រព្យសម្បត្តិដូចគ្នា i.e. បន្ទាប់មកពីសមភាពវាដូចខាងក្រោមថាធាតុពិតជាមានតែមួយគត់ (ទាក់ទងនឹង ) ។ នេះអនុញ្ញាតឱ្យយើងនិយាយអំពី បញ្ច្រាសធាតុ , ទៅ (បញ្ច្រាស) ធាតុ , ជាមួយនឹងលក្ខណៈសម្បត្តិ: , .

ប្រសិនបើ , គឺជាធាតុបញ្ច្រាសនៃម៉ូណូអ៊ីត , , , នោះផលិតផលរបស់ពួកគេក៏ជាធាតុមិនបញ្ច្រាស់ដែរ ចាប់តាំងពី , . ជាក់ស្តែងវាគឺជាធាតុដែលមិនអាចត្រឡប់វិញបាន។ ដូច្នេះមាន

ទ្រឹស្តីបទ។សំណុំនៃធាតុបញ្ច្រាសទាំងអស់នៃ monooid , , ត្រូវបានបិទនៅក្រោមប្រតិបត្តិការ ∗ និងបង្កើតជា submonoid នៅក្នុង , , .

ក្រុម

និយមន័យនៃក្រុម។ម៉ូណូអ៊ីត , , ធាតុទាំងអស់របស់វាត្រូវបានដាក់បញ្ច្រាសត្រូវបានគេហៅថា ក្រុម។

ម្យ៉ាងវិញទៀត ក្រុមមួយគឺជាសំណុំដែលមានប្រតិបត្តិការគោលពីរដែល axioms ខាងក្រោមមាន៖

. (ប្រតិបត្តិការបិទ.) , .

. (សមាគមប្រតិបត្តិការ.) ,

. (អត្ថិភាពនៃធាតុអព្យាក្រឹត.) ∃ .

. (អត្ថិភាពនៃធាតុបញ្ច្រាស.) .

មតិយោបល់។ត្រលប់ទៅរចនាសម្ព័ន្ធពិជគណិតដែលបានណែនាំខាងលើ យើងសង្កេតមើលឋានានុក្រមខាងក្រោមក្នុងចំណោមពួកគេ៖ គូ , គឺ ជាក្រុមប្រសិនបើ axiom ពេញចិត្ត; ក្រុមពាក់កណ្តាលប្រសិនបើ axioms និង ; ម៉ូណូអ៊ីដប្រសិនបើ axioms និង ; ក្រុមប្រសិនបើ axioms , , និង .

កម្រិតនៃធាតុដែលមានលក្ខណៈសម្បត្តិជាក់ស្តែងត្រូវបានកំណត់តាមវិធីធម្មជាតិ៖

(ម្តង),

; , ( , , .

និយាយជាទូទៅ វាមិនអាចទៅរួចទេក្នុងការរៀបចំធាតុនៅក្នុងកន្សោម (ឧ. ) ប្រសិនបើ បន្ទាប់មកធាតុត្រូវបានគេហៅថា អាចផ្លាស់ប្តូរបាន។, ឬ ការធ្វើដំណើរ. ប្រសិនបើធាតុពីរនៃការធ្វើដំណើរជាក្រុម នោះក្រុមត្រូវបានគេហៅថា ផ្លាស់ប្តូរ, ឬ អាបៀន(ជាកិត្តិយសរបស់គណិតវិទូន័រវេស Riehl Henrik Abel (-))។

ប្រតិបត្តិការនៅក្នុងក្រុមមួយត្រូវបានចង្អុលបង្ហាញជាញឹកញាប់បំផុតដោយនិមិត្តសញ្ញា (បន្ថែម) ឬនិមិត្តសញ្ញា (គុណ)។ ក្នុងករណីនេះក្រុមត្រូវបានហៅតាម សារធាតុបន្ថែមឬ ពហុគុណធាតុអព្យាក្រឹតរបស់វារៀងៗខ្លួន សូន្យ() ឬ ឯកតា( ). នៅក្នុងក្រុមបន្ថែម ធាតុ ធាតុបញ្ច្រាស ត្រូវបានគេហៅថា ទល់មុខហើយត្រូវបានគេកំណត់ ប៉ុន្តែជំនួសវិញពួកគេសរសេរ។ នៅក្នុងក្រុមពហុគុណ ពួកគេជាធម្មតាសរសេរជំនួសវិញ ដោយលុបនិមិត្តសញ្ញាប្រតិបត្តិការ។

ឧទាហរណ៍នៃក្រុមបន្ថែម។ 1) , , , , , , , , - ក្រុមបន្ថែមនៃសង្វៀន និងវាល , , . ពួកគេគ្រាន់តែសរសេរ , , , . 2) ចិញ្ចៀនណាមួយដោយការបន្ថែមគឺជាក្រុម Abelian ។ ជាពិសេស ring of polynomials ,…, ] និង ring of matrices of order over a field គឺជាក្រុម Abelian ។ 3) ចន្លោះវ៉ិចទ័រណាមួយនៅលើវាលដែលទាក់ទងនឹងការបន្ថែមគឺជាក្រុម Abelian ។ 4) , 1, … , – ប្រព័ន្ធពេញលេញនៃសំណល់ម៉ូឌុលដែលមិនអវិជ្ជមានយ៉ាងតិចជាមួយនឹងប្រតិបត្តិការបន្ថែមម៉ូឌុល។

ឧទាហរណ៍នៃក្រុមពហុគុណ។ 1) , , គឺជាក្រុមពហុគុណនៃវាល , , . 2) គឺជាសំណុំនៃធាតុបញ្ច្រាសនៃចិញ្ចៀនណាមួយជាមួយនឹងការរួបរួមនៅក្រោមការគុណ។ ជាពិសេស, = ; , គឺជាសំណុំនៃម៉ាទ្រីសបញ្ច្រាសពី . 3) - ឫសទាំងអស់ (ពិតនិងស្មុគស្មាញ)

, , 1 , … , , - ឯកតាស្រមើលស្រមៃ,

សមីការគឺជាក្រុម Abelian ពហុគុណ។ 4) - សំណុំនៃការបង្វិលនៃ -gon ធម្មតានៅក្នុងយន្តហោះនិងក្នុងលំហ - ក្រុមដែលមិនផ្លាស់ប្តូរ (សម្រាប់ ) ។

លើសពីនេះ ទម្រង់ពហុគុណនៃការកត់ត្រាប្រតិបត្តិការគឺត្រូវបានប្រើប្រាស់ញឹកញាប់ជាង។ ជាធម្មតាក្រុមត្រូវបានកំណត់ដោយអក្សរតែមួយដោយមិនបញ្ជាក់ប្រតិបត្តិការ។ សំណុំនៃធាតុទាំងអស់នៃក្រុមត្រូវបានគេហៅថា សំណុំសំខាន់នៃក្រុមហើយត្រូវបានតំណាងដោយអក្សរដូចគ្នា។ ប្រសិនបើសំណុំមូលដ្ឋានត្រូវបានកំណត់ នោះក្រុមត្រូវបានហៅ ចុងក្រោយ; បើមិនដូច្នោះទេវាត្រូវបានគេហៅថា គ្មានទីបញ្ចប់. ធាតុលេខនៃក្រុមកំណត់ត្រូវបានគេហៅថារបស់វា។ នៅក្នុងលំដាប់. ក្រុមនៃលំដាប់ 1 ត្រូវបានហៅ នៅលីវ, ឬ T គូប្រជែង. ក្រុមគ្មានកំណត់មួយត្រូវបានគេនិយាយថាមាន លំដាប់គ្មានកំណត់. ដើម្បីចង្អុលបង្ហាញលំដាប់នៃក្រុម (ខានៃសំណុំមេ) និមិត្តសញ្ញាស្មើគ្នា កាត (លេខខា) និង () ត្រូវបានប្រើ។

ប្រសិនបើ , គឺជាសំណុំរង (នៃសំណុំសំខាន់) នៃក្រុម នោះយើងដាក់

, , .

ក្រុមរងនៃក្រុមគឺជាសំណុំរងដែលខ្លួនវាផ្ទាល់ជាក្រុមទាក់ទងនឹងប្រតិបត្តិការដូចគ្នាដូចនៅក្នុង . ម្យ៉ាងវិញទៀត សំណុំរងគឺជាក្រុមរងប្រសិនបើ និងបានតែប្រសិនបើ (មួយក្នុង ) ហើយត្រូវបានបិទក្រោមការគុណ និងគ្នាទៅវិញទៅមក ពោលគឺឧ។ , (តាមពិតមានសូម្បីតែសមភាពនៅទីនេះ) ។ ប្រសិនបើជាក្រុមរងនៅក្នុង នោះសរសេរ ; ប្រសិនបើនៅពេលជាមួយគ្នានោះវាត្រូវបានគេហៅថា ផ្ទាល់ខ្លួនក្រុមរង ហើយនេះត្រូវបានតំណាងថាជា .

មុខងារ Möbius  (ន) កន្លែងណា ន- លេខធម្មជាតិយកតម្លៃដូចខាងក្រោមៈ

អនុគមន៍ Möbius អនុញ្ញាតឱ្យអ្នកសរសេរអនុគមន៍អយល័រជាផលបូក៖

ការបូកសរុបគឺលើផ្នែកទាំងអស់នៃ n (ហើយមិនគ្រាន់តែលើសការបែងចែកបឋមទេ)។

ឧទាហរណ៍។ចូរយើងគណនា φ (100) ដោយប្រើមុខងារ Möbius ។

ការបែងចែកទាំងអស់នៃ 100 គឺ (1, 2, 4, 5, 10, 20, 25, 50, 100) ។

(2) = (-1) 1 = −1 (ពីរមានមេចែកមួយ − 2)

(4) = 0 (4 ចែកនឹងការេនៃពីរ)

(5) = (-1) 1 = -1 (5 មានមេចែកបឋមមួយ − 5)

(10) = (-1) 2 = 1 (10 មានកត្តាសំខាន់ពីរគឺ 2 និង 5)

(20) = 0 (20 ចែកនឹងការេនៃពីរ)

(25) = 0 (25 ចែកនឹងការេនៃប្រាំ)

(50) = 0 (50 ត្រូវបានបែងចែកដោយ 2 2 និង 5 5)

(100) = 0 (100 ត្រូវបានបែងចែកដោយ 2 2 និង 5 5)

ដូច្នេះ

ទ្រព្យសម្បត្តិនៃមុខងារMöbius៖.

ឧទាហរណ៍, ន=100, {1, 2, 4, 5, 10, 20, 25, 50, 100}.

16 ទ្រឹស្តីបទអំពីចំនួនវិធីដើម្បីជ្រើសរើសធាតុ k ដែលក្នុងនោះមិនមានពីរនៅជាប់គ្នាទេ ពីធាតុ n ដែលរៀបចំជាជួរ។ បញ្ជាក់ដោយទទួលបានរូបមន្តកើតឡើងវិញ។

17 ចំនួននៃបន្សំជាមួយពាក្យដដែលៗ

ចំនួន r- បន្សំជាមួយពាក្យដដែលៗពី ន- សំណុំគឺស្មើគ្នា

– ភស្តុតាងដោយប្រើរូបមន្តកើតឡើងវិញ។

វិធីសាស្រ្តគឺផ្អែកលើការទទួលបានរូបមន្តដែលអនុញ្ញាតឱ្យអ្នកគណនាតម្លៃនៃបរិមាណដែលចង់បានមួយជំហានម្តងៗ ដោយផ្អែកលើតម្លៃដំបូងដែលគេស្គាល់ និងតម្លៃដែលបានគណនាក្នុងជំហានមុនៗ។

រូបមន្តកើតឡើងវិញ។r - លំដាប់- រូបមន្តនៃទម្រង់

ក ន = f(ន, ក n- 1 , ក n- 2 , … , ក n-r).

រូបមន្តបង្ហាញនៅ n>rសមាជិកនីមួយៗនៃលំដាប់ ( ក ខ្ញុំ) តាមរយៈមុន។ rសមាជិក។ ការសាងសង់រូបមន្តកើតឡើងវិញមានជំហានដូចខាងក្រោម។

1. ការអភិវឌ្ឍន៍លក្ខខណ្ឌដំបូងផ្អែកលើទំនាក់ទំនងជាក់ស្តែងណាមួយ។

ចូរយើងបញ្ជាក់ដោយ f(n,r) វាច្បាស់ណាស់។

2. ហេតុផលឡូជីខល។អនុញ្ញាតឱ្យយើងជួសជុលធាតុមួយចំនួននៅក្នុងសំណុំ ស. បន្ទាប់មកទាក់ទងទៅនឹងណាមួយ។ r- បន្សំជាមួយពាក្យដដែលៗពី ន- សំណុំ សយើងអាចដឹងថាតើវាមានធាតុថេរដែលបានផ្តល់ឱ្យឬអត់។

ប្រសិនបើ មានបន្ទាប់មកនៅសល់ ( r-1) ធាតុអាចត្រូវបានជ្រើសរើស f(ន,r-1) វិធី។

ប្រសិនបើ មិនមាន(ធាតុនេះមិនមាននៅក្នុងជម្រើសទេ) បន្ទាប់មក r- ការរួមបញ្ចូលគ្នានៃធាតុ ( ន-1) - សំណុំ (សំណុំ សលើកលែងតែធាតុថេរនេះ) ។ ចំនួននៃបន្សំបែបនេះ f(ន-1,r).

ដោយសារតែ ករណីទាំងនេះគឺផ្តាច់មុខទៅវិញទៅមក បន្ទាប់មកយោងតាមច្បាប់បូក

3. ពិនិត្យរូបមន្តលើតម្លៃមួយចំនួន និងកាត់លំនាំទូទៅ.

1) ចូរយើងគណនា f (ន ,0) . ពី (2) វាធ្វើតាម

បន្ទាប់មក f(ន,0)=f(ន,1)-f(ន-១,១)។ ពី (1) f(ន,1)=n,f(ន-1,1)=ន-1.

អាស្រ័យហេតុនេះ f(ន,0)=ន-(ន-1)=1=.

2) f (ន ,1) =f(ន,0)+f(ន-1,1) = 1+n- 1 =ន==.

3) f (ន ,2) =f(ន,1)+f(ន-1,2) =ន+f(ន-1,1)+f(ន-2,2) =ន+(ន-1)+f(ន-2,1)+f(ន-3,2) = … =

= ន+(ន-1)+…+2+1 =.

(ផលបូកនៃដំណើរការនព្វន្ធ)

4) f (ន ,3) =f(ន,2)+f(ន-1,3) =+f(ន-1,2)+f(ន-2,3) =++f(ន-2,2)+f(ន-3,3) = … =

(ផលបូកនៃវឌ្ឍនភាពធរណីមាត្រ)

5) f (ន ,4) =

ដោយផ្អែកលើករណីជាក់លាក់វាអាចត្រូវបានសន្មត់ថា

4. ពិនិត្យលក្ខខណ្ឌដំបូងដោយប្រើរូបមន្តលទ្ធផល។

ដែលស្របនឹង (1) #

19, 20) ចំនួនដើមឈើគោលពីរដែលមានចំនុចកំពូលគឺស្មើនឹង C(n) ដែល C(n) ជាលេខ Catalan ទី n ។

ចំនួនដើមឈើគោលពីរដែលមានចំនុចកំពូលត្រូវបានគេហៅថាលេខ Catalan ដែលមានលក្ខណៈសម្បត្តិគួរឱ្យចាប់អារម្មណ៍ជាច្រើន។ លេខ Nth Catalan ត្រូវបានគណនាដោយប្រើរូបមន្ត (2n)! / (n+1)!n!, ដែលលូតលាស់ជាអិចស្ប៉ូណង់ស្យែល។ (វិគីភីឌាផ្តល់នូវភស្តុតាងជាច្រើនដែលថានេះគឺជាទម្រង់នៃលេខកាតាឡាន។) ចំនួនដើមឈើគោលពីរនៃទំហំដែលបានផ្តល់ឱ្យ 0 1 1 1 2 2 4 14 8 1430 12 208012 16 35357670

ការជំនួស

ទៅ: ការរុករក, ស្វែងរក

នេះគឺជាអត្ថបទអំពីការជំនួសជាប្រតិបត្តិការវាក្យសម្ព័ន្ធនៅលើកំដៅ . អ្នកប្រហែលជាចាប់អារម្មណ៍ការរៀបចំឡើងវិញ .

IN គណិតវិទ្យានិង វិទ្យាសាស្ត្រកុំព្យូទ័រ ការជំនួស- នេះគឺជាប្រតិបត្តិការ វាក្យសម្ព័ន្ធការជំនួសនៃលក្ខខណ្ឌរងដែលបានផ្តល់ឱ្យ ពាក្យលក្ខខណ្ឌផ្សេងទៀត យោងតាមច្បាប់ជាក់លាក់។ ជាធម្មតាយើងកំពុងនិយាយអំពីការជំនួសពាក្យជំនួសវិញ។ អថេរ.

និយមន័យនិងសញ្ញាណ

មិនមានសញ្ញាណដែលយល់ព្រមជាសកលសម្រាប់ការជំនួស ហើយក៏មិនមាននិយមន័យស្តង់ដារដែរ។ គោលគំនិតនៃការជំនួសមិនគ្រាន់តែនៅក្នុងផ្នែកប៉ុណ្ណោះទេប៉ុន្តែថែមទាំងនៅកម្រិតនៃការបោះពុម្ពបុគ្គលផងដែរ។ ជាទូទៅយើងអាចបន្លិច ការជំនួសបរិបទនិង ជំនួស "ជំនួស". ក្នុងករណីដំបូងកន្លែងនៅក្នុងពាក្យដែលការជំនួសកើតឡើងត្រូវបានផ្តល់ឱ្យ បរិបទនោះគឺជាផ្នែកមួយនៃពាក្យ "ជុំវិញ" កន្លែងនេះ។ ជាពិសេសគំនិតនៃការជំនួសនេះត្រូវបានប្រើនៅក្នុង ការសរសេរឡើងវិញ. ជម្រើសទីពីរគឺជារឿងធម្មតាជាង។ ក្នុងករណីនេះ ការជំនួសជាធម្មតាត្រូវបានបញ្ជាក់ដោយមុខងារមួយចំនួនពីសំណុំនៃអថេរទៅជាសំណុំនៃពាក្យ។ ដើម្បីចង្អុលបង្ហាញ សកម្មភាពជំនួសតាមក្បួនមួយប្រើ កំណត់ចំណាំ postfix. ឧទាហរណ៍ មានន័យថាលទ្ធផលនៃសកម្មភាពជំនួសលើពាក្យមួយ។

ក្នុងករណីភាគច្រើនលើសលប់ វាត្រូវបានទាមទារឱ្យមានការជំនួសមានក្រុមហ៊ុនដឹកជញ្ជូនកំណត់ ពោលគឺសំណុំ មានកំណត់។ ក្នុងករណីនេះវាអាចត្រូវបានបញ្ជាក់ដោយគ្រាន់តែរាយបញ្ជីគូ "តម្លៃអថេរ". ដោយសារការជំនួសនីមួយៗអាចត្រូវបានកាត់បន្ថយទៅជាលំដាប់នៃការជំនួសដែលជំនួសតែអថេរមួយប៉ុណ្ណោះ ដោយមិនបាត់បង់ភាពទូទៅ យើងអាចសន្មត់ថាការជំនួសត្រូវបានផ្តល់ឱ្យដោយគូមួយ។ "តម្លៃអថេរ"ដែលជាធម្មតាត្រូវបានធ្វើ។

និយមន័យចុងក្រោយនៃការជំនួសគឺប្រហែលជាធម្មតាបំផុត និងត្រូវបានគេប្រើញឹកញាប់បំផុត។ ទោះយ៉ាងណាក៏ដោយ ក៏មិនមានសញ្ញាណដែលទទួលយកជាទូទៅសម្រាប់វាដែរ។ ភាគច្រើនត្រូវបានគេប្រើដើម្បីចង្អុលបង្ហាញការជំនួស កជំនួសអោយ xវ tការថតត្រូវបានប្រើប្រាស់ t[ក/x], t[x:=ក] ឬ t[x←ក].

ការជំនួសអថេរនៅក្នុងλ-គណនា

នៅក្នុង λ-calculus ការជំនួសត្រូវបានកំណត់ដោយការបញ្ចូលរចនាសម្ព័ន្ធ។ សម្រាប់វត្ថុបំពាន និងអថេរបំពាន លទ្ធផលនៃការជំនួសការកើតឡើងដោយសេរីត្រូវបានគណនា ការជំនួសនិងត្រូវបានកំណត់ដោយការណែនាំលើការសាងសង់៖

(i) មូលដ្ឋាន៖៖ វត្ថុត្រូវគ្នានឹងអថេរ។ បន្ទាប់មក;

(ii) មូលដ្ឋាន៖៖ វត្ថុត្រូវគ្នានឹងថេរ។ បន្ទាប់មកសម្រាប់អាតូមបំពាន;

(iii) ជំហាន៖ ៖ វត្ថុមិនមែនជាអាតូមិច ហើយមានរូបរាងនៃកម្មវិធី។ បន្ទាប់មក;

(iv) ជំហាន៖៖ វត្ថុមិនមែនជាអាតូមិក និងជាអរូបី។ បន្ទាប់មក [;

(v) ជំហាន៖៖ វត្ថុមិនមែនជាអាតូមិក ហើយជាអរូបី លើសពីនេះទៅទៀត ។ បន្ទាប់មក៖

សម្រាប់ Andor;

ការជំនួសអថេរក្នុងការសរសេរកម្មវិធី

ការជំនួសអថេរ ( ភាសាអង់គ្លេស ការជំនួស) វ កម្មវិធីអនុវត្តត្រូវបានយល់ដូចខាងក្រោម។ ដើម្បីគណនាតម្លៃនៃអនុគមន៍ fនៅលើអាគុយម៉ង់ vការចូលត្រូវបានអនុវត្ត f(v)) កន្លែងណា fកំណត់ដោយការរចនា f(x) = e. កត់ត្រា f(v)ក្នុងករណីនេះមានន័យថានៅក្នុងកន្សោម អ៊ីកំពុងកើតឡើង ការជំនួសឬការជំនួសអថេរ xនៅលើ v. ការជំនួសត្រូវបានអនុវត្តស្របតាម semantics នៃការគណនា.

ការជំនួសអថេរ ( ភាសាអង់គ្លេស កិច្ចការ) វ ការសរសេរកម្មវិធីយល់ថាជា កិច្ចការ. ប្រតិបត្តិករការចាត់តាំងគឺជាការបង្ហាញពីឥទ្ធិពលនៃការរារាំងរបស់ von Neumann សម្រាប់ភាសាសរសេរកម្មវិធីប្រពៃណី . ទំនេរពីនេះ។ ប្រព័ន្ធកុំព្យូទ័រអនុវត្ត.

http://math.nsc.ru/LBRT/u3/bard/fails/Brenner_Evans.pdf

21 ការបង្កើតមុខងារ។ការបង្កើតអនុគមន៍ (លេខរៀង) និងការរាប់បញ្ចូលមុខងារបង្កើតសម្រាប់បន្សំដោយគ្មានពាក្យដដែលៗ។

ការបង្កើតមុខងារ៖ 1) ការផ្លាស់ប្តូរ Z 2) ម៉ាស៊ីនភ្លើង 3) បង្កើតមុខងារ 4) បង្កើតមុខងារនៃលំដាប់ (a r) នៅលើមូលដ្ឋាន (g r) - មុខងារ f នៅពេលដែលពង្រីកទៅជាស៊េរីនៃមុខងារនៃមូលដ្ឋានថេរ (g r) ។ លំដាប់នៃមេគុណ (a r) ត្រូវបានបង្កើតឡើង …………*)

ស៊េរីនេះគឺផ្លូវការ។ ឈ្មោះផ្លូវការមានន័យថាយើងចាត់ទុករូបមន្ត *) ជាសញ្ញាណងាយស្រួលសម្រាប់លំដាប់របស់យើង - ក្នុងករណីនេះវាមិនមានបញ្ហាដែលតម្លៃ (សកម្មភាព និងភាពស្មុគស្មាញ) ដែលវាបញ្ចូលគ្នានោះទេ។ តួនាទីរបស់ t ត្រូវបានកាត់បន្ថយទៅជាការបែងចែកមេគុណនៃលំដាប់ A0, A1,…Ar…. ដូច្នេះហើយនៅក្នុងទ្រឹស្តីនៃការបង្កើតមុខងារ តម្លៃនៃស៊េរីនេះមិនដែលត្រូវបានគណនាសម្រាប់តម្លៃជាក់លាក់នៃអថេរ t ។ មានតែប្រតិបត្តិការមួយចំនួនប៉ុណ្ណោះដែលត្រូវបានអនុវត្តនៅលើស៊េរីបែបនេះ ហើយបន្ទាប់មកមានតែប្រតិបត្តិការមួយចំនួននៅលើស៊េរីបែបនេះប៉ុណ្ណោះដែលត្រូវបានកំណត់ ហើយបន្ទាប់មកមេគុណត្រូវបានកំណត់សម្រាប់អំណាចបុគ្គលនៃអថេរ t ។

ជាធម្មតាដូច

22 ការបង្កើតមុខងារ។ ការបង្កើតអនុគមន៍ (លេខរៀង) និងការរាប់បញ្ចូលមុខងារបង្កើតសម្រាប់បន្សំជាមួយពាក្យដដែលៗ។

កន្លែងផលិតសម្រាប់៖

ច្បាប់សំណង់

1) ប្រសិនបើធាតុនៃប្រភេទ i អាចត្រូវបានរួមបញ្ចូលនៅក្នុងបន្សំ K 1 ឬ K 2 ឬ ... K i ដង នោះវាមានមេគុណដែលត្រូវគ្នា

3) វានៅសល់ដើម្បីរកមេគុណ។ នៅ

អនុគមន៍បង្កើតអិចស្ប៉ូណង់ស្យែលសម្រាប់ច្បាប់សំណង់កន្លែង

25) លេខបន្សំក៏រួមបញ្ចូលផងដែរ។ លេខ Stirlingនៃប្រភេទទីមួយនិងទីពីរ។ លេខទាំងនេះត្រូវបានកំណត់ជាមេគុណនៅក្នុងសមភាព

និងមានអត្ថន័យបន្សំសាមញ្ញ - ស្មើនឹងចំនួនធាតុនៃក្រុម permutation ដែលជាផលិតផលពិតប្រាកដ k disjoint cycles និងស្មើនឹងចំនួនភាគថាស n-ធាតុដែលបានកំណត់ kសំណុំរងមិនទទេ។ វាច្បាស់ណាស់។ ផលបូកស្រដៀងគ្នានៃលេខ Stirling នៃប្រភេទទីពីរត្រូវបានគេហៅថា ន- លេខកណ្ដឹង និងស្មើនឹងចំនួនភាគថាសទាំងអស់។ ន- សំណុំធាតុ។ រូបមន្តកើតឡើងវិញមានសុពលភាពសម្រាប់លេខ Bell ។

នៅពេលដោះស្រាយបញ្ហាបន្សំវាច្រើនតែមានប្រយោជន៍ រូបមន្តរាប់បញ្ចូល - មិនរាប់បញ្ចូល

ដែលអនុញ្ញាតឱ្យមនុស្សម្នាក់ស្វែងរក cardinality នៃ union of sets ប្រសិនបើ cardinality នៃចំនុចប្រសព្វរបស់ពួកគេត្រូវបានគេស្គាល់។ អនុញ្ញាតឱ្យយើងប្រើរូបមន្តការរាប់បញ្ចូល - ការបដិសេធដើម្បីទទួលបានរូបមន្តច្បាស់លាស់សម្រាប់លេខ Stirling នៃប្រភេទទីពីរ។

លេខ Stirling នៃប្រភេទទីមួយ

សម្ភារៈពីវិគីភីឌា - សព្វវចនាធិប្បាយឥតគិតថ្លៃ

ទៅ: ការរុករក, ស្វែងរក

លេខ Stirling នៃប្រភេទទីមួយ(មិនបានចុះហត្ថលេខា) - បរិមាណ ការផ្លាស់ប្តូរលំដាប់ នជាមួយ k វដ្ត.

និយមន័យ

លេខ Stirling នៃប្រភេទទីមួយ(មានសញ្ញា) s(n, k)ត្រូវបានគេហៅថាមេគុណ ពហុនាម:

កន្លែងណា ( x) ន - និមិត្តសញ្ញា Pochhammer (ថយចុះ Factorial):

ដូចដែលអាចមើលឃើញពីនិយមន័យ លេខមានសញ្ញាឆ្លាស់គ្នា។ តម្លៃដាច់ខាតរបស់ពួកគេបញ្ជាក់លេខ ការផ្លាស់ប្តូរសំណុំរួមមាន នធាតុជាមួយ k វដ្ត.

ទំនាក់ទំនងកើតឡើងវិញ។

លេខ Stirling នៃប្រភេទទីមួយត្រូវបានផ្តល់ឱ្យ កើតឡើងវិញ។សមាមាត្រ៖

ស(ន,ន) = 1, សម្រាប់ n ≥ 0,

ស(ន,0) = 0, សម្រាប់ n > 0,

សម្រាប់ 0< k < ន.

ភស្តុតាង។

សម្រាប់ ន=1 សមភាពនេះត្រូវបានពិនិត្យដោយផ្ទាល់។ អនុញ្ញាតឱ្យការផ្លាស់ប្តូរ ( ន-1) លំដាប់ទីមួយត្រូវបានរលាយចូលទៅក្នុង kវដ្ត។ ចំនួន នអាចត្រូវបានបន្ថែមបន្ទាប់ពីលេខណាមួយនៅក្នុងរង្វិលជុំដែលត្រូវគ្នា។ ការបំប្លែងលទ្ធផលទាំងអស់គឺខុសគ្នា ហើយមានវដ្ត k ចំនួនរបស់ពួកគេ ( ន-1) · ស(ន-1, k) ពីការផ្លាស់ប្តូរណាមួយ ( ន-1) លំដាប់ដែលមាន k-1 វដ្ដ ការផ្លាស់ប្តូរតែមួយអាចត្រូវបានបង្កើតឡើង នលំដាប់ដែលមាន kវដ្តដោយបន្ថែមវដ្ដដែលបង្កើតឡើងដោយលេខឯកវចនៈ ន. ជាក់ស្តែង សំណង់នេះពិពណ៌នាអំពីការផ្លាស់ប្តូរទាំងអស់។ ន- លំដាប់ដែលមាន kវដ្ត។ ដូច្នេះសមភាពត្រូវបានបញ្ជាក់។

ឧទាហរណ៍

ជួរទីមួយ៖

IN ឧបករណ៍ផ្សំ លេខ Stirling នៃប្រភេទទីពីរពី នដោយ kតំណាងដោយ ឬ គឺជាចំនួននៃ unordered ភាគថាស ន- ធាតុ សំណុំនៅលើ kសំណុំរងមិនទទេ។

រូបមន្តកើតឡើងវិញ។

លេខ Stirling នៃប្រភេទទីពីរពេញចិត្ត កើតឡើងវិញ។សមាមាត្រ៖

សម្រាប់ n ≥ 0,

សម្រាប់ n > 0,

រូបមន្តច្បាស់លាស់

ឧទាហរណ៍

តម្លៃដំបូងនៃលេខ Stirling នៃប្រភេទទីពីរត្រូវបានផ្តល់ឱ្យក្នុងតារាង:

ទ្រព្យសម្បត្តិ

គោលបំណងការធ្វើផែនទីគឺជាការគូសផែនទីដែលមានលក្ខណៈសម្បត្តិនៃការចាក់បញ្ចូល និងទស្សន៍ទាយក្នុងពេលតែមួយ។

1. ចូរយើងរំលឹកឡើងវិញនូវនិយមន័យនៃអនុគមន៍លេខទ្រឹស្តីសំខាន់-Möbiu

1 ប្រសិនបើ n = 1

µ (n) = 0 បើមានលេខបឋម p, p2 n (-1)k ប្រសិនបើ n = p1 ... pk គឺជាផលនៃកត្តាបឋមផ្សេងគ្នា k ។

ចូរយើងបង្ហាញពីលក្ខណៈសម្បត្តិសំខាន់នៃមុខងារ Möbius៖

ទ្រឹស្តីបទ ១.

♦ប្រសិនបើ n = 1 នោះការបែងចែកតែមួយគត់គឺ d = 1 ហើយ (1) គឺពិត ពីព្រោះ µ (1) = 1. ឥឡូវឲ្យ n > 1. ចូរយើងតំណាងវាក្នុងទម្រង់

n = p1 s 1 ps 2 2 K ps k k ,

ដែល pi, i 1, k ជាលេខបឋម, si គឺជាអំណាចរបស់ពួកគេ។ ប្រសិនបើ d ជាការបែងចែក n នោះ d = p1 d 1 pd 2 2 K pd k k ,

ដែល 0 ≤ di ≤ si, i 1, k ។ ប្រសិនបើ di > 1 សម្រាប់ខ្លះ i 1, k បន្ទាប់មក µ (d) = 0 ។ នេះមានន័យថាក្នុង (1) យើងត្រូវពិចារណាតែ d ដែល di ≤ 1, i 1, k ។ ការបែងចែកបែបនេះនីមួយៗ

មានផលិតផលនៃលេខបឋមផ្សេងគ្នា r ដែល r 1, k និងការរួមចំណែករបស់វាចំពោះផលបូក

(1) ស្មើនឹង (-1)r ហើយមាន k សរុប។ ដូច្នេះយើងទទួលបាន


	µ (d) = 1 −	K + (− 1) ក	0. ♦



	ទ្រឹស្តីបទ 2. (រូបមន្តបញ្ច្រាស Mobius) ។ អនុញ្ញាតឱ្យ f(n) និង g(n) ជាមុខងារនៃធម្មជាតិ
អាគុយម៉ង់ ral ។ បន្ទាប់មកសមភាព
			∑f(d)

គឺពិតប្រសិនបើសមភាពគឺពិត
			∑ µ (d)g(
			∑ µ (d)g(

♦ ចូរ (2) ពិតសម្រាប់ n ។ បន្ទាប់មក

g(d n) = ∑ f(d′)

ឃ ឃ ន

ជំនួសដោយផ្នែកខាងស្តាំនៃ (3) យើងទទួលបាន

∑ µ (d)g(	) = ∑ µ (d) ∑ f (d′ )

		ឃ

ការបូកសរុបពីរដងនៅខាងស្តាំត្រូវបានអនុវត្តលើគូទាំងអស់ d, d′ នោះ d d′ n ។ ប្រសិនបើអ្នកជ្រើសរើស d ' នោះ d នឹងរត់តាមផ្នែកទាំងអស់ d n ' ។ ដូច្នេះ

∑ µ (d)g(

) = ∑ f(d′ ) ∑ µ (d′ )

ឃ

n > d '

ប៉ុន្តែយោងទៅតាម (1) យើងមាន ∑

µ (d′) =

n = d′

ឃ

នេះមានន័យថាសមភាព (៣) ត្រូវបានបង្កើតឡើង។ ឥឡូវនេះសូមឱ្យ (3) ជាការពិតសម្រាប់ n ។ បន្ទាប់មក

∑ f(d) =

∑ ∑ µ (d′ )g(

) d′ = d d′ - គឺជាការបែងចែក n ហើយផលបូកទ្វេអាច

ឃ

n d'

ត្រូវបានសរសេរឡើងវិញជា

∑ µ(d′)g(d′) =

∑ g(d′)

∑ µ(d′)

ឃ'

n d '

ឃ'

ឃ

ឃ'

យោងតាម (1) ផលបូកចុងក្រោយប្រែទៅជាឯកភាពនៅក្នុងករណី d′ = n ក្នុងករណីផ្សេងទៀត។

ក្នុងករណីណាក៏ដោយវាគឺសូន្យ។ នេះបញ្ជាក់ (២)។ ♦ 2. ពិចារណាលើការអនុវត្តនៃការបញ្ច្រាសMöbius។

សូមឱ្យអក្សរ A នៃអក្សរ s ត្រូវបានផ្តល់ឱ្យ។ មានពាក្យ sn នៃប្រវែង n នៅក្នុងអក្ខរក្រមដែលបានផ្តល់ឱ្យ។ សម្រាប់ពាក្យនីមួយៗ w0 = a1 a2 … n - 1 ពាក្យអាចត្រូវបានកំណត់

w1 = a2 a3 … a1 , w2 = a3 a4 … a1 a2 , … , wk-1 = an a1 … an-1 , ទទួលបានពីគ្នាទៅវិញទៅមកដោយការផ្លាស់ប្តូររង្វិល។ នៅលើសំណុំនៃពាក្យ sn ទាំងអស់ យើងណែនាំទំនាក់ទំនងសមមូល៖ យើងប្រកាសពាក្យពីរដែលសមមូល ប្រសិនបើពាក្យមួយត្រូវបានទទួលពីមួយទៀតដោយការផ្លាស់ប្តូរវដ្ត។ យើងនឹងចាប់អារម្មណ៍លើចំនួនថ្នាក់ដែលមានពាក្យ n យ៉ាងពិតប្រាកដ។ បញ្ហានេះកើតឡើងនៅក្នុងទ្រឹស្តីនៃការធ្វើសមកាលកម្មកូដ។

យើងនឹងហៅពាក្យ w degenerate ប្រសិនបើថ្នាក់សមមូលដែលមាន w មានពាក្យតិចជាង n ។ អនុញ្ញាតឱ្យយើងហៅ w តាមកាលកំណត់ប្រសិនបើមានពាក្យ u និងលេខធម្មជាតិ m ដូចជា w = u u ... u (m ដង) ។

ទ្រឹស្តីបទ 3. ពាក្យ w គឺតាមកាលកំណត់ ប្រសិនបើ និង លុះត្រាតែវាខូច។

ដូចដែលអ្នកអាចយក a 1 a 2 … a p និងជា m =

♦ វាច្បាស់ណាស់ថាប្រសិនបើ w មករដូវ នោះវាខូច។ ចូរយើងក្លាយជាមនុស្សខូច។ ឲ្យ p ជាចំនួនគត់អប្បបរមា ដូចនោះ w = wp ។ បន្ទាប់មកប្រសិនបើ

w = a1 a2 … an បន្ទាប់មក wp = a1+p a2+p … an+p (indices modulo n) ។ ពីទីនេះយើងទទួលបានវានៅក្នុង n p ។ (វាងាយមើលថា p n)។ ♦ ផ្ទាំងរូបភាព

សំខាន់តាមរយៈ M (d) - ចំនួនការ៉េដែលមានពាក្យ d ។ ពីមុនយើងមាន

ឃ ន. ដូច្នេះរូបមន្តមានសុពលភាព∑ dM(d) = s n . ឃ ន

ចូរយើងអនុវត្តរូបមន្តបញ្ច្រាសMöbiusសម្រាប់ករណី g(n) = sn , f(d) = dM(d) ។ បន្ទាប់មកយើងទទួលបាន

nM(n) = ∑ µ (d)s n d d n

∑ µ (d)sn ឃ

ដូច្នេះ M(n) គឺជាលេខដែលយើងចាប់អារម្មណ៍។ ប្រសិនបើ n = p ជាលេខបឋម នោះ

-s)

មានកំណែពហុគុណនៃការបញ្ច្រាសMöbius។ យុត្តិធម៌

ទ្រឹស្តីបទ 4. អនុញ្ញាតឱ្យ f(n) និង g(n) ជាមុខងារនៃអាគុយម៉ង់ធម្មជាតិដែលទាក់ទងគ្នាតាម

ពាក់

f(n) = ∏g(d)

µ(ន

g(n) = ∏f(d)

និង ផ្ទុយទៅវិញពី (5) ដូចខាងក្រោម (4) ។

ដោយប្រើរូបមន្តបញ្ច្រាសMöbius មនុស្សម្នាក់អាចដោះស្រាយបញ្ហាសំខាន់ជាក់ស្តែងនៃចំនួនពហុនាមដែលមិនអាចកាត់ថ្លៃបាននៃសញ្ញាបត្រថេរលើវាលកំណត់មួយ។ អនុញ្ញាតឱ្យ GF(q) ជាវាលនៃធាតុ q ហើយ m ជាលេខធម្មជាតិ។ បន្ទាប់មកសម្រាប់លេខ

Φ m (q) នៃពហុនាមដែលមិនអាចកាត់ថ្លៃបានលើវាល GF(q) រូបមន្តខាងក្រោមមាន៖

ចូរយើងបង្ហាញតារាងនៃតម្លៃពីរបីដំបូងនៃអនុគមន៍Φ m (2)


Φ m (2)

§ 5. អចិន្រ្តៃយ៍ និងពាក្យសុំរបស់ពួកគេចំពោះអ្នករាប់បញ្ចូល

1. អចិន្រ្តៃយ៍ត្រូវបានប្រើដើម្បីដោះស្រាយបញ្ហាបន្សំជាច្រើន។ ពិចារណាម៉ាទ្រីសលេខ

A = (ai, j), i = 1, n, j = 1, m, n ≤ m

ម៉ាទ្រីសអចិន្រ្តៃយ៍ A (ការកំណត់ - ក្នុងមួយ A) ត្រូវបានកំណត់ដោយសមភាព

ក្នុងមួយ A = ∑			a 2 j L a nj
(j1,K,jn)
(j1,K,jn)

ដែលជាកន្លែងដែលការបូកសរុបត្រូវបានអនុវត្តលើ n-permutation ទាំងអស់នៃធាតុ m 1, 2, m ។ និយាយម្យ៉ាងទៀតអចិន្ត្រៃយ៍នៃម៉ាទ្រីសគឺស្មើនឹងផលបូកនៃផលិតផលនៃធាតុដែលបានយកមួយពីជួរនីមួយៗនិងជួរឈរផ្សេងៗគ្នា។

ពីរូបមន្ត (1) លក្ខណៈសម្បត្តិជាក់ស្តែងមួយចំនួននៃការធ្វើតាមអចិន្ត្រៃយ៍ ស្រដៀងទៅនឹងលក្ខណៈសម្បត្តិនៃកត្តាកំណត់សម្រាប់ម៉ាទ្រីសការ៉េ។

1. ប្រសិនបើមួយក្នុងចំណោមបន្ទាត់(n × m) ម៉ាទ្រីស A (n ≤ m) មានសូន្យ បន្ទាប់មកក្នុងមួយ A = 0 ។ សម្រាប់ n = m គឺដូចគ្នាសម្រាប់ជួរឈរ។

2. នៅពេលដែលធាតុទាំងអស់នៃជួរដេកមួយនៃម៉ាទ្រីស A ត្រូវបានគុណនឹងចំនួនជាក់លាក់ តម្លៃនៃ A អចិន្ត្រៃយ៍ត្រូវបានគុណនឹងចំនួនដូចគ្នា។

3. អចិន្ត្រៃយ៍មិនផ្លាស់ប្តូរទេ នៅពេលដែលជួរដេក និងជួរឈររបស់វាត្រូវបានរៀបចំឡើងវិញ។

អនុញ្ញាតឱ្យយើងបង្ហាញដោយ Aij ម៉ាទ្រីសដែលទទួលបានពី A ដោយលុបជួរ i-th និងជួរឈរ j-th ។

4. រូបមន្តសម្រាប់បំបែកអចិន្ត្រៃយ៍ក្នុងជួរ i-th មានសុពលភាព៖ per A = ai1 per Ai1 + ai2 per Ai2 + ... + aim per Aim (2)

ដូច្នេះ លក្ខណៈសម្បត្តិជាច្រើនរបស់អចិន្ត្រៃយ៍គឺស្រដៀងនឹងកត្តាកំណត់។

ទោះយ៉ាងណាក៏ដោយ ទ្រព្យសម្បត្តិសំខាន់នៃកត្តាកំណត់ det(A B) = detA detB មិនពេញចិត្តចំពោះអចិន្ត្រៃយ៍ទេ ហើយកាលៈទេសៈនេះធ្វើឱ្យការគណនារបស់ពួកគេពិបាកខ្លាំងណាស់។


ឧទាហរណ៍,


	2, ក្នុងមួយ


ទោះយ៉ាងណាក៏ដោយ 4 = ក្នុងមួយ		≠ក្នុងមួយ

ចូរយើងពិចារណាកម្មវិធីដ៏សំខាន់បំផុតមួយនៃគំនិតអចិន្ត្រៃយ៍នៅក្នុងបញ្ហាផ្សំ។

dachas សូមឲ្យ X = (x1, xm) ជាសំណុំកំណត់ ហើយ X1, …, Xn ជាប្រព័ន្ធនៃសំណុំរង

ក្នុងករណីនេះធាតុ xi ត្រូវបានគេនិយាយថាតំណាងឱ្យសំណុំ Xi ។ តម្រូវការក្នុងការស្វែងរកប្រព័ន្ធនៃអ្នកតំណាងផ្សេងៗគ្នាកើតឡើងនៅពេលដោះស្រាយបញ្ហាដែលបានអនុវត្តជាច្រើន។ ពិចារណាបញ្ហាសរសេរកូដខាងក្រោម។ សូមឱ្យមានសំណើមួយចំនួន, i.e. សំណុំពាក្យតាមលំដាប់លំដោយនៅក្នុងអក្ខរក្រមមួយចំនួន។ វាត្រូវបានទាមទារដើម្បីអ៊ិនកូដប្រយោគនេះ ដូច្នេះពាក្យនីមួយៗត្រូវបានចាត់ចែងមួយអក្សរ ហើយអក្សរនេះត្រូវតែជាផ្នែកនៃពាក្យនេះ ហើយអក្សរផ្សេងគ្នាត្រូវតែត្រូវគ្នានឹងពាក្យផ្សេងគ្នា។

ឧទាហរណ៍៖ ប្រយោគ a bc ab d abe c de cd e អាចត្រូវបានអ៊ិនកូដជា abecd ។ ក្នុងពេលជាមួយគ្នានោះ ប្រយោគ ab ab bc abc bcd មិនអាចត្រូវបានអ៊ិនកូដតាមរបៀបនេះទេ ព្រោះពាក្យទាំងបួនដំបូងរួមគ្នាមានត្រឹមតែបីអក្សរប៉ុណ្ណោះ។

សម្រាប់ប្រព័ន្ធនៃសំណុំ X1 , … , Xn យើងកំណត់ ម៉ាទ្រីសឧប្បត្តិហេតុ A = (aij), i = 1, n,


	1 ប្រសិនបើ xi
a ij =
	0 បើមិនដូច្នេះទេ។
យុត្តិធម៌
ទ្រឹស្តីបទ 1. ចូរឱ្យ A = (aij), i =		(n ≤ m) ម៉ាទ្រីសឧប្បត្តិហេតុ
ទ្រឹស្តីបទ 1. ចូរឱ្យ A = (aij), i =		(n ≤ m) ម៉ាទ្រីសឧប្បត្តិហេតុ

កំណត់ X1, …, Xn, ដែល Xi X, i = 1, n, X = (x1, …, xm) ។ បន្ទាប់មកសម្រាប់ចំនួនប្រព័ន្ធ

អ្នកតំណាងផ្ទាល់ខ្លួន R(X1 , … , Xn ) នៃសំណុំ X1 , … , Xn ទទួលបានសមភាពដូចខាងក្រោមៈ

R(X1 , … , Xn ) = ក្នុងមួយ A

♦ ជាការពិត ចាប់តាំងពីក្នុងម៉ាទ្រីស A ធាតុ aij = 1 ប្រសិនបើ xj Xi និង aij = 0 ។

ប្រសិនបើ xj

K, ស៊ី

) ធាតុ X គឺជាប្រព័ន្ធនៃបុព្វបទផ្សេងៗ។

ស៊ី បន្ទាប់មកសំណុំ (xi

បច្ច័យសម្រាប់ X1 , … , Xn

ប្រសិនបើ និងប្រសិនបើ a1i

K, នី

ប៉ូលីស a1i

K, នី

ស្ថិតនៅក្នុងជួរផ្សេងគ្នានៃម៉ាទ្រីស A. ចូរយើងបូកសរុបលេខ

a1i ,K ,a ni

លើការផ្លាស់ប្តូរ n ទាំងអស់នៃធាតុ 1, 2, …, m ។ បន្ទាប់មកយើងទទួលបានពីមួយរយ

rons ចំនួននៃប្រព័ន្ធនៃអ្នកតំណាងផ្សេងគ្នាសម្រាប់ X1, ..., Xn និងម្យ៉ាងវិញទៀតតម្លៃនៃ per-

ម៉ានិតម៉ាទ្រិច A. ♦

a 1i 1 a 2i 2 L a ni n

ផលវិបាក។ ប្រព័ន្ធនៃអ្នកតំណាងផ្សេងគ្នាសម្រាប់ X1, …, Xn មានប្រសិនបើ ហើយប្រសិនបើសម្រាប់ឧប្បត្តិហេតុម៉ាទ្រីសដែលត្រូវគ្នា A គឺពេញចិត្ត៖

ដោយសារនៅក្នុងរូបមន្ត (1) មាន m(m - 1) ... (m - n +1) ការគណនាអចិន្ត្រៃយ៍ដោយផ្អែកលើនិយមន័យគឺពិបាក។ ចូរយើងបង្ហាញរូបមន្តទូទៅសម្រាប់គោលបំណងនេះ។

2. ចូរយើងកំណត់ខ្លួនយើងដោយពិចារណាលើម៉ាទ្រីសលេខការេ A = (aij), i, j = 1, n ។

បន្ទាប់មកក្នុងមួយ A = ∑

(i1,K,in)

ដែលផលបូកលាតសន្ធឹងលើការផ្លាស់ប្តូរទាំងអស់ i1 , … , នៅក្នុងធាតុ

១, ២, … , ន. អនុញ្ញាតឱ្យយើងអនុវត្តរូបមន្តនៃការរាប់បញ្ចូល - ការបដិសេធដើម្បីគណនាអចិន្រ្តៃយ៍នៃម៉ាទ្រីស A. យើងកំណត់ទៅសំណុំនីមួយៗ i1, ..., ក្នុងទម្ងន់ស្មើនឹង a1i 1,K,a ni n ។

នេះមានន័យថាអចិន្រ្តៃយ៍ A គឺជាផលបូកនៃទម្ងន់នៃសំណុំទាំងនោះដែលត្រូវគ្នាទៅនឹងការផ្លាស់ប្តូរ។ ចូរយើងណែនាំ n លក្ខណៈសម្បត្តិ P1 , … , Pn លើសំណុំនៃបណ្តុំទាំងអស់ i1 , i2 , … , ក្នុង 1, 2, … , n ដែលទ្រព្យសម្បត្តិ Pi មានន័យថាគ្មានធាតុ i នៅក្នុងការប្រមូល i1 , … , ក្នុង ដូច្នេះអចិន្រ្តៃយ៍ A គឺជាផលបូកនៃទម្ងន់នៃសំណុំ i1, ..., in ដែលមិនមានលក្ខណៈសម្បត្តិណាមួយ P1, ..., Pn ។ វានៅសល់ដើម្បីកំណត់ផលបូកនៃទម្ងន់ W (Pi 1, K, Pi k) នៃសំណុំដែលមានលក្ខណៈសម្បត្តិ k

Pi 1 , K , Pi k ។ យើងមានសម្រាប់ផលបូកនៃទម្ងន់ W (0) នៃសំណុំទាំងអស់ i1 , … , ik ។
W(0) = ∑		K, អានី	= (a 11 + L + a 1n )(a 21 + L + a 2n ) L (a n1 + L + a nn )
i1,K,in
i1,K,in

W(N(Pi)) =		a1i ,K ,a ni		= (a 11 + L + a 1i	L + a1n )L (a n1 + L a ni + L + a nn ) (9)

	≠i

ដែលសញ្ញា ^ ខាងលើធាតុនៃម៉ាទ្រីស A មានន័យថាធាតុនេះគួរតែត្រូវបានលុបចោល។ ស្រដៀងគ្នានេះដែរសម្រាប់ sij (i< j) имеем


W(N(Pi , Pj )) = (a11 + L + a1i	L+a 1j	L + a1n )L (a n1 + L a ni + L + a nj + L + a nn ) (10)

ឥឡូវនេះ ដោយប្រើរូបមន្តមិនរាប់បញ្ចូលការរាប់បញ្ចូល យើងទទួលបានរូបមន្ត Raiser សម្រាប់អចិន្ត្រៃយ៍ A៖


ក្នុងមួយ A = ∏ i n = 1 (ai1 + L + ain ) − ∑∏ k n = 1 (a k1 + L + a ki + L + a kn ) + L +

+ (− ១) ស	∑∏ ន
+ (− ១) ស	∑∏ ន	(a k1 + L + a ki1	L+a ki	L + a kn) + L
	1≤ i1< L < is ≤ k n= 1

ការគណនាអចិន្ត្រៃយ៍ដោយប្រើរូបមន្ត Raiser អាចត្រូវបានរៀបចំតាមរបៀបដែលវាទាមទារ

(2n - 1)(n - 4) គុណ និង (2n - 2)(n + 1) ការបន្ថែម។ ទោះបីជាតម្លៃនេះកើនឡើងយ៉ាងឆាប់រហ័សនៅពេលដែល n កើនឡើងក៏ដោយ រូបមន្តនេះផ្តល់នូវវិធីដ៏មានប្រសិទ្ធភាពបំផុតក្នុងការគណនាអចិន្ត្រៃយ៍។

3. ឥឡូវនេះ ចូរយើងស្រាយចម្ងល់នៃលក្ខខណ្ឌសម្រាប់ម៉ាទ្រីសអចិន្ត្រៃយ៍ (0, 1) ស្មើនឹងសូន្យ។ ចូរយើងដាក់កម្រិតខ្លួនយើងចំពោះករណីនៃម៉ាទ្រីសការ៉េ។

ទ្រឹស្តីបទ 2. ចូរឱ្យ A = (aij ), i, j = 1, n be a (0, 1) matrix of order n. បន្ទាប់មក

ក្នុងមួយ A= 0 ប្រសិនបើ A មានអនុម៉ាទ្រីសនៃលេខសូន្យនៃទំហំ s × t ដែល s + t = n + 1 ។

♦ សូមអោយសូន្យ submatrix បែបនេះមាននៅក្នុង A ។ ដោយសារអចិន្ត្រៃយ៍មិនផ្លាស់ប្តូរដោយសារការផ្លាស់ប្តូរជួរដេក និងជួរឈរ យើងអាចសន្មត់ថា submatrix នេះមានទីតាំងនៅជ្រុងខាងឆ្វេងខាងក្រោម i.e.

ដែល O - (s × t) ជាម៉ាទ្រីសនៃសូន្យ អនុម៉ាទ្រីស B មានទំហំ (n - s) × t ។ សមាជិកនីមួយៗនៃ A អចិន្ត្រៃយ៍ត្រូវតែមានធាតុមួយពីជួរ t ដំបូង។ ដូច្នេះប្រសិនបើយើងស្វែងរកពាក្យវិជ្ជមាននៃអចិន្ត្រៃយ៍ នោះធាតុនៃជួរឈរទាំងនេះត្រូវតែជារបស់ជួរផ្សេងគ្នាជាគូជាមួយលេខ 1, 2, ..., n - s ។ ទោះយ៉ាងណាក៏ដោយ n - s = t - 1< t и поэтому данное условие выполнить нельзя, т.е. per A = 0.

ឥឡូវនេះក្នុងមួយ A = 0 ។ យើងបង្ហាញទ្រឹស្ដីដោយការបញ្ចូលនៅលើ n ។ សម្រាប់ n = 1 សេចក្តីថ្លែងការណ៍គឺជាក់ស្តែង (A = (0)) ។ សូមឱ្យវាជាការពិតសម្រាប់ការបញ្ជាទិញទាំងអស់តិចជាង n ។ ប្រសិនបើ A ជាម៉ាទ្រីសសូន្យនៃលំដាប់ n នោះសេចក្តីថ្លែងការណ៍គឺជាក់ស្តែង។ ប្រសិនបើ A មិនមែនជាម៉ាទ្រីសសូន្យទេ នោះសូមឱ្យ aij = 1 ។ ចូរយើងសរសេរ decomposition នៃ A តាមជួរ i៖

per A = ai1 Ai1 + … + ain Ain

ចាប់តាំងពីក្នុងមួយ A = 0 បន្ទាប់មកក្នុងមួយ Aij = 0 ។ ប៉ុន្តែ Aij មានទំហំ (n − 1) × (n − 1) ហើយដោយសម្មតិកម្មនៃការបញ្ចូលមានអនុម៉ាទ្រីសនៃទំហំសូន្យ។

s1 × t1 ដែលមាន s1 + t1 = n − 1 + 1 = n ។ ចូររៀបចំជួរដេក និងជួរឈរឡើងវិញ ដើម្បីកុំឱ្យម៉ាទ្រីសរងសូន្យនេះនៅជ្រុងខាងឆ្វេងខាងក្រោម៖


A → B =

ដែល O ជាអនុម៉ាទ្រីសសូន្យនៃទំហំ s1 × t1, s1 + t1 = n, C - មានទំហំ (n − s1) × t1, D -

មានទំហំ s1 × (n - t) ។ នេះមានន័យថាម៉ាទ្រីស C និង D គឺជាការ៉េ និងមានលំដាប់ (t1 × t1) និង (s1 × s1) រៀងគ្នា។ យោងតាមនិយមន័យនៃអចិន្រ្តៃយ៍យើងមានក្នុងមួយ B = per A និង,

per B = per C per D ហើយដូច្នេះពី A = 0 វាធ្វើតាមថា per C = 0 ឬ per D = 0 ។

អនុញ្ញាតឱ្យក្នុងមួយ C = 0. តាមសម្មតិកម្មអាំងឌុចស្យុង មានអនុម៉ាទ្រីសសូន្យនៃទំហំ

u × v, ដែល u + v = t1 + 1. ឲ្យវាស្ថិតនៅជួរដែលមានលេខ i1, …, iu និងជួរឈរដែលមានលេខ j1, …, jv ។ ពិចារណា submatrix B ដែលមានជួរ

i1, …, iu, t1 + 1, …, n និងជួរឈរ j1, …, jv ។ នេះគឺជាលេខសូន្យនៃទំហំ (u + n - t1) × v,

ដែល u + n − t1 + v = n + +1 ។ ដូច្នេះ ម៉ាទ្រីស B មានលេខសូន្យនៃទំហំ s × t ដែល s + t = n + 1 ។ ដោយសារម៉ាទ្រីស A និង B ខុសគ្នាក្នុងការផ្លាស់ប្តូរជួរដេក និងជួរឈរ ទ្រឹស្តីបទត្រូវបានបង្ហាញឱ្យឃើញ។ ♦

ឥឡូវនេះ ចូរយើងពិចារណាករណីពិសេសសំខាន់មួយនៃម៉ាទ្រីស A. ចូរយើងបញ្ជាក់ដោយ A(k,n) ម៉ាទ្រីសនៃ 0.1 ធាតុនៃទំហំ n × n ជាមួយ k មួយសម្រាប់ជួរនីមួយៗ និងជួរឈរនីមួយៗ (k > 0)។

ទ្រឹស្តីបទ 3. សម្រាប់ម៉ាទ្រីសណាមួយ A(k,n) ក្នុងមួយ A(k,n) > 0 ។

◆ ចូរយើងសន្មត់ផ្ទុយថាក្នុងមួយ A(k,n) = 0។ បន្ទាប់មក តាមទ្រឹស្តីបទ 2 មានសូន្យ -

submatrix នៃទំហំ s × t ដែល s + t = n + 1. បន្ទាប់មក ការរៀបចំជួរដេក និងជួរឈរនៃម៉ាទ្រីស A(k, n) ឡើងវិញ យើងទទួលបានម៉ាទ្រីស

ដែល O ជាម៉ាទ្រីសសូន្យ (s × t) ។

ចូររាប់ចំនួនមួយក្នុងម៉ាទ្រីស B និង D។ ដោយសារ A(k,n) មាន k ក្នុងជួរនីមួយៗ និងជួរឈរនីមួយៗ ដូច្នេះមាន k ពិតប្រាកដនៅក្នុងជួរឈរ B និងជួរនីមួយៗនៃ D

ឯកតា។ មាន n k សរុបនៅក្នុង A(k,n) ដូច្នេះ nk ≥ tk + sk = (t + s)n ។ ផ្លូវនេះ

som, n ≥ t + s, ដែលមិនអាចទៅរួចទេព្រោះ s + t = n + 1 ពីភាពផ្ទុយគ្នានេះវាធ្វើតាមនោះ។

សុពលភាពនៃសេចក្តីថ្លែងការណ៍។ ◆ វាត្រូវបានបញ្ជាក់តាមរបៀបស្រដៀងគ្នា

ទ្រឹស្តីបទ ៣ ក. អនុញ្ញាតឱ្យ A ជាម៉ាទ្រីស (0,1) នៃទំហំ n × m (n≤ m) ។ បន្ទាប់មក perA = 0 ប្រសិនបើវាមានលេខសូន្យនៃទំហំ s × t ដែល s + t = m + 1 ។

4. ឥឡូវនេះ ចូរយើងពិចារណាលើការអនុវត្តបញ្ហាដែលកំពុងពិចារណាលើការសាងសង់ឡ-

ទីណាការ៉េ។ ឡាតាំង (n × ម) - ចតុកោណលើសំណុំ X = (x1,…,xm)

ត្រូវបានគេហៅថា (n × m) -matrix នៃធាតុ X ដែលក្នុងនោះជួរនីមួយៗគឺជា n-permutation នៃ X ហើយជួរឈរនីមួយៗគឺជា m-permutation នៃសំណុំ X។ សម្រាប់ n=m ចតុកោណឡាតាំងត្រូវបានគេហៅថា ការ៉េឡាតាំង។

វាច្បាស់ណាស់ថាសម្រាប់ n = 1 ចំនួននៃចតុកោណកែង 1 × m គឺស្មើនឹង m ! នៅពេល n=2 បន្ទាប់ពីជួរទីមួយត្រូវបានជ្រើសរើស ការផ្លាស់ប្តូរណាមួយអាចត្រូវបានយកជាជួរទីពីរ។

ផលិតផលថ្មីដែលផ្ទុយនឹងជម្រើសដែលបានជ្រើសរើស។ ចំនួននៃការផ្លាស់ប្តូរបែបនេះគឺ Dm ដូច្នេះលេខ 2 × m គឺ

ចតុកោណឡាតាំងស្មើនឹង m! ឃ.

សំណួរធម្មជាតិមួយកើតឡើងទាក់ទងនឹងការសាងសង់អាំងឌុចទ័នៃការ៉េឡាតាំង។ អនុញ្ញាតឱ្យយើងសាងសង់ឡាតាំង (n × m) - ចតុកោណកែង (n< m). Можно ли его расширить до ((n+1)× m) -прямоугольника добавлением (n+1)-й строки?

យុត្តិធម៌

ទ្រឹស្តីបទ 4. រាល់ឡាតាំង (n×m)-rectangle n

♦ សូមឲ្យ X=(x1,…,xm) និង L-Latin (n×m)-ចតុកោណកែងជាមួយធាតុពី X។ ពិចារណាលើសំណុំ A1,…,Am ដែល Ai ជាធាតុនៃជួរឈរ i-th នៃ ចតុកោណកែងឡាតាំង L. សូមឱ្យ A ជាម៉ាទ្រីសឧប្បត្តិហេតុនៃប្រព័ន្ធកំណត់ A1 ,… ,Am ។ វាមានទំហំ m × m ហើយជួរនីមួយៗនៃម៉ាទ្រីស A មាន n ពិតប្រាកដ ចាប់តាំងពី Ai = n, i = 1, m ។ ធាតុនីមួយៗ xi X អាចបង្ហាញក្នុងជួរ L មិនលើសពី m ដង បើមិនដូច្នេះទេ វានឹងមានជួរដែលធាតុនេះលេចឡើងពីរដង។ ចំនួនសរុបនៃធាតុ

L គឺស្មើនឹង m n ដូច្នេះធាតុនីមួយៗ xi X បង្ហាញយ៉ាងពិតប្រាកដ n ដងក្នុងជួរឈរ។ វាធ្វើតាមថាជួរឈរនីមួយៗនៃម៉ាទ្រីស A មាន n ពិតប្រាកដ។ ឥឡូវនេះ ចូរយើងពិចារណាម៉ាទ្រីស A ដែលទទួលបានដោយជំនួសលេខមួយដោយសូន្យ និងសូន្យនីមួយៗជាមួយមួយ។

ម៉ាទ្រីស A គឺជាម៉ាទ្រីសឧប្បត្តិហេតុនៃប្រព័ន្ធនៃសំណុំ X1, …, Xn ដែល Xi = X\Ai,

i = 1, m ។ វាមានឯកតា m - n ក្នុងជួរនីមួយៗ និងក្នុងជួរនីមួយៗ។ តាមទ្រឹស្តីបទ

> 0. អនុញ្ញាតឱ្យ ai1

…ខ្ញុំ

≠ 0 ។ បន្ទាប់មកយើងមាន xi X1 ,K , xi

Xm និងធាតុទាំងអស់។

ស៊ី, ខេ, ស៊ី

ខុសគ្នាជាគូ។ បន្ទាត់

ស៊ី, ខេ, ស៊ី

អាចត្រូវបានយកជា (n + 1)th

សម្រាប់ Latin (n × m)-rectangle L. ការបន្តនីតិវិធីនេះ យើងទទួលបានឡាតាំង

ការ៉េមេឃ។ ♦

អនុញ្ញាតឱ្យយើងសម្គាល់ l n - ចំនួនការ៉េឡាតាំងនៃលំដាប់ n ជាមួយនឹងធាតុពីសំណុំ X = (1, 2, ..., n) ដែលធាតុនៃជួរទីមួយនិងជួរទីមួយស្ថិតនៅក្នុងលំដាប់ធម្មជាតិ។ នេះគឺជាតារាងនៃតម្លៃដែលគេស្គាល់ជាច្រើននៃចំនួន l n: