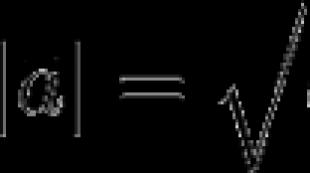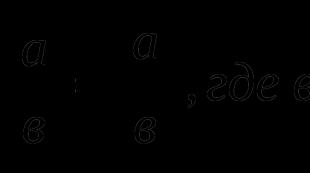№17 Иванов орта мектебінің МБОУ

« Модульдік теңдеулер»
Әдістемелік өңдеу

Құрастырылған

математика мұғалімі

Лебедева Н.В.

20010

түсіндірме жазба

1-тарау Кіріспе

2-бөлім. Негізгі мүмкіндіктер Бөлім 3. Санның модулі түсінігінің геометриялық түсіндірмесі 4-бөлім. y = |x| функциясының графигі 5-бөлім Конвенциялар

2-тарау

1-бөлім. |F(х)| түріндегі теңдеулер = м (қарапайымдылар) 2-бөлім. F(|х|) = m түріндегі теңдеулер 3-бөлім. |F(х)| түріндегі теңдеулер = G(x) 4-бөлім. |F(х)| түріндегі теңдеулер = ± F(x) (әдемі) 5-бөлім. |F(х)| түріндегі теңдеулер = |G(x)| Бөлім 6. Стандартты емес теңдеулерді шешу мысалдары 7-бөлім. |F(х)| түріндегі теңдеулер + |G(x)| = 0 8-бөлім. |а 1 x ± в 1 | түріндегі теңдеулер ± |a 2 x ± в 2 | ± …|a n x ± in n | = м 9-бөлім. Құрамында бірнеше модуль бар теңдеулер

3-тарау. Модульі бар әртүрлі теңдеулерді шешу мысалдары.

Бөлім 1. Тригонометриялық теңдеулер 2-бөлім. Көрсеткіштік теңдеулер 3-бөлім. Логарифмдік теңдеулер 4-бөлім. Иррационал теңдеулер 5-бөлім. Күрделілігі жоғары тапсырмалар Жаттығулардың жауаптары Әдебиеттер тізімі

Түсіндірме жазба.

Нақты санның абсолютті мәні (модуль) ұғымы оның маңызды сипаттамаларының бірі болып табылады. Бұл ұғым физика, математика және техника ғылымдарының әртүрлі салаларында кеңінен қолданылады. Ресей Федерациясы Қорғаныс министрлігінің Бағдарламасына сәйкес орта мектепте математика курсын оқыту тәжірибесінде «санның абсолютті мәні» түсінігі бірнеше рет кездеседі: 6-сыныпта модульдің анықтамасы. , оның геометриялық мағынасы таныстырылады; 8-сыныпта абсолютті қате туралы түсінік қалыптасады, модулі бар қарапайым теңдеулер мен теңсіздіктерді шешу қарастырылады, арифметикалық квадрат түбірдің қасиеттері оқытылады; 11-сыныпта «Түбір nші дәреже».Оқыту тәжірибесі көрсеткендей, студенттер осы материалды білуді талап ететін тапсырмаларды шешуде жиі қиындықтарға кезігеді және орындай бастамай-ақ жиі өткізіп жібереді. 9-11-сыныптар курсы бойынша емтихан тапсырмаларының мәтіндерінде де осыған ұқсас тапсырмалар берілген. Сонымен қатар, университеттердің мектеп түлектеріне қоятын талаптары әртүрлі, яғни мектеп бағдарламасының талаптарынан жоғары деңгейде. Қазіргі қоғамдағы өмір үшін белгілі бір психикалық дағдыларда көрінетін ойлаудың математикалық стилін қалыптастыру өте маңызды. Модульдермен есептерді шешу барысында жалпылау және нақтылау, талдау, жіктеу және жүйелеу, аналогия сияқты әдіс-тәсілдерді қолдана білу қажет. Мұндай тапсырмаларды шешу мектеп курсының негізгі бөлімдері бойынша білімдерін, логикалық ойлау деңгейін, зерттеудің бастапқы дағдыларын тексеруге мүмкіндік береді. Бұл жұмыс бөлімдердің бірі – модулі бар теңдеулерді шешуге арналған. Ол үш тараудан тұрады. Бірінші тарауда негізгі ұғымдар мен маңызды теориялық есептеулер берілген. Екінші тарауда модуль бар теңдеулердің тоғыз негізгі түрі ұсынылады, оларды шешу әдістері қарастырылады және күрделіліктің әртүрлі деңгейлерінің мысалдары талданады. Үшінші тарауда анағұрлым күрделі және стандартты емес теңдеулер (тригонометриялық, көрсеткіштік, логарифмдік және иррационалдық) ұсынылған. Теңдеулердің әрбір түрі үшін өз бетінше шешуге арналған жаттығулар бар (жауаптар мен нұсқаулар қоса беріледі). Бұл жұмыстың негізгі мақсаты мұғалімдерге сабаққа дайындалуда және факультативтік курстарды ұйымдастыруда әдістемелік көмек көрсету болып табылады. Материалды жоғары сынып оқушылары үшін оқу құралы ретінде де пайдалануға болады. Жұмыста ұсынылған тапсырмалар қызықты және әрқашан оңай шешілмейді, бұл студенттердің оқу мотивациясын саналы етуге, олардың қабілеттерін тексеруге, мектеп түлектерінің жоғары оқу орындарына түсуге дайындық деңгейін арттыруға мүмкіндік береді. Ұсынылған жаттығуларды сараланған таңдау материалды игерудің репродуктивті деңгейінен шығармашылық деңгейге көшуді, сондай-ақ стандартты емес есептерді шешуде өз білімін қолдануды үйрету мүмкіндігін білдіреді.

1-тарау. Кіріспе.

1-бөлім. Абсолюттік шаманы анықтау .

Анықтама : Нақты санның абсолютті мәні (модуль). Атеріс емес сан деп аталады: Анемесе -А. Белгіленуі: │ А │ Жазба келесідей оқылады: «a санының модулі» немесе «а санының абсолютті мәні»

│ a, егер a > 0

│a│ = │ 0, егер a = 0 (1)

│ - а, егер а
Мысалдар: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Өрнек модулін кеңейту:

а) │x - 8│, егер x > 12 б) │2x + 3│, егер x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

2-бөлім. Негізгі қасиеттер.

Абсолюттік шаманың негізгі қасиеттерін қарастырайық. №1 қасиет: Қарама-қарсы сандар бірдей модульдерге ие, яғни. │а│=│-а│Теңдіктің дұрыстығын көрсетейік. Санның анықтамасын жазып алайық - А : │- a│= (2) (1) және (2) жиындарын салыстырайық. Сандардың абсолютті мәндерінің анықтамалары анық АЖәне - Асәйкестендіріңіз. Демек, │а│=│-а│
Төмендегі қасиеттерді қарастырған кезде біз олардың тұжырымдарымен шектелеміз, өйткені олардың дәлелі келтірілген №2 қасиет: Нақты сандардың соңғы санының қосындысының абсолютті мәні терминдердің абсолютті мәндерінің қосындысынан аспайды: №3 қасиет: Екі нақты санның айырмашылығының абсолюттік мәні олардың абсолюттік мәндерінің қосындысынан аспайды: │а - в│ ≤│а│+│в│ №4 мүлік: Нақты сандардың ақырлы санының көбейтіндісінің абсолютті мәні мына факторлардың абсолютті мәндерінің көбейтіндісіне тең: │а · в│=│а│·│в│ №5 мүлік: Нақты сандар бөлігінің абсолютті мәні олардың абсолюттік мәндерінің бөліміне тең:

Бөлім 3. Санның модулі түсінігінің геометриялық түсіндірмесі.

Әрбір нақты санды сан түзуіндегі нүктемен байланыстыруға болады, ол осы нақты санның геометриялық көрінісі болады. Сандық түзудегі әрбір нүкте оның басынан қашықтығына сәйкес келеді, яғни. кесіндінің басынан берілген нүктеге дейінгі ұзындығы. Бұл қашықтық әрқашан теріс емес мән ретінде қарастырылады. Демек, сәйкес кесіндінің ұзындығы берілген нақты санның абсолютті мәнінің геометриялық түсіндірмесі болады

Ұсынылған геометриялық иллюстрация №1 сипатты анық растайды, яғни. қарама-қарсы сандардың модульдері тең. Осы жерден теңдіктің дұрыстығын оңай түсінуге болады: │x - a│= │a - x│. Сондай-ақ │х│= m теңдеуін шешу айқынырақ болады, мұндағы m ≥ 0, атап айтқанда x 1,2 = ± m. Мысалдар: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

4-бөлім. y \u003d │х│ функциясының графигі

Бұл функцияның анықталу облысы барлық нақты сандар болып табылады.

5-бөлім. Рәміздер.

Болашақта теңдеулерді шешу мысалдарын қарастыру кезінде келесі конвенциялар қолданылады: ( - жүйе белгісі [ - орнату белгісі Теңдеулер (теңсіздіктер) жүйесін шешу кезінде жүйеге кіретін теңдеулердің (теңсіздіктердің) шешімдерінің қиылысуы табылады. Теңдеулер (теңсіздіктер) жиынын шешу кезінде жиынға кіретін теңдеулердің (теңсіздіктердің) шешімдерінің бірігуі табылады.

2-тарау

Бұл тарауда біз бір немесе бірнеше модульден тұратын теңдеулерді шешудің алгебралық жолдарын қарастырамыз.

1-бөлім. │F (х) │= m түріндегі теңдеулер

Бұл түрдегі теңдеу ең қарапайым деп аталады. Оның шешімі m ≥ 0 болған жағдайда ғана болады. Модульдің анықтамасы бойынша бастапқы теңдеу екі теңдеудің қосындысына тең: │ Ф(x)│=м
Мысалдар:
№1. Теңдеуді шешіңіз: │7x - 2│= 9


Жауабы: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 \u003d 0; x 2 = -3 Жауабы: түбірлердің қосындысы – 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 x 2 = m, m ≥ 0 x = 0 деп белгілейді; ±√5 м 2 – 5м + 4 = 0 м = 1; 4 – екі мән де m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 шартын қанағаттандырады Жауабы: 7-теңдеудің түбірлерінің саны. Жаттығулар:
№1. Теңдеуді шешіп, түбірлердің қосындысын көрсет: │x - 5│= 3 №2 . Теңдеуді шешіп, кіші түбірін көрсетіңіз: │x 2 + x │ \u003d 0 №3 . Теңдеуді шешіп, үлкенірек түбірін көрсетіңіз: │x 2 - 5x + 4 │ \u003d 4 №4 .Теңдеуді шешіп, бүтін түбірді көрсет: │2x 2 - 7x + 6│ \u003d 1 №5 .Теңдеуді шешіп, түбірлер санын көрсет: │x 4 - 13x 2 + 50 │ = 14

2-бөлім. F(│х│) = m түріндегі теңдеулер

Сол жағындағы функция аргументі модуль белгісінің астында, ал оң жағы айнымалыға тәуелсіз. Осы түрдегі теңдеулерді шешудің екі әдісін қарастырайық. 1 жол:Абсолюттік шаманың анықтамасы бойынша бастапқы теңдеу екі жүйенің жиынтығына тең. Олардың әрқайсысында субмодуль өрнекіне шарт қойылады. Ф(│х│) =м
F(│х│) функциясы барлық анықтау облысында жұп болғандықтан, F(х) = m және F(-х) = m теңдеулерінің түбірлері қарама-қарсы сандар жұптары болып табылады. Сондықтан жүйенің біреуін шешу жеткілікті (мысалдарды осылай қарастырғанда бір жүйенің шешімі беріледі). 2 жол:Жаңа айнымалыны енгізу әдісін қолдану. Бұл жағдайда │х│= a белгілеу енгізіледі, мұнда a ≥ 0. Бұл әдіс конструкцияда аз көлемді.
Мысалдар: №1 . Теңдеуді шешіңіз: 3x 2 - 4│x│ = - 1 Жаңа айнымалы енгізуді қолданайық. │x│= a деп белгілеңіз, мұндағы a ≥ 0. 3a 2 - 4a + 1 = 0 теңдеуін аламыз D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 Бастапқы айнымалыға ораламыз: │x │ = 1 және │х│= 1/3. Әрбір теңдеудің екі түбірі болады. Жауабы: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Теңдеуді шешіңіз: 5x 2 + 3│x│- 1 \u003d 1/2 │x│ + 3x 2
Бірінші жиын жүйесінің шешімін табайық: 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 x 2 орындайтынын ескеріңіз. x ≥ 0 шартын қанағаттандырмайды. Шешімі бойынша екінші жүйе қарама-қарсы x 1 саны болады. Жауабы: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Теңдеуді шешіңіз: x 4 - │х│= 0 │х│= a деп белгілеңіз, мұндағы a ≥ 0. a 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d 0 теңдеуін аламыз. a 2 \u003d 1 Біз бастапқы айнымалыға ораламыз: │х│=0 және │х│= 1 x = 0; ± 1 Жауабы: x 1 = 0; X 2 = 1; X 3 = - 1.
Жаттығулар: №6. Теңдеуді шешіңіз: 2│х│ - 4,5 = 5 - 3/8 │х│ №7 . Теңдеуді шешіңіз, жауапта түбірлер санын көрсетіңіз: 3x 2 - 7│x│ + 2 = 0 №8 . Теңдеуді шешіңіз, жауапта барлық шешімдерді көрсетіңіз: x 4 + │х│ - 2 = 0

3-бөлім. │F(х)│ = G(х) түріндегі теңдеулер

Бұл түрдегі теңдеудің оң жағы айнымалыға тәуелді және сондықтан, егер оң жағы G(x) ≥ 0 функциясы болса ғана шешімі болады. Бастапқы теңдеуді екі жолмен шешуге болады: 1 жол:Стандарт, оның анықтамасына негізделген модульді ашуға негізделген және екі жүйенің тіркесіміне эквивалентті өтуден тұрады. │ Ф(x)│ =Г(X)

Бұл әдісті G(x) функциясы үшін күрделі өрнек және F(x) функциясы үшін күрделі өрнек болған жағдайда қолдану ұтымды, өйткені ол теңсіздіктерді F(x) функциясымен шешу керек. 2 жол:Ол оң жаққа шарт қойылған эквивалентті жүйеге көшуден тұрады. │ Ф(x)│= Г(x)

Бұл әдісті қолдану ыңғайлырақ, егер G(x) функциясының өрнегі F(x) функциясына қарағанда күрделірек болса, өйткені G(x) ≥ 0 теңсіздігінің шешімі қабылданған.Сонымен қатар, жағдайда бірнеше модульдерден, бұл әдіс екінші опцияны пайдалану ұсынылады. Мысалдар: №1. Теңдеуді шешіңіз: │x + 2│= 6 -2x
(1 жол) Жауабы: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(2 жол) Жауабы: Тамырлардың көбейтіндісі 3-ке тең.
№3. Теңдеуді шеш, жауапта түбірлердің қосындысын жаз:
│x - 6 │ \u003d x 2 - 5x + 9

Жауабы: түбірлердің қосындысы 4-ке тең.
Жаттығулар: №9. │x + 4│= - 3x №10. Теңдеуді шешіңіз, жауапта шешімдер санын көрсетіңіз: │x 2 + x - 1 │ \u003d 2x - 1 №11 . Теңдеуді шешіңіз, жауапта түбірлердің көбейтіндісін көрсетіңіз: │x + 3 │ \u003d x 2 + x - 6

4-бөлім. │F(x)│= F(x) және │F(x)│= - F(x) түріндегі теңдеулер

Бұл түрдегі теңдеулерді кейде «әдемі» деп те атайды. Теңдеулердің оң жағы айнымалыға тәуелді болғандықтан, оң жағы теріс емес болса ғана шешімдер бар. Демек, бастапқы теңдеулер теңсіздіктерге тең:
│F(x)│= F(x) F(x) ≥ 0 және │F(x)│= - F(x) F(x) Мысалдар: №1 . Теңдеуді шешіңіз, жауапта кіші бүтін түбірді көрсетіңіз: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Жауабы: x = 1№2. Теңдеуді шешіңіз, жауапта аралық ұзындығын көрсетіңіз: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] Жауабы: саңылаудың ұзындығы 6.№3 . Теңдеуді шешіңіз, жауапта бүтін шешімдердің санын көрсетіңіз: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] Жауабы: 4 бүтін шешім.№4 . Теңдеуді шешіңіз, жауапта ең үлкен түбірді көрсетіңіз:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1,2 \u003d
≈ 1,4

Жауабы: x = 3.

Жаттығулар: №12. Теңдеуді шешіңіз, жауапта бүтін түбірді көрсетіңіз: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. Теңдеуді шешіңіз, жауапта бүтін шешімдердің санын көрсетіңіз: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. Теңдеуді шешіңіз, жауапта теңдеудің түбірі болып табылмайтын бүтін санды көрсетіңіз:

5-бөлім. │F(x)│= │G(x)│ түріндегі теңдеулер

Теңдеудің екі жағы да теріс емес болғандықтан, шешім екі жағдайды қарастырады: ішкі модуль өрнектері таңбалары бойынша тең немесе қарама-қарсы. Демек, бастапқы теңдеу екі теңдеудің қосындысына тең: │ Ф(x)│= │ Г(x)│
Мысалдар: №1. Теңдеуді шешіңіз, жауапта толық түбірді көрсетіңіз: │x + 3│ \u003d │2x - 1│
Жауабы: бүтін түбір x = 4.№2. Теңдеуді шеш: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Жауабы: x = 2.№3 . Теңдеуді шешіңіз, жауапта түбірлердің көбейтіндісін көрсетіңіз:




4x 2 + 2x - 1 \u003d 0 x 1,2 \u003d - 1±√5 / 4 теңдеуінің түбірлері Жауабы: түбірлердің көбейтіндісі 0,25. Жаттығулар: №15 . Теңдеуді шешіңіз, жауапта барлық шешімді көрсетіңіз: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. Теңдеуді шешіңіз, жауапта кіші түбірді көрсетіңіз: │5x - 3│=│7 - x│ №17 . Теңдеуді шеш, жауапта түбірлердің қосындысын жаз:

Бөлім 6. Стандартты емес теңдеулерді шешу мысалдары

Бұл бөлімде стандартты емес теңдеулердің мысалдарын қарастырамыз, оларды шешуде өрнектің абсолюттік мәні анықтамасы арқылы ашылады. Мысалдар:

№1. Теңдеуді шешіңіз, жауапта түбірлердің қосындысын көрсетіңіз: x │x│- 5x - 6 \u003d 0
Жауабы: түбірлердің қосындысы 1-ге тең №2. . Теңдеуді шешіңіз, жауапта кіші түбірді көрсетіңіз: x 2 - 4x
- 5 = 0
Жауабы: кіші түбір x = - 5. №3. Теңдеуді шеш:

Жауабы: x = -1. Жаттығулар: №18. Теңдеуді шешіп, түбірлердің қосындысын жаз: x │3x + 5│= 3x 2 + 4x + 3
№19. Теңдеуді шешіңіз: x 2 - 3x \u003d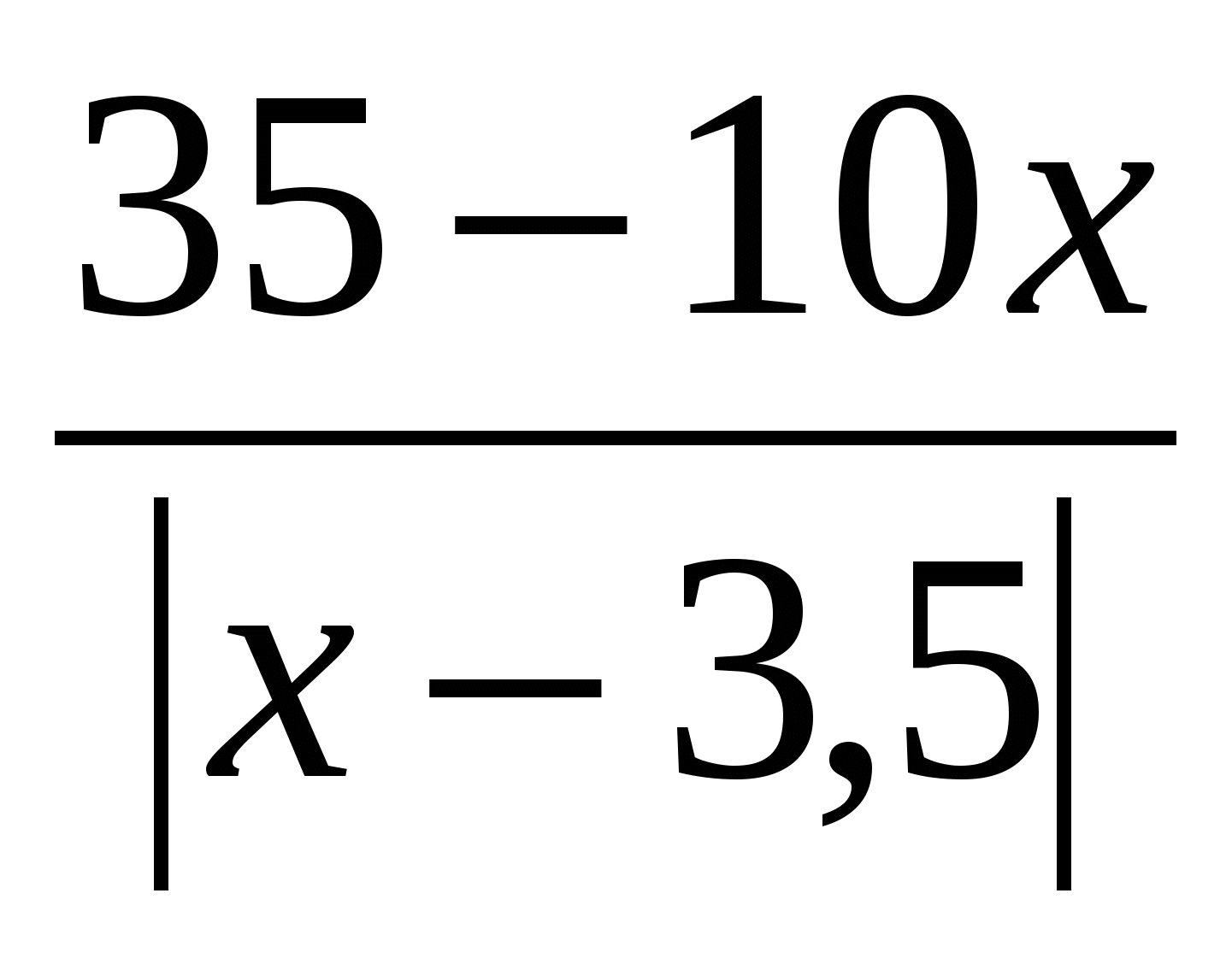

№20. Теңдеуді шеш:

7-бөлім. │F(x)│+│G(x)│=0 түріндегі теңдеулер

Бұл түрдегі теңдеудің сол жағында теріс емес шамалардың қосындысы болатынын байқау қиын емес. Демек, бастапқы теңдеудің шешімі екі мүшесі бір уақытта нөлге тең болған жағдайда ғана болады. Теңдеу теңдеулер жүйесіне эквивалентті: │ Ф(x)│+│ Г(x)│=0
Мысалдар: №1 . Теңдеуді шеш:
Жауабы: x = 2. №2. Теңдеуді шеш: Жауабы: x = 1. Жаттығулар: №21. Теңдеуді шеш: №22 . Теңдеуді шеш, жауапта түбірлердің қосындысын жаз: №23 . Теңдеуді шешіңіз, жауапта шешімдер санын көрсетіңіз:

8-бөлім. Пішіннің теңдеуі

Бұл түрдегі теңдеулерді шешу үшін интервалдар әдісі қолданылады. Егер ол модульдерді дәйекті кеңейту арқылы шешілсе, онда біз аламыз nжүйелер жиынтығы, бұл өте ауыр және қолайсыз. Интервал әдісінің алгоритмін қарастырайық: 1). Айнымалы мәндерді табыңыз X, ол үшін әрбір модуль нөлге тең (ішкі модуль өрнектерінің нөлдері):
2). Табылған мәндер аралықтарға бөлінген сан жолында белгіленеді (тиісінше интервалдар саны тең n+1 ) 3). Әрбір алынған аралықта әрбір модуль қандай белгімен ашылатынын анықтаңыз (шешімді жасаған кезде ондағы белгілерді белгілей отырып, сандық сызықты қолдануға болады) 4). Бастапқы теңдеу жиынға эквивалентті n+1 жүйелер, олардың әрқайсысында айнымалының мүшелігі көрсетілген Xаралықтардың бірі. Мысалдар: №1 . Теңдеуді шешіңіз, жауапта ең үлкен түбірді көрсетіңіз:
1). Ішкі модульдік өрнектердің нөлдерін табайық: x = 2; x = -3 2). Табылған мәндерді сандық сызықта белгілейміз және алынған интервалдарда әрбір модуль қандай белгімен ашылатынын анықтаймыз:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- шешімі жоқ Теңдеудің екі түбірі бар. Жауабы: ең үлкен түбір х = 2. №2. Теңдеуді шешіңіз, жауапта түбірді түгел жазыңыз:
1). Ішкі модуль өрнектерінің нөлдерін табайық: x = 1,5; x = - 1 2). Табылған мәндерді сандық сызықта белгілейміз және алынған интервалдарда әрбір модуль қандай белгімен ашылатынын анықтаймыз: x + 1 x + 1 x + 1 - + +
-1 1,5 х 2х – 3 2х – 3 2х – 3 - - +
3).
Соңғы жүйенің шешімі жоқ, сондықтан теңдеудің екі түбірі бар. Теңдеуді шешкен кезде екінші модульдің алдындағы «-» белгісіне назар аудару керек. Жауабы: бүтін түбір x = 7. №3. Теңдеуді шешіңіз, жауапта түбірлердің қосындысын көрсетіңіз: 1). Ішкі модуль өрнектерінің нөлдерін табайық: x = 5; x = 1; x = - 2 2). Табылған мәндерді сандық сызықта белгілейміз және алынған аралықтарда әрбір модуль қандай белгімен ашылатынын анықтаймыз: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Теңдеудің x = 0 және 2 екі түбірі бар. Жауабы: түбірлердің қосындысы 2-ге тең. №4 . Теңдеуді шешіңіз: 1). Ішкі модуль өрнектерінің нөлдерін табайық: x = 1; x = 2; x = 3. 2). Алынған аралықтарда әрбір модуль кеңейтілетін белгіні анықтайық. 3).
Біз алғашқы үш жүйенің шешімдерін біріктіреміз. Жауап: ; x = 5.
Жаттығулар: №24. Теңдеуді шеш:
№25. Теңдеуді шеш, жауапта түбірлердің қосындысын жаз: №26. Теңдеуді шешіңіз, жауапта кіші түбірді көрсетіңіз: №27. Теңдеуді шешіңіз, жауабыңызда үлкенірек түбірін беріңіз:

9-бөлім. Құрамында бірнеше модуль бар теңдеулер

Бірнеше модульден тұратын теңдеулер ішкі модуль өрнектерінде абсолютті мәндердің болуын болжайды. Бұл түрдегі теңдеулерді шешудің негізгі принципі «сыртқыдан» бастап модульдерді тізбектей ашу болып табылады. Шешім барысында No1, No3 бөлімдерде қарастырылған әдістер қолданылады.

Мысалдар: №1. Теңдеуді шеш:
Жауабы: x = 1; - он бір. №2. Теңдеуді шеш:
Жауабы: x = 0; 4; - 4. №3. Теңдеуді шешіңіз, жауапта түбірлердің көбейтіндісін көрсетіңіз:
Жауабы: Тамырлардың көбейтіндісі 8-ге тең. №4. Теңдеуді шеш:
Басымдық теңдеулерді белгілеңіз (1) Және (2) және дизайнға ыңғайлы болу үшін олардың әрқайсысының шешімін бөлек қарастырыңыз. Екі теңдеуде бірнеше модуль бар болғандықтан, жүйелер жиынына эквивалентті көшуді жүзеге асыру ыңғайлы. (1)

(2)


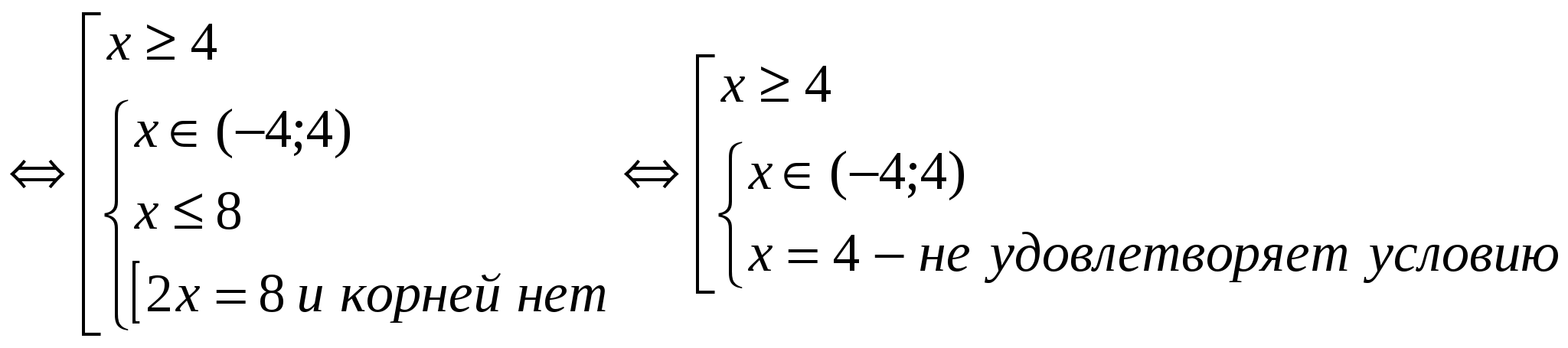Жауап:
Жаттығулар: №36. Теңдеуді шешіңіз, жауапта түбірлердің қосындысын көрсетіңіз: 5 │3x-5│ \u003d 25 x №37. Теңдеуді шешіңіз, егер бірден көп түбір болса, жауапта түбірлердің қосындысын көрсетіңіз: │x + 2│ x - 3x - 10 = 1 №38. Теңдеуді шешіңіз: 3 │2x -4│ \u003d 9 │x│ №39. Теңдеуді шешіңіз, жауапта түбірлер санын көрсетіңіз: 2 │ sin x │ = √2 №40 . Теңдеуді шешіңіз, жауапта түбірлер санын көрсетіңіз:

3-бөлім. Логарифмдік теңдеулер.

Келесі теңдеулерді шешпес бұрын логарифмдердің қасиеттерін және логарифмдік функцияны қарастыру қажет. Мысалдар: №1. Теңдеуді шешіңіз, жауапта түбірлердің көбейтіндісін көрсетіңіз: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

1-жағдай: егер x ≥ - 1 болса, онда log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – x ≥ - 1 2 шартын қанағаттандырады: егер x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – x - 1 шартын қанағаттандырады
Жауабы: Тамырлардың көбейтіндісі 15-ке тең.
№2. Теңдеуді шешіңіз, жауапта түбірлердің қосындысын көрсетіңіз: lg
О.Д.З.

Жауабы: түбірлердің қосындысы 0,5.
№3. Теңдеуді шешіңіз: log 5
О.Д.З.

Жауабы: x = 9. №4. Теңдеуді шешіңіз: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Басқа негізге көшу формуласын қолданайық. │2 - журнал 5 x│+ 3 = │1 + журнал 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Ішкі модуль өрнектерінің нөлдерін табайық: x = 25; x \u003d Бұл сандар рұқсат етілген мәндердің ауданын үш интервалға бөледі, сондықтан теңдеу үш жүйенің жиынтығына тең.
Жауап:)