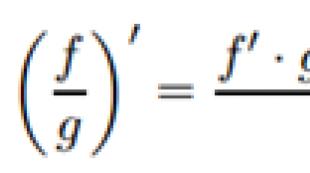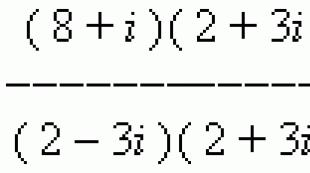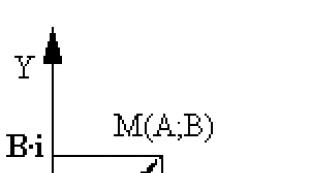Күрделі сандар

Қиял Және күрделі сандар. Абцисса және ордината

күрделі сан. Біріктірілген күрделі сандар.

Комплекс сандармен амалдар. Геометриялық

күрделі сандарды бейнелеу. күрделі жазықтық.

Комплекс санның модулі және аргументі. тригонометриялық

күрделі сан түрі. Кешенді операциялар

тригонометриялық формадағы сандар. Моевр формуласы.

туралы негізгі мәліметтер ойдан шығарылған Және күрделі сандар «Елес және күрделі сандар» бөлімінде берілген. Бұл жаңа типтегі сандарға қажеттілік жағдайға квадрат теңдеулерді шешу кезінде пайда болдыD< 0 (здесь Dквадрат теңдеудің дискриминанты болып табылады). Ұзақ уақыт бойы бұл сандар физикалық қолдануды таппады, сондықтан оларды «ойдан шығарылған» сандар деп атады. Дегенмен, қазір олар физиканың әртүрлі салаларында өте кең қолданылады.

және технология: электротехника, гидро- және аэродинамика, серпімділік теориясы және т.б.

Күрделі сандар былай жазылады:a+bi. Мұнда аЖәне б – нақты сандар , А мен – ойша бірлік. e. мен 2 = –1. Сан ашақырды абсцисса, а b - ординатакүрделі санa + b .Екі күрделі санa+biЖәне а-би шақырды конъюгаткүрделі сандар.

Негізгі келісімдер:

1. Нақты санАтүрінде де жазылуы мүмкінкүрделі сан:a + 0 меннемесе а - 0 мен. Мысалы, 5 + 0 жазбаларыменжәне 5 - 0 менбірдей санды білдіреді 5 .

2. Күрделі сан 0 + бишақырды таза ойдан шығарылған саны. Жазылуби0 дегенді білдіреді + би.

3. Екі күрделі санa+bi Жәнеc + diтең деп есептеледі, егерa = cЖәне b = d. Әйтпесе күрделі сандар тең емес.

Қосу. Күрделі сандардың қосындысыa+biЖәне c + diкүрделі сан деп аталады (a+c ) + (b+d ) мен.Осылайша, қосылған кезде күрделі сандар, олардың абциссалары мен ординаталары бөлек қосылады.

Бұл анықтама кәдімгі көпмүшелермен жұмыс істеу ережелерін сақтайды.

Алу. Екі күрделі санның айырмашылығыa+bi(қысқартылған) және c + di(алу) күрделі сан деп аталады (a-c ) + (б-д ) мен.

Осылайша, екі күрделі санды азайтқанда олардың абциссалары мен ординаталары бөлек алынып тасталады.

Көбейту. Күрделі сандардың көбейтіндісіa+biЖәне c + di күрделі сан деп аталады.

(ac-bd ) + (ad+bc ) мен.Бұл анықтама екі талаптан туындайды:

1) сандар a+biЖәне c + diалгебралық сияқты көбейту керекбиномдар,

2) саны меннегізгі қасиеті бар:мен 2 = – 1.

МЫСАЛ ( a + bi )(а-би) = а 2 +б 2 . Демек, жұмыс

екі конъюгаттық күрделі сан нақтыға тең

оң сан.

Бөлім. Күрделі санды бөлa+bi (бөлінетін) басқаc + di(бөлгіш) - үшінші санды табу дегенді білдіредіe + fi(чат), ол бөлгішке көбейтілгендеc + di, бұл дивидендке әкеледіa + b .

Егер бөлгіш нөл болмаса, бөлу әрқашан мүмкін.

МЫСАЛ Табу (8+мен ) : (2 – 3 мен) .

Шешуі.Бұл қатынасты бөлшек түрінде қайта жазайық:

Оның алымы мен бөлімін 2 + 3-ке көбейтумен

ЖӘНЕ барлық түрлендірулерді орындағаннан кейін біз аламыз:

Комплекс сандардың геометриялық кескіні. Нақты сандар сан түзуіндегі нүктелермен көрсетіледі:

Мәселе мынада А-3 санын, нүктені білдіредіБсаны 2, және О- нөл. Керісінше, комплекс сандар координаталық жазықтықтағы нүктелер арқылы көрсетіледі. Ол үшін екі осьте бірдей масштабтары бар тікбұрышты (декарттық) координаталарды таңдаймыз. Содан кейін күрделі санa+bi нүкте арқылы бейнеленеді абсциссасы бар P а және ординатасы b (суретті қараңыз). Бұл координаттар жүйесі деп аталады күрделі жазықтық .

модуль күрделі сан вектордың ұзындығы деп аталадыОП, координатасында күрделі санды бейнелейді ( біріктірілген) жазықтық. Күрделі сан модуліa+bi| арқылы белгіленеді a+bi| немесе хат r

Квадрат теңдеуді қарастырайық.

Оның тамырын анықтайық.

Квадраты -1 болатын нақты сан жоқ. Бірақ егер формула операторды анықтаса менойша бірлік ретінде, онда бұл теңдеудің шешімін түрінде жазуға болады . Бола тұра Және - күрделі сандар, онда -1 нақты бөлік, 2 немесе екінші жағдайда -2 елестетілген бөлік. Ойша бөлік те нақты (нақты) сан болып табылады. Елестеткіш бірлікке көбейтілген елестетілген бөлік қазірдің өзінде дегенді білдіреді ойдан шығарылған сан.

Жалпы алғанда, күрделі санның пішіні болады

z = x + iy ,

Қайда x, yнақты сандар болып табылады, жорамал бірлік болып табылады. Бірқатар қолданбалы ғылымдарда, мысалы, электротехникада, электроникада, сигналдар теориясында елестету бірлігі былай белгіленеді. j. Нақты сандар x = Re(z)Және у=мен(z)шақырды нақты және қиял бөліктерісандар z.Өрнек деп аталады алгебралық пішінкүрделі санның белгіленуі.

Кез келген нақты сан формадағы күрделі санның ерекше жағдайы болып табылады . Күрделі сан да күрделі санның ерекше жағдайы болып табылады. .

Комплекс сандар жиынының анықтамасы С

Бұл өрнек келесідей оқылады: set МЕН, осындай элементтерден тұрады xЖәне жнақты сандар жиынына жатады Ржәне елестетілген бірлік болып табылады. Назар аударыңыз, т.б.

Екі күрделі сан Және олардың нақты және елестетілген бөліктері тең болған жағдайда ғана тең болады, яғни. Және .

Күрделі сандар мен функциялар ғылым мен техникада, атап айтқанда, механикада, айнымалы ток тізбектерін талдау мен есептеуде, аналогтық электроникада, сигналдар теориясы мен өңдеуде, автоматты басқару теориясында және басқа қолданбалы ғылымдарда кеңінен қолданылады.

1. Күрделі сандардың арифметикасы

Екі күрделі санды қосу олардың нақты және жорамал бөліктерін қосудан тұрады, яғни.

Сәйкесінше, екі күрделі санның айырмасы

Күрделі сан шақырды кешен конъюгатсаны z=x +i.y.

Күрделі конъюгаттық z және z * сандары елестетілген бөліктің белгілері бойынша ерекшеленеді. Ол анық

.

Күрделі өрнектер арасындағы кез келген теңдік, егер бұл теңдік барлық жерде болса, жарамды болып қалады менауыстырылды - мен, яғни. жалғаулық сандардың теңдігіне өтіңіз. Сандар менЖәне – меналгебралық тұрғыдан ажыратылмайды, өйткені .

Екі күрделі санның көбейтіндісін (көбейтіндісін) келесідей есептеуге болады:

Екі күрделі санның бөлімі:

Мысал:

1. Күрделі жазықтық

Күрделі санды тікбұрышты координаталар жүйесінде графикалық түрде көрсетуге болады. Жазықтыққа тікбұрышты координаталар жүйесін орнатайық (x, y).

осьте Өгізбіз нақты бөліктерді реттейміз x, деп аталады нақты (нақты) ось, осьте Ой– ойдан шығарылған бөліктер жкүрделі сандар. Ол есімді алып жүр қиял осі. Оның үстіне әрбір күрделі сан жазықтықтың белгілі бір нүктесіне сәйкес келеді және мұндай жазықтық деп аталады күрделі жазықтық. Нүкте Акүрделі жазықтық векторға сәйкес болады О.А.

Сан xшақырды абсциссакүрделі сан, сан ж – ордината.

Күрделі конъюгаттық сандар жұбы нақты оське қатысты симметриялы орналасқан нүктелер түрінде көрсетіледі.

Егер ұшақта орнатылған болса полярлық координаталар жүйесі, содан кейін әрбір күрделі сан zполярлық координаталар арқылы анықталады. Бола тұра модульсандар нүктенің полярлық радиусы және бұрышы болып табылады - оның полярлық бұрышы немесе комплекс сан аргументі z.

Күрделі сан модулі әрқашан теріс емес. Күрделі санның аргументі біркелкі анықталмаған. Аргументтің негізгі мәні шартты қанағаттандыруы керек . Күрделі жазықтықтың әрбір нүктесі аргументтің жалпы мәніне де сәйкес келеді . 2π еселігімен ерекшеленетін аргументтер тең деп есептеледі. Нөл сандық аргументі анықталмаған.

Аргументтің негізгі мәні мына өрнектермен анықталады:

Ол анық

Бола тұра
, .

Күрделі санды ұсыну zтүрде

шақырды тригонометриялық пішінкүрделі сан.

Мысал.

1. Комплекс сандардың көрсеткіштік түрі

ыдырау Маклаурин сериясынақты аргумент функциялары үшін ұқсайды:

Күрделі аргументтің көрсеткіштік функциясы үшін zыдырауы ұқсас

.

Елестетілген аргументтің экспоненциалды функциясы үшін Маклаурин сериясының кеңеюін келесідей көрсетуге болады.

Алынған сәйкестік деп аталады Эйлер формуласы.

Теріс аргумент үшін бұл ұқсайды

Осы өрнектерді біріктіру арқылы синус пен косинус үшін келесі өрнектерді анықтай аламыз

.

Эйлер формуласын пайдаланып, күрделі сандарды бейнелеудің тригонометриялық түрінен

қолжетімді демонстрациялықКүрделі санның (көрсеткіштік, полярлық) түрі, яғни. түрінде оның көрінісі

,

Қайда - тікбұрышты координаталары бар нүктенің полярлық координаталары ( x,ж).

Күрделі санның жалғауы көрсеткіштік түрде былай жазылады.

Көрсеткіштік форма үшін күрделі сандарды көбейту және бөлу үшін келесі формулаларды анықтау оңай.

Яғни, экспоненциалды түрде күрделі сандарды көбейту және бөлу алгебралық түрге қарағанда оңайырақ. Көбейту кезінде факторлардың модульдері көбейтіледі, ал аргументтер қосылады. Бұл ереже факторлардың кез келген санына қолданылады. Атап айтқанда, күрделі санды көбейту кезінде zқосулы менвекторы zсағат тіліне қарсы 90 бұрылады

Бөлу кезінде алым модулі бөлгіш модуліне бөлінеді, ал алым аргументінен бөлгіш аргумент алынады.

Күрделі сандардың экспоненциалды түрін пайдалана отырып, белгілі тригонометриялық сәйкестіктердің өрнектерін алуға болады. Мысалы, жеке басынан

Эйлер формуласын қолданып жаза аламыз

Бұл өрнектегі нақты және жорамал бөлшектерді теңестіре отырып, бұрыштар қосындысының косинусы мен синусы үшін өрнектерді аламыз.

1. Күрделі сандардың дәрежелері, түбірлері және логарифмдері

Комплекс санды натурал дәрежеге көтеру nформуласы бойынша өндіріледі

Мысал. Есептеу .

Санды елестетіңіз тригонометриялық түрде

’

Көрсеткіштік формуланы қолданып, аламыз

Өрнектегі мәнді қою r= 1, біз деп аталатынды аламыз Де Мойвр формуласы, оның көмегімен бірнеше бұрыштардың синусы мен косинустарының өрнектерін анықтауға болады.

Түбір nкүрделі санның th дәрежесі zОнда бар nөрнек арқылы анықталатын әртүрлі мәндер

Мысал. Табайық.

Ол үшін күрделі санды () тригонометриялық түрге келтіреміз

.

Күрделі санның түбірін есептеу формуласы бойынша біз аламыз

Күрделі санның логарифмі zсан болып табылады w, ол үшін. Күрделі санның натурал логарифмінде мәндердің шексіз саны бар және формула бойынша есептеледі

Нақты (косинус) және жорамал (синус) бөліктерден тұрады. Мұндай кернеуді ұзындық векторы ретінде көрсетуге болады У м, бастапқы фаза (бұрыш), бұрыштық жылдамдықпен айналу ω .

Оның үстіне күрделі функциялар қосылса, олардың нақты және елес бөліктері қосылады. Егер күрделі функция тұрақты немесе нақты функцияға көбейтілсе, оның нақты және жорамал бөліктері бірдей көбейткішке көбейтіледі. Мұндай күрделі функцияның дифференциалдануы/интегралуы нақты және елес бөліктерінің дифференциациясына/интегралына келтіріледі.

Мысалы, күрделі екпінді өрнектің дифференциациясы

көбейту болып табылады iω – f(z) функциясының нақты бөлігі және функцияның елестетілген бөлігі болып табылады. Мысалдар: .

Мағынасы zкомплекс z жазықтығындағы нүктемен және сәйкес мәнмен көрсетіледі w- күрделі жазықтықтағы нүкте w. Көрсетілген кезде w = f(z)жазық сызықтар zжазықтықтың сызықтарына өтеді w, бір жазықтықтың фигуралары басқасының фигураларына айналады, бірақ сызықтардың немесе фигуралардың пішіндері айтарлықтай өзгеруі мүмкін.

		Комплекс санның алгебралық белгіленуі.................................................................................
		Комплекс сандар жазықтығы..................................................................................................................
		Күрделі құрмалас сандар ...................................................................................................
	Алгебралық түрдегі күрделі сандармен амалдар.................................................................
		Күрделі сандарды қосу ...................................................................................................
		Күрделі сандарды азайту......................................................................................................................
		Күрделі сандарды көбейту..................................................................................................................
		Күрделі сандарды бөлу..................................................................................................................
	Комплекс санның тригонометриялық түрі ......................................................................
	Тригонометриялық түрдегі күрделі сандармен амалдар ......................................................
		Комплекс сандарды тригонометриялық түрдегі көбейту...................................................................
		Комплекс сандарды тригонометриялық түрге бөлу ...................................................................
		Комплекс санды бүтін натурал дәрежеге көтеру
		Күрделі саннан натурал дәреженің түбірін алу
		Комплекс санды рационал дәрежеге шығару ...................................................................
		Күрделі қатар .................................................................................................................................
		Күрделі сандар қатары..................................................................................................................
		Күрделі жазықтықтағы қуат қатары................................................................................
		Күрделі жазықтықтағы екі жақты қуат сериясы .................................................................
		Күрделі айнымалының функциялары .................................................................................................................
		Негізгі элементар функциялар ...................................................................................................
		Эйлер формулалары.................................................................................................................................
		Комплекс санды көрсетудің көрсеткіштік түрі ................................................................
		Тригонометриялық және гиперболалық функциялар арасындағы байланыс ................................................
		Логарифмдік функция..................................................................................................................
		Жалпы көрсеткіштік және жалпы дәрежелік функциялар .................................................................................
	Күрделі айнымалының функцияларын дифференциалдау......................................................
		Коши-Риман шарттары .................................................................................................................
		Туындыны есептеу формулалары ...................................................................................
		Дифференциалдау операциясының қасиеттері .................................................................................................................
		Аналитикалық функцияның нақты және жорамал бөліктерінің қасиеттері .................................................

	Күрделі айнымалының функциясын оның нақты немесе жорамалынан қалпына келтіру
		№1 әдіс. Қисықсызықты интегралды қолдану.................................................................
		№2 әдіс. Коши-Риман шарттарын тікелей қолдану......................................
		№3 әдіс. Қажетті функцияның туындысы арқылы ...................................................................
	Күрделі айнымалы функцияларды интегралдау ...................................................................
	Интегралдық Коши формуласы.................................................................................................................
	Тейлор және Лоран қатарындағы функцияларды кеңейту ..............................................................................
	Күрделі айнымалы функцияның нөлдері мен дара нүктелері......................................................................
		Күрделі айнымалы функцияның нөлдері ................................................................................
		Күрделі айнымалы функцияның оқшауланған сингулярлық нүктелері .................................................

14.3 Күрделі айнымалы функцияның дара нүктесі ретінде шексіздік нүктесі

	Шығындар..................................................................................................................................................
		Соңғы нүктедегі шегерім ...................................................................................................................
		Функцияның шексіздік нүктесіндегі қалдығы ......................................................................
	Қалдықтарды пайдаланып интегралдарды есептеу ...................................................................................
	Өзін-өзі тексеруге арналған сұрақтар .................................................................................................................
	Әдебиет..................................................................................................................................
	Пәндік көрсеткіш.................................................................................................................

Алғы сөз

Емтиханның немесе модульді сертификаттаудың теориялық және практикалық бөліктеріне дайындалу үшін уақыт пен күш-жігерді дұрыс бөлу өте қиын, әсіресе сессия кезінде әрқашан уақыт жеткіліксіз болғандықтан. Тәжірибе көрсеткендей, мұны бәрі бірдей жеңе алмайды. Нәтижесінде емтихан кезінде кейбір студенттер есептерді дұрыс шығарса, ең қарапайым теориялық сұрақтарға жауап беру қиынға соғады, ал басқалары теореманы тұжырымдай алады, бірақ оны қолдана алмайды.

Күрделі айнымалы функциялар теориясы (ТҚТ) курсы бойынша емтиханға дайындалуға арналған осы әдістемелік ұсыныстар осы қарама-қайшылықты шешуге және курстың теориялық және практикалық материалдарының бір мезгілде қайталануын қамтамасыз етуге талпыныс болып табылады. «Тәжірибесіз теория өлі, теориясыз практика соқыр» деген қағиданы басшылыққа ала отырып, олар анықтамалар мен тұжырымдар деңгейінде курстың теориялық ұстанымдарын да, әрбір берілген теориялық ұстанымды қолдануды суреттейтін мысалдарды да қамтиды, осылайша есте сақтау мен түсінуді жеңілдетеді.

Ұсынылған әдістемелік ұсыныстардың мақсаты студентке емтиханға базалық деңгейде дайындалуға көмектесу болып табылады. Басқаша айтқанда, TFKT курсының сабақтарында қолданылатын және үй тапсырмасын орындау және бақылау іс-шараларына дайындалу кезінде қажет негізгі ойларды қамтитын кеңейтілген жұмыс нұсқаулығы құрастырылды. Студенттердің өзіндік жұмыстарымен қатар, бұл электронды оқу басылымын электронды тақтаны пайдалана отырып интерактивті түрде сабақтарды өткізу немесе қашықтықтан оқыту жүйесіне орналастыру үшін пайдалануға болады.

Бұл жұмыс оқулықтарды немесе дәріс конспектісін алмастырмайтынын ескеріңіз. Материалды тереңірек зерттеу үшін Мәскеу мемлекеттік техникалық университетінде жарияланған басылымның тиісті бөлімдеріне жүгіну ұсынылады. Н.Е. Бауманның негізгі оқулығы.

Нұсқаулықтың соңында ұсынылатын әдебиеттер тізімі және мәтінде көрсетілгендердің барлығын қамтитын пәндік индекс бар. қалың курсившарттар. Индекс осы терминдер қатаң түрде анықталған немесе сипатталған және олардың қолданылуын көрсету үшін мысалдар келтірілген бөлімдерге гиперсілтемелерден тұрады.

Әдістемелік құрал ММУ барлық факультеттерінің 2 курс студенттеріне арналған. Н.Е. Бауман.

1. Комплекс санды жазудың алгебралық түрі

z \u003d x + iy түріндегі жазу, мұндағы x, y - нақты сандар, i - елестетілген бірлік (яғни i 2 = − 1)

z комплекс санының алгебралық түрі деп аталады. Бұл жағдайда x күрделі санның нақты бөлігі деп аталады және Re z (x \u003d Re z) деп белгіленеді, y күрделі санның елестетілген бөлігі деп аталады және Im z (y \u003d Im z) деп белгіленеді.

Мысал. z = 4 − 3i күрделі санның нақты бөлігі Re z = 4 , ал елестетілген бөлігі Im z = − 3 .

2. Комплекс сандар жазықтығы

IN күрделі айнымалы функциялар теорияларын қарастырадыкүрделі сандар жазықтығы, ол не белгіленеді немесе z, w, т.б. күрделі сандарды білдіретін әріптер қолданылады.

Күрделі жазықтықтың горизонталь осі деп аталады нақты ось, онда z = x + 0 i = x нақты сандар орналасқан.

Күрделі жазықтықтың тік осі қиял осі деп аталады, ол бар

3. Күрделі құрмалас сандар

z = x + iy және z = x − iy сандары аталады күрделі конъюгат. Күрделі жазықтықта олар нақты оське қатысты симметриялы нүктелерге сәйкес келеді.

4. Алгебралық түрдегі күрделі сандармен амалдар

4.1 Күрделі сандарды қосу

Екі күрделі санның қосындысы

z 1 = x 1 + iy 1

ал z 2 = x 2 + iy 2 күрделі сан деп аталады

z1 + z2

= (x 1 + iy 1 ) + (x 2 + iy 2 ) = (x 1 + x 2 ) + i (y 1 + y 2 ) .

операция

толықтырулар

күрделі сандар алгебралық биномдарды қосу операциясына ұқсас.

Мысал. Екі күрделі санның қосындысы z 1 = 3 + 7i және z 2

= −1 +2 i

күрделі сан болады

z 1 + z 2 = (3 +7 i ) +(−1 +2 i ) = (3 −1 ) +(7 +2 ) i = 2 +9 i .

Әлбетте,

кешендегі сома

конъюгацияланған

болып табылады

жарамды

z + z = (x + iy) + (x − iy) = 2 x = 2 Rez .

4.2 Күрделі сандарды азайту

Екі күрделі санның айырмасы z 1 = x 1 + iy 1

X 2 +iy 2

шақырды

жан-жақты

саны z 1 − z 2 = (x 1 + iy 1 ) − (x 2 + iy 2 ) = (x 1 - x 2 ) + i (y 1 - y 2 ) .

Мысал. Екі күрделі санның айырмашылығы

z 1 = 3 −4 i

және z2

= −1 +2 i

жан-жақты болады

саны z 1 − z 2 = (3 − 4i ) − (− 1+ 2i ) = (3 − (− 1) ) + (− 4 − 2) i = 4 − 6i .

айырмашылық

күрделі конъюгат

болып табылады

z − z = (x + iy) − (x − iy) = 2 iy = 2 i Im z .

4.3 Күрделі сандарды көбейту

Екі күрделі санның көбейтіндісі

z 1 = x 1 + iy 1

және z 2 = x 2 + iy 2

күрделі деп аталады

z 1z 2 = (x 1 + iy 1 )(x 2 + iy 2 ) = x 1x 2 + iy 1x 2 + iy 2 x 1 + i 2 y 1 y 2

= (x 1x 2 − y 1 y 2 ) + i (y 1x 2 + y 2 x ) .

Сонымен, күрделі сандарды көбейту операциясы i 2 = − 1 болатынын ескере отырып, алгебралық биномдарды көбейту операциясына ұқсас.

АНЫҚТАУ

Комплекс санның алгебралық түрі \(\ z \) күрделі санды \(\ z=x+i y \) түрінде жазу болып табылады, мұндағы \(\ x \) және \(\ y \) нақты сандар, \(\ i \) - \(\ i^(2)=-1 \) қатынасын қанағаттандыратын жорамал бірлік.

\(\ x \) саны күрделі санның нақты бөлігі \(\ z \) деп аталады және \(\ x=\operatorname(Re) z \) деп белгіленеді.

\(\ y \) саны \(\ z \) күрделі санның елестетілген бөлігі деп аталады және \(\ y=\оператор аты(Im) z \) деп белгіленеді.

Мысалы:

Комплекс саны \(\ z=3-2 i \) және оған байланысты \(\ \overline(z)=3+2 i \) алгебралық түрде жазылған.

\(\ z=5 i \) елестету мәні алгебралық түрде жазылады.

Сонымен қатар, шешілетін мәселеге байланысты күрделі санды тригонометриялық немесе көрсеткіштік санға түрлендіруге болады.

Тапсырма

\(\ z=\frac(7-i)(4)+13 \) санын алгебралық түрде жазыңыз, оның нақты және жорамал бөліктерін, сонымен қатар жалғаулық санын табыңыз.

Шешім.

Бөлшектерді бөлу терминін және бөлшектерді қосу ережесін қолданып, мынаны аламыз:

\(\ z=\frac(7-i)(4)+13=\frac(7)(4)+13-\frac(i)(4)=\frac(59)(4)-\frac(1)(4) i \)

Демек, күрделі санның нақты бөлігі \(\ z=\frac(5 g)(4)-\frac(1)(4) i \) \(\ x=\operatorname(Re) z=\frac(59)(4) \) , елестетілген бөлігі \(\ y=\operatorname(Im)(Im)\(4)\1 саны болып табылады.

Конъюгаттық сан: \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)

Жауап

\(\ z=\frac(59)(4)-\frac(1)(4) i \), \(\ \оператор аты(Re) z=\frac(59)(4) \), \(\ \оператор аты(Im) z=-\frac(1)(4) \), \(\ \overline(z)=\frac(1)(1)(59)\

Комплекс сандардың алгебралық түрдегі салыстыру әрекеттері

Екі күрделі сандар \(\ z_(1)=x_(1)+i y_(1) \) тең деп аталады, егер \(\ x_(1)=x_(2) \), \(\ y_(1)=y_(2) \) яғни. Олардың нақты және қиял бөліктері тең.

Тапсырма

\(\ z_(1)=13+y i \) және \(\ z_(2)=x+5 i \) қандай x және y екі күрделі сандар тең екенін анықтаңыз.

Шешім

Анықтау бойынша екі күрделі сан тең, егер олардың нақты және жорамал бөліктері тең болса, яғни. \(\ x=13 \), \(\ y=5 \).

Жауабы \(\ x=13 \), \(\ y=5 \)

қосу

\(\ z_(1)=x_(1)+i y_(1) \) күрделі сандарды қосу нақты және жорамал бөлшектерді тура қосу арқылы орындалады:

\(\ z_(1)+z_(2)=x_(1)+i y_(1)+x_(2)+i y_(2)=\сол(x_(1)+x_(2)\оң)+i\сол(y_(1)+y_(2)\оң) \)

Тапсырма

\(\ z_(1)=-7+5 i \), \(\ z_(2)=13-4 i \) күрделі сандардың қосындысын табыңыз.

Шешім.

Күрделі санның \(\ z_(1)=-7+5 i \) нақты бөлігі \(\ x_(1)=\операторname(Re) z_(1)=-7 \) саны, елестетілген бөлігі \(\ y_(1)=\mathrm(Im) \), \(\ z_)(1)=5 саны. \(\ z_(2)=13-4 i \) күрделі санның нақты және жорамал бөліктері сәйкесінше \(\ x_(2)=\operatorname(Re) z_(2)=13 \) және \(\ y_(2)=\operatorname(Im) z_(2)=-4 \) болады.

Демек, күрделі сандардың қосындысы:

\(\ z_(1)+z_(2)=\сол(x_(1)+x_(2)\оң)+i\сол(y_(1)+y_(2)\оң)=(-7+13)+i(5-4)=6+i \)

Жауап

\(\z_(1)+z_(2)=6+i \)

Күрделі сандарды қосу туралы қосымша ақпаратты бөлек мақалада оқыңыз: Күрделі сандарды қосу.

Алу

\(\ z_(1)=x_(1)+i y_(1) \) және \(\ z_(2)=x_(2)+i y_(2) \) күрделі сандарды азайту нақты және жорамал бөлшектерді тура алу арқылы орындалады:

\(\ z_(1)-z_(2)=x_(1)+i y_(1)-\сол(x_(2)+i y_(2)\оң)=x_(1)-x_(2)+\сол(i y_(1)-i y_(2)\оң)=\сол(x_(1)\оң)=\сол(x_(1)-left(x_(1)-le)_(i)\y(1)\x дұрыс)\)

Тапсырма

күрделі сандардың айырмасын табыңдар \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \)

Шешім.

Күрделі сандардың нақты және жорамал бөліктерін табыңыз \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \) :

\(\ x_(1)=\оператор аты(Re) z_(1)=17, x_(2)=\оператор аты(Re) z_(2)=15 \)

\(\ y_(1)=\оператор аты(Im) z_(1)=-35, y_(2)=\оператор аты(Im) z_(2)=5 \)

Сонымен, күрделі сандардың айырмашылығы:

\(\ z_(1)-z_(2)=\сол(x_(1)-x_(2)\оң)+i\сол(y_(1)-y_(2)\оң)=(17-15)+i(-35-5)=2-40 i \)

Жауап

\(\ z_(1)-z_(2)=2-40 i \) көбейту

\(\ z_(1)=x_(1)+i y_(1) \) және \(\ z_(2)=x_(2)+i y_(2) \) күрделі сандарды көбейту \(\ i^(2) \) елестетілген бірлік қасиетін ескере отырып, алгебралық түрде сандарды тура генерациялау арқылы орындалады:

\(\ z_(1) \cdot z_(2)=\left(x_(1)+i y_(1)\оң) \cdot\left(x_(2)+i y_(2)\оң)=x_(1) \cdot x_(2)+i^(2) \cdot y_(1) _ fut \(1) do y _(2)+x_(2) \cdot i y_(1)\оң)= \)

\(\ =\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2) \cdot y_(1)\оң) \)

Тапсырма

Күрделі сандардың көбейтіндісін табыңыз \(\ z_(1)=1-5 i \)

Шешім.

Комплекс сандар кешені:

\(\ z_(1) \cdot z_(2)=\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2) \cdot y_(1)\c)(5)(5) істеу \c= \cdot 2+(-5) \cdot 5)=15-23 i \)

Жауап

\(\ z_(1) \cdot z_(2)=15-23 i \) бөлу

Күрделі сан коэффициенті \(\ z_(1)=x_(1)+i y_(1) \) және \(\ z_(2)=x_(2)+i y_(2) \) алым мен азайтқышты бөлгіштің жалғаулығына көбейту арқылы анықталады:

\(\ \frac(z_(1))(z_(2))=\frac(x_(1)+i y_(1))(x_(2)+i y_(2))=\frac(\left(x_(1)+i y_(1)\оң)\сол(x_(2)-i y_)(2)y(оң)_(2) 2)\le сол жақ(x_ (2)-i y_(2)\оң))=\frac(x_(1) \cdot x_(2)+y_(1) \cdot y_(2))(x_(2)^(2)+y_(2)^(2))+i \frac(x_(2) \cdot y_(1)(2) \cdot y_(1)(_) 2)+y_(2)^ (2)) \)

Тапсырма

1 санын күрделі санға бөлу үшін \(\ z=1+2 i \).

Шешім.

Нақты 1 санның ойша бөлігі нөлге тең болғандықтан, көбейткіш:

\(\ \frac(1)(1+2 i)=\frac(1 \cdot 1)(1^(2)+2^(2))-i \frac(1 \cdot 2)(1^(2)+2^(2))=\frac(1)(5)-i \frac(2)(5) \)

Жауап

\(\ \frac(1)(1+2 i)=\frac(1)(5)-i \frac(2)(5) \)

Сабақ жоспары.

1. Ұйымдастыру кезеңі.

2. Материалды таныстыру.

3. Үйге тапсырма.

4. Сабақты қорытындылау.

Сабақтар кезінде

I. Ұйымдастыру кезеңі.

II. Материалды таныстыру.

Мотивация.

Нақты сандар жиынының кеңеюі нақты сандарға жаңа сандар (ойдан алынған) қосылуынан тұрады. Бұл сандарды енгізу нақты сандар жиынындағы теріс саннан түбір алу мүмкін еместігімен байланысты.

Комплекс сан ұғымымен таныстыру.

Нақты сандарды толықтыратын ойша сандар былай жазылады би, Қайда менойша бірлік болып табылады, және i 2 = - 1.

Осының негізінде күрделі санның келесі анықтамасын аламыз.

Анықтама. Күрделі сан – пішіннің өрнегі a+bi, Қайда аЖәне бнақты сандар. Бұл жағдайда келесі шарттар орындалады:

а) Екі күрделі сан a 1 + b 1 iЖәне a 2 + b 2 iтең болса және тек егер a 1 = a 2, b1=b2.

б) Күрделі сандардың қосылуы мына ережемен анықталады:

(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.

в) Күрделі сандарды көбейту мына ережемен анықталады:

(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.

Комплекс санның алгебралық түрі.

Күрделі санды пішінде жазу a+biкүрделі санның алгебралық түрі деп аталады, мұндағы А- нақты бөлігі биқиял бөлігі болып табылады және бнақты сан болып табылады.

Күрделі сан a+biнөлге тең деп есептеледі, егер оның нақты және жорамал бөліктері нөлге тең болса: a=b=0

Күрделі сан a+biсағ b = 0нақты сан болып есептеледі а: a + 0i = a.

Күрделі сан a+biсағ a = 0таза елестету деп аталады және белгіленеді би: 0 + bi = bi.

Екі күрделі сан z = a + biЖәне = а – би, тек қиял бөлігінің таңбасымен ғана ерекшеленетін сыңарлары құрмалас деп аталады.

Алгебралық түрдегі күрделі сандарға әрекеттер.

Алгебралық түрде күрделі сандарға келесі амалдарды орындауға болады.

1) Қосымша.

Анықтама. Күрделі сандардың қосындысы z 1 = a 1 + b 1 iЖәне z 2 = a 2 + b 2 iкүрделі сан деп аталады z, оның нақты бөлігі нақты бөліктерінің қосындысына тең z1Және z2, ал қиял бөлігі сандардың елестетілген бөліктерінің қосындысы болып табылады z1Және z2, яғни z = (a 1 + a 2) + (b 1 + b 2)i.

Сандар z1Және z2терминдер деп аталады.

Күрделі сандарды қосудың келесі қасиеттері бар:

1º. Коммутативтілік: z1 + z2 = z2 + z1.

2º. Ассоциативтілік: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).

3º. Күрделі сан -а -бикүрделі санға қарама-қарсы сан деп аталады z = a + bi. Күрделі санға қарама-қарсы күрделі сан z, белгіленген -z. Күрделі сандардың қосындысы zЖәне -zнөлге тең: z + (-z) = 0

1-мысал: Қосу (3 - i) + (-1 + 2i).

(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.

2) Алу.

Анықтама.Күрделі саннан алу z1күрделі сан z2 z,Не z + z 2 = z 1.

Теорема. Күрделі сандардың айырмашылығы бар және оның үстіне бірегей.

2-мысал: Алу (4 - 2i) - (-3 + 2i).

(4 - 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 - 4i.

3) Көбейту.

Анықтама. Күрделі сандардың көбейтіндісі z 1 =a 1 +b 1 iЖәне z 2 \u003d a 2 + b 2 iкүрделі сан деп аталады z, теңдігімен анықталады: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.

Сандар z1Және z2факторлар деп аталады.

Күрделі сандарды көбейту келесі қасиеттерге ие:

1º. Коммутативтілік: z 1 z 2 = z 2 z 1.

2º. Ассоциативтілік: (z 1 z 2)z 3 = z 1 (z 2 z 3)

3º. Көбейтудің қосуға қатысты үлестірімділігі:

(z 1 + z 2) z 3 \u003d z 1 z 3 + z 2 z 3.

4º. z \u003d (a + bi) (a - bi) \u003d a 2 + b 2нақты сан болып табылады.

Практикада күрделі сандарды көбейту қосындыны қосындыға көбейту және нақты және жорамал бөлшектерді бөлу ережесі бойынша жүзеге асырылады.

Келесі мысалда күрделі сандарды екі жолмен көбейтуді қарастырайық: ереже бойынша және қосындыны қосындыға көбейту.

3-мысал: Көбейту (2 + 3i) (5 – 7i).

1 жол. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15)i = 31 + i.

2 жол. (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.

4) Бөлім.

Анықтама. Күрделі санды бөл z1күрделі санға z2, осындай күрделі санды табуды білдіреді z, Не z z 2 = z 1.

Теорема.Күрделі сандардың бөлімі бар және бірегей, егер болса z2 ≠ 0 + 0i.

Практикада күрделі сандардың бөлімі алымы мен бөлімін бөлгіштің жалғауына көбейту арқылы табылады.

Болсын z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, Содан кейін

.

Келесі мысалда формула бойынша бөлуді және көбейту ережесін бөлгіштің жалғауы арқылы орындаймыз.

Мысал 4. Бөліндіні табыңыз .

5) Оң бүтін дәрежеге көтеру.

а) Елестету бірлігінің күштері.

Теңдікті пайдалану i 2 \u003d -1, ойша бірліктің кез келген оң бүтін дәрежесін анықтау оңай. Бізде бар:

i 3 \u003d i 2 i \u003d -i,

i 4 \u003d i 2 i 2 \u003d 1,

i 5 \u003d i 4 i \u003d i,

i 6 \u003d i 4 i 2 \u003d -1,

i 7 \u003d i 5 i 2 \u003d -i,

i 8 = i 6 i 2 = 1және т.б.

Бұл дәреже мәндерін көрсетеді мен н, Қайда n- индикатор артқанда мерзімді түрде қайталанатын натурал сан 4 .

Сондықтан санын көбейту меноң бүтін дәрежеге, көрсеткішті мынаға бөліңіз 4 және тұрғызу менкөрсеткіші бөлімнің қалдығы болатын дәрежеге.

5-мысал Есептеңіз: (i 36 + i 17) i 23.

i 36 = (i 4) 9 = 1 9 = 1,

i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 i = i.

i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 i 3 = - i.

(i 36 + i 17) i 23 \u003d (1 + i) (- i) \u003d - i + 1 \u003d 1 - i.

б) Комплекс санды бүтін натурал дәрежеге көтеру биномдық мәнді сәйкес дәрежеге көтеру ережесі бойынша жүзеге асырылады, өйткені бұл бірдей күрделі көбейткіштерді көбейтудің ерекше жағдайы.

6-мысал Есептеңіз: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.