परिकथाएं

एक त्रिभुज की ऊंचाई के समीकरण दिए गए हैं। विश्लेषणात्मक ज्यामिति में समस्याओं को हल करना कैसे सीखें? समतल पर त्रिभुज के साथ विशिष्ट समस्या

समस्या 1 - 20 में त्रिभुज ABC के शीर्ष दिए गए हैं।
ज्ञात करें: 1) भुजा AB की लंबाई; 2) भुजाओं AB और AC के समीकरण और उनके कोणीय गुणांक; 3) 0.01 की सटीकता के साथ रेडियन में आंतरिक कोण ए; 4) सीडी की ऊंचाई और उसकी लंबाई के लिए समीकरण; 5) एक वृत्त का समीकरण जिसकी ऊंचाई सीडी व्यास है; 6) त्रिभुज ABC को परिभाषित करने वाली रैखिक असमानताओं की एक प्रणाली।

त्रिभुज की भुजाओं की लंबाई:
|एबी| = 15
|एसी| = 11.18
|बीसी| = 14.14
बिंदु M से दूरी d: d = 10
त्रिभुज के शीर्षों के निर्देशांक दिए गए हैं: A(-5,2), B(7,-7), C(5,7).
2) त्रिभुज की भुजाओं की लंबाई
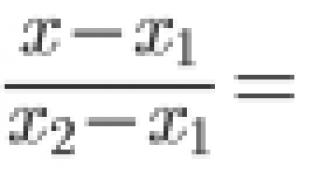
बिंदु M 1 (x 1 ; y 1) और M 2 (x 2 ; y 2) के बीच की दूरी d सूत्र द्वारा निर्धारित की जाती है:

8) एक रेखा का समीकरण
बिंदु A 1 (x 1 ; y 1) और A 2 (x 2 ; y 2) से गुजरने वाली एक सीधी रेखा को समीकरणों द्वारा दर्शाया जाता है:

रेखा AB का समीकरण

या

या
y = -3 / 4 x -7 / 4 या 4y + 3x +7 = 0
लाइन एसी का समीकरण
रेखा का विहित समीकरण:

या

या
y = 1 / 2 x + 9 / 2 या 2y -x - 9 = 0
रेखा BC का समीकरण
रेखा का विहित समीकरण:

या

या
y = -7x + 42 या y + 7x - 42 = 0
3) सीधी रेखाओं के बीच का कोण
सीधी रेखा AB का समीकरण:y = -3 / 4 x -7 / 4
रेखा समीकरण AC:y = 1/2 x + 9/2
कोणीय गुणांक y = k 1 x + b 1 और y 2 = k 2 x + b 2 वाले समीकरणों द्वारा दिए गए दो सीधी रेखाओं के बीच के कोण की गणना सूत्र द्वारा की जाती है:

इन रेखाओं का ढलान -3/4 और 1/2 है। आइए सूत्र का उपयोग करें, और इसका दाहिना ओर मॉड्यूल लें:

टीजी φ = 2
φ = आर्कटान(2) = 63.44 0 या 1.107 रेड।
9) शीर्ष C से होकर ऊँचाई का समीकरण
बिंदु N 0 (x 0 ;y 0) से गुजरने वाली सीधी रेखा और सीधी रेखा Ax + By + C = 0 के लंबवत एक दिशा वेक्टर (A;B) है और इसलिए, समीकरणों द्वारा दर्शाया गया है:

इस समीकरण को दूसरे तरीके से पाया जा सकता है. ऐसा करने के लिए, आइए सीधी रेखा AB का ढलान k 1 ज्ञात करें।
एबी समीकरण: y = -3 / 4 x -7 / 4, यानी। के 1 = -3/4
आइए दो सीधी रेखाओं की लंबवतता की स्थिति से लंबवत का कोणीय गुणांक k ज्ञात करें: k 1 *k = -1।
k 1 के स्थान पर इस रेखा की ढलान को प्रतिस्थापित करने पर, हम पाते हैं:
-3 / 4 k = -1, जहाँ से k = 4 / 3
चूँकि लम्ब बिंदु C(5,7) से होकर गुजरता है और इसमें k = 4/3 है, हम इसके समीकरण को इस रूप में देखेंगे: y-y 0 = k(x-x 0)।
x 0 = 5, k = 4/3, y 0 = 7 को प्रतिस्थापित करने पर हमें प्राप्त होता है:
y-7 = 4/3 (x-5)
या
y = 4 / 3 x + 1 / 3 या 3y -4x - 1 = 0
आइए रेखा AB के साथ प्रतिच्छेदन बिंदु ज्ञात करें:
हमारे पास दो समीकरणों की एक प्रणाली है:
4y + 3x +7 = 0
3y -4x - 1 = 0
पहले समीकरण से हम y व्यक्त करते हैं और इसे दूसरे समीकरण में प्रतिस्थापित करते हैं।
हम पाते हैं:
एक्स = -1
y=-1
डी(-1;-1)
9) शीर्ष C से खींचे गए त्रिभुज की ऊंचाई की लंबाई
बिंदु M 1 (x 1 ;y 1) से सीधी रेखा Ax + By + C = 0 की दूरी d मात्रा के पूर्ण मान के बराबर है:

बिंदु C(5;7) और रेखा AB (4y + 3x +7 = 0) के बीच की दूरी ज्ञात करें

ऊंचाई की लंबाई की गणना एक अन्य सूत्र का उपयोग करके की जा सकती है, जैसे बिंदु C(5;7) और बिंदु D(-1;-1) के बीच की दूरी।
दो बिंदुओं के बीच की दूरी सूत्र द्वारा निर्देशांक के रूप में व्यक्त की जाती है:

5) एक वृत्त का समीकरण जिसकी ऊंचाई सीडी व्यास है;
बिंदु E(a;b) पर केंद्र के साथ त्रिज्या R के एक वृत्त का समीकरण इस प्रकार है:
(एक्स-ए) 2 + (वाई-बी) 2 = आर 2
चूँकि CD वांछित वृत्त का व्यास है, इसका केंद्र E खंड CD का मध्यबिंदु है। किसी खंड को आधे में विभाजित करने के सूत्रों का उपयोग करते हुए, हम पाते हैं:

इसलिए, E(2;3) और R = CD / 2 = 5. सूत्र का उपयोग करके, हम वांछित वृत्त का समीकरण प्राप्त करते हैं: (x-2) 2 + (y-3) 2 = 25

6) त्रिभुज ABC को परिभाषित करने वाली रैखिक असमानताओं की एक प्रणाली।
रेखा AB का समीकरण: y = -3 / 4 x -7 / 4
रेखा AC का समीकरण: y = 1/2 x + 9/2
रेखा BC का समीकरण: y = -7x + 42

विश्लेषणात्मक ज्यामिति में समस्याओं को हल करना कैसे सीखें?
समतल पर त्रिभुज के साथ विशिष्ट समस्या

यह पाठ समतल की ज्यामिति और अंतरिक्ष की ज्यामिति के बीच भूमध्य रेखा के दृष्टिकोण पर बनाया गया है। फिलहाल, संचित जानकारी को व्यवस्थित करने और एक बहुत ही महत्वपूर्ण प्रश्न का उत्तर देने की आवश्यकता है: विश्लेषणात्मक ज्यामिति में समस्याओं को हल करना कैसे सीखें?कठिनाई यह है कि आप ज्यामिति में अनंत संख्या में समस्याएं लेकर आ सकते हैं, और किसी भी पाठ्यपुस्तक में सभी उदाहरणों की भीड़ और विविधता शामिल नहीं होगी। क्या नहीं है किसी फ़ंक्शन का व्युत्पन्नविभेदीकरण के पांच नियमों, एक तालिका और कई तकनीकों के साथ...

एक समाधान है! मैं इस तथ्य के बारे में जोर से नहीं बोलूंगा कि मैंने किसी प्रकार की भव्य तकनीक विकसित की है, हालांकि, मेरी राय में, विचाराधीन समस्या के लिए एक प्रभावी दृष्टिकोण है, जो एक पूर्ण डमी को भी अच्छे और उत्कृष्ट परिणाम प्राप्त करने की अनुमति देता है। कम से कम, ज्यामितीय समस्याओं को हल करने के लिए सामान्य एल्गोरिदम ने मेरे दिमाग में बहुत स्पष्ट रूप से आकार ले लिया।

आपको क्या जानने और करने में सक्षम होने की आवश्यकता है
ज्यामिति समस्याओं को सफलतापूर्वक हल करने के लिए?

इससे कोई बच नहीं सकता है - अपनी नाक से बटनों को बेतरतीब ढंग से न चुभाने के लिए, आपको विश्लेषणात्मक ज्यामिति की मूल बातों में महारत हासिल करने की आवश्यकता है। इसलिए, यदि आपने अभी-अभी ज्यामिति का अध्ययन शुरू किया है या इसे पूरी तरह से भूल गए हैं, तो कृपया पाठ से शुरुआत करें डमी के लिए वेक्टर. सदिशों और उनके साथ होने वाली क्रियाओं के अलावा, आपको विशेष रूप से समतल ज्यामिति की बुनियादी अवधारणाओं को जानने की आवश्यकता है, एक समतल में एक रेखा का समीकरणऔर । अंतरिक्ष की ज्यामिति लेखों में प्रस्तुत की गई है समतल समीकरण, अंतरिक्ष में एक रेखा के समीकरण, एक सीधी रेखा और एक समतल पर बुनियादी समस्याएं और कुछ अन्य पाठ। दूसरे क्रम की घुमावदार रेखाएँ और स्थानिक सतहें कुछ हद तक अलग-अलग खड़ी होती हैं, और उनके साथ इतनी अधिक विशिष्ट समस्याएँ नहीं होती हैं।

आइए मान लें कि छात्र के पास विश्लेषणात्मक ज्यामिति की सबसे सरल समस्याओं को हल करने का बुनियादी ज्ञान और कौशल पहले से ही है। लेकिन ऐसा होता है: आप समस्या का विवरण पढ़ते हैं, और... आप पूरी चीज़ को पूरी तरह से बंद कर देना चाहते हैं, इसे दूर कोने में फेंक देना चाहते हैं और एक बुरे सपने की तरह इसे भूल जाना चाहते हैं। इसके अलावा, यह मूल रूप से आपकी योग्यता के स्तर पर निर्भर नहीं करता है; समय-समय पर मेरे सामने ऐसे कार्य आते हैं जिनका समाधान स्पष्ट नहीं होता है। ऐसे मामलों में क्या करें? जिस काम को आप नहीं समझते उससे डरने की कोई जरूरत नहीं है!

पहले तो, स्थापित किया जाना चाहिए - क्या यह एक "सपाट" या स्थानिक समस्या है?उदाहरण के लिए, यदि शर्त में दो निर्देशांक वाले वेक्टर शामिल हैं, तो, निश्चित रूप से, यह एक विमान की ज्यामिति है। और यदि शिक्षक ने कृतज्ञ श्रोता पर पिरामिड लाद दिया, तो अंतरिक्ष की ज्यामिति स्पष्ट रूप से दिखाई देती है। पहले चरण के परिणाम पहले से ही काफी अच्छे हैं, क्योंकि हम इस कार्य के लिए अनावश्यक जानकारी की एक बड़ी मात्रा को काटने में कामयाब रहे!

दूसरा. यह स्थिति आमतौर पर आपको किसी ज्यामितीय आकृति से चिंतित करेगी। वास्तव में, अपने मूल विश्वविद्यालय के गलियारों में चलें, और आपको बहुत सारे चिंतित चेहरे दिखाई देंगे।

"सपाट" समस्याओं में, स्पष्ट बिंदुओं और रेखाओं का उल्लेख न करते हुए, सबसे लोकप्रिय आकृति एक त्रिकोण है। हम इसका विस्तृत विश्लेषण करेंगे. इसके बाद समांतर चतुर्भुज आता है, और आयत, वर्ग, समचतुर्भुज, वृत्त और अन्य आकृतियाँ बहुत कम आम हैं।

स्थानिक समस्याओं में, समान सपाट आकृतियाँ + स्वयं विमान और समान्तर चतुर्भुज वाले सामान्य त्रिकोणीय पिरामिड उड़ सकते हैं।

प्रश्न दो - क्या आप इस आंकड़े के बारे में सब कुछ जानते हैं?मान लीजिए कि स्थिति एक समद्विबाहु त्रिभुज के बारे में बात करती है, और आपको बहुत अस्पष्ट रूप से याद है कि यह किस प्रकार का त्रिभुज है। हम एक स्कूल की पाठ्यपुस्तक खोलते हैं और एक समद्विबाहु त्रिभुज के बारे में पढ़ते हैं। क्या करें...डॉक्टर ने कहा रोम्बस, मतलब रोम्बस। विश्लेषणात्मक ज्यामिति विश्लेषणात्मक ज्यामिति है, लेकिन समस्या का समाधान आकृतियों के ज्यामितीय गुणों से स्वयं हो जाएगा, जो हमें स्कूली पाठ्यक्रम से ज्ञात है। यदि आप नहीं जानते कि त्रिभुज के कोणों का योग कितना होता है, तो आप लंबे समय तक पीड़ित रह सकते हैं।

तीसरा. हमेशा ड्राइंग का अनुसरण करने का प्रयास करें(ड्राफ्ट/फिनिश कॉपी पर/मानसिक रूप से), भले ही यह शर्त के अनुसार आवश्यक न हो। "सपाट" समस्याओं में, यूक्लिड ने स्वयं एक रूलर और एक पेंसिल लेने का आदेश दिया - और न केवल स्थिति को समझने के लिए, बल्कि आत्म-परीक्षण के उद्देश्य से भी। इस मामले में, सबसे सुविधाजनक पैमाना 1 इकाई = 1 सेमी (2 नोटबुक सेल) है। आइए लापरवाह छात्रों और कब्रों में घूमते गणितज्ञों के बारे में बात न करें - ऐसी समस्याओं में गलती करना लगभग असंभव है। स्थानिक कार्यों के लिए, हम एक योजनाबद्ध चित्रण करते हैं, जो स्थिति का विश्लेषण करने में भी मदद करेगा।

एक रेखाचित्र या योजनाबद्ध रेखाचित्र अक्सर आपको किसी समस्या को हल करने का तरीका तुरंत देखने की अनुमति देता है। निःसंदेह, इसके लिए आपको ज्यामिति की नींव जानने और ज्यामितीय आकृतियों के गुणों को समझने की आवश्यकता है (पिछला पैराग्राफ देखें)।

चौथी. समाधान एल्गोरिथम का विकास. कई ज्यामिति समस्याएं बहु-चरणीय होती हैं, इसलिए समाधान और उसके डिज़ाइन को बिंदुओं में विभाजित करना बहुत सुविधाजनक होता है। अक्सर शर्त पढ़ने या ड्राइंग पूरा करने के बाद एल्गोरिदम तुरंत दिमाग में आता है। कठिनाइयों के मामले में, हम कार्य के प्रश्न से शुरुआत करते हैं. उदाहरण के लिए, शर्त के अनुसार "आपको एक सीधी रेखा बनाने की आवश्यकता है..."। यहां सबसे तार्किक प्रश्न यह है: "इस सीधी रेखा को बनाने के लिए क्या जानना पर्याप्त है?" मान लीजिए, "हम बिंदु जानते हैं, हमें दिशा वेक्टर जानने की जरूरत है।" हम निम्नलिखित प्रश्न पूछते हैं: “इस दिशा वेक्टर को कैसे खोजें? कहाँ?" वगैरह।

कभी-कभी एक "बग" होता है - समस्या हल नहीं होती है और बस इतना ही। रुकने के कारण निम्नलिखित हो सकते हैं:

– बुनियादी ज्ञान में गंभीर अंतर. दूसरे शब्दों में, आप किसी बहुत ही साधारण सी चीज़ को नहीं जानते और/या नहीं देखते हैं।

- ज्यामितीय आकृतियों के गुणों की अज्ञानता।

- कार्य कठिन था। हाँ, ऐसा होता है. घंटों तक भाप लेने और रूमाल में आँसू इकट्ठा करने का कोई मतलब नहीं है। अपने शिक्षक, साथी छात्रों से सलाह लें या मंच पर प्रश्न पूछें। इसके अलावा, अपने कथन को ठोस बनाना बेहतर है - समाधान के उस हिस्से के बारे में जिसे आप नहीं समझते हैं। "समस्या का समाधान कैसे करें?" के रूप में एक पुकार बहुत अच्छा नहीं लग रहा है... और, सबसे बढ़कर, आपकी अपनी प्रतिष्ठा के लिए।

चरण पांच. हम निर्णय लेते हैं-जांचते हैं, निर्णय लेते हैं-जांचते हैं, निर्णय लेते हैं-जांचते हैं-उत्तर देते हैं। कार्य के प्रत्येक बिन्दु की जांच करना लाभकारी रहता है इसके पूरा होने के तुरंत बाद. इससे आपको तुरंत त्रुटि पहचानने में मदद मिलेगी. स्वाभाविक रूप से, कोई भी पूरी समस्या को जल्दी से हल करने से मना नहीं करता है, लेकिन सब कुछ फिर से लिखने का जोखिम होता है (अक्सर कई पृष्ठ)।

ये, शायद, सभी मुख्य विचार हैं जिनका समस्याओं को हल करते समय पालन किया जाना चाहिए।

पाठ का व्यावहारिक भाग समतल ज्यामिति में प्रस्तुत किया गया है। केवल दो उदाहरण होंगे, लेकिन यह पर्याप्त नहीं लगेगा =)

आइए एल्गोरिथम के उस सूत्र पर गौर करें जिसे मैंने अभी अपने छोटे वैज्ञानिक कार्य में देखा है:

उदाहरण 1

एक समांतर चतुर्भुज के तीन शीर्ष दिए गए हैं। शीर्ष खोजें.

आइए समझना शुरू करें:

पहला कदम: यह स्पष्ट है कि हम एक "सपाट" समस्या के बारे में बात कर रहे हैं।

दूसरा चरण: समस्या एक समांतर चतुर्भुज से संबंधित है। क्या सभी को यह समांतर चतुर्भुज आकृति याद है? मुस्कुराने की जरूरत नहीं है, बहुत से लोग 30-40-50 या उससे अधिक उम्र में शिक्षा प्राप्त करते हैं, इसलिए साधारण तथ्य भी स्मृति से मिटाए जा सकते हैं। समांतर चतुर्भुज की परिभाषा पाठ के उदाहरण संख्या 3 में पाई जाती है सदिशों की रैखिक (गैर) निर्भरता। सदिशों का आधार.

तीसरा कदम: आइए एक चित्र बनाएं जिस पर हम तीन ज्ञात शीर्षों को चिह्नित करें। यह मज़ेदार है कि वांछित बिंदु को तुरंत बनाना मुश्किल नहीं है:

बेशक, इसका निर्माण अच्छा है, लेकिन समाधान विश्लेषणात्मक रूप से तैयार किया जाना चाहिए।

चरण चार: एक समाधान एल्गोरिथ्म का विकास. पहली बात जो दिमाग में आती है वह यह है कि एक बिंदु को रेखाओं के प्रतिच्छेदन के रूप में पाया जा सकता है। हम उनके समीकरण नहीं जानते, इसलिए हमें इस मुद्दे से निपटना होगा:

1) सम्मुख भुजाएँ समान्तर हैं। अंकों के हिसाब से आइए इन भुजाओं का दिशा सदिश ज्ञात करें। यह सबसे सरल समस्या है जिस पर कक्षा में चर्चा की गई थी। डमी के लिए वेक्टर.

टिप्पणी: "एक पक्ष वाली रेखा का समीकरण" कहना अधिक सही है, लेकिन यहां और आगे संक्षिप्तता के लिए मैं "एक पक्ष का समीकरण," "एक पक्ष का दिशा वेक्टर" आदि वाक्यांशों का उपयोग करूंगा।

3) सम्मुख भुजाएँ समान्तर हैं। बिंदुओं का उपयोग करके, हम इन भुजाओं का दिशा सदिश ज्ञात करते हैं।

4) आइए एक बिंदु और एक दिशा वेक्टर का उपयोग करके एक सीधी रेखा का समीकरण बनाएं

पैराग्राफ 1-2 और 3-4 में, हमने वास्तव में एक ही समस्या को दो बार हल किया; वैसे, इस पर पाठ के उदाहरण संख्या 3 में चर्चा की गई थी समतल पर सीधी रेखा की सबसे सरल समस्याएँ. एक लंबा रास्ता अपनाना संभव था - पहले रेखाओं के समीकरण खोजें और उसके बाद ही उनमें से दिशा सदिशों को "बाहर निकालें"।

5) अब रेखाओं के समीकरण ज्ञात हैं। जो कुछ बचा है वह रैखिक समीकरणों की संगत प्रणाली को बनाना और हल करना है (उसी पाठ के उदाहरण संख्या 4, 5 देखें) समतल पर सीधी रेखा की सबसे सरल समस्याएँ).

बात तो मिल गयी.

कार्य काफी सरल है और इसका समाधान स्पष्ट है, लेकिन एक छोटा रास्ता भी है!

दूसरा उपाय:

समांतर चतुर्भुज के विकर्णों को उनके प्रतिच्छेदन बिंदु द्वारा विभाजित किया जाता है। मैंने बिंदु को चिह्नित किया, लेकिन चित्र को अव्यवस्थित न करने के लिए, मैंने विकर्ण स्वयं नहीं बनाए।

आइए बिंदु दर बिंदु पक्ष का समीकरण बनाएं :

जाँच करने के लिए, आपको मानसिक रूप से या ड्राफ्ट पर प्रत्येक बिंदु के निर्देशांक को परिणामी समीकरण में प्रतिस्थापित करना चाहिए। आइए अब ढलान ज्ञात करें। ऐसा करने के लिए, हम ढलान गुणांक वाले समीकरण के रूप में सामान्य समीकरण को फिर से लिखते हैं:

इस प्रकार, ढलान है:

इसी प्रकार, हम पक्षों के समीकरण पाते हैं। मुझे उसी चीज़ का वर्णन करने का कोई मतलब नहीं दिखता, इसलिए मैं तुरंत अंतिम परिणाम दूंगा:

2) भुजा की लंबाई ज्ञात करें। यह कक्षा में शामिल सबसे सरल समस्या है। डमी के लिए वेक्टर. अंक के लिए हम सूत्र का उपयोग करते हैं:

उसी सूत्र का उपयोग करके अन्य भुजाओं की लंबाई ज्ञात करना आसान है। एक नियमित रूलर से जाँच बहुत जल्दी की जा सकती है।

हम सूत्र का उपयोग करते हैं .

आइए वेक्टर खोजें:

इस प्रकार:

वैसे, रास्ते में हमें भुजाओं की लंबाई मिली।

नतीजतन:

खैर, यह सच प्रतीत होता है; आश्वस्त होने के लिए, आप कोने पर एक चांदा लगा सकते हैं।

ध्यान! त्रिभुज के कोण को सीधी रेखाओं के बीच के कोण के साथ भ्रमित न करें। त्रिभुज का कोण अधिक हो सकता है, लेकिन सीधी रेखाओं के बीच का कोण नहीं हो सकता (लेख का अंतिम पैराग्राफ देखें)। समतल पर सीधी रेखा की सबसे सरल समस्याएँ). हालाँकि, किसी त्रिभुज का कोण ज्ञात करने के लिए आप उपरोक्त पाठ के सूत्रों का भी उपयोग कर सकते हैं, लेकिन खुरदरापन यह है कि वे सूत्र हमेशा न्यून कोण देते हैं। उनकी मदद से, मैंने ड्राफ्ट में इस समस्या को हल किया और परिणाम प्राप्त किया। और अंतिम प्रति पर मुझे अतिरिक्त बहाने लिखने होंगे, कि।

4) रेखा के समानांतर एक बिंदु से गुजरने वाली रेखा के लिए एक समीकरण लिखें।

मानक कार्य, पाठ के उदाहरण संख्या 2 में विस्तार से चर्चा की गई है समतल पर सीधी रेखा की सबसे सरल समस्याएँ. रेखा के सामान्य समीकरण से आइए गाइड वेक्टर निकालें। आइए एक बिंदु और एक दिशा वेक्टर का उपयोग करके एक सीधी रेखा का समीकरण बनाएं:

त्रिभुज की ऊँचाई कैसे ज्ञात करें?

5) आइए ऊंचाई के लिए एक समीकरण बनाएं और इसकी लंबाई ज्ञात करें।

सख्त परिभाषाओं से कोई बच नहीं सकता, इसलिए आपको स्कूल की पाठ्यपुस्तक से चोरी करनी होगी:

त्रिभुज की ऊंचाई त्रिभुज के शीर्ष से विपरीत भुजा वाली रेखा पर खींचा गया लंब कहलाता है।

अर्थात् शीर्ष से भुजा पर खींचे गए लम्ब के लिए एक समीकरण बनाना आवश्यक है। इस कार्य की चर्चा पाठ के उदाहरण संख्या 6, 7 में की गई है समतल पर सीधी रेखा की सबसे सरल समस्याएँ. Eq से. सामान्य वेक्टर हटाएँ. आइए एक बिंदु और एक दिशा वेक्टर का उपयोग करके ऊंचाई समीकरण बनाएं:

कृपया ध्यान दें कि हम बिंदु के निर्देशांक नहीं जानते हैं।

कभी-कभी ऊंचाई का समीकरण लंबवत रेखाओं के कोणीय गुणांक के अनुपात से पाया जाता है:। इस मामले में, तो: . आइए एक बिंदु और एक कोणीय गुणांक का उपयोग करके ऊंचाई समीकरण बनाएं (पाठ की शुरुआत देखें)। समतल पर एक सीधी रेखा का समीकरण):

ऊंचाई की लंबाई दो प्रकार से ज्ञात की जा सकती है।

वहाँ एक गोल चक्कर रास्ता है:

ए) खोजें - ऊंचाई और भुजा का प्रतिच्छेदन बिंदु;
बी) दो ज्ञात बिंदुओं का उपयोग करके खंड की लंबाई ज्ञात करें।

लेकिन क्लास में समतल पर सीधी रेखा की सबसे सरल समस्याएँएक बिंदु से एक रेखा की दूरी के लिए एक सुविधाजनक सूत्र पर विचार किया गया। बात ज्ञात है: , रेखा का समीकरण भी ज्ञात है: , इस प्रकार:

6) त्रिभुज के क्षेत्रफल की गणना करें। अंतरिक्ष में, त्रिभुज के क्षेत्रफल की गणना पारंपरिक रूप से उपयोग करके की जाती है सदिशों का सदिश गुणनफल, लेकिन यहां हमें एक समतल पर एक त्रिभुज दिया गया है। हम स्कूल फॉर्मूला का उपयोग करते हैं:
- एक त्रिभुज का क्षेत्रफल उसके आधार और उसकी ऊंचाई के आधे गुणनफल के बराबर होता है।

इस मामले में:

त्रिभुज की माध्यिका कैसे ज्ञात करें?

7) आइए माध्यिका के लिए एक समीकरण बनाएं।

एक त्रिभुज की माध्यिका त्रिभुज के शीर्ष को विपरीत भुजा के मध्य से जोड़ने वाला खंड कहलाता है।

a) बिंदु खोजें - भुजा के मध्य में। हम उपयोग करते हैं किसी खंड के मध्यबिंदु के निर्देशांक के लिए सूत्र. खंड के सिरों के निर्देशांक ज्ञात हैं: , फिर मध्य के निर्देशांक:

इस प्रकार:

आइए माध्यिका समीकरण को बिंदु दर बिंदु बनाते हैं :

समीकरण की जाँच करने के लिए, आपको उसमें बिंदुओं के निर्देशांक को प्रतिस्थापित करना होगा।

8) ऊँचाई और माध्यिका का प्रतिच्छेदन बिंदु ज्ञात कीजिए। मुझे लगता है कि हर कोई पहले ही सीख चुका है कि बिना गिरे फिगर स्केटिंग के इस तत्व को कैसे निष्पादित किया जाए:

समस्या 1. त्रिभुज ABC के शीर्षों के निर्देशांक दिए गए हैं: A(4; 3), B(16;-6), C(20; 16). ज्ञात करें: 1) भुजा AB की लंबाई; 2) भुजाओं AB और BC के समीकरण और उनके कोणीय गुणांक; 3) दो अंकों की सटीकता के साथ रेडियन में कोण बी; 4) ऊंचाई सीडी और उसकी लंबाई का समीकरण; 5) माध्यिका AE का समीकरण और ऊँचाई CD के साथ इस माध्यिका के प्रतिच्छेदन के बिंदु K के निर्देशांक; 6) भुजा AB के समानांतर बिंदु K से गुजरने वाली एक सीधी रेखा का समीकरण; 7) बिंदु एम के निर्देशांक, सीधी रेखा सीडी के सापेक्ष बिंदु ए के सममित रूप से स्थित हैं।

समाधान:

1. बिंदु A(x 1 ,y 1) और B(x 2 ,y 2) के बीच की दूरी d सूत्र द्वारा निर्धारित की जाती है

(1) को लागू करने पर, हम भुजा AB की लंबाई ज्ञात करते हैं:

2. बिंदु A(x 1 ,y 1) और B(x 2 ,y 2) से गुजरने वाली रेखा का समीकरण इस प्रकार है

(2)

बिंदु A और B के निर्देशांकों को (2) में प्रतिस्थापित करने पर, हमें भुजा AB का समीकरण प्राप्त होता है:

Y के लिए अंतिम समीकरण को हल करने के बाद, हम कोणीय गुणांक के साथ एक सीधी रेखा समीकरण के रूप में भुजा AB का समीकरण पाते हैं:

कहाँ

बिंदु B और C के निर्देशांकों को (2) में प्रतिस्थापित करने पर, हमें सीधी रेखा BC का समीकरण प्राप्त होता है:

या

3. यह ज्ञात है कि दो सीधी रेखाओं, जिनके कोणीय गुणांक क्रमशः बराबर हैं, के बीच के कोण की स्पर्शरेखा की गणना सूत्र द्वारा की जाती है

(3)

वांछित कोण B सीधी रेखाओं AB और BC से बनता है, जिसके कोणीय गुणांक पाए जाते हैं: (3) लगाने पर, हम प्राप्त करते हैं

या ख़ुशी है.

4. किसी दिए गए बिंदु से एक निश्चित दिशा में गुजरने वाली सीधी रेखा के समीकरण का रूप होता है

(4)

ऊंचाई CD भुजा AB पर लंबवत है। ऊंचाई सीडी का ढलान ज्ञात करने के लिए, हम रेखाओं की लंबवतता की स्थिति का उपयोग करते हैं। के बाद से (4) में बिंदु सी के निर्देशांक और ऊंचाई के पाए गए कोणीय गुणांक को प्रतिस्थापित करने पर, हम प्राप्त करते हैं

ऊँचाई CD की लंबाई ज्ञात करने के लिए, हम पहले बिंदु D के निर्देशांक निर्धारित करते हैं - सीधी रेखाओं AB और CD का प्रतिच्छेदन बिंदु। सिस्टम को एक साथ हल करना:

हम देखतें है वे। डी(8;0).

सूत्र (1) का उपयोग करके हम ऊँचाई CD की लंबाई ज्ञात करते हैं:

5. माध्यिका AE का समीकरण ज्ञात करने के लिए, हम पहले एक खंड को दो समान भागों में विभाजित करने के सूत्रों का उपयोग करके बिंदु E के निर्देशांक निर्धारित करते हैं, जो कि भुजा BC का मध्य है:

(5)

इस तरह,

बिंदु A और E के निर्देशांकों को (2) में प्रतिस्थापित करने पर, हम माध्यिका के लिए समीकरण पाते हैं:

ऊंचाई सीडी और माध्यिका एई के प्रतिच्छेदन बिंदु के निर्देशांक खोजने के लिए, हम समीकरणों की प्रणाली को एक साथ हल करते हैं

हम देखतें है।

6. चूँकि वांछित सीधी रेखा भुजा AB के समानांतर है, इसका कोणीय गुणांक सीधी रेखा AB के कोणीय गुणांक के बराबर होगा। (4) में पाए गए बिंदु K के निर्देशांक और कोणीय गुणांक को प्रतिस्थापित करने पर हमें प्राप्त होता है

3x + 4y – 49 = 0 (KF)

7. चूँकि सीधी रेखा AB सीधी रेखा CD पर लंबवत है, वांछित बिंदु M, सीधी रेखा CD के सापेक्ष बिंदु A के सममित रूप से स्थित है, सीधी रेखा AB पर स्थित है। इसके अलावा, बिंदु D, खंड AM का मध्यबिंदु है। सूत्र (5) का उपयोग करके, हम वांछित बिंदु M के निर्देशांक पाते हैं:

चित्र में xOy निर्देशांक प्रणाली में त्रिभुज ABC, ऊंचाई CD, माध्यिका AE, सीधी रेखा KF और बिंदु M का निर्माण किया गया है। 1.

कार्य 2. उन बिंदुओं के स्थान के लिए एक समीकरण बनाएं जिनकी किसी दिए गए बिंदु A(4; 0) और दी गई रेखा x=1 से दूरी 2 के बराबर है।

समाधान:

xOy समन्वय प्रणाली में, हम बिंदु A(4;0) और सीधी रेखा x = 1 का निर्माण करते हैं। मान लें कि M(x;y) बिंदुओं के वांछित ज्यामितीय स्थान का एक मनमाना बिंदु है। आइए दी गई रेखा x = 1 पर लंबवत एमबी को कम करें और बिंदु बी के निर्देशांक निर्धारित करें। चूंकि बिंदु बी दी गई रेखा पर स्थित है, इसका भुज 1 के बराबर है। बिंदु बी की कोटि बिंदु एम के कोटि के बराबर है। .इसलिए, B(1;y) (चित्र 2)।

समस्या की स्थितियों के अनुसार |MA|: |MV| = 2. दूरियाँ |एमए| और |एमबी| हम समस्या 1 के सूत्र (1) से पाते हैं:

बाएँ और दाएँ पक्षों का वर्ग करने पर, हमें प्राप्त होता है

परिणामी समीकरण एक अतिपरवलय है जिसमें वास्तविक अर्ध-अक्ष a = 2 है, और काल्पनिक अर्ध-अक्ष है

आइए हाइपरबोला की नाभियों को परिभाषित करें। अतिपरवलय के लिए, समानता संतुष्ट होती है। इसलिए, और - अतिशयोक्तिपूर्ण तरकीबें। जैसा कि आप देख सकते हैं, दिया गया बिंदु A(4;0) हाइपरबोला का सही फोकस है।

आइए हम परिणामी हाइपरबोला की विलक्षणता निर्धारित करें:

हाइपरबोला अनंतस्पर्शी समीकरणों का रूप और होता है। इसलिए, या और हाइपरबोला के स्पर्शोन्मुख हैं। हाइपरबोला का निर्माण करने से पहले, हम इसके अनंतस्पर्शी का निर्माण करते हैं।

समस्या 3. बिंदु A(4; 3) और सीधी रेखा y = 1 से समदूरस्थ बिंदुओं के बिंदुपथ के लिए एक समीकरण बनाएं। परिणामी समीकरण को उसके सरलतम रूप में कम करें।

समाधान:मान लीजिए M(x; y) बिंदुओं के वांछित ज्यामितीय स्थान के बिंदुओं में से एक है। आइए हम बिंदु M से इस सीधी रेखा y = 1 पर लंबवत MB को छोड़ें (चित्र 3)। आइए हम बिंदु B के निर्देशांक निर्धारित करें। स्पष्ट रूप से, बिंदु B का भुज बिंदु M के भुज के बराबर है, और बिंदु B का कोटि 1 के बराबर है, अर्थात B(x; 1)। समस्या की स्थितियों के अनुसार |MA|=|MV| नतीजतन, बिंदुओं के वांछित ज्यामितीय स्थान से संबंधित किसी भी बिंदु M(x;y) के लिए, निम्नलिखित समानता सत्य है:

परिणामी समीकरण बिंदु पर एक शीर्ष के साथ एक परवलय को परिभाषित करता है। परवलय समीकरण को उसके सरलतम रूप में लाने के लिए, आइए सेट करें और y + 2 = Y, फिर परवलय समीकरण रूप लेता है:

अभ्यास 1

57. त्रिभुज ABC के शीर्ष दिये गये हैं। खोजो

) भुजा AB की लंबाई;

) भुजाओं AB और AC के समीकरण और उनके कोणीय गुणांक;

) आंतरिक कोण ए;

) शीर्ष B से खींचे गए माध्यिका का समीकरण;

) ऊंचाई सीडी और उसकी लंबाई का समीकरण;

) एक वृत्त का समीकरण जिसकी ऊँचाई CD व्यास है और भुजा AC के साथ इस वृत्त का प्रतिच्छेदन बिंदु है;

) आंतरिक कोण A के समद्विभाजक का समीकरण;

) त्रिभुज ABC का क्षेत्रफल;

) त्रिभुज ABC को परिभाषित करने वाली रैखिक असमानताओं की एक प्रणाली।

एक चित्र बनाओ.

ए(7,9); बी(-2, -3); सी(-7,7)

समाधान:

1) आइए वेक्टर की लंबाई ज्ञात करें

= (एक्स बी - एक्स ए )2+ (य बी -य ए )2 = ((-2)-7)2 + (-3 - 9)2 = 92 + 122 = 225

= = 15 - भुजा AB की लंबाई

2) आइए भुजा AB का समीकरण ज्ञात करें

बिंदुओं से गुजरने वाली रेखा का समीकरण

ओह ए ; पर वी ) और बी(x ए ; पर वी ) सामान्य रूप में

आइए सीधी रेखा के इस समीकरण में बिंदु A और B के निर्देशांकों को प्रतिस्थापित करें

एस अब = (- 3, - 4) को सरल रेखा AB का दिशा सदिश कहते हैं। यह वेक्टर रेखा AB के समानांतर है।

4(x - 7) = - 3(y - 9)

4x + 28 = - 3y + 27

4x + 3y + 1 = 0 - रेखा AB का समीकरण

यदि समीकरण इस रूप में लिखा गया है: y = एक्स - तब हम इसके कोणीय गुणांक को अलग कर सकते हैं: k 1 =4/3

वेक्टर एन अब = (-4,3) को रेखा AB का सामान्य सदिश कहा जाता है।

वेक्टर एन अब = (-4,3) रेखा AB पर लम्ब है।

इसी प्रकार, हम भुजा AC का समीकरण ज्ञात करते हैं

एस एसी = (- 7, - 1) - एसी पक्ष का दिशा सदिश

(x - 7) = - 7(y - 9)

x + 7 = - 7y + 63

x + 7y - 56 = 0 - भुजा AC का समीकरण

य = = x + 8 जहाँ से ढलान k है 2 = 1/7

वेक्टर एन एसी। = (- 1, 7) - रेखा AC का सामान्य सदिश।

वेक्टर एन एसी। = (- 1, 7) रेखा AC पर लम्ब है।

3) आइए कोण A ज्ञात करें

आइए सदिशों के अदिश गुणनफल का सूत्र लिखें और

* = *क्योंकि ∟ए

कोण A ज्ञात करने के लिए इस कोण की कोज्या ज्ञात करना पर्याप्त है। पिछले सूत्र से हम कोण A की कोज्या के लिए व्यंजक लिखते हैं

क्योंकि ∟A =

सदिशों का अदिश गुणनफल ज्ञात करना और

= (एक्स वी - एक्स ए ; पर वी - वाई ए ) = (- 2 - 7; - 3 - 9) = (-9, -12)

= (एक्स साथ - एक्स ए ; पर साथ - वाई ए ) = (- 7 - 7; 7 - 9) = (-14; -2)

9*(-14) + (-12)*(-2) = 150

वेक्टर लंबाई = 15 (पहले पाया गया)

आइए वेक्टर की लंबाई ज्ञात करें

= (एक्स साथ - एक्स ए )2+ (य साथ -य ए )2 = (-14)2 + (-2)2 = 200

= = 14.14 - भुजा की लंबाई AC

तब cos ∟A = = 0,7072

∟ए = 45 0

4) आइए बिंदु B से भुजा AC तक खींची गई माध्यिका BE का समीकरण ज्ञात करें

सामान्य रूप में माध्यिका समीकरण

अब आपको सीधी रेखा BE का दिशा सदिश ज्ञात करना होगा।

आइए हम त्रिभुज ABC को समांतर चतुर्भुज ABCD तक पूरा करें, ताकि भुजा AC इसका विकर्ण हो। समांतर चतुर्भुज में विकर्णों को आधे में विभाजित किया जाता है, अर्थात AE = EC। इसलिए, बिंदु E रेखा BF पर स्थित है।

सदिश BE को सीधी रेखा BE के दिशा सदिश के रूप में लिया जा सकता है , जो हम पाएंगे।

= +

= (एक्स सी - एक्स बी ; पर सी - वाई बी ) = (- 7- (-2); 7 - (-3)) = (-5. 10)

= + = (-5 + 9; 10 + 12) = (4; 22)

आइए समीकरण में स्थानापन्न करें

आइए बिंदु C के निर्देशांक को प्रतिस्थापित करें (-7; 7)

(x + 7) = 2(y - 7)

x + 77 = 2y - 14

x - 2y + 91 = 0 - माध्यिका BE का समीकरण

चूँकि बिंदु E, भुजा AC का मध्य है, इसके निर्देशांक हैं

एक्स इ = (एक्स ए + एक्स साथ )/2 = (7 - 7)/2 = 0

पर इ = (य ए + वाई साथ )/2 = (9 + 7)/2 = 8

बिंदु E के निर्देशांक (0; 8)

5) आइए ऊंचाई सीडी और इसकी लंबाई के लिए समीकरण खोजें

सामान्य समीकरण

सीधी रेखा CD का दिशा सदिश ज्ञात करना आवश्यक है

सीधी रेखा CD सीधी रेखा AB के लंबवत है, इसलिए, सीधी रेखा CD का दिशा वेक्टर सीधी रेखा AB के सामान्य वेक्टर के समानांतर है

सीडी ‖अब

अर्थात्, सीधी रेखा AB के सामान्य वेक्टर को सीधी रेखा CD के दिशात्मक वेक्टर के रूप में लिया जा सकता है

वेक्टर अब पहले पाया: अब (-4, 3)

आइए बिंदु C के निर्देशांकों को प्रतिस्थापित करें, (- 7; 7)

(x + 7) = - 4(y - 7)

x + 21 = - 4y + 28

x + 4y - 7 = 0 - ऊंचाई का समीकरण C D

बिंदु डी निर्देशांक:

बिंदु D, रेखा AB से संबंधित है, इसलिए, बिंदु D(x) के निर्देशांक हैं डी . य डी ) को पहले पाए गए सीधी रेखा AB के समीकरण को संतुष्ट करना होगा

बिंदु D, रेखा CD से संबंधित है, इसलिए, बिंदु D(x) के निर्देशांक हैं डी . य डी ) को सीधी रेखा CD के समीकरण को संतुष्ट करना होगा,

आइए इसके आधार पर समीकरणों की एक प्रणाली बनाएं

निर्देशांक डी(1; 1)

सीधी रेखा CD की लंबाई ज्ञात कीजिए

= (एक्स डी - एक्स सी )2+ (य डी -य सी )2 = (1 + 7)2 + (1 - 7)2 = 64 +36 = 100

= = 10 - सीधी रेखा सीडी की लंबाई

6) सीडी व्यास वाले वृत्त का समीकरण ज्ञात कीजिए

यह स्पष्ट है कि सीधी रेखा CD निर्देशांक के मूल से होकर गुजरती है क्योंकि इसका समीकरण -3x - 4y = 0 है, इसलिए, एक वृत्त का समीकरण इस रूप में लिखा जा सकता है

(एक्स - ए) 2 + (वाई - बी) 2= आर 2- बिंदु (ए; बी) पर केंद्र के साथ एक वृत्त का समीकरण

यहाँ R = СD/2 = 10 /2 = 5

(एक्स - ए) 2 + (वाई - बी) 2 = 25

वृत्त O (a; b) का केंद्र खंड CD के मध्य में स्थित है। आइए इसके निर्देशांक खोजें:

एक्स 0= ए = = = - 3;

य 0= बी = = = 4

वृत्त समीकरण:

(एक्स + 3) 2 + (वाई - 4) 2 = 25

आइए AC भुजा वाले इस वृत्त का प्रतिच्छेदन ज्ञात करें:

बिंदु K वृत्त और रेखा AC दोनों से संबंधित है

x + 7y - 56 = 0 - पहले पाया गया सीधी रेखा AC का समीकरण।

आइए एक सिस्टम बनाएं