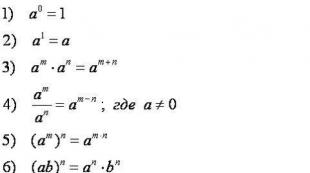क्यूबा में एक बी। घन का निर्माण। संक्षिप्त गुणा के सूत्र कहां से आते हैं
अभ्यास एक ऑपरेशन है, गुणा से निकटता से संबंधित है, यह ऑपरेशन किसी भी संख्या के एकाधिक गुणा का परिणाम है। मैं सूत्र को चित्रित करूंगा: ए 1 * ए 2 * ... * ए \u003d ए।
उदाहरण के लिए, ए \u003d 2, एन \u003d 3: 2 * 2 * 2 \u003d 2 ^ 3 \u003d 8।
आम तौर पर, प्रदर्शनी अक्सर गणित और भौतिकी में विभिन्न सूत्रों में उपयोग की जाती है। इस सुविधा में चार मुख्य से अधिक वैज्ञानिक गंतव्य है: अतिरिक्त, घटाव, गुणा, विभाजन।
निर्माण
संख्या का निर्माण जटिल नहीं है। यह गुणा और अतिरिक्त के समान गुणा से जुड़ा हुआ है। रिकॉर्डिंग एन-वें का सारांश है, संख्याओं की संख्या "ए" एक दूसरे से गुणा की गई है।
परिसर में जाने वाले सबसे आसान उदाहरणों तक व्यायाम पर विचार करें।
उदाहरण के लिए, 42. 42 \u003d 4 * 4 \u003d 16। चार वर्ग (दूसरी डिग्री) सोलह है। यदि आप 4 * 4 के गुणा को समझ में नहीं आते हैं, तो गुणा के बारे में बनने के लिए हमारी पढ़ें।
एक और उदाहरण पर विचार करें: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125 । क्यूबा में पांच (तीसरी डिग्री में) एक सौ पच्चीस के बराबर है।
एक और उदाहरण: 9 ^ 3। 9^3 = 9 * 9 * 9 = 81 * 9 = 729 । क्यूबा में नौ सात सैकड़ों बीस नौ के बराबर है।
सूत्रों
हद तक सक्षम होने के लिए, आपको नीचे सूचीबद्ध सूत्रों को याद रखने और जानने की आवश्यकता है। प्राकृतिक पर कुछ भी नहीं है, मुख्य बात सार को समझना है और फिर उन्हें न केवल याद किया जाएगा, बल्कि वे प्रकाश प्रतीत होंगे।

खड़ी
क्या अकेले खुद का प्रतिनिधित्व करता है? यह किसी भी मात्रा में संख्याओं और चर का एक उत्पाद है। उदाहरण के लिए, दो - Unrochene। और यह इस तरह के माहौल का निर्माण इस लेख है।
डिग्री के लिए सार्वभौमिक निर्माण की गणना करने के लिए अभ्यास के लिए सूत्रों का लाभ लेना मुश्किल नहीं होगा।
उदाहरण के लिए, (3x ^ 2y ^ 3) ^ 2 \u003d 3 ^ 2 * x ^ 2 * 2 * y ^ (3 * 2) \u003d 9x ^ 4y ^ 6; यदि यह डिग्री के लिए व्यस्त है, तो प्रत्येक समग्र डिग्री में unobed है।
डिग्री चर के लिए आसान पहले से ही डिग्री है, डिग्री गुणा किया जाता है। उदाहरण के लिए, (x ^ 2) ^ 3 \u003d x ^ (2 * 3) \u003d x ^ 6;
नकारात्मक
नकारात्मक डिग्री - विपरीत संख्या। विपरीत संख्या क्या है? कोई भी संख्या x रिवर्स 1 / x होगा। वह है, एक्स -1 \u003d 1 / एक्स। यह एक नकारात्मक डिग्री का सार है।
एक उदाहरण पर विचार करें (3Y) ^ - 3:
(3Y) ^ - 3 \u003d 1 / (27y ^ 3)।
ऐसा क्यों है? चूंकि डिग्री के लिए एक ऋण है, तो यह अभिव्यक्ति केवल denominator में स्थानांतरित कर दिया गया है, और फिर अपनी तीसरी डिग्री में बनाया गया है। बस सही?
क्रॉस-डिग्री
आइए किसी विशिष्ट उदाहरण पर इस मुद्दे पर विचार करना शुरू करें। 43/2। डिग्री 3/2 क्या है? 3 - न्यूमरेटर, क्यूब में संख्या (इस मामले में 4) का निर्माण का अर्थ है। संख्या 2 denominator है, यह दूसरी डिग्री की जड़ का निष्कर्षण है (इस मामले में 4)।
फिर हमें 43 \u003d 2 ^ 3 \u003d 8 का वर्गमूल मिलता है। उत्तर: 8।
इसलिए, फ्रैक्शनल डिग्री का संप्रदाय 3 और 4 और किसी भी संख्या से अनंत तक हो सकता है और यह संख्या निर्दिष्ट संख्या से निकाली गई स्क्वायर रूट की डिग्री निर्धारित करती है। बेशक, denominator शून्य नहीं हो सकता है।
तेजी से जड़
यदि रूट को रूट की डिग्री के बराबर डिग्री में बनाया जाता है, तो जवाब एक भोजन अभिव्यक्ति होगी। उदाहरण के लिए, (√h) 2 \u003d x। और इसलिए किसी भी मामले में जड़ की डिग्री और जड़ के निर्माण की डिग्री की समानता।
यदि (√x) ^ 4। वह (√x) ^ 4 \u003d x ^ 2। निर्णय की जांच करने के लिए अभिव्यक्ति को एक आंशिक डिग्री के साथ अभिव्यक्ति में स्थानांतरित करें। चूंकि रूट वर्ग है, denominator 2. है और यदि रूट चौथी डिग्री में बनाया गया है, तो संख्या 4. हमें 4/2 \u003d 2 मिलता है। उत्तर: x \u003d 2।
किसी भी मामले में, सबसे अच्छा विकल्प बस एक आंशिक डिग्री के साथ अभिव्यक्ति में स्थानांतरित किया जाता है। यदि अंश कम नहीं होता है, तो यह जवाब होगा और होगा, बशर्ते निर्दिष्ट संख्या की जड़ आवंटित न हो।
एकीकृत संख्या की डिग्री में उत्तराधिकारी
एक व्यापक संख्या क्या है? एक जटिल संख्या एक अभिव्यक्ति है जिसमें फॉर्मूला ए + बी * I; ए, बी - मान्य संख्या। I - संख्या जो संख्या -1 वर्ग में देता है।
एक उदाहरण पर विचार करें। (2 + 3i) ^ 2।
(2 + 3i) ^ 2 \u003d 22 +2 * 2 * 3i + (3i) ^ 2 \u003d 4 + 12i ^ -9 \u003d -5 + 12i।
पाठ्यक्रम के लिए साइन अप करें "मौखिक खाता को तेज करें, मानसिक अंकगणित नहीं" सीखने के लिए कि कैसे जल्दी और सही ढंग से गुना, कटौती, गुणा करना, विभाजित करना, संख्या को एक वर्ग में खड़ा करना और जड़ों को निकालने के लिए। 30 दिनों के लिए, आप सीखेंगे कि अंकगणितीय परिचालनों को सरल बनाने के लिए आसान तकनीकों का उपयोग कैसे करें। प्रत्येक पाठ में, नई तकनीक, समझने योग्य उदाहरण और उपयोगी कार्यों में।
ऑनलाइन
हमारे कैलकुलेटर की मदद से, आप डिग्री के निर्माण की गणना की गणना कर सकते हैं:
श्रेणी 7
अभ्यास केवल सातवीं कक्षा में स्कूली बच्चों को पारित करना शुरू कर रहा है।
अभ्यास एक ऑपरेशन है, गुणा से निकटता से संबंधित है, यह ऑपरेशन किसी भी संख्या के एकाधिक गुणा का परिणाम है। मैं सूत्र को चित्रित करूंगा: ए 1 * ए 2 * ... * ए \u003d ए।
उदाहरण के लिए, ए \u003d 2, एन \u003d 3: 2 * 2 * 2 \u003d 2 ^ 3 \u003d 8.
हल करने के लिए उदाहरण:

प्रस्तुतीकरण
सातवें ग्रेडर पर गणना की गई सीमा तक अभ्यास पर प्रस्तुति। प्रस्तुति कुछ समझ में आने वाले क्षणों को स्पष्ट कर सकती है, लेकिन शायद हमारे लेख के लिए ऐसा कोई क्षण नहीं होगा।
परिणाम
हमने गणित को बेहतर ढंग से समझने के लिए हिमशैल के शीर्ष की समीक्षा की - हमारे पाठ्यक्रम के लिए साइन अप करें: मौखिक खाते में तेजी लाने के लिए एक मानसिक अंकगणित नहीं है।
पाठ्यक्रम से आप केवल सरलीकृत और तेज़ गुणन, जोड़, गुणा, डिवीजनों, ब्याज की गणना करने के लिए दर्जनों तकनीकों को पहचान नहीं पाएंगे, बल्कि उन्हें विशेष कार्यों और शैक्षिक खेलों में भी काम करेंगे! मौखिक खाते को भी बहुत ध्यान और सांद्रता की आवश्यकता होती है जो दिलचस्प कार्यों को हल करने में सक्रिय रूप से प्रशिक्षित होते हैं।
गणितीय अभिव्यक्ति (सूत्र) संक्षिप्त गुणा (वर्ग रकम और मतभेद, घन रकम और मतभेद, वर्गों का अंतर, क्यूब्स की राशि और अंतर) को सटीक विज्ञान के कई क्षेत्रों में बेहद प्रतिस्थापित किया जाता है। इन 7 वर्ण रिकॉर्डिंग को अभिव्यक्तियों को सरल बनाने, समीकरणों को हल करने, बहुपदों के गुणा के साथ, भिन्नताओं को कम करने, अभिन्न और कई अन्य चीजों को हल करने के साथ प्रतिस्थापित नहीं किया जाता है। तो यह पता लगाने के लिए बहुत उपयोगी होगा कि वे कैसे प्राप्त किए जाते हैं, जिसके लिए उन्हें आवश्यक है, और सबसे महत्वपूर्ण बात यह है कि उन्हें कैसे याद रखें और फिर आवेदन करें। फिर लागू करें संक्षिप्त गुणा के सूत्र व्यवहार में, सबसे मुश्किल यह देखेंगे कि क्या है एचऔर वाई क्या है। जाहिर है, के लिए कोई प्रतिबंध नहीं ए। तथा बीनहीं, जिसका मतलब है कि यह कोई संख्यात्मक या अक्षर अभिव्यक्ति हो सकता है।
और इसलिए वे यहां:
प्रथम एक्स 2 - यू 2। \u003d (x - y) (x + y) । हिसाब करना वर्ग अंतर दो अभिव्यक्तियों को इन अभिव्यक्तियों के बीच अंतर को उनके रकम पर गुणा करने की आवश्यकता है।
दूसरा (x + y) 2 \u003d x 2 + 2H + 2 में । ढूँढ़ने के लिए वर्ग राशि दूसरी अभिव्यक्ति के वर्ग को दूसरे अभिव्यक्ति के वर्ग पर पहली अभिव्यक्ति के एक डबल उत्पाद जोड़ने के लिए पहली अभिव्यक्ति के वर्ग में दो अभिव्यक्तियों को जोड़ा जाना चाहिए।
तीसरा (x - y) 2 \u003d x 2 - 2 एच + 2 में। हिसाब करना वर्ग अंतरदूसरी अभिव्यक्ति के वर्ग से दूसरी अभिव्यक्ति के एक डबल उत्पाद को दूसरे अभिव्यक्ति के वर्ग को दूर करने के लिए पहली अभिव्यक्ति के वर्ग से दो अभिव्यक्तियों की आवश्यकता होती है।
चौथी (x + y) 3 \u003d x 3। + 3 एक्स 2 वाई + 3 एच 2 + 3। हिसाब करना घन राशिदूसरी अभिव्यक्ति के वर्ग प्लस क्यूब पर पहली अभिव्यक्ति के तीन गुना उत्पाद के दूसरे स्थान पर पहली अभिव्यक्ति के तीन गुना उत्पाद को जोड़ने के लिए पहली अभिव्यक्ति के क्यूबा में दो अभिव्यक्तियों को जोड़ा जाना चाहिए।
पांचवां (x - y) 3 \u003d x 3। - 3 एक्स 2 वाई + 3 एच 2 - 3।। हिसाब करना घन अंतरपहली अभिव्यक्ति घन से दो अभिव्यक्ति आवश्यक हैं कि दूसरी अभिव्यक्ति के दूसरे शून्य घन पर पहली अभिव्यक्ति के त्रिभुज उत्पाद के दूसरे स्थान पर पहली अभिव्यक्ति के तीन गुना उत्पाद के तीन गुणों को लेने के लिए।
छह x 3 + 3। \u003d (x + y) (x 2) - हू + यू 2) हिसाब करना क्यूब्स की मात्रादो अभिव्यक्तियों को इन अभिव्यक्तियों के अंतर के अधूरे वर्ग पर पहली और दूसरी अभिव्यक्ति की रकम को गुणा करने की आवश्यकता होती है।
सातवीं x 3 - 3। \u003d (x - y) (x 2) + हू + यू 2) गणना करने के लिए घन मतभेदइन अभिव्यक्तियों के योग के अपूर्ण वर्ग पर पहली और दूसरी अभिव्यक्ति के बीच अंतर को गुणा करने की आवश्यकता होती है।
यह याद रखना मुश्किल नहीं है कि सभी सूत्रों को गणना के काम और विपरीत दिशा में लागू किया जाता है (दाएं से बाएं)।
लगभग 4 हजार साल पहले इन पैटर्न के अस्तित्व पर। प्राचीन बाबुल और मिस्र के निवासियों द्वारा उनका व्यापक रूप से उपयोग किया जाता था। लेकिन उन युगों में, उन्होंने मौखिक रूप से या ज्यामितीय रूप से व्यक्त किया और गणनाओं के दौरान अक्षरों का उपयोग नहीं किया।
हम समझेंगे स्क्वायर सममा का प्रमाण(ए + बी) 2 \u003d एक 2 + 2 एबी + बी 2।
पहले यह गणितीय पैटर्न एक प्राचीन यूनानी वैज्ञानिक यूकलाइड को साबित किया, जिन्होंने III शताब्दी ईसा पूर्व में अलेक्जेंड्रिया में काम किया, उन्होंने फॉर्मूला को विकसित करने के लिए एक ज्यामितीय तरीका का उपयोग किया, क्योंकि प्राचीन इलाला के वैज्ञानिकों ने संख्याओं को नामित करने के लिए पत्रों का उपयोग नहीं किया था। वे सार्वभौमिक रूप से "ए 2" नहीं थे, लेकिन "सेगमेंट ए पर स्क्वायर", "एबी" नहीं, लेकिन "आयताकार, सेगमेंट ए और बी के बीच निष्कर्ष निकाला गया"।
पिछले पाठ में, हमने गुणक के अपघटन के साथ निपटाया। दो तरीकों से महारत हासिल की गई: कोष्ठक और समूह के लिए एक आम कारक बनाना। इस पाठ में - अगला शक्तिशाली तरीका: संक्षिप्त गुणा के सूत्र। एक संक्षिप्त रिकॉर्ड में - एफएसयू।
संक्षिप्त गुणा के सूत्र (योग और अंतर का वर्ग, राशि और अंतर का घन, वर्गों का अंतर, योग और क्यूब्स का अंतर) गणित के सभी वर्गों में बेहद जरूरी है। वे अभिव्यक्तियों को सरल बनाने, समीकरणों को हल करने, बहुपदों का गुणा, भिन्नता में कमी, इंटीग्रल को सुलझाने आदि में उपयोग किया जाता है। आदि। संक्षेप में, उनके साथ निपटने का हर कारण है। यह समझने के लिए कि उन्हें कैसे लिया जाता है, उन्हें क्यों चाहिए, उन्हें कैसे याद रखें और आवेदन कैसे करें।
हम समझते है?)
संक्षिप्त गुणा सूत्र कहां से आते हैं?
समानता 6 और 7 बहुत परिचित नहीं लिखी गई हैं। जैसे कि इसके विपरीत। यह विशेष रूप से है।) कोई भी समानता बाएं से दाएं और दाएं से बाईं ओर दोनों काम करती है। ऐसे रिकॉर्ड में, यह स्पष्ट है कि एफएसयू कहां से आता है।
उन्हें गुणा से लिया जाता है।) उदाहरण के लिए:
(ए + बी) 2 \u003d (ए + बी) (ए + बी) \u003d एक 2 + एबी + बीए + बी 2 \u003d ए 2 + 2 एबी + बी 2
यह सब, कोई वैज्ञानिक चाल नहीं है। बस कोष्ठक बदलें और इन्हें दें। तो यह पता चला संक्षिप्त गुणा के सभी सूत्र। संक्षिप्त गुणा है क्योंकि सूत्रों में स्वयं को ब्रैकेट का कोई गुणा नहीं है और समान लाने के लिए नहीं है। कम।) तुरंत परिणाम दिया।
एफएसयू को दिल से जानने की जरूरत है। पहले तीन के बिना, आप ट्रूका के बारे में नहीं देख सकते हैं, बाकी के बिना - पांच के साथ चौथे के बारे में।)
संक्षिप्त गुणा के सूत्रों को क्यों चाहिए?
इन सूत्रों को प्राप्त करने के लिए भी दो कारण हैं, सीखें। पहला - मशीन पर समाप्त उत्तर तेजी से त्रुटियों की संख्या को कम कर देता है। लेकिन यह मुख्य कारण नहीं है। लेकिन दूसरा ...
अगर आपको यह साइट पसंद है ...
वैसे, मेरे पास आपके लिए एक और कुछ दिलचस्प साइटें हैं।)
इसे उदाहरणों को हल करने और अपने स्तर को खोजने में पहुंचा जा सकता है। तत्काल चेक के साथ परीक्षण। जानें - ब्याज के साथ!)
आप सुविधाओं और डेरिवेटिव से परिचित हो सकते हैं।
बड़े बीजगणित अभिव्यक्तियों की गणना करने की तेज प्रक्रिया के लिए सूत्रों या संक्षिप्त गुणा नियमों का उपयोग बीजगणित में, या बीजगणित में किया जाता है। सूत्र स्वयं बीजगणित में मौजूदा नियमों से प्राप्त होते हैं ताकि कई बहुपद गुणा हो सके।
इन सूत्रों का उपयोग विभिन्न गणितीय कार्यों का काफी परिचालन समाधान प्रदान करता है, और अभिव्यक्तियों को सरल बनाने में भी मदद करता है। बीजगणितीय परिवर्तनों के नियम आपको अभिव्यक्तियों के साथ कुछ कुशलताओं को करने की अनुमति देते हैं, जिसके बाद समानता के बाएं हिस्से में दाईं ओर एक अभिव्यक्ति प्राप्त करना संभव है, या समानता के दाएं हाथ के हिस्से को परिवर्तित करना संभव है (एक प्राप्त करने के लिए) अभिव्यक्ति जो समानता संकेत के बाद बाईं ओर खड़ी होती है)।
संक्षिप्त गुणा के लिए उपयोग किए जाने वाले सूत्रों को जानना सुविधाजनक है, साथ ही साथ उन्हें अक्सर समस्याओं और समीकरणों को हल करने में उपयोग किया जाता है। नीचे इस सूची में शामिल मूल सूत्र हैं, और उनका नाम।
वर्ग राशि
राशि के वर्ग की गणना करने के लिए, पहली अवधि के वर्ग को शामिल करने वाली राशि को ढूंढना आवश्यक है, दूसरे के दूसरे और वर्ग पर पहले कार्यकाल के उत्पाद को दोगुना कर दिया गया है। अभिव्यक्ति के रूप में, यह नियम निम्नानुसार लिखा गया है: (ए + सी) ² \u003d A² + 2AS + C²।
वर्ग अंतर
अंतर के वर्ग की गणना करने के लिए, पहले संख्या के वर्ग (विपरीत संकेत के साथ लिया गया) और दूसरी संख्या के वर्ग के वर्ग को पहले संख्या के वर्ग से युक्त राशि की गणना करना आवश्यक है। अभिव्यक्ति के रूप में, यह नियम निम्नानुसार है: (ए - सी) ² \u003d A² - 2AS + C²।
वर्ग अंतर
वर्ग में बनाए गए दो संख्याओं के अंतर के लिए सूत्र इन संख्याओं के योग की राशि के बराबर है। अभिव्यक्ति के रूप में, यह नियम निम्नानुसार है: A² - c² \u003d (a + c) · (ए - सी)।
घन राशि
दो घटकों की रकम के घन की गणना करने के लिए, पहले अवधि के घन, पहली अवधि के वर्ग के तीन गुना और पहली अवधि के तीन गुना उत्पाद और दूसरी अवधि के तीन गुना उत्पाद की गणना करना आवश्यक है। वर्ग में दूसरा, साथ ही दूसरे कार्यकाल के घन। अभिव्यक्ति के रूप में, यह नियम निम्नानुसार है: (ए + सी) ³ \u003d A³ + 3A² + 3AS² + C³।

क्यूब्स की मात्रा
सूत्र के अनुसार, यह अंतर के अपूर्ण वर्ग पर घटकों की शर्तों की राशि की राशि के बराबर है। अभिव्यक्ति के रूप में, यह नियम निम्नानुसार है: A³ + c³ \u003d (a + c) · (A² - AC + C²)।
उदाहरण। आकार की मात्रा की गणना करना आवश्यक है, जो दो क्यूब्स के अतिरिक्त द्वारा गठित किया जाता है। केवल उनकी पार्टियों के मूल्यों को भी जाना जाता है।
यदि पार्टियों के मूल्य छोटे होते हैं, तो गणना करें।
यदि पार्टियों की लंबाई भारी संख्या में व्यक्त की जाती है, तो इस मामले में "क्यूब्स की मात्रा" सूत्र को लागू करना आसान होता है, जो गणनाओं को काफी सरल बना देगा।

घन अंतर
घन अंतर के लिए अभिव्यक्ति इस तरह लगता है: पहली अवधि की तीसरी डिग्री के रूप में, दूसरे पर पहले सदस्य के वर्ग के तीन गुना नकारात्मक काम, दूसरे और नकारात्मक के वर्ग के पहले सदस्य के तीन गुना काम दूसरे कार्यकाल का घन। गणितीय अभिव्यक्ति के रूप में एक घन अंतर इस तरह दिखता है: (ए - सी) ³ \u003d A³ - 3a² + 3as² - c³।

घन मतभेद
क्यूब अंतर फॉर्मूला केवल एक संकेत क्यूब्स की मात्रा से अलग है। इस प्रकार, क्यूब्स का अंतर उनके अपूर्ण वर्ग योग के बीच डेटा अंतर के उत्पाद के बराबर एक सूत्र है। क्यूब्स का अंतर निम्नानुसार है: 3 - 3 \u003d (ए - सी) (और 2 + एसी + सी 2) से।
उदाहरण। पीले रंग की एक पीले रूपरेखा आंकड़े के नीले घन की मात्रा से घटाने के बाद बने आंकड़े की मात्रा की गणना करना आवश्यक है, जो एक घन भी है। केवल एक छोटे और बड़े घन के किनारे की परिमाण ज्ञात है।
यदि पार्टियों के मूल्य छोटे होते हैं, तो गणना काफी सरल होती है। और यदि पार्टियों की लंबाई महत्वपूर्ण संख्या में व्यक्त की जाती है, तो "क्यूब्स के मतभेद" (या "अंतर के" घन ") नामक सूत्र को लागू करना आवश्यक है, जो गणनाओं को काफी सरल बनाएगा।
तीन दोष, जिनमें से प्रत्येक बराबर है एक्स। (\\ displaystyle x।) इस अंकगणितीय ऑपरेशन को "क्यूब में निर्माण" कहा जाता है, इसका परिणाम इंगित किया जाता है x 3 (\\ displaysstyle x ^ (3)):
x 3 \u003d x ⋅ x ⋅ x (\\ displaysstyle x ^ (3) \u003d x \\ cdot x \\ cdot x)घन रिवर्स ऑपरेशन के निर्माण के लिए घन रूट का निष्कर्षण है। तीसरी डिग्री का ज्यामितीय नाम " घन"इस तथ्य के कारण है कि प्राचीन गणितज्ञों ने क्यूब्स को माना घन संख्या, संख्याओं की सूची के बाद से विशेष प्रकार की अनुमानित संख्याएं (नीचे देखें) X (\\ displaystyle x) पसलियों की लंबाई के बराबर घन की मात्रा के बराबर X (\\ displaystyle x).
घन अनुक्रम
, , , , , 125, 216, 343, 512, 729, , 1331, , 2197, 2744, 3375, 4096, 4913, 5832, 6859, 8000, 9261, 10648, 12167, 13824, 15625, 17576, 19683, 21952, 24389, 27000, 29791, 32768, 35937, 39304, 42875, 46656, 50653, 54872, 59319, 64000, 68921, 74088, 79507, 85184, 91125, 97736, 103823, 110592, 117649, 125000, 132651, 140608, 148877, 157464, 166375, 175616, 185193, 195112, 205379, 216000, 226981, 238328…पहले क्यूब्स की राशि N (\\ displaystyle n) सकारात्मक प्राकृतिक संख्याओं की गणना सूत्र द्वारा की जाती है:
Σ i \u003d 1 ni 3 \u003d 1 3 + 2 3 + 3 3 + ... + n 3 \u003d (n (n + 1) 2) 2 (\\ displaystyle \\ sum _ (i \u003d 1) ^ (n) i ^ (3) \u003d 1 ^ (3) + 2 ^ (3) + 3 ^ (3) + \\ ldots + n ^ (3) \u003d \\ bept (((\\ frac (n + 1)) (2)) \\ अधिकार) ^ (2))फॉर्मूला की वापसी
क्यूब्स की मात्रा गुणा तालिका और अंकगणितीय प्रगति के योग का उपयोग करके प्रदर्शित की जा सकती है। विधि के चित्रण के रूप में विचार करते हुए, दो गुणा तालिका 5 × 5, एन × एन की तालिकाओं के लिए तर्क को पूरा करते हैं।
|
|
K-OH (K \u003d 1,2, ...) में संख्याओं की संख्या पहली तालिका का चयनित क्षेत्र:
के 2 + 2 के σ एल \u003d 1 के - 1 एल \u003d के 2 + 2 केके (के - 1) 2 \u003d के 3 (\\ डिस्प्लेस्टाइल के ^ (2) + 2k \\ sum _ (l \u003d 1) ^ (के- 1) l \u003d k ^ (2) + 2k (\\ frac (k (के - 1)) (2)) \u003d k ^ (3))और के-ओएच (के \u003d 1,2, ...) में संख्याओं का योग दूसरी तालिका का चयनित क्षेत्र, जो अंकगणितीय प्रगति है:
k σ l \u003d 1 n l \u003d k n (n + 1) 2 (\\ displaystyle k \\ sum _ (l \u003d 1) ^ (n) l \u003d k (\\ frac (n (n + 1)) (2)))पहली तालिका के सभी चयनित क्षेत्रों के माध्यम से संक्षेप में, हमें दूसरी तालिका के सभी चयनित क्षेत्रों पर एक ही संख्या मिलती है:
Σ के \u003d 1 एनके 3 \u003d σ के \u003d 1 एनकेएन (एन + 1) 2 \u003d एन (एन + 1) 2 σ के \u003d 1 एनके \u003d (एन (एन + 1) 2) 2 (\\ डिस्प्लेस्टाइल \\ योग _ (के) \u003d 1) ^ (n) k ^ (3) \u003d \\ sum _ (k \u003d 1) ^ (n) k (\\ frac (n (n + 1)) (2)) \u003d (\\ frac (n +) 1)) (2)) \\ sum _ (k \u003d 1) ^ (n) k \u003d \\ bept (((\\ frac (n (n + 1)) (2)) \\ राइट) ^ (2))कुछ गुण
- दशमलव रिकॉर्ड में, घन किसी भी अंक (वर्ग के विपरीत) पर समाप्त हो सकता है
- दशमलव रिकॉर्ड में, दो अंतिम क्यूब्स 00, 01, 03, 04, 07, 08, 09, 11, 1 9, 21, 23, 2 9, 2 9, 21, 23, 23, 31 32, 33, 36, हो सकते हैं 37, 39, 41, 43, 44, 47, 52, 53, 51, 52, 59, 61, 51, 52, 53, 61, 73, 75, 76, 77, 79, 81, 83, 84, 87, 88, 89, 91, 92, 9 3, 9 6, 9 7, 99। बाद वाले से घन के अंतिम अंक की निर्भरता को निम्नलिखित तालिका के रूप में दर्शाया जा सकता है:
घुमावदार संख्या के रूप में क्यूबा
"क्यूबिक संख्या" Q n \u003d n 3 (\\ displaystyle q_ (n) \u003d n ^ (3)) ऐतिहासिक रूप से, इसे विभिन्न स्थानिक आकृति संख्या माना जाता था। इसे लगातार त्रिकोणीय संख्याओं के वर्गों के अंतर के रूप में दर्शाया जा सकता है। T n (\\ displaystyle t_ (n)):
क्यू एन \u003d (टी एन) 2 - (टी एन - 1) 2, एन ⩾ 2 (\\ डिस्प्लेस्टाइल क्यू_ (एन) \u003d (टी_ (एन)) ^ (2) - (टी_ (एन - 1)) ^ (2), n \\ geqslant 2) क्यू 1 + क्यू 2 + क्यू 3 + ⋯ + क्यू एन \u003d (टी एन) 2 (\\ डिस्प्लेस्टाइल क्यू_ (1) + क्यू_ (2) + क्यू_ (3) + \\ डॉट्स + क्यू_ (एन) \u003d (टी_ (एन)) ^ (2)दो आसन्न घन संख्या के बीच का अंतर एक केंद्रित हेक्सागोनल संख्या है।
टेट्राहेड्रल के माध्यम से एक घन संख्या की अभिव्यक्ति Π एन (3) (\\ Displaystyle \\ Pi _ (n) ^ ((3))).