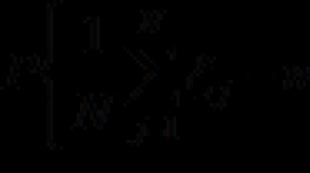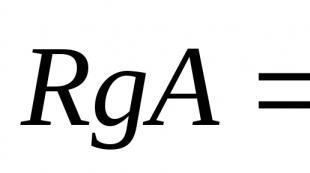Development methods

Möbius function. Möbius inversion formula. Mobius strip - amazing discovery "Magic" of Mobius strip

Municipal budgetary educational institution secondary school with in-depth study of individual

items with. Terbuny

the Mobius strip

Completed by: Chepurina Anna Vitalievna,

10th grade student

Head: Kirikova M.A.

first math teacher

qualification category

Terbuny village

2015

Introduction……………………………………………………………. .................3

Historical background………………………………………………………4

Möbius strip – the beginning of a new science of topology..................................5

Making a Mobius strip……………………………........6

Experiments with Mobius strip.................................................... .................9

Topological properties of the Möbius strip……………………..11

Theorems on the Möbius strip…………………………………….12

Tricks with Mobius strip………………………………………………………15

Application of the Möbius strip……………………………………..16

Conclusion................................................. ........................................23

List of used literature......................................................... .25

Application

Introduction

Nowadays, it is important to study the various properties and non-standard applications of unusual figures.

Have you ever heard of a Möbius strip? How it can be made, how it is related to mathematics and where it is used in life.

While doing this work, I came to the conclusion that although the Möbius strip was discovered back in the 19th century, it was relevant both in the 20th and 20th centuries. The amazing properties of the Möbius strip have been and are used in cooking, technology, physics, painting, architecture, and in the design of jewelry and costume jewelry. He inspired the creativity of many writers and artists.

Interest in the Möbius strip has not faded to this day. In Moscow, in September 2006, the Festival of Artistic Mathematics took place. The speech of a professor from Tokyo was received with great success.

I was very interested and intrigued by this topic. I studied the literature, then made a Mobius strip myself, and then conducted research, conducting experiments, studying its magical, extraordinary properties.

A Möbius strip is a strip of paper with one end turned half a turn (i.e. 180 degrees) and glued to the other end. Millions of people in all parts of the world do not even realize that they use a Möbius strip every day.

Target : tell and show your classmates that a seemingly simple ribbon, turned

half-turn with glued ends, can contain a lot

surprises.

Object of study: Möbius strip.

Tasks: identify sources and literature on this topic and analyze them;

get acquainted with the history of the Mobius strip;

learn how to make a Mobius strip;

study the various properties of the Möbius strip;

While working on the topic, I used the following methods: analysis, synthesis,

observation, experiment, comparison and sociological survey.

CHAPTER I

"Möbius strip - the beginning of a new science"

1. 1. Historical background

The mysterious and famous Möbius strip was invented in 1858 by a German geometerAugust Ferdinand Mobius . They say that Mobius was helped to open his “leaf” by a maid who sewed the ends of a long ribbon incorrectly. He waited seven years for his work to be reviewed and, without waiting, published its results.

At the same time as Möbius, another student of K. F. Gauss invented this leaf -Johann Benedict Listing, Professor at the University of Göttingen. He published his work three years earlier than Mobius, in 1862. A. F. Mobius was born in the city of Schulpforte. For some time, under the guidance of K. Gauss, he studied astronomy. He began to conduct independent astronomical observations at the Pleisenburg Observatory in 1818. became its director. In those days, mathematics was not supported, and astronomy provided enough money not to think about them, and left time for one’s own thoughts. Becoming a professor at the University of Leipzig, in 1816, Möbius first introduced projective geometry, a coordinate system and analytical methods of research; established the existence of one-sided surfaces (Möbius strips), polyhedra, for which the “law of edges” does not apply and which have no volume. Möbius is one of the founders of the theory of geometric transformations, as well as topology. He obtained important results in number theory (the Möbius function) and became one of the leading geometers of his time.

1.2. Möbius strip - the beginning of a new science of topology

From the moment the German mathematician A. F. Möbius discovered the existence of an amazing one-sided sheet of paper, a whole new branch of mathematics began to develop, called topology. The term “topology” can be attributed to two branches of mathematics. One topology, the founder of which was Poincaré, was called combinatorial for a long time. The other, whose origins were the German scientist Georg Cantor, was given the name general or set-theoretic.

Combinatorial topology is a branch of geometry. “Geometry” is a Greek word, translated into Russian means “land surveying” (“geo” means earth in Greek, and “metreo” means to measure) studies the properties of figures. Like any science, geometry is divided into sections.

1. Planimetry (Latin word, “planum” - surface + geometry), a section of geometry that studies the properties of figures on a plane (triangle, square, circle, circle, etc.)

2. Stereometry (Greek, “stereos” - space + geometry) - a section of geometry that studies the properties of figures in space (sphere, cube, parallelepiped, etc.)

H. Topology (Greek “topos” - place, terrain + logic) is one of the “youngest” sections of modern geometry, which studies the properties of such figures that do not change if they are bent, stretched, compressed, but not glued and do not tear, i.e. do not change when deformed. Examples of topological objects are: the letters I and H, thin long balloons.

Combinatorial topology studies the properties of geometric figures that remain unchanged under one-to-one and continuous mappings. For a long time, topology was perceived as a science far from life, intended only to “glorify the human mind.” But in our time it has become clear that it is directly related to explaining the structure of the universe.

General topology is adjacent to set theory and lies at the foundation of mathematics. This is an axiomatic theory designed to explore concepts such as “limit”, “convergence”, “continuity”, etc. The foundations of the axiomatics of topological space were laid by Felix Hausdorff and completed by the Russian mathematician Pavel Sergeevich Alexandrov.

1.3. How to make a Möbius strip

● The Möbius strip is one of the (mathematical surprises). To make a Möbius strip, take a rectangular strip ABCD, twist it 180 degrees and glue the opposite sides AB andCD, i.e. so points A and will coincideC and dots D and V.

See adj. eleven.

● Shapes and sizes of paper strips for the Möbius strip.

The strip should be narrow and long, with the greatest possible length to width ratio. You can't make a Möbius strip from a square sheet of paper. This is true, but it should not be underestimated that size restrictions matter when the paper is not allowed to wrinkle. If crumpling the paper is not prohibited, then a Möbius strip can be glued not only from a square, but from a rectangle of any size - the glued sides can even be any number of times longer than the non-glued ones.

● Development surface.

Since the requirement not to wrinkle the paper is important, let's see what its mathematical meaning is.

It is easy to understand that the prohibition against crumpling paper significantly limits

the ability to manipulate a sheet of paper. For example, a sheet of paper can be rolled into a tube or folded in half without creasing, but cannot be folded into four. You can make a cone from a sheet of paper without crumpling it, but you cannot make a sphere or even a piece of it: press the sheet of paper against the globe, and folds will certainly appear. As you can see, a sheet of paper cannot be given any shape. See adj. 2.

Surfaces that can be made from a sheet of paper by bending it without crushing it are called developable surfaces by mathematicians. In mathematics, developable surfaces are defined differently: in the metamathematical language there are no words “paper”, “crumple”, “make”. There is a whole theory of developable surfaces, among the achievements of which is a satisfactory answer to the question of what they can be; mathematicians call this "classification" (the answer belongs to Leonardo Euler). Let us present only some properties of developable surfaces as experimental facts.

See adj. 3

1. Through each point A of a developable surface that does not lie on its boundary, there passes a segment lying on the surface that does not end at A. In other words, to each point on a developable surface (a curved but not crumpled sheet of paper) a knitting needle can be attached so that it adjacent to the surface for some extent on both sides of the taken point. Such a segment is called a generatrix of the surface (let us agree that this name applies only to segments of maximum length that lie entirely on the surface, that is, to segments that are not contained in large segments with this property).

2. If two different generators pass through a point A that does not lie on the boundary of a surface, and A is not the end of either of them, then a sufficiently small piece of the surface surrounding A is flat. In this case, we will call point A flat.

3. If point A, which does not lie on the boundary of the surface, is the end of some generator, say,A , then the neighborhood of point A is structured like this: through point A there passes the only generatrix that does not end there, let’s sayb . This generatrix divides the surface into two parts. On the other side of the generatrixb , with which the generatrix is locateda , to the generator b a flat piece is adjacent, on the other side ofb , arbitrarily from point A, there are non-flat points. In this situation we will call point A semi-flat.

We emphasize that if a point on a surface is neither boundary nor flat, then there passes through it a single generatrix that does not end at it, and the ends of this generatrix lie on the boundary of the surface.

●Examples: A sheet of paper rolled into a cylinder or cone does not have flat (or semi-flat) points. For a cylinder, the generators form a family of parallel segments; for a cone, they form a family of segments fanning out from one point. More complex arrangements of generatrices are possible.

See adj. 4 .

For example, the generators and flat points of a developing surface are shown in the figure (in which the surface is unfolded into a flat sheet of paper): thin lines are generators, and the shaded areas consist of flat points.

Points lying on the boundary of a region of flat points are either boundary points for the entire surface or semi-flat. If a surface is made of a paper polygon (say, a rectangle), then the planar points make up one or more planar polygons, each of these polygons having vertices lying on the boundary of the surface and sides either lying on the boundary or consisting of semi-planar points.

CHAPTER 2

2.1. Experiments with Mobius strip

Each of us has an intuitive idea of what “surface” is. The surface of a sheet of paper, the surface of the walls of a classroom, the surface of the globe are known to everyone. Can there be anything mysterious in such an ordinary concept? Yes, maybe an example is the Möbius strip. To study its properties, I conducted several experiments (dividing them into two groups) on my own.

I group of experiments

Experiment No. 1. We are accustomed to the fact that at any surface from which

we are dealing (sheet of paper, bicycle or volleyball tube) –

two sides.

I started painting the Mobius strip without turning it over.

Result . The Möbius strip was completely painted over.

"If anyone decides to color only one side

surface of the Möbius strip, let him immediately immerse it all in a bucket of paint,” - writes Richard Courant and Herbert Robins in an excellent

book "What is mathematics?"

Experience No. 2. I made a spider and a fly out of paper and sent it “for a walk” around

an ordinary ring, but forbade them to cross the borders.

Result. The spider couldn't get to the fly.

Experiment No. 3. I sent these spider and fly only along the Mobius strip. AND

forbade them to crawl across the border.

Result.The poor fly will be eaten if, of course, the spider is running

faster!

Experience No. 4. I made a little man out of paper and sent him to travel along the Mobius strip.

Result. The little man will return to the point of departure, where he would meet his mirror image.

II group of experiments

associated with cutting the Möbius strip, the results are listed in the table

experience

Description of the experience

Result

I cut a simple ring lengthwise down the middle.

I got two simple rings, the same length, twice as wide, with two borders.

The Möbius strip was cut lengthwise down the middle.

I received 1 ring, the length of which is twice as long, the width is twice as narrow, twisted 1 full turn, with one border.

Möbius strip width

5cm cut lengthwise at a distance of 1cm from the edge.

I received two rings linked to each other: 1) a Mobius strip - length = the length of the original one, width 3 cm; 2) width 1cm, length twice the original, twisted two full turns, with two borders.

Möbius strip width

5cm cut lengthwise at a distance of 2cm from the edge.

I received two rings linked to each other: 1) the ring is a Möbius strip 1 cm wide, length = the length of the original one; 2) ring - 2 cm wide, twice as long as the original one, twisted by two full turns, with two borders.

A Möbius strip 5cm wide, cut lengthwise at a distance of 3cm from the edge.

I got two rings linked to each other: 1) the ring is a Möbius strip with the width

1 cm of the same length; 2) ring – 2 cm wide, its length is twice the original, twisted two full turns.

The results of a sociological survey with 10th grade students.

Questions

Yes

Have you heard

1.Do you know what topology is?

2. Do you know what a Mobius strip is?

3.Did you know properties of a Mobius strip?

Only 5% of 10th grade students know what topology is. 30% of students know what a Mobius strip is. 20% have heard of it. 50% have no idea about the Mobius strip. 25% of students know the properties of the strip, 10% have heard about them, 65% know nothing about the properties of the Möbius strip.

2.2.Topological properties of the Möbius strip

Based on the results of the experiments, we can formulate the following topological properties of the Möbius strip related to mathematical surprises.

One-sidedness is a topological property of the Möbius strip, characteristic only of it.

Continuity - on a Möbius strip, any point can be connected

with any other point. There are no breaks - complete continuity.

From a topological point of view, a circle is indistinguishable from a square,

because they are easy to transform one into another without breaking

continuity.

Connectivity – two cuts will be required to halve the ring. As for the Möbius strip, the number of connections is replaced depending on the change in the number of turns of the tape: if one turn is doubly connected, if two turns are simply connected, if three turns are doubly connected, etc. But to divide the square into two parts, we only need one cut. Connectivity is usually assessed by the Betti number, or sometimes the Euler characteristic is used.

4. Orientation is a property that is absent in the Möbius strip. So, if a person could travel along all the bends of the Mobius strip, then he would return to the starting point, but would turn into his mirror image.

5. “Chromatic number” is the maximum number of areas that can be drawn on a surface so that each of them has a common border with all the others. The chromatic number of the Möbius strip is six.

6.Theorems on the Möbius strip

Theorem 1: λ ≥ π/2

Due to the complexity of the proof, I do not consider it in my work.

Theorem 2: λ ≤ √3

This theorem is simpler than the previous one: to prove it, it is enough to explain how to glue a Möbius strip from a strip whose length is greater than √3. Let us first assume that its length is exactly √3. Then you can place two regular triangles on this strip. Let's fold the strip along the sides of these triangles, alternating fold directions. The edges AB and CD of the strip will align, and point A will align with point D, and point B with point C. The result will be a Möbius strip, the edges of which are positioned end-to-end (see Appendix 1.2)

In this construction, the main rule was violated - do not wrinkle the paper. But it is easy to understand that if the length of the strip is at least a little more than √3, then the break along the generatrix can be replaced by bending performed in a narrow section. In short, we are not afraid of a kink along a straight segment: it can be replaced by a bend close to it. (Irreparable creasing of paper occurs when two fold lines intersect, i.e. when the sheet is folded like a handkerchief - all this is known to us from everyday experience.) Its structure can be imagined as follows: three identical regular triangles ABC, A"B"C", A"B"C" lie parallel to each other, the corresponding vertices are above the corresponding vertices; sides AB and A"B", B"C" and B"C", C"A" and CA are connected by jumpers. The gluing line runs along the median of one of the triangles.

Why can't we find λ more accurately?

Until the problem is solved, it is difficult to say why it is not solved. Nevertheless, sometimes in various unsolved problems it is possible to trace common difficulties, to mark, so to speak, difficult places on a mathematical map, which sometimes makes it possible to predict success or failure in solving a particular problem

Theorem 3. A Möbius strip with self-intersections can be glued together from a strip of any length greater than π/2.

It's done like this. Let's take a sufficiently large odd n and construct a regular n-gon inscribed in a circle of diameter 1. Consider, further, n triangles containing the center of the circle, each of which is limited by a side and two diagonals of the n-gon (n=7). These triangles cover our n-gon, some of its places several times. Let us now apply these n triangles to each other, after which we cut off half of the leftmost triangle along the long median and apply it to the rightmost triangle. The result is a rectangular strip with a ratio of length to width greater than π/2 and tending to π/2 as n, tending to ∞ (the width of the strip tends to 1, and the length to π/2). Consistently fold this strip along all the lines drawn on it, alternating the folding directions. Segments AB and CD will almost coincide - there will be only a few layers of folded paper between them. In this “almost alignment,” point A will align with D, and point B will align with C, so if we could “pass the tape through” and glue |AB| with |CD|, then the result would be a Möbius strip. If you take the tape a little longer, you can avoid folds, just as we did in the proof of Theorem 2. We have obtained a Möbius strip, the edges of which are separated by several layers of paper, see Appendix 1.3. But let's return to the Möbius strip. Theorem 1, as we have seen, actually applies to self-intersecting bands. It is unlikely that the no-self-intersection condition would have no effect on λ; however, it is not possible to take this effect into account, since mathematics does not have sufficient technical means to study self-intersections in three-dimensional space. On the contrary, it is quite likely that Theorem 2 cannot be improved. After all, improving it means coming up with a new tape design. Experience shows that optimal constructions are simple and harmonious, which is what the construction from the proof of Theorem 2 is. It is natural to assume that if the best construction existed, it would have been found - after so many years!

This is why we can expect λ = √3.

Moebius strip tricks

Problem tying knots

How to tie a knot in a scarf without letting go of its ends? It can be done like this. Place the scarf on the table. Cross your arms over your chest. Continuing to hold them in this position, bend over the table and take one end of the scarf with each hand in turn. After the arms are spread apart, a knot will form automatically in the middle of the scarf. Using topological terminology, we can say that the viewer's hands, his body and scarf form a closed curve in the form of a “three-leaf” knot. When spreading the arms, the knot only moves from the hands to the scarf.

Tie a knot in the scarf with one hand, without letting go of the end of the scarf from your hand. The answer to this puzzle can be found in the book “Mathematical Wonders and Mysteries” by M. Gardner.

From a topological point of view, the vest can be considered as a two-sided surface with three non-interlocking edges, each of which is an ordinary closed curve. The buttoned vest is a double-sided surface with four edges.

Mysterious loop.

The spectator wearing the vest has a loop placed on his hand and is then asked to place his thumb in the bottom pocket of the vest. Now you can invite those present to remove the loop from your hand without removing your finger from your vest pocket. The solution is this: the loop needs to be pulled into the vest hole for the sleeve, thrown over the viewer's head, pulled out through the second hole for the sleeve and moved under the second arm. As a result of these actions, the loop will be under the vest, surrounding the chest. Lower it until it appears from under the vest, and then let it fall to the floor.

Turning the vest inside out without removing it from the person.

The owner of the vest needs to clasp his fingers behind his back. Those around you should turn the vest inside out without separating the owner’s hands. To demonstrate this experience, it is necessary to unfasten the vest and pull it over the hands behind the wearer's back. The vest will dangle in the air, but, of course, will not come off, because the hands are clasped. Now you need to take the left hem of the vest and, trying not to wrinkle the vest, push it as far as possible into the right armhole. Then take the right armhole and insert it into the same armhole and in the same direction. All that remains is to straighten the vest and pull it on the owner. The vest will be turned inside out. We performed this trick and filmed it with our classmates. It is contained in the presentation "Mobius Strip".

2.3. Application of the Möbius strip

∞ At the entrance to the Museum of History and Technology in Washington, a steel ribbon twisted half a turn slowly rotates on a pedestal. In 1967, when the International Mathematical Congress took place in Brazil, its organizers issued a commemorative stamp in denominations of five centavos. It depicted a Möbius strip. Both the monument, more than two meters high, and the tiny stamp are unique monuments to the German mathematician and astronomer August Ferdinand Möbius.

See Appendix 5.

The Patent Service has registered many inventions based on the same one-sided surface.

∞ The Möbius strip is used in many inventions inspired by careful study of the properties of a one-sided surface. The conveyor belt strip, made in the form of a Möbius strip, allows it to work twice as long because the entire surface of the sheet wears out evenly. In 1923, a patent was issued to inventor Lee de Force, who proposed recording sound on film without changing reels on both sides at once. Cassettes for tape recorders were invented, where the tape is twisted and glued into a ring, which makes it possible to record or read information from both sides at once, which doubles the capacity of the cassette and, accordingly, the playing time. In dot matrix printers, the ink ribbon was shaped like a Möbius strip to increase shelf life. This provides significant savings. The Möbius strip is used in cycling and volleyball tubes.

∞ More recently, they found another use for it - it began to play the role of a spring, only a special spring. As you know, a charged spring fires in the opposite direction. The Mobius strip, contrary to all laws, does not change the direction of operation, like mechanisms with two stable positions. Such a spring could become invaluable in wind-up toys - it cannot be twisted like an ordinary one - a kind of perpetual motion machine.

See adj. 6.

∞ In 1971, inventor from the Urals P.N. Chesnokov. applied a filter in the form of a Mobius strip.

∞ The Mobius leaf is used in cooking to create an interesting and appetizing look for buns, crackers, and brushwood. And also in the manufacture of tools for preparing and decorating various dishes, power structures (stirrer).

See adj. 7.

∞ With the help of a Möbius strip, entire masterpieces are created.

The Möbius strip served as inspiration for sculptures and graphic art. Escher was one of the artists who especially loved it and dedicated several of his lithographs to this mathematical object. One famous one shows ants crawling across the surface of a Möbius strip.

See appendix 9.

∞ The Möbius strip also appears regularly in science fiction, such as in Arthur C. Clarke's story "The Wall of Darkness." Sometimes science fiction stories suggest that our Universe may be some kind of generalized Möbius strip. In the story by author A.J. Deitch, the Boston subway is building a new line, the route of which becomes so confusing that it turns into a Mobius strip, after which trains begin to disappear on this line.

∞ There is a hypothesis that the DNA spiral itself is also a fragment of a Mobius strip, and that is the only reason why the genetic code is so difficult to decipher and perceive. Moreover, such a structure quite logically explains the reason for the onset of biological death: the spiral closes on itself, and self-destruction occurs.

Appendix 10.

∞ The Möbius strip was liked not only by mathematicians, but also by magicians

For over 100 years, the Möbius strip has been used to perform various magic tricks and entertainment. The amazing properties of the leaf were demonstrated even in the circus, where bright ribbons glued together in the form of Möbius strips were suspended. The magician lit a cigarette and with the burning end touched the middle line of each ribbon, which was made of potassium nitrate. The fiery path turned the first ribbon into a longer one, and the second into two ribbons, threaded one into the other. (In this case, the magician cut the Mobius strip not in the middle, but at a distance of one-third of its width).

∞ Physicists claim that all optical laws are based on the properties of the Mobius strip, in particular, reflection in a mirror is a kind of transfer in time, short-term, lasting hundredths of a second, because we see in front of us... that's right, our mirror double.

∞There is a hypothesis that our Universe is quite likely closed in the same Mobius strip, according to the theory of relativity, the greater the mass, the greater the curvature of space. This theory fully confirms the assumption that a spaceship, flying straight all the time, can return to the starting point, this confirms the unlimitedness and finitude of the Universe.

See adj. eleven.

∞ Interest in the Möbius strip has not faded to this day. The Festival of Artistic Mathematics took place in Moscow in September 2006. The speech of professor from Tokyo Jin Akiyama was received with great success. His performance was reminiscent of an illusionist’s show, where there was a place for the Möbius strip (work with paper “Möbius strip and its modifications”).

SPORT

Manual expander "Robur"

See adj. 12 .

One offavorite things of all school physical education teachers, which according to themin his own words, “trains notonly the muscles of the hand, butand brain muscle."Carpal expander fromArtemy Lebedev studio repeats the shape of a Möbius strip. An excellent remedy for relieving stress, thinking aboutinfinity andjust a useful way to keep your hands busy.

PERFUME

Bugatti perfume

See adj. 13

CompanyBugattibegan producing not only ultra-expensive cars (modelVeyroncosts 1.3 million euros), but also... perfume. Each bottle, made of crystal and covered with real gold, is designed in the form of an unusual Möbius strip, which has only one side. Price of perfumeBugattiis 3500 euros.

Perfume Loewe Quzas, Quizas, Quizas

See adj. 14 .

In the fall of 2011, a crimson version of the fragrance was released, the bottle of which is wrapped in a Mobius strip - a symbol of the cycle of passions in nature. The richness of the composition consists of the freshness of Asian oranges, bergamot, red berries, continues with a floral heart of magnolia, freesia and orange petals, and ends with a sensual trail of cashmere wood, golden amber and vetiver.

Perfume UFO Limited Edition, Kenzo

See adj. 15 .

Fragrance presentationKenzotook place in 2009 at a retrospective exhibition of works by Ron Arad (RonArad) at the Pompidou Center in Paris. It was this artist and architect who came up with the cosmic design of the bottle in the form of a Mobius strip. It is designed to fit exactly in the palm of your hand.UnidentifiedFragranceObject, or “Unidentified Aromatic Object,” is limited to just 180 pieces and retails for $188.

FURNITURE

Mobius table

See adj. 16

A table with one surface at which you can stand, sit and lie comfortably.

Bookshelf Infinity

See adj. 17.

Designer Job Kelevius broke the mold when he designed his Infinity bookcase. Using the mathematical concept of Lemniscate, and something similar to the Möbius strip, the designer embodied the physical concept of infinity in the Infinity Shelf. This means that if you have read all the books on this shelf, consider that you have comprehended the entire infinity of literature.

Mobius sofa

See adj. 18.

Born under the motto "Double chair - double pleasure", the sofa chairMoebiusDoubleArmchaircreated by designerGaetanVandeWyerfrom Belgium and brings a fresh vision of furniture for lovers.

LOGOS

Woolmark company logo

See adj. 19.

The logo was created in 1964 as a result of a design competition. Jury memberFrancoGrignanicouldn’t resist and offered his own version, hiding under a pseudonymFrancescoSeraglio. This logo resembles a Mobius strip and is a symbol of the eternity and flexibility of the company.

Recycling symbol

See adj. 20.

The international symbol for recycling is the Möbius strip. Recycling (other terms: recycling, waste recycling, recycling and recycling)- reuse or return into circulation of industrial waste or garbage. The most common are secondary, tertiary and T. e. recycling on one scale or another of materials such as glass, paper, aluminum, asphalt, iron, fabrics and various types of plastic. Organic agricultural and household waste has also been used in agriculture since ancient times.

Mathematics symbol

See adj. 21.

The Möbius strip is considered a symbol of modern mathematics, since it was he who gave impetus to new mathematical research.

CLOTHING AND FOOTWEAR

Shoes

See adj. 22.

Founded in 2003 by architect Ram Di Koolhaase and shoemaker Galahad ClarkUnitedNudespecializes in the production of innovative designer shoes. One of the most successful developments of the company are shoesMobius , named after the geometer August Möbius and his idea of a one-sided surface. The idea of the shoes is this: the leather upper of the shoes and the sole are a single ribbon, twisted in a certain way.

Mobius scarf

See adj. 23.

An interesting thing is the Möbius scarf that appears in the wardrobes of the 21st century. You can make a Möbius scarf yourself by tying the ends of the scarf and twisting it one turn.

PAINTING

Graffiti

See adj. 24.

A modern Möbius strip is painted on a wall in Prague, Czech Republic.   Two types of vehicles move along the tape: tanks and road construction equipment. A symbol of modern civilization: destroy-build-destroy-build..

ARCHITECTURE

Library building

See adj. 25.

A project to build a library in the form of a Mobius strip in Kazakhstan is currently being considered.

The curves of the building form a Möbius strip, thus the internal space flows into the external and vice versa; in a similar way, the walls transform into the roof, and the roof transforms back into walls. Natural light enters the interior corridors through geometric openings in the outer shell, creating beautifully lit spaces ideal for reading.

Attractions

See adj. 26.

The roller coaster ride resembles the shape of a Mobius strip. In Moscow there is the world's largest inverted roller coaster, where a person sits in a suspended chair and his legs are in the air. Speed - 81 km/h, height 30 m. The height, compared to foreign analogues, is small, but it more than pays off with the abundance of spirals, rings and loops.

Film reel

See adj. 27.

In 1923, a patent was issued to inventor Lee de Force, who proposed recording sound on film without changing reels, from both sides at once.

Cassette

See adj. 28.

Cassettes were invented for tape recorders, where the tape is twisted and glued into a ring, which makes it possible to record or read information from both sides at once, which increases the capacity of the cassette and, accordingly, the playing time.

Toyota MOB car

See adj. 29.

The Möbius strip is designed by Spanish designer Jorge Marti Vidal and combines the beauty and mystery of a Möbius strip. The unique body shape provides the racing car with good aerodynamics

Matrix printer

See adj. thirty.

In many matrix printers, the ink ribbon also has the form of a Mobius strip to increase its resource.

Möbius resistor

See adj. 31.

This is a newly invented electronic element that has no inductance of its own.

Sanding belt

See adj. 32.

In 1969, Soviet inventor Gubaidullin proposed an endless sanding belt in the form of a Möbius strip.

Conclusion

The Möbius strip is the first one-sided surface that a scientist discovered. Later, mathematicians discovered a whole series of one-sided surfaces. But

this one, the very first, which laid the foundation for a whole direction in geometry, continues to attract the attention of scientists, inventors, artists and our students. I was very interested in the open properties of the Möbius strip:

The Mobius strip has one edge, one side

A Möbius strip is a topological object. Like any topological figure, it does not change its properties until it is cut, torn, or its individual pieces are glued together.

One edge and one side of the Mobius strip are not related to its position in space, and are not related to the concepts of distance.

The Möbius strip finds numerous applications in cooking, technology, physics, painting, architecture, jewelry design and the study of the properties of the Universe. He inspired the creativity of many writers and artists.

μ( n) is defined for all natural numbers n and takes values depending on the nature of the expansion of the number n to simple factors:

μ( n) = 1 if n free from squares (i.e. no prime number is divisible by the square) and the decomposition n an even number of factors;
μ( n) = − 1 if n free from squares and decomposition n into prime factors consists of an odd number of factors;
μ( n) = 0 if n not free from squares.

By definition, we also assume μ(1) = 1.

Properties and Applications

The Möbius function is multiplicative: for any coprime numbers a And b equality holds μ( ab) = μ( a)μ( b) .

The sum of the values of the Möbius function over all divisors of an integer n, not equal to one, is equal to zero

Style="max-width: 98%; height: auto; width: auto;" src="/pictures/wiki/files/49/1bee8d0f6bd91176912a8cedc63e174b.png" border="0">

From here, in particular, it follows that for any non-empty finite set, the number of different subsets consisting of an odd number of elements is equal to the number of different subsets consisting of an even number of elements - a fact used in the proof.

The Möbius function is related to the Mertens function by the relation

The Mertens function, in turn, is closely related to the problem of zeros of the Riemann zeta function, see the article Mertens hypothesis.

Mobius inversion

First Möbius inversion formula

For arithmetic functions f And g ,

g(n) =	∑	f(d)
	d \| n

then and only when

Second Möbius inversion formula

For real-valued functions f(x) And g(x) defined at ,

then and only when

Here the amount is interpreted as .

Wikimedia Foundation. 2010.

See what the “Mobius function” is in other dictionaries:

The Möbius function μ(n) is a multiplicative arithmetic function used in number theory and combinatorics, named after the German mathematician Möbius, who first considered it in 1831. Contents 1 Definition 2 Properties and applications ... Wikipedia

Type of transformations on the complex plane (gray) and the Riemann sphere (black) Contents 1 Definition 2 Algebraic properties ... Wikipedia

A fractional linear function is a function of the form where z = (z1,...,zn) are complex or real variables, ai,b,ci,d are complex or real coefficients. Often the term “fractional linear function” is used for its special case of transformation... ... Wikipedia

Möbius series is a functional series of the form This series was studied by Möbius, who found an inversion formula for this series: where μ(s) is the Möbius function ... Wikipedia

METHODS OF MEDICAL RESEARCH- I. General principles of medical research. The growth and deepening of our knowledge, more and more technical equipment of the clinic, based on the use of the latest achievements of physics, chemistry and technology, the associated complication of methods... ... Great Medical Encyclopedia

A pathological condition that developed during childbirth and is characterized by damage to the tissues and organs of the child, accompanied, as a rule, by a disorder of their functions. Factors predisposing to the development of R. so-called are incorrect... ... Medical encyclopedia

Lemma.

Proof. The statement is obvious. Let and be the canonical expansion of the number . Then, taking into account that the divisors have the form , where , ,…, ; , we get

because the

Theorem. (Additive Möbius inversion formula.) Let and be functions of the natural argument . Then if

Proof. We have

Let . Then the fixed one runs through all the values of the divisors of the number . This means that the summation signs in the last double sum can be reversed, i.e.

Now, given that

we get

There is another form of the proven theorem:

Theorem. (Multiplicative Möbius inversion formula.) Let

where the symbol denotes the product extended to all divisors of the number.

Proof:

Examples of using the Möbius inversion formula:

Problem on the number of ring sequences. See: Hall M. Combinatorics. M.: Mir, , § .

The number of irreducible polynomials of a given degree over a finite field of elements. See: Berlekamp E. Algebraic coding theory. − M.: Mir, 1970, Ch. 3.

Glukhov M. M., Elizarov V. P., Nechaev A. A. Algebra. In the t. M.: Helios, . T. , § .

For self-study:

Möbius inversion on partially ordered sets. The inclusion-exclusion principle as a special case of the Möbius inversion formula. See: Hall M. Combinatorics. M.: Mir, , § ; Bender E., Goldman J. On applications of Möbius inversion in combinatorial analysis. In the book: Enumerative problems of combinatorial analysis. M.: Mir, 1971. S. - .

Comparisons for number combinations

Let be a prime number.

Lemma.

Proof. When the numerator in the formula

Consequence.

Proof.

Lemma. Let , , , be non-negative integers, and let , . Then

Proof. We have

On the other side,

Comparing the coefficients at the same degrees, we obtain the required result. ∎

− representations of non-negative integers and radix. (Here is any integer for which , ). On the set of non-negative integers we define the partial order relation (the relation precedence) , assuming , if and only if

Lucas's theorem ( ).

Proof. According to the previous lemma,

Where , . Applying the lemma repeatedly the appropriate number of times, we obtain the required result. ∎

Comment. The theorem is not true for unprime ones. For example (see Berlekamp, p.),

Consequence.

II . Algebraic structures

II. 1. Sets with binary operations. Groupoids, semigroups, monoids

Binary algebraic operation(or law of composition) on a non-empty set S called mapping : , matching a pair of elements to a uniquely defined element. Many operations can be specified on a set. (If, for example, of course, then the number of ways is equal to , where is the number of elements in .) If you want to highlight one of them, for example, write , . Such an object is called binary algebra, or groupoid. Instead of , they often write , and the operation itself is denoted by some symbol ( , , , etc.).

Comment. Along with binary operations, more general -ary operations are considered (unary at, ternary at, etc.). The algebraic structures (systems) associated with them constitute the subject of research of the so-called. universal algebras.

A binary operation on a set is called associative, If

, for any , , .

A groupoid with an associative operation is called semigroup.

An example of a non-associative groupoid. On the set we define the operation as . The operation is non-associative: , but .

Theorem. If a binary operation on a set is associative, then the value of the expression does not depend on the placement of parentheses in it.

Proof. With , or the statement is obvious. For it is sufficient to show, using induction, that

for any , . By the induction hypothesis, the placement of brackets in

Not significant; in particular, .

If, then.

If , then

The right-hand side of the equality being proved (1) is also reduced to the same form. ∎

The element is called neutral regarding the operation, if

for anyone .

A semigroup with an element is called monoid(or semigroup with identity) and denote , , .

A semigroup (groupoid) can have at most one neutral element: if

, are neutral elements, then

A groupoid (semigroup) is called subgroupoid (subsemigroup) groupoid (semigroup), , if

And for any , .

In this case they say that the subset closed under operation. Monoid is called submonoid monoid , , , if and .

The element of the monoid, , is called reversible, if there is an element such that (obviously, then we will reverse it). If the element has the same property, i.e. , then from the equalities it follows that the element is actually unique (with respect to ). This allows us to talk about reverse element , to (invertible) element , with properties: , .

If , are invertible elements of the monoid , , , then their product is also an invertible element, since , . Obviously, it is an invertible element. Therefore, there is

Theorem. The set of all invertible elements of the monoid , , is closed under the operation ∗ and forms a submonoid in , , .

Groups

Definition of a group. A monoid , , , all of whose elements are invertible is called group.

In other words, a group is a set with a binary operation for which the following axioms hold:

. (Closed operation.) , .

. (Operation associativity.) ,

. (Existence of a neutral element.) ∃ .

. (Existence of an inverse element.) .

Comment. Returning to the algebraic structures introduced above, we observe the following hierarchy among them: the pair , is groupoid, if the axiom is satisfied; semigroup, if axioms and ; monoid, if axioms , and ; group, if the axioms , , and .

The degrees of elements with obvious properties are determined in a natural way:

( once),

; , ( , , .

Generally speaking, it is impossible to rearrange elements in an expression (i.e. ). If , then the elements are called permutable, or commuting. If any two elements of a group commute, then the group is called commutative, or Abelian(in honor of the Norwegian mathematician Riehl Henrik Abel ( - )).

An operation in a group is most often indicated by either a symbol (addition) or a symbol (multiplication). In this case, the group is called accordingly additive or multiplicative, its neutral element is respectively zero() or unit(). In an additive group, the element, the inverse of the element, is called opposite and is designated , but instead they write . In a multiplicative group, they usually write instead, omitting the operation symbol.

Examples of additive groups. 1) , , , , , , , – additive groups of the ring and fields , , . They simply write , , , . 2) Any ring by addition is an Abelian group. In particular, the ring of polynomials ,…, ] and the ring of matrices of order over a field are Abelian groups. 3) Any vector space over a field with respect to addition is an Abelian group. 4) , 1,…, – a complete system of least non-negative modulo residues with the modulo addition operation.

Examples of multiplicative groups. 1) , , are multiplicative groups of fields , , . 2) is the set of invertible elements of any ring with unity under multiplication. In particular, = ; , is the set of invertible matrices from . 3) − all (real and complex) roots

, , 1,…, , − imaginary unit,

equation is a multiplicative Abelian group. 4) - the set of rotations of a regular -gon in the plane and in space - a non-commutative group (for ).

Further, the multiplicative form of recording the operation is more often used. The group is usually designated by a single letter without specifying the operation. The set of all elements of a group is called main set of the group and is denoted by the same letter. If the base set is finite, then the group is called ultimate; otherwise it is called endless. The number element of a finite group is called its in order. A group of order 1 is called single, or T rivial. An infinite group is said to have infinite order. To indicate the order of the group (the cardinality of the main set), the equal symbols Card (cardinal number), and () are used.

If , are subsets (of the main set) of the group, then we put

, , .

Subgroup of a group is a subset in which is itself a group with respect to the same operation as in . In other words, a subset is a subgroup if and only if ( one in ) and is closed under multiplication and reciprocal, i.e. , (in fact there are even equalities here). If is a subgroup in , then write ; if at the same time, then it is called own subgroup and this is denoted as .

Möbius function  (n), Where n– a natural number, takes the following values:

The Möbius function allows you to write the Euler function as a sum:

The summation is over all divisors of n (and not just over prime divisors).

Example. Let's calculate φ (100) using the Möbius function.

All divisors of 100 are (1, 2, 4, 5, 10, 20, 25, 50, 100).

(2) = (-1) 1 = -1 (two has one prime divisor – 2)

(4) = 0 (4 is divided by the square of two)

(5) = (-1) 1 = -1 (5 has one prime divisor – 5)

(10) = (-1) 2 = 1 (10 has two prime factors – 2 and 5)

(20) = 0 (20 divided by the square of two)

(25) = 0 (25 divided by the square of five)

(50) = 0 (50 is divisible by both 2 2 and 5 5)

(100) = 0 (100 is divisible by both 2 2 and 5 5)

Thus,

Property of the Möbius function:.

For example, n=100, {1, 2, 4, 5, 10, 20, 25, 50, 100}.

16 A theorem on the number of ways to select k-elements, among which there are not two adjacent ones, from n elements arranged in a row. Prove by obtaining a recurrence formula.

17 Number of combinations with repetitions

Number r-combinations with repetitions from n-sets are equal

– proof using a recurrence formula.

The method is based on obtaining a formula that allows you to calculate the values of the desired quantity step by step, based on the known initial values and values calculated in previous steps.

Recurrence formular -th order– formula of the form

a n = f(n, a n- 1 , a n- 2 , … , a n-r).

The formula expresses at n>r each member of the sequence ( a i) through previous r members. The construction of a recurrent formula consists of the following steps.

1. Development of initial conditions based on any obvious relationships.

Let us denote by f(n,r). It's obvious that

2. Logical reasoning. Let us fix some element in the set S. Then relative to any r- combinations with repetitions from n-sets S we can tell whether it contains a given fixed element or not.

If contains, then the rest ( r-1) item can be selected f(n,r-1) ways.

If does not contain(this element is not in the selection), then r- a combination made up of elements ( n-1)-sets (set S except for this fixed element). Number of such combinations f(n-1,r).

Because these cases are mutually exclusive, then according to the sum rule

3. Checking the formula on some values and deducing a general pattern.

1) Let's calculate f (n ,0) . From (2) it follows

Then f(n,0)=f(n,1)-f(n-1,1). From (1) f(n,1)=n,f(n-1,1)=n-1.

Hence, f(n,0)=n-(n-1)=1=.

2) f (n ,1) =f(n,0)+f(n-1,1) = 1+n- 1 =n==.

3) f (n ,2) =f(n,1)+f(n-1,2) =n+f(n-1,1)+f(n-2,2) =n+(n-1)+f(n-2,1)+f(n-3,2) = … =

= n+(n-1)+…+2+1 =.

(sum of arithmetic progression)

4) f (n ,3) =f(n,2)+f(n-1,3) =+f(n-1,2)+f(n-2,3) =++f(n-2,2)+f(n-3,3) = … =

(sum of geometric progression)

5) f (n ,4) =

Based on particular cases, it can be assumed that

4. Checking the initial conditions using the resulting formula.

which is consistent with (1) #

19, 20) The number of binary trees with n vertices is equal to C(n), where C(n) is the nth Catalan number.

The number of binary trees with n vertices is called the Catalan number, which has many interesting properties. The Nth Catalan number is calculated using the formula (2n)! / (n+1)!n!, which grows exponentially. (Wikipedia offers several proofs that this is a form of the Catalan number.) Number of binary trees of a given size 0 1 1 1 2 2 4 14 8 1430 12 208012 16 35357670

Substitution

Go to: navigation, search

This is an article about substitution as a syntactic operation ontherms . You might be interested inrearrangement .

IN mathematics And computer science substitution- this is an operation syntactic replacement of subterms of a given terma other terms, according to certain rules. Usually we are talking about substituting a term instead of variable.

Definitions and notations

There is no universal, agreed-upon notation for substitution, nor is there a standard definition. The concept of substitution varies not only within sections, but also at the level of individual publications. In general, we can highlight context substitution And substitution "instead of". In the first case, the place in the term where the replacement occurs is given context, that is, part of the terma “surrounding” this place. In particular, this concept of substitution is used in rewriting. The second option is more common. In this case, the substitution is usually specified by some function from a set of variables into a set of terms. To indicate substitution actions, as a rule, use postfix notation. For example, means the result of a substitution action on a term.

In the overwhelming majority of cases, it is required that the substitution have a finite carrier, that is, that the set was finite. In this case, it can be specified by simply listing the pairs "variable-value". Since each such substitution can be reduced to a sequence of substitutions that replace only one variable each, without loss of generality we can assume that the substitution is given by one pair "variable-value", which is what is usually done.

The last definition of substitution is probably the most typical and frequently used. However, there is no single generally accepted notation for it either. Most often used to indicate substitution a instead of x V t recording is used t[a/x], t[x:=a] or t[x←a].

Variable substitution inλ-calculus

In λ-calculus, substitution is determined by structural induction. For arbitrary objects and an arbitrary variable, the result of replacing an arbitrary free occurrence is calculated substitution and is determined by induction on the construction:

(i) basis:: object matches variable. Then;

(ii) basis:: object matches constant. Then for arbitrary atomic ones;

(iii) step: : the object is non-atomic and has the appearance of an application. Then;

(iv) step:: object is non-atomic and is an abstraction. Then [;

(v) step:: the object is non-atomic and is an abstraction, moreover. Then:

for andor;

Variable Substitution in Programming

Substitution variable ( English substitution) V applicative programming is understood as follows. To calculate the value of a function f on the argument v entry is applied f(v)), Where f determined by design f(x) = e. Record f(v) in this case means that in the expression e is happening substitution, or variable substitution x on v. The substitution is performed in accordance with semantics of calculations.

Substitution variable ( English assignment) V programming understood as assignment. The assignment operator is a manifestation of the von Neumann bottleneck effect for traditional programming languages . Free from this applicative computing systems.

http://math.nsc.ru/LBRT/u3/bard/fails/Brenner_Evans.pdf

21 Generating functions.Generating function (numerator) and enumerating generating function for combinations without repetitions.

Generating functions: 1) Z-transforms 2) generator 3) generating function 4) generating function of the sequence (a r ) on the basis (g r ) - function f, when expanded into a series of functions of a fixed basis (g r ), this sequence of coefficients (a r ) is formed …………*)

This series is formal. The name formal means that we treat the formula *) as a convenient notation for our sequence - in this case it does not matter for which (actions and complex) values it converges. The role of t is reduced to distinguishing the coefficients of the sequence A0, A1,…Ar….therefore, in the theory of generating functions, the values of this series are never calculated for a specific value of the variable t. Only some operations are performed on such series, and then only some operations on such series are determined, and then the coefficients are determined for individual powers of the variable t.

Usually as

22 Generating function. Generating function (numerator) and enumerating generating function for combinations with repetitions.

Manufacturing facility for:

Construction rule

1) If an element of type i can be included in combinations K 1 or K 2 or... K i times, then it has a corresponding multiplier

3) It remains to find the coefficient. at

exponential generating function for placements construction rule

25) Combinatorial numbers also include Stirling numbers of the first and second kind. These numbers are defined as coefficients in the equalities

and have a simple combinatorial meaning - equal to the number of elements of the permutation group that are products of exactly k disjoint cycles, and equal to the number of partitions n- element set on k non-empty subsets. It's obvious that. A similar sum of Stirling numbers of the second kind is called n- Bell number and equal to the number of all partitions n-element set. The recurrence formula is valid for Bell numbers.

When solving combinatorial problems it is often useful inclusion-exclusion formula

which allows one to find the cardinality of the union of sets if the cardinality of their intersections is known. Let us use the inclusion-exclusion formula to obtain an explicit formula for the Stirling numbers of the second kind.

Stirling numbers of the first kind

Material from Wikipedia - the free encyclopedia

Go to: navigation, search

Stirling numbers of the first kind(unsigned) - quantity permutations order n With k cycles.

Definition

Stirling numbers of the first kind(with sign) s(n, k) are called coefficients polynomial:

Where ( x) n - Pochhammer symbol (decreasing factorial):

As can be seen from the definition, numbers have an alternating sign. Their absolute values specify the number permutations set consisting of n elements with k cycles.

Recurrence relation

Stirling numbers of the first kind are given recurrent ratio:

s(n,n) = 1, for n ≥ 0,

s(n,0) = 0, for n > 0,

for 0< k < n.

Proof.

For n=1 this equality is checked directly. Let the permutation ( n-1)th order decomposes into k cycles. Number n can be added after any number in the appropriate loop. All the resulting permutations are different and contain k cycles, their number ( n-1)· s(n-1, k). From any permutation ( n-1)th order containing k-1 cycle, a single permutation can be formed n order containing k cycles by adding a cycle formed by a singular number n. Obviously, this construction describes all permutations n-th order containing k cycles. Thus equality is proven.

Example

First rows:

IN combinatorics Stirling number of the second kind from n By k, denoted by or, is the number of unordered partitions n-elemental sets on k non-empty subsets.

Recurrence formula

Stirling numbers of the second kind satisfy recurrent ratio:

For n ≥ 0,

For n > 0,

Explicit formula

Example

The initial values of the Stirling numbers of the second kind are given in the table:

Properties

Bijective A mapping is a mapping that has the properties of being injective and surjective at the same time.

1. Let us first recall the definition of the important number-theoretic Möbiu function

1 if n = 1

µ (n)=0, if there is a prime number p, p2 n (-1)k, if n = p1 ... pk is the product of k different prime factors.

Let us prove the main property of the Möbius function:

Theorem 1.

♦ If n = 1, then the only divisor is d = 1 and (1) is true, because µ (1) = 1. Now let n > 1. Let us represent it in the form

n = p1 s 1 ps 2 2 K ps k k ,

where pi, i 1, k are prime numbers, si are their powers. If d is a divisor of n, then d = p1 d 1 pd 2 2 K pd k k ,

where 0 ≤ di ≤ si, i 1, k. If di > 1 for some i 1, k, then µ (d) = 0. This means that in (1) we need to consider only those d for which di ≤ 1, i 1, k. Each such divisor co-

consists of the product of r different prime numbers, where r 1, k, and its contribution to the sum

(1) is equal to (-1)r and there are k in total. Thus, we get


	µ (d) = 1 −	K + (− 1) k	0. ♦



	Theorem 2. (Mobius inversion formula). Let f(n) and g(n) be functions of natural
ral argument. Then equality
			∑f(d)

is true if and only if the equality is true
			∑ µ (d)g(
			∑ µ (d)g(

♦ Let (2) be true for any n. Then

g(d n ) = ∑ f(d′ )

d ′ d n

Substituting into the right side of (3), we get

∑ µ (d)g(	) = ∑ µ (d) ∑ f(d′ )

		d′

Double summation on the right is carried out over all pairs d, d′ such that d d′ n. If you choose d ′ , then d will run through all divisors d n ′ . Thus

∑ µ (d)g(

) = ∑ f(d′ ) ∑ µ (d′ )

d′

n > d′

But according to (1) we have ∑

µ (d′ ) =

n = d′

d′

This means that equality (3) is established. Now let (3) be true for any n. Then

∑ f(d) =

∑ ∑ µ (d′ )g(

) , d′′ = d d ′ - is a divisor of n and the double sum can

d′

n d′

be rewritten as

∑ µ (d′ )g(d′′ ) =

∑ g(d′′ )

∑ µ(d′)

d′′

n d ′

d′′

d′

d′′

According to (1), the last sum turns to unity in the case d′′ = n, in other cases

In any case, it is zero. This proves (2). ♦ 2. Consider an application of the Möbius inversion.

Let an alphabet A of s letters be given. There are sn words of length n in a given alphabet. For each word w0 = a1 a2 … an n - 1 words can be defined

w1 = a2 a3 … an a1 , w2 = a3 a4 … a1 a2 , … , wk-1 = an a1 … an-1 , obtained from one another by cyclic shifts. On the set of all sn words we introduce an equivalence relation: we declare two words equivalent if one is obtained from the other by a cyclic shift. We will be interested in the number of classes that contain exactly n words. This problem arises in the theory of synchronizing codes.

We will call a word w degenerate if the equivalence class containing w consists of less than n words. Let us call w periodic if there exists a word u and a natural number m such that w = u u … u (m times).

Theorem 3. A word w is periodic if and only if it is degenerate.

as u we can take a 1 a 2 … a p , and as m =

♦ It is clear that if w is periodic, then it is degenerate. Let w be degenerate. Let p be the minimal integer such that w = wp. Then if

w = a1 a2 … an , then wp = a1+p a2+p … an+p (indices modulo n). From here we get that in n p . (It is easy to see that p n). ♦ Wallpaper

significant through M(d) - the number of squares that contain d words. From the previous we have

d n. Thus, the formula is valid∑ dM(d) = s n . d n

Let us apply the Möbius inversion formula for the case g(n) = sn , f(d) = dM(d). Then we get

nM(n) = ∑ µ (d)s n d d n

∑ µ (d)sn d

Thus, M(n) is the number we are interested in. If n = p is a prime number, then

− s)

There is a multiplicative version of the Möbius inversion. Fair

Theorem 4. Let f(n) and g(n) be functions of a natural argument related accordingly

wearing

f(n) = ∏g(d)

µ(n

g(n) = ∏f(d)

And conversely, from (5) follows (4).

Using the Möbius inversion formula, one can solve the practically important problem of the number of irreducible polynomials of a fixed degree over a finite field. Let GF(q) be a field of q elements and m be a natural number. Then for the number

Φ m (q) of irreducible polynomials over the field GF(q) the following formula holds:

Let us present a table of the first few values of the function Φ m (2)


Φ m (2)

§ 5. Permanents and their application to enumerative ones

1. Permanents are used to solve many combinatorial problems. Consider the numeric matrix

A = (ai, j), i = 1, n, j = 1, m, n ≤ m

The permanent matrix A (designation - per A) is determined by the equality

per A = ∑			a 2 j L a nj
(j1 ,K , jn )
(j1 ,K , jn )

where the summation is performed over all n-permutations of m elements 1, 2, m. In other words, the permanent of the matrix is equal to the sum of the products of the elements taken one from each row and different columns.

From formula (1) some obvious properties of the permanent follow, similar to the properties of the determinant for square matrices.

1. If one of the lines(n× m) matrix A (n ≤ m) consists of zeros, then per A = 0. For n = m the same is true for the columns.

2. When all elements of one of the rows of matrix A are multiplied by a certain number, the value of permanent A is multiplied by the same number.

3. A permanent does not change when its rows and columns are rearranged.

Let us denote by Aij the matrix obtained from A by deleting the i-th row and j-th column.

4. The formula for decomposing the permanent in the i-th row is valid: per A = ai1 per Ai1 + ai2 per Ai2 + ... + aim per Aim (2)

thus, many properties of permanents are similar to those of determinants.

However, the main property of determinants det(A B) = detA detB is not satisfied for permanents, and this circumstance makes their calculation very difficult.


For example,


	2, per


However, 4 = per		≠per

Let us consider one of the most important applications of the concept of permanent in combinatorial problems.

dachas Let X = (x1, xm) be a finite set, and X1, …, Xn be a system of subsets

In this case, the element xi is said to represent the set Xi. The need to find a system of different representatives arises when solving many applied problems. Consider the following coding problem. Let there be some proposal, i.e. an ordered set of words in some alphabet. It is required to encode this sentence so that each word is assigned one letter, and this letter must be part of this word, and different letters must correspond to different words.

Example: The sentence a bc ab d abe c de cd e can be encoded as abecd. At the same time, the sentence ab ab bc abc bcd cannot be encoded in this way, since the first four words together contain only three letters.

For a system of sets X1 , … , Xn we define incidence matrix A = (aij), i = 1, n,


	1 if xi
a ij =
	0 otherwise.
Fair
Theorem 1. Let A = (aij), i =		(n ≤ m) incidence matrix
Theorem 1. Let A = (aij), i =		(n ≤ m) incidence matrix

sets X1, …, Xn, where Xi X, i = 1, n, X = (x1, …, xm). Then for the number of systems

personal representatives R(X1 , … , Xn ) of the sets X1 , … , Xn the following equality holds:

R(X1 , … , Xn ) = per A

♦ Indeed, since in matrix A the element aij = 1, if xj Xi and aij = 0,

if xj

K, xi

) elements X is a system of various pre-

Xi, then the set (xi

suffixes for X1 , … , Xn

if and only if a1i

K ,a ni

cops a1i

K ,a ni

are in different columns of matrix A. Let’s sum up the numbers

a1i ,K ,a ni

over all n-permutations of elements 1, 2, …, m. Then we get from one hundred

rons, the number of systems of different representatives for X1, ..., Xn, and on the other hand, the value of the per-

manenta matrix A. ♦

a 1i 1 a 2i 2 L a ni n

Consequence. A system of different representatives for X1, …, Xn exists if and only if for the corresponding matrix incident A is satisfied:

Since in formula (1) there are m(m - 1) ... (m - n +1) terms, calculating the permanent based on the definition is difficult. Let us present a general formula for this purpose.

2. Let us limit ourselves to considering square numerical matrices A = (aij), i, j = 1, n.

Then per A = ∑

(i1 ,K ,in )

where the sum extends over all permutations i1 , … , in elements

1, 2, … , n. Let us apply the inclusion-exclusion formula to calculate the permanent of matrix A. We assign to each set i1, ..., in a weight equal to a1i 1,K,a ni n.

This means that the permanent A is the sum of the weights of those sets that correspond to the permutations. Let us introduce n properties P1 , … , Pn on the set of all collections i1 , i2 , … , in of 1, 2, … , n, where the property Pi means that there is no element i in the collection i1 , … , in. Thus, the permanent A is the sum of the weights of the sets i1, ..., in, which do not have any of the properties P1, ..., Pn. It remains to determine the sum of weights W(Pi 1 ,K , Pi k ) of sets having k properties

Pi 1 ,K , Pi k . We have for the sum of the weights W(0) of all sets i1 , … , ik .
W(0) = ∑		K, ani	= (a 11 + L + a 1n )(a 21 + L + a 2n ) L (a n1 + L + a nn )
i1 ,K ,in
i1 ,K ,in

W(N(Pi )) =		a1i ,K ,a ni		= (a 11 + L + a 1i	L + a1n )L (a n1 + L a ni + L + a nn ) (9)

	≠i

where the ^ sign above an element of matrix A means that this element should be omitted. Similarly for sij (i< j) имеем


W(N(Pi , Pj )) = (a11 + L + a1i	L+a 1j	L + a1n )L (a n1 + L a ni + L + a nj + L + a nn ) (10)

Now, using the inclusion-exclusion formula, we obtain the Raiser formula for permanent A:


per A = ∏ i n = 1 (ai1 + L + ain ) − ∑∏ k n = 1 (a k1 + L + a ki + L + a kn )+ L +

+ (− 1)s	∑∏n
+ (− 1)s	∑∏n	(a k1 + L + a ki1	L+a ki	L +a kn ) +L
	1≤ i1< L < is ≤ k n= 1

The calculation of the permanent using the Raiser formula can be organized in such a way that it requires

(2n - 1)(n - 4) multiplications and (2n - 2)(n + 1) additions. Although this value grows quickly as n increases, this formula provides the most efficient way to calculate permanents.

3. Let us now clarify the question of the conditions for the permanent (0, 1) matrix to be equal to zero. Let us restrict ourselves to the case of a square matrix.

Theorem 2. Let A = (aij ), i, j = 1, n be a (0, 1) matrix of order n. Then

per A= 0 if and only if A contains a submatrix of zeros of size s × t, where s + t = n + 1.

♦ Let such a zero submatrix exist in A. Since the permanent does not change due to permutations of rows and columns, we can assume that this submatrix is located in the lower left corner, i.e.

where O - (s × t) is a matrix of zeros, submatrix B has size (n - s) × t. Each member of permanent A must contain one element from the first t columns. Therefore, if we look for a positive term of the permanent, then the elements of these columns must belong to pairwise different rows with numbers 1, 2, ..., n - s. However n - s = t - 1< t и поэтому данное условие выполнить нельзя, т.е. per A = 0.

Let now per A = 0. We prove the theorem by induction on n. For n = 1 the statement is obvious (A = (0)). Let it be true for all orders less than n. If A is a zero matrix of order n, then the statement is obvious. If A is not a zero matrix, then let aij = 1. Let us write the decomposition of A along row i:

per A = ai1 Ai1 + … + ain Ain

Since per A = 0, then per Aij = 0. But Aij has size (n - 1) × (n - 1) and by the induction hypothesis there is a submatrix of zeros of size

s1 × t1, with s1 + t1 = n - 1 + 1 = n. Let's rearrange the rows and columns so that this zero submatrix is in the lower left corner:


A → B =

where O is the zero submatrix of size s1 × t1, s1 + t1 = n, C - has size (n - s1) × t1, D -

has size s1 × (n - t) . This means that matrices C and D are square and have order (t1 × t1) and (s1 × s1), respectively. According to the definition of a permanent, we have per B = per A and,

per B = per C per D and therefore from per A = 0 it follows that either per C = 0 or per D = 0.

Let per C = 0. By the induction hypothesis, there is a zero submatrix of size

u × v, where u + v = t1 + 1. Let it be located in rows with numbers i1, …, iu and columns with numbers j1, …, jv. Consider a submatrix B consisting of rows

i1, …, iu, t1 + 1, …, n and columns j1, …, jv. This is a zero submatrix of size (u + n - t1) × v,

where u + n - t1 + v = n + +1. So, matrix B contains a zero submatrix of size s × t, where s + t = n + 1. Since matrices A and B differ in the permutation of rows and columns, the theorem is proven. ♦

Let us now consider an important special case of the matrix A. Let us denote by A(k, n) a matrix of 0.1 elements of size n × n with k ones for each row and each column (k > 0).

Theorem 3. For any matrix A(k, n) per A(k, n) > 0.

♦ Let us assume the opposite, that per A(k, n) = 0. Then, by Theorem 2, there exists a zero-

submatrix of size s × t, where s + t = n + 1. Then, rearranging the rows and columns of the matrix A(k, n) we obtain the matrix

where O is the zero (s × t) matrix.

Let's count the number of ones in matrices B and D. Since A(k, n) has k ones in each row and each column, then there are exactly k ones in each column of B and each row of D

units. There are n k units in total in A(k, n), so nk ≥ tk + sk = (t + s)n. This way

som, n ≥ t + s, which is impossible, because s + t = n + 1 From this contradiction it follows that

validity of the statement. ♦ It is proved in a similar way

Theorem 3a. Let A be a (0,1) matrix of size n× m (n≤ m). Then perA = 0 if and only if it contains a zero submatrix of size s×t, where s+t=m+1.

4. Let us now consider the application of the issues under consideration to the construction of la-

Tina squares. Latin (n × m)-rectangle over the set X=(x1 ,…,xm )

is called an (n× m) -matrix of elements X, in which each row is an n-permutation of X, and each column is an m-permutation of the set X. For n=m, the Latin rectangle is called Latin square.

It is clear that for n=1 the number of Latin 1×m rectangles is equal to m!. When n=2, after the first row is selected, any permutation can be taken as the second row.

new product that contradicts the chosen one. The number of such permutations is Dm, so the number 2× m is

of Latin rectangles is equal to m! Dm.

A natural question arises in connection with the inductive construction of Latin squares. Let us construct a Latin (n× m)-rectangle (n< m). Можно ли его расширить до ((n+1)× m) -прямоугольника добавлением (n+1)-й строки?

Fair

Theorem 4. Every Latin (n× m)-rectangle n

♦ Let X=(x1,…,xm) and an L-Latin (n×m)-rectangle with elements from X. Consider a set of sets A1,…,Am where Ai are the elements of the i-th column of the Latin rectangle L. Let A be incidence matrix of the set system A1 ,… ,Am . It has size m×m, and each row of matrix A contains exactly n ones, since Ai = n, i = 1, m. Each element xi X can appear in the columns of L no more than m times, otherwise there would be a row in which this element appears twice. Total number of elements

L is equal to m n, so each element xi X appears exactly n times in the columns. It follows that each column of matrix A contains exactly n ones. Let us now consider the matrix A obtained by replacing each one with a zero and each zero with a one.

Matrix A is the incidence matrix of the system of sets X1, …, Xn, where Xi = X\Ai,

i = 1, m. It contains m - n units in each row and in each column. By theorem

> 0. Let ai1

…a mi

≠ 0 . Then we have xi X1 ,K , xi

Xm and all elements

xi ,K ,xi

pairwise different. Line

xi ,K ,xi

can be taken as the (n + 1)th

for a Latin (n × m)-rectangle L. Continuing this procedure, we obtain a Latin

sky square. ♦

Let us denote l n - the number of Latin squares of order n, with elements from the set X = (1, 2, ..., n), in which the elements of the first column and first row are in natural order. Here is a table of several known values of the number l n:

5. A matrix A = (aij) of size n × n with real, non-negative elements is called twice stochastic, If