Static modeling method of Monte Carlo formulas. How Monte Carlo simulation is performed. There are no concepts in the “object-model” relationship

Encyclopedic YouTube

1 / 5

✪ RuleOfThumb - Monte Carlo Method

✪ Dmitry Kazakov - Quarks

✪ [Colloquium]: The brilliance and poverty of mathematical methods in applied research

✪ Lecture 1: Calculation errors

✪ Elena Brown - The Myth of Richard lll

Subtitles

Story

Buffon's algorithm for determining Pi

	Number of throws	Number of intersections	Needle length	Distance between lines	Rotation	Pi value	Error
First try	500	236	3	4	absent	3.1780	+3,6⋅10 -2
Second try	530	253	3	4	present	3.1423	+7,0⋅10 -4
Third try	590	939	5	2	present	3.1416	+4,7⋅10 -5

Comments:

Relationship between stochastic processes and differential equations

The creation of the mathematical apparatus of stochastic methods began at the end of the 19th century. In 1899, Lord Rayleigh showed that a one-dimensional random walk on an infinite lattice could give an approximate solution to a type of parabolic differential equation. Andrei Nikolaevich Kolmogorov in 1931 gave a big impetus to the development of stochastic approaches to solving various mathematical problems, since he was able to prove that Markov chains are related to certain integro-differential equations. In 1933, Ivan Georgievich Petrovsky showed that the random walk forming a Markov chain is asymptotically related to the solution of an elliptic partial differential equation. After these discoveries, it became clear that stochastic processes can be described by differential equations and, accordingly, studied using well-developed mathematical methods for solving these equations at that time.

Birth of the Monte Carlo method at Los Alamos

The idea was developed by Ulam, who, while playing solitaire while convalescing from illness, wondered what the likelihood was that the solitaire game would work out. Instead of using the usual combinatorics considerations for such problems, Ulam suggested that one could simply perform the experiment a large number of times and, by counting the number of successful outcomes, estimate the probability. He also proposed using computers for Monte Carlo calculations.

The advent of the first electronic computers, which could generate pseudorandom numbers at high speed, dramatically expanded the range of problems for which the stochastic approach turned out to be more effective than other mathematical methods. After this, a big breakthrough occurred, and the Monte Carlo method was used in many problems, but its use was not always justified due to the large number of calculations required to obtain an answer with a given accuracy.

The birth year of the Monte Carlo method is considered to be 1949, when the article by Metropolis and Ulam “The Monte Carlo Method” was published. The name of the method comes from the name of a commune in the Principality of Monaco, widely known for its numerous casinos, since roulette is one of the most widely known random number generators. Stanislaw Ulam writes in his autobiography, Adventures of a Mathematician, that the name was suggested by Nicholas Metropolis in honor of his uncle, who was a gambler.

Further development and modernity

Monte Carlo integration

Suppose we need to take the integral of some function. Let's use an informal geometric description of the integral and understand it as the area under the graph of this function.

To determine this area, you can use one of the usual numerical integration methods: divide the segment into subsegments, calculate the area under the graph of the function on each of them and add. Let's assume that for the function presented in Figure 2, it is enough to split it into 25 segments and, therefore, calculate 25 function values. Let's imagine now that we are dealing with n (\displaystyle n)-dimensional function. Then we need 25 n (\displaystyle 25^(n)) segments and the same number of calculations of the function value. When the function dimension is greater than 10, the problem becomes enormous. Since high-dimensional spaces occur, in particular, in string theory problems, as well as many other physical problems where there are systems with many degrees of freedom, it is necessary to have a solution method whose computational complexity does not depend so strongly on the dimension. This is precisely the property that the Monte Carlo method has.

Conventional Monte Carlo integration algorithm

Suppose you need to calculate a definite integral ∫ a b f (x) d x (\displaystyle \int \limits _(a)^(b)f(x)\,dx)

Consider the random variable u (\displaystyle u), uniformly distributed on the integration interval. Then it will also be a random variable, and its mathematical expectation is expressed as
E f (u) = ∫ a b f (x) φ (x) d x (\displaystyle \mathbb (E) f(u)=\int \limits _(a)^(b)f(x)\varphi (x) \,dx), Where φ (x) (\displaystyle \varphi (x))- distribution density of a random variable u (\displaystyle u), equal 1 b − a (\displaystyle (\frac (1)(b-a))) Location on [ a , b ] (\displaystyle ).

Thus, the required integral is expressed as
∫ a b f (x) d x = (b − a) E f (u) (\displaystyle \int \limits _(a)^(b)f(x)\,dx=(b-a)\mathbb (E) f( u)).

But the mathematical expectation of a random variable f (u) (\displaystyle f(u)) can be easily estimated by simulating this random variable and calculating the sample mean.

So, let's quit N (\displaystyle N) points evenly distributed over [ a , b ] (\displaystyle ), for each point u i (\displaystyle u_(i)) calculate f (u i) (\displaystyle f(u_(i))). Then we calculate the sample mean: 1 N ∑ i = 1 N f (u i) (\displaystyle (\frac (1)(N))\sum _(i=1)^(N)f(u_(i))).

As a result, we obtain an estimate of the integral: ∫ a b f (x) d x ≈ b − a N ∑ i = 1 N f (u i) (\displaystyle \int \limits _(a)^(b)f(x)\,dx\approx (\frac (b-a) (N))\sum _(i=1)^(N)f(u_(i)))

The accuracy of the estimate depends only on the number of points N (\displaystyle N).

This method also has a geometric interpretation. It is very similar to the deterministic method described above, with the difference that instead of uniformly dividing the integration region into small intervals and summing the areas of the resulting “columns”, we throw random points at the integration region, on each of which we build the same “column”, determining its width How b − a N (\displaystyle (\frac (b-a)(N))), and sum up their areas.

Geometric Monte Carlo integration algorithm

To determine the area under the graph of a function, you can use the following stochastic algorithm:

For a small number of dimensions of the integrable function, the performance of Monte Carlo integration is much lower than the performance of deterministic methods. However, in some cases, when the function is specified implicitly, and it is necessary to determine the region specified in the form of complex inequalities, the stochastic method may be more preferable.

Using significance sampling

With the same number of random points, the accuracy of calculations can be increased by bringing the area limiting the desired function closer to the function itself. To do this, it is necessary to use random variables with a distribution whose shape is as close as possible to the shape of the function being integrated. This is the basis of one of the methods for improving convergence in Monte Carlo calculations: significance sampling.

Optimization

Variations of the Monte Carlo method can be used to solve optimization problems. For example, the simulated annealing algorithm.

Application in physics

Computer simulation plays an important role in modern physics and the Monte Carlo method is one of the most common in many fields from quantum physics to solid state physics, plasma physics and astrophysics.

Metropolis algorithm

Traditionally, the Monte Carlo method has been used to determine various physical parameters of systems in a state of thermodynamic equilibrium. Let us assume that there is a set of possible states of a physical system S (\displaystyle S). To determine the average value A ¯ (\displaystyle (\overline (A))) some size A (\displaystyle A) needs to be calculated A ¯ = ∑ S A (S) P (S) (\displaystyle (\overline (A))=\sum _(S)A(S)P(S)), where the summation is performed over all states S (\displaystyle S) from W (S) (\displaystyle W(S)), P (S) (\displaystyle P(S))- state probability S (\displaystyle S).

Dynamic (kinetic) formulation

Direct Monte Carlo Simulation

Direct Monte Carlo modeling of any physical process involves modeling the behavior of individual elementary parts of a physical system. In essence, this direct modeling is close to solving the problem from first principles, but usually, to speed up calculations, the use of some physical approximations is allowed. An example is the calculation of various processes using the molecular dynamics method: on the one hand, the system is described through the behavior of its elementary components, on the other hand, the interaction potential used is often empirical.

Examples of direct Monte Carlo simulation:

• Modeling of irradiation of solids by ions in the binary collision approximation.
• Direct Monte Carlo simulation of rarefied gases.
• Most kinetic Monte Carlo models are direct (in particular, the study of molecular beam epitaxy).

Quantum Monte Carlo method

The quantum Monte Carlo method is widely used to study complex molecules and solids. This name combines several different methods. The first of them is the variational Monte Carlo method, which is essentially the numerical integration of multidimensional integrals that arise when solving the Schrödinger equation. Solving a problem involving 1000 electrons requires taking 3000-dimensional integrals, and for solving such problems the Monte Carlo method has a huge performance advantage over other numerical integration methods. Another variation of the Monte Carlo method is the diffusion Monte Carlo method.

Lecture 5.

Monte Carlo method

Topic 3. Queuing processes in economic systems

1. Introductory remarks. 1

2. General scheme of the Monte Carlo method. 2

3. An example of calculating a queuing system using the Monte Carlo method. 4

Test questions... 5

1. Introductory remarks

The method of statistical modeling on a computer is the main method of obtaining results using simulation models of stochastic systems, using limit theorems of probability theory as a theoretical basis. The basis is the Monte Carlo statistical test method.

The Monte Carlo method can be defined as a method of simulating random variables in order to calculate the characteristics of their distributions. As a rule, it is assumed that modeling is carried out using electronic computers (computers), although in some cases success can be achieved using devices such as a tape measure, pencil and paper.

The term "Monte Carlo method" (coined by J. von Neumann and in the 1940s) refers to the simulation of processes using a random number generator. The term Monte Carlo (a city widely known for its casinos) comes from the fact that the "number of odds" (Monte Carlo simulation techniques) were used for the purpose of finding integrals of complex equations in the development of the first nuclear bombs (quantum mechanics integrals). By generating large samples of random numbers from, for example, several distributions, the integrals of these (complex) distributions can be approximated from the (generated) data.

The emergence of the idea of ​​using random phenomena in the field of approximate calculations is usually attributed to 1878, when Hall's work appeared on determining the numbers p by randomly throwing a needle onto paper marked with parallel lines. The essence of the matter is to experimentally reproduce an event, the probability of which is expressed through the number p, and to approximately estimate this probability.

Domestic works on the Monte Carlo method appeared in the years. Over two decades, an extensive bibliography using the Monte Carlo method has been accumulated, which includes more than 2000 titles. Moreover, even a quick glance at the titles of works allows one to draw a conclusion about the applicability of the Monte Carlo method for solving applied problems from a large number of fields of science and technology.

Initially, the Monte Carlo method was used mainly to solve problems in neutron physics, where traditional numerical methods turned out to be of little use. Further, his influence spread to a wide class of problems in statistical physics, very different in content. The branches of science where the Monte Carlo method is increasingly used include problems in the theory of queuing, problems in game theory and mathematical economics, problems in the theory of message transmission in the presence of interference, and a number of others.

The Monte Carlo method has had and continues to have a significant influence on the development of the method of computational mathematics (for example, the development of numerical integration methods) and, in solving many problems, is successfully combined with other computational methods and complements them. Its use is justified primarily in those problems that allow a probabilistic theoretical description. This is explained both by the naturalness of obtaining an answer with a certain given probability in problems with probable content, and by a significant simplification of the solution procedure. The difficulty of solving a particular problem on a computer is determined to a large extent by the difficulty of translating it into the “language” of a machine. The creation of automatic programming languages ​​has significantly simplified one of the stages of this work. Therefore, the most difficult stages at present are: a mathematical description of the phenomenon under study, the necessary simplifications of the problem, the selection of a suitable numerical method, the study of its error and the recording of the algorithm. In cases where there is a probability-theoretic description of the problem, the use of the Monte Carlo method can significantly simplify the mentioned intermediate stages. However, as will follow from what follows, in many cases it is also useful for strictly deterministic problems to build a probabilistic model (randomize the original problem) in order to further use the Monte Carlo method.

2. General scheme of the Monte Carlo method

Suppose we need to calculate some unknown quantity m, and we want to do this by considering a random variable such that its mathematical expectation is M, = m. Let the variance of this random variable be D = b.

Let's consider N random independent variables,,..., whose distributions coincide with the distribution of the random variable under consideration ξ..gif" width="247" height="48">

The last relation can be rewritten as

The resulting formula gives a method for calculating m and an estimate of the error of this method.

The essence of using the Monte Carlo method is to determine the results based on statistics obtained at the time of making a certain decision.

For example. Let E1 and E2 be the only two possible implementations of some random process, and p1 is the probability of outcome E1, and p2 = 1 – p1 is the probability of outcome E2. To determine which of the two events, e1 or E2, takes place in this case, we take a random number in the interval between 0 and 1, uniformly distributed in the interval (0, 1), and perform a test. Outcome E1 will occur if , and outcome E2 will occur otherwise.

Thus, the reliability of the results obtained using the Monte Carlo method is decisively determined by the quality of the random number generator.

To obtain random numbers on a computer, generation methods are used, which are usually based on repeating a certain operation many times. The sequence obtained in this way is more appropriately called pseudorandom numbers, since the generated sequence is periodic and, starting from a certain moment, the numbers will begin to repeat. This follows from the fact that only a finite number of different numbers can be written in computer code. Consequently, in the end one of the generated numbers γ1 will coincide with one of the previous members of the sequence γL. And since generation is carried out according to a formula of the form

γк+1 = F(γk),

from this moment on, the remaining members of the sequence will be repeated.

The use of uniformly distributed random numbers forms the basis of Monte Carlo simulation. We can say that if a certain random variable was determined using the Monte Carlo method, then a sequence of uniformly distributed random numbers was used to calculate it.

Uniformly distributed random numbers range from 0 to 1 and are selected at random according to the distribution function

F(x) = Рr(Х< х} = х, .

With this distribution, the occurrence of any values ​​of a random variable in the interval (0, 1) is equally plausible. Here Pr(X< х} - вероятность того, что случайная величина X примет значение меньше х.

The main method of obtaining random numbers is their modulo generation. Let m, a, c, x0 be integers such that m > x0 and a, c, x0 > 0. The pseudo-random number xi from the sequence (xi) is obtained using the recurrence relation

xi = a xi-1 + c (mod m).

The stochastic characteristics of the numbers generated depend decisively on the choice of m, a and c. Their poor choice leads to erroneous results in Monte Carlo simulations.

Numerical simulations often require a large number of random numbers. Therefore, the period of the sequence of generated random numbers, after which the sequence begins to repeat, must be quite large. It must be significantly larger than the number of random numbers required for modeling, otherwise the results obtained will be distorted.

Most computers and software packages contain a random number generator. However, most statistical tests show correlation between the resulting random numbers.

There is a quick test that you can use to check each generator. The quality of a random number generator can be demonstrated by filling a completely d-dimensional lattice (for example, two- or three-dimensional). A good generator should fill the entire space of the hypercube.

Another approximate way to check the uniformity of the distribution of N random numbers xi is to calculate their mathematical expectation and variance. According to this criterion, for uniform distribution the following conditions must be met:

There are many statistical tests that can be used to test whether a sequence will be random. The spectral criterion is considered the most accurate. For example, a very common criterion called the KS criterion, or the Kolmogorov-Smirnov criterion. The check shows that, for example, the random number generator in Excel spreadsheets does not meet this criterion.

In practice, the main problem is to build a simple and reliable random number generator that you can use in your programs. To do this, the following procedure is suggested.

At the beginning of the program, the entire variable X is assigned a certain value X0. Then random numbers are generated according to the rule

X = (aX + c) mod m. (1)

The selection of parameters should be made using the following basic principles.

1. The initial number X0 can be chosen arbitrarily. If the program is used several times and each time requires different sources of random numbers, you can, for example, assign X0 the value of the X last obtained in the previous run.

2. The number m must be large, for example, 230 (since it is this number that determines the period of the generated pseudo-random sequence).

3.If m is a power of two, choose a such that a mod8 = 5. If m is a power of ten, choose a such that a mod10 = 21. This choice ensures that the random number generator will produce all m possible values ​​before they start repeating.

4.Multiplier A the preferred choice is between 0.01m and 0.99m, and its binary or decimal digits should not have a simple regular structure. The multiplier must pass the spectral criterion and, preferably, several other criteria.

5.If a is a good multiplier, the value of c is not significant, except that c should not have a common multiplier with m if m is the computer word size. You can, for example, choose c = 1 or c = a.

6. You can generate no more than m/1000 random numbers. After this, a new circuit must be used, for example a new multiplier A.

The listed rules mainly relate to machine programming language. For a high-level programming language, such as C++, another option (1) is often used: a prime number m is selected that is close to the largest easily computable integer, the value of a is set to be equal to the antiderivative root of m, and c is taken to be zero. For example, you can take a= 48271 and t =

3. An example of calculating a queuing system using the Monte Carlo method

Let's consider the simplest queuing system (QS), which consists of n lines (otherwise called channels or service points). At random times, requests are received into the system. Each application arrives on line No. 1. If at the time of receipt of the appearance Tk this line is free, the application is serviced at time t3 (line busy time). If the line is busy, the request is instantly transferred to line No. 2, etc. If all n lines are currently busy, then the system issues a refusal.

A natural task is to determine the characteristics of a given system by which its effectiveness can be assessed: the average waiting time for service, the percentage of system downtime, the average queue length, etc.

For such systems, practically the only calculation method is the Monte Carlo method.

https://pandia.ru/text/78/241/images/image013_34.gif" width="373" height="257">

Algorithms are used to obtain random numbers on a computer, therefore such sequences, which are essentially deterministic, are called pseudorandom. The computer operates with n-bit numbers, therefore, instead of a continuous collection of uniform random numbers of the interval (0,1), a discrete sequence of 2n random numbers of the same interval is used on the computer - the distribution law of such a discrete sequence is called quasi-uniform distribution.

Requirements for an ideal random number generator:

1. The sequence must consist of quasi-uniformly distributed numbers.

2. The numbers must be independent.

3. Random number sequences must be reproducible.

4. Sequences must have non-repeating numbers.

5. Sequences should be obtained with minimal computational resources.

The greatest application in computer modeling practice for generating sequences of pseudo-random numbers is found in algorithms of the form:

which are recurrent relations of the first order.

For example. x0 = 0.2152, (x0)2=0, x1 = 0.6311, (x1)2=0, x2=0.8287, etc.

The disadvantage of such methods is the presence of correlation between the numbers in the sequence, and sometimes there is no randomness at all, for example:

x0 = 0.4500, (x0)2=0, x1 = 0.2500, (x1)2=0, x2=0.2500, etc.

Congruent procedures for generating pseudorandom sequences have become widely used.

Two integers a and b are congruent (comparable) modulo m, where m is an integer, if and only if there is an integer k such that a-b=km.

1984º4 (mod 10), 5008º8 (mod 103).

Most congruent random number generation procedures are based on the following formula:

where are non-negative integers.

Using the integers of the sequence (Xi), we can construct a sequence (xi)=(Xi/M) of rational numbers from the unit interval (0,1).

Before modeling, the random number generators used must undergo thorough preliminary testing for uniformity, stochasticity and independence of the resulting sequences of random numbers.

Methods for improving the quality of random number sequences:

1. Using recurrent formulas of order r:

But the use of this method leads to an increase in the cost of computing resources to obtain numbers.

2. Perturbation method:

.

5. Modeling random impacts on systems

1. It is necessary to realize a random event A that occurs with a given probability p. Let us define A as the event that the selected value xi of a random variable uniformly distributed over the interval (0,1) satisfies the inequality:

Then the probability of event A will be https://pandia.ru/text/78/241/images/image019_31.gif" width="103" height="25">,

The test simulation procedure in this case consists of sequential comparison of random numbers xi with the values ​​of lr. If the condition is met, the outcome of the test is the event Am.

3. Consider independent events A and B with probabilities of occurrence pA and pB. Possible outcomes of joint trials in this case will be events AB, with probabilities pArB, (1-pA)pB, pA(1-pB), (1-pA)(1-pB). To simulate joint tests, two variants of the procedure can be used:

Consistent execution of the procedure discussed in paragraph 1.

Determination of one of the outcomes of AB, by lot with the corresponding probabilities, i.e., the procedure discussed in paragraph 2.

The first option will require two numbers xi and two comparisons. With the second option, you can get by with one number xi, but more comparisons may be required. From the point of view of convenience of constructing a modeling algorithm and saving the number of operations and computer memory, the first option is more preferable.

4. Events A and B are dependent and occur with probabilities pA and pB. Let us denote by pA(B) the conditional probability of the occurrence of event B, provided that event A has occurred.

Control questions

1) How can you define the Monte Carlo method?

2) Practical significance of the Monte Carlo method.

3) General scheme of the Monte Carlo method.

4) An example of calculating a queuing system using the Monte Carlo method.

5) Methods for generating random numbers.

6) What are the requirements for an ideal random number generator?

7) Methods for improving the quality of random number sequences.

is an integral part of any decision we make. We are constantly faced with uncertainty, ambiguity and variability. And even with unprecedented access to information, we cannot accurately predict the future. Monte Carlo simulation (also known as the Monte Carlo method) allows you to consider all the possible consequences of your decisions and evaluate the impact of risk, allowing you to make better decisions under conditions of uncertainty.

What is Monte Carlo Simulation?
Monte Carlo simulation is an automated mathematical technique designed to incorporate risk into the quantitative analysis and decision-making process. This methodology is used by professionals in various fields such as finance, project management, energy, manufacturing, engineering, R&D, insurance, oil and gas, transportation and environmental protection.

Each time in the process of choosing a course of further action, Monte Carlo simulation allows the decision maker to consider a whole range of possible consequences and assess the likelihood of their occurrence. This method demonstrates the possibilities that lie at opposite ends of the spectrum (the results of going all-in and taking the most conservative measures), as well as the likely consequences of moderate decisions.

This method was first used by scientists involved in the development of the atomic bomb; it was named after Monte Carlo, a resort in Monaco famous for its casinos. Having become widespread during the Second World War, the Monte Carlo method began to be used to simulate all kinds of physical and theoretical systems.

View reviews
Douglas Hubbard
Hubbard Decision Research
Time: 00:35 sec

“Monte Carlo simulation is the only way to analyze critical decisions under conditions of uncertainty.”

John Zhao
Suncor Energy
Time: 02:36 min

“Conducting Monte Carlo simulations to estimate capital costs has become [at Suncor] a requirement for any major project.”

How Monte Carlo Simulation is Performed
Within the Monte Carlo method, risk analysis is performed using models of possible outcomes. When creating such models, any factor that is characterized by uncertainty is replaced by a range of values ​​- a probability distribution. The results are then calculated multiple times, each time using a different set of random probability function values. Sometimes, to complete a simulation, it may be necessary to make thousands or even tens of thousands of recalculations, depending on the number of uncertainties and the ranges set for them. Monte Carlo simulation allows one to obtain distributions of values ​​of possible consequences.

When using probability distributions, variables can have different probabilities of different consequences occurring. Probability distributions are a much more realistic way of describing the uncertainty of variables in the risk analysis process. The most common probability distributions are listed below.

Normal distribution(or "Baussian curve"). To describe the deviation from the mean, the user defines the mean or expected value and the standard deviation. Values ​​located in the middle, next to the average, are characterized by the highest probability. The normal distribution is symmetrical and describes many common phenomena - for example, the height of people. Examples of variables that are described by normal distributions include inflation rates and energy prices.

Lognormal distribution. The values ​​are positively skewed and, unlike a normal distribution, are asymmetrical. This distribution is used to reflect quantities that do not fall below zero, but can take on unlimited positive values. Examples of variables described by lognormal distributions include real estate values, stock prices, and oil reserves.

Uniform distribution. All quantities can take one value or another with equal probability; the user simply determines the minimum and maximum. Examples of variables that may be uniformly distributed include production costs or revenues from future sales of a new product.

Triangular distribution. The user defines the minimum, most likely and maximum values. The values ​​located near the point of maximum probability have the highest probability. Variables that can be described by a triangular distribution include historical sales per unit time and inventory levels.

PERT distribution. The user defines the minimum, most likely and maximum values ​​- the same as with a triangular distribution. The values ​​located near the point of maximum probability have the highest probability. However, values ​​in the range between the most likely and the extreme values ​​are more likely to appear than with a triangular distribution, that is, there is no emphasis on the extreme values. An example of the use of the PERT distribution is to describe the duration of a task within a project management model.

Discrete distribution. The user determines specific values ​​from among the possible ones, as well as the probability of obtaining each of them. An example would be the outcome of a lawsuit: 20% chance of a favorable decision, 30% chance of a negative decision, 40% chance of an agreement between the parties and 10% chance of annulment of the trial.

In a Monte Carlo simulation, values ​​are selected randomly from the original probability distributions. Each sample of values ​​is called an iteration; the result obtained from the sample is recorded. During the modeling process, this procedure is performed hundreds or thousands of times, and the result is a probability distribution of possible consequences. Thus, Monte Carlo simulation provides a much more complete picture of possible events. It allows you to judge not only what can happen, but also what the likelihood of such an outcome is.

Monte Carlo simulation has a number of advantages over deterministic or point estimate analysis:

• Probabilistic results.The results show not only possible events, but also the likelihood of their occurrence.
• Graphic representation of results. The nature of the data obtained using the Monte Carlo method allows the creation of graphs of various consequences, as well as the probabilities of their occurrence. This is important when communicating results to other stakeholders.
• Sensitivity analysis. With few exceptions, deterministic analysis makes it difficult to determine which variable influences results most. When running a Monte Carlo simulation, it is easy to see which inputs have the greatest impact on the final results.
• Scenario analysis. In deterministic models, it is very difficult to simulate different combinations of quantities for different input values, and therefore assess the impact of truly different scenarios. Using the Monte Carlo method, analysts can determine exactly what inputs lead to certain values ​​and trace the occurrence of certain consequences. This is very important for further analysis.
• Correlation of source data. The Monte Carlo method allows you to model interdependent relationships between input variables. To obtain reliable information, it is necessary to imagine in which cases, when some factors increase, others correspondingly increase or decrease.

You can also improve your Monte Carlo simulation results by sampling using the Latin Hypercube method, which selects more accurately from the entire range of distribution functions.

Palisade Modeling Products
using the Monte Carlo method
The emergence of applications designed to work with spreadsheets on personal computers has opened up wide opportunities for specialists to use the Monte Carlo method when conducting analysis in everyday activities. Microsoft Excel is one of the most common spreadsheet analytical tools, and the program is Palisade's main plug-in for Excel, which allows you to perform Monte Carlo simulations. @RISK was first introduced for Lotus 1-2-3 on the DOS operating system in 1987 and immediately earned an excellent reputation for its accuracy, modeling flexibility and ease of use. The advent of Microsoft Project led to the creation of another logic application for applying the Monte Carlo method. His main task was to analyze the uncertainties and risks associated with managing large projects.

Statistical modeling is a basic modeling method that involves testing a model with a set of random signals with a given probability density. The goal is to statistically determine the output results. Statistical modeling is based on method Monte Carlo. Let us remember that imitation is used when other methods cannot be used.

Monte Carlo method

Let's consider the Monte Carlo method using the example of calculating an integral, the value of which cannot be found analytically.

Task 1. Find the value of the integral:

In Fig. 1.1 shows the graph of the function f (x). To calculate the value of the integral of this function means to find the area under this graph.

Rice. 1.1

We limit the curve from above, to the right and to the left. We randomly distribute points in the search rectangle. Let us denote by N 1 the number of points accepted for testing (that is, falling into a rectangle, these points are shown in Fig. 1.1 in red and blue), and through N 2 - the number of points under the curve, that is, falling into the shaded area under the function (these points are shown in red in Fig. 1.1). Then it is natural to assume that the number of points falling under the curve in relation to the total number of points is proportional to the area under the curve (the value of the integral) in relation to the area of ​​the test rectangle. Mathematically this can be expressed as follows:

These reasonings, of course, are statistical and the more correct the greater the number of test points we take.

A fragment of the Monte Carlo method algorithm in the form of a block diagram looks as shown in Fig. 1.2

Rice. 1.2

Values r 1 and r 2 in Fig. 1.2 are uniformly distributed random numbers from the intervals ( x 1 ; x 2) and ( c 1 ; c 2) accordingly.

The Monte Carlo method is extremely efficient and simple, but requires a "good" random number generator. The second problem in applying the method is determining the sample size, that is, the number of points required to provide a solution with a given accuracy. Experiments show that to increase accuracy by 10 times, the sample size needs to be increased by 100 times; that is, the accuracy is approximately proportional to the square root of the sample size:

Scheme for using the Monte Carlo method in studying systems with random parameters

Having built a model of a system with random parameters, input signals from a random number generator (RNG) are supplied to its input, as shown in Fig. 1.3 The RNG is designed in such a way that it produces evenly distributed random numbers r pp from the interval . Since some events may be more probable, others less probable, uniformly distributed random numbers from the generator are fed to a random number law converter (RLC), which converts them into given user of the probability distribution law, for example, the normal or exponential law. These converted random numbers x fed to the model input. The model processes the input signal x according to some law y = ts (x) and receives the output signal y, which is also random.

statistical modeling random variable

Rice. 1.3

Filters and counters are installed in the statistics accumulation block (BNStat). A filter (some logical condition) determines by value y, whether a certain event was realized in a specific experiment (the condition was fulfilled, f= 1) or not (the condition was not met, f= 0). If the event occurs, the event counter is incremented by one. If the event is not realized, then the counter value does not change. If you need to monitor several different types of events, then you will need several filters and counters for statistical modeling N i. A counter of the number of experiments is always kept - N.

Further relation N i To N, calculated in the block for calculating statistical characteristics (BVSH) using the Monte Carlo method, gives an estimate of the probability p i occurrence of an event i, that is, indicates the frequency of its occurrence in a series of N experiments. This allows us to draw conclusions about the statistical properties of the modeled object.

For example, event A occurred as a result of 200 experiments performed 50 times. This means, according to the Monte Carlo method, that the probability of an event occurring is: p A = 50/200 = 0.25. The probability that the event will not occur is, respectively, 1 - 0.25 = 0.75.

Please pay attention: when they talk about probability obtained experimentally, it is called frequency; the word probability is used when they want to emphasize that we are talking about a theoretical concept.

With a large number of experiments N the frequency of occurrence of an event, obtained experimentally, tends to the value of the theoretical probability of occurrence of the event.

In the reliability assessment block (RAB), the degree of reliability of statistical experimental data taken from the model is analyzed (taking into account the accuracy of the result e, specified by the user) and determine the number of statistical tests required for this. If fluctuations in the values ​​of the frequency of occurrence of events relative to the theoretical probability are less than the specified accuracy, then the experimental frequency is taken as the answer, otherwise the generation of random input influences continues, and the modeling process is repeated. With a small number of tests, the result may be unreliable. But the more tests, the more accurate the answer, according to the central limit theorem.

Note that the evaluation is carried out using the worst frequency. This provides reliable results for all measured characteristics of the model at once.

Example 1. Let's solve a simple problem. What is the probability of a coin landing heads up when dropped randomly from a height?

Let's start tossing a coin and recording the results of each throw (see Table 1.1).

Table 1.1.

Coin toss test results

We will calculate the frequency of heads as the ratio of the number of cases of heads to the total number of observations. Look in the table. 1.1 cases for N = 1, N = 2, N= 3 - at first the frequency values ​​cannot be called reliable. Let's try to build a dependence graph P o from N- and let's see how the frequency of heads changes depending on the number of experiments performed. Of course, different experiments will produce different tables and, therefore, different graphs. In Fig. 1.4 shows one of the options.

Rice. 1.4

Let's draw some conclusions.

• 1. It can be seen that at small values N, For example, N = 1, N = 2, N= 3 The answer cannot be trusted at all. For example, P o = 0 at N= 1, that is, the probability of getting heads in one throw is zero! Although everyone knows well that this is not so. That is, so far we have received a very rude answer. However, look at the graph: in progress savings information, the answer is slowly but surely approaching the correct one (it is highlighted with a dotted line). Fortunately, in this particular case, we know the correct answer: ideally, the probability of getting heads is 0.5 (in other, more complex problems, the answer, of course, will be unknown to us). Let's assume that we need to know the answer with precision e= 0.1. Let's draw two parallel lines, separated from the correct answer 0.5 by a distance of 0.1 (see Fig. 1.4). The width of the resulting corridor will be 0.2. As soon as the curve P O ( N) will enter this corridor in such a way that it will never leave it, you can stop and see for what value N it happened. That's what it is experimentally calculated critical meaning required number of experiments N kr e to determine the answer with accuracy e = 0.1; e- the neighborhood in our reasoning plays the role of a kind of precision tube. Please note that the answers P o (91), P o (92) and so on no longer change their values ​​much (see Fig. 1.4); at least the first digit after the decimal point, which we are obliged to trust according to the conditions of the problem, does not change.
• 2. The reason for this behavior of the curve is the action central ultimate theorems. For now, here we will formulate it in the simplest version: “The sum of random variables is a non-random quantity.” We used the average P o, which carries information about the sum of experiments, and therefore gradually this value becomes more and more reliable.
• 3. If you do this experiment again from the beginning, then, of course, its result will be a different type of random curve. And the answer will be different, although approximately the same. Let's conduct a whole series of such experiments (see Fig. 1.5). Such a series is called an ensemble of realizations. Which answer should you ultimately believe? After all, although they are close, they still differ. In practice, they act differently. The first option is to calculate the average of the responses over several implementations (see Table 1.2).

Rice. 1.5

We set up several experiments and determined each time how many experiments needed to be done, that is N cr e. 10 experiments were carried out, the results of which were summarized in table. 1.2 Based on the results of 10 experiments, the average value was calculated N cr e.

Table 1.2.

Experimental data on the required number of coin tosses to achieve accuracy e

Thus, after carrying out 10 implementations of different lengths, we determined that it is sufficient V average it was possible to make 1 realization with a length of 94 coin tosses.

Another important fact. Take a close look at the graph in Fig. 21.5. It shows 100 realizations - 100 red lines. Mark the abscissa on it N= 94 vertical bar. There is a certain percentage of red lines that did not have time to cross e-neighborhood, that is ( P exp - e ? P theory? P exp + e), and enter the corridor exactly up to the moment N= 94. Please note that there are 5 such lines. This means that 95 out of 100, that is, 95%, lines reliably entered the designated interval.

Thus, after carrying out 100 implementations, we achieved approximately 95% confidence in the experimentally obtained probability of heads, determining it with an accuracy of 0.1.

To compare the obtained result, let’s calculate the theoretical value N kr t theoretically. However, for this we will have to introduce the concept of confidence probability Q F, which shows how willing we are to believe the answer.

For example, when Q F= 0.95 we are ready to believe the answer in 95% of cases out of 100. It looks like: N cr t = k (Q F) · p· (1 - p) /e 2 where k (Q F) - Laplace coefficient, p- probability of getting heads, e- accuracy (confidence interval). In table 1.3 shows the values ​​of the theoretical value of the number of necessary experiments for different Q F(for accuracy e= 0.1 and probability p = 0.5).

Table 1.3.

Theoretical calculation of the required number of coin flips to achieve accuracy e= 0.1 when calculating the probability of getting heads

As you can see, the estimate we obtained for the length of the implementation, equal to 94 experiments, is very close to the theoretical one, equal to 96. Some discrepancy is explained by the fact that, apparently, 10 implementations are not enough for an accurate calculation N cr e. If you decide that you want a result that you should trust more, then change the confidence value. For example, the theory tells us that if there are 167 experiments, then only 1-2 lines from the ensemble will not be included in the proposed accuracy tube. But keep in mind, the number of experiments increases very quickly with increasing accuracy and reliability.

The second option used in practice is to carry out one implementation and increase received For her N cr uh V 2 times. This is considered a good guarantee of the accuracy of the answer (see Figure 1.6).

Rice. 1.6. Illustration of the experimental determination of N cr e using the “multiply by two” rule

If you look closely at ensemble random implementations, then we can find that the convergence of the frequency to the value of the theoretical probability occurs along a curve corresponding to the inverse quadratic dependence on the number of experiments (see Fig. 1.7).

Rice. 1.7

This actually works out this way in theory. If you change the specified accuracy e and examine the number of experiments required to provide each of them, you get table. 1.4

Table 1.4.

Theoretical dependence of the number of experiments required to ensure a given accuracy at Q F = 0.95

Let's build according to the table. 1.4 dependency graph N crt ( e) (see Fig. 1.8).

Rice. 1.8 Dependence of the number of experiments required to achieve a given accuracy e at a fixed Q F = 0.95

So, the considered graphs confirm the above assessment:

Note that there can be several accuracy estimates.

Example 2. Finding the area of ​​a figure using the Monte Carlo method. Using the Monte Carlo method, determine the area of ​​a pentagon with angle coordinates (0, 0), (0.10), (5, 20), (10,10), (7, 0).

Let's draw the given pentagon in two-dimensional coordinates, inscribing it in a rectangle, whose area, as you might guess, is (10 - 0) · (20 - 0) = 200 (see Fig. 1.9).

Rice. 1.9

Using a table of random numbers to generate pairs of numbers R, G, uniformly distributed in the range from 0 to 1. Number R X (0 ? X? 10), therefore, X= 10 · R. Number G will simulate the coordinate Y (0 ? Y? 20), therefore, Y= 20 · G. Let's generate 10 numbers R And G and display 10 points ( X; Y) in Fig. 1.9 and in table. 1.5

Table 1.5.

Solving the problem using the Monte Carlo method

The statistical hypothesis is that the number of points included in the contour of the figure is proportional to the area of ​​the figure: 6: 10 = S: 200. That is, according to the formula of the Monte Carlo method, we find that the area S pentagon is equal to: 200 · 6/10 = 120.

Let's see how the value changed S from experience to experience (see Table 1.6).

Table 1.6.

Response accuracy assessment

Since the value of the second digit in the answer is still changing, the possible inaccuracy is still more than 10%. The calculation accuracy can be increased with increasing number of tests (see Fig. 1.10).

Rice. 1.10 Illustration of the process of convergence of an experimentally determined answer to a theoretical result

Lecture 2. Random number generators

The Monte Carlo method (see Lecture 1. Statistical modeling) is based on the generation of random numbers, which should be uniformly distributed in the interval (0;1).

If the generator produces numbers that are shifted to some part of the interval (some numbers appear more often than others), then the result of solving a problem solved by the statistical method may turn out to be incorrect. Therefore, the problem of using a good generator of truly random and truly uniformly distributed numbers is very acute.

Expected value m r and variance D r such a sequence consisting of n random numbers r i, should be as follows (if these are truly uniformly distributed random numbers in the range from 0 to 1):

If the user needs a random number x was in the interval ( a; b), different from (0;

• 1), you need to use the formula x = a + (b - a) · r, Where r- random number from the interval (0;
• 1). The legality of this transformation is demonstrated in Fig. 2.1

Rice. 2.1

1) in the interval (a; b)

Now x- a random number uniformly distributed in the range from a before b.

Behind random number generator standard(RNG) a generator is adopted that generates subsequence random numbers with uniform distribution law in the interval (0;

• 1). For one call, this generator returns one random number. If you observe such a RNG for a sufficiently long time, it turns out that, for example, in each of the ten intervals (0; 0.1), (0.1; 0.2), (0.2; 0.3), ..., (0.9;
• 1) there will be almost the same number of random numbers - that is, they will be distributed evenly over the entire interval (0;
• 1). If shown on a graph k= 10 intervals and frequencies N i hits them, you will get an experimental distribution density curve of random numbers (see Fig. 2.2).

Rice. 2.2

Note that ideally the random number distribution density curve would look as shown in Fig. 2.3. That is, ideally, each interval contains the same number of points: N i = N/k, Where N- total number of points, k- number of intervals, i = 1, …, k.

Rice. 2.3

It should be remembered that generating an arbitrary random number consists of two stages:

• · generation of a normalized random number (that is, uniformly distributed from 0 to 1);
• · transformation of normalized random numbers r i to random numbers x i, which are distributed according to the (arbitrary) distribution law required by the user or in the required interval.

Random number generators according to the method of obtaining numbers are divided into:

• · physical;
• · tabular;
• · algorithmic.

Not long ago I read a wonderful book by Douglas Hubbard. In the brief synopsis of the book, I promised that I would devote a separate note to one of the sections - Risk Assessment: An Introduction to Monte Carlo Simulation. Yes, everything somehow didn’t work out. And recently I began to more carefully study methods of managing currency risks. In materials devoted to this topic, Monte Carlo simulation is often mentioned. So the promised material is in front of you.

I will give a simple example of Monte Carlo simulation for those who have never worked with it before, but have some understanding of using Excel spreadsheets.

Let's say you want to rent a new machine. The annual rental cost for the machine is $400,000, and the contract must be signed for several years. Therefore, even if you haven’t reached , you still won’t be able to immediately return the machine. You are about to sign a contract, thinking that modern equipment will save on labor costs and the cost of raw materials and supplies, and you also think that the logistics and technical maintenance of the new machine will be cheaper.

Download the note in format, examples in format

Your calibrated estimators have given the following ranges of expected savings and annual production:

Annual savings will be: (MS + LS + RMS) x PL

Of course, this example is too simple to be realistic. The volume of production changes every year, some costs will decrease when workers finally master the new machine, etc. But in this example we deliberately sacrificed realism for the sake of simplicity.

If we take the median (average) of each value interval, we get the annual savings: (15 + 3 + 6) x 25,000 = 600,000 (dollars)

It looks like we not only broke even, but also made some profit, but remember, there are uncertainties. How to assess the riskiness of these investments? Let's first define what risk is in this context. To derive risk, we must outline future outcomes with their inherent uncertainties, some of them with the likelihood of suffering quantifiable harm. One way to look at risk is to imagine the likelihood that we will not break even, that is, that our savings will be less than the annual cost of leasing the machine. The more we fall short of covering our rental costs, the more we will lose. Amount 600,000 dollars. is the median of the interval. How to determine the real range of values ​​​​and calculate from it the probability that we will not reach the break-even point?

Since precise data is not available, simple calculations cannot be made to answer the question of whether we can achieve the required savings. There are methods that, under certain conditions, allow one to find the range of values ​​of the resulting parameter from the ranges of values ​​of the initial data, but for most real-life problems such conditions, as a rule, do not exist. Once we start summing and multiplying different types of distributions, the problem usually becomes what mathematicians call an intractable problem, or one that cannot be solved by conventional mathematical methods. Therefore, instead we use the method of direct selection of possible options, made possible by the advent of computers. From the available intervals, we select at random a set (thousands) of exact values ​​of the initial parameters and calculate the set of exact values ​​of the desired indicator.

Monte Carlo simulation is an excellent way to solve problems like this. We just have to randomly select values ​​in the specified intervals, substitute them into the formula to calculate annual savings and calculate the total. Some results will be above our calculated median of $600,000, while others will be below. Some will be even below the $400,000 required to break even.

You can easily run a Monte Carlo simulation on a personal computer using Excel, but it requires a little more information than a 90% confidence interval. It is necessary to know the shape of the distribution curve. For different quantities, curves of one shape are more suitable than others. In the case of a 90% confidence interval, a normal (Gaussian) distribution curve is usually used. This is the familiar bell-shaped curve, in which most possible outcome values ​​are clustered in the central part of the graph and only a few, less likely ones, are distributed, tapering off towards its edges (Figure 1).

This is what a normal distribution looks like:

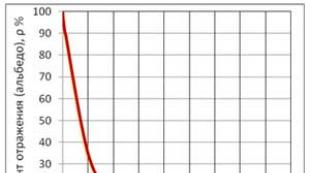
Fig.1. Normal distribution. The abscissa axis is the number of sigma.

Peculiarities:

• values ​​located in the central part of the graph are more likely than values ​​at its edges;
• the distribution is symmetrical; the median is exactly halfway between the upper and lower limits of the 90% confidence interval (CI);
• the “tails” of the graph are endless; values ​​outside the 90% confidence interval are unlikely, but still possible.

To build a normal distribution in Excel, you can use the function =NORMIDIST(X; Average; Standard_deviation; Integral), where
X – value for which the normal distribution is constructed;
Mean – arithmetic mean of the distribution; in our case = 0;
Standard_deviation – standard deviation of the distribution; in our case = 1;
Integral – a logical value that determines the form of the function; if cumulative is TRUE, NORMDIST returns the cumulative distribution function; if this argument is FALSE, the density function is returned; in our case = FALSE.

Speaking about the normal distribution, it is necessary to mention such a related concept as standard deviation. Obviously, not everyone has an intuitive understanding of what this is, but since the standard deviation can be replaced by a number calculated from a 90% confidence interval (which many people intuitively understand), I won’t go into detail about it here. Figure 1 shows that there are 3.29 standard deviations in one 90% confidence interval, so we'll just need to do the conversion.

In our case, we should create a random number generator in a spreadsheet for each value interval. Let's start, for example, with MS - savings on material and technical services. Let's use the Excel formula: =NORMINV(probability,average,standard_deviation), where
Probability – probability corresponding to a normal distribution;
Mean – arithmetic mean of the distribution;
Standard_deviation – standard deviation of the distribution.

In our case:
Mean (median) = (Upper limit of 90% CI + Lower limit of 90% CI)/2;
Standard deviation = (Upper limit of 90% CI – Lower limit of 90% CI)/3.29.

For the MS parameter, the formula has the form: =NORMIN(RAND();15,(20-10)/3.29), where
RAND – a function that generates random numbers in the range from 0 to 1;
15 – arithmetic mean of the MS range;
(20-10)/3.29 = 3.04 – standard deviation; Let me remind you that the meaning of the standard deviation is as follows: 90% of all values ​​of the random variable (in our case MS) fall into the interval 3.29*Standard_deviation, located symmetrically to the relative average.

Distribution of savings on logistics for 100 random normally distributed values:

Rice. 2. Probability of distribution of MS over ranges of values; For information on how to construct such a distribution using a pivot table, see

Since we "only" used 100 random values, the distribution was not that symmetrical. However, about 90% of the values ​​fell within the MS savings range of $10 to $20 (91% to be exact).

Let's build a table based on the confidence intervals of the parameters MS, LS, RMS and PL (Fig. 3). The last two columns show the results of calculations based on the data in the other columns. The Total Savings column shows the annual savings calculated for each row. For example, if Scenario 1 were implemented, the total savings would be (14.3 + 5.8 + 4.3) x 23,471 = $570,834. The “Are you breaking even?” column. you don't really need it. I've included it just for informational purposes. Let's create 10,000 script lines in Excel.

Rice. 3. Calculation of scenarios using the Monte Carlo method in Excel

To evaluate the results obtained, you can use, for example, a pivot table that allows you to count the number of scenarios in each 100 thousand range. Then you build a graph displaying the calculation results (Figure 4). This graph shows what proportion of 10,000 scenarios will have annual savings in a given value range. For example, about 3% of scenarios will provide annual savings of more than $1M.

Rice. 4. Distribution of total savings across value ranges. The x-axis shows 100-thousandth ranges of savings, and the y-axis shows the share of scenarios falling within the specified range.

Of all the annual savings obtained, approximately 15% will be less than $400K. This means there is a 15% chance of damage. This number represents a meaningful risk assessment. But risk does not always boil down to the possibility of negative investment returns. When assessing the size of a thing, we determine its height, mass, girth, etc. Likewise, there are several useful risk indicators. Further analysis shows: there is a 4% probability that the plant, instead of saving, will lose $100K annually. However, a complete lack of income is practically impossible. This is what is meant by risk analysis - we must be able to calculate the probabilities of damage of different scales. If you are truly measuring risk, this is what you should do.

In some situations, you can take a shorter route. If all the distributions of values ​​we are working with are normal and we just need to add the intervals of these values ​​(for example, intervals of costs and benefits) or subtract them from each other, then we can do without Monte Carlo simulation. When it comes to adding up the three savings from our example, a simple calculation needs to be done. To get the interval you are looking for, use the six steps listed below:

1) subtract the average value of each value interval from its upper limit; to save on logistics 20 – 15 = 5 (dollars), to save on labor costs – 5 dollars. and to save on raw materials and materials – 3 dollars;

2) square the results of the first step 5 2 = 25 (dollars), etc.;

3) summarize the results of the second step 25 + 25 + 9 = 59 (dollars);

4) take the square root of the resulting amount: it turns out to be 7.7 dollars;

5) add up all average values: 15 + 3 + 6 = 24 (dollars);

6) add the result of step 4 to the sum of average values ​​and get the upper limit of the range: 24 + 7.7 = 31.7 dollars; subtract the result of step 4 from the sum of average values ​​and get the lower limit of the range 24 - 7.7 = 16.3 dollars.

Thus, the 90% confidence interval for the sum of the three 90% confidence intervals for each type of savings is $16.3–$31.7.

We used the following property: the range of the total interval is equal to the square root of the sum of the squares of the ranges of individual intervals.

Sometimes something similar is done by summing up all the “optimistic” values ​​of the upper limit and the “pessimistic” values ​​of the lower limit of the interval. In this case, based on our three 90% confidence intervals, we would get a total interval of $11–$37. This interval is somewhat wider than 16.3–31.7 dollars. When such calculations are made to justify a design with dozens of variables, the expansion of the interval becomes too much to ignore. Taking the most “optimistic” values ​​for the upper bound and “pessimistic” ones for the lower one is like thinking: if we throw several dice, in all cases we will get only “1” or only “6”. In reality, some combination of low and high values ​​will appear. Excessive expansion of the interval is a common mistake, which, of course, often leads to uninformed decisions. At the same time, the simple method I described works great when we have several 90% confidence intervals that need to be summed.

However, our goal is not only to sum the intervals, but also to multiply them by the production volume, the values ​​of which are also given in the form of a range. The simple summation method is only suitable for subtracting or adding intervals of values.

Monte Carlo simulation is also required when not all distributions are normal. Although other types of distributions are not included in the subject of this book, we will mention two of them - uniform and binary (Fig. 5, 6).

Rice. 5. Uniform distribution (not ideal, but built using the RAND function in Excel)

Peculiarities:

• the probability of all values ​​is the same;
• the distribution is symmetrical, without distortions; the median is exactly halfway between the upper and lower limits of the interval;
• values ​​outside the interval are not possible.

To construct this distribution in Excel, the formula was used: RAND()*(UB – LB) + LB, where UB is the upper limit; LB – lower limit; followed by dividing all values ​​into ranges using a pivot table.

Rice. 6. Binary distribution (Bernoulli distribution)

Peculiarities:

• only two values ​​are possible;
• there is a single probability of one value (in this case 60%); the probability of the other value is equal to one minus the probability of the first value

To construct a random distribution of this type in Excel, the function was used: =IF(RAND()<Р;1;0), где Р - вероятность выпадения «1»; вероятность выпадения «0» равна 1–Р; с последующим разбиением всех значений на два значения с помощью сводной таблицы.

The method was first used by mathematician Stanislav Ulam (see).

Douglas Hubbard further lists several programs designed for Monte Carlo simulation. Among them is the Crystal Ball from Decisioneering, Inc., Denver, Colorado. The book in English was published in 2007. Now this program belongs to Oracle. A demo version of the program is available for downloading from the company's website. We'll talk about its capabilities.

See Chapter 5 of the book mentioned by Douglas Hubbard

Here, Douglas Hubbard defines range as the difference between the upper limit of the 90% confidence interval and the mean value of this interval (or between the mean value and the lower limit, since the distribution is symmetrical). Typically, range is understood as the difference between the upper and lower boundaries.