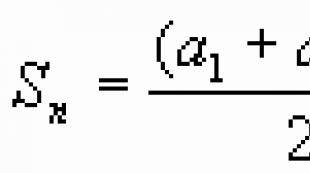Crafts

Arithmetic progression formula an. Arithmetic progression: what is it? Terms and designations

Attention!
There are additional
materials in Special Section 555.
For those who are "not very ..."
And for those who "very much ...")

An arithmetic progression is a series of numbers in which each number is greater (or less) than the previous one by the same amount.

This topic is often difficult and incomprehensible. Indices for letters, the n-th term of the progression, the difference in the progression - all this is somehow confusing, yes ... Let's figure out the meaning of the arithmetic progression and everything will work out right away.)

Arithmetic progression concept.

Arithmetic progression is a very simple and clear concept. Doubt? In vain.) See for yourself.

I'll write an unfinished series of numbers:

1, 2, 3, 4, 5, ...

Can you extend this row? What numbers will go next, after the five? Everyone ... uh-uh ..., in short, everyone will realize that the numbers 6, 7, 8, 9, etc. will go further.

Let's complicate the task. I give an unfinished series of numbers:

2, 5, 8, 11, 14, ...

You will be able to catch the pattern, extend the series, and name seventh row number?

If you figured out that this number is 20 - I congratulate you! Not only did you feel key points of the arithmetic progression, but also successfully used them in business! If you haven't figured it out, read on.

Now let's translate the key points from sensation to mathematics.)

First key point.

Arithmetic progression deals with series of numbers. This is confusing at first. We are used to solving equations, plotting graphs and all that ... And then extend the series, find the number of the series ...

It's OK. Just progressions are the first acquaintance with a new branch of mathematics. The section is called "Rows" and works with series of numbers and expressions. Get used to it.)

Second key point.

In an arithmetic progression, any number is different from the previous one by the same amount.

In the first example, this difference is one. Whatever number you take, it is one more than the previous one. In the second - three. Any number greater than the previous one by three. Actually, it is this moment that gives us the opportunity to catch the pattern and calculate the subsequent numbers.

The third key point.

This moment is not striking, yes ... But it is very, very important. Here it is: each number in the progression stands in its place. There is the first number, there is the seventh, there is the forty-fifth, etc. If they are confused at random, the pattern will disappear. The arithmetic progression will also disappear. There will be just a row of numbers.

That's the whole point.

Of course, new terms and designations appear in the new topic. You need to know them. Otherwise, you will not understand the task. For example, you have to decide something like:

Write out the first six terms of the arithmetic progression (a n), if a 2 = 5, d = -2.5.

Does it inspire?) Letters, some indexes ... And the task, by the way - couldn't be easier. You just need to understand the meaning of terms and designations. Now we will master this business and return to the task.

Terms and designations.

Arithmetic progression is a series of numbers in which each number is different from the previous one by the same amount.

This quantity is called ... Let's deal with this concept in more detail.

Difference of arithmetic progression.

Difference of arithmetic progression is the amount by which any number of the progression more the previous one.

One important point. Please pay attention to the word "more". Mathematically, this means that each number in the progression is obtained adding the difference of the arithmetic progression to the previous number.

For calculation, let's say second number of the series, it is necessary to the first the number add this very difference of the arithmetic progression. For calculation fifth- the difference is necessary add To fourth, well, etc.

Difference of arithmetic progression may be positive, then each number of the row will turn out really more than the previous one. This progression is called increasing. For example:

8; 13; 18; 23; 28; .....

Here every number is obtained adding positive number, +5 to the previous one.

The difference can be negative, then each number in the row will turn out less than the previous one. Such a progression is called (you won't believe it!) decreasing.

For example:

8; 3; -2; -7; -12; .....

Here every number is obtained too adding to the previous, but already negative number, -5.

By the way, when working with a progression, it is very useful to immediately determine its nature - whether it is increasing or decreasing. It helps a lot to navigate the solution, to detect your mistakes and fix them before it's too late.

Difference of arithmetic progression denoted, as a rule, by the letter d.

How to find d? Very simple. It is necessary to subtract from any number of the series previous number. Subtract. By the way, the result of the subtraction is called the "difference".)

We define, for example, d for increasing arithmetic progression:

2, 5, 8, 11, 14, ...

We take any number of the row that we want, for example, 11. Subtract from it previous number, those. eight:

This is the correct answer. For this arithmetic progression, the difference is three.

You can take exactly any number of progression, since for a specific progression d -always the same. At least somewhere in the beginning of the row, at least in the middle, at least anywhere. You cannot take only the very first number. Just because the very first number there is no previous one.)

By the way, knowing that d = 3, it is very easy to find the seventh number of this progression. Add 3 to the fifth number - we get the sixth, it will be 17. Add three to the sixth number, we get the seventh number - twenty.

We define d for a decreasing arithmetic progression:

8; 3; -2; -7; -12; .....

I remind you that, regardless of the signs, to determine d it is necessary from any number take away the previous one. We choose any number of the progression, for example -7. The previous one is -2. Then:

d = -7 - (-2) = -7 + 2 = -5

The difference of the arithmetic progression can be any number: whole, fractional, irrational, whatever.

Other terms and designations.

Each number in the series is called a member of an arithmetic progression.

Each member of the progression has its own number. The numbers are strictly in order, without any tricks. First, second, third, fourth, etc. For example, in the progression 2, 5, 8, 11, 14, ... two is the first term, five is the second, eleven is the fourth, well, you understand ...) Please understand clearly - the numbers themselves can be absolutely any, whole, fractional, negative, whatever, but numbering of numbers- strictly in order!

How to record a general progression? No problem! Each number in the row is written as a letter. As a rule, the letter is used to denote an arithmetic progression a... The member number is indicated by an index at the bottom right. We write members separated by commas (or semicolons), like this:

a 1, a 2, a 3, a 4, a 5, .....

a 1 is the first number, a 3- third, etc. Nothing tricky. You can briefly write this series like this: (a n).

Progressions are finite and endless.

The ultimate the progression has a limited number of members. Five, thirty-eight, whatever. But - a finite number.

Endless progression - has an infinite number of members, as you might guess.)

You can write the final progression through a series like this, all the members and a dot at the end:

a 1, a 2, a 3, a 4, a 5.

Or so, if there are many members:

a 1, a 2, ... a 14, a 15.

In a short entry, you will have to additionally indicate the number of members. For example (for twenty members), like this:

(a n), n = 20

An endless progression can be recognized by the ellipsis at the end of the row, as in the examples in this lesson.

Now you can solve tasks. The tasks are simple, purely for understanding the meaning of the arithmetic progression.

Examples of tasks on arithmetic progression.

Let's analyze the task in detail, which is given above:

1. Write down the first six terms of the arithmetic progression (a n), if a 2 = 5, d = -2.5.

We translate the task into an understandable language. An infinite arithmetic progression is given. The second number of this progression is known: a 2 = 5. The difference in progression is known: d = -2.5. It is necessary to find the first, third, fourth, fifth and sixth members of this progression.

For clarity, I will write down a series according to the condition of the problem. The first six terms, where the second term is a five:

a 1, 5, a 3, a 4, a 5, a 6, ....

a 3 = a 2 + d

Substitute into expression a 2 = 5 and d = -2.5... Do not forget about the minus!

a 3=5+(-2,5)=5 - 2,5 = 2,5

The third term is smaller than the second. Everything is logical. If the number is greater than the previous one by negative value, then the number itself will turn out to be less than the previous one. The progression is decreasing. Okay, let's take it into account.) We consider the fourth member of our series:

a 4 = a 3 + d

a 4=2,5+(-2,5)=2,5 - 2,5 = 0

a 5 = a 4 + d

a 5=0+(-2,5)= - 2,5

a 6 = a 5 + d

a 6=-2,5+(-2,5)=-2,5 - 2,5 = -5

So, the terms from the third to the sixth are calculated. The result is such a series:

a 1, 5, 2.5, 0, -2.5, -5, ....

It remains to find the first term a 1 according to the well-known second. This is a step in the other direction, to the left.) Hence, the difference of the arithmetic progression d need not add to a 2, a take away:

a 1 = a 2 - d

a 1=5-(-2,5)=5 + 2,5=7,5

That's all there is to it. Task answer:

7,5, 5, 2,5, 0, -2,5, -5, ...

Along the way, I will note that we solved this task recurrent way. This scary word only means searching for a member of the progression. by the previous (adjacent) number. We will consider other ways of working with progression later.

One important conclusion can be drawn from this simple task.

Remember:

If we know at least one term and the difference of an arithmetic progression, we can find any member of this progression.

Remember? This simple conclusion allows you to solve most of the tasks of the school course on this topic. All tasks revolve around three main parameters: member of arithmetic progression, difference of the progression, number of the member of the progression. Everything.

Of course, all the previous algebra is not canceled.) Inequalities, equations, and other things are attached to the progression. But by the very progression- everything revolves around three parameters.

Let's take a look at some of the popular assignments on this topic as an example.

2. Write down the final arithmetic progression as a series if n = 5, d = 0.4, and a 1 = 3.6.

Everything is simple here. Everything has already been given. You need to remember how the members of an arithmetic progression are counted, count, and write them down. It is advisable not to miss the words in the condition of the task: "final" and " n = 5". Not to count until completely blue in the face.) There are only 5 (five) members in this progression:

a 2 = a 1 + d = 3.6 + 0.4 = 4

a 3 = a 2 + d = 4 + 0.4 = 4.4

a 4 = a 3 + d = 4.4 + 0.4 = 4.8

a 5 = a 4 + d = 4.8 + 0.4 = 5.2

It remains to write down the answer:

3,6; 4; 4,4; 4,8; 5,2.

Another task:

3. Determine whether the number 7 is a member of the arithmetic progression (a n), if a 1 = 4.1; d = 1.2.

Hmm ... Who knows? How to determine something?

How, how ... Yes, write down the progression in the form of a series and see if there will be a seven there or not! We consider:

a 2 = a 1 + d = 4.1 + 1.2 = 5.3

a 3 = a 2 + d = 5.3 + 1.2 = 6.5

a 4 = a 3 + d = 6.5 + 1.2 = 7.7

4,1; 5,3; 6,5; 7,7; ...

Now it is clearly seen that we are just a seven slipped through between 6.5 and 7.7! The seven did not get into our series of numbers, and, therefore, the seven will not be a member of the given progression.

The answer is no.

And here is a task based on a real version of the GIA:

4. Several consecutive members of the arithmetic progression are written out:

...; 15; NS; nine; 6; ...

A row is written here without end and beginning. No member numbers, no difference d... It's OK. To solve the problem, it is enough to understand the meaning of the arithmetic progression. We look and think about what is possible to know from this series? What are the three main parameters?

Member numbers? There is not a single number here.

But there are three numbers and - attention! - word "consecutive" in the condition. This means that the numbers are strictly in order, without gaps. Are there two in this row neighboring known numbers? Yes there is! These are 9 and 6. So we can calculate the difference of the arithmetic progression! We subtract from the six previous number, i.e. nine:

There are mere trifles left. What is the previous number for the X? Fifteen. This means that x can be easily found by simple addition. Add the difference of the arithmetic progression to 15:

That's all. Answer: x = 12

We solve the following problems ourselves. Note: these problems are not about formulas. Purely for understanding the meaning of an arithmetic progression.) We just write down a series of numbers-letters, look and think.

5. Find the first positive term of the arithmetic progression if a 5 = -3; d = 1.1.

6. It is known that the number 5.5 is a member of the arithmetic progression (a n), where a 1 = 1.6; d = 1.3. Determine the number n of this member.

7. It is known that in the arithmetic progression a 2 = 4; a 5 = 15.1. Find a 3.

8. Written out several consecutive members of the arithmetic progression:

...; 15.6; NS; 3.4; ...

Find the term in the progression indicated by the letter x.

9. The train started moving from the station, steadily increasing its speed by 30 meters per minute. What will the train speed be in five minutes? Give your answer in km / h.

10. It is known that in the arithmetic progression a 2 = 5; a 6 = -5. Find a 1.

Answers (in disarray): 7.7; 7.5; 9.5; nine; 0.3; 4.

Everything worked out? Wonderful! You can master the arithmetic progression at a higher level in the following lessons.

Not everything worked out? No problem. In Special Section 555, all these tasks are sorted out to pieces.) And, of course, a simple practical technique is described that immediately highlights the solution of such tasks clearly, clearly, as if in the palm of your hand!

By the way, in the puzzle about the train there are two problems that people often stumble on. One is purely in progression, and the second is common for any problems in mathematics, and physics too. This is a translation of dimensions from one to another. In it is shown how these problems should be solved.

In this lesson, we examined the elementary meaning of the arithmetic progression and its main parameters. This is enough to solve almost all problems on this topic. Add d to the numbers, write a series, everything will be decided.

The finger solution works well for very short pieces of a row, as in the examples in this lesson. If the row is longer, the calculations become more complicated. For example, if in problem 9 in the question, replace "five minutes" on "thirty five minutes" the problem will become significantly angrier.)

And there are also tasks that are simple in essence, but incredible in terms of calculations, for example:

You are given an arithmetic progression (a n). Find a 121 if a 1 = 3 and d = 1/6.

And what, we will add many, many times by 1/6 ?! You can kill yourself !?

You can.) If you do not know a simple formula, according to which such tasks can be solved in a minute. This formula will be in the next lesson. And this problem is solved there. In a minute.)

If you like this site ...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Instant validation testing. Learning - with interest!)

you can get acquainted with functions and derivatives.

Mathematics has its own beauty, just like painting and poetry.

Russian scientist, mechanic N.E. Zhukovsky

Problems related to the concept of arithmetic progression are very common problems in entrance examinations in mathematics. To successfully solve such problems, it is necessary to know well the properties of the arithmetic progression and have certain skills in their application.

We first recall the main properties of the arithmetic progression and present the most important formulas, related to this concept.

Definition. Numerical sequence, in which each subsequent term differs from the previous one by the same number, called arithmetic progression. Moreover, the numbercalled the difference in progression.

For an arithmetic progression, the following formulas are valid

, (1)

where . Formula (1) is called the formula for the general term of an arithmetic progression, and formula (2) is the main property of an arithmetic progression: each term of the progression coincides with the arithmetic mean of its neighboring terms and.

Note that it is precisely because of this property that the considered progression is called "arithmetic".

The above formulas (1) and (2) are generalized as follows:

(3)

To calculate the amount the first members of the arithmetic progressionusually the formula is applied

(5) where and.

Taking into account the formula (1), then formula (5) implies

If we denote, then

where . Since, then formulas (7) and (8) are a generalization of the corresponding formulas (5) and (6).

In particular , formula (5) implies, what

The property of the arithmetic progression, formulated by means of the following theorem, is among the little-known to most students.

Theorem. If, then

Proof. If, then

The theorem is proved.

For example , using the theorem, it can be shown that

Let's move on to considering typical examples of solving problems on the topic "Arithmetic progression".

Example 1. Let and. Find .

Solution. Applying formula (6), we obtain. Since and, then or.

Example 2. Let it be three times more, and when dividing by in the quotient, we get 2 and remainder 8. Determine and.

Solution. The condition of the example implies the system of equations

Since,, and, then from the system of equations (10) we obtain

The solution to this system of equations is and.

Example 3. Find if and.

Solution. According to formula (5), we have or. However, using property (9), we obtain.

Since and, then from the equality the equation follows or .

Example 4. Find if.

Solution.By formula (5), we have

However, using the theorem, one can write

From this and formula (11) we obtain.

Example 5. Given:. Find .

Solution. Since, then. However, therefore.

Example 6. Let, and. Find .

Solution. Using formula (9), we obtain. Therefore, if, then or.

Since and, then here we have the system of equations

Solving which, we get and.

The natural root of the equation is an .

Example 7. Find if and.

Solution. Since by formula (3) we have that, then the problem statement implies the system of equations

If you substitute the expressioninto the second equation of the system, then we get or.

The roots of the quadratic equation are and .

Let's consider two cases.

1. Let, then. Since and, then.

In this case, according to formula (6), we have

2. If, then, and

Answer: and.

Example 8. It is known that and. Find .

Solution. Taking into account formula (5) and the condition of the example, we write down and.

Hence follows the system of equations

If we multiply the first equation of the system by 2, and then add it to the second equation, we get

According to formula (9), we have... In this connection, from (12) it follows or .

Since and, then.

Answer: .

Example 9. Find if and.

Solution. Since, and by condition, then or.

From formula (5) it is known, what . Since, then.

Hence , here we have a system of linear equations

Hence we get and. Taking into account formula (8), we write.

Example 10. Solve the equation.

Solution. From the given equation it follows that. Suppose that,, and. In this case .

According to formula (1), you can write or.

Since, then equation (13) has a single suitable root.

Example 11. Find the maximum value provided that and.

Solution. Since, the considered arithmetic progression is decreasing. In this regard, the expression takes on the maximum value when it is the number of the minimum positive term of the progression.

We use formula (1) and the fact, as. Then we get that or.

Since, then either ... However, in this inequalitygreatest natural number, therefore .

If the values, and are substituted in the formula (6), then we get.

Answer: .

Example 12. Determine the sum of all two-digit natural numbers that, when divided by 6, give a remainder of 5.

Solution. Let us denote by the set of all two-digit natural numbers, i.e. ... Next, we construct a subset consisting of those elements (numbers) of the set that, when divided by 6, give the remainder 5.

It is not difficult to establish, what . Obviously , that the elements of the setform an arithmetic progression, in which and.

To establish the cardinality (number of elements) of a set, we assume that. Since and, then from formula (1) it follows or. Taking into account formula (5), we get.

The above examples of solving problems in no way can claim to be exhaustive. This article is written on the basis of an analysis of modern methods for solving typical problems on a given topic. For a deeper study of methods for solving problems associated with arithmetic progression, it is advisable to refer to the list of recommended literature.

1. Collection of problems in mathematics for applicants to technical colleges / Ed. M.I. Skanavi. - M .: Peace and Education, 2013 .-- 608 p.

2. Suprun V.P. Mathematics for high school students: additional sections of the school curriculum. - M .: Lenand / URSS, 2014 .-- 216 p.

3. Medynsky M.M. Complete course of elementary mathematics in problems and exercises. Book 2: Number sequences and progressions. - M .: Editus, 2015 .-- 208 p.

Still have questions?

To get help from a tutor - register.

site, with full or partial copying of the material, a link to the source is required.

Someone is wary of the word "progression", as a very complex term from the branches of higher mathematics. Meanwhile, the simplest arithmetic progression is the work of the taxi meter (where they still remain). And to understand the essence (and in mathematics there is nothing more important than "understanding the essence") of the arithmetic sequence is not so difficult, having analyzed several elementary concepts.

Math number sequence

It is customary to name a series of numbers by a numerical sequence, each of which has its own number.

a 1 - the first member of the sequence;

and 2 is the second member of the sequence;

and 7 is the seventh member of the sequence;

and n is the nth member of the sequence;

However, we are not interested in any arbitrary set of numbers and numbers. We will focus our attention on the numerical sequence, in which the value of the nth term is associated with its ordinal number by a dependence that can be clearly formulated mathematically. In other words: the numerical value of the n-th number is some function of n.

a - value of a member of a numerical sequence;

n is its serial number;

f (n) is a function where the ordinal in the numerical sequence n is an argument.

Definition

It is customary to call an arithmetic progression a numerical sequence in which each subsequent term is greater (less) than the previous one by the same number. The formula for the nth member of an arithmetic sequence is as follows:

a n - the value of the current member of the arithmetic progression;

a n + 1 - the formula for the next number;

d - difference (a certain number).

It is easy to determine that if the difference is positive (d> 0), then each subsequent term of the series under consideration will be larger than the previous one, and such an arithmetic progression will be increasing.

In the graph below, it is easy to see why the number sequence is called “ascending”.

In cases where the difference is negative (d<0), каждый последующий член по понятным причинам будет меньше предыдущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убывающей.

The value of the specified member

Sometimes it is necessary to determine the value of any arbitrary member a n of an arithmetic progression. You can do this by calculating sequentially the values of all members of the arithmetic progression, starting from the first to the desired one. However, this path is not always acceptable if, for example, it is necessary to find the meaning of the five-thousandth or eight-millionth member. The traditional calculation will take a long time. However, a specific arithmetic progression can be investigated using specific formulas. There is also a formula for the nth term: the value of any member of an arithmetic progression can be defined as the sum of the first term of the progression with the difference of the progression, multiplied by the number of the sought term, decreased by one.

The formula is universal for both increasing and decreasing progression.

An example of calculating the value of a given member

Let's solve the following problem of finding the value of the nth term of an arithmetic progression.

Condition: there is an arithmetic progression with parameters:

The first term in the sequence is 3;

The difference in the number series is 1.2.

Assignment: you need to find the value of 214 members

Solution: to determine the value of a given term, we use the formula:

a (n) = a1 + d (n-1)

Substituting the data from the problem statement into the expression, we have:

a (214) = a1 + d (n-1)

a (214) = 3 + 1.2 (214-1) = 258.6

Answer: The 214th term in the sequence is 258.6.

The advantages of this calculation method are obvious - the whole solution takes no more than 2 lines.

Sum of a given number of members

Very often, in a given arithmetic series, it is required to determine the sum of the values of a certain segment of it. This also does not require calculating the values of each term and then summing. This method is applicable if the number of terms to be found is small. In other cases, it is more convenient to use the following formula.

The sum of the members of the arithmetic progression from 1 to n is equal to the sum of the first and nth members, multiplied by the number of the member n and divided by two. If in the formula the value of the nth term is replaced by the expression from the previous paragraph of the article, we get:

Calculation example

For example, let's solve a problem with the following conditions:

The first term in the sequence is zero;

The difference is 0.5.

In the problem, you need to determine the sum of the members of the series from 56th to 101.

Solution. Let's use the formula for determining the sum of the progression:

s (n) = (2 ∙ a1 + d ∙ (n-1)) ∙ n / 2

First, we determine the sum of the values of 101 members of the progression, substituting the data of their conditions of our problem into the formula:

s 101 = (2 ∙ 0 + 0.5 ∙ (101-1)) ∙ 101/2 = 2 525

Obviously, in order to find out the sum of the members of the progression from 56th to 101st, it is necessary to subtract S 55 from S 101.

s 55 = (2 ∙ 0 + 0.5 ∙ (55-1)) ∙ 55/2 = 742.5

Thus, the sum of the arithmetic progression for this example:

s 101 - s 55 = 2,525 - 742.5 = 1,782.5

An example of practical application of arithmetic progression

At the end of the article, let's go back to the example of the arithmetic sequence given in the first paragraph - a taximeter (taxi car meter). Let's consider an example.

Boarding a taxi (which includes 3 km of run) costs 50 rubles. Each subsequent kilometer is paid at the rate of 22 rubles / km. Travel distance 30 km. Calculate the cost of the trip.

1. Let's discard the first 3 km, the price of which is included in the landing price.

30 - 3 = 27 km.

2. Further calculation is nothing more than an analysis of an arithmetic number series.

Member number - the number of kilometers traveled (minus the first three).

The member value is the sum.

The first term in this problem will be equal to a 1 = 50 p.

Difference in progression d = 22 p.

the number we are interested in is the value of the (27 + 1) -th term of the arithmetic progression - the counter reading at the end of the 27th kilometer is 27.999… = 28 km.

a 28 = 50 + 22 ∙ (28 - 1) = 644

Calculations of calendar data for an arbitrarily long period are based on formulas describing certain numerical sequences. In astronomy, the length of the orbit is geometrically dependent on the distance of the celestial body to the luminary. In addition, various numerical series are successfully used in statistics and other applied branches of mathematics.

Another type of number sequence is geometric

Geometric progression is characterized by large, in comparison with arithmetic, rates of change. It is no coincidence that in politics, sociology, medicine, they often say that the process develops exponentially in order to show the high rate of spread of a phenomenon, for example, a disease during an epidemic.

The Nth term of the geometric numerical series differs from the previous one in that it is multiplied by some constant number - the denominator, for example, the first term is 1, the denominator is 2, respectively, then:

n = 1: 1 ∙ 2 = 2

n = 2: 2 ∙ 2 = 4

n = 3: 4 ∙ 2 = 8

n = 4: 8 ∙ 2 = 16

n = 5: 16 ∙ 2 = 32,

b n - the value of the current member of the geometric progression;

b n + 1 - the formula of the next term of the geometric progression;

q is the denominator of a geometric progression (constant number).

If the graph of the arithmetic progression is a straight line, then the geometric one paints a slightly different picture:

As in the case of arithmetic, a geometric progression has a formula for the value of an arbitrary term. Any n-th term of the geometric progression is equal to the product of the first term by the denominator of the progression to the power of n, reduced by one:

Example. We have a geometric progression with the first term equal to 3 and the denominator of the progression equal to 1.5. Find the 5th term of the progression

b 5 = b 1 ∙ q (5-1) = 3 ∙ 1.5 4 = 15.1875

The sum of a given number of members is calculated in the same way using a special formula. The sum of the first n terms of a geometric progression is equal to the difference between the product of the nth term of the progression and its denominator and the first term of the progression, divided by the denominator reduced by one:

If b n is replaced using the formula considered above, the value of the sum of the first n terms of the considered numerical series will take the form:

Example. The geometric progression starts with the first term equal to 1. The denominator is set equal to 3. Find the sum of the first eight terms.

s8 = 1 ∙ (3 8 -1) / (3-1) = 3 280

So let's sit down and start writing some numbers. For example:
You can write any numbers, and there can be as many as you like (in our case, them). No matter how many numbers we write, we can always say which one is the first, which is the second, and so on to the last, that is, we can number them. This is an example of a number sequence:

Numerical sequence
For example, for our sequence:

The assigned number is specific to only one number in the sequence. In other words, there are no three second numbers in the sequence. The second number (like the -th number) is always one.
The number with the number is called the th member of the sequence.

We usually call the entire sequence some letter (for example,), and each member of this sequence is the same letter with an index equal to the number of this member:.

In our case:

Let's say we have a numerical sequence in which the difference between adjacent numbers is the same and equal.
For example:

etc.
This number sequence is called an arithmetic progression.
The term "progression" was introduced by the Roman author Boethius back in the 6th century and was understood in a broader sense as an endless number sequence. The name "arithmetic" was carried over from the theory of continuous proportions, which was occupied by the ancient Greeks.

This is a numerical sequence, each member of which is equal to the previous one, added to the same number. This number is called the difference of the arithmetic progression and is denoted by.

Try to determine which number sequences are arithmetic progression and which are not:

a)
b)
c)
d)

Understood? Let's compare our answers:
Is an arithmetic progression - b, c.
Is not arithmetic progression - a, d.

Let's return to the given progression () and try to find the value of its th member. Exists two the way to find it.

1. Method

We can add to the previous value of the number of the progression until we reach the th term of the progression. It's good that we don't have much left to summarize - only three values:

So, the th member of the described arithmetic progression is equal to.

2. Method

What if we needed to find the value of the th term in the progression? The summation would take us more than one hour, and it is not a fact that we would not be mistaken when adding numbers.
Of course, mathematicians have come up with a way in which you do not need to add the difference of the arithmetic progression to the previous value. Take a closer look at the drawn picture ... Surely you have already noticed a certain pattern, namely:

For example, let's see how the value of the th member of this arithmetic progression is added:

In other words:

Try to find by yourself in this way the value of a member of a given arithmetic progression.

Calculated? Compare your notes to the answer:

Please note that you got exactly the same number as in the previous method, when we successively added the members of the arithmetic progression to the previous value.
Let's try to "depersonalize" this formula - we will bring it into general form and get:

Arithmetic progression equation.

Arithmetic progressions are ascending and sometimes decreasing.

Ascending- progressions in which each subsequent value of the members is greater than the previous one.
For example:

Decreasing- progressions in which each subsequent value of the members is less than the previous one.
For example:

The derived formula is used in calculating the terms in both increasing and decreasing terms of an arithmetic progression.
Let's check it out in practice.
We are given an arithmetic progression consisting of the following numbers: Let's check what the th number of this arithmetic progression will turn out if we use our formula to calculate it:

Since, then:

Thus, we made sure that the formula works in both decreasing and increasing arithmetic progression.
Try to find the th and th terms of this arithmetic progression on your own.

Let's compare the results obtained:

Arithmetic progression property

Let's complicate the task - we will derive the property of the arithmetic progression.
Let's say we are given the following condition:
- arithmetic progression, find the value.
Easy, you say and start counting according to the formula you already know:

Let, a, then:

Absolutely right. It turns out that we first find, then we add it to the first number and get what we are looking for. If the progression is represented by small values, then there is nothing complicated about it, but if we are given numbers in the condition? Admit it, there is a chance of making a mistake in the calculations.
Now think, is it possible to solve this problem in one action using any formula? Of course, yes, and it is her that we will try to withdraw now.

Let's denote the required term of the arithmetic progression as, we know the formula for finding it - this is the same formula we derived at the beginning:
, then:

the previous member of the progression is:
the next member of the progression is:

Let's summarize the previous and subsequent members of the progression:

It turns out that the sum of the previous and subsequent members of the progression is the doubled value of the member of the progression located between them. In other words, in order to find the value of a member of the progression with known previous and consecutive values, it is necessary to add them up and divide by.

That's right, we got the same number. Let's fix the material. Calculate the value for the progression yourself, because it's not difficult at all.

Well done! You know almost everything about progression! There is only one formula left to learn, which, according to legend, was easily deduced for himself by one of the greatest mathematicians of all time, the "king of mathematicians" - Karl Gauss ...

When Karl Gauss was 9 years old, a teacher engaged in checking the work of students in other grades asked the following task in the lesson: "Calculate the sum of all natural numbers from up to (according to other sources up to) inclusive." Imagine the teacher's surprise when one of his students (it was Karl Gauss) gave the correct answer to the problem in a minute, while most of the daredevil's classmates, after long calculations, received the wrong result ...

Young Karl Gauss noticed a certain pattern that you can easily notice.
Let's say we have an arithmetic progression consisting of -th members: We need to find the sum of the given members of the arithmetic progression. Of course, we can manually sum all the values, but what if in the task it is necessary to find the sum of its members, as Gauss was looking for?

Let's draw a given progression. Look closely at the highlighted numbers and try to perform various mathematical operations with them.

Have you tried it? What have you noticed? Right! Their sums are equal

Now tell me, how many such pairs are there in the given progression? Of course, exactly half of all numbers, that is.
Based on the fact that the sum of two members of the arithmetic progression is equal, and similar equal pairs, we get that the total sum is:
.
Thus, the formula for the sum of the first terms of any arithmetic progression will be as follows:

In some problems, we do not know the th term, but we know the difference in the progression. Try to substitute in the formula for the sum, the formula of the th term.
What did you do?

Well done! Now let's return to the problem that was asked to Karl Gauss: calculate yourself what is the sum of the numbers starting from the -th, and the sum of the numbers starting from the -th.

How much did you get?
Gauss found that the sum of the members is equal, and the sum of the members. Is that how you decided?

In fact, the formula for the sum of the members of an arithmetic progression was proved by the ancient Greek scientist Diophantus back in the 3rd century, and throughout this time, witty people were using the properties of an arithmetic progression with might and main.
For example, imagine Ancient Egypt and the most ambitious construction site of that time - the construction of the pyramid ... The figure shows one side of it.

Where is the progression here you say? Look closely and find a pattern in the number of sand blocks in each row of the pyramid wall.

Isn't it an arithmetic progression? Calculate how many blocks are needed to build one wall if block bricks are placed in the base. I hope you won't count by running your finger across the monitor, do you remember the last formula and everything we said about the arithmetic progression?

In this case, the progression looks like this:.
Difference of arithmetic progression.
The number of members of the arithmetic progression.
Let's substitute our data into the last formulas (we will count the number of blocks in 2 ways).

Method 1.

Method 2.

And now you can calculate on the monitor: compare the obtained values with the number of blocks that are in our pyramid. Did it come together? Well done, you have mastered the sum of the terms of the arithmetic progression.
Of course, you can't build a pyramid from blocks at the base, but from? Try to calculate how many sand bricks are needed to build a wall with this condition.
Did you manage?
The correct answer is blocks:

Workout

Tasks:

Masha is getting in shape by the summer. Every day she increases the number of squats by. How many times will Masha squat in weeks, if at the first workout she did squats.
What is the sum of all the odd numbers contained in.
When storing logs, lumberjacks stack them in such a way that each top layer contains one log less than the previous one. How many logs are in one masonry, if logs serve as the basis of the masonry.

Answers:

Let's define the parameters of the arithmetic progression. In this case
(weeks = days).
Answer: After two weeks, Masha should squat once a day.
First odd number, last number.
Difference of arithmetic progression.
The number of odd numbers in is half, however, we will check this fact using the formula for finding the -th term of an arithmetic progression:
The numbers do contain odd numbers.
Substitute the available data into the formula:
Answer: The sum of all odd numbers contained in is equal to.
Let's remember the pyramid problem. For our case, a, since each top layer is reduced by one log, then only in a bunch of layers, that is.
Let's substitute the data into the formula:
Answer: There are logs in the masonry.

Let's sum up

- a numerical sequence in which the difference between adjacent numbers is the same and equal. It can be ascending and decreasing.
Finding formula-th member of the arithmetic progression is written by the formula -, where is the number of numbers in the progression.
Property of members of an arithmetic progression- - where is the number of numbers in the progression.
The sum of the members of an arithmetic progression can be found in two ways:

, where is the number of values.

ARITHMETIC PROGRESSION. AVERAGE LEVEL

Numerical sequence

Let's sit down and start writing some numbers. For example:

You can write any numbers, and there can be as many as you like. But you can always say which one is the first, which is the second, and so on, that is, we can number them. This is an example of a number sequence.

Numerical sequence is a set of numbers, each of which can be assigned a unique number.

In other words, each number can be associated with a certain natural number, and the only one. And we will not assign this number to any other number from this set.

The number with the number is called the th member of the sequence.

We usually call the entire sequence some letter (for example,), and each member of this sequence is the same letter with an index equal to the number of this member:.

It is very convenient if the th term of the sequence can be specified by some formula. For example, the formula

specifies the sequence:

And the formula is the following sequence:

For example, an arithmetic progression is a sequence (the first term here is equal, and the difference). Or (, difference).

Nth term formula

We call recurrent a formula in which to find out the th member, you need to know the previous or several previous ones:

To find, for example, the th term of the progression using such a formula, we will have to calculate the previous nine. For example, let. Then:

Well, what is the formula now?

In each line we add to, multiplied by some number. For what? Very simple: this is the number of the current member minus:

Much more convenient now, right? We check:

Decide for yourself:

In an arithmetic progression, find the formula for the nth term and find the hundredth term.

Solution:

The first term is equal. What is the difference? And here's what:

(it is because it is called the difference, which is equal to the difference of the successive members of the progression).

So the formula is:

Then the hundredth term is:

What is the sum of all natural numbers from to?

According to legend, the great mathematician Karl Gauss, being a 9-year-old boy, calculated this amount in a few minutes. He noticed that the sum of the first and last numbers is equal, the sum of the second and the last but one is the same, the sum of the third and the third from the end is the same, and so on. How many such pairs will there be? That's right, exactly half the number of all numbers, that is. So,

The general formula for the sum of the first terms of any arithmetic progression would be:

Example:
Find the sum of all two-digit multiples.

Solution:

The first such number is. Each next is obtained by adding to the previous number. Thus, the numbers of interest to us form an arithmetic progression with the first term and the difference.

The th term formula for this progression is:

How many members are in the progression if they all have to be double digits?

Very easy: .

The last term in the progression will be equal. Then the sum:

Answer: .

Now decide for yourself:

Every day, the athlete runs more m than the previous day. How many kilometers will he run in weeks if he ran km m on the first day?
A cyclist drives more kilometers every day than the previous one. On the first day, he drove km. How many days does he need to travel to cover the km? How many kilometers will he travel in the last day of the journey?
The price of a refrigerator in a store decreases by the same amount every year. Determine how much the price of the refrigerator decreased every year, if, put up for sale for rubles, six years later it was sold for rubles.

Answers:

The most important thing here is to recognize the arithmetic progression and determine its parameters. In this case, (weeks = days). You need to determine the sum of the first members of this progression:
.
Answer:
It is given here:, it is necessary to find.
Obviously, you need to use the same sum formula as in the previous problem:
.
Substitute the values:
The root obviously doesn't fit, so the answer is.
Let's calculate the distance traveled for the last day using the th term formula:
(km).
Answer:
Given:. Find: .
It couldn't be easier:
(rub).
Answer:

ARITHMETIC PROGRESSION. BRIEFLY ABOUT THE MAIN

This is a numerical sequence in which the difference between adjacent numbers is the same and equal.

Arithmetic progression can be ascending () and decreasing ().

For example:

The formula for finding the n-th term of an arithmetic progression

written by the formula, where is the number of numbers in the progression.

Property of members of an arithmetic progression

It allows you to easily find a member of the progression if its neighboring members are known - where is the number of numbers in the progression.

The sum of the members of an arithmetic progression

There are two ways to find the amount:

Where is the number of values.

THE REMAINING 2/3 ARTICLES ARE AVAILABLE ONLY TO YOUCLEVER STUDENTS!

Become a YouClever student,

Prepare for the USE or USE in mathematics at the price of "a cup of coffee per month",

And also get unlimited access to the "YouClever" textbook, the "100gia" training program (reshebnik), an unlimited trial USE and OGE, 6000 problems with analysis of solutions and to other YouClever and 100gia services.

The sum of an arithmetic progression.

The sum of an arithmetic progression is a simple thing. Both in meaning and in formula. But there are all sorts of tasks on this topic. From elementary to quite solid.

First, let's figure out the meaning and the formula for the sum. And then we'll fix it. For your pleasure.) The meaning of the sum is simple, like a hum. To find the sum of an arithmetic progression, you just need to carefully add all its members. If these terms are few, you can add without any formulas. But if there is a lot, or a lot ... addition is annoying.) In this case, the formula saves.

The sum formula looks simple:

Let's figure out what letters are included in the formula. This will clarify a lot.

S n - the sum of the arithmetic progression. Addition result of all members with the first on last. It is important. Add up exactly all members in a row, without gaps and jumps. And, namely, starting with first. In tasks such as finding the sum of the third and eighth terms, or the sum of the fifth to twentieth terms, the direct application of the formula will be disappointing.)

a 1 - first member of the progression. Everything is clear here, it's simple first row number.

a n- last member of the progression. The last number of the row. Not a very familiar name, but, when applied to the amount, it is even very suitable. Then you will see for yourself.

n - the number of the last member. It is important to understand that in the formula this number coincides with the number of added members.

Let's define the concept the last member a n... Backfill question: which member will be the last one if given endless arithmetic progression?)

For a confident answer, you need to understand the elementary meaning of the arithmetic progression and ... read the assignment carefully!)

In the task of finding the sum of an arithmetic progression, the last term always appears (directly or indirectly), which should be limited. Otherwise, the final, specific amount just doesn't exist. For the solution, it is not important which progression is given: finite or infinite. It doesn't matter how it is set: by a number of numbers, or by the formula of the n-th term.

The most important thing is to understand that the formula works from the first term of the progression to the number c. n. Actually, the full name of the formula looks like this: the sum of the first n terms of an arithmetic progression. The number of these very first members, i.e. n, is determined exclusively by the task. In the task, all this valuable information is often encrypted, yes ... But nothing, in the examples below we will reveal these secrets.)

Examples of tasks for the sum of an arithmetic progression.

First of all, some useful information:

The main difficulty in tasks for the sum of an arithmetic progression lies in the correct definition of the elements of the formula.

The authors of the tasks encrypt these very elements with boundless imagination.) The main thing here is not to be afraid. Understanding the essence of the elements, it is enough to simply decipher them. Let's take a closer look at a few examples. Let's start with an assignment based on a real GIA.

1. An arithmetic progression is specified by the condition: a n = 2n-3.5. Find the sum of its first 10 members.

Good assignment. Easy.) What do we need to know to determine the amount by the formula? First term a 1, last term a n, yes the number of the last member n.

Where to get the number of the last member n? Yes there, in the condition! It says: find the amount first 10 members. Well, what number will be last, tenth member?) You won't believe, its number is tenth!) So, instead of a n in the formula we will substitute a 10 and instead of n- ten. Again, the number of the last member is the same as the number of members.

It remains to determine a 1 and a 10... It is easily calculated by the formula of the nth term, which is given in the problem statement. Not sure how to do this? Visit the previous lesson, without it - nothing.

a 1= 2 1 - 3.5 = -1.5

a 10= 210 - 3.5 = 16.5

S n = S 10.

We found out the meaning of all elements of the formula for the sum of an arithmetic progression. It remains to substitute them, and count:

That's all there is to it. Answer: 75.

Another task based on the GIA. A little more complicated:

2. You are given an arithmetic progression (a n), the difference of which is 3.7; a 1 = 2.3. Find the sum of the first 15 members.

We immediately write the formula for the amount:

This formula allows us to find the value of any member by its number. We are looking for a simple substitution:

a 15 = 2.3 + (15-1) 3.7 = 54.1

It remains to substitute all the elements in the formula for the sum of the arithmetic progression and calculate the answer:

Answer: 423.

By the way, if in the formula the sum instead of a n just substitute the formula for the nth term, we get:

We give similar ones, we get a new formula for the sum of the members of an arithmetic progression:

As you can see, the nth term is not required here. a n... In some tasks, this formula helps a lot, yes ... You can remember this formula. Or you can simply display it at the right time, like here. After all, the formula for the sum and the formula for the nth term must be remembered in every way.)

Now the task is in the form of a short encryption):

3. Find the sum of all positive two-digit numbers that are multiples of three.

How! Neither the first member, nor the last, nor the progression at all ... How to live !?

You have to think with your head and pull out all the elements of the sum of the arithmetic progression from the condition. We know what two-digit numbers are. They consist of two digits.) What two-digit number will be the first? 10, I suppose.) last thing two-digit number? 99, of course! Three-digit ones will follow him ...

Multiples of three ... Hm ... These are numbers that are divisible by three altogether, here! Ten is not divisible by three, 11 is not divisible ... 12 ... is divisible! So, something looms. It is already possible to write a series by the condition of the problem:

12, 15, 18, 21, ... 96, 99.

Will this series be an arithmetic progression? Of course! Each member differs from the previous one strictly by three. If we add 2 or 4 to the term, say, the result, i.e. the new number will no longer be divided entirely by 3. To the heap, you can immediately determine the difference of the arithmetic progression: d = 3. It will come in handy!)

So, you can safely write down some parameters of the progression:

What will be the number n last member? Anyone who thinks that 99 is fatally mistaken ... Numbers - they always go in a row, and our members jump over the top three. They do not match.

There are two ways to solve it. One way is for the super hardworking. You can paint the progression, the whole series of numbers, and count the number of members with your finger.) The second way is for the thoughtful. We need to remember the formula for the nth term. If we apply the formula to our problem, we get that 99 is the thirtieth term of the progression. Those. n = 30.

We look at the formula for the sum of an arithmetic progression:

We look, and we are happy.) We pulled out everything necessary to calculate the amount from the problem statement:

a 1= 12.

a 30= 99.

S n = S 30.

Elementary arithmetic remains. We substitute numbers in the formula and count:

Answer: 1665

Another type of popular puzzles:

4. An arithmetic progression is given:

-21,5; -20; -18,5; -17; ...

Find the sum of members from twentieth to thirty-fourth.

We look at the formula for the sum and ... we get upset.) The formula, let me remind you, calculates the amount from the first member. And in the problem you need to calculate the sum from the twentieth ... The formula will not work.

You can, of course, paint the entire progression in a row, and add members from 20 to 34. But ... it's somehow stupid and takes a long time, right?)

There is a more elegant solution. Let's split our row into two parts. The first part will be from the first member to the nineteenth. Second part - from the twentieth to thirty-fourth. It is clear that if we calculate the sum of the members of the first part S 1-19, yes we add with the sum of the terms of the second part S 20-34, we get the sum of the progression from the first term to the thirty-fourth S 1-34... Like this:

S 1-19 + S 20-34 = S 1-34

This shows that to find the sum S 20-34 can be simple subtraction

S 20-34 = S 1-34 - S 1-19

Both amounts on the right side are considered from the first member, i.e. the standard sum formula is quite applicable to them. Getting started?

We take out the parameters of the progression from the problem statement:

d = 1.5.

a 1= -21,5.

To calculate the sums of the first 19 and first 34 members, we will need the 19th and 34th members. We count them according to the formula of the nth term, as in problem 2:

a 19= -21.5 + (19-1) 1.5 = 5.5

a 34= -21.5 + (34-1) 1.5 = 28

There is nothing left. Subtract 19 members from the total of 34 members:

S 20-34 = S 1-34 - S 1-19 = 110.5 - (-152) = 262.5

Answer: 262.5

One important note! There is a very useful trick in solving this problem. Instead of direct settlement what you need (S 20-34), we counted what, it would seem, is not needed - S 1-19. And then they determined and S 20-34, discarding the unnecessary from the complete result. This "trick with the ears" often saves in evil tasks.)

In this lesson, we examined the problems, for the solution of which it is enough to understand the meaning of the sum of an arithmetic progression. Well, you need to know a couple of formulas.)

Practical advice:

When solving any problem for the sum of an arithmetic progression, I recommend immediately writing out two main formulas from this topic.

Formula of the nth term:

These formulas will immediately tell you what to look for, in which direction to think in order to solve the problem. It helps.

And now tasks for an independent solution.

5. Find the sum of all two-digit numbers that are not divisible by three.

Cool?) The tip is hidden in the note to task 4. Well, task 3 will help.

6. The arithmetic progression is specified by the condition: a 1 = -5.5; a n + 1 = a n +0.5. Find the sum of the first 24 members.

Unusual?) This is a recurring formula. You can read about it in the previous lesson. Do not ignore the link, such tasks are often found in the GIA.

7. Vasya has saved up money for the Holiday. As much as 4550 rubles! And I decided to give my most beloved person (myself) a few days of happiness). To live beautifully, without denying yourself anything. Spend 500 rubles on the first day, and spend 50 rubles more on each subsequent day than on the previous one! Until the supply of money runs out. How many days of happiness did Vasya get?

Difficult?) An additional formula from problem 2 will help.

Answers (in disarray): 7, 3240, 6.