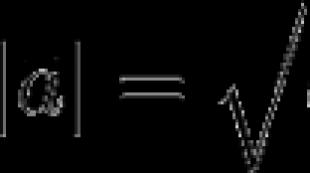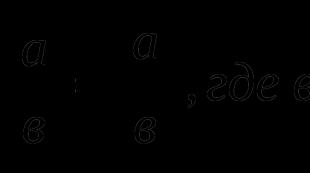Приказки

Формула за дължина на вектора. Намиране на дължината на вектор по координати. Формулата за определяне на координатите на вектор за пространствени задачи

Да намерим дължината на вектора по неговите координати (в правоъгълна координатна система), по координатите на точките на началото и края на вектора и по косинусовата теорема (дадени са 2 вектора и ъгълът между тях).

вектор е насочена отсечка.Дължината на този сегмент определя числената стойност на вектора и се наричавекторна дължина или векторен модул.

1. Изчисляване на дължината на вектор от неговите координати

Ако векторните координати са дадени в плоска (двумерна) правоъгълна координатна система, т.е. a x и a y са известни, тогава дължината на вектора може да се намери по формулата

В случай на вектор в пространството се добавя трета координата

В MS EXCEL израз =ROOT(SUMSQ(B8:B9))ви позволява да изчислите модула на вектора (предполага се, че векторните координатори са въведени в клетките B8: B9, вижте примерния файл ).

Функцията SUMSQ() връща сумата от квадратите на аргументите, т.е. в този случай, еквивалентно на формулата =B8*B8+B9*B9 .

Примерният файл също изчислява дължината на вектора в пространството.

Алтернативна формула е изразът =КОРЕН(СУМА ПРОДУКТ(B8:B9,B8:B9)).

2. Намиране на дължината на вектор чрез координатите на точки

Ако векторът се дава чрез координатите на началната и крайната му точка, тогава формулата ще бъде различна =ROOT(SUMDIFF(C28:C29;B28:B29))

Формулата предполага, че координатите на началната и крайната точка са въведени в диапазоните C28:C29 И B28: B29 съответно.

функция SUMMQVAR() вВръща сумата от квадратите на разликите на съответните стойности в два масива.

Всъщност формулата първо изчислява координатите на вектора (разликата между съответните координати на точките), след което изчислява сумата от техните квадрати.

3. Намиране на дължината на вектор чрез косинусовата теорема

Ако искате да намерите дължината на вектор с помощта на косинусовата теорема, тогава обикновено се дават 2 вектора (техните модули и ъгълът между тях).

Намерете дължината на вектора с помощта на формулата =ROOT(SUMQ(B43:C43)-2*B43*C43*COS(B45))

В клетки B43: B43 съдържа дължините на векторите a и b и клетката B45 - ъгълът между тях в радиани (в части от числото PI() ).

Ако ъгълът е даден в градуси, тогава формулата ще бъде малко по-различна. =ROOT(B43*B43+C43*C43-2*B43*C43*COS(B46*PI()/180))

Забележка: за по-голяма яснота, в клетка със стойност на ъгъл в градуси, можете да използвате, вижте например статията

Окси

ОТНОСНО А ОА.

, където ОА .

По този начин, .

Помислете за пример.

Пример.

Решение.

Отговор:

Oxyzв космоса.

А ОАще бъде диагонал.

В този случай (защото ОА ОА .

По този начин, дължина на вектора .

Пример.

Изчислете дължината на вектора

Решение.

, следователно,

Отговор:

Права на равнина

Общо уравнение

Ax + By + C (> 0).

вектор = (A; B)е вектор с нормална линия.

Във векторна форма: + C = 0, където е радиус-векторът на произволна точка на права линия (фиг. 4.11).

Специални случаи:

1) Чрез + C = 0- права линия, успоредна на оста вол;

2) Ax+C=0- права линия, успоредна на оста Ой;

3) Ax + By = 0- линията минава през началото;

4) y=0- ос вол;

5) х=0- ос Ой.

Уравнение на права линия в отсечки

Където а, б- размерът на сегментите, отрязани от права линия на координатните оси.

Нормално уравнение на права линия(фиг. 4.11)

където е ъгълът, образуван нормално спрямо правата и оста вол; стре разстоянието от началото на координатите до правата.

Привеждане на общото уравнение на права линия до нормална форма:

Тук е нормализираният фактор на директната линия; знакът е избран срещу знака ° С, ако и произволно, ако C=0.

Намиране на дължината на вектор по координати.

Дължината на вектора ще бъде означена с . Поради тази нотация дължината на вектора често се нарича модул на вектора.

Нека започнем с намирането на дължината на вектора в равнината по координатите.

Въвеждаме на равнината правоъгълна декартова координатна система Окси. Нека в него е даден вектор и той има координати. Нека получим формула, която ви позволява да намерите дължината на вектора чрез координатите и .

Отделете от началото на координатите (от точката ОТНОСНО) вектор . Означете проекциите на точката Ана координатните оси като и съответно и разгледайте правоъгълник с диагонал ОА.

По силата на Питагоровата теорема равенството , където . От дефиницията на координатите на вектор в правоъгълна координатна система можем да твърдим, че и , и по конструкция дължината ОАе равно на дължината на вектора, следователно, .

По този начин, формула за намиране на дължината на векторв своите координати в равнината има формата .

Ако векторът се представи като разлагане в координатни вектори , тогава дължината му се изчислява по същата формула , тъй като в този случай коефициентите и са координатите на вектора в дадената координатна система.

Помислете за пример.

Пример.

Намерете дължината на вектора, даден в декартови координати.

Решение.

Незабавно приложете формулата, за да намерите дължината на вектора по координати :

Отговор:

Сега получаваме формула за намиране на дължината на вектор по своите координати в правоъгълна координатна система Oxyzв космоса.

Отделете вектора от началото и означете проекциите на точката Апо координатните оси, както и . След това можем да построим върху страните и правоъгълен паралелепипед, в който ОАще бъде диагонал.

В този случай (защото ОАе диагоналът на правоъгълен паралелепипед), откъдето . Определянето на координатите на вектора ни позволява да напишем равенствата , и дължината ОАе равно на желаната дължина на вектора, следователно, .

По този начин, дължина на вектора в пространството е равно на корен квадратен от сумата от квадратите на неговите координати, тоест се намира по формулата .

Пример.

Изчислете дължината на вектора , където са ортите на правоъгълната координатна система.

Решение.

Дадено ни е разширението на вектор по отношение на координатните вектори на формата , следователно, . Тогава, според формулата за намиране на дължината на вектор по координати, имаме .

На абсцисата и ординатната ос се наричат координати вектор. Координатите на вектора обикновено се посочват във формуляра (x, y), а самият вектор като: = (x, y).

Формулата за определяне на координатите на вектор за двумерни задачи.

В случай на двумерна задача, вектор с известни координати на точки A(x 1; y 1)И Б(х 2 ; г 2 ) може да се изчисли:

\u003d (x 2 - x 1; y 2 - y 1).

Формулата за определяне на координатите на вектор за пространствени задачи.

В случай на пространствен проблем, вектор с известни координати на точкиА (x 1; y 1;z 1 ) и Б (х 2 ; г 2 ; z 2 ) може да се изчисли по формулата:

= (х 2 - х 1 ; г 2 - г 1 ; z 2 - z 1 ).

Координатите дават цялостно описание на вектора, тъй като е възможно да се конструира самият вектор от координатите. Познавайки координатите, е лесно да се изчисли и дължина на вектора. (Имот 3 по-долу).

Свойства на векторните координати.

1. Всякакви равни векторив една координатна система имат равни координати.

2. Координати колинеарни векторипропорционален. При условие, че нито един от векторите не е равен на нула.

3. Квадратът на дължината на произволен вектор е равен на сумата от неговите квадрати координати.

4.Когато операцията векторни умноженияНа реално числовсяка негова координата се умножава по това число.

5. По време на операцията на векторно добавяне, ние изчисляваме сумата на съответния векторни координати.

6. Скаларно произведениена два вектора е равно на сумата от произведенията на съответните им координати.

Дължината на вектора a → ще бъде означена с a → . Тази нотация е подобна на модула на число, така че дължината на вектор се нарича още модул на вектор.

За да се намери дължината на вектор в равнината по неговите координати, е необходимо да се разгледа правоъгълна декартова координатна система O x y . Нека съдържа някакъв вектор a → с координати a x ; a y . Въвеждаме формула за намиране на дължината (модула) на вектора a → по отношение на координатите a x и a y .

Отделете вектора O A → = a → от началото. Нека дефинираме съответните проекции на точка A върху координатните оси като A x и A y . Сега разгледайте правоъгълник O A x A A y с диагонал O A .

От Питагоровата теорема следва равенството O A 2 = O A x 2 + O A y 2 , откъдето O A = O A x 2 + O A y 2 . От вече известната дефиниция на координатите на вектор в правоъгълна декартова координатна система получаваме, че O A x 2 = a x 2 и O A y 2 = a y 2 , като по построение дължината на O A е равна на дължината на вектор O A → , следователно O A → = O A x 2 + O A y 2.

Следователно се оказва, че формула за намиране на дължината на вектор a → = a x ; a y има съответния вид: a → = a x 2 + a y 2 .

Ако векторът a → е даден като разширение в координатни вектори a → = a x i → + a y j → , тогава неговата дължина може да се изчисли по същата формула a → = a x 2 + a y 2 , в този случай коефициентите a x и a y са като координатите на вектора a → в дадената координатна система.

Пример 1

Да се изчисли дължината на вектора a → = 7 ; e , дадени в правоъгълна координатна система.

Решение

За да намерим дължината на вектор, ще използваме формулата за намиране на дължината на вектор по координати a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e

Отговор: a → = 49 + e .

Формула за намиране на дължината на вектор a → = a x ; a y ; a z чрез неговите координати в декартовата координатна система Oxyz в пространството, се извежда подобно на формулата за случая в равнината (вижте фигурата по-долу)

В този случай O A 2 \u003d O A x 2 + O A y 2 + O A z 2 (тъй като OA е диагоналът на правоъгълен паралелепипед), следователно O A \u003d O A x 2 + O A y 2 + O A z 2. От дефиницията на координатите на вектора можем да запишем следните равенства O A x = a x ; O A y = a y ; O A z = a z ; , а дължината на OA е равна на дължината на вектора, който търсим, следователно O A → = O A x 2 + O A y 2 + O A z 2 .

От това следва, че дължината на вектора a → = a x ; a y ; a z е равно на a → = a x 2 + a y 2 + a z 2 .

Пример 2

Изчислете дължината на вектора a → = 4 i → - 3 j → + 5 k → , където i → , j → , k → са единичните вектори на правоъгълната координатна система.

Решение

Дадено е разлагане на вектор a → = 4 i → - 3 j → + 5 k → , неговите координати са a → = 4 , - 3 , 5 . Използвайки формулата по-горе, получаваме a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 .

Отговор: a → = 5 2 .

Дължината на вектор по отношение на координатите на началната и крайната му точка

По-горе бяха получени формули, които ви позволяват да намерите дължината на вектор по неговите координати. Разглеждали сме случаи в равнината и в триизмерното пространство. Нека ги използваме, за да намерим координатите на вектора по координатите на началната и крайната му точка.

И така, дадени точки с дадени координати A (a x; a y) и B (b x; b y), следователно векторът A B → има координати (b x - a x; b y - a y), което означава, че неговата дължина може да се определи по формулата: A B → = ( b x - a x) 2 + (b y - a y) 2

И ако са дадени точки с дадени координати A (a x; a y; a z) и B (b x; b y; b z) в триизмерното пространство, тогава дължината на вектора A B → може да се изчисли по формулата

A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2

Пример 3

Намерете дължината на вектора A B → ако в правоъгълна координатна система A 1 , 3 , B-3 , 1 .

Решение

Използвайки формулата за намиране на дължината на вектора от координатите на началната и крайната точка на равнината, получаваме A B → = (b x - a x) 2 + (b y - a y) 2: A B → = (- 3 - 1) 2 + (1 - 3) 2 = 20 - 2 3 .

Второто решение предполага последователно прилагане на тези формули: A B → = (- 3 - 1; 1 - 3) = (- 4; 1 - 3) ; A B → = (- 4) 2 + (1 - 3) 2 = 20 - 2 3 . -

Отговор: A B → = 20 - 2 3 .

Пример 4

Определете за какви стойности дължината на вектора A B → е равна на 30, ако A (0 , 1 , 2) ; B (5 , 2 , λ 2) .

Решение

Първо, нека запишем дължината на вектора A B → според формулата: A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2 = (5 - 0) 2 + (2 - 1) 2 + (λ 2 - 2) 2 = 26 + (λ 2 - 2) 2

След това приравняваме получения израз на 30, от тук намираме желания λ:

26 + (λ 2 - 2) 2 = 30 26 + (λ 2 - 2) 2 = 30 (λ 2 - 2) 2 = 4 λ 2 - 2 = 2 и l и λ 2 - 2 = - 2 λ 1 = - 2, λ 2 = 2, λ 3 = 0.

Отговор: λ 1 \u003d - 2, λ 2 \u003d 2, λ 3 \u003d 0.

Намиране на дължината на вектор чрез косинусния закон

Уви, координатите на вектор не винаги са известни в задачите, така че нека разгледаме други начини за намиране на дължината на вектор.

Нека са дадени дължините на два вектора A B → , A C → и ъгълът между тях (или косинусът на ъгъла) и се изисква да се намери дължината на вектора B C → или C B → . В този случай трябва да използвате косинусовата теорема в триъгълника △ A B C , да изчислите дължината на страната B C , която е равна на желаната дължина на вектора.

Нека разгледаме такъв случай в следния пример.

Пример 5

Дължините на векторите A B → и A C → са съответно равни на 3 и 7, а ъгълът между тях е равен на π 3 . Изчислете дължината на вектора B C → .

Решение

Дължината на вектора B C → в този случай е равна на дължината на страната B C на триъгълника △ A B C . Дължините на страните A B и A C на триъгълника са известни от условието (те са равни на дължините на съответните вектори), известен е и ъгълът между тях, така че можем да използваме косинусовата теорема: B C 2 = A B 2 + A C 2 - 2 A B A C cos ∠ (A B , → A C →) = 3 2 + 7 2 - 2 3 7 cos π 3 = 37 ⇒ B C = 37 Така, B C → = 37 .

Отговор: B C → = 37 .

И така, за да намерите дължината на вектор по координати, има следните формули a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2, според координатите на точките на началото и края на вектора A B → = (b x - a x) 2 + ( b y - a y) 2 или A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2, в някои случаи косинусовата теорема трябва да се използва.

Ако забележите грешка в текста, моля, маркирайте я и натиснете Ctrl+Enter

6.4. Някои приложения на точковия продукт

11. Изразяване на скаларното произведение на вектор чрез координатите на факторите. Теорема.

12. Дължина на вектор, дължина на отсечка, ъгъл между векторите, условие за перпендикулярност на векторите.

13. Векторно произведение на вектори, неговите свойства. Площта на успоредник.

14. Смесено произведение на вектори, неговите свойства. Условието за векторна компланарност. Обемът на паралелепипеда. Обемът на пирамидата.

15. Методи за нанасяне на права върху равнина.

16. Нормално уравнение на права върху равнина (извод). Геометричният смисъл на коефициентите.

17. Уравнението на права линия на равнина в сегменти (заключение).

Намаляване на общото уравнение на равнината до уравнението на равнината в сегменти.

18. Уравнение на права линия в равнина с наклон (изход).

19. Уравнение на права на равнина, минаваща през две точки (извод).

20. Ъгъл между прави в равнина (заключение).

21. Разстояние от точка до права в равнина (изход).

22. Условия на успоредност и перпендикулярност на прави в равнина (заключение).

23. Уравнението на равнината. Нормално уравнение на равнината (извод). Геометричният смисъл на коефициентите.

24. Уравнението на равнината в сегменти (заключение).

25. Уравнение на равнина, минаваща през три точки (изход).

26. Ъгъл между равнините (изход).

27. Разстояние от точка до равнина (изход).

28. Условия на паралелност и перпендикулярност на равнините (заключение).

29. Уравнения на права линия в r3. Уравнения на права, минаваща през две неподвижни точки (извод).

30. Канонични уравнения на права линия в пространството (извеждане).

Съставяне на канонични уравнения на права линия в пространството.

Частни случаи на канонични уравнения на права линия в пространството.

Канонични уравнения на права, минаваща през две дадени точки в пространството.

Преход от канонични уравнения на права линия в пространството към други видове уравнения на права линия.

31. Ъгъл между прави (изход).

32. Разстояние от точка до права в равнина (изход).

Разстояние от точка до права в равнина - теория, примери, решения.

Първият начин за намиране на разстоянието от дадена точка до дадена права линия на равнина.

Вторият метод, който ви позволява да намерите разстоянието от дадена точка до дадена линия на равнината.

Решаване на задачи за намиране на разстоянието от дадена точка до дадена права в равнина.

Разстояние от точка до права линия в пространството - теория, примери, решения.

Първият начин за намиране на разстоянието от точка до линия в пространството.

Вторият метод, който ви позволява да намерите разстоянието от точка до права линия в пространството.

33. Условия на успоредност и перпендикулярност на правите в пространството.

34. Взаимно разположение на прави в пространството и права с равнина.

35. Класическото уравнение на елипса (извод) и неговото построяване. Каноничното уравнение на елипса има формата, където са положителни реални числа, освен това Как да построим елипса?

36. Класическото уравнение на хипербола (извод) и неговото построяване. Асимптоти.

37. Канонично уравнение на парабола (извеждане) и построяване.

38. Функция. Основни определения. Графики на основни елементарни функции.

39. Цифрови поредици. Границата на числовата последователност.

40. Безкрайно малки и безкрайно големи количества. Теорема за връзката между тях, свойства.

41. Теореми за действия върху променливи с крайни граници.

42. Номер e.

Съдържание

Методи за определяне

Имоти

История

Приближения

43. Дефиниция на лимит на функция. Разкриване на несигурности.

44. Забележителни граници, тяхното заключение. Еквивалентни безкрайно малки количества.

Съдържание

Първият прекрасен лимит

Втората прекрасна граница

45. Едностранни граници. Непрекъснатост и прекъсване на функцията. Едностранни ограничения

Лява и дясна граница на функция

Точка на прекъсване от първи род

Точка на прекъсване от втори род

Точка на пречупване

46. Дефиниция на производна. Геометричен смисъл, механичен смисъл на производната. Допирателни и нормални уравнения за крива и точка.

47. Теореми за производната на обратните, комплексни функции.

48. Производни на най-простите елементарни функции.

49. Диференциране на параметрични, неявни и експоненциални функции.

21. Диференциране на неявни и параметрично дефинирани функции

21.1. Неявна функция

21.2. Параметрично дефинирана функция

50. Производни от по-високи разряди. Формула на Тейлър.

51. Диференциал. Приложение на диференциала за приближени изчисления.

52. Теореми на Рол, Лагранж, Коши. Правилото на L'Hopital.

53. Теорема за необходимите и достатъчни условия за монотонност на функция.

54. Определяне на максимум, минимум на функция. Теореми за необходими и достатъчни условия за съществуване на екстремум на функция.

Теорема (необходимо екстремално условие)

55. Изпъкналост и вдлъбнатост на кривите. Инфлексни точки. Теореми за необходими и достатъчни условия за съществуване на инфлексни точки.

Доказателство

57. Детерминанти от n-ти ред, техните свойства.

58. Матрици и действия върху тях. Ранг на матрицата.

Определение

Свързани определения

Имоти

Линейна трансформация и ранг на матрицата

59. Обратна матрица. Теорема за съществуването на обратна матрица.

60. Системи линейни уравнения. Матрично решение на системи от линейни уравнения. Правилото на Крамър. Метод на Гаус. Теоремата на Кронекер-Капели.

Решаване на системи от линейни алгебрични уравнения, методи за решаване, примери.

Дефиниции, понятия, обозначения.

Решаване на елементарни системи линейни алгебрични уравнения.

Решаване на системи от линейни уравнения по метода на Крамер.

Решаване на системи от линейни алгебрични уравнения по матричен метод (с помощта на обратната матрица).

Решаване на системи линейни уравнения по метода на Гаус.

Решаване на системи от линейни алгебрични уравнения от общ вид.

Теорема на Кронекер-Капели.

Метод на Гаус за решаване на системи от линейни алгебрични уравнения от общ вид.

Записване на общото решение на хомогенни и нехомогенни линейни алгебрични системи с помощта на векторите на основната система от решения.

Решаване на системи от уравнения, свеждащи се до слоу.

Примери за задачи, които се свеждат до решаване на системи от линейни алгебрични уравнения.

12. Дължина на вектор, дължина на отсечка, ъгъл между векторите, условие за перпендикулярност на векторите.

вектор - това е насочен сегмент, свързващ две точки в пространството или в равнина.Векторите обикновено се означават или с малки букви, или с начална и крайна точка. Отгоре обикновено има тире.

Например вектор, насочен от точка Акъм основния въпрос б, може да се означи а ,

Нулев вектор 0 или 0 - е вектор, чиято начална и крайна точка са еднакви, т.е. А = б. Оттук, 0 = – 0 .

Дължина (модул) на вектораа е дължината на сегмента, който го представлява AB, означено с |а | . По-специално | | 0 | = 0.

Векторите се наричат колинеаренако насочените им отсечки лежат на успоредни прави. Колинеарни вектори а И b са определени а || b .

Извикват се три или повече вектора компланаренако лежат в една равнина.

Добавяне на вектори. Тъй като векторите са насоченисегменти, тогава може да се извърши тяхното добавяне геометрично. (Алгебричното добавяне на вектори е описано по-долу, в параграфа "Единични ортогонални вектори"). Нека се преструваме, че

а = АВи b = CD,

тогава векторът __ __

а + b = AB+ CD

е резултат от две операции:

а)паралелен трансфередин от векторите, така че началната му точка да съвпада с крайната точка на втория вектор;

b)геометрично добавяне, т.е. конструиране на получения вектор, преминаващ от началната точка на фиксирания вектор до крайната точка на транслирания вектор.

Изваждане на вектори. Тази операция се свежда до предишната чрез заместване на извадения вектор с противоположния: а – b =а + (– b ) .

Законите на събирането.

аз а + b = b + а (Величимо право).

II. (а + b ) + ° С = а + (b + ° С ) (Комбинирано право).

III. а + 0 = а .

IV. а + (– а ) = 0 .

Закони за умножение на вектор с число.

аз 1 · а = а , 0 · а = 0 , м· 0 = 0 , (– 1) · а = – а .

II. ма = а м,| ма | = | м | · | a | .

III. m(nа ) = (m n)а . (Комбиниран

закон за умножение).

IV. (m+n) а = ма +nа , (Дистрибутор

м(а + b ) = ма + мb . закон за умножение).

Скаларно произведение на вектори. __ __

Ъгъл между ненулеви вектори ABИ CDе ъгълът, образуван от векторите по време на тяхното успоредно пренасяне, докато точките се изравнят АИ C. Точково произведение на векториа И b наречено число, равно на произведението на техните дължини по косинуса на ъгъла между тях:

Ако един от векторите е нула, тогава тяхното скаларно произведение, в съответствие с дефиницията, е нула:

(а , 0 ) = ( 0 , b ) = 0 .

Ако и двата вектора са различни от нула, тогава косинусът на ъгъла между тях се изчислява по формулата:

Скаларен продукт ( a , a ) равно на | а | 2 се нарича скаларен квадрат.Дължина на вектора а и неговият скаларен квадрат са свързани с:

Точково произведение на два вектора:

- положителноако ъгълът между векторите пикантен;

- отрицателенако ъгълът между векторите тъп.

Тогава скаларното произведение на два ненулеви вектора е нула и то само ако ъгълът между тях е прав, т.е. когато тези вектори са перпендикулярни (ортогонални):

Свойства на скаларното произведение. За всякакви вектори а , b, c и произволно число мважат следните отношения:

аз (а , b ) = (б, а ) . (Величимо право)

II. (ма , b ) = м(а , b ) .

III.(a + b, c ) = (а , ° С ) + (б, ° С ). (Закон за разпределение)

Единични ортогонални вектори. Във всяка правоъгълна координатна система можете да въведете единични по двойки ортогонални векториаз , й И к свързани с координатните оси: аз - с ос х, й - с ос YИ к - с ос З. Според това определение:

(аз , дж ) = (аз , к ) = (й , к ) = 0,

| аз | =| j | =| k | = 1.

Всеки вектор а може да се изрази чрез тези вектори по уникален начин: а = хаз + гj + zк . Друга форма на писане: а = (x, y, z). Тук х, г, z-координативектор а в тази координатна система. В съответствие с последното отношение и свойства на единичните ортогонални вектори i, j , к скаларното произведение на два вектора може да се изрази по различен начин.

Позволявам а = (x, y, z); b = (u, v, w). Тогава ( а , b ) = xi +yv +zw.

Скаларното произведение на два вектора е равно на сумата от произведенията на съответните координати.

Дължина (модул) на вектора а = (х, г, z ) е равно на:

Освен това вече сме в състояние алгебриченоперациите върху вектори, а именно добавяне и изваждане на вектори, могат да се извършват чрез координати:

а + b= (x + u, y + v, z + w) ;

а – b= (х–u, y– v, z–w) .

Векторно произведение на вектори. векторно изкуство [а, b ] векториа Иb (в този ред) се нарича вектор:

Има друга формула за дължината на вектора [ а, б ] :

| [ а, б ] | = | а | | b | грях( а, б ) ,

т.е. дължина ( модул ) кръстосано произведение на векториа Иb е равно на произведението на дължините (модулите) на тези вектори и синуса на ъгъла между тях.С други думи: дължина (модул) на вектор[ а, б ] числено равна на площта на успоредника, изграден върху векторите а Иb .