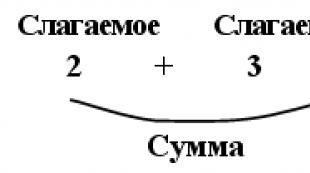
İki inandırıcı təsadüfi və qeyri-mümkün hadisə ilə gəlin. Özünüz iki etibarlı, təsadüfi və qeyri-mümkün hadisə ilə gəlin. Yeni materialın öyrənilməsi
Dərsin mövzusu: "Təsadüfi, etibarlı və mümkün olmayan hadisələr"
Kurikulumda dərsin yeri: “Kombinatorika. Təsadüfi hadisələr "dərs 5/8
Dərs növü: Yeni biliklərin formalaşmasında dərs
Dərsin məqsədləri:
Təhsil:
o təsadüfi, etibarlı və tərifini təqdim edir mümkün olmayan hadisə;
o real vəziyyət prosesində ehtimal nəzəriyyəsinin şərtlərini müəyyən etməyi öyrətmək: etibarlı, qeyri-mümkün, bərabər ehtimal olunan hadisələr;
İnkişaf edir:
o məntiqi təfəkkürün inkişafına kömək etmək,
o tələbələrin idrak marağı,
o müqayisə və təhlil etmək bacarığı,
Təhsil:
o riyaziyyatın öyrənilməsinə marağı artırmaq,
o tələbələrin dünyagörüşünün inkişafı.
o intellektual bacarıqlara və əqli əməliyyatlara sahib olmaq;
Tədris üsulları: izahlı və illüstrativ, reproduktiv, riyazi diktə.
UMK: Riyaziyyat: 6-cı sinif üçün dərslik. və başqalarının redaktorluğu ilə “Təhsil” nəşriyyatı, 2008, Riyaziyyat, 5-6: kitab. müəllim üçün / [, [ ,]. - M.: Təhsil, 2006.
Didaktik material: lövhədə plakatlar.
Ədəbiyyat:
1. Riyaziyyat: dərslik. 6 cl üçün. ümumi təhsil. qurumlar / və s.]; red. ,; Böyüdü. akad. Elmlər, Ros. akad. təhsil, “Təhsil” nəşriyyatı. - 10-cu nəşr. - M.: Təhsil, 2008.-302 s.: xəstə. - (Akademik məktəb dərsliyi).
2. Riyaziyyat, 5-b: kitab. müəllim üçün / [,]. - M.: Təhsil, 2006 .-- 191 s. : xəstə.
4. Statistikada, kombinatorikada və ehtimal nəzəriyyəsində məsələlərin həlli. 7-9 sinif. / müəllif - komp. ... Ed. 2-ci, rev. - Volqoqrad: Müəllim, 2006.-428 s.
5. Riyaziyyatdan informasiya texnologiyalarından istifadə etməklə dərslər. 5-10 siniflər. Metodik - elektron tətbiqi olan dərslik / s. 2-ci nəşr, Stereotip. - M .: "Globus" nəşriyyatı, 2010. - 266 s. (Müasir məktəb).
6. Müasir məktəblərdə riyaziyyatın tədrisi. Təlimatlar... Vladivostok: PIPPKRO nəşriyyatı, 2003.
DƏRS PLANI
I. Təşkilati məqam.
II. Şifahi iş.
III. Yeni materialın öyrənilməsi.
IV. Bacarıq və bacarıqların formalaşdırılması.
V. Dərsin xülasəsi.
V. Ev tapşırığı.
DƏRSLƏR zamanı
1. Təşkilati məqam
2. Biliklərin yenilənməsi
15*(-100) |
Şifahi iş:
3. Yeni materialın izahı
Müəllim: Həyatımız çox şansdır. Belə bir elm var “Ehtimallar nəzəriyyəsi”. Onun dilindən istifadə edərək bir çox hadisələri və vəziyyəti təsvir edə bilərsiniz.
Makedoniyalı İskəndər və ya Dmitri Donskoy kimi qədim generallar döyüşə hazırlaşarkən təkcə döyüşçülərin şücaətinə və bacarığına deyil, həm də şansa arxalanırdılar.
Bir çox insanlar riyaziyyatı əbədi həqiqətlərə görə sevirlər ki, iki dəfə iki həmişə dörddür, cüt ədədlərin cəmi cütdür, düzbucaqlının sahəsi onun bitişik tərəflərinin hasilinə bərabərdir və s. Həll etdiyiniz hər hansı bir məsələdə hamı eyni cavab - yalnız həllində səhv etmək lazım deyil.
Real həyat o qədər də sadə və sadə deyil. Bir çox hadisələrin nəticələrini əvvəlcədən proqnozlaşdırmaq mümkün deyil. Məsələn, atılan sikkənin hansı tərəfə düşəcəyini, gələn il ilk qarın nə vaxt yağacağını və ya yaxın bir saat ərzində şəhərdə neçə nəfərin zəng etmək istəyəcəyini dəqiq söyləmək mümkün deyil. Belə gözlənilməz hadisələrə deyilir təsadüfi .
Bununla belə, işin də öz qanunları var ki, onlar təsadüfi hadisələrin dəfələrlə təkrarlanması ilə özünü göstərməyə başlayır. Bir sikkəni 1000 dəfə çevirsəniz, "başlar" vaxtın təxminən yarısında düşəcək, bunu iki və ya hətta on atış haqqında söyləmək olmaz. “Təxminən” yarım demək deyil. Bu, bir qayda olaraq, belə də ola bilər, olmaya da bilər. Qanun qətiyyən heç nəyi ifadə etmir, lakin hər hansı təsadüfi hadisənin baş verəcəyinə müəyyən dərəcədə əminlik verir.
Bu cür nümunələr riyaziyyatın xüsusi bölməsi tərəfindən öyrənilir - Ehtimal nəzəriyyəsi . Onun köməyi ilə həm ilk qarın yağma tarixini, həm də telefon zənglərinin sayını proqnozlaşdırmaq daha böyük dərəcədə inamla (lakin hələ də dəqiq deyil) mümkündür.
Ehtimal nəzəriyyəsi bizimlə ayrılmaz şəkildə bağlıdır Gündəlik həyat... Bu, bizə bir çox ehtimal qanunları yaratmaq üçün gözəl imkan verir. empirik olaraq təsadüfi təcrübələri dəfələrlə təkrarlamaqla. Bu təcrübələr üçün materiallar çox vaxt adi sikkə, zər, domino dəsti, nərd, rulet və ya hətta kart göyərtəsi olacaqdır. Bu maddələrin hər biri bir növ oyunlarla bağlıdır. Fakt budur ki, iş burada ən çox rast gəlinən formada görünür. Və ilk ehtimal problemləri oyunçuların qalib gəlmək şanslarının qiymətləndirilməsi ilə bağlı idi.
Müasir ehtimal nəzəriyyəsi qumardan uzaqlaşdı, lakin onun rekvizitləri hələ də şansın ən sadə və ən etibarlı mənbəyidir. Rulet çarxı və zərlə məşq etdikdən sonra siz real həyat vəziyyətlərində təsadüfi hadisələrin baş vermə ehtimalını necə hesablamağı öyrənəcəksiniz ki, bu da sizə uğur şanslarınızı qiymətləndirməyə, fərziyyələri yoxlamağa və təkcə oyunlarda və lotereyalarda deyil, optimal qərarlar qəbul etməyə imkan verəcək. .
Ehtimal məsələlərini həll edərkən çox diqqətli olun, atdığınız hər addımı əsaslandırmağa çalışın, çünki riyaziyyatın başqa heç bir sahəsində bu qədər paradoks yoxdur. Ehtimal nəzəriyyəsi kimi. Və bəlkə də bunun əsas izahı onun yaşadığımız real dünya ilə əlaqəsidir.
Bir çox oyunlarda hər üzdə 1-dən 6-ya qədər fərqli sayda nöqtə olan zardan istifadə olunur.Oyunçu zar atır, neçə nöqtənin düşdüyünə baxır (üstdə olan üzdə) və müvafiq sayda hərəkət edir. : 1,2,3 , 4,5 və ya 6. Zərbə atmaq təcrübə, təcrübə, sınaq sayıla bilər və əldə edilən nəticə hadisədir. İnsanlar adətən bir hadisənin başlanğıcını təxmin etməkdə, onun nəticəsini proqnozlaşdırmaqda çox maraqlıdırlar. Onlar zar atarkən hansı proqnozları verə bilərlər?
İlk proqnoz: 1, 2, 3, 4, 5 rəqəmlərindən biri çıxacaq, yoxsa 6. Sizcə, proqnozlaşdırılan hadisə gələcək, ya yox? Təbii ki, mütləq gələcək.
Bu təcrübədə mütləq baş verəcək bir hadisə deyilir etibarlı hadisə.
İkinci proqnoz : 7 nömrə düşəcək.Sizcə proqnozlaşdırılan hadisə gələcək ya yox? Əlbəttə ki, olmayacaq, sadəcə mümkün deyil.
Verilmiş təcrübədə baş verə bilməyən hadisəyə deyilir qeyri-mümkün hadisə.
Üçüncü proqnoz : 1 nömrə düşəcək.Sizcə proqnozlaşdırılan hadisə gələcək ya yox? Biz bu suala tam əminliklə cavab verə bilmərik, çünki proqnozlaşdırılan hadisə baş verə bilər və ya olmaya da bilər.
Eyni şəraitdə baş verə bilən və ya olmaya bilən hadisələr çağırılır təsadüfi.
Misal. Qutuda 5 şirniyyat mavi qablaşdırmada və biri ağda var. Qutuya baxmadan təsadüfi bir konfet çıxarırlar. Bunun hansı rəngdə olacağını əvvəlcədən deyə bilərsinizmi?
Məşq edin : Aşağıdakı tapşırıqlarda qeyd olunan hadisələri təsvir edin. Nə qədər etibarlı, qeyri-mümkün və ya təsadüfi.
1. Sikkə çevirin. Gerb göründü. (təsadüfi)
2. Ovçu canavarı vurub vurdu. (təsadüfi)
3. Tələbə hər axşam gəzintiyə çıxır. Bazar ertəsi gəzinti zamanı üç tanışı ilə rastlaşıb. (təsadüfi)
4. Gəlin zehni olaraq aşağıdakı təcrübəni həyata keçirək: su stəkanını tərs çevirin. Əgər bu təcrübə kosmosda deyil, evdə və ya sinifdə aparılsa, o zaman su töküləcək. (etibarlı)
5. Hədəfə üç atəş açıldı”. Beş hit oldu " (mümkün deyil)
6. Daşı yuxarı atın. Daş havada asılı vəziyyətdə qalır. (mümkün deyil)
Misal Petya natural ədəd yaratdı. Tədbir aşağıdakı kimidir:
a) cüt ədəd nəzərdə tutulur; (təsadüfi)
b) tək ədəd düşünülür; (təsadüfi)
c) nə cüt, nə də tək olmayan ədəd nəzərdə tutulur; (mümkün deyil)
d) tək və ya cüt olan ədəd. (etibarlı)
Bu şərtlər altında şansları bərabər olan hadisələr deyilir bərabər ehtimal.
Şansları bərabər olan təsadüfi hadisələr çağırılır eyni dərəcədə mümkündür və ya bərabər ehtimal .
Lövhədə poster yerləşdirin.
Şifahi imtahanda tələbə qarşısında qoyulmuş biletlərdən birini götürür. İmtahan biletlərindən hər hansı birini götürmək şansları bərabərdir. Zər atarkən 1-dən 6-ya qədər istənilən sayda xal, həmçinin sikkə atarkən "başlar" və ya "quyruqlar" əldə etmək eyni dərəcədə mümkündür.
Ancaq bütün hadisələr belə deyil eyni dərəcədə mümkündür... Siqnal çalmaya bilər, lampa sönə bilər, avtobus xarab ola bilər, amma normal şəraitdə belə hadisələr çətin. Çox güman ki, həyəcan siqnalı çalacaq, işıq yanacaq və avtobus hərəkət edəcək.
Bəzi hadisələr şanslar daha çox, bu o deməkdir ki, onlar daha çox ehtimal olunur - etibarlılığa daha yaxındır. Digərlərinin şansları daha azdır, onların ehtimalı azdır - mümkünsüzə yaxındır.
Mümkün olmayan hadisələrin baş vermə şansı yoxdur və etibarlı hadisələrin baş verməsi üçün hər cür şans var, müəyyən şərtlər daxilində mütləq baş verəcəklər.
Misal Petya və Kolya ad günlərini müqayisə edirlər. Tədbir aşağıdakı kimidir:
a) ad günləri uyğun gəlmir; (təsadüfi)
b) onların doğum günləri eynidir; (təsadüfi)
d) hər ikisinin ad günü bayramlara düşür - Yeni il(1 yanvar) və Rusiyanın Müstəqillik Günü (12 iyun). (təsadüfi)
3. Bacarıq və bacarıqların formalaşdırılması
Dərslikdəki məsələ 000. Aşağıdakı təsadüfi hadisələrdən hansı etibarlıdır, mümkündür:
a) tısbağa danışmağı öyrənəcək;
b) sobanın üzərindəki çaydandakı su qaynayacaq;
d) lotereyada iştirak etməklə udmuş olursunuz;
e) uduş-uduş lotereyasında iştirak etməklə qalib gəlməyəcəksiniz;
f) şahmat oyununda uduzacaqsınız;
g) sabah bir yadplanetli ilə qarşılaşacaqsınız;
h) gələn həftə hava pisləşəcək; i) zəngə basdınız, lakin zəng çalmadı; j) bu gün cümə axşamıdır;
k) cümə axşamından sonra cümə günü olacaq; m) Cümə günündən sonra cümə axşamı olacaqmı?
Qutularda 2 qırmızı, I sarı və 4 yaşıl top var. Qutudan təsadüfi olaraq üç top çıxarılır. Aşağıdakı hadisələrdən hansı qeyri-mümkün, təsadüfi, etibarlıdır:
A: üç yaşıl top çəkiləcək;
S: üç qırmızı top çəkiləcək;
C: iki rəngli toplar çəkiləcək;
D: eyni rəngli toplar çəkiləcək;
E: uzadılmış toplar arasında mavi var;
F: uzadılmışlar arasında üç rəngli toplar var;
G: Uzadılanlar arasında iki sarı top varmı?
Özünüzü sınayın. (riyaziyyatdan diktə)
1) Aşağıdakı hadisələrdən hansının qeyri-mümkün, hansının etibarlı, hansının təsadüfi olduğunu göstərin:
· “Spartak” – “Dinamo” futbol matçı heç-heçə başa çatacaq (təsadüfi)
Qalib-qazan lotereyasında iştirak etməklə qazanacaqsınız ( etibarlı)
Qar gecə yarısı yağacaq və 24 saatdan sonra günəş parlayacaq (mümkün deyil)
· Sabah riyaziyyatdan imtahan olacaq. (təsadüfi)
· Siz ABŞ prezidenti seçiləcəksiniz. (mümkün deyil)
· Siz Rusiyanın prezidenti seçiləcəksiniz. (təsadüfi)
2) Siz mağazada televizor aldınız, ona istehsalçı iki il zəmanət verir. Aşağıdakı hadisələrdən hansı qeyri-mümkün, hansı təsadüfi, hansı etibarlıdır?
· Televizor bir il ərzində xarab olmayacaq. (təsadüfi)
Televizor iki il xarab olmayacaq ... (təsadüfi)
· İki il ərzində televizorun təmiri üçün pul ödəməli olmayacaqsınız. (etibarlı)
· Üçüncü ildə televizor xarab olacaq. (təsadüfi)
3) 15 sərnişin daşıyan avtobus 10 dayanacaq etməli olacaq. Aşağıdakı hadisələrdən hansı qeyri-mümkün, hansı təsadüfi, hansı etibarlıdır?
· Bütün sərnişinlər müxtəlif dayanacaqlarda avtobusdan düşəcəklər. (mümkün deyil)
· Bütün sərnişinlər bir dayanacaqda enəcəklər. (təsadüfi)
· Hər dayanacaqda heç olmasa kimsə düşür. (təsadüfi)
· Heç kimin düşmədiyi bir dayanacaq olacaq. (təsadüfi)
· Bütün dayanacaqlarda bərabər sayda sərnişin ayrılacaq. (mümkün deyil)
· Bütün dayanacaqlarda tək sayda sərnişin ayrılacaq. (mümkün deyil)
Dərsin xülasəsi
Tələbələrə suallar:
Hansı hadisələr təsadüfi adlanır?
Hansı hadisələrə bərabər ehtimal deyilir?
Hansı hadisələr inandırıcı adlanır? qeyri-mümkün?
Hansı hadisələr daha çox ehtimal adlanır? az ehtimal?
Ev tapşırığı : səh 9.3
№ 000. Etibarlı, qeyri-mümkün hadisələrin, eləcə də mütləq baş verəcəyini söyləmək mümkün olmayan hadisələrin üç nümunəsini düşünün.
902. Qutuda 10 qırmızı, 1 yaşıl və 2 göy qələm var. Qutudan təsadüfi olaraq iki tutacaq çıxarılır. Aşağıdakı hadisələrdən hansı qeyri-mümkündür, etibarlıdır:
A: iki qırmızı tutacaq çıxarılacaq; S: iki yaşıl tutacaq çıxarılacaq; C: iki mavi tutacaq çıxarılacaq; D: Müxtəlif rəngli iki tutacaq çıxarılacaq;
E: iki karandaş çıxarılacaq? 03. Eqor və Danila razılaşdılar: dönər masanın oxu (şək. 205) ağ sahədə dayanarsa, Yeqor hasarı rəngləyəcək, mavi sahədəsə - Danila. Hansı oğlanın hasarın rənglənməsi ehtimalı daha çoxdur?
Dərsin məqsədi:
- Etibarlı, qeyri-mümkün və təsadüfi hadisələr anlayışını təqdim edin.
- Hadisələrin növünü müəyyən etmək üçün bilik və bacarıqları formalaşdırmaq.
- İnkişaf etdirin: hesablama bacarığı; Diqqət; təhlil etmək, əsaslandırmaq, nəticə çıxarmaq bacarığı; qrupla iş bacarıqları.
Dərslər zamanı
1) Təşkilati məqam.
İnteraktiv məşq: uşaqlar nümunələri həll etməli və sözləri deşifrə etməli, nəticələrə görə qruplara bölünürlər (etibarlı, qeyri-mümkün və təsadüfi) və dərsin mövzusunu müəyyənləşdirirlər.
1 kart.
| 0,5 | 1,6 | 12,6 | 5,2 | 7,5 | 8 | 5,2 | 2,08 | 0,5 | 9,54 | 1,6 |
2 kart
| 0,5 | 2,1 | 14,5 | 1,9 | 2,1 | 20,4 | 14 | 1,6 | 5,08 | 8,94 | 14 |
3 kart
| 5 | 2,4 | 6,7 | 4,7 | 8,1 | 18 | 40 | 9,54 | 0,78 |
2) Öyrənilən biliklərin yenilənməsi.
Alqış oyunu: cüt ədəd - əl çalmaq, tək - ayağa qalxmaq.
Tapşırıq: verilmiş ədədlər seriyasından 42, 35, 8, 9, 7, 10, 543, 88, 56, 13, 31, 77, ... cüt və təki təyin edin.
3) Yeni mövzunun öyrənilməsi.
Masalarınızda kublar var. Gəlin onlara daha yaxından nəzər salaq. Nə görürsən?
Zarlar harada istifadə olunur? Necə?
Qrup işi.
Eksperimentin aparılması.
Zərləri atarkən hansı proqnozları verə bilərsiniz?
İlk proqnoz: 1,2,3,4,5 və ya 6 rəqəmlərindən biri atılacaq.
Bu təcrübədə mütləq baş verəcək bir hadisə deyilir etibarlı.
İkinci proqnoz: 7 nömrəsi silinəcək.
Sizcə, proqnozlaşdırılan hadisə gələcək, ya yox?
Bu mümkün deyil!
Verilmiş təcrübədə baş verə bilməyən hadisəyə deyilir qeyri-mümkün.
Üçüncü proqnoz: 1 nömrə atılacaq.
Bu hadisə gələcəkmi?
Müəyyən bir təcrübədə baş verə bilən və ya olmaya bilən bir hadisə deyilir təsadüfi.
4) Öyrənilən materialın konsolidasiyası.
I. Hadisənin növünü müəyyənləşdirin
-Sabah qırmızı qar yağacaq.
Sabah güclü qar yağacaq.
Sabah iyul olsa da qar yağacaq.
Sabah iyul olsa da, qar yağmayacaq.
Sabah qar yağacaq, çovğun olacaq.
II. Bu cümləyə bir söz əlavə edin ki, hadisə qeyri-mümkün olsun.
Kolya tarixdən A aldı.
Saşa testdə heç bir tapşırığı yerinə yetirmədi.
Oksana Mixaylovna (tarix müəllimi) yeni mövzunu izah edəcək.
III. Qeyri-mümkün, təsadüfi və etibarlı hadisələrə nümunələr verin.
IV. Dərsliyə uyğun işləyin (qruplarda).
Aşağıdakı tapşırıqlarda istinad edilən hadisələri ağlabatan, qeyri-mümkün və ya təsadüfi olaraq təsvir edin.
No 959. Petya natural ədəd yaratdı. Tədbir aşağıdakı kimidir:
a) cüt ədəd nəzərdə tutulur;
b) tək ədəd düşünülür;
c) nə cüt, nə də tək olmayan ədəd nəzərdə tutulur;
d) tək və ya cüt olan ədəd.
№ 960. Siz bu dərsliyi istənilən səhifədə açdınız və qarşınıza çıxan ilk isim seçdiniz. Tədbir aşağıdakı kimidir:
a) seçilmiş sözün yazılışında sait var;
b) seçilmiş sözün yazılışında “o” hərfi var;
c) seçilmiş sözün yazılışında sait yoxdur;
d) seçilmiş sözün yazılışında yumşaq işarə var.
Həll edin No 961, No 964.
Həll edilmiş vəzifələrin müzakirəsi.
5) Refeksiya.
1.Dərsdə hansı hadisələrlə qarşılaşdınız?
2. Aşağıdakı hadisələrdən hansının etibarlı, hansının qeyri-mümkün və hansının təsadüfi olduğunu göstərin:
a) yay tətili olmayacaq;
b) sendviç yağı aşağı düşəcək;
c) dərs ili nə vaxtsa başa çatacaq.
6) Ev tapşırığı:
İki etibarlı, təsadüfi və qeyri-mümkün hadisə ilə gəlin.
Onlardan birinə rəsm çəkin.
Ehtimal nəzəriyyəsi, riyaziyyatın hər hansı bir sahəsi kimi, müəyyən bir anlayış diapazonu ilə işləyir. Ehtimal nəzəriyyəsinin əksər anlayışlarına tərif verilir, lakin bəziləri həndəsədə nöqtə, düz xətt, müstəvidə olduğu kimi müəyyən edilməmiş əsas kimi qəbul edilir. Ehtimal nəzəriyyəsinin əsas anlayışı hadisədir. Hadisə, müəyyən bir vaxtdan sonra iki şeydən yalnız birinin deyilə biləcəyi bir şey kimi başa düşülür:
- · Bəli, baş verdi.
- · Xeyr, baş vermədi.
Məsələn, mənim lotereya biletim var. Lotereya tirajının nəticələri dərc olunandan sonra məni maraqlandıran hadisə odur ki, min rubl uduş ya olur, ya da olmur. Hər hansı bir hadisə sınaq (və ya təcrübə) nəticəsində baş verir. Test (və ya təcrübə) hadisə ilə nəticələnən şərtlərə aiddir. Məsələn, sikkə atmaq sınaqdır, onun üzərində “gerb”in görünməsi isə hadisədir. Tədbir adətən böyük Latın hərfləri ilə təyin olunur: A, B, C,…. Maddi aləmdəki hadisələri üç kateqoriyaya bölmək olar - etibarlı, qeyri-mümkün və təsadüfi.
Etibarlı hadisə baş verməsi əvvəlcədən bilinən bir hadisədir. W hərfi ilə işarələnir. Deməli, adi zər atarkən altıdan çox olmayan xal almaq etibarlıdır, tərkibində yalnız ağ toplar olan qabdan çıxarıldıqda ağ topun görünməsi və s.
Qeyri-mümkün hadisə baş verməyəcəyi əvvəlcədən bilinən hadisədir. E hərfi ilə işarələnir. Qeyri-mümkün hadisələrə misal olaraq adi kart göyərtəsindən dörddən çox eysin çıxarılması, yalnız ağ və qara topların olduğu qabdan qırmızı topun görünməsi və s.
Təsadüfi hadisə sınaq nəticəsində baş verə bilən və ya olmaya bilən hadisədir. A və B hadisələri, əgər onlardan birinin başlaması digərinin baş vermə ehtimalını istisna edərsə, uyğunsuz adlanır. Beləliklə, zər atarkən istənilən mümkün xal sayının görünməsi (A hadisəsi) fərqli nömrənin (B hadisəsi) görünüşü ilə uyğun gəlmir. Cüt sayda xal tək nömrə ilə uyğun gəlmir. Əksinə, cüt xalların itirilməsi (A hadisəsi) və üçə (B hadisəsi) çox olan xalların sayı uyğunsuz olmayacaq, çünki altı xalın itirilməsi həm A, həm də B hadisələrinin baş verməsi deməkdir. belə ki, onlardan birinin baş verməsi digərinin baş verməsini istisna etməsin. Hadisələrlə əməliyyatlar həyata keçirə bilərsiniz. İki hadisənin birləşməsi C = AUB hadisəsi C hadisəsidir və yalnız bu A və B hadisələrindən ən azı biri baş verdikdə baş verir.İki hadisənin kəsişməsi D = A ?? B yalnız və yalnız həm A, həm də B hadisələri olduqda baş verən hadisə adlanır.
Müşahidə etdiyimiz hadisələri (hadisələri) aşağıdakı üç növə bölmək olar: etibarlı, qeyri-mümkün və təsadüfi.
Etibarlı müəyyən şərtlər toplusunun S yerinə yetirildiyi təqdirdə mütləq baş verəcək hadisə adlanır.Məsələn, bir gəmidə normal atmosfer təzyiqində və 20 ° temperaturda su varsa, o zaman "qabdakı suyun maye vəziyyətdə olması" hadisəsi ” etibarlıdır. Bu nümunədə müəyyən edilmiş atmosfer təzyiqi və suyun temperaturu S şərtlər toplusudur.
Mümkün deyilşərtlər toplusunun S yerinə yetirildiyi təqdirdə baş verməyəcək hadisə adlanır.Məsələn, “qabdakı su bərk vəziyyətdədir” hadisəsi əvvəlki misalın şərtlər toplusu yerinə yetirildikdə, əlbəttə ki, baş verməyəcək.
Təsadüfi bir hadisədir ki, S şərtlər toplusu yerinə yetirildikdə ya baş verə bilər, ya da olmaya bilər. Məsələn, bir sikkə atılırsa, o zaman düşə bilər ki, üstündə ya gerb, ya da yazı olsun. Buna görə də, hadisə "sikkə atılanda" gerb "düşdü - təsadüfi. Hər bir təsadüfi hadisə, xüsusən də “gerb”in düşməsi çoxlu təsadüfi səbəblərin təsirinin nəticəsidir (bizim nümunəmizdə: sikkənin atıldığı qüvvə, sikkənin forması və s. ). Bütün bu səbəblərin nəticəyə təsirini nəzərə almaq qeyri-mümkündür, çünki onların sayı çox böyükdür və fəaliyyət qanunları naməlumdur. Buna görə də ehtimal nəzəriyyəsi tək bir hadisənin baş verib-verməyəcəyini proqnozlaşdırmaq vəzifəsi qoymur - o, sadəcə olaraq bunu edə bilməz.
Eyni S şəraitində dəfələrlə müşahidə oluna bilən təsadüfi hadisələr nəzərə alınarsa, yəni kütləvi bircins təsadüfi hadisələrdən danışırıqsa, vəziyyət fərqlidir. Belə çıxır ki, kifayət qədər çox sayda homojen təsadüfi hadisələr, spesifik təbiətindən asılı olmayaraq, müəyyən qanunlara, yəni ehtimal qanunlarına tabe olur. Bu qanunauyğunluqların qurulması ehtimal nəzəriyyəsi ilə məşğul olur.
Beləliklə, ehtimal nəzəriyyəsinin mövzusu kütləvi bircins təsadüfi hadisələrin ehtimal qanunlarının öyrənilməsidir.
Ehtimal nəzəriyyəsi üsulları təbiət elminin və texnologiyanın müxtəlif sahələrində geniş istifadə olunur. Ehtimal nəzəriyyəsi həm də riyazi və tətbiqi statistikanın əsaslandırılmasına xidmət edir.
Təsadüfi hadisələrin növləri... Hadisələr adlanır ziddiyyətli onlardan birinin baş verməsi eyni məhkəmə prosesində digər hadisələrin baş verməsini istisna edərsə.
Misal. Bir sikkə atılır. “Gerbin” görünüşü yazının görünüşünü istisna edir. “gerb çıxdı” və “yazı çıxdı” hadisələri bir-birinə uyğun gəlmir.
Bir neçə hadisə meydana gəlir tam qrup test nəticəsində onlardan ən azı biri meydana çıxdıqda. Xüsusilə, tam qrup təşkil edən hadisələr qoşa uyğunsuzluq təşkil edərsə, sınaq nəticəsində bu hadisələrdən biri və yalnız biri meydana çıxacaq. Aşağıda istifadə edildiyi üçün bu xüsusi hal bizi daha çox maraqlandırır.
Misal 2. İki pul lotereya bileti alınır. Aşağıdakı hadisələrdən biri və yalnız biri mütləq baş verəcək: "qələbə birinci biletə düşdü və ikinciyə düşmədi", "qələbə birinci biletə düşmədi və ikinciyə düşdü", "qələbə düşdü" hər iki biletdə", "hər iki biletdə uduşlar silinməyib." Bu hadisələr cüt-cüt uyğun gəlməyən hadisələrin tam qrupunu təşkil edir.
Misal 3. Atıcı hədəfə atəş açdı. Aşağıdakı iki hadisədən biri mütləq baş verəcək: hit, miss. Bu iki uyğunsuz hadisə tam bir qrup təşkil edir.
Hadisələr adlanır eyni dərəcədə mümkündür onların heç birinin digərindən daha mümkün olmadığına inanmaq üçün əsas varsa.
Misal 4. Sikkə atılan zaman “gerb”in görünməsi və yazının görünməsi eyni dərəcədə mümkün hadisələrdir. Həqiqətən də, hesab edilir ki, sikkə bircins materialdan hazırlanıb, müntəzəm silindrik formaya malikdir və zərb alətlərinin olması sikkənin bu və ya digər tərəfinin düşməsinə təsir göstərmir.
Öz latın əlifbasının böyük hərfləri ilə işarələnir: A, B, C, .. A 1, A 2 ..
Tam qrup təşkil edən yalnız iki mümkün varlıq əks adlanır. Əgər iki əksdən biri. hadisələr A, sonra digərləri A ' ilə işarələnir.
Nümunə 5. Hədəfə - əks sahəyə atəş açarkən vurma və itmə. so-i.
1.1. Kombinatorikadan bəzi məlumatlar
1.1.1. Yerləşdirmə
Bir sıra obyektlərin seçimi və yeri ilə əlaqəli ən sadə anlayışları nəzərdən keçirin.
Bu hərəkətlərin həyata keçirilə biləcəyi üsulların sayını hesablamaq çox vaxt ehtimal məsələlərini həll edərkən aparılır.
Tərif... Yerləşdirmə n tərəfindən elementlər k (k ≤n) hər hansı sıralanmış alt çoxluq adlanır k ibarət çoxluğun elementləri n müxtəlif elementlər.
Misal. Aşağıdakı nömrə ardıcıllığı çoxluğun 3 elementindən (1; 2; 3) 2 elementli yerləşdirmələrdir: 12, 13, 23, 21, 31, 32.
Qeyd edək ki, yerləşdirmələr onların tərkib elementlərinin sırasına və tərkibinə görə fərqlənir. 12 və 21-ci yerləşdirmələr eyni nömrələri ehtiva edir, lakin onların sırası fərqlidir. Buna görə də bu yerləşdirmələr fərqli hesab olunur.
Müxtəlif yerləşdirmələrin sayı n tərəfindən elementlər k düsturla işarələnir və hesablanır:
,
harada n! = 1∙2∙...∙(n - 1)∙n(oxuyur " n- faktorial ").
Nömrə ikirəqəmli ədədlər, 1, 2, 3 rəqəmlərindən ibarət ola bilər, bir şərtlə ki, təkrarlanan heç bir rəqəm bərabər deyil:.
1.1.2. Permütasyonlar
Tərif... Permutasiyalar n elementlərə belə yerləşdirmələr deyilir n yalnız elementlərin düzülüşündə fərqlənən elementlər.
Permütasyonların sayı n elementləri P n düsturla hesablanır: P n=n!
Misal. 5 nəfər neçə yolla növbəyə dura bilər? Yolların sayı 5 elementin dəyişdirilməsinin sayına bərabərdir, yəni.
P 5 =5!=1∙2∙3∙4∙5=120.
Tərif... Əgər arasında n elementləri k eynidir, sonra bunları yenidən təşkil edin n elementlərə təkrarlarla permutasiya deyilir.
Misal. 6 kitab arasında 2 eyni kitab olsun. Rəfdəki bütün kitabların hər hansı bir tərtibatı - təkrarlarla permutasiya.
Təkrarlarla müxtəlif permutasiyaların sayı (dan n elementləri, o cümlədən k eyni) düsturu ilə hesablanır:.
Bizim nümunəmizdə kitabları rəfdə yerləşdirməyin yollarının sayı:
1.1.3. Kombinasiyalar
Tərif... birləşmələri n tərəfindən elementlər k belə yerləşdirmələrdən n tərəfindən elementlər k bir-birindən ən azı bir elementlə fərqlənən.
Müxtəlif birləşmələrin sayı n tərəfindən elementlər k düsturu ilə işarələnir və hesablanır:.
Tərifinə görə, 0! = 1.
Aşağıdakı xüsusiyyətlər birləşmələr üçün etibarlıdır:
1.
2.
3.
4.
Misal. Müxtəlif rənglərdə 5 çiçək var. Buket üçün 3 çiçək seçilir. 5 çiçəkdən 3 çiçəkdən ibarət müxtəlif buketlərin sayı bərabərdir:.
1.2. Təsadüfi hadisələr
1.2.1. Hadisələr
Təbiət elmlərində reallığın idrakı sınaqlar (təcrübə, müşahidə, təcrübə) nəticəsində baş verir.
Test
və ya təcrübə müəyyən şərtlər toplusunun həyata keçirilməsidir və istənilən qədər təkrarlana bilər.
Təsadüfi
hansısa sınaq (təcrübə) nəticəsində baş verə bilən və ya olmaya bilən hadisə adlanır.
Beləliklə, hadisə sınaq nəticəsi kimi qəbul edilir.
Misal. Sikkə atmaq bir problemdir. Atılanda qartalın görünməsi bir hadisədir.
Müşahidə etdiyimiz hadisələr baş vermə ehtimalı dərəcəsi və bir-biri ilə əlaqə xarakteri ilə fərqlənir.
Tədbir adlanır etibarlı
bu test nəticəsində mütləq baş verəcəksə.
Misal.İmtahan adi qaydalara uyğun gedirsə, tələbənin imtahandan müsbət və ya mənfi qiymət alması etibarlı hadisədir.
Tədbir adlanır qeyri-mümkün
bu sınaq nəticəsində baş verə bilməzsə.
Misal. Yalnız rəngli (ağ olmayan) topların olduğu qabdan ağ topun çıxarılması qeyri-mümkün bir hadisədir. Qeyd edək ki, digər eksperimental şəraitdə ağ topun görünüşü istisna edilmir; beləliklə, bu hadisə yalnız bizim təcrübəmizin şərtləri ilə mümkün deyil.
Bundan sonra təsadüfi hadisələr böyük Latın dili ilə işarələnəcək A, B, C hərfləri... Etibarlı hadisə Ω hərfi ilə, qeyri-mümkün - Ø ilə işarələnəcək.
İki və ya daha çox hadisə çağırılır eyni dərəcədə mümkündür
bu sınaqda, bu hadisələrin heç birinin digərlərindən daha çox və ya daha az mümkün olmadığına inanmaq üçün əsas varsa.
Misal. Zərlərin bir atışı ilə 1, 2, 3, 4, 5 və 6 xalların görünməsi - bütün bu hadisələr eyni dərəcədə mümkündür. Əlbəttə ki, zərlərin vahid materialdan hazırlandığı və düzgün formaya malik olduğu güman edilir.
İki hadisə çağırılır ziddiyyətli
verilmiş testdə, əgər onlardan birinin görünüşü digərinin görünüşünü istisna edirsə və birgə
əks halda.
Misal. Qutuda standart və qeyri-standart hissələr var. Uğurlar üçün bir detalı götürək. Standart hissənin görünüşü qeyri-standart hissənin görünüşünü aradan qaldırır. Bu hadisələr bir-birinə ziddir.
Bir neçə hadisə meydana gəlir hadisələrin tam qrupu
bu testdə, əgər bu test nəticəsində onlardan ən azı biri mütləq meydana çıxacaq.
Misal. Nümunədəki hadisələr eyni dərəcədə mümkün və qoşa uyğun gəlməyən hadisələrin tam qrupunu təşkil edir.
Müəyyən bir sınaqda hadisələrin tam qrupunu təşkil edən iki uyğunsuz hadisə deyilir əks hadisələr.
Onlardan biri ilə işarələnərsə A, onda digəri adətən ilə işarələnir (oxumaq "yox A»).
Misal. Bir hədəfə bir atəşlə vurmaq və itmək əks hadisələrdir.
1.2.2. Ehtimalın klassik tərifi
Hadisə ehtimalı
- onun hücum ehtimalının ədədi ölçüsü.
Hadisə Açağırdı əlverişli
hadisə V hər hansı bir hadisə baş verərsə A, hadisə də gəlir V.
Hadisələr A 1 , A 2 , ..., An forma hal diaqramı
, əgər onlar:
1) eyni dərəcədə mümkündür;
2) cüt-cüt uyğunsuzluq;
3) tam qrup yaratmaq.
İşlərin sxemində (və yalnız bu sxemdə) ehtimalın klassik tərifi var P(A) hadisələr A... Burada eyni dərəcədə mümkün və qoşa uyğun gəlməyən hadisələrin seçilmiş tam qrupuna aid hadisələrin hər biri hal adlanır.
Əgər n Sxemdəki bütün halların sayıdır və m- hadisə üçün əlverişli halların sayı A, sonra hadisə ehtimalı
A bərabərliklə müəyyən edilir:
Aşağıdakı xüsusiyyətlər ehtimalın tərifindən irəli gəlir:
1. Etibarlı hadisənin baş vermə ehtimalı birə bərabərdir.
Həqiqətən də, əgər hadisə müəyyəndirsə, hadisələrin sxemindəki hər bir hadisə hadisəyə üstünlük verir. Bu halda m = n və buna görə də ![]()
2. Qeyri-mümkün hadisənin baş vermə ehtimalı sıfırdır.
Doğrudan da, əgər hadisə qeyri-mümkündürsə, o zaman hadisələrin sxemindəki hadisələrin heç biri hadisəyə üstünlük vermir. Belə ki m= 0 və buna görə də ![]()
Təsadüfi hadisənin baş vermə ehtimalı sıfırdan birə qədər olan müsbət ədəddir.
Həqiqətən, iş sxemindəki işlərin ümumi sayının yalnız bir hissəsi təsadüfi bir hadisəyə üstünlük verir. Buna görə də 0<m<n, və buna görə də 0<m/n<1 и, следовательно, 0 < P (A) < 1.
Beləliklə, hər hansı bir hadisənin ehtimalı bərabərsizlikləri ödəyir
0 ≤ P (A) ≤ 1.
Hazırda ehtimalın xassələri A.N. Kolmoqorov.
Ehtimalın klassik tərifinin əsas üstünlüklərindən biri hadisənin baş vermə ehtimalını birbaşa hesablamaq qabiliyyətidir, yəni. məntiqi əsaslandırma ilə əvəzlənən təcrübələrə müraciət etmədən.
Ehtimalların birbaşa hesablanması məsələləri
Tapşırıq 1.1... Bir atışda cüt sayda nöqtələrin (A hadisəsinin) baş vermə ehtimalı nədir?
Həll... Hadisələri nəzərdən keçirin Ai- düşdü i xal, i= 1, 2, ..., 6. Aydındır ki, bu hadisələr bir vəziyyət diaqramını təşkil edir. Sonra bütün halların sayı n= 6. Cüt sayda xal hallar tərəfindən üstünlük təşkil edir A 2 , A 4 , A 6, yəni. m= 3. Sonra ![]() .
.
Tapşırıq 1.2... Qabda 5 ağ və 10 qara top var. Toplar yaxşıca qarışdırılır və sonra təsadüfi olaraq 1 top çıxarılır. Çıxarılan topun ağ olması ehtimalı nədir?
Həll... Cəmi 15 hal var ki, bunlar iş diaqramını təşkil edir. Üstəlik, gözlənilən hadisə A- ağ topun görünüşü, buna görə də onlardan 5-i üstünlük təşkil edir ![]() .
.
Tapşırıq 1.3... Uşaq əlifbanın altı hərfi ilə oynayır: A, A, E, K, P, T. Onun təsadüfən CARETA sözünü əlavə edə bilməsi ehtimalını tapın (A hadisəsi).
Həll... Qərar hərflər arasında eyni - iki "A" hərfinin olması ilə çətinləşir. Buna görə də, bu testdə bütün mümkün halların sayı 6 hərfin təkrarlanması ilə permütasyonların sayına bərabərdir:
.
Bu hallar eyni dərəcədə mümkündür, cüt-cüt uyğun gəlmir və hadisələrin tam qrupunu təşkil edir, yəni. hal diaqramını yaradın. Yalnız bir hadisə bir hadisəyə üstünlük verir A... Belə ki
.
Tapşırıq 1.4... Tanya və Vanya Yeni ili 10 nəfərlik şirkətdə qeyd etməyə razılaşıblar. İkisi də bir-birinin yanında oturmaq istəyirdilər. Dostları arasında yerləri püşkatma yolu ilə bölüşdürmək adətdirsə, onların istəklərinin yerinə yetirilməsi ehtimalı nədir?
Həll... ilə işarə edək A hadisə "Tanya və Vanyanın istəklərinin yerinə yetirilməsi". 10 nəfər masada 10 nəfər əyləşə bilər! fərqli yollar. Bunların neçəsi n= 10! Tanya və Vanya üçün eyni dərəcədə əlverişli yollar varmı? Bir-birinin yanında oturan Tanya və Vanya 20 müxtəlif mövqe tuta bilirlər. Eyni zamanda, onların səkkiz dostu 8-ci masada otura bilər! müxtəlif yollarla, buna görə də m= 20 ∙ 8 !. Beləliklə, ![]() .
.
Tapşırıq 1.5... 5 qadın və 20 kişidən ibarət qrup üç nümayəndə seçir. Eyni ehtimalla iştirak edənlərin hər birinin seçilə biləcəyini fərz etsək, iki qadın və bir kişinin seçilmə ehtimalını tapın.
Həll... Eyni dərəcədə ehtimal olunan sınaq nəticələrinin ümumi sayı 25 nəfərdən üç nümayəndənin seçilə biləcəyi yolların sayına bərabərdir, yəni. ... İndi əlverişli halların sayını sayaq, yəni. maraq hadisəsinin baş verdiyi halların sayı. Kişi nümayəndə iyirmi yolla seçilə bilər. Bu halda, digər iki nümayəndə qadın olmalıdır və siz beş qadından iki qadın seçə bilərsiniz. Beləliklə, . Belə ki
.
Tapşırıq 1.6. Dörd top təsadüfi olaraq dörd dəliyə səpələnmişdir, hər bir top eyni ehtimalla və digərlərindən asılı olmayaraq bir və ya digər dəliyə dəyir (bir neçə top üçün eyni çuxura dəyməyə heç bir maneə yoxdur). Çuxurların birində üç, biri digərində, digər iki çuxurda isə top olmama ehtimalını tapın.
Həll. İşlərin ümumi sayı n= 4 4. Üç top ilə bir çuxur seçə biləcəyiniz yolların sayı. Bir topun olacağı bir çuxur seçə biləcəyiniz yolların sayı. Dörd topdan seçə biləcəyiniz yolların sayı onları ilk çuxura qoymaq üçün üçdür. Əlverişli halların ümumi sayı. Hadisə ehtimalı: ![]()
Tapşırıq 1.7. Qutuda 1, 2,…, 10 rəqəmləri ilə işarələnmiş 10 eyni top var. Uğur üçün altı top çəkilib. Çıxarılan toplar arasında olma ehtimalını tapın: a) top №1; b) №1 və №2 toplar.
Həll... a) Mümkün elementar test nəticələrinin ümumi sayı on topdan altı top çıxarmaq üsullarının sayına bərabərdir, yəni.
Bizi maraqlandıran hadisə üçün əlverişli nəticələrin sayını tapaq: seçilmiş altı top arasında №1 top var və buna görə də digər beş topun fərqli nömrələri var. Belə nəticələrin sayı açıq-aydın beş topun qalan doqquzdan seçilə biləcəyi yolların sayına bərabərdir, yəni.
İstənilən ehtimal, nəzərdən keçirilən hadisə üçün əlverişli nəticələrin sayının mümkün elementar nəticələrin ümumi sayına nisbətinə bərabərdir:
b) Bizi maraqlandıran hadisə üçün əlverişli nəticələrin sayı (seçilmiş toplar arasında №1 və №2 toplar var, buna görə də dörd topun fərqli nömrələri var) dörd topun çıxarıla biləcəyi yolların sayına bərabərdir qalan səkkizdən, yəni Ehtimal axtarışı ![]()
1.2.3. Statistik ehtimal
Ehtimalın statistik tərifi təcrübənin nəticələrinin eyni dərəcədə mümkün olmadığı hallarda istifadə olunur.
Hadisənin nisbi tezliyi
A bərabərliklə müəyyən edilir:
,
harada m- hadisənin baş verdiyi sınaqların sayı A gəldi n- yerinə yetirilən testlərin ümumi sayı.
J. Bernoulli sübut etdi ki, təcrübələrin sayının qeyri-məhdud artması ilə hadisənin baş vermə tezliyi praktiki olaraq müəyyən sabit ədəddən az fərqlənəcəkdir. Məlum oldu ki, bu sabit rəqəm bir hadisənin baş vermə ehtimalıdır. Buna görə də təbii olaraq, əvvəllər təqdim edilmiş ehtimaldan fərqli olaraq, kifayət qədər çox sayda sınaqla hadisənin baş verməsinin nisbi tezliyi statistik ehtimal adlanır.
Misal 1.8... Göldəki balıqların təxmini sayını necə hesablamaq olar?
Gölə buraxın X balıq. Biz toru atırıq və deyək ki, içində tapırıq n balıq. Onların hər birini qeyd edirik və geri buraxırıq. Bir neçə gündən sonra eyni havada, eyni yerdə eyni toru atdıq. Tutaq ki, orada m balıq tapırıq, onların arasında k etiketli. Hadisə olsun A- “tutulmuş balıq etiketlənir”. Sonra nisbi tezliyin tərifi ilə.
Amma göldə olsa X balıq və biz ona buraxdıq n etiketli, sonra.
Çünki R * (A) » R(A), sonra .
1.2.4. Hadisələr üzərində əməliyyatlar. Ehtimal toplama teoremi
Məbləğ, və ya bir neçə hadisənin birləşməsinə bu hadisələrdən ən azı birinin (eyni sınaqda) baş verməsindən ibarət hadisə deyilir.
məbləğ A 1 + A 2 + … + An aşağıdakı kimi qeyd olunur: ![]() və ya
və ya ![]() .
.
Misal... İki zar atılır. Hadisə olsun A 1 ölüm və hadisə üzrə 4 xal itkisindən ibarətdir V- Payızda 5 bal digər ölür. Hadisələr A və V birgədirlər. Buna görə də hadisə A +V eyni zamanda birinci zarda 4 xal və ya ikinci zarda 5 xal və ya birinci zarda 4 xal və ikincidə 5 xal atmaqdan ibarətdir.
Misal. Hadisə A- 1 kredit üzrə uduş, hadisə V- 2-ci kredit üzrə uduşlar. Sonra hadisə A + B- ən azı bir kredit udmaq (ehtimal ki, eyni anda iki).
Məhsula görə yaxud bir neçə hadisənin kəsişməsi bütün bu hadisələrin (eyni sınaqda) birgə görünməsindən ibarət hadisədir.
iş V hadisələr A 1 , A 2 , …, An aşağıdakı kimi qeyd olunur:
.
Misal. Hadisələr A və V instituta daxil olarkən müvafiq olaraq I və II turları uğurla başa vurmaqdan ibarətdir. Sonra hadisə A× B hər iki turu uğurla başa vurmaqdan ibarətdir.
Hadisələrin cəmi və hasili anlayışları aydın həndəsi şərhə malikdir. Hadisə olsun Aərazidə vuruş nöqtəsi var A və hadisə V- ərazidə bir nöqtəyə vurmaq V... Sonra hadisə A + B bu sahələrin birliyində bir nöqtənin vuruşu var (Şəkil 2.1), və hadisə AV bu sahələrin kəsişməsində nöqtənin vuruşu var (şək. 2.2).
düyü. 2.1 Şek. 2.2
teorem... Əgər hadisələr A i(i = 1, 2, …, n) cüt-cüt uyğunsuzdur, onda hadisələrin cəminin ehtimalı bu hadisələrin ehtimallarının cəminə bərabərdir: ![]() .
.
Qoy A və Ā
- əks hadisələr, yəni. A + Ā= Ω, burada Ω etibarlı hadisədir. Əlavə teoremindən belə nəticə çıxır
P (Ω) = R(A) + R(Ā
) = 1, buna görə də
R(Ā
) = 1 – R(A).
Əgər hadisələr A 1 və A 2 ardıcıldır, onda iki birgə hadisənin cəminin ehtimalı belədir:
R(A 1 + A 2) = R(A 1) + R(A 2) - P ( A 1 × A 2).
Ehtimalların toplanması teoremləri ehtimalların birbaşa hesablanmasından mürəkkəb hadisələrin baş vermə ehtimallarının müəyyən edilməsinə keçməyə imkan verir.
Tapşırıq 1.8... Atıcı hədəfə bir atəş atır. 10 xal əldə etmə ehtimalı (hadisə A), 9 xal (hadisə V) və 8 xal (hadisə İLƏ) müvafiq olaraq 0,11-ə bərabərdir; 0,23; 0.17. Bir atışla atıcının 8 xaldan az xal toplaması ehtimalını tapın (hadisə D).
Həll... Gəlin əks hadisəyə keçək - bir atışla atıcı ən azı 8 xal qazanacaq. Hadisə baş verərsə baş verir A və ya V, və ya İLƏ, yəni. ... Hadisələrdən bəri A, B, İLƏ qoşa uyğunsuzdur, onda əlavə teoreminə görə,
, harada.
Tapşırıq 1.9... 6 kişi və 4 qadından ibarət briqadanın kollektivindən iki nəfər həmkarlar ittifaqı konfransına seçilir. Seçilmiş ən azı bir qadının (hadisə A).
Həll... Bir hadisə baş verərsə A, onda aşağıdakı uyğunsuz hadisələrdən biri mütləq baş verəcək: V- “bir kişi və bir qadın seçildi”; İLƏ- “iki qadın seçildi”. Beləliklə, yaza bilərik: A = B + C... Hadisələrin baş vermə ehtimalını tapın V və İLƏ... 10 nəfərdən ikisi yollarla seçilə bilər. 4 qadından ikisi yollarla seçilə bilər. Kişi və qadın 6 × 4 şəkildə seçilə bilər. Sonra . Hadisələrdən bəri V və İLƏ uyğunsuzdur, onda əlavə teoreminə görə,
P (A) = P (B + C) = P (B) + P (C) = 8/15 + 2/15 = 2/3.
Tapşırıq 1.10. On beş dərslik kitabxananın rəfinə təsadüfi şəkildə düzülüb, onlardan beşi cildlənib. Kitabxanaçı təsadüfi olaraq üç dərsliyi götürür. Alınan dərsliklərdən ən azı birinin bağlanma ehtimalını tapın (hadisə A).
Həll... Birinci yol. Tələb - götürülmüş üç cildli dərslikdən ən azı biri - aşağıdakı üç uyğunsuz hadisədən hər hansı biri baş verərsə yerinə yetiriləcəkdir: V- bir cildli dərslik, İLƏ- iki cildli dərslik, D- üç cildli dərslik.
Bizi maraqlandıran hadisə A hadisələrin cəmi kimi təqdim edilə bilər: A = B + C + D... Əlavə teoreminə görə,
P (A) = P (B) + P (C) + P (D). (2.1)
Hadisələrin baş vermə ehtimalını tapın B, C və D(kombinator sxemlərinə baxın): 
Bu ehtimalları bərabərlikdə (2.1) təmsil edərək nəhayət əldə edirik
P (A)= 45/91 + 20/91 + 2/91 = 67/91.
İkinci yol. Hadisə A(götürülmüş üç dərslikdən ən azı biri cildlidir) və Ā
(alınan dərsliklərin heç biri cildli deyil) əksdir, belə ki P (A) + P (Ā) = 1 (iki əks hadisənin ehtimallarının cəmi 1-dir). Buradan P (A) = 1 – P (Ā). Hadisə ehtimalı Ā
(alınan dərsliklərin heç biri cildli deyil)
Ehtimal axtarışı
P (A) = 1 - P (Ā) = 1 – 24/91 = 67/91.
1.2.5. Şərti ehtimal. Ehtimalların vurma teoremi
Şərti ehtimal P (B/A) A hadisəsinin artıq baş verdiyi fərziyyəsi ilə hesablanmış B hadisəsinin ehtimalıdır.
teorem... İki hadisənin birgə baş verməsi ehtimalı, birinci hadisənin artıq baş verdiyi fərziyyəsi ilə hesablanan onlardan birinin ehtimallarının digərinin şərti ehtimalına hasilinə bərabərdir:
P (A∙B) = P (A) ∙ Р ( V/A). (2.2)
İki hadisə müstəqil adlanır, əgər onlardan hər hansı birinin baş verməsi digərinin baş vermə ehtimalını dəyişməzsə, yəni.
P (A) = P (A / B) və ya P (B) = P (B/A). (2.3)
Əgər hadisələr A və V müstəqildir, onda (2.2) və (2.3) düsturları nəzərdə tutur
P (A∙B) = P (A)∙P (B). (2.4)
Bunun əksi də doğrudur, yəni. iki hadisə üçün bərabərlik (2.4) yerinə yetirilirsə, bu hadisələr müstəqildir. Həqiqətən də (2.4) və (2.2) düsturları nəzərdə tutur
P (A∙B) = P (A)∙P (B) = P (A) × P (B/A), harada P (A) = P (B/A).
Formula (2.2) sonlu sayda hadisələr üçün ümumiləşdirilə bilər A 1 , A 2 ,…,A n:
P (A 1 ∙A 2 ∙…∙A n)=P (A 1)∙P (A 2 /A 1)∙P (A 3 /A 1 A 2)∙…∙P (A n/A 1 A 2 …A n -1).
Tapşırıq 1.11... 5 ağ və 10 qara top olan qabdan ardıcıl olaraq iki top çıxarın. Hər iki topun ağ olması ehtimalını tapın (hadisə A).
Həll... Hadisələri nəzərdən keçirin: V- ilk çıxarılan top ağdır; İLƏ- çıxarılan ikinci top ağdır. Sonra A = BC.
Təcrübə iki şəkildə edilə bilər:
1) geri qaytarılma ilə: çıxarılan top, rəngi düzəltdikdən sonra qaba qaytarılır. Bu vəziyyətdə hadisələr V və İLƏ müstəqil:
P (A) = P (B)∙P (C) = 5/15 × 5/15 = 1/9;
2) geri qaytarılmır: çıxarılan top yan tərəfə qoyulur. Bu vəziyyətdə hadisələr V və İLƏ asılı:
P (A) = P (B)∙P (C/V).
Bir hadisə üçün Vşərtlər eynidir və üçün İLƏ vəziyyət dəyişdi. baş verdi V, buna görə də qabda 14 top qalıb, onlardan 4-ü ağdır.
Belə ki, .
Tapşırıq 1.12... 50 işıq lampası arasında 3-ü qeyri-standartdır. Eyni anda alınan iki lampanın qeyri-standart olma ehtimalını tapın.
Həll... Hadisələri nəzərdən keçirin: A- birinci işıq qeyri-standartdır, V- ikinci işıq qeyri-standartdır, İLƏ- hər iki lampa qeyri-standartdır. Aydındır ki C = A∙V... Hadisə A 50 haldan 3-ü əlverişlidir, yəni. P (A) = 3/50. Əgər hadisə A artıq gəldi, sonra hadisə V 49 haldan ikisi əlverişlidir, yəni. P (B/A) = 2/49. Beləliklə,
.
Hədəf 1.13... İki idmançı bir-birindən asılı olmayaraq bir hədəfə atəş açır. Birinci idmançının hədəfini vurma ehtimalı 0,7, ikincinin isə 0,8-dir. Hədəfin vurulma ehtimalı nə qədərdir?
Həll... Hədəf ya birinci atıcıya, ya da ikinciyə və ya hər ikisini birlikdə vurarsa vurulacaq, yəni. hadisə baş verəcək A + B hadisə haradadır A hədəfə ilk vuran idmançı və hadisədir V- ikinci. Sonra
P (A+V)=P (A)+P (B)–P (A∙V)=0, 7+0, 8–0, 7∙0,8=0,94.
Tapşırıq 1.14. Oxu zalında ehtimal nəzəriyyəsi üzrə altı dərslik var, onlardan üçü cildlidir. Kitabxanaçı təsadüfi iki dərslik götürdü. İki dərsliyin bağlanma ehtimalını tapın.
Həll... Hadisələrin qeydini təqdim edək : A- alınan ilk dərslik cildlidir; V- ikinci dərslik cildlidir. İlk dərsliyin bağlı olma ehtimalı
P (A) = 3/6 = 1/2.
Alınan ilk dərsliyin cildli olması şərti ilə ikinci dərsliyin bağlanma ehtimalı, yəni. hadisənin şərti ehtimalı V, budur: P (B/A) = 2/5.
Hər iki dərsliyin bağlı olması ehtimalını axtararaq, hadisələrin ehtimalları üçün vurma teoremi ilə bərabərdir.
P (AB) = P (A) ∙ P (B/A)= 1/2 · ∙ 2/5 = 0,2.
Tapşırıq 1.15. Sexdə 7 kişi və 3 qadın çalışır. Üç nəfər şəxsi heyət nömrələri ilə təsadüfi seçildi. Bütün seçilmiş şəxslərin kişi olma ehtimalını tapın.
Həll... Hadisələrin qeydini təqdim edək: A- ilk adam seçildi, V- ikinci adam seçildi, İLƏ -üçüncü kişidir. Kişinin ilk seçilmə ehtimalı, P (A) = 7/10.
Kişinin ikinci seçilmə ehtimalı, bir şərtlə ki, bir kişi artıq birinci seçilib, yəni. hadisənin şərti ehtimalı V növbəti : P (B / A) = 6/9 = 2/3.
Bir kişinin üçüncü seçilmə ehtimalı, bir şərtlə ki, iki kişi artıq seçilib, yəni. hadisənin şərti ehtimalı İLƏ budur: P (C/AB) = 5/8.
Seçilmiş hər üç şəxsin kişi olması ehtimalını axtararaq, P (ABC) = P (A) P (B/A) P (C/AB) = 7/10 2/3 5/8 = 7/24.
1.2.6. Ümumi ehtimal düsturu və Bayes düsturu
Qoy B 1 , B 2 ,…, B n- qoşa uyğunsuz hadisələr (hipotezalar) və A- yalnız onlardan biri ilə birlikdə baş verə bilən hadisə.
Bundan əlavə, biz bilək P (B i) və P (A/B i) (i = 1, 2, …, n).
Bu şərtlərdə aşağıdakı düsturlar etibarlıdır: ![]() (2.5)
(2.5) (2.6)
(2.6)
Formula (2.5) adlanır ümumi ehtimal düsturu
... Bir hadisənin baş vermə ehtimalını hesablayır A(tam ehtimal).
Formula (2.6) adlanır Bayes düsturu
... Bu, hadisə baş verərsə, fərziyyələrin ehtimallarını yenidən hesablamağa imkan verir A baş verdi.
Nümunələr tərtib edərkən, fərziyyələrin tam bir qrup təşkil etdiyini güman etmək rahatdır.
Hədəf 1.16... Səbətdə eyni növdən dörd ağacdan alma var. Birincidən - bütün almaların 15% -i, ikincidən - 35%, üçüncüdən - 20%, dördüncüdən - 30%. Yetişmiş almalar müvafiq olaraq 99%, 97%, 98%, 95% təşkil edir.
a) Təsadüfən alınan almanın yetişmə ehtimalı nədir (hadisə A).
b) Bir şərtlə ki, təsadüfi götürülmüş alma yetişmiş olsun, onun birinci ağacdan olması ehtimalını hesablayın.
Həll... a) 4 hipotezimiz var:
B 1 - təsadüfi götürülmüş alma 1-ci ağacdan çıxarılır;
B 2 - təsadüfi götürülmüş alma 2-ci ağacdan çıxarılır;
B 3 - təsadüfi götürülmüş alma 3-cü ağacdan çıxarılır;
B 4 - təsadüfi götürülmüş alma 4-cü ağacdan götürülür.
Şərtə görə onların ehtimalları: P (B 1) = 0,15; P (B 2) = 0,35; P (B 3) = 0,2; P (B 4) = 0,3.
Şərti hadisə ehtimalları A:
P (A/B 1) = 0,99; P (A/B 2) = 0,97; P (A/B 3) = 0,98; P (A/B 4) = 0,95.
Təsadüfən alınan almanın yetişmə ehtimalı ümumi ehtimal düsturu ilə tapılır:
P (A)=P (B 1)∙P (A/B 1)+P (B 2)∙P (A/B 2)+P (B 3)∙P (A/B 3)+P (B 4)∙P (A/B 4)=0,969.
b) Bizim vəziyyətimiz üçün Bayes düsturu belə görünür: ![]() .
.
Tapşırıq 1.17. Ağ top iki top olan qaba atılır, ondan sonra təsadüfi bir top ondan alınır. Topların ilkin tərkibi (rənginə görə) ilə bağlı bütün mümkün fərziyyələr eyni dərəcədə mümkün olarsa, çıxarılan topun ağ olma ehtimalını tapın.
Həll... ilə işarə edək A hadisə - ağ top çıxarılır. Topların ilkin tərkibi ilə bağlı aşağıdakı fərziyyələr (fərziyyələr) mümkündür: B 1- ağ toplar yoxdur, 2-də- bir ağ top, AT 3- iki ağ top.
Ümumilikdə üç fərziyyə olduğundan və fərziyyələrin ehtimallarının cəmi 1-ə bərabər olduğundan (onlar tam hadisələr qrupunu təşkil etdiyinə görə) fərziyyələrin hər birinin ehtimalı 1/3-ə bərabərdir, yəni.
P (B 1) = P (B 2)= P (B 3) = 1/3.
Ağ topun çəkilməsinin şərti ehtimalı, bir şərtlə ki, əvvəlcə qabda ağ toplar yox idi, P (A/B 1) = 1/3. Ağ topun çəkilməsinin şərti ehtimalı, əvvəlcə qabda bir ağ top olduğunu nəzərə alsaq, P (A/B 2) = 2/3. Əvvəlcə qabda iki ağ top olması şərti ilə ağ topun çəkilmə ehtimalı P (A/B 3)=3/ 3=1.
Ümumi ehtimal üçün düsturdan istifadə edərək ağ topun çəkilmə ehtimalını tapırıq:
R(A)=P (B 1)∙P (A/B 1)+P (B 2)∙P (A/B 2)+P (B 3)∙P (A/B 3) = 1/3 1/3 + 1/3 2/3 + 1/3 1 = 2/3 .
Hədəf 1.18... İki maşın ümumi konveyerə gedən eyni hissələri istehsal edir. Birinci maşının məhsuldarlığı ikincidən iki dəfədir. Birinci avtomatik maşın əla keyfiyyətli hissələrin orta hesabla 60%, ikincisi isə 84% istehsal edir. Konveyerdən təsadüfi götürülən hissə əla keyfiyyətə malik oldu. Bu hissənin birinci maşın tərəfindən istehsal olunma ehtimalını tapın.
Həll... ilə işarə edək A tədbir əla keyfiyyətli elementdir. İki fərziyyə irəli sürmək olar: B 1- hissə birinci maşın tərəfindən istehsal olunur, üstəlik (çünki birinci maşın ikincidən iki dəfə çox hissə istehsal edir) P (A/B 1) = 2/3; B 2 - hissə ikinci maşın tərəfindən istehsal olunur və P (B 2) = 1/3.
İlk avtomatik maşın tərəfindən istehsal edildiyi təqdirdə hissənin əla keyfiyyətə malik olmasının şərti ehtimalı, P (A/B 1)=0,6.
İkinci avtomatik maşın tərəfindən istehsal edildiyi təqdirdə hissənin əla keyfiyyətə malik olmasının şərti ehtimalı, P (A/B 1)=0,84.
Ümumi ehtimal düsturuna görə təsadüfi götürülmüş hissənin əla keyfiyyətə malik olması ehtimalı belədir.
P (A)=P (B 1) ∙P (A/B 1)+P (B 2) ∙P (A/B 2) = 2/3 0,6 + 1/3 0,84 = 0,68.
Alınan əla hissənin ilk avtomat tərəfindən istehsal olunma ehtimalını axtararaq, Bayes düsturuna görə bərabərdir.
Hədəf 1.19... Hər biri 20 hissədən ibarət üç çox hissə var. Birinci, ikinci və üçüncü lotlardakı standart hissələrin sayı müvafiq olaraq 20, 15, 10-dur. Standart olan hissə təsadüfi olaraq seçilmiş lotdan çıxarılıb. Hissələr partiyaya qaytarılır və ikinci dəfə bir hissə təsadüfi olaraq eyni partiyadan çıxarılır ki, bu da standartdır. Üçüncü partiyadan hissələrin çıxarılması ehtimalını tapın.
Həll... ilə işarə edək A hadisə - iki testin hər birində (qaytarma ilə) standart bir hissə çıxarıldı. Üç fərziyyə (hipoteza) irəli sürmək olar: B 1 - hissələr ilk partiyadan çıxarılır, V 2
- hissələr ikinci partiyadan çıxarılır, V 3 - hissələr üçüncü partiyadan çıxarılır.
Təfərrüatlar alınan partiyadan təsadüfi olaraq götürülüb, ona görə də fərziyyələrin ehtimalları eynidir: P (B 1) = P (B 2) = P (B 3) = 1/3.
Şərti ehtimalı tapın P (A/B 1), yəni. iki standart hissənin ardıcıl olaraq birinci partiyadan çıxarılması ehtimalı. Bu hadisə etibarlıdır, çünki birinci partiyada bütün hissələr standartdır, buna görə də P (A/B 1) = 1.
Şərti ehtimalı tapın P (A/B 2), yəni. iki standart hissənin ikinci partiyadan ardıcıl olaraq (qaytarılmaqla) çıxarılması ehtimalı: P (A/B 2)= 15/20 ∙ 15/20 = 9/16.
Şərti ehtimalı tapın P (A/B 3), yəni. iki standart hissənin üçüncü partiyadan ardıcıl olaraq (qaytarılmaqla) çıxarılması ehtimalı: P (A/B 3) = 10/20 10/20 = 1/4.
Bayes düsturundan istifadə edərək, hər iki çıxarılan standart hissənin üçüncü partiyadan olması ehtimalını axtarmaq 
1.2.7. Təkrarlanan testlər
Bir neçə test aparılarsa və hadisənin baş vermə ehtimalı A hər sınaqda digər sınaqların nəticələrindən asılı deyil, o zaman belə sınaqlar deyilir hadisə ilə bağlı müstəqil A. Müxtəlif müstəqil sınaqlarda, hadisə A müxtəlif ehtimallara və ya eyni ehtimala malik ola bilər. Biz daha sonra yalnız belə müstəqil testləri nəzərdən keçirəcəyik A eyni ehtimala malikdir.
Qoy istehsal olunsun P müstəqil testlər, hər birində bir hadisə A görünə bilər və ya görünməyə bilər. Gəlin bir hadisənin baş vermə ehtimalını qəbul edək A hər testdə eynidir, yəni bərabərdir R. Buna görə də hadisənin baş verməməsi ehtimalı A hər testdə də sabit və 1-ə bərabərdir R. Belə bir ehtimal sxemi deyilir Bernoulli sxemi... Bunun üçün ehtimalı hesablamaq vəzifəsini özümüzə qoyaq P Bernoulli test hadisəsi A tam gerçəkləşəcək k bir dəfə ( k Uğurların sayıdır) və buna görə də həyata keçirilməyəcək P- bir dəfə. Bu hadisənin tələb olunmadığını vurğulamaq vacibdir A dəqiq təkrarlanır k dəfələr müəyyən ardıcıllıqla. Tələb olunan ehtimal ilə işarələnir P n (k).
Məsələn, simvol R 5 (3) beş sınaqda hadisənin tam olaraq 3 dəfə görünməsi və buna görə də 2 dəfə baş verməyəcəyi ehtimalı deməkdir.
Problem sözdə istifadə edərək həll edilə bilər Bernoulli düsturları, bu kimi görünür: ![]() .
.
Tapşırıq 1.20. Bir gün ərzində elektrik enerjisi istehlakının müəyyən edilmiş normadan artıq olmama ehtimalı bərabərdir R= 0,75. Növbəti 6 gündə 4 gün ərzində enerji sərfiyyatının normadan artıq olmama ehtimalını tapın.
Həll. Hər 6 gün ərzində normal elektrik istehlakı ehtimalı sabit və bərabərdir R= 0,75. Nəticə etibarilə, gündə həddindən artıq elektrik istehlakı ehtimalı da sabit və bərabərdir q = 1–R=1–0,75=0,25.
Bernoulli düsturu ilə istənilən ehtimaldır
.
Hədəf 1.21... İki bərabər şahmatçı şahmat oynayır. Hansı daha çox ehtimal olunur: altı oyundan dörd və ya üç oyundan ikisini qazanmaq (heçə-heçə nəzərə alınmır)?
Həll... Ekvivalent şahmatçılar oynayır, buna görə də qazanma ehtimalı R= 1/2, buna görə də itirmək ehtimalı q həm də 1/2-dir. Çünki bütün oyunlarda qalib gəlmə ehtimalı sabitdir və oyunların hansı ardıcıllıqla qalib gələcəyinin fərqi yoxdur, o zaman Bernoulli düsturu tətbiq olunur.
Dörd oyundan ikisinin qalib gəlməsi ehtimalını tapaq:
Altı oyundan üçünün qalib gəlmə ehtimalını tapaq:
Çünki P 4 (2) > P 6 (3), altı oyundan üçdən dörd oyundan ikisini qazanma ehtimalı daha yüksəkdir.
Bununla belə, böyük dəyərlər üçün Bernoulli düsturundan istifadə edildiyini görmək olar n bu olduqca çətindir, çünki düstur böyük sayda hərəkətlər etməyi tələb edir və buna görə də hesablamalar prosesində səhvlər toplanır; nəticədə yekun nəticə həqiqi olandan əhəmiyyətli dərəcədə fərqlənə bilər.
Bu problemi həll etmək üçün çoxlu sayda testlər üçün istifadə olunan bir neçə limit teoremləri var.
1. Puasson teoremi
Bernoulli sxeminə uyğun olaraq çox sayda sınaq apararkən (ile n=> ∞) və az sayda əlverişli nəticələrlə k(bu halda müvəffəqiyyət ehtimalının olduğu güman edilir səh kiçikdir), Bernulli düsturu Puasson düsturuna yaxınlaşır ![]() .
.
Misal 1.22.İstehsal vahidi müəssisə tərəfindən istehsal edildikdə nikah ehtimalı bərabərdir səh= 0,001. 5000 ədəd məhsulun buraxılması ilə 4-dən az qüsurlu olması ehtimalı nədir (hadisə A Həll... Çünki n böyükdürsə, biz yerli Laplas teoremindən istifadə edirik: ![]()
Gəlin hesablayaq x:
Funksiya ![]() - hətta, buna görə də φ (–1,67) = φ (1,67).
- hətta, buna görə də φ (–1,67) = φ (1,67).
Əlavə A.1-dəki cədvələ əsasən, φ (1,67) = 0,0989 tapırıq.
Ehtimal axtarışı P 2400 (1400) = 0,0989.
3. Laplasın inteqral teoremi
Ehtimal olarsa R hadisənin baş verməsi A Bernoulli sxeminə görə hər bir testdə sabit və sıfırdan və birdən fərqlidir, sonra çox sayda test ilə n, ehtimal P n (k 1 , k 2) hadisənin baş verməsi A olan bu testlərdə k 1-ə k 2 dəfə təxminən bərabərdir
R p(k 1 , k 2) = Φ ( x "") – Φ ( x "), harada ![]() - Laplas funksiyası,
- Laplas funksiyası,
Laplas funksiyasında müəyyən inteqral analitik funksiyalar sinfində hesablanmır, ona görə də onu hesablamaq üçün Cədvəl 1-dən istifadə olunur. A.2, əlavədə verilmişdir.
Misal 1.24. Yüz müstəqil sınaqdan hər birində hadisənin baş vermə ehtimalı sabit və bərabərdir səh= 0,8. Hadisənin baş vermə ehtimalını tapın: a) ən azı 75 dəfə və 90 dəfədən çox olmamaqla; b) ən azı 75 dəfə; c) 74 dəfədən çox olmayaraq.
Həll... Laplasın inteqral teoremindən istifadə edəcəyik:
R p(k 1 , k 2) = Φ ( x "") – Φ( x "), burada Ф ( x) Laplas funksiyasıdır,
a) şərtlə, n = 100, səh = 0,8, q = 0,2, k 1 = 75, k 2 = 90. Hesablayın x "" və x " :![]()
![]()
Laplas funksiyasının tək olduğunu nəzərə alsaq, yəni. Ф (- x) = - Ф ( x), alırıq
P 100 (75; 90) = Ф (2,5) - Ф (–1,25) = Ф (2,5) + Ф (1,25).
Cədvələ görə. A.2. proqramları tapacağıq:
F (2,5) = 0,4938; Ф (1,25) = 0,3944.
Ehtimal axtarışı
P 100 (75; 90) = 0,4938 + 0,3944 = 0,8882.
b) Hadisənin ən azı 75 dəfə görünməsi tələbi o deməkdir ki, hadisənin baş vermə sayı 75 və ya 76, ... və ya 100-ə bərabər ola bilər. Beləliklə, bu halda qəbul edilməlidir. k 1 = 75, k 2 = 100. Sonra ![]()
![]() .
.
Cədvələ görə. A.2. tətbiqlər, biz F (1.25) = 0.3944 tapırıq; Ф (5) = 0,5.
Ehtimal axtarışı
P 100 (75;100) = (5) – (–1,25) = (5) + (1,25) = 0,5 + 0,3944 = 0,8944.
c) Hadisə - " Aən azı 75 dəfə "və" göründü A 74 dəfədən çox görünməmiş "əksdir, buna görə də bu hadisələrin ehtimallarının cəmi 1-dir. Buna görə də arzu olunan ehtimal
P 100 (0;74) = 1 – P 100 (75; 100) = 1 – 0,8944 = 0,1056.