Matematična analiza.

Delavnica.

Za študente na specialnosti:

"državna in občinska uprava"

T.Z. Pavlova

Kolpaševo 2008

Poglavje 1. Uvod v analizo

1.1 Funkcije. Splošne lastnosti

1.2 Teorija mej

1.3 Kontinuiteta delovanja

2.1 Opredelitev izpeljanke

2.4 Raziskovanje funkcij

2.4.1 Celoten študijski načrt

2.4.2 Primeri študije funkcij

2.4.3. Največja in najmanjša vrednost funkcije na segmentu

2.5 L'Hôpitalovo pravilo

3.1 Nedoločen integral

3.1.1 Definicije in lastnosti

3.1.2 Tabela integralov

3.1.3 Osnovne metode integracije

3.2 Določen integral

3.2.2 Metode za izračun določenega integrala

Poglavje 4. Funkcije več spremenljivk

4.1 Osnovni pojmi

4.2 Meje in kontinuiteta funkcij več spremenljivk

4.3.3 Skupni diferencial in njegova uporaba za približne izračune

Poglavje 5. Klasične metode optimizacije

6.1 Funkcija uporabnosti.

6.2 Črte brezbrižnosti

6.3 Določen proračun

Domače naloge

1.1 Funkcije. Splošne lastnosti

Številčna funkcija je definirana na množici realnih števil D, če je vsaka vrednost spremenljivke povezana z neko dobro definirano realno vrednostjo spremenljivke y, kjer je D domena funkcije.

Analitična predstavitev funkcije:

izrecno:;

implicitno:;

v parametrični obliki:

različne formule na področju definicije:

Lastnosti.

Enakomerna funkcija:. Na primer, funkcija je soda, saj ...

čudna funkcija: ... Na primer, funkcija je čudna, saj ...

Periodična funkcija: , kjer je T obdobje funkcije,. Na primer trigonometrične funkcije.

Monotona funkcija. Če za katero koli področje definicije - funkcija narašča, - pada. Na primer, - naraščajoče in - padajoče.

Omejena funkcija. Če obstaja število M, tako da. Na primer funkcije in od .

Primer 1. Poiščite področje definicije funkcij.

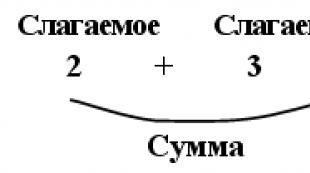
+ 2 – 3 +

1.2 Teorija mej

Opredelitev 1... Meja funkcije pri je število b, če je za katero koli (- poljubno majhno pozitivno število) mogoče najti takšno vrednost argumenta, pri kateri je neenakost izpolnjena.

Oznaka:.

Opredelitev 2... Meja funkcije pri je število b, če za katero koli (je poljubno majhno pozitivno število) obstaja tako pozitivno število, da za vse vrednosti x, ki izpolnjujejo neenakost, velja neenakost.

Oznaka:.

Opredelitev 3. Funkcija se imenuje neskončno mala za ali, če ali.

Lastnosti.

1. Algebraična vsota končnega števila neskončno majhnih količin je neskončno majhna količina.

2. Zmnožek neskončno majhne količine z omejeno funkcijo (konstanta, druga neskončno majhna količina) je neskončno majhna količina.

3. Kvocient deljenja neskončno majhne količine s funkcijo, katere meja ni nič, je neskončno majhna količina.

Opredelitev 4. Funkcija se imenuje neskončno velika pri, če.

Lastnosti.

1. Zmnožek neskončno velike količine s funkcijo, katere meja ni nič, je neskončno velika količina.

2. Vsota neskončno velike vrednosti in omejene funkcije je neskončno velika vrednost.

3. Kvocient deljenja neskončno velike količine s funkcijo, ki ima mejo, je neskončno velika količina.

Izrek.(Razmerje med neskončno majhno količino in neskončno veliko količino.) Če je funkcija neskončno majhna pri (), potem je funkcija neskončno velika količina pri (). In obratno, če je funkcija neskončno velika pri (), potem je funkcija neskončno majhna pri ().

Mejni izreki.

1. Funkcija ne more imeti več kot ene omejitve.

2. Meja algebraične vsote več funkcij je enaka algebrski vsoti mej teh funkcij:

3. Meja produkta več funkcij je enaka zmnožku mej teh funkcij:

4. Meja stopnje je enaka stopnji meje:

5. Omejitev količnika je enaka količniku mej, če obstaja meja delitelja:

.

6. Prva izjemna meja.

posledice:

7. Druga izjemna meja:

posledice:

Ekvivalentne neskončno male vrednosti za:

Izračun mej.

Pri izračunu mej se uporabljajo osnovni izreki o mejah, lastnosti zveznih funkcij in pravila, ki izhajajo iz teh izrekov in lastnosti.

1. pravilo. Da bi našli mejo na točki funkcije, ki je na tej točki neprekinjena, je treba njeno mejo vrednost nadomestiti v funkciji pod predznakom meje namesto argumenta x.

Primer 2. Najdi

2. pravilo.Če je pri iskanju meje ulomka meja imenovalca nič in meja števca ni nič, potem je meja takšne funkcije.

Primer 3. Najdi

3. pravilo.Če je pri iskanju meje ulomka meja imenovalca enaka in je meja števca drugačna od nič, je meja takšne funkcije nič.

Primer 4. Najdi

Pogosto zamenjava mejne vrednosti za argument povzroči nedefinirane izraze, kot je

.

Iskanje meje funkcije v teh primerih se imenuje razkritje negotovosti. Za razkritje negotovosti je treba ta izraz preoblikovati, preden gremo do meje. Za razkrivanje negotovosti se uporabljajo različne tehnike.

4. pravilo... Negotovost tipa se razkrije s preoblikovanjem podmejne funkcije, da izberemo faktor v števcu in imenovalcu, katerega meja je nič, in po zmanjšanju ulomka najdemo mejo količnika. Da bi to naredili, se števec in imenovalec bodisi pomnožita ali pomnožita z izrazi, konjugiranimi s števcem in imenovalcem.

5. pravilo.Če izraz sublimit vsebuje trigonometrične funkcije, se prva izjemna meja uporablja za razkrivanje negotovosti vrste.

.

6. pravilo... Da bi razkrili negotovost oblike pri, je treba števec in imenovalec podmejnega ulomka deliti z najvišjo stopnjo argumenta in nato najti mejo količnika.

Možni rezultati:

1) želena meja je enaka razmerju koeficientov pri najvišjih potenjih argumenta števca in imenovalca, če sta ti stopnji enaki;

2) meja je enaka neskončnosti, če je stopnja argumenta števca višja od stopnje argumenta imenovalca;

3) meja je nič, če je stopnja argumenta števca nižja od stopnje argumenta imenovalca.

a)

od

Stopnje so enake, kar pomeni, da je meja enaka razmerju koeficientov pri višjih stopnjah, t.j. ...

b)

Stopnja števca, imenovalec je 1, kar pomeni, da je meja

v)

Stopnja števca je 1, stopnja imenovalca je, zato je meja 0.

7. pravilo... Da bi razkrili negotovost obrazca, je treba števec in imenovalec podmejnega ulomka pomnožiti s konjugiranim izrazom.

Primer 10.

8. pravilo... Druga izjemna meja in njene posledice se uporabljajo za odkrivanje negotovosti vrste.

To je mogoče dokazati

Primer 11.

Primer 12.

Primer 13.

9. pravilo... Pri razkrivanju negotovosti, katerih subliminalna funkcija vsebuje neskončno malo, je treba zamenjati meje teh neskončnosti. na mejah neskončno majhnih elementov, ki so jim enakovredni.

Primer 14.

Primer 15.

Pravilo 10. L'Hôpitalovo pravilo (glej 2.6).

1.3 Kontinuiteta delovanja

Funkcija je na točki neprekinjena, če meja funkcije, ko se argument teži k a, obstaja in je enaka vrednosti funkcije na tej točki.

Enakovredni pogoji:

1. ;

3.

Razvrstitev prelomnih točk:

prelom prve vrste

Za enkratno uporabo – enostranske omejitve obstajajo in so enake;

Fatalni (skok) - enostranske meje niso enake;

diskontinuiteta druge vrste: meja funkcije v točki ne obstaja.

Primer 16. Ugotovite naravo diskontinuitete funkcije v točki ali dokažite kontinuiteto funkcije na tej točki.

saj funkcija ni definirana, zato na tej točki ni neprekinjena. Ker in ustrezno, , potem je točka odstranljive diskontinuitete prve vrste.

b)

v primerjavi z nalogo (a) je funkcija razširjena na točki, tako da , zato je ta funkcija na tej točki neprekinjena.

Ko funkcija ni definirana;

.

Ker ena od enostranskih mej je neskončna, potem je prelomna točka druge vrste.

Poglavje 2. Diferencialni račun

2.1 Opredelitev izpeljanke

Definicija izpeljanke

Ali izpeljanka dane funkcije je meja razmerja prirastka funkcije in ustreznega prirastka argumenta, ko se prirast argumenta nagiba k nič:

ali .

Mehanski pomen derivata je hitrost spremembe funkcije. Geometrijski pomen izpeljanke je tangenta kota naklona tangente na graf funkcije:

2.2 Osnovna pravila za razlikovanje

ime	Funkcija	Izpeljanka
Množenje s konstantnim faktorjem
Algebraična vsota dveh funkcij
Produkt dveh funkcij
Zasebni dve funkciji
Kompleksna funkcija

Izpeljanke osnovnih elementarnih funkcij

P / p št.	Ime funkcije	Funkcija in njen derivat
1	stalna
2	močna funkcija posebni primeri
3	eksponentna funkcija poseben primer
4	logaritemska funkcija poseben primer
5	trigonometrične funkcije
6	vzvratno trigonometrično

b)

2.3 Izvedeni finančni instrumenti višjega reda

Izvod funkcije drugega reda

Izpeljanka funkcije drugega reda:

Primer 18.

a) Poišči izpeljavo funkcije drugega reda.

Rešitev. Najprej poiščimo izpeljanko prvega reda .

Vzemimo izpeljanko izvoda prvega reda.

Primer 19. Poiščite izpeljanko tretjega reda funkcije.

2.4 Raziskovanje funkcij

2.4.1 Načrt za celotno študijo funkcije:

Celoten študijski načrt:

1. Osnovna raziskava:

Poiščite domeno in obseg vrednosti;

Ugotovite splošne lastnosti: parnost (neparnost), periodičnost;

Poiščite presečišča s koordinatnimi osemi;

Določite območja konstantnosti.

2. Asimptote:

Poiščite navpične asimptote, če;

Poiščite poševne asimptote:.

Če je število, potem - horizontalne asimptote.

3. Raziskovanje z uporabo:

Poiščite kritične točke, tiste. točke, na katerih ali ne obstajajo;

Določite intervale povečanja, tiste. intervali, pri katerih in padajoče funkcije -;

Določite ekstreme: točke, pri prehodu skozi katere spremeni predznak iz "+" v "-", so največje točke, od "-" do "+" - minimalne.

4. Raziskovanje z uporabo:

Poiščite točke, na katerih ali ne obstajajo;

Poiščite območja konveksnosti, t.j. intervali, v katerih so konkavnosti;

Poiščite pregibne točke, t.j. točke pri prehodu skozi katere se spremeni predznak.

1. Posamezni elementi študije so na grafu izrisani postopoma, kot se najdejo.

2. Če pride do težav pri gradnji grafa funkcije, se vrednosti funkcije najdejo na nekaterih dodatnih točkah.

3. Namen študije je opisati naravo obnašanja funkcije. Zato se ne gradi natančen graf, temveč njegova aproksimacija, na kateri so najdeni elementi (ekstremi, pregibne točke, asimptote itd.) jasno označeni.

4. Zgornjega načrta se ni treba strogo držati; pomembno je, da ne spregledamo značilnih elementov obnašanja funkcije.

2.4.2 Primeri študije funkcije:

1)

2) Funkcija je čudna:

.

3) Asimptote.

- navpične asimptote, ker

Poševna asimptota.

5)

- pregibna točka.

2) Funkcija je čudna:

3) Asimptote: navpičnih asimptot ni.

nagnjeno:

- poševne asimptote

4) - funkcija se poveča.

- pregibna točka.

Shematski diagram te funkcije:

2) Splošna funkcija

3) Asimptote

- brez poševnih asimptot

- horizontalna asimptota pri

- pregibna točka

Shematski diagram te funkcije:

2) Asimptote.

- navpična asimptota, ker

- brez poševnih asimptot

, - horizontalna asimptota

Shematski diagram te funkcije:

2) Asimptote

- navpična asimptota pri, saj

- brez poševnih asimptot

, - horizontalna asimptota

3) - funkcija se v vsakem od intervalov zmanjšuje.

Shematski diagram te funkcije:

Če želite najti največjo in najmanjšo vrednost funkcije na segmentu, lahko uporabite diagram:

1. Poiščite izvod funkcije.

2. Poiščite kritične točke funkcije, na katerih ali ne obstajajo.

3. Poišči vrednost funkcije na kritičnih točkah, ki pripadajo danemu segmentu in na njegovih koncih, ter izberi največjo in najmanjšo izmed njih.

Primer. Poiščite najmanjšo in največjo vrednost funkcije na danem segmentu.

25. vmes

2) - kritične točke

26. vmes.

Izpeljanka ne obstaja pri, vendar 1 ne pripada temu intervalu. Funkcija se v intervalu zmanjšuje, kar pomeni, da ni največje vrednosti, ampak najmanjša vrednost.

2.5 L'Hôpitalovo pravilo

Izrek. Meja razmerja dveh neskončno majhnih ali neskončno velikih funkcij je enaka meji razmerja njunih izvodov (končnih ali neskončnih), če slednja obstaja v navedenem pomenu.

tiste. pri razkrivanju negotovosti vrste ali pa lahko uporabite formulo:

.

27.

Poglavje 3. Integralni račun

3.1 Nedoločen integral

3.1.1 Definicije in lastnosti

Definicija 1. Funkcija se imenuje antiderivativna za if.

Definicija 2. Nedoločen integral funkcije f (x) je zbirka vseh antiderivov za to funkcijo.

Oznaka: , kjer je c poljubna konstanta.

Neomejene integralne lastnosti

1. Izvod nedoločnega integrala:

2. Diferencial nedoločenega integrala:

3. Nedoločen integral diferenciala:

4. Nedoločen integral vsote (razlike) dveh funkcij:

5. Premik konstantnega faktorja preko predznaka nedoločnega integrala:

3.1.2 Tabela integralov

.1.3 Osnovne metode integracije

1. Uporaba lastnosti nedoločenega integrala.

Primer 29.

2. Pripeljemo pod diferencialni znak.

Primer 30.

3. Spremenljiva metoda zamenjave:

a) zamenjava v integralu

kje - funkcija, ki jo je lažje integrirati kot prvotno; - funkcija obratna funkciji; je antiderivat funkcije.

Primer 31.

b) zamenjava v integralu oblike:

Primer 32.

Primer 33.

4. Metoda integracije po delih:

Primer 34.

Primer 35.

Vzemimo ločeno integral

Vrnimo se k našemu integralu:

3.2 Določen integral

3.2.1 Pojem določenega integrala in njegove lastnosti

Opredelitev. Naj je podana neprekinjena funkcija na nekem intervalu. Sestavimo njen graf.

Slika, ki je zgoraj omejena s krivuljo, levo in desno z ravnimi črtami, od spodaj pa z odsekom abscisne osi med točkama a in b, se imenuje ukrivljen trapez.

S - območje - ukrivljen trapez.

Interval razdelite s pikami in dobite:

Celotna vsota:

Opredelitev. Določen integral je meja integralne vsote.

Določene integralne lastnosti:

1. Konstantni faktor je mogoče vzeti iz predznaka integrala:

2. Integral algebraične vsote dveh funkcij je enak algebraični vsoti integralov teh funkcij:

3. Če je odsek integracije razdeljen na dele, je integral na celotnem segmentu enak vsoti integralov za vsak od nastalih delov, tj. za vse a, b, c:

4. Če na segmentu, potem

5. Meje integracije se lahko zamenjajo, medtem ko se predznak integrala spremeni:

6.

7. Integral v točki je enak 0:

8.

9. (»o povprečju«) Naj bo y = f (x) funkcija, ki je integrabilna na. Potem , kjer je f (c) povprečna vrednost f (x) na:

10. Newton-Leibnizova formula

,

kjer je F (x) antiderivat za f (x).

3.2.2 Metode za izračun določenega integrala.

1. Neposredna integracija

Primer 35.

a)

b)

v)

e)

2. Sprememba spremenljivk pod predznakom določenega integrala .

Primer 36.

2. Integracija po delih v določenem integralu .

Primer 37.

a)

b)

e)

3.2.3 Uporaba določenega integrala

Značilnost	Vrsta funkcije	Formula
	v kartezijanskih koordinatah
ukrivljeno sektorsko območje	v polarnih koordinatah
ukrivljeno trapezno območje	v parametrični obliki
dolžina loka	v kartezijanskih koordinatah
dolžina loka	v polarnih koordinatah
dolžina loka	v parametrični obliki
volumen telesa rotacija	v kartezijanskih koordinatah
telesni volumen z danim prečnim prečni prerez

Primer 38. Izračunajte površino oblike, omejene s črtami: in .

rešitev: Poiščimo presečišča grafov teh funkcij. Za to enačimo funkcije in rešimo enačbo

Torej, presečišča in.

S formulo najdemo površino figure

.

V našem primeru

Odgovor: površina je enaka (kvadratne enote).

4.1 Osnovni pojmi

Opredelitev. Če se po nekem pravilu vsakemu paru neodvisnih števil iz določenega niza dodeli ena ali več vrednosti spremenljivke z, se spremenljivka z imenuje funkcija dveh spremenljivk.

Opredelitev. Domena funkcije z je množica parov, za katere funkcija z obstaja.

Domena funkcije dveh spremenljivk je niz točk na koordinatni ravnini Oxy. Koordinato z imenujemo applicate, nato pa je funkcija sama prikazana kot neka površina v prostoru E 3. Na primer:

Primer 39. Poiščite domeno funkcije.

a)

Izraz na desni strani je smiseln samo za. To pomeni, da je domena te funkcije zbirka vseh točk, ki ležijo znotraj in na meji kroga s polmerom R s središčem v izhodišču.

Domena te funkcije so vse točke ravnine, razen točk ravnih črt, t.j. koordinatne osi.

Opredelitev. Črte na ravni funkcij so družina krivulj na koordinatni ravnini, opisanih z enačbami v obliki.

Primer 40. Poiščite vrstice ravni funkcije .

Rešitev. Nivelirne črte dane funkcije so družina krivulj v ravnini, ki jo opisuje enačba

Zadnja enačba opisuje družino krogov s središčem v točki O 1 (1, 1) polmera. Površina vrtenja (paraboloid), ki jo opisuje ta funkcija, postane "strmejša", ko se odmika od osi, kar je podano z enačbami x = 1, y = 1. (slika 4)

4.2 Meje in kontinuiteta funkcij več spremenljivk.

1. Meje.

Opredelitev. Število A imenujemo meja funkcije, saj se točka nagiba k točki, če za vsako poljubno majhno število obstaja število, tako da je pogoj resničen za katero koli točko, in pogoj ... Zapišejo: .

Primer 41. Poiščite meje:

tiste. meja je odvisna od in zato ne obstaja.

2. Kontinuiteta.

Opredelitev. Naj točka pripada domeni definicije funkcije. Potem se funkcija imenuje neprekinjena v točki if

(1)

poleg tega se točka na poljuben način nagiba k točki.

Če v kateri koli točki pogoj (1) ni izpolnjen, se ta točka imenuje točka prekinitve funkcije. To je lahko v naslednjih primerih:

1) Funkcija v točki ni definirana.

2) Ni omejitev.

3) Ta meja obstaja, vendar ni enaka.

Primer 42. Ugotovite, ali je podana funkcija neprekinjena v točki, če.

Razumem zato je ta funkcija v točki neprekinjena.

meja je odvisna od k, t.j. na določeni točki ne obstaja, kar pomeni, da ima funkcija na tej točki diskontinuiteto.

4.3 Izpeljanke in diferenciali funkcij več spremenljivk

4.3.1 Delni izpeljanki prvega reda

Delni izvod funkcije glede na argument x je običajen izvod funkcije ene spremenljivke x za fiksno vrednost spremenljivke y in je označen:

Delni odvod funkcije glede na argument y je običajen izvod funkcije ene spremenljivke y pri fiksni vrednosti spremenljivke x in je označen:

Primer 43. Poišči delne izpeljanke funkcij.

4.3.2 Delni izpeljanki drugega reda

Delne izpeljanke drugega reda so delne izpeljanke delnih izpeljank prvega reda. Za funkcijo dveh spremenljivk oblike so možne štiri vrste delnih izpeljank drugega reda:

Delne izpeljanke drugega reda, pri katerih se izvaja diferenciacija glede na različne spremenljivke, imenujemo mešane izpeljanke. Mešani odvodki drugega reda dvakrat diferencibilne funkcije so enaki.

Primer 44. Poišči delne izpeljanke drugega reda.

4.3.3 Skupni diferencial in njegova uporaba za približne izračune.

Opredelitev. Diferencial prvega reda funkcije dveh spremenljivk najdemo s formulo

.

Primer 45. Poiščite skupno diferencial za funkcijo.

Rešitev. Poiščimo delne izpeljanke:

.

Za majhne prirastke argumentov x in y funkcija pridobi prirast približno enak dz, t.j. ...

Formula za iskanje približne vrednosti funkcije v točki, če je njena natančna vrednost v točki znana:

Primer 46. Najdi .

Rešitev. Pustiti ,

Nato uporabimo formulo

Odgovori. .

Primer 47. Približno izračunaj.

Rešitev. Razmislimo o funkciji. Imamo

Primer 48. Približno izračunaj.

Rešitev. Razmislite o funkciji ... Dobimo:

Odgovori. .

4.3.4 Implicitna diferenciacija funkcij

Opredelitev. Funkcija se imenuje implicitna, če je podana z enačbo, ki ni rešljiva glede na z.

Delne izpeljanke takšne funkcije najdemo s formulami:

Primer 49. Poišči delne izvode funkcije z, ki jo poda enačba .

Rešitev.

Opredelitev. Funkcija se imenuje implicitna, če je podana z enačbo, ki ni rešljiva glede na y.

Izvod takšne funkcije najdemo s formulo:

.

Primer 50. Poiščite izpeljanke teh funkcij.

5.1 Lokalni ekstrem funkcije več spremenljivk

Definicija 1. Funkcija ima maksimum v točki if

Definicija 2. Funkcija ima minimum na točki if za vse točke, ki so dovolj blizu točki in so od nje različne.

Potreben pogoj za ekstrem. Če funkcija v točki doseže ekstrem, potem delni derivati ​​funkcije izginejo ali pa na tej točki ne obstajajo.

Točke, na katerih delne izpeljanke izginejo ali ne obstajajo, se imenujejo kritične.

Zadosten znak ekstremuma. Naj bo funkcija definirana v neki soseščini kritične točke in ima na tej točki neprekinjene delne izpeljanke drugega reda

1) ima lokalni maksimum na točki, če in;

2) ima lokalni minimum na točki, če in;

3) nima lokalnega ekstremuma na točki, če;

Shema študije za ekstrem funkcije dveh spremenljivk.

1. Poišči delne izpeljanke funkcije: in.

2. Rešite sistem enačb in poiščite kritične točke funkcije.

3. Poiščite delne derivate drugega reda, izračunajte njihove vrednosti na kritičnih točkah in z zadostnim pogojem sklepajte o prisotnosti ekstremov.

4. Poiščite ekstreme funkcije.

Primer 51. Poišči ekstreme funkcije .

1) Poiščite delne izpeljanke.

2) Rešite sistem enačb

4) Poiščite delne derivate drugega reda in njihove vrednosti na kritičnih točkah:. Na točki dobimo:

zato na točki ni ekstrema. Na točki dobimo:

torej na točki obstaja minimum.

5.2 Globalni ekstrem (najvišja in najnižja vrednost funkcije)

Največje in najmanjše vrednosti funkcije več spremenljivk, neprekinjene na neki zaprti množici, se dosežejo bodisi na ekstremnih točkah bodisi na meji množice.

Shema za iskanje najvišje in najnižje vrednosti.

1) Poiščite kritične točke, ki ležijo znotraj regije, izračunajte vrednost funkcije na teh točkah.

2) Raziščite funkcijo na meji območja; če je meja sestavljena iz več različnih črt, je treba študijo izvesti za vsako lokacijo posebej.

3) Primerjajte dobljene vrednosti funkcije in izberite največjo in najmanjšo.

Primer 52. Poiščite največjo in najmanjšo vrednost funkcije v pravokotniku.

Rešitev. 1) Poiščite kritične točke funkcije, za to poiščemo delne odvodke:, in rešimo sistem enačb:

Prejeto kritično točko A. Nastala točka leži znotraj določenega območja,

Meja območja je sestavljena iz štirih segmentov: in. poiščite največjo in najmanjšo vrednost funkcije na vsakem segmentu.

4) Primerjajte dobljene rezultate in jih poiščite na točkah .

Poglavje 6. Model izbire potrošnikov

Predvidevamo, da obstaja n različnih izdelkov. Potem bo določen niz blaga označen z n-dimenzionalnim vektorjem , kjer je količina i-tega produkta. Množico vseh množic blaga X imenujemo prostor.

Za izbiro posameznega potrošnika je značilno razmerje preferenc: verjame se, da potrošnik lahko reče o poljubnih dveh nizih, kar je bolj zaželeno, ali pa ne vidi razlike med njima. Preferenčna relacija je prehodna: če je množica boljša od množice in je množica boljša od množice, je množica boljša od množice. Predvidevamo, da je vedenje potrošnikov v celoti opisano z aksiomom posameznega potrošnika: vsak posamezni potrošnik se na podlagi svojega sistema preferenc odloča o porabi, nakupih itd.

6.1 Funkcija uporabnosti

Na množici potrošniških nizov X je funkcija definirana , katerega vrednost je na potrošniškem naboru enaka potrošnikovi oceni posameznika za ta sklop. Funkcija se imenuje funkcija uporabnosti potrošnika ali funkcija potrošnikove preference. tiste. vsak potrošnik ima svojo funkcijo uporabnosti. Toda celotno množico potrošnikov lahko razdelimo na določene razrede potrošnikov (po starosti, premoženjskem statusu itd.) in vsakemu razredu lahko dodelimo kakšno, morda povprečno funkcijo uporabnosti.

Funkcija je torej ocena potrošnika oziroma stopnja zadovoljevanja potreb posameznika ob nakupu določenega kompleta. Če je niz boljši od nabora za danega posameznika, potem.

Lastnosti uporabne funkcije.

1.

Prve delne izpeljanke funkcije uporabnosti imenujemo mejna koristnost izdelkov. Iz te lastnosti izhaja, da povečanje porabe enega izdelka, medtem ko poraba drugih izdelkov ostane nespremenjena, vodi v povečanje ocene potrošnikov. Vektor je gradient funkcije, kaže smer največje rasti funkcije. Za funkcijo je njen gradient vektor mejnih uporabnosti izdelkov.

2.

tiste. mejna koristnost katerega koli blaga se z naraščajočo potrošnjo zmanjšuje.

3.

tiste. mejna koristnost vsakega proizvoda narašča s količino drugega proizvoda.

Nekatere vrste pomožnih funkcij.

1) Neoklasični:.

2) Kvadrat: kjer je matrika negativno določena in za .

3) Logaritemska funkcija:.

6.2 Črte brezbrižnosti

Pri aplikativnih problemih in modelih izbire potrošnikov se pogosto uporablja poseben primer nabora dveh dobrin, tj. ko je funkcija koristnosti odvisna od dveh spremenljivk. Črta brezbrižnosti je linija, ki povezuje potrošniške sklope, ki imajo enak nivo zadovoljevanja potreb posameznika. V bistvu so črte brezbrižnosti črte ravni funkcije. Enačbe indiferentne črte: .

Osnovne lastnosti indiferentnih linij.

1. Črte brezbrižnosti, ki ustrezajo različnim stopnjam zadovoljevanja potreb, se ne dotikajo in ne križajo.

2. Črte brezbrižnosti se zmanjšujejo.

3. Črte brezbrižnosti so izbočene navzdol.

Lastnost 2 implicira pomembno približno enakost.

To razmerje kaže, za koliko bi moral posameznik povečati (zmanjšati) porabo drugega izdelka, hkrati pa zmanjšati (povečati) porabo prvega izdelka za eno enoto, ne da bi spremenil stopnjo zadovoljevanja svojih potreb. Razmerje se imenuje stopnja zamenjave prvega izdelka z drugim, vrednost pa mejna stopnja zamenjave prvega izdelka z drugim.

Primer 53. Če je mejna koristnost prvega blaga 6, drugega pa 2, potem je treba z zmanjšanjem porabe prvega blaga za eno enoto povečati porabo drugega blaga za 3 enote z enaka raven zadovoljevanja potreb.

6.3 Določen proračun

Pustiti - vektor cen za nabor n izdelkov; I - dohodek posameznika, ki ga je pripravljen porabiti za nakup nabora izdelkov. Nabor nizov blaga, ki stanejo največ I po danih cenah, se imenuje proračunski niz B. Poleg tega se množica naborov blaga, ki stane I, imenuje meja G proračunskega niza B. množica B je omejena z mejo G in naravnimi omejitvami.

Proračunski niz je opisan s sistemom neenakosti:

V primeru niza dveh blaga je proračunski niz B (slika 1) trikotnik v koordinatnem sistemu, omejen s koordinatnimi osmi in premo črto.

6.4 Teorija povpraševanja potrošnikov

V teoriji potrošnje se domneva, da potrošnik vedno stremi k maksimiranju svoje uporabnosti in edina omejitev zanj je omejen dohodek I, ki ga lahko porabi za nakup nabora blaga. Na splošno je problem izbire potrošnikov (problem racionalnega vedenja potrošnikov na trgu) oblikovan takole: poišči potrošniški nabor , ki maksimizira svojo funkcijo uporabnosti za dano proračunsko omejitev. Matematični model tega problema:

V primeru kompleta dveh izdelkov:

Geometrijsko je rešitev tega problema stična točka med mejo proračunskega niza G in črto brezbrižnosti.

Rešitev tega problema je zmanjšana na reševanje sistema enačb:

(1)

Rešitev tega sistema je rešitev problema izbire potrošnikov.

Rešitev problema izbire potrošnikov se imenuje točka povpraševanja. Ta točka povpraševanja je odvisna od cen in dohodka I. To je. točka povpraševanja je funkcija povpraševanja. Po drugi strani je funkcija povpraševanja nabor n funkcij, od katerih je vsaka odvisna od argumenta:

Te funkcije imenujemo funkcije povpraševanja po ustreznem blagu.

Primer 54. Za niz dveh blaga na trgu, znanih cen zanje in dohodka I, poiščite funkcije povpraševanja, če ima funkcija koristnosti obliko .

Rešitev. Razlikujemo funkcijo uporabnosti:

.

Dobljene izraze nadomestimo v (1) in dobimo sistem enačb:

V tem primeru bo strošek za vsak izdelek polovica dohodka potrošnika, znesek kupljenega izdelka pa je enak znesku, porabljenemu zanj, deljeno s ceno izdelka.

Primer 55. Naj deluje koristnost za prvo dobro, drugo,

cena prvega izdelka, cena drugega. Dohodek . Koliko naj potrošnik kupi, da poveča uporabnost?

Rešitev. Poiščimo izpeljanke funkcij koristnosti, jih nadomestimo v sistem (1) in ga rešimo:

Ta sklop blaga je optimalen za potrošnika v smislu maksimiranja uporabnosti.

Preizkus je treba izvesti v skladu z možnostjo, izbrano z zadnjo števko evidenčne številke v ločenem zvezku. Vsaka težava naj vsebuje pogoj, podrobno rešitev in sklep.

1. Uvod v račun

Naloga 1. Poiščite domeno funkcije.

5.

Problem 2. Poiščite meje funkcij.

.

Naloga 3. Poiščite prelomne točke funkcije in določite njihov tip.

1. 2. 3.

Poglavje 2. Diferencialni račun funkcije ene spremenljivke

Naloga 4. Poišči izpeljanke teh funkcij.

1.a); b) c) y =;

d) y = x 6 + + + 5; e) y = x tg x + ln sin x + e 3x;

f) y = 2 x - arcsin x.

2.a) ; b) y =; c) y =; d) y = x 2 - + 3; e) y = e cos; f) y =.

3.a) y = lnx; b) y =; c) y = ln;

4. a) y =; b) y = (e 5 x - 1) 6; c) y =; d) y =; e) y = x 8 ++ + 5; f) y = 3 x - arcsin x.

5.a) y = 2x 3 - + e x; b) y =; c) y =;

d) y =; e) y = 2 cos; f) y =.

6.a) y = lnx; b) y =; c) y = ln;

d) y =; e) y = x 7 + + 1; f) y = 2.

7.a) ; b) y =; c) y =; d) y = x 2 + xsinx +; e) y = e cos; f) y =.

8. a) y =; b) y = (3 x - 4) 6; c) y = sintg;

d) y = 3x 4 - - 9+ 9; e) y =;

f) y = x 2 + arcsin x - x.

9.a); b) ; c) y =; d) y = 5 sin 3 x; e) y = x 3 - - 6+ 3; f) y = 4x 4 + ln.

10.a) b) y =; c) y = (3 x - 4) 6; d) y =; e) y = x 2 - x; f) y = e sin 3 x + 2.

Naloga 5. Raziščite funkcijo in zgradite njen graf.

1. a) b) c).

2.a) b) v) .

3.a) b) v) .

4.b) v)

5.a) b) v) .

6.a) b) v) .

7. a) b) c).

8. a) b) c).

9.a) b) c).

10. a) b) v) .

Naloga 6. Poišči največjo in najmanjšo vrednost funkcije na danem segmentu.

1. .

3. .

6. .

8. .

9. .

10. .

Poglavje 3. Integralni račun

Problem 7. Poišči nedoločene integrale.

1.a) b);

2.a) ; b) c) d).

4. G)

5.a) ; b); v) ; G).

6.a) ; b); v); G)

7.a) ; b) ; v) ; G)

8.a) ; b); v) ; G) .

9.a) ; b) c); G).

10.a) b) v) ; G) .

Problem 8. Izračunaj določene integrale.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

Problem 9. Poišči nepravilne integrale ali dokaži, da se razhajajo.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Problem 10. Poišči površino območja, omejenega s krivuljami

1. .2. .

5. 6.

7. , .8..

10. , .

Poglavje 4. Diferencialni račun funkcije več spremenljivk.

Naloga 11. Poišči domeno funkcije (prikaži na risbi).

Problem 12. Raziščite kontinuiteto funkcije za

Problem 13. Poišči izpeljanko implicitno definirane funkcije.

Problem 14. Približno izračunaj

1.a); b) ; v)

2.a) ; b); v) .

3.a) ; b) ; v) .

4.a) ; b) ; v) .

5. a); b) ; v) .

6. a); b); v) .

7. a); b) ; v) .

8.a); b) ; v)

9.a) ; b); v) .

10. a); b) ; v)

Problem 15. Raziščite funkcijo za ekstreme.

7. .

8. .

9. .

10. .

Naloga 16. Poišči največjo in najmanjšo vrednost funkcije v danem zaprtem območju.

1.v pravokotniku

2.

3.v pravokotniku

4.v območju, omejenem s parabolo

In abscisa.

5.kvadrat

6.v trikotniku, omejenem s koordinatnimi osmi in premo

7.v trikotniku, omejenem s koordinatnimi osmi in premico

8. v trikotniku, omejenem s koordinatnimi osemi in premo

9.v območju, omejenem s parabolo

In abscisa.

10.v območju, omejenem s parabolo

In abscisa.

Glavni

1. M.S. Crassus, B.P. Chuprynov. Osnove matematike in njena uporaba v ekonomski vzgoji: Učbenik. - 4. izd., Isp. - M .: Delo, 2003.

2. M.S. Crassus, B.P. Chuprynov. Matematika za ekonomske specialnosti: Učbenik. - 4. izd., Isp. - M .: Delo, 2003.

3. M.S. Crassus, B.P. Chuprynov. Matematika za dodiplomski študij ekonomije. Učbenik. - 4. izd., Isp. - M .: Delo, 2005.

4. Višja matematika za ekonomiste. Učbenik za univerze / N.Sh. Kremer, B.A. Putko, I.M. Trishin, M.N. Friedman; Ed. prof. N.Sh. Kremer, - 2. izd., Revidirano. in dodaj. - M: ENOTNOST, 2003.

5. Kremer N.Sh, Putko BA, Trishin IM, Fridman MN Višja matematika za ekonomske specialnosti. Učbenik in delavnica (I. in II. del) / Ed. prof. N.Sh. Kremer, - 2. izd., Revidirano. in dodaj. - M: Visokošolsko izobraževanje, 2007. - 893str. - (Osnove znanosti)

6. Danko P.E., Popov A.G., Kozhevnikova T.Ya. Višja matematika v vajah in problemih. M. gimnazija. 1999.

Dodatni

1. I.I. Bavrin, V.L. mornarji. Višja matematika. Humanitarno založniško središče Vlados, 2002.

2. I.A. Zajcev. Višja matematika. "Srednja šola", 1998.

3. A.S. Solodovnikov, V.A. Babaytsev, A.V. Brailov, I.G. Shandra. Matematika v ekonomiji / v dveh delih /. M. Finance in statistika. 1999.

za študente medicinski, pediatrični, zobozdravniški

in fakultete za preventivno medicino

na laboratorijsko delo

"Osnovni koncepti matematične analize"

1. Znanstvena in metodološka utemeljitev teme:

Izvedeni in diferencialni koncepti so eden od osnovnih konceptov matematične analize. Računanje izpeljank je potrebno pri reševanju številnih problemov iz fizike in matematike (iskanje hitrosti, pospeška, tlaka itd.). Pomen koncepta izpeljanke je zlasti določen z dejstvom, da izpeljanka funkcije označuje hitrost spremembe te funkcije, ko se njen argument spremeni.

Uporaba diferenciala omogoča izvedbo približnih izračunov, pa tudi oceno napak.

Metode za iskanje odvodov in diferencialov funkcij ter njihova uporaba predstavljajo glavni problem diferencialnega računa. Potreba po konceptu derivata se pojavi v povezavi s formulacijo problema izračuna hitrosti gibanja in iskanja kota tangente na krivuljo. Možna je tudi inverzna težava: določite prevoženo razdaljo s hitrostjo in poiščite ustrezno funkcijo s tangentom naklona tangente. Ta inverzni problem vodi do koncepta nedoločenega integrala.

Koncept določenega integrala se uporablja v številnih praktičnih problemih, zlasti pri problemih izračunavanja površin ravninskih figur, izračuna dela, ki ga opravi spremenljiva sila, in iskanja povprečne vrednosti funkcije.

Pri matematičnem opisu različnih fizikalnih, kemičnih, bioloških procesov in pojavov se pogosto uporabljajo enačbe, ki vsebujejo ne le preučevane količine, temveč tudi njihove derivate različnih vrstnih redov teh veličin. Na primer, po najpreprostejši različici zakona o razmnoževanju bakterij je stopnja razmnoževanja sorazmerna s številom bakterij v določenem trenutku. Če to količino označimo z N (t), potem je v skladu s fizičnim pomenom derivata hitrost razmnoževanja bakterij derivat N (t), na podlagi zgornjega zakona pa lahko zapišemo razmerje N "(t) = k ∙ N, kjer je k> 0 - koeficient sorazmernosti. Nastala enačba ni algebraična, saj vsebuje ne le neznano funkcijo N (t), ampak tudi njen izvod prvega reda.

2. Kratka teorija:

1. Problemi, ki vodijo do koncepta izpeljanke

1. Problem iskanja hitrosti v materialne točke... Neka materialna točka naj izvaja pravocrtno gibanje. V trenutku t 1 točka je na položaju M 1. V trenutku t 2 noseča M 2 . Označimo interval M 1 , M 2 čez ΔS; t 2 - t 1 = Δt... Vrednost se imenuje povprečna hitrost gibanja. Najti trenutno hitrost točke na položaju M 1 potrebno Δt težijo k ničli. Matematično to pomeni, da

, (1)

Tako je za iskanje trenutne hitrosti materialne točke potrebno izračunati mejo razmerja prirastka funkcije ΔS na prirast argumenta Δt pod pogojem, da Δt → 0.

2. Problem iskanja nagibnega kota tangente na graf funkcije.

Slika 1

Razmislite o grafu neke funkcije y = f (x). Kakšen je nagibni kot
tangenta na točki M 1 ? Na točki M 1 narišite tangento na graf funkcije. Izberite poljubno točko na grafu M 2 in nariši sekanto. Nagnjena je proti osi OH pod kotom α 1 ... Razmislite ΔM 1 M 2 O:

, (2)

Če točka M 1 popraviti in poudariti M 2 približati se M 1 , nato sekans M 1 M 2 bo šel na tangento na graf funkcije v točki M 1 in lahko napišeš:

, (3)

Tako je treba izračunati mejo razmerja prirastka funkcije in prirastka argumenta, če se prirast argumenta nagiba k nič.

Meja razmerja med prirastkom Δy funkcije y = f (x) in prirastkom argumenta Δx v dani točki x 0 ker Δx teži k nič, se imenuje izpeljanka funkcije v dani točki.

Izpeljan zapis: y ", f" (x), ... Po definiciji

, (4)

kjer je Δx = x 2 -x 1 prirast argumenta (razlika med dvema naslednjima dovolj bližnjima vrednostima argumenta), Δy = y 2 -y 1 je prirast funkcije (razlika med vrednostma funkcije, ki ustreza tem vrednostim argumenta).

Iskanje izpeljanke dane funkcije imenujemo njena diferenciacijo... Diferenciacija glavnih elementarnih funkcij se izvaja po že pripravljenih formulah (glej tabelo), pa tudi z uporabo pravila:

Izpeljanka algebraične vsote funkcije enaka vsoti izpeljank teh funkcij:

(u+ υ )"= u" + υ "

2. Odvod produkta dveh funkcij je enak vsoti zmnožkov druge funkcije z odvodkom prve in prve funkcije z izpeljanko druge:

(u ∙υ ) "= u"υ + uυ "

3. Izpeljanka količnika dveh funkcij je enak ulomku, katerega števec je razlika med zmnožki imenovalca z izpeljanko števca in števcem z odvodkom imenovalca, imenovalec pa je kvadrat imenovalca:

Fizični pomen izpeljanke. Primerjava (4) in (1) pomeni, da je trenutna hitrost premočrtnega gibanja materialne točke enaka derivatu odvisnosti njene koordinate od časa.

Splošni pomen izpeljanke funkcije je, da označuje hitrost (hitrost) spremembe funkcije za dano spremembo argumenta. Hitrost fizikalnih, kemičnih in drugih procesov, na primer hitrost hlajenja telesa, hitrost kemične reakcije, hitrost razmnoževanja bakterij itd., je izražena tudi z izpeljanko.

Geometrijski pomen izpeljanke. Velikost tangenta kota naklona tangente, ki je narisana na graf funkcije, se v matematiki imenuje naklon tangente.

Naklon tangente na graf diferenciabilne funkcije v neki točki je številčno enak izvodu funkcije v tej točki.

Ta izjava se imenuje geometrijski pomen izpeljanke.

Vsebina članka

MATEMATIČNA ANALIZA, veja matematike, ki zagotavlja metode za kvantitativno preučevanje različnih procesov sprememb; se ukvarja s preučevanjem hitrosti spreminjanja (diferencialni račun) in določanjem dolžin krivulj, površin in volumnov figur, omejenih z ukrivljenimi konturami in površinami (integralni račun). Za probleme matematične analize je značilno, da je njihova rešitev povezana s pojmom meje.

Matematično analizo sta začela leta 1665 I. Newton in (približno 1675) neodvisno G. Leibniz, čeprav so pomembna pripravljalna dela opravili I. Kepler (1571–1630), F. Cavalieri (1598–1647), P. Ferma (1601– 1665), J. Wallis (1616–1703) in I. Barrow (1630–1677).

Da bo predstavitev bolj živahna, se bomo zatekli k jeziku grafov. Zato bo bralcu morda koristno, da si pred branjem tega članka pogleda članek ANALITIČNA GEOMETRIJA.

DIFERENCIALNI RAČUN

Tangente.

Na sl. 1 prikazuje delček krivulje y = 2x – x 2, sklenjeno med x= –1 in x= 3. Dovolj majhni segmenti te krivulje izgledajo naravnost. Z drugimi besedami, če R Je poljubna točka te krivulje, potem je neka ravna črta, ki poteka skozi to točko in je približek krivulje v majhni soseščini točke R, in manjša kot je soseska, boljši je približek. Taka ravna črta se imenuje tangenta na krivuljo v točki R... Glavna naloga diferencialnega računa je zgraditi splošno metodo, ki vam omogoča, da najdete smer tangente na kateri koli točki na krivulji, kjer tangenta obstaja. Ni si težko predstavljati krivine z ostrim prelomom (slika 2). Če R- vrh takega preloma, potem lahko zgradite približno ravno črto PT 1 - desno od točke R in še ena približna črta RT 2 - levo od točke R... Toda skozi točko ne poteka nobena ravna črta R, ki se je enako dobro približal krivulji v bližini točke P tako v desno kot v levo, od tod tangenta na točki P ne obstaja.

Na sl. 1 tangenta IZ vlečeno skozi izvor O= (0,0). Naklon te črte je 2, t.j. ko se abscisa spremeni za 1, se ordinata poveča za 2. Če x in y- koordinate poljubne točke na IZ, nato pa se odmakne od O na daljavo X enote na desno, odmikamo se O na 2 y enote navzgor. zato y/x= 2 oz y = 2x... To je tangentna enačba IZ na krivuljo y = 2x – x 2 na točki O.

Zdaj je treba pojasniti, zakaj iz množice premic, ki potekajo skozi točko O, je bila izbrana ravna črta IZ... Kakšna je razlika med ravno črto z naklonom 2 in drugimi ravnimi črtami? Obstaja en preprost odgovor in težko se upremo skušnjavi, da bi uporabili analogijo tangente na krog: tangenta IZ ima samo eno skupno točko s krivuljo, medtem ko katera koli druga nenavpična ravna črta, ki poteka skozi to točko O, dvakrat seka krivuljo. To je mogoče preveriti na naslednji način.

Od izraza y = 2x – x 2 lahko dobimo z odštevanjem X 2 od y = 2x(enačbe premice IZ), nato vrednosti y za graf je manj znanja y za ravno črto v vseh točkah, razen v točki x= 0. Zato je graf povsod, razen točke O ki se nahaja spodaj IZ, ta vrstica in graf pa imata samo eno skupno točko. Poleg tega, če y = mx- enačba neke druge premice, ki poteka skozi točko O, potem sta zagotovo dve presečni točki. res, mx = 2x – x 2 ne samo za x= 0, ampak tudi za x = 2 – m... In šele ko m= 2 obe presečni točki sovpadata. Na sl. 3 prikazuje primer, ko m manj kot 2, torej desno od O obstaja druga točka križišča.

Kaj IZ- edina nenavpična ravna črta, ki poteka skozi točko O in ima z grafom samo eno skupno točko, ne pa njegove najpomembnejše lastnosti. Dejansko, če se obrnemo na druge grafe, bo kmalu postalo jasno, da lastnost tangente, ki smo jo zabeležili v splošnem primeru, ni izpolnjena. Na primer, iz sl. 4 je razvidno, da je blizu točke (1,1) graf krivulje y = x 3 je dobro aproksimirana z ravno črto RT, ki pa ima z njim več skupnih točk. Vendar pa bi radi razmislili RT tangenta na ta graf v točki R... Zato je treba poiskati kakšen drug način za poudarjanje tangente od tistega, ki nam je tako dobro služil v prvem primeru.

Recimo, da skozi točko O in poljubna točka Q = (h,k) na grafu krivulje y = 2x – x 2 (slika 5) je narisana ravna črta (imenovana sekanta). Nadomestitev vrednosti v enačbo krivulje x = h in y = k, to razumemo k = 2h – h 2, je torej naklon sekante

Z zelo majhnimi h pomen m blizu 2. Poleg tega izbira h dovolj blizu 0, kar lahko storimo m poljubno blizu 2. Lahko rečemo, da m"Nagiba se k meji", ki je enaka 2, ko h nagiba k nič, ali kakršna koli je meja m enako 2 for h teži k ničli. To je simbolično zapisano takole:

Nato tangenta na graf v točki O opredeljena kot ravna črta, ki poteka skozi točko O, z naklonom, enakim tej meji. Ta definicija tangente je splošno uporabna.

Pokažimo prednosti tega pristopa z drugim primerom: poiščite naklon tangente na graf krivulje y = 2x – x 2 na poljubni točki P = (x,y), da se ne omejujemo na najpreprostejši primer, ko P = (0,0).

Pustiti Q = (x + h, y + k) - druga točka na grafikonu, ki se nahaja na daljavo h desno od R(slika 6). Potrebno je najti pobočje k/h sekansa PQ... Dot Q je na daljavo

nad osjo X.

Če razširimo oklepaje, najdemo:

Odštevanje od te enačbe y = 2x – x 2, najdemo navpično razdaljo od točke R do točke Q:

Zato naklon m sekansa PQ je enako

Zdaj ko h teži k ničli, m teži k 2-2 x; zadnjo vrednost bomo vzeli kot naklon tangente PT... (Isti rezultat bo dosežen, če h ima negativne vrednosti, kar ustreza izbiri točke Q na levi strani P.) Upoštevajte, da za x= 0 rezultat je enak prejšnjemu.

Izraz 2 - 2 x se imenuje izpeljanka od 2 x – x 2. V starih časih so izpeljanko imenovali tudi "diferencialno razmerje" in "diferencialni koeficient". Če izraz 2 x – x 2 določiti f(x), tj.

potem lahko izpeljanko označimo

Da bi ugotovili naklon tangente na graf funkcije y = f(x) na neki točki, ga je treba nadomestiti z fў ( x) vrednost, ki ustreza tej točki X... Torej naklon fў (0) = 2 for X = 0, fў (0) = 0 for X= 1 in fў (2) = –2 for X = 2.

Izpeljanka je tudi označena priў , dy/dx, D x y in Du.

Dejstvo, da je krivulja y = 2x – x 2 blizu dane točke se praktično ne razlikuje od svoje tangente na tej točki, nam omogoča, da govorimo o naklonu tangente kot o "nagibu krivulje" na točki tangente. Tako lahko trdimo, da ima naklon obravnavane krivulje na točki (0,0) naklon 2. Prav tako lahko rečemo, da je pri x= 0 stopnja spremembe y relativno x je 2. V točki (2,0) je naklon tangente (in krivulje) –2. (Znak minus pomeni, da kot x spremenljivka y pada.) V točki (1,1) je tangenta vodoravna. Pravimo krivulja y = 2x – x 2 ima na tej točki stacionarno vrednost.

Vzponi in padci.

Pravkar smo pokazali, da je krivulja f(x) = 2x – x 2 miruje v točki (1,1). Ker fў ( x) = 2 – 2x = 2(1 – x), jasno je, da za x manj kot 1, fў ( x) je pozitiven in zato y poveča; pri x, velika 1, fў ( x) je negativna in zato y zmanjša. Tako je v bližini točke (1,1), prikazane na sl. 6 črka M, pomen pri raste do točke M, nepremičen na točki M in se po točki zmanjša M... Ta točka se imenuje "maksimum", ker je vrednost pri na tej točki presega katero koli od svojih vrednosti v dovolj majhni okolici. Podobno je "minimum" opredeljen kot točka, v bližini katere so vse vrednosti y več kot število pri prav na tej točki. Lahko se tudi zgodi, da čeprav izpeljanka od f(x) na neki točki in izgine, se njegov predznak v bližini te točke ne spremeni. Takšna točka, ki ni niti maksimum niti minimum, se imenuje pregibna točka.

Kot primer poiščimo stacionarno točko krivulje

Izpeljanka te funkcije je

in izgine pri x = 0, X= 1 in X= –1; tiste. pri točkah (0,0), (1, –2/15) in (–1, 2/15). Če X nekoliko manj kot -1, torej fў ( x) je negativna; če X nekoliko več kot -1, torej fў ( x) je pozitiven. Zato je točka (–1, 2/15) maksimum. Podobno lahko pokažemo, da je točka (1, –2/15) minimum. Toda izpeljanka fў ( x) je negativen pred in za točko (0,0). Zato je (0,0) pregibna točka.

Izvedena študija oblike krivulje, pa tudi dejstva, da krivulja seka os X pri f(x) = 0 (tj. za X= 0 ali) vam omogoča, da predstavite njegov graf približno, kot je prikazano na sl. 7.

Na splošno, če izvzamemo nenavadne primere (krivulje, ki vsebujejo ravne odseke ali neskončno število zavojev), obstajajo štiri možnosti za relativni položaj krivulje in tangente v bližini tangentne točke R. (cm... riž. 8, kjer ima tangenta pozitiven naklon.)

1) Na obeh straneh točke R krivulja leži nad tangento (slika 8, a). V tem primeru pravijo, da je krivulja na točki R konveksno navzdol ali konkavno.

2) Na obeh straneh točke R krivulja se nahaja pod tangento (slika 8, b). V tem primeru pravimo, da je krivulja konveksna navzgor ali preprosto konveksna.

3) in 4) Krivulja se nahaja nad tangento na eni strani točke R in spodaj - na drugi strani. V tem primeru R- pregibna točka.

Primerjava vrednosti fў ( x) na obeh straneh R s svojo vrednostjo na točki R, je mogoče določiti, kateri od teh štirih primerov je treba obravnavati v določenem problemu.

Aplikacije.

Vse našteto najde pomembne aplikacije na različnih področjih. Na primer, če se telo vrže navpično navzgor z začetno hitrostjo 200 čevljev na sekundo, potem višina s na katerem se bodo nahajali skozi t sekund v primerjavi z začetno točko bo

Ugotovimo, da delujemo na enak način kot v primerih, ki smo jih obravnavali

ta vrednost izgine pri c. Izpeljanka fў ( x) je pozitiven do vrednosti c in negativen po tem času. zato s naraste na, nato postane stacionarno in nato zmanjša. To je splošen opis gibanja telesa, vrženega navzgor. Iz nje vemo, kdaj telo doseže najvišjo točko. Nadalje, zamenjava t= 25/4 in f(t), dobimo 625 čevljev, največje dviganje. V tej nalogi fў ( t) ima fizični pomen. Ta izpeljanka kaže hitrost, s katero se telo giblje v trenutku t.

Poglejmo si še eno vrsto aplikacije (slika 9). Iz lista kartona s površino 75 cm 2 je potrebno narediti škatlo s kvadratnim dnom. Kako velika mora biti ta škatla, da ima največjo prostornino? Če X- stran dna škatle in h- njegova višina, potem je prostornina škatle V = x 2 h, površina pa je 75 = x 2 + 4xh... S preoblikovanjem enačbe dobimo:

Izpeljano iz V se izkaže za enako

in izgine pri X= 5. Potem

in V= 125/2. Funkcijski graf V = (75x – x 3) / 4 je prikazano na sl. 10 (negativne vrednosti X izpuščen, ker v tem problemu nima fizičnega pomena).

Odvod.

Pomembna naloga diferencialnega računa je ustvarjanje metod, ki vam omogočajo hitro in priročno iskanje izpeljank. To je na primer enostavno izračunati

(Izvod konstante je seveda nič.) Ni težko izpeljati splošnega pravila:

kje n- poljubno celo število ali ulomek. na primer,

(Ta primer prikazuje, kako uporabni so ulomni eksponenti.)

Tukaj je nekaj najpomembnejših formul:

Obstajajo tudi naslednja pravila: 1) če vsaka od obeh funkcij g(x) in f(x) ima izpeljanke, potem je odvod njihove vsote enak vsoti odvodov teh funkcij, izpeljanka razlike pa je enaka razliki izpeljank, t.j.

2) izvod produkta dveh funkcij se izračuna po formuli:

3) izpeljanka razmerja obeh funkcij ima obliko

4) odvod funkcije, pomnožen s konstanto, je enak konstanti, pomnoženi z odvodom te funkcije, t.j.

Pogosto se zgodi, da je treba vrednosti funkcije izračunati po fazah. Na primer za izračun greha x 2, najprej moramo najti u = x 2 in nato izračunajte sinus števila u... Izvod tako zapletenih funkcij najdemo s pomočjo tako imenovanega "verižnega pravila":

V našem primeru f(u) = greh u, fў ( u) = cos u, torej,

Ta in druga podobna pravila omogočajo, da takoj zapišemo izpeljanke številnih funkcij.

Linearni približki.

Dejstvo, da lahko ob poznavanju izpeljanke na tej točki v mnogih primerih zamenjamo graf funkcije blizu neke točke njene tangente, je zelo pomembno, saj je z ravnimi črtami lažje delati.

Ta ideja najde neposredno uporabo pri izračunu približnih vrednosti funkcij. Na primer, precej težko je izračunati vrednost kdaj x= 1,033. Lahko pa izkoristite dejstvo, da je število 1,033 blizu 1 in to. Zapri x= 1 lahko zamenjamo graf tangentne krivulje brez resne napake. Naklon takšne tangente je enak vrednosti izpeljanke ( x 1/3) ў = (1/3) x–2/3 pri x = 1, tj 1/3. Ker točka (1,1) leži na krivulji in je naklon tangente na krivuljo na tej točki 1/3, ima enačba tangente obliko

Na tej vrstici na X = 1,033

Nastala vrednost y mora biti zelo blizu resnični vrednosti y; in dejansko je le 0,00012 več kot res. V matematični analizi so bile razvite metode za izboljšanje natančnosti te vrste linearnega približevanja. Te metode zagotavljajo zanesljivost naših približnih izračunov.

Pravkar opisani postopek predlaga uporaben zapis. Pustiti P- točka, ki ustreza na grafu funkcije f spremenljivka X in pusti funkcijo f(x) je diferenciran. Zamenjajte graf krivulje blizu točke R tangenta nanjo, narisana na tej točki. Če X spremeniti glede na znesek h, potem se bo ordinata tangente spremenila za vrednost h H f ў ( x). Če h je zelo majhna, potem je slednja vrednost dober približek resnični spremembi ordinate y grafike. Če namesto h zapisali bomo simbol dx(to ni produkt!), ampak sprememba ordinate y označujejo dy, potem dobimo dy = f ў ( x)dx, oz dy/dx = f ў ( x) (cm... riž. enajst). Zato namesto Dy oz f ў ( x) simbol se pogosto uporablja za označevanje izpeljanke dy/dx... Priročnost tega zapisa je odvisna predvsem od eksplicitnega videza verižnega pravila (diferenciacija kompleksne funkcije); v novem zapisu je ta formula videti takole:

kjer se namiguje, da pri odvisno od u, a u posledično odvisno od X.

Velikost dy imenujemo diferencial pri; pravzaprav je odvisno od dve spremenljivke, in sicer: od X in prirastki dx... Ko se prirastek dx zelo majhna, velikost dy je blizu ustrezni spremembi vrednosti y... Toda predpostaviti, da je prirast dx malo, ni potrebno.

Izpeljana funkcija y = f(x) smo označili f ў ( x) oz dy/dx... Pogosto je mogoče vzeti derivat derivata. Rezultat se imenuje druga izpeljanka od f (x) in označeno f ўў ( x) oz d 2 y/dx 2. Na primer, če f(x) = x 3 – 3x 2, torej f ў ( x) = 3x 2 – 6x in f ўў ( x) = 6x- 6. Podobne oznake se uporabljajo za izpeljanke višjega reda. Da bi se izognili velikemu številu pomišljajev (enako vrstnemu redu izpeljanke), lahko četrto izpeljanko (na primer) zapišemo kot f (4) (x), in izpeljanka n-ti vrstni red kot f (n) (x).

Lahko se pokaže, da je krivulja v točki konveksna navzdol, če je druga izpeljanka pozitivna, in konveksna navzgor, če je druga izpeljanka negativna.

Če ima funkcija drugo izpeljanko, potem sprememba količine y ki ustreza prirastku dx spremenljivka X, lahko približno izračunamo po formuli

Ta približek je na splošno boljši od tistega, ki ga daje diferencial fў ( x)dx... To ustreza zamenjavi dela krivulje s parabolo in ne z ravno črto.

Če je funkcija f(x) torej obstajajo izpeljanke višjih vrst

Preostanek je

kje x- neka številka med x in x + dx... Zgornji rezultat se imenuje Taylorjeva formula za preostanek. Če f(x) ima izpeljanke vseh vrstnih redov, potem običajno R n® 0 za n ® Ґ .

INTEGRALNI RAČUN

Kvadrati.

Pri preučevanju področij krivolinijskih ravninskih figur se odkrijejo novi vidiki matematične analize. Takšne težave so poskušali rešiti celo stari Grki, za katere je bila na primer določitev površine kroga ena najtežjih nalog. Velik uspeh pri reševanju tega problema je dosegel Arhimed, ki mu je uspelo najti tudi površino paraboličnega segmenta (slika 12). S pomočjo zelo zapletenega sklepanja je Arhimed dokazal, da je površina paraboličnega segmenta 2/3 površine opisanega pravokotnika in je zato v tem primeru enaka (2/3) (16) = 32/3. Kot bomo videli kasneje, je ta rezultat mogoče zlahka dobiti z metodami matematične analize.

Predhodniki Newtona in Leibniza, predvsem Kepler in Cavalieri, so rešili problem izračunavanja površin krivolinijskih figur z metodo, ki jo težko imenujemo logična, a se je izkazala za izjemno plodno. Ko je Wallis leta 1655 združil metode Keplerja in Cavalierija z Descartesovimi metodami (analitična geometrija) in uporabil novorojeno algebro, je bil oder za pojav Newtona popolnoma pripravljen.

Wallis je sliko, katere površino je bilo treba izračunati, razdelil na zelo ozke trakove, od katerih je vsak približno veljal za pravokotnik. Nato je seštel površine aproksimacijskih pravokotnikov in v najpreprostejših primerih dobil vrednost, h kateri teži vsota površin pravokotnikov, ko se število črt nagiba k neskončnosti. Na sl. 13 prikazuje pravokotnike, ki ustrezajo neki delitvi na trakove površine pod krivuljo y = x 2 .

Glavni izrek.

Veliko odkritje Newtona in Leibniza je omogočilo izključitev napornega procesa prehoda na mejo vsote površin. To je bilo storjeno zahvaljujoč novemu pogledu na koncept kvadrata. Bistvo je v tem, da si moramo zamisliti površino pod krivuljo, kot jo generira ordinata, ki se premika od leve proti desni, in vprašati, kako hitro se spreminja območje, ki ga ordinate pometejo. Ključ do odgovora na to vprašanje bomo dobili, če upoštevamo dva posebna primera, v katerih je območje vnaprej znano.

Začnimo s površino pod grafom linearne funkcije y = 1 + x ker je v tem primeru mogoče površino izračunati z uporabo elementarne geometrije.

Pustiti A(x) Je del ravnine, zaprt med ravno črto y = 1 + x in segment OQ(slika 14). Med vožnjo QP desno območje A(x) poveča. Kako hitro? Na to vprašanje ni težko odgovoriti, saj vemo, da je površina trapeza enaka zmnožku njegove višine s polovično vsoto njegovih osnov. zato

Stopnja spremembe območja A(x) je določena s svojo izpeljanko

To vidimo Aў ( x) sovpada z ordinato pri točke R... Je to naključje? Poskusimo preveriti parabolo, prikazano na sl. 15. Kvadrat A (x) pod parabolo pri = X 2 v razponu od 0 do X je enako A(x) = (1 / 3)(x)(x 2) = x 3/3. Hitrost spremembe tega območja je določena z izrazom

ki natančno sovpada z ordinato pri premikajoča se točka R.

Če predpostavimo, da je to pravilo na splošno izpolnjeno tako, da

je stopnja spremembe površine pod grafom funkcije y = f(x), potem lahko to uporabite za izračune in druga področja. Pravzaprav razmerje Aў ( x) = f(x) izraža temeljni izrek, ki bi ga lahko formulirali na naslednji način: izvod ali stopnja spremembe površine kot funkcija X, je enak vrednosti funkcije f (x) na točki X.

Na primer, če želite poiskati območje pod grafom funkcije y = x 3 od 0 do X(slika 16), damo

Možen odgovor je:

saj izpeljanka od X 4/4 je res enako X 3. Poleg tega A(x) je enak nič za X= 0, kot bi moralo biti, če A(x) je res območje.

Matematična analiza dokazuje, da je poleg zgornjega izraza za še en odgovor A(x), ne obstaja. Pokažimo, da je ta izjava verjetna z naslednjim hevrističnim (nerigoroznim) sklepanjem. Recimo, da obstaja druga rešitev V(x). Če A(x) in V(x) "Začni" hkrati od nič vrednosti pri X= 0 in se ves čas spreminjajo z enako hitrostjo, nato pa njihove vrednosti na št X ne more postati drugačen. Povsod morajo biti enaki; zato obstaja samo ena rešitev.

Kako je mogoče upravičiti razmerje? Aў ( x) = f(x) na splošno? Na to vprašanje je mogoče odgovoriti le s preučevanjem hitrosti spreminjanja površine kot funkcije X na splošno. Pustiti m- najmanjša vrednost funkcije f (x) v razponu od X prej ( x + h), a M- največja vrednost te funkcije v istem intervalu. Nato prirast površine na prehodu X do ( x + h) mora biti zaprta med površinama dveh pravokotnikov (slika 17). Osnovi obeh pravokotnikov sta enaki h... Manjši pravokotnik ima višino m in območje mh, večji oz. M in Mh... Na ploskvi površine proti X(slika 18) je razvidno, da ko se abscisa spremeni za h, se vrednost ordinate (tj. površine) poveča za znesek, ki je med mh in Mh... Sekantni naklon v tem grafu je med m in M... kaj se zgodi, ko h teži k ničli? Če je graf funkcije y = f(x) je neprekinjena (tj. ne vsebuje diskontinuitet), torej M, in m nagnjeni k f(x). Zato naklon Aў ( x) ploskev površine kot funkcija X je enako f(x). Prav do takega zaključka je bilo treba priti.

Leibniz je predlagal območje pod krivuljo y = f(x) od 0 do a poimenovanje

S strogim pristopom je treba ta tako imenovani določen integral definirati kot mejo določenih vsot na Wallisov način. Glede na zgornji rezultat je jasno, da je ta integral izračunan pod pogojem, da lahko najdemo takšno funkcijo A(x), ki izgine pri X= 0 in ima izpeljanko Aў ( x) enako f (x). Iskanje takšne funkcije se običajno imenuje integracija, čeprav bi bilo to operacijo bolj primerno poimenovati antidiferenciacija, kar pomeni, da je v nekem smislu inverzna diferenciaciji. V primeru polinoma je integracija enostavna. Na primer, če

kar je enostavno preveriti z diferenciacijo A(x).

Za izračun površine A 1 pod krivuljo y = 1 + x + x 2/2, zaprto med ordinatama 0 in 1, preprosto zapišemo

in nadomeščanje X= 1, dobimo A 1 = 1 + 1/2 + 1/6 = 5/3. Kvadrat A(x) od 0 do 2 je enako A 2 = 2 + 4/2 + 8/6 = 16/3. Kot je razvidno iz sl. 19 je območje med ordinatama 1 in 2 A 2 – A 1 = 11/3. Običajno je zapisan kot določen integral

Zvezki.

S podobnim sklepanjem je presenetljivo preprosto izračunati prostornine vrtilnih teles. Pokažimo to na primeru izračuna prostornine žoge, še enega klasičnega problema, ki so ga stari Grki z velikimi težavami uspeli rešiti z znanimi metodami.

Zavrtite del ravnine, ki je zaprt znotraj četrtine kroga polmera r, pod kotom 360 ° okoli osi X... Kot rezultat dobimo hemisfero (slika 20), katere volumen označujemo V(x). Treba je določiti stopnjo, s katero se V(x) z naraščanjem x... Nadaljujemo od X Za X + h, je enostavno preveriti, da je prirast glasnosti manjši od prostornine str(r 2 – x 2)h polmer in višina krožnega valja h, in več kot volumen str[r 2 – (x + h) 2 ]h polmer in višina valja h... Zato na grafu funkcije V(x) naklon sekansa je med str(r 2 – x 2) in str[r 2 – (x + h) 2]. Kdaj h teži k nič, naklon teži k

Pri x = r dobimo

za prostornino hemisfere in torej 4 p r 3/3 za prostornino celotne krogle.

Podobna metoda vam omogoča iskanje dolžin krivulj in površin ukrivljenih površin. Na primer, če a(x) - dolžina loka PR na sl. 21, potem je naša naloga izračunati aў( x). Na hevristični ravni uporabljamo trik, ki nam omogoča, da se ne zatečemo k običajnemu prehodu do meje, ki je nujna za strog dokaz rezultata. Recimo, da je stopnja spremembe funkcije a(x) na točki R je enak, kot bi bil, če bi krivuljo nadomestila njena tangenta PT na točki P... Toda iz sl. 21 je mogoče neposredno videti, ko stopite h desno ali levo od točke X skupaj RT pomen a(x) spremeni v

Zato je hitrost spremembe funkcije a(x) je

Da bi našli samo funkcijo a(x), je potrebno le integrirati izraz na desni strani enakosti. Izkazalo se je, da je večino funkcij težko integrirati. Zato razvoj integralnih računskih metod predstavlja velik del matematične analize.

Antiderivati.

Vsaka funkcija, katere izpeljanka je enaka dani funkciji f(x), se imenuje antiderivat (ali primitiven) za f(x). na primer, X 3/3 je antiderivat za funkcijo X 2, saj ( x 3/3) ў = x 2. Seveda X 3/3 ni edini antiderivat funkcije X 2 od takrat x 3 /3 + C je tudi izpeljanka za X 2 za katero koli konstanto Z... Vendar se bomo v nadaljevanju strinjali, da takšne aditivne konstante izpustimo. Na splošno

kje n Je pozitivno celo število, saj ( x n + 1/(n+ 1)) ў = x n... Relacija (1) velja v še bolj splošnem smislu, če n zamenjajte s katerim koli racionalnim številom k razen -1.

Arbitrarna antiderivativna funkcija za dano funkcijo f(x) se običajno imenuje nedoločen integral od f(x) in ga označimo kot

Na primer, ker (greh x) ў = cos x, formula velja

V mnogih primerih, ko obstaja formula za nedoločen integral dane funkcije, jo lahko najdemo v številnih široko objavljenih tabelah nedoločenih integralov. Integrali elementarnih funkcij so tabelarični (vključujejo potenke, logaritme, eksponentno funkcijo, trigonometrične funkcije, inverzne trigonometrične funkcije, pa tudi njihove končne kombinacije, pridobljene z operacijami seštevanja, odštevanja, množenja in deljenja). S pomočjo tabelarnih integralov lahko izračunate integrale bolj zapletenih funkcij. Obstaja veliko načinov za izračun nedoločenih integralov; najpogostejša med njimi je variabilna substitucija ali substitucijska metoda. Sestavljen je v tem, da če želimo zamenjati v nedoločenem integralu (2) x na neki diferenciabilni funkciji x = g(u), da se integral ne spremeni, je potrebno x zamenjan z gў ( u)du... Z drugimi besedami, enakost

(zamenjava 2 x = u, od koder 2 dx = du).

Tu je še ena metoda integracije - metoda integracije po delih. Temelji na že znani formuli

Ob integraciji leve in desne strani in ob upoštevanju tega

Ta formula se imenuje formula za integracijo po delih.

Primer 2. Potrebno je najti. Ker cos x= (greh x) ў, to lahko zapišemo

Od (5), nastavitev u = x in v= greh x, dobimo

In ker (–cos x) ў = greh x najdemo to in

Poudariti je treba, da smo se omejili le na zelo kratek uvod v zelo obsežno temo, v kateri so se nabrale številne duhovite tehnike.

Funkcije dveh spremenljivk.

Zaradi krivulje y = f(x) obravnavali smo dve nalogi.

1) Poiščite naklon tangente na krivuljo v dani točki. Ta problem se reši z izračunom vrednosti izpeljanke fў ( x) na določeni točki.

2) Poiščite površino pod krivuljo nad segmentom osi X omejeno z navpičnimi črtami X = a in X = b... Ta problem je rešen z izračunom določenega integrala.

Vsaka od teh težav ima analog v primeru površine z = f(x,y).

1) Poiščite tangentno ravnino na površino v dani točki.

2) Poiščite prostornino pod površino nad delom ravnine hu omejeno s krivuljo Z, in s strani - pravokotnici na ravnino xy ki poteka skozi točke mejne krivulje Z (cm... riž. 22).

Naslednji primeri prikazujejo, kako se te naloge izvajajo.

Primer 4. Poiščite tangentno ravnino na površino

na točki (0,0,2).

Ravnina je definirana, če sta podani dve sekajoči se premici, ki ležita v njej. Ena od teh vrstic ( l 1) vstopimo v letalo xz (pri= 0), drugi ( l 2) - v letalu yz (x = 0) (cm... riž. 23).

Najprej, če pri= 0, torej z = f(x,0) = 2 – 2x – 3x 2. Izpeljanka glede na X označeno z fў x(x,0) = –2 – 6x, pri X= 0 ima vrednost –2. naravnost l 1 podano z enačbami z = 2 – 2x, pri= 0 - tangenta na Z 1, linije preseka površine z ravnino pri= 0. Podobno, če X= 0, torej f(0,y) = 2 – y – y 2, in izpeljanka glede na pri ima obliko

Ker fў y(0,0) = –1, krivulja Z 2 - črta presečišča površine z ravnino yz- ima tangento l 2 podane z enačbami z = 2 – y, X= 0. Želena tangentna ravnina vsebuje obe ravni črti l 1 in l 2 in je zapisana z enačbo

To je enačba ravnine. Poleg tega dobimo ravne črte l 1 in l 2, nastavitev oz. pri= 0 in X = 0.

Dejstvo, da enačba (7) resnično opredeljuje tangentno ravnino, lahko preverimo na hevristični ravni, če opazimo, da ta enačba vsebuje člene prvega reda, vključene v enačbo (6), in da je člene drugega reda mogoče predstaviti v oblika -. Ker je ta izraz negativen za vse vrednosti X in pri, Poleg tega X = pri= 0, površina (6) leži povsod pod ravnino (7), razen točke R= (0,0,0). Lahko rečemo, da je površina (6) v točki konveksna navzgor R.

Primer 5. Poiščite tangentno ravnino na površino z = f(x,y) = x 2 – y 2 v izvoru 0.

Na površini pri= 0 imamo: z = f(x,0) = x 2 in fў x(x,0) = 2x... Na Z 1, presečišča, z = x 2. Na točki O naklon je fў x(0,0) = 0. Na ravnini X= 0 imamo: z = f(0,y) = –y 2 in fў y(0,y) = –2y... Na Z 2, presečišča, z = –y 2. Na točki O naklon krivulje Z 2 je enako fў y(0,0) = 0. Ker so tangente na Z 1 in Z 2 sta osi X in pri, je tangentna ravnina, ki jih vsebuje, ravnina z = 0.

Vendar v bližini izhodišča naša površina ni na eni strani tangentne ravnine. Pravzaprav krivulja Z 1 povsod, razen točke 0, leži nad tangentno ravnino in krivuljo Z 2 - oziroma pod njim. Površina seka tangentno ravnino z= 0 v ravnih črtah pri = X in pri = –X... Takšna površina naj bi imela v izhodišču sedlo (slika 24).

Delne izpeljanke.

V prejšnjih primerih smo uporabili izpeljanke iz f (x,y) na X in po pri... Poglejmo zdaj takšne izpeljanke bolj splošno. Če imamo funkcijo dveh spremenljivk, npr. F(x,y) = x 2 – xy, potem lahko v vsaki točki definiramo dva njena "delna izpeljanka", enega z diferenciacijo funkcije glede na X in popravljanje pri, drugi z razlikovanjem glede na pri in popravljanje X... Prva od teh izpeljank je označena kot fў x(x,y) ali ¶ f/¶ x; drugič - kako f f ў y... Če oba mešana izpeljanka (by X in pri, na pri in X) so neprekinjeni, potem ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x; v našem primeru ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x = –1.

Delna izpeljanka fў x(x,y) označuje hitrost spremembe funkcije f na točki ( x,y) v smeri naraščanja X, a fў y(x,y) Je hitrost spremembe funkcije f naraščajoča smer pri... Stopnja spremembe funkcije f na točki ( X,pri) v smeri premice, ki tvori kot q s pozitivno smerjo osi X, se imenuje izpeljanka funkcije f proti; njena vrednost je kombinacija dveh delnih izvodov funkcije f v tangentni ravnini je skoraj enak (za majhne dx in dy) resnična sprememba z na površini, vendar je izračun diferenciala običajno lažji.

Formula, ki smo jo že obravnavali iz metode spremenljivke spremembe, znane kot izpeljanka kompleksne funkcije ali verižno pravilo, v enodimenzionalnem primeru, ko pri odvisno od X, a X odvisno od t, ima obliko:

Za funkcije dveh spremenljivk je podobna formula:

Koncepte in oznake delne diferenciacije je enostavno posplošiti na višje dimenzije. Zlasti, če je površina implicitno podana z enačbo f(x,y,z) = 0, lahko enačbo tangentne ravnine na površino dobimo bolj simetrično obliko: enačbo tangentne ravnine v točki ( x (x 2/4)], potem je integriran preko X 0 proti 1. Končni rezultat je 3/4.

Formulo (10) lahko interpretiramo tudi kot tako imenovani dvojni integral, tj. kot meja vsote volumnov elementarnih "celic". Vsaka taka celica ima bazo D x D y in višino, ki je enaka višini površine nad neko točko pravokotne osnove ( cm... riž. 26). Lahko se pokaže, da sta obe stališči na formulo (10) enakovredni. Dvojni integrali se uporabljajo za iskanje težišč in številnih momentov, ki jih najdemo v mehaniki.

Strožja utemeljitev matematičnega aparata.

Doslej smo koncepte in metode računanja predstavili na intuitivni ravni in se nismo obotavljali zateči k geometrijskim oblikam. Ostaja nam še, da na kratko razmislimo o strožjih metodah, ki so se pojavile v 19. in 20. stoletju.

Na začetku 19. stoletja, ko se je končala doba jurišnih in jurišnih "ustvarjanja matematične analize", so se v ospredje postavila vprašanja njene utemeljitve. V delih Abela, Cauchyja in številnih drugih izjemnih matematikov so bili pojmi "meje", "neprekinjene funkcije", "konvergentne serije" natančno opredeljeni. To je bilo potrebno za vzpostavitev logičnega reda na podlagi matematične analize, da bi postala zanesljivo raziskovalno orodje. Potreba po temeljiti utemeljitvi je postala še bolj očitna, ko je leta 1872 Weierstrass odkril povsod neprekinjene, vendar nikjer diferencialne funkcije (graf takšnih funkcij ima prelom na vsaki točki). Ta rezultat je naredil izjemen vtis na matematike, saj je očitno nasprotoval njihovi geometrijski intuiciji. Še bolj izrazit primer nezanesljivosti geometrijske intuicije je bila neprekinjena krivulja, ki jo je zgradil D. Peano, ki v celoti zapolni določen kvadrat, t.j. ki poteka skozi vse svoje točke. Ta in druga odkritja so dala povod za program »aritmetizacije« matematike, t.j. narediti bolj zanesljivo z utemeljitvijo vseh matematičnih konceptov s pojmom števila. Skoraj puritanska abstinenca od jasnosti v delih o temeljih matematike je imela svojo zgodovinsko utemeljitev.

Po sodobnih kanonih logične strogosti je nedopustno govoriti o površini pod krivuljo. y = f(x) in nad segmentom osi X, celo f- neprekinjeno funkcijo, ne da bi prej opredelili točen pomen izraza "območje" in ne ugotovili, da tako določeno območje res obstaja. Ta problem je leta 1854 uspešno rešil B. Riemann, ki je natančno opredelil pojem določenega integrala. Od takrat je bila ideja seštevanja za pojmom določenega integrala predmet številnih poglobljenih študij in posploševanj. Posledično je danes mogoče dati pomen določenemu integralu, tudi če je integrand povsod diskontinuiran. Novi koncepti integracije, k nastanku katerih so veliko prispevali A. Lebesgue (1875–1941) in drugi matematiki, so povečali moč in lepoto sodobne matematične analize.

Komaj bi bilo primerno, da se spuščamo v podrobnosti vseh teh in drugih konceptov. Omejili se bomo le na podajanje strogih definicij mejnega in določenega integrala.

Za zaključek naj povemo, da matematična analiza, ki je izjemno dragoceno orodje v rokah znanstvenika in inženirja, še danes pritegne pozornost matematikov kot vir plodnih idej. Hkrati se zdi, da sodobni razvoj kaže, da se matematična analiza v 20. stoletju vse bolj absorbira s takšnimi dominanti. veje matematike, kot sta abstraktna algebra in topologija.

Popolnoma nemogoče je reševati fizične probleme ali primere v matematiki brez poznavanja izvoda in metod za njegovo računanje. Izpeljanka je eden najpomembnejših konceptov matematične analize. Odločili smo se, da današnji članek posvetimo tej temeljni temi. Kaj je izpeljanka, kakšen je njen fizični in geometrijski pomen, kako izračunati izvod funkcije? Vsa ta vprašanja je mogoče združiti v eno: kako razumeti izpeljanko?

Geometrijski in fizični pomen izpeljanke

Naj obstaja funkcija f (x) podano v nekem intervalu (a, b) ... Točki х in х0 pripadata temu intervalu. Ko se x spremeni, se spremeni funkcija sama. Spreminjanje argumenta - razlika med njegovimi vrednostmi x-x0 ... Ta razlika je zapisana kot delta x in se imenuje prirast argumenta. Sprememba ali povečanje funkcije je razlika v vrednostih funkcije na dveh točkah. Definicija izpeljanke:

Derivat funkcije v točki je meja razmerja med prirastkom funkcije v dani točki in prirastkom argumenta, ko slednji teži k nič.

Sicer pa se lahko zapiše takole:

Kakšen je smisel iskati takšno mejo? In tukaj:

odvod funkcije v točki je enak tangentu kota med osjo OX in tangenti na graf funkcije v tej točki.

Fizični pomen izpeljanke: izpeljanka poti glede na čas je enaka hitrosti premočrtnega gibanja.

Dejansko že od šolskih časov vsi vedo, da je hitrost zasebna pot. x = f (t) in čas t ... Povprečna hitrost v določenem časovnem obdobju:

Da bi ugotovili hitrost gibanja naenkrat t0 morate izračunati mejo:

Prvo pravilo: odstranite konstanto

Konstanto je mogoče premakniti izven predznaka odvoda. Poleg tega je treba to storiti. Pri reševanju primerov iz matematike vzemite praviloma - če lahko poenostavite izraz, se prepričajte, da ga poenostavite .

Primer. Izračunajmo izpeljanko:

Drugo pravilo: izpeljanka vsote funkcij

Derivat vsote dveh funkcij je enak vsoti izpeljank teh funkcij. Enako velja za izvod razlike funkcij.

Tega izreka ne bomo dokazovali, ampak raje razmislimo o praktičnem primeru.

Poiščite izpeljavo funkcije:

Tretje pravilo: izpeljanka produkta funkcij

Izvod produkta dveh diferenciabilnih funkcij se izračuna po formuli:

Primer: poiščite izpeljanko funkcije:

rešitev:

Tukaj je pomembno povedati o izračunu izvodov kompleksnih funkcij. Odvod kompleksne funkcije je enak zmnožku odvoda te funkcije glede na vmesni argument z izvodom vmesnega argumenta glede na neodvisno spremenljivko.

V zgornjem primeru srečamo izraz:

V tem primeru je vmesni argument 8x na peto potenco. Da bi izračunali izvod takega izraza, najprej izračunamo izvod zunanje funkcije glede na vmesni argument, nato pa pomnožimo z izpeljanko neposrednega vmesnega argumenta glede na neodvisno spremenljivko.

Četrto pravilo: količnik izpeljanke dveh funkcij

Formula za določanje izvoda količnika dveh funkcij:

Poskušali smo vam povedati o izpeljankah za lutke iz nič. Ta tema ni tako preprosta, kot se sliši, zato bodite opozorjeni: v primerih so pogosto pasti, zato bodite previdni pri izračunu izpeljank.

Za vsa vprašanja o tej in drugih temah se lahko obrnete na študentski servis. V kratkem času vam bomo pomagali rešiti najtežji test in se spopasti z nalogami, tudi če se še nikoli niste ukvarjali z izračunom izpeljank.

Na kateri smo analizirali najpreprostejše izpeljanke, seznanili pa se tudi s pravili diferenciacije in nekaterimi tehnikami iskanja izpeljank. Če torej niste prav veliko z izpeljankami funkcij ali nekatere točke tega članka niso povsem jasne, potem najprej preberite zgornjo lekcijo. Prosim, nastavite se na resno razpoloženje - gradivo ni enostavno, a vseeno ga bom poskušal predstaviti na preprost in dostopen način.

V praksi se moraš z izpeljanko kompleksne funkcije ukvarjati zelo pogosto, rekel bi celo, skoraj vedno, ko dobiš naloge, da najdeš izpeljanke.

V tabeli pogledamo pravilo (št. 5) za razlikovanje kompleksne funkcije:

Razumevanje. Najprej bodimo pozorni na posnetek. Tukaj imamo dve funkciji - in poleg tega je funkcija, figurativno rečeno, vgrajena v funkcijo. Tovrstna funkcija (ko je ena funkcija ugnezdena v drugo) se imenuje kompleksna funkcija.

Poklical bom funkcijo zunanja funkcija in funkcija - notranja (ali ugnezdena) funkcija.

! Te definicije niso teoretične in se ne bi smele pojavljati v končni zasnovi nalog. Neformalne izraze "zunanja funkcija", "notranja" funkcija uporabljam samo zato, da vam olajšam razumevanje snovi.

Če želite razjasniti situacijo, upoštevajte:

Primer 1

Poiščite izvod funkcije

Pod sinusom nimamo samo črke "X", ampak celoštevilski izraz, zato iz tabele izpeljanke ne bo mogoče najti takoj. Opazimo tudi, da je tukaj nemogoče uporabiti prva štiri pravila, zdi se, da obstaja razlika, a dejstvo je, da ne morete "raztrgati" sinusa:

V tem primeru je že iz mojih razlag intuitivno jasno, da je funkcija kompleksna funkcija, polinom pa notranja funkcija (gnezdenje) in zunanja funkcija.

Prvi korak, ki ga je treba izvesti pri iskanju izvoda kompleksne funkcije, je to ugotoviti, katera funkcija je notranja in katera zunanja.

V primeru preprostih primerov se zdi jasno, da je polinom ugnezden pod sinus. Toda kaj, če ni vse očitno? Kako natančno določiti, katera funkcija je zunanja in katera notranja? Za to predlagam uporabo naslednje tehnike, ki jo lahko naredite v mislih ali na osnutku.

Predstavljajte si, da moramo na kalkulatorju izračunati vrednost izraza pri (namesto enega je lahko poljubno število).

Kaj bomo najprej izračunali? Najprej boste morali izvesti naslednje dejanje:, zato bo polinom notranja funkcija:

Drugič bo treba najti, zato bo sinus zunanja funkcija:

Potem ko smo Ugotovljeno pri notranjih in zunanjih funkcijah je čas, da uporabimo pravilo diferenciacije kompleksne funkcije .

Začnemo se odločati. Iz lekcije Kako najdem izpeljanko? spomnimo se, da se zasnova rešitve katere koli izpeljanke vedno začne tako - izraz zapremo v oklepaje in v zgornjem desnem kotu postavimo črto:

Prvič poiščite izvod zunanje funkcije (sinus), poglejte v tabelo odvodov elementarnih funkcij in opazite, da. Vse tabelarične formule so uporabne, tudi če je "x" zamenjan s kompleksnim izrazom, v tem primeru:

Upoštevajte, da je notranja funkcija se ni spremenilo, se je ne dotikamo.

No, to je povsem očitno

Rezultat uporabe formule v končnem dizajnu izgleda takole:

Konstantni faktor je običajno postavljen na začetek izraza:

Če pride do zmede, zapišite rešitev in še enkrat preberite pojasnila.

Primer 2

Poiščite izvod funkcije

Primer 3

Poiščite izvod funkcije

Kot vedno zapišemo:

Ugotovimo, kje imamo zunanjo funkcijo in kje notranjo. Če želite to narediti, poskusite (miselno ali na osnutku) izračunati vrednost izraza pri. Kaj je treba najprej narediti? Najprej morate izračunati, čemu je enaka osnova: kar pomeni, da je polinom notranja funkcija:

In šele nato se izvede eksponentacija, zato je funkcija moči zunanja funkcija:

Po formuli , najprej morate najti izvod zunanje funkcije, v tem primeru stopnjo. V tabeli iščemo zahtevano formulo:. Še enkrat ponavljamo: katera koli tabelarična formula ne velja samo za "x", ampak tudi za kompleksen izraz... Tako je rezultat uporabe pravila diferenciacije kompleksne funkcije Naslednji:

Ponovno poudarjam, da ko vzamemo izpeljanko zunanje funkcije, se notranja funkcija za nas ne spremeni:

Zdaj je treba najti zelo preprosto izpeljanko notranje funkcije in malo "prečesati" rezultat:

Primer 4

Poiščite izvod funkcije

To je primer za samostojno rešitev (odgovor na koncu vadnice).

Za utrjevanje razumevanja izpeljanke kompleksne funkcije bom dal primer brez pripomb, poskusite ga ugotoviti sami, ugibati, kje je zunanja in kje notranja funkcija, zakaj so bile naloge rešene na ta način?

Primer 5

a) Poišči izvod funkcije

b) Poišči izvod funkcije

Primer 6

Poiščite izvod funkcije

Tukaj imamo koren, in da ga lahko razlikujemo, ga moramo predstaviti kot stopnjo. Tako najprej spravimo funkcijo v obliko, primerno za diferenciacijo:

Z analizo funkcije pridemo do zaključka, da je vsota treh členov notranja funkcija, eksponentacija pa zunanja funkcija. Uporabljamo pravilo diferenciacije kompleksne funkcije :

Stopnja je ponovno predstavljena kot radikal (koren), za izvod notranje funkcije pa uporabimo preprosto pravilo za razlikovanje vsote:

Pripravljen. Izraz lahko pripeljete tudi do skupnega imenovalca v oklepaju in vse zapišete v en ulomek. Lepo, seveda, a ko dobimo okorne dolge izpeljanke, je bolje, da tega ne storite (lahko se zmedete, naredite nepotrebno napako in učitelju bo neprijetno preverjati).

Primer 7

Poiščite izvod funkcije

To je primer za samostojno rešitev (odgovor na koncu vadnice).

Zanimivo je, da lahko včasih namesto pravila za razlikovanje kompleksne funkcije uporabimo pravilo za razlikovanje količnika , vendar bo takšna rešitev videti nenavadno kot perverzija. Tukaj je tipičen primer:

Primer 8

Poiščite izvod funkcije

Tukaj lahko uporabite pravilo za razlikovanje količnika , vendar je veliko bolj donosno najti izvod s pravilom diferenciacije kompleksne funkcije:

Funkcijo pripravimo za diferenciacijo - minus premaknemo izven predznaka odvoda in dvignemo kosinus na števec:

Kosinus je notranja funkcija, eksponentacija je zunanja funkcija.
Uporabljamo naše pravilo :

Poiščite izvod notranje funkcije, ponastavite kosinus nazaj:

Pripravljen. V obravnavanem primeru je pomembno, da se ne zmedete v znakih. Mimogrede, poskusite to rešiti s pravilom , se morajo odgovori ujemati.

Primer 9

Poiščite izvod funkcije

To je primer za samostojno rešitev (odgovor na koncu vadnice).

Do sedaj smo si ogledali primere, ko smo imeli samo eno prilogo v kompleksni funkciji. Pri praktičnih nalogah lahko pogosto najdete izpeljanke, kjer je, tako kot gnezdenice, ena v drugi, ugnezdenih 3 ali celo 4-5 funkcij hkrati.

Primer 10

Poiščite izvod funkcije

Razumimo priloge te funkcije. Poskus oceniti izraz s testno vrednostjo. Kako bi računali na kalkulator?

Najprej morate najti, kar pomeni, da je arcsin najgloblje gnezdenje:

Potem je treba ta arcsin od ena na kvadrat:

In končno, dvignite 7 na moč:

To pomeni, da imamo v tem primeru tri različne funkcije in dve prilogi, medtem ko je najbolj notranja funkcija arksinus, najbolj zunanja funkcija pa je eksponentna funkcija.

Začnemo reševati

Po pravilu najprej morate vzeti izpeljanko zunanje funkcije. Pogledamo tabelo izpeljank in najdemo izpeljanko eksponentne funkcije: Edina razlika je v tem, da imamo namesto "x" kompleksen izraz, ki ne izniči veljavnosti te formule. Torej, rezultat uporabe pravila diferenciacije kompleksne funkcije Naslednji.