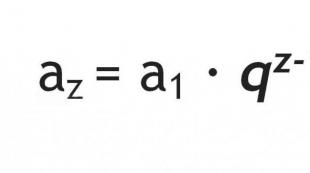Jazykolamy

Štvorrozmerná kocka. Kyberkocka - prvý krok do štvrtej dimenzie Ako sa volá kocka s rôznymi stranami

Tesseract je štvorrozmerná hyperkocka – kocka v štvorrozmernom priestore.
Podľa Oxfordského slovníka slovo tesseract vymyslel a použil v roku 1888 Charles Howard Hinton (1853-1907) vo svojej knihe A New Age of Thought. Neskôr niektorí ľudia nazvali ten istý obrazec tetrakocka (grécky τετρα - štyri) - štvorrozmerná kocka.
Obyčajný tesseract v euklidovskom štvorrozmernom priestore je definovaný ako konvexný obal bodov (±1, ±1, ±1, ±1). Inými slovami, môže byť reprezentovaný ako nasledujúca množina:
[-1, 1]^4 = ((x_1,x_2,x_3,x_4) : -1 = Tesseract je ohraničený ôsmimi nadrovinami x_i= +- 1, i=1,2,3,4 , ktorých priesečník so samotným tesseractom ho definuje 3D plochy (čo sú pravidelné kocky) Každý pár nerovnobežných 3D plôch sa pretína a vytvára 2D plochy (štvorce) atď. Nakoniec má tesseract 8 3D plôch, 24 2D plôch, 32 hrán a 16 vrcholy.
Populárny popis
Skúsme si predstaviť, ako bude vyzerať hyperkocka bez toho, aby sme opustili trojrozmerný priestor.
V jednorozmernom „priestore“ - na priamke - vyberieme úsečku AB dĺžky L. Na dvojrozmernej rovine vo vzdialenosti L od AB nakreslíme úsečku DC rovnobežnú s ňou a ich konce spojíme. Výsledkom je štvorcový CDBA. Opakovaním tejto operácie s rovinou získame trojrozmernú kocku CDBAGHFE. A posunutím kocky v štvrtom rozmere (kolmo na prvé tri) o vzdialenosť L dostaneme hyperkocku CDBAGHFEKLJIOPNM.
Jednorozmerný segment AB slúži ako strana dvojrozmerného štvorca CDBA, štvorec - ako strana kocky CDBAGHFE, ktorá bude naopak stranou štvorrozmernej hyperkocky. Priamka úsečka má dva hraničné body, štvorec má štyri vrcholy, kocka osem. V štvorrozmernej hyperkocke teda bude 16 vrcholov: 8 vrcholov pôvodnej kocky a 8 posunutého vo štvrtom rozmere. Má 32 hrán – každá z nich 12 udáva počiatočnú a konečnú polohu pôvodnej kocky a ďalších 8 hrán „kreslí“ jej osem vrcholov, ktoré sa presunuli do štvrtej dimenzie. Rovnaké uvažovanie možno urobiť pre steny hyperkocky. V dvojrozmernom priestore je len jeden (samotný štvorec), kocka ich má 6 (dve tváre z posunutého štvorca a ďalšie štyri, ktoré opisujú jeho strany). Štvorrozmerná hyperkocka má 24 štvorcových plôch – 12 políčok pôvodnej kocky v dvoch polohách a 12 políčok od jej dvanástich hrán.
Tak, ako sú strany štvorca 4 jednorozmerné segmenty a strany (tváre) kocky sú 6 dvojrozmernými štvorcami, tak pre „štvorrozmernú kocku“ (tesseract) sú strany 8 trojrozmerných kociek. . Priestory protiľahlých párov kociek tesseract (teda trojrozmerné priestory, do ktorých tieto kocky patria) sú rovnobežné. Na obrázku sú to kocky: CDBAGHFE a KLJIOPNM, CDBAKLJI a GHFEOPNM, EFBAMNJI a GHDCOPLK, CKIAGOME a DLJBHPNF.
Podobným spôsobom môžeme pokračovať v úvahách pre hyperkocky väčšieho počtu rozmerov, no oveľa zaujímavejšie je sledovať, ako bude štvorrozmerná hyperkocka vyzerať pre nás, obyvateľov trojrozmerného priestoru. Na to použijeme už známu metódu analógií.
Vezmeme drôtenú kocku ABCDHEFG a pozrieme sa na ňu jedným okom zo strany okraja. Uvidíme a môžeme nakresliť dva štvorce na rovine (jej blízke a vzdialené okraje), spojené štyrmi čiarami - bočnými okrajmi. Podobne štvorrozmerná hyperkocka v trojrozmernom priestore bude vyzerať ako dve kubické „škatule“ vložené do seba a spojené ôsmimi hranami. V tomto prípade sa samotné „boxy“ – trojrozmerné tváre – premietnu do „nášho“ priestoru a čiary, ktoré ich spájajú, sa roztiahnu v smere štvrtej osi. Môžete si tiež skúsiť predstaviť kocku nie v projekcii, ale v priestorovom obrázku.
Tak ako je trojrozmerná kocka tvorená štvorcom posunutým o dĺžku jeho plochy, kocka posunutá do štvrtého rozmeru vytvorí hyperkocku. Je ohraničený ôsmimi kockami, ktoré budú v perspektíve vyzerať ako nejaký dosť zložitý obrazec. Samotná štvorrozmerná hyperkocka pozostáva z nekonečného počtu kociek, rovnako ako trojrozmernú kocku možno „rozrezať“ na nekonečné množstvo plochých štvorcov.
Rozrezaním šiestich plôch trojrozmernej kocky ju môžete rozložiť na plochú postavu - vývoj. Bude mať štvorec na každej strane pôvodnej tváre plus jeden ďalší - tvár oproti nemu. A trojrozmerný vývoj štvorrozmernej hyperkocky bude pozostávať z pôvodnej kocky, šiestich kociek, ktoré z nej „rastú“, plus jednej ďalšej - konečnej „hyperface“.
Vlastnosti tesseractu predstavujú pokračovanie vlastností geometrických útvarov nižšej dimenzie do štvorrozmerného priestoru.

Body (±1, ±1, ±1, ±1). Inými slovami, môže byť reprezentovaný ako nasledujúca množina:

Tesseract je ohraničený ôsmimi nadrovinami, ktorých priesečník so samotným tesseractom definuje jeho trojrozmerné plochy (čo sú obyčajné kocky). Každý pár nerovnobežných 3D plôch sa pretína a vytvára 2D plochy (štvorce) atď. Nakoniec má tesseract 8 3D plôch, 24 2D plôch, 32 hrán a 16 vrcholov.

Populárny popis

Skúsme si predstaviť, ako bude vyzerať hyperkocka bez toho, aby sme opustili trojrozmerný priestor.

Stavba tesseractu na rovine

Jednorozmerný segment AB slúži ako strana dvojrozmerného štvorca CDBA, štvorec - ako strana kocky CDBAGHFE, ktorá bude naopak stranou štvorrozmernej hyperkocky. Priamka úsečka má dva hraničné body, štvorec má štyri vrcholy, kocka osem. V štvorrozmernej hyperkocke teda bude 16 vrcholov: 8 vrcholov pôvodnej kocky a 8 posunutého vo štvrtom rozmere. Má 32 hrán – každá z nich 12 udáva počiatočnú a konečnú polohu pôvodnej kocky a ďalších 8 hrán „kreslí“ jej osem vrcholov, ktoré sa presunuli do štvrtej dimenzie. Rovnaké uvažovanie možno urobiť pre steny hyperkocky. V dvojrozmernom priestore je len jeden (samotný štvorec), kocka ich má 6 (dve tváre z posunutého štvorca a ďalšie štyri, ktoré opisujú jeho strany). Štvorrozmerná hyperkocka má 24 štvorcových plôch – 12 políčok pôvodnej kocky v dvoch polohách a 12 políčok od jej dvanástich hrán.

Tak, ako sú strany štvorca 4 jednorozmerné segmenty a strany (tváre) kocky sú 6 dvojrozmernými štvorcami, tak pre „štvorrozmernú kocku“ (tesseract) sú strany 8 trojrozmerných kociek. . Priestory protiľahlých párov kociek tesseract (teda trojrozmerné priestory, do ktorých tieto kocky patria) sú rovnobežné. Na obrázku sú to kocky: CDBAGHFE a KLJIOPNM, CDBAKLJI a GHFEOPNM, EFBAMNJI a GHDCOPLK, CKIAGOME a DLJBHPNF.

Podobným spôsobom môžeme pokračovať v úvahách pre hyperkocky väčšieho počtu rozmerov, no oveľa zaujímavejšie je sledovať, ako bude štvorrozmerná hyperkocka vyzerať pre nás, obyvateľov trojrozmerného priestoru. Na to použijeme už známu metódu analógií.

Vezmeme drôtenú kocku ABCDHEFG a pozrieme sa na ňu jedným okom zo strany okraja. Uvidíme a môžeme nakresliť dva štvorce na rovine (jej blízke a vzdialené okraje), spojené štyrmi čiarami - bočnými okrajmi. Podobne štvorrozmerná hyperkocka v trojrozmernom priestore bude vyzerať ako dve kubické „škatule“ vložené do seba a spojené ôsmimi hranami. V tomto prípade sa samotné „boxy“ – trojrozmerné tváre – premietnu do „nášho“ priestoru a čiary, ktoré ich spájajú, sa roztiahnu v smere štvrtej osi. Môžete si tiež skúsiť predstaviť kocku nie v projekcii, ale v priestorovom obrázku.

Tak ako je trojrozmerná kocka tvorená štvorcom posunutým o dĺžku jeho plochy, kocka posunutá do štvrtého rozmeru vytvorí hyperkocku. Je ohraničený ôsmimi kockami, ktoré budú v perspektíve vyzerať ako nejaký dosť zložitý obrazec. Samotná štvorrozmerná hyperkocka pozostáva z nekonečného počtu kociek, rovnako ako trojrozmernú kocku možno „rozrezať“ na nekonečné množstvo plochých štvorcov.

Rozrezaním šiestich plôch trojrozmernej kocky ju môžete rozložiť na plochú postavu - vývoj. Bude mať štvorec na každej strane pôvodnej tváre plus jeden ďalší - tvár oproti nemu. A trojrozmerný vývoj štvorrozmernej hyperkocky bude pozostávať z pôvodnej kocky, šiestich kociek, ktoré z nej „rastú“, plus jednej ďalšej - konečnej „hyperface“.

Vlastnosti tesseractu predstavujú pokračovanie vlastností geometrických útvarov nižšej dimenzie do štvorrozmerného priestoru.

Projekcie

Do dvojrozmerného priestoru

Táto štruktúra je ťažko predstaviteľná, ale je možné premietnuť tesseract do dvojrozmerných alebo trojrozmerných priestorov. Okrem toho premietanie do roviny uľahčuje pochopenie polohy vrcholov hyperkocky. Týmto spôsobom je možné získať obrázky, ktoré už neodrážajú priestorové vzťahy v rámci tesseractu, ale ilustrujú štruktúru spojenia vrcholov, ako v nasledujúcich príkladoch:

Tretí obrázok ukazuje tesseract v izometrii vzhľadom na konštrukčný bod. Táto reprezentácia je zaujímavá pri použití tesseractu ako základu pre topologickú sieť na prepojenie viacerých procesorov pri paralelnom výpočte.

Do trojrozmerného priestoru

Jedna z projekcií tesseractu do trojrozmerného priestoru predstavuje dve vnorené trojrozmerné kocky, ktorých zodpovedajúce vrcholy sú spojené segmentmi. Vnútorná a vonkajšia kocka majú v trojrozmernom priestore rôzne veľkosti, no v štvorrozmernom priestore sú to rovnaké kocky. Na pochopenie rovnosti všetkých kociek tesseractu bol vytvorený rotujúci model tesseractu.

Šesť zrezaných pyramíd pozdĺž okrajov tesseractu sú obrazy rovnakých šiestich kociek. Tieto kocky sú však pre tesseract ako štvorce (tváre) pre kocku. Ale v skutočnosti môže byť tesseract rozdelený na nekonečný počet kociek, rovnako ako kocka môže byť rozdelená na nekonečný počet štvorcov alebo štvorec na nekonečný počet segmentov.

Ďalšou zaujímavou projekciou tesseractu do trojrozmerného priestoru je kosoštvorcový dvanástnik so štyrmi uhlopriečkami spájajúcimi dvojice protiľahlých vrcholov pod veľkými uhlami kosoštvorcov. V tomto prípade sa 14 zo 16 vrcholov tesseractu premieta do 14 vrcholov kosoštvorcového dvanástnika a projekcie zvyšných 2 sa zhodujú v jeho strede. Pri takejto projekcii do trojrozmerného priestoru je zachovaná rovnosť a rovnobežnosť všetkých jednorozmerných, dvojrozmerných a trojrozmerných strán.

Stereo pár

Stereo pár tesseractu je znázornený ako dve projekcie do trojrozmerného priestoru. Tento obrázok tesseractu bol navrhnutý tak, aby predstavoval hĺbku ako štvrtý rozmer. Stereo pár sa pozerá tak, že každé oko vidí iba jeden z týchto obrázkov, objaví sa stereoskopický obraz, ktorý reprodukuje hĺbku tesseractu.

Tesseract sa rozbaľuje

Povrch tesseractu sa dá rozložiť na osem kociek (podobne ako sa dá povrch kocky rozložiť na šesť štvorcov). Existuje 261 rôznych dizajnov tesseract. Rozvinutie tesseractu možno vypočítať vynesením spojených uhlov do grafu.

Tesseract v umení

V „New Abbott Plain“ od Edwiny A. hyperkocka pôsobí ako rozprávač.
V jednej epizóde Dobrodružstva Jimmyho Neutrona „chlapec génius“ Jimmy vynájde štvorrozmernú hyperkocku identickú so skladacou skrinkou z románu Glory Road (1963) od Roberta Heinleina.
Robert E. Heinlein spomenul hyperkocky najmenej v troch sci-fi príbehoch. V "The House of Four Dimensions" ("The House That Teal Built") opísal dom postavený ako nezabalený tesseract, ktorý sa potom v dôsledku zemetrasenia "zložil" do štvrtej dimenzie a stal sa z neho "skutočný" tesseract. .
Heinleinov román Glory Road popisuje hyperveľkú krabicu, ktorá bola väčšia zvnútra ako zvonka.
Príbeh Henryho Kuttnera „All Tenali Borogov“ opisuje vzdelávaciu hračku pre deti z ďalekej budúcnosti, podobnú štruktúre ako tesseract.
V románe Alexa Garlanda () sa termín „tesseract“ používa na trojrozmerné rozvinutie štvorrozmernej hyperkocky, a nie samotnej hyperkocky. Toto je metafora navrhnutá tak, aby ukázala, že kognitívny systém musí byť širší ako poznateľný.
Dej hry Cube 2: Hypercube sa sústreďuje na osem cudzincov uväznených v „hyperkocke“ alebo sieti spojených kociek.
Televízny seriál Andromeda používa generátory tesseract ako zápletkové zariadenie. Sú primárne určené na manipuláciu s priestorom a časom.
Obraz „Ukrižovanie“ (Corpus Hypercubus) od Salvadora Dalího ().
Komiks Nextwave zobrazuje vozidlo, ktoré obsahuje 5 zón tesseract.
Na albume Voivod Nothingface sa jedna zo skladieb volá „In my hypercube“.
V románe Anthonyho Pearcea Route Cube sa jeden z obiehajúcich mesiacov Medzinárodnej asociácie pre rozvoj nazýva tesseract, ktorý bol stlačený do 3 rozmerov.
V sérii „Black Hole School“ v tretej sezóne je epizóda „Tesseract“. Lucas stlačí tajné tlačidlo a škola sa začne „formovať ako matematický tesseract“.
Pojem „tesseract“ a jeho odvodený výraz „tesseract“ sa nachádza v príbehu Madeleine L’Engle „A Wrinkle in Time“.
TesseracT je názov britskej djentovej kapely.
Vo filmovej sérii Marvel Cinematic Universe je Tesseract kľúčovým dejovým prvkom, kozmickým artefaktom v tvare hyperkocky.
V príbehu Roberta Sheckleyho „Slečna Myška a štvrtá dimenzia“ sa ezoterický spisovateľ, známy autora, pokúša vidieť tesserakt tak, že celé hodiny hľadí na zariadenie, ktoré navrhol: loptičku na nohe a do nej zapichnuté tyče. ktoré kocky sú namontované, prelepené všelijakými ezoterickými symbolmi. Príbeh spomína Hintonovu prácu.
Vo filmoch The First Avenger, The Avengers. Tesseract - energia celého vesmíru

Ostatné mená

Hexadekachorón Hexadekachorón)
Octochoron (anglicky) Octachoron)
Tetracube
4-kocka
Hyperkocka (ak nie je zadaný počet rozmerov)

Poznámky

Literatúra

Charles H. Hinton. Štvrtá dimenzia, 1904. ISBN 0-405-07953-2
Martin Gardner, Matematický karneval, 1977. ISBN 0-394-72349-X
Ian Stewart, Concepts of Modern Mathematics, 1995. ISBN 0-486-28424-7

Odkazy

V ruštine

Program Transformator4D. Tvorba modelov trojrozmerných projekcií štvorrozmerných objektov (vrátane Hyperkocky).
Program, ktorý implementuje konštrukciu tesseractu a všetky jeho afinné transformácie so zdrojovým kódom v C++.

V angličtine

Mushware Limited – výstupný program tesseract ( Tréner Tesseract, licencia kompatibilná s GPLv2) a strieľačka z pohľadu prvej osoby v štvorrozmernom priestore ( Adanaxis; grafika je hlavne trojrozmerná; V úložiskách OS je verzia GPL).

Polyhedra

Správne
(Platónske pevné látky)

Hviezdicový dvanásťsten Hviezdicový ikoziddekaedrón Hviezdicový dvadsaťsten Hviezdicový mnohosten Hviezdicový osemsten

Konvexné

Archimedove pevné látky	Kuboktaedrón Ikoziddekaedrón Zrezaný štvorsten Zrezaný osemsten Zrezaný dvadsaťsten Zrezaný kváder Zrezaný dvanásťsten Rhombocuboktahedrón Kosoštvorcový kosoštvorcový zrezaný koboktaedrón kosoštvorcový kosoštvorcový zrezaný ikosidodekaedrón Trubectahedrón Trubectahedón doboctahedón desaťsten Pravidelný hranol Antihranol
Katalánske telá	kosodĺžnik kosoštvorcový kosoštvorcový štvorsten Triakistetrahedron štvorsten štvorsten päťsten trojstenný trojsten triakisikosaedrón deltový dvojstenný štvorsten Deltový dvojstenný štvorsten hexexontahedrón päťuholníkový ikosittrahedron dispergovaný štvorhranný štvorsten Distagonálny konštrukciadodekahedrón
Bez úplnej priestorovej symetrie	Pyramída Hranol Dvojpyramída Antihranol Zonohedrón Rovnobežník Rhomboedr Prizmatoid Zrezaná pyramída
Pentagondodecahedron Rovnobežník

vzorce,
vety,
teórie

Iné

Hneď ako som po operácii mohol prednášať, prvá otázka, ktorú študenti položili, bola:

Kedy nám nakreslíte 4-rozmernú kocku? Ilyas Abdulkhaevič nám to sľúbil!

Pamätám si, že moji drahí priatelia majú občas radi chvíľku matematicko-vzdelávacích aktivít. Preto tu napíšem časť mojej prednášky pre matematikov. A pokúsim sa bez toho, aby som bol nudný. V niektorých momentoch som prednášku čítal, samozrejme, prísnejšie.

Najprv sa dohodnime. 4-rozmerný, a ešte viac 5-6-7- a všeobecne k-rozmerný priestor nám nie je daný v zmyslových vnemoch.
„Sme úbohí, pretože sme iba trojrozmerní,“ povedal môj učiteľ v nedeľnej škole, ktorý mi ako prvý povedal, čo je 4-rozmerná kocka. Nedeľná škola bola, prirodzene, mimoriadne nábožensko – matematická. V tom čase sme študovali hyperkocky. Týždeň pred tým matematická indukcia, týždeň po nej hamiltonovské cykly v grafoch - podľa toho ide o 7. ročník.

Nemôžeme sa dotýkať, cítiť, počuť alebo vidieť 4-rozmernú kocku. Čo s tým môžeme robiť? Vieme si to predstaviť! Pretože náš mozog je oveľa zložitejší ako naše oči a ruky.

Aby sme teda pochopili, čo je 4-rozmerná kocka, poďme najprv pochopiť, čo máme k dispozícii. Čo je to 3-rozmerná kocka?

DOBRE DOBRE! Nežiadam vás o jasnú matematickú definíciu. Len si predstavte najjednoduchšiu a najobyčajnejšiu trojrozmernú kocku. Predstavený?

Dobre.
Aby sme pochopili, ako zovšeobecniť 3-rozmernú kocku do 4-rozmerného priestoru, poďme zistiť, čo je 2-rozmerná kocka. Je to také jednoduché - je to štvorec!

Štvorec má 2 súradnice. Kocka má tri. Štvorcové body sú body s dvoma súradnicami. Prvá je od 0 do 1. A druhá je od 0 do 1. Body kocky majú tri súradnice. A každé je ľubovoľné číslo od 0 do 1.

Je logické si predstaviť, že 4-rozmerná kocka je vec, ktorá má 4 súradnice a všetko je od 0 do 1.

/* Je okamžite logické predstaviť si 1-rozmernú kocku, ktorá nie je ničím iným ako jednoduchým segmentom od 0 do 1. */

Tak počkaj, ako nakreslíš 4-rozmernú kocku? Nemôžeme predsa nakresliť 4-rozmerný priestor v rovine!
Ale ani 3-rozmerný priestor nekreslíme v rovine, my ho kreslíme projekcia na 2-rozmernú rovinu kreslenia. Tretiu súradnicu (z) umiestnime pod uhlom, pričom si predstavíme, že os z roviny kreslenia ide „smerom k nám“.

Teraz je úplne jasné, ako nakresliť 4-rozmernú kocku. Rovnakým spôsobom, ako sme umiestnili tretiu os pod určitým uhlom, zoberme štvrtú os a tiež ju umiestnime pod určitým uhlom.
A - voila! -- premietanie 4-rozmernej kocky na rovinu.

Čo? Čo je to vôbec? Vždy počujem šepot zo zadných stolov. Dovoľte mi podrobnejšie vysvetliť, čo je táto spleť riadkov.
Najprv sa pozrite na trojrozmernú kocku. čo sme urobili? Vzali sme štvorec a pretiahli ho pozdĺž tretej osi (z). Je to ako veľa, veľa papierových štvorcov zlepených dohromady v stohu.
Rovnako je to aj so 4-rozmernou kockou. Nazvime štvrtú os pre pohodlie a pre sci-fi „časová os“. Musíme vziať obyčajnú trojrozmernú kocku a pretiahnuť ju časom z času „teraz“ do času „za hodinu“.

Máme "teraz" kocku. Na obrázku je ružová.

A teraz to ťaháme po štvrtej osi - po časovej osi (ukázal som to zelenou farbou). A dostaneme kocku budúcnosti – modrú.

Každý vrchol „kocky teraz“ zanecháva stopu v čase - segment. Spája svoju prítomnosť s budúcnosťou.

Stručne povedané, bez akýchkoľvek textov: nakreslili sme dve rovnaké 3-rozmerné kocky a spojili zodpovedajúce vrcholy.
Presne tak, ako to urobili s 3-rozmernou kockou (nakreslite 2 rovnaké 2-rozmerné kocky a spojte vrcholy).

Ak chcete nakresliť 5-rozmernú kocku, budete musieť nakresliť dve kópie 4-rozmernej kocky (4-rozmernú kocku s piatou súradnicou 0 a 4-rozmernú kocku s piatou súradnicou 1) a spojiť zodpovedajúce vrcholy s hranami. Pravda, na rovine bude taká spleť hrán, že bude takmer nemožné ničomu rozumieť.

Keď sme si predstavili 4-rozmernú kocku a dokonca sme ju dokázali nakresliť, môžeme ju skúmať rôznymi spôsobmi. Nezabudnite to preskúmať vo svojej mysli aj z obrázka.
Napríklad. 2-rozmerná kocka je ohraničená na 4 stranách 1-rozmernými kockami. Je to logické: pre každú z 2 súradníc má začiatok aj koniec.
3-rozmerná kocka je ohraničená na 6 stranách 2-rozmernými kockami. Pre každú z troch súradníc má začiatok a koniec.
To znamená, že 4-rozmerná kocka musí byť obmedzená ôsmimi 3-rozmernými kockami. Pre každú zo 4 súradníc - na oboch stranách. Na obrázku vyššie jasne vidíme 2 tváre, ktoré ho obmedzujú pozdĺž súradnice „času“.

Tu sú dve kocky (sú mierne šikmé, pretože majú 2 rozmery premietnuté do roviny pod uhlom), ktoré obmedzujú našu hyperkocku vľavo a vpravo.

Je tiež ľahké si všimnúť „horné“ a „dolné“.

Najťažšie je vizuálne pochopiť, kde sú „predné“ a „zadné“. Predná časť začína od predného okraja „kocky teraz“ a po predný okraj „kocky budúcnosti“ - je červená. Zadná časť je fialová.

Najťažšie sa spozorujú, pretože sa pod nohami pletú ďalšie kocky, ktoré obmedzujú hyperkocku na inej premietnutej súradnici. Ale všimnite si, že kocky sú predsa len iné! Tu je opäť obrázok, kde sú zvýraznené „kocka súčasnosti“ a „kocka budúcnosti“.

Samozrejme je možné premietnuť 4-rozmernú kocku do 3-rozmerného priestoru.
Prvý možný priestorový model je jasný, ako vyzerá: treba zobrať 2 rámy kocky a spojiť ich zodpovedajúce vrcholy novou hranou.
Tento model momentálne nemám na sklade. Na prednáške študentom ukazujem trochu iný 3-rozmerný model 4-rozmernej kocky.

Viete, ako sa kocka premieta do roviny, ako je táto.
Je to ako keby sme sa pozerali na kocku zhora.

Blízky okraj je, samozrejme, veľký. A vzdialená hrana vyzerá menšia, vidíme ju cez blízku.

Takto môžete premietnuť 4-rozmernú kocku. Kocka je teraz väčšia, v diaľke vidíme kocku budúcnosti, takže vyzerá menšia.

Na druhej strane. Z vrchnej strany.

Priamo presne zo strany okraja:

Zo strany rebier:

A posledný uhol, asymetrický. Z časti „povedz mi, že som sa mu pozrel medzi rebrá“.

No potom sa dá vymyslieť čokoľvek. Napríklad tak, ako sa vyvíja 3-rozmerná kocka na rovinu (je to ako vystrihnutie listu papiera tak, že po zložení dostanete kocku), to isté sa deje s vývojom 4-rozmernej kocky do priestor. Je to ako rezať kus dreva tak, že jeho zložením v 4-rozmernom priestore dostaneme tesseract.

Môžete študovať nielen 4-rozmernú kocku, ale n-rozmerné kocky vo všeobecnosti. Je napríklad pravda, že polomer gule opísanej okolo n-rozmernej kocky je menší ako dĺžka hrany tejto kocky? Alebo tu je jednoduchšia otázka: koľko vrcholov má n-rozmerná kocka? Koľko hrán (jednorozmerných plôch)?

Tesseract (zo starogréčtiny τέσσερες ἀκτῖνες - štyri lúče) je štvorrozmerná hyperkocka - analóg kocky v štvorrozmernom priestore.

Obraz je projekcia (perspektíva) štvorrozmernej kocky do trojrozmerného priestoru.

Podľa Oxfordského slovníka slovo „tesseract“ vymyslel a použil v roku 1888 Charles Howard Hinton (1853–1907) vo svojej knihe A New Age of Thought. Neskôr niektorí ľudia nazvali tú istú postavu „tetracube“.

Geometria

Obyčajný tesseract v euklidovskom štvorrozmernom priestore je definovaný ako konvexný obal bodov (±1, ±1, ±1, ±1). Inými slovami, môže byť reprezentovaný ako nasledujúca množina:

Tesseract je ohraničený ôsmimi nadrovinami, ktorých priesečník so samotným tesseractom definuje jeho trojrozmerné plochy (čo sú obyčajné kocky). Každý pár nerovnobežných 3D plôch sa pretína a vytvára 2D plochy (štvorce) atď. Nakoniec má tesseract 8 3D plôch, 24 2D plôch, 32 hrán a 16 vrcholov.

Populárny popis

Skúsme si predstaviť, ako bude vyzerať hyperkocka bez toho, aby sme opustili trojrozmerný priestor.

V jednorozmernom „priestore“ - na priamke - vyberieme úsečku AB dĺžky L. Na dvojrozmernej rovine vo vzdialenosti L od AB nakreslíme úsečku DC rovnobežnú s ňou a ich konce spojíme. Výsledkom je štvorec ABCD. Opakovaním tejto operácie s rovinou získame trojrozmernú kocku ABCDHEFG. A posunutím kocky v štvrtom rozmere (kolmo na prvé tri) o vzdialenosť L dostaneme hyperkocku ABCDEFGHIJKLMNOP.
http://upload.wikimedia.org/wikipedia/ru/1/13/Construction_tesseract.PNG

Jednorozmerný segment AB slúži ako strana dvojrozmerného štvorca ABCD, štvorec - ako strana kocky ABCDHEFG, ktorá bude naopak stranou štvorrozmernej hyperkocky. Priamy segment má dva hraničné body, štvorec má štyri vrcholy a kocka osem. V štvorrozmernej hyperkocke teda bude 16 vrcholov: 8 vrcholov pôvodnej kocky a 8 posunutého vo štvrtom rozmere. Má 32 hrán – každá z nich 12 udáva počiatočnú a konečnú polohu pôvodnej kocky a ďalších 8 hrán „kreslí“ jej osem vrcholov, ktoré sa presunuli do štvrtej dimenzie. Rovnaké uvažovanie možno urobiť pre steny hyperkocky. V dvojrozmernom priestore je len jeden (samotný štvorec), kocka ich má 6 (dve tváre z posunutého štvorca a ďalšie štyri, ktoré opisujú jeho strany). Štvorrozmerná hyperkocka má 24 štvorcových plôch – 12 políčok pôvodnej kocky v dvoch polohách a 12 políčok od jej dvanástich hrán.

Tesseract sa rozbaľuje

Vezmeme drôtenú kocku ABCDHEFG a pozrieme sa na ňu jedným okom zo strany okraja. Uvidíme a môžeme nakresliť dva štvorce na rovine (jej blízke a vzdialené okraje), spojené štyrmi čiarami - bočnými okrajmi. Podobne štvorrozmerná hyperkocka v trojrozmernom priestore bude vyzerať ako dve kubické „škatule“ vložené do seba a spojené ôsmimi hranami. V tomto prípade sa samotné „boxy“ – trojrozmerné tváre – premietnu do „nášho“ priestoru a čiary, ktoré ich spájajú, sa roztiahnu vo štvrtej dimenzii. Môžete si tiež skúsiť predstaviť kocku nie v projekcii, ale v priestorovom obrázku.

Tak ako je trojrozmerná kocka tvorená štvorcom posunutým o dĺžku jeho plochy, kocka posunutá do štvrtého rozmeru vytvorí hyperkocku. Je ohraničený ôsmimi kockami, ktoré budú v perspektíve vyzerať ako nejaký dosť zložitý obrazec. Časť, ktorá zostala v „našom“ priestore, je nakreslená plnými čiarami a časť, ktorá prešla do hyperpriestoru, je nakreslená bodkovanými čiarami. Samotná štvorrozmerná hyperkocka pozostáva z nekonečného počtu kociek, rovnako ako trojrozmernú kocku možno „rozrezať“ na nekonečné množstvo plochých štvorcov.

Vlastnosti tesseractu predstavujú pokračovanie vlastností geometrických útvarov nižšej dimenzie do štvorrozmerného priestoru.

Projekcie

Do dvojrozmerného priestoru

Projekcia tesseractu do trojrozmerného priestoru predstavuje dve vnorené trojrozmerné kocky, ktorých zodpovedajúce vrcholy sú spojené segmentmi. Vnútorná a vonkajšia kocka majú v trojrozmernom priestore rôzne veľkosti, no v štvorrozmernom priestore sú to rovnaké kocky. Na pochopenie rovnosti všetkých kociek tesseractu bol vytvorený rotujúci model tesseractu.

Šesť zrezaných pyramíd pozdĺž okrajov tesseractu sú obrazy rovnakých šiestich kociek.
Stereo pár

Tesseract v umení

V „New Abbott Plain“ od Edwiny A. hyperkocka pôsobí ako rozprávač.
V jednej epizóde The Adventures of Jimmy Neutron: "Boy Genius" Jimmy vynájde štvorrozmernú hyperkocku identickú so skladacou skrinkou z Heinleinovho románu Glory Road z roku 1963.
Robert E. Heinlein spomenul hyperkocky najmenej v troch sci-fi príbehoch. V The House of Four Dimensions (The House That Teal Built) (1940) opísal dom postavený ako nezabalený tesseract.
Heinleinov román Glory Road opisuje jedlá nadmernej veľkosti, ktoré boli väčšie zvnútra ako zvonku.
Príbeh Henryho Kuttnera „Mimsy Were the Borogoves“ opisuje vzdelávaciu hračku pre deti z ďalekej budúcnosti, podobnú štruktúre ako tesseract.
V románe Alexa Garlanda (1999) sa termín „tesseract“ používa na trojrozmerné rozvinutie štvorrozmernej hyperkocky, a nie samotnej hyperkocky. Toto je metafora navrhnutá tak, aby ukázala, že kognitívny systém musí byť širší ako poznateľný.
Dej hry Cube 2: Hypercube sa sústreďuje na osem cudzincov uväznených v „hyperkocke“ alebo sieti spojených kociek.
Televízny seriál Andromeda používa generátory tesseract ako zápletkové zariadenie. Sú primárne určené na manipuláciu s priestorom a časom.
Obraz „Ukrižovanie“ (Corpus Hypercubus) od Salvadora Dalího (1954)
Komiks Nextwave zobrazuje vozidlo, ktoré obsahuje 5 zón tesseract.
Na albume Voivod Nothingface sa jedna zo skladieb volá „In my hypercube“.
V románe Anthonyho Pearcea Route Cube sa jeden z obiehajúcich mesiacov Medzinárodnej asociácie pre rozvoj nazýva tesseract, ktorý bol stlačený do 3 rozmerov.
V sérii „Black Hole School“ v tretej sezóne je epizóda „Tesseract“. Lucas stlačí tajné tlačidlo a škola sa začne formovať ako matematický tesseract.
Termín „tesseract“ a jeho odvodený výraz „tesserate“ sa nachádzajú v príbehu „A Wrinkle in Time“ od Madeleine L’Engle.

Evolúcia ľudského mozgu prebiehala v trojrozmernom priestore. Preto je pre nás ťažké predstaviť si priestory s rozmermi väčšími ako tri. V skutočnosti si ľudský mozog nedokáže predstaviť geometrické objekty s rozmermi väčšími ako tri. A zároveň si ľahko predstavíme geometrické objekty s rozmermi nielen tri, ale aj s rozmermi dva a jedna.

Rozdiel a analógia medzi jednorozmernými a dvojrozmernými priestormi, ako aj rozdiel a analógia medzi dvojrozmernými a trojrozmernými priestormi nám umožňujú mierne pootvárať clonu tajomstva, ktoré nás oddeľuje od priestorov vyšších dimenzií. Aby ste pochopili, ako sa táto analógia používa, zvážte veľmi jednoduchý štvorrozmerný objekt - hyperkocku, teda štvorrozmernú kocku. Aby sme boli konkrétni, povedzme, že chceme vyriešiť konkrétny problém, konkrétne spočítať počet štvorcových plôch štvorrozmernej kocky. Všetky ďalšie úvahy budú veľmi laxné, bez akýchkoľvek dôkazov, čisto analogicky.

Aby ste pochopili, ako sa z obyčajnej kocky skladá hyperkocka, musíte sa najprv pozrieť na to, ako sa z obyčajného štvorca skladá bežná kocka. Kvôli originalite pri prezentácii tohto materiálu tu budeme obyčajný štvorec nazývať SubCube (a nebudeme si ho mýliť so succubusom).

Ak chcete postaviť kocku z podkocky, musíte podkocku predĺžiť v smere kolmom na rovinu podkocky v smere tretieho rozmeru. V tomto prípade z každej strany počiatočnej podkocky vyrastie podkocka, čo je bočná dvojrozmerná plocha kocky, ktorá obmedzí trojrozmerný objem kocky na štyroch stranách, dvoch kolmých na každý smer v rovina podkocky. A pozdĺž novej tretej osi sú tiež dve podkocky, ktoré obmedzujú trojrozmerný objem kocky. Toto je dvojrozmerná plocha, kde sa pôvodne nachádzala naša podkocka, a dvojrozmerná plocha kocky, ku ktorej sa podkocka dostala na konci konštrukcie kocky.

To, čo ste práve čítali, je podané príliš podrobne a s množstvom vysvetlení. A z dobrého dôvodu. Teraz urobíme taký trik, formálne nahradíme niektoré slová v predchádzajúcom texte týmto spôsobom:
kocka -> hyperkocka
podkocka -> kocka
rovina -> objem
tretí -> štvrtý
dvojrozmerný -> trojrozmerný
štyri -> šesť
trojrozmerný -> štvorrozmerný
dva -> tri
rovina -> priestor

Výsledkom je nasledujúci zmysluplný text, ktorý sa už nezdá byť príliš podrobný.

Ak chcete postaviť hyperkocku z kocky, musíte kocku natiahnuť v smere kolmom na objem kocky v smere štvrtého rozmeru. V tomto prípade vyrastie kocka z každej strany pôvodnej kocky, čo je bočná trojrozmerná plocha hyperkocky, ktorá obmedzí štvorrozmerný objem hyperkocky na šiestich stranách, tri kolmé na každý smer v priestor kocky. A pozdĺž novej štvrtej osi sú tiež dve kocky, ktoré obmedzujú štvorrozmerný objem hyperkocky. Toto je trojrozmerná plocha, kde bola pôvodne umiestnená naša kocka, a trojrozmerná plocha hyperkocky, kde sa kocka dostala na konci konštrukcie hyperkocky.

Prečo sme si tak istí, že sme dostali správny popis konštrukcie hyperkocky? Áno, pretože presne rovnakou formálnou zámenou slov dostaneme opis konštrukcie kocky z opisu konštrukcie štvorca. (Presvedčte sa o tom sami.)

Teraz je jasné, že ak by z každej strany kocky mala vyrásť ďalšia trojrozmerná kocka, potom by z každej hrany pôvodnej kocky mala vyrásť tvár. Celkovo má kocka 12 hrán, čo znamená, že na tých 6 kockách, ktoré obmedzujú štvorrozmerný objem pozdĺž troch osí trojrozmerného priestoru, sa objaví ďalších 12 nových plôch (podkociek). A zostali ďalšie dve kocky, ktoré obmedzujú tento štvorrozmerný objem zdola a zhora pozdĺž štvrtej osi. Každá z týchto kociek má 6 tvárí.

Celkovo zistíme, že hyperkocka má 12+6+6=24 štvorcových plôch.

Nasledujúci obrázok ukazuje logickú štruktúru hyperkocky. Je to ako projekcia hyperkocky do trojrozmerného priestoru. To vytvára trojrozmerný rám rebier. Na obrázku samozrejme vidíte projekciu tohto rámu do roviny.

Na tomto ráme je vnútorná kocka ako počiatočná kocka, z ktorej stavba začala a ktorá obmedzuje štvorrozmerný objem hyperkocky pozdĺž štvrtej osi zdola. Túto počiatočnú kocku natiahneme nahor pozdĺž štvrtej osi merania a ide do vonkajšej kocky. Takže vonkajšia a vnútorná kocka z tohto obrázku obmedzujú hyperkocku pozdĺž štvrtej osi merania.

A medzi týmito dvoma kockami môžete vidieť ďalších 6 nových kociek, ktoré sa dotýkajú spoločných tvárí s prvými dvoma. Týchto šesť kociek spájalo našu hyperkocku pozdĺž troch osí trojrozmerného priestoru. Ako vidíte, nie sú v kontakte len s prvými dvoma kockami, ktoré sú vnútornou a vonkajšou kockou na tomto trojrozmernom ráme, ale sú v kontakte aj navzájom.

Môžete počítať priamo na obrázku a uistiť sa, že hyperkocka má skutočne 24 tvárí. Ale vyvstáva táto otázka. Tento rám hyperkocky v trojrozmernom priestore je vyplnený ôsmimi trojrozmernými kockami bez akýchkoľvek medzier. Ak chcete vytvoriť skutočnú hyperkocku z tejto trojrozmernej projekcie hyperkocky, musíte tento rám otočiť naruby tak, aby všetkých 8 kociek spájalo 4-rozmerný objem.

Robí sa to takto. Pozývame na návštevu obyvateľa štvorrozmerného priestoru a žiadame ho, aby nám pomohol. Chytí vnútornú kocku tohto rámu a posunie ho v smere štvrtej dimenzie, ktorá je kolmá na náš trojrozmerný priestor. V našom trojrozmernom priestore to vnímame, akoby zmizol celý vnútorný rám a zostal len rám vonkajšej kocky.

Ďalej náš štvorrozmerný asistent ponúka asistenciu v pôrodniciach pri bezbolestnom pôrode, no naše tehotné ženy straší predstava, že bábätko jednoducho zmizne zo žalúdka a skončí v paralelnom trojrozmernom priestore. Preto je štvorrozmerná osoba zdvorilo odmietnutá.

A lámeme si hlavu nad otázkou, či sa nám niektoré kocky nerozpadli, keď sme rám hyperkocky otočili naruby. Ak sa totiž niektoré trojrozmerné kocky obklopujúce hyperkocku svojimi tvárami dotknú svojich susedov na ráme, budú sa dotýkať aj tými istými tvárami, ak štvorrozmerná kocka obráti rám naruby?

Vráťme sa opäť k analógii s priestormi nižších dimenzií. Porovnajte obraz rámu hyperkocky s priemetom trojrozmernej kocky do roviny znázornenej na nasledujúcom obrázku.

Obyvatelia dvojrozmerného priestoru postavili na rovine rám na premietanie kocky do roviny a vyzvali nás, trojrozmerných obyvateľov, aby sme tento rám obrátili naruby. Vezmeme štyri vrcholy vnútorného štvorca a posunieme ich kolmo na rovinu. Dvojrozmerní obyvatelia vidia úplné zmiznutie celého vnútorného rámu a zostane im iba rám vonkajšieho štvorca. Pri takejto operácii sa všetky štvorce, ktoré boli v kontakte s ich okrajmi, naďalej dotýkajú rovnakých okrajov.

Preto dúfame, že logická schéma hyperkocky tiež nebude narušená pri otáčaní rámu hyperkocky naruby a počet štvorcových plôch hyperkocky sa nezvýši a bude stále rovný 24. To samozrejme , nie je vôbec dôkazom, ale čisto analógiou.

Po všetkom, čo ste si tu prečítali, môžete ľahko nakresliť logický rámec päťrozmernej kocky a vypočítať počet vrcholov, hrán, plôch, kociek a hyperkociek, ktoré má. Nie je to vôbec ťažké.