Matematinė analizė.

Seminaras.

Universiteto studentams pagal specialybę:

„Valstybės ir savivaldybių administracija“

T.Z. Pavlova

Kolpashevo 2008 m

1 skyrius. Analizės įvadas

1.1 Funkcijos. Bendrosios savybės

1.2 Ribų teorija

1.3 Funkcijos tęstinumas

2.1 Išvestinės priemonės apibrėžimas

2.4 Funkcijų tyrinėjimas

2.4.1 Visas funkcijų tyrimo planas

2.4.2 Funkcijų tyrimo pavyzdžiai

2.4.3. Didžiausia ir mažiausia funkcijos reikšmė segmente

2.5 L'Hôpital taisyklė

3.1 Neapibrėžtas integralas

3.1.1 Apibrėžimai ir savybės

3.1.2 Integralų lentelė

3.1.3 Pagrindiniai integravimo metodai

3.2 Apibrėžiamasis integralas

3.2.2 Apibrėžtinio integralo skaičiavimo metodai

4 skyrius. Kelių kintamųjų funkcijos

4.1 Pagrindinės sąvokos

4.2 Kelių kintamųjų funkcijų ribos ir tęstinumas

4.3.3 Bendras skirtumas ir jo taikymas apytiksliems skaičiavimams

5 skyrius. Klasikiniai optimizavimo metodai

6.1 Naudingumo funkcija.

6.2 Abejingumo linijos

6.3 Biudžeto rinkinys

Namų darbų užduotys

1.1 Funkcijos. Bendrosios savybės

Skaitinė funkcija apibrėžiama realiųjų skaičių D aibėje, jei kiekviena kintamojo reikšmė yra susieta su kokia nors tiksliai apibrėžta realia kintamojo y reikšme, kur D yra funkcijos sritis.

Analitinis funkcijos vaizdavimas:

aiškiai:;

netiesiogiai:;

parametrine forma:

skirtingos formulės apibrėžimo srityje:

Savybės.

Lygi funkcija:. Pavyzdžiui, funkcija yra lyginė, nes ...

Nelyginė funkcija: ... Pavyzdžiui, funkcija yra nelyginė, nes ...

Periodinė funkcija: , kur T yra funkcijos periodas,. Pavyzdžiui, trigonometrinės funkcijos.

Monotoniška funkcija. Jei kuriai nors iš apibrėžimo srities - funkcija didėja, - mažėja. Pavyzdžiui, - didėja ir - mažėja.

Ribota funkcija. Jei yra toks skaičius M, kad. Pavyzdžiui, funkcijos ir, kadangi .

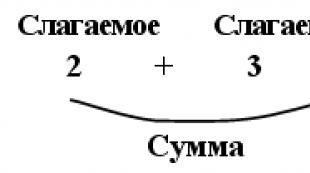
1 pavyzdys. Raskite funkcijų apibrėžimo sritį.

+ 2 – 3 +

1.2 Ribų teorija

1 apibrėžimas... Funkcijos at riba yra skaičius b, jei bet kuriam (- savavališkai mažam teigiamam skaičiui) galima rasti tokią argumento reikšmę, pradedant nuo kurios tenkinama nelygybė.

Pavadinimas:.

2 apibrėžimas... Funkcijos at riba yra skaičius b, jei bet kuriam (yra savavališkai mažas teigiamas skaičius) yra toks teigiamas skaičius, kad visoms x reikšmėms, atitinkančioms nelygybę, galioja nelygybė.

Pavadinimas:.

3 apibrėžimas. Funkcija vadinama be galo maža arba, jei arba.

Savybės.

1. Baigtinio skaičiaus be galo mažų dydžių algebrinė suma yra be galo mažas dydis.

2. Be galo mažo kiekio sandauga iš ribojančios funkcijos (pastovi, kitas be galo mažas dydis) yra be galo mažas dydis.

3. Be galo mažo dydžio dalijimosi iš funkcijos, kurios riba yra nulis, koeficientas yra be galo mažas dydis.

4 apibrėžimas. Funkcija vadinama be galo didele, jei.

Savybės.

1. Be galo didelio kiekio sandauga iš funkcijos, kurios riba nėra lygi nuliui, yra be galo didelis dydis.

2. Be galo didelės reikšmės ir ribojančios funkcijos suma yra be galo didelė reikšmė.

3. Be galo didelio kiekio dalijimo iš funkcijos, kuri turi ribą, koeficientas yra be galo didelis dydis.

Teorema.(Ryšys tarp be galo mažo ir be galo didelio kiekio.) Jei funkcija yra be galo maža ties (), tai funkcija yra be galo didelis dydis taške (). Ir atvirkščiai, jei funkcija yra be galo didelė ties (), tada funkcija yra be galo maža ties ().

Ribinės teoremos.

1. Funkcija negali turėti daugiau nei vienos ribos.

2. Kelių funkcijų algebrinės sumos riba lygi šių funkcijų ribų algebrinei sumai:

3. Kelių funkcijų sandaugos riba lygi šių funkcijų ribų sandaugai:

4. Laipsnio riba lygi ribos laipsniui:

5. Dalinio riba lygi ribų daliniui, jei yra daliklio riba:

.

6. Pirmoji nepaprasta riba.

Pasekmės:

7. Antra reikšminga riba:

Pasekmės:

Lygiavertės be galo mažos vertės:

Ribų skaičiavimas.

Skaičiuojant ribas, naudojamos pagrindinės teoremos apie ribas, tęstinių funkcijų savybes ir iš šių teoremų bei savybių kylančios taisyklės.

1 taisyklė. Norint rasti ribą funkcijos taške, kuris yra tęstinis šiame taške, reikia pakeisti jos ribinę reikšmę funkcijoje po ribos ženklu, o ne argumentu x.

2 pavyzdys. Rasti

2 taisyklė. Jeigu, randant trupmenos ribą, vardiklio riba lygi nuliui, o skaitiklio – ne nuliui, tai tokios funkcijos riba yra.

3 pavyzdys. Rasti

3 taisyklė. Jeigu, randant trupmenos ribą, vardiklio riba yra lygi, o skaitiklio riba skiriasi nuo nulio, tai tokios funkcijos riba lygi nuliui.

4 pavyzdys. Rasti

Dažnai argumento ribinės vertės pakeitimas sukelia neapibrėžtas išraiškas, pvz

.

Funkcijos ribos nustatymas šiais atvejais vadinamas neapibrėžtumo atskleidimu. Norint atskleisti neapibrėžtumą, prieš pereinant prie ribos šią išraišką būtina transformuoti. Neapibrėžtumui atskleisti naudojami įvairūs metodai.

4 taisyklė... Tipo neapibrėžtumas atskleidžiamas transformuojant sublimito funkciją, taigi, norint skaitiklyje ir vardiklyje pasirinkti koeficientą, kurio riba lygi nuliui, ir, juo sumažinus trupmeną, rasti dalinio ribą. Norėdami tai padaryti, skaitiklis ir vardiklis padauginami arba padauginami iš išraiškų, susietų su skaitikliu ir vardikliu.

5 taisyklė. Jei sublimito išraiškoje yra trigonometrinių funkcijų, tada pirmoji žymi riba naudojama rūšies neapibrėžtumui atskleisti.

.

6 taisyklė... Norint atskleisti formos neapibrėžtumą, reikia padalyti poribinės trupmenos skaitiklį ir vardiklį iš didžiausio argumento laipsnio, tada reikia rasti koeficiento ribą.

Galimi rezultatai:

1) norima riba lygi koeficientų santykiui esant didžiausiems skaitiklio ir vardiklio argumento laipsniams, jei šie laipsniai yra vienodi;

2) riba lygi begalybei, jei skaitiklio argumento laipsnis didesnis už vardiklio argumento laipsnį;

3) riba lygi nuliui, jei skaitiklio argumento laipsnis yra mažesnis už vardiklio argumento laipsnį.

a)

nuo

Laipsniai yra lygūs, vadinasi, riba lygi koeficientų santykiui prie aukštesnių laipsnių, t.y. ...

b)

Skaitiklio laipsnis, vardiklis yra 1, tai reiškia, kad riba yra

v)

Skaitiklio laipsnis yra 1, vardiklio laipsnis yra, taigi riba yra 0.

7 taisyklė... Norint atskleisti formos neapibrėžtumą, ribinės trupmenos skaitiklį ir vardiklį reikia padauginti iš konjuguotos išraiškos.

10 pavyzdys.

8 taisyklė... Antroji nepaprasta riba ir jos pasekmės naudojamos rūšies neapibrėžtumui atskleisti.

Tai galima įrodyti

11 pavyzdys.

12 pavyzdys.

13 pavyzdys.

9 taisyklė... Atskleidžiant neapibrėžtumus, kurių pasąmoninėje funkcijoje yra begalybė, būtina pakeisti šių begalybių ribas. apie be galo mažų jiems lygiaverčių elementų ribas.

14 pavyzdys.

15 pavyzdys.

10 taisyklė. L'Hôpital taisyklė (žr. 2.6).

1.3 Funkcijos tęstinumas

Funkcija yra ištisinė taške, jei funkcijos, kaip argumento, riba yra linkusi į a, egzistuoja ir yra lygi funkcijos reikšmei šiame taške.

Lygiavertės sąlygos:

1. ;

3.

Lūžio taškų klasifikacija:

pirmos rūšies pertrauka

Vienkartiniai – vienpusės ribos egzistuoja ir yra lygios;

Fatalinis (šuolis) – vienpusės ribos nėra lygios;

antrosios rūšies nenuoseklumas: funkcijos riba taške neegzistuoja.

16 pavyzdys. Nustatykite funkcijos nepertraukiamumo pobūdį taške arba įrodykite funkcijos tęstinumą šiame taške.

nes funkcija neapibrėžta, todėl šiuo metu ji nėra tęstinė. Nes ir atitinkamai, , tada yra pirmosios rūšies pašalinamo pertrūkio taškas.

b)

lyginant su užduotimi (a), funkcija išplečiama taške taip, kad , todėl ši funkcija šiuo metu yra nuolatinė.

Kai funkcija neapibrėžta;

.

Nes viena iš vienpusių ribų yra begalinė, tada ji yra antrojo tipo lūžio taškas.

2 skyrius. Diferencialinis skaičiavimas

2.1 Išvestinės priemonės apibrėžimas

Išvestinis apibrėžimas

Nurodytos funkcijos arba išvestinė yra funkcijos prieaugio ir atitinkamo argumento prieaugio santykio riba, kai argumento prieaugis linkęs į nulį:

Arba .

Mechaninė išvestinės reikšmė yra funkcijos kitimo greitis. Geometrinė išvestinės reikšmė yra funkcijos grafiko liestinės polinkio kampo liestinė:

2.2 Pagrindinės diferencijavimo taisyklės

vardas	Funkcija	Darinys
Padauginimas iš pastovaus koeficiento
Dviejų funkcijų algebrinė suma
Dviejų funkcijų produktas
Privačios dvi funkcijos
Sudėtinga funkcija

Pagrindinių elementariųjų funkcijų išvestiniai

P/p Nr.	Funkcijos pavadinimas	Funkcija ir jos išvestinė
1	pastovus
2	galios funkcija ypatingi atvejai
3	eksponentinė funkcija ypatinga byla
4	logaritminė funkcija ypatinga byla
5	trigonometrinės funkcijos
6	atvirkščiai trigonometrinis

b)

2.3 Aukštesnės eilės išvestinės finansinės priemonės

Funkcijos antros eilės išvestinė

Funkcijos antros eilės išvestinė:

18 pavyzdys.

a) Raskite funkcijos antros eilės išvestinę.

Sprendimas. Pirmiausia suraskime pirmosios eilės išvestinę .

Paimkime pirmosios eilės išvestinę.

19 pavyzdys. Raskite funkcijos trečiosios eilės išvestinę.

2.4 Funkcijų tyrinėjimas

2.4.1 Viso funkcijų tyrimo planas:

Visas funkcijų studijų planas:

1. Elementarus tyrimas:

Raskite domeną ir reikšmių diapazoną;

Išsiaiškinti bendrąsias savybes: paritetą (keistumą), periodiškumą;

Raskite susikirtimo taškus su koordinačių ašimis;

Nustatykite pastovumo sritis.

2. Asimptotės:

Rasti vertikalius asimptotus if;

Raskite pasvirusius asimptotus:.

Jei koks nors skaičius, tai – horizontalios asimptotės.

3. Tyrimas naudojant:

Raskite kritinius taškus, tuos. taškai, kuriuose nėra arba nėra;

Nustatykite didėjimo intervalus, tuos. intervalai, kuriais ir mažėjančios funkcijos -;

Nustatykite kraštutinumą: taškai, per kuriuos einant keičia ženklą iš „+“ į „-“, yra didžiausi taškai, nuo „-“ iki „+“ – minimumas.

4. Tyrimas naudojant:

Rasti taškus, kurių nėra arba nėra;

Raskite išgaubimo sritis, t.y. intervalai, kuriuose yra įdubimai;

Raskite vingio taškus, t.y. taškai, kai praeina per kuriuos keičiasi ženklas.

1. Atskiri tyrimo elementai grafike brėžiami palaipsniui, juos surandant.

2. Jei kyla sunkumų sudarant funkcijos grafiką, tada funkcijos reikšmės randamos kai kuriuose papildomuose taškuose.

3. Tyrimo tikslas – apibūdinti funkcijos elgsenos pobūdį. Todėl statomas ne tikslus grafikas, o jo aproksimacija, kurioje aiškiai nurodomi rasti elementai (ekstremumai, vingio taškai, asimptotės ir kt.).

4. Nebūtina griežtai laikytis aukščiau pateikto plano; svarbu nepamiršti būdingų funkcijos elgsenos elementų.

2.4.2 Funkcijų tyrimo pavyzdžiai:

1)

2) Funkcija yra nelyginė:

.

3) Asimptotės.

- vertikalios asimptotės, nes

Įstrižas asimptotas.

5)

- Vingio taškas.

2) Funkcija yra nelyginė:

3) Asimptotės: vertikalių asimptočių nėra.

Pasviręs:

- įstrižai asimptotai

4) - funkcija padidėja.

- Vingio taškas.

Šios funkcijos schema:

2) Bendroji funkcija

3) Asimptotės

- nėra įstrižų asimptotų

- horizontalus asimptotas ties

- Vingio taškas

Šios funkcijos schema:

2) Asimptotės.

- vertikali asimptota, nes

- nėra įstrižų asimptotų

, - horizontali asimptotė

Šios funkcijos schema:

2) Asimptotės

- vertikali asimptote ties, nuo

- nėra įstrižų asimptotų

, - horizontali asimptotė

3) - funkcija mažėja kiekvienu intervalu.

Šios funkcijos schema:

Norėdami rasti didžiausią ir mažiausią segmento funkcijos reikšmę, galite naudoti diagramą:

1. Raskite funkcijos išvestinę.

2. Raskite funkcijos kritinius taškus, kuriuose yra arba nėra.

3. Raskite funkcijos reikšmę duotam atkarpai priklausančiuose kritiniuose taškuose ir jo galuose ir pasirinkite didžiausią bei mažiausią iš jų.

Pavyzdys. Raskite mažiausią ir didžiausią funkcijos reikšmę duotame segmente.

25. tarp

2) - kritiniai taškai

26. tarpais.

Išvestinė neegzistuoja, bet 1 nepriklauso šiam intervalui. Funkcija intervale mažėja, o tai reiškia, kad yra ne didžiausia reikšmė, o mažiausia.

2.5 L'Hôpital taisyklė

Teorema. Dviejų be galo mažų arba be galo didelių funkcijų santykio riba lygi jų išvestinių (baigtinių arba begalinių) santykio ribai, jei pastaroji nurodyta prasme egzistuoja.

Tie. atskleisdami tipo neapibrėžtumus arba galite naudoti formulę:

.

27.

3 skyrius. Integralinis skaičiavimas

3.1 Neapibrėžtas integralas

3.1.1 Apibrėžimai ir savybės

Apibrėžimas 1. Funkcija vadinama antiderivatine, jei.

2 apibrėžimas. Neapibrėžtas funkcijos f (x) integralas yra visų šios funkcijos antidarinių rinkinys.

Pavadinimas: , kur c yra savavališka konstanta.

Neapibrėžtos integralinės savybės

1. Neapibrėžtinio integralo išvestinė:

2. Neapibrėžto integralo diferencialas:

3. Neapibrėžtas diferencialo integralas:

4. Dviejų funkcijų sumos (skirtumo) neapibrėžtasis integralas:

5. Pastovaus koeficiento perkėlimas už neapibrėžto integralo ženklo:

3.1.2 Integralų lentelė

.1.3 Pagrindiniai integravimo metodai

1. Naudojant neapibrėžtinio integralo savybes.

29 pavyzdys.

2. Atvedimas po diferencialo ženklu.

30 pavyzdys.

3. Kintamasis pakeitimo būdas:

a) pakeitimas integralu

kur - funkcija, kurią lengviau integruoti nei originalią; - funkcija atvirkščiai; yra funkcijos antidarinys.

31 pavyzdys.

b) pakeitimas formos integralu:

32 pavyzdys.

33 pavyzdys.

4. Integravimo būdas dalimis:

34 pavyzdys.

35 pavyzdys.

Paimkime atskirai integralą

Grįžkime prie mūsų integralo:

3.2 Apibrėžiamasis integralas

3.2.1 Apibrėžtinio integralo sąvoka ir jo savybės

Apibrėžimas. Tegu tam tikrame intervale duota tolydi funkcija. Sukurkime jos grafiką.

Figūra, kurią iš viršaus riboja kreivė, iš kairės ir į dešinę – tiesios linijos, o iš apačios – abscisių ašies atkarpa tarp taškų a ir b, vadinama lenkta trapecija.

S – plotas – lenkta trapecija.

Padalinkite intervalą taškais ir gaukite:

Integrali suma:

Apibrėžimas. Apibrėžiamasis integralas yra integralo sumos riba.

Apibrėžtos integralinės savybės:

1. Iš integralo ženklo galima paimti pastovų koeficientą:

2. Dviejų funkcijų algebrinės sumos integralas yra lygus šių funkcijų integralų algebrinei sumai:

3. Jei integralinis segmentas yra padalintas į dalis, tai visos atkarpos integralas yra lygus kiekvienos iš susidariusios dalies integralų sumai, t. bet kuriam a, b, c:

4. Jei segmente, tada

5. Integracijos ribos gali būti keičiamos, o integralo ženklas keičiasi:

6.

7. Integralas taške lygus 0:

8.

9. („Apie vidurkį“) Tegul y = f (x) yra funkcija, kurią galima integruoti. Tada , kur f (c) yra vidutinė f (x) reikšmė:

10. Niutono-Leibnizo formulė

,

kur F (x) yra f (x) antidarinys.

3.2.2 Apibrėžtinio integralo skaičiavimo metodai.

1. Tiesioginė integracija

35 pavyzdys.

a)

b)

v)

e)

2. Kintamųjų po apibrėžtuoju integralo ženklu keitimas .

36 pavyzdys.

2. Integravimas dalimis į apibrėžtąjį integralą .

37 pavyzdys.

a)

b)

e)

3.2.3 Apibrėžtinio integralo taikymai

Charakteristika	Funkcijos tipas	Formulė
	Dekarto koordinatėmis
lenktas sektoriaus plotas	poliarinėse koordinatėse
išlenktas trapecijos plotas	parametrine forma
arkos ilgis	Dekarto koordinatėmis
arkos ilgis	poliarinėse koordinatėse
arkos ilgis	parametrine forma
kūno apimtis sukimasis	Dekarto koordinatėmis
kūno tūris su tam tikra skersine skerspjūvis

38 pavyzdys. Apskaičiuokite linijomis apribotos figūros plotą: ir .

Sprendimas: Raskime šių funkcijų grafikų susikirtimo taškus. Norėdami tai padaryti, sulyginame funkcijas ir išsprendžiame lygtį

Taigi, susikirtimo taškai ir.

Figūros plotą randame pagal formulę

.

Mūsų atveju

Atsakymas: plotas lygus (kvadratiniais vienetais).

4.1 Pagrindinės sąvokos

Apibrėžimas. Jei pagal tam tikrą taisyklę kiekvienai nepriklausomų skaičių porai iš tam tikros aibės priskiriama viena ar daugiau kintamojo z reikšmių, tada kintamasis z vadinamas dviejų kintamųjų funkcija.

Apibrėžimas. Funkcijos z sritis yra porų, kurioms egzistuoja funkcija z, rinkinys.

Dviejų kintamųjų funkcijos sritis yra taškų rinkinys koordinačių plokštumoje Oxy. Z koordinatė vadinama aplikacija, o tada pati funkcija vaizduojama kaip kažkoks paviršius erdvėje E 3. Pavyzdžiui:

39 pavyzdys. Raskite funkcijos sritį.

a)

Išraiška dešinėje yra reikšminga tik. Tai reiškia, kad šios funkcijos sritis yra visų taškų, esančių R spindulio apskritimo, kurio centras yra pradinis taškas, viduje ir ant ribos.

Šios funkcijos sritis – visi plokštumos taškai, išskyrus tiesių taškus, t.y. koordinačių ašys.

Apibrėžimas. Funkcijos lygio linijos yra kreivių šeima koordinačių plokštumoje, aprašyta formos lygtimis.

40 pavyzdys. Raskite funkcijos lygio eilutes .

Sprendimas. Tam tikros funkcijos lygio linijos yra kreivių šeima lygtimi aprašytoje plokštumoje

Paskutinė lygtis apibūdina apskritimų šeimą, kurios centras yra spindulio O 1 (1, 1) taške. Šia funkcija aprašytas apsisukimo paviršius (paraboloidas) tampa „statesnis“, toldamas nuo ašies, o tai duodama lygtimis x = 1, y = 1. (4 pav.)

4.2 Kelių kintamųjų funkcijų ribos ir tęstinumas.

1. Ribos.

Apibrėžimas. Skaičius A vadinamas funkcijos riba, nes taškas linkęs į tašką, jei kiekvienam savavališkai mažam skaičiui yra toks skaičius, kad sąlyga yra teisinga bet kuriam taškui, o sąlyga ... Jie užrašo: .

41 pavyzdys. Raskite ribas:

tie. riba priklauso nuo, todėl jos nėra.

2. Tęstinumas.

Apibrėžimas. Tegul taškas priklauso funkcijos apibrėžimo sričiai. Tada funkcija vadinama tęstine taške if

(1)

be to, taškas savavališkai linksta į tašką.

Jei bet kuriame taške netenkinama sąlyga (1), tada šis taškas vadinamas funkcijos nepertraukiamumo tašku. Tai gali būti šiais atvejais:

1) Funkcija taške neapibrėžta.

2) Nėra jokių apribojimų.

3) Ši riba egzistuoja, bet ji nėra lygi.

42 pavyzdys. Nustatykite, ar duotoji funkcija yra tolydi taške, jei.

Supratau vadinasi, ši funkcija yra nuolatinė taške.

riba priklauso nuo k, t.y. ji neegzistuoja tam tikrame taške, o tai reiškia, kad funkcija šiame taške yra nenuosekli.

4.3 Kelių kintamųjų funkcijų išvestinės ir diferencialai

4.3.1 Pirmosios eilės dalinės išvestinės

Dalinė funkcijos išvestinė argumento x atžvilgiu yra įprastinė vieno kintamojo x funkcijos išvestinė fiksuotai kintamojo y vertei ir žymima:

Dalinė funkcijos išvestinė argumento y atžvilgiu yra įprastinė vieno kintamojo y funkcijos išvestinė esant fiksuotai kintamojo x vertei ir žymima:

43 pavyzdys. Raskite funkcijų dalines išvestines.

4.3.2 Antrosios eilės dalinės išvestinės

Antrosios eilės daliniai išvestiniai yra pirmosios eilės dalinių darinių daliniai išvestiniai. Dviejų formos kintamųjų funkcijai galimi keturi antros eilės dalinių išvestinių tipai:

Antrosios eilės dalinės išvestinės, kuriose diferencijavimas atliekamas skirtingų kintamųjų atžvilgiu, vadinamos mišriomis išvestinėmis. Du kartus diferencijuojamos funkcijos antrosios eilės mišrios išvestinės yra lygios.

44 pavyzdys. Raskite antros eilės dalines išvestines.

4.3.3 Bendras skirtumas ir jo taikymas apytiksliems skaičiavimams.

Apibrėžimas. Dviejų kintamųjų funkcijos pirmosios eilės diferencialas randamas pagal formulę

.

45 pavyzdys. Raskite funkcijos bendrą skirtumą.

Sprendimas. Raskime dalines išvestines:

.

Mažiems argumentų x ir y prieaugiams funkcija įgyja prieaugį, maždaug lygų dz, t.y. ...

Apytikslės funkcijos reikšmės taške radimo formulė, jei žinoma tiksli jos reikšmė taške:

46 pavyzdys. Rasti .

Sprendimas. Leisti ,

Tada mes naudojame formulę

Atsakymas. .

47 pavyzdys. Apskaičiuokite apytikslę.

Sprendimas. Panagrinėkime funkciją. Mes turime

48 pavyzdys. Apskaičiuokite apytikslę.

Sprendimas. Apsvarstykite funkciją ... Mes gauname:

Atsakymas. .

4.3.4 Numanomas funkcijų diferencijavimas

Apibrėžimas. Funkcija vadinama numanoma, jei ji pateikta lygtimi, kuri nėra išsprendžiama z atžvilgiu.

Tokios funkcijos dalinės išvestinės randamos pagal formules:

49 pavyzdys. Raskite lygties pateiktos funkcijos z dalines išvestines .

Sprendimas.

Apibrėžimas. Funkcija vadinama numanoma, jei ji pateikiama lygtimi, kuri nėra išsprendžiama y atžvilgiu.

Tokios funkcijos išvestinė randama pagal formulę:

.

50 pavyzdys. Raskite šių funkcijų išvestines.

5.1 Kelių kintamųjų funkcijos lokalus ekstremumas

Apibrėžimas 1. Funkcija turi maksimumą taške, jei

Apibrėžimas 2. Funkcija turi minimumą taške if visiems pakankamai arti taško ir skiriasi nuo jo taškams.

Būtina ekstremumo sąlyga. Jei funkcija taške pasiekia ekstremumą, tai dalinės funkcijos išvestinės išnyksta arba šiame taške neegzistuoja.

Taškai, kuriuose dalinės išvestinės išnyksta arba neegzistuoja, vadinami kritiniais.

Pakankamas ekstremumo požymis. Tegul funkcija yra apibrėžta kurioje nors kritinio taško kaimynystėje ir šiame taške turi ištisines antros eilės dalines išvestines

1) turi vietinį maksimumą taške, jei ir;

2) turi vietinį minimumą taške, jei ir;

3) neturi vietinio ekstremumo taške if;

Dviejų kintamųjų funkcijos ekstremumo tyrimo schema.

1. Raskite funkcijos: ir dalines išvestines.

2. Išspręskite lygčių sistemą ir raskite funkcijos kritinius taškus.

3. Raskite antros eilės dalines išvestis, apskaičiuokite jų reikšmes kritiniuose taškuose ir, pasinaudoję pakankama sąlyga, padarykite išvadą apie ekstremalių buvimą.

4. Raskite funkcijos kraštutinumą.

51 pavyzdys. Raskite funkcijos kraštutinumus .

1) Raskite dalines išvestines.

2) Išspręskite lygčių sistemą

4) Raskite antros eilės dalines išvestis ir jų reikšmes kritiniuose taškuose:. Tuo momentu gauname:

vadinasi, taške nėra ekstremumo. Tuo momentu gauname:

vadinasi, taške yra minimumas.

5.2 Visuotinis ekstremumas (aukščiausia ir mažiausia funkcijos reikšmės)

Didžiausia ir mažiausia kelių kintamųjų funkcijos reikšmės, nuolatinės tam tikroje uždaroje aibėje, pasiekiamos ekstremaliuose taškuose arba aibės ribose.

Didžiausių ir mažiausių verčių radimo schema.

1) Raskite regiono viduje esančius kritinius taškus, apskaičiuokite funkcijos reikšmę šiuose taškuose.

2) Ištirkite funkciją ant teritorijos ribos; jei sieną sudaro kelios skirtingos linijos, tada tyrimas turi būti atliekamas kiekvienai vietai atskirai.

3) Palyginkite gautas funkcijos reikšmes ir pasirinkite didžiausią ir mažiausią.

52 pavyzdys. Raskite didžiausią ir mažiausią funkcijų reikšmes stačiakampyje.

Sprendimas. 1) Raskite funkcijos kritinius taškus, tam randame dalines išvestines: ir išspręskite lygčių sistemą:

Gautas kritinis taškas A. Gautas taškas yra nurodytoje srityje,

Teritorijos riba sudaryta iš keturių segmentų: ir. raskite didžiausią ir mažiausią funkcijos reikšmę kiekviename segmente.

4) Palyginkite gautus rezultatus ir raskite tai taškuose .

6 skyrius. Vartotojo pasirinkimo modelis

Darysime prielaidą, kad yra n skirtingų prekių. Tada tam tikra prekių rinkinys bus pažymėtas n-mačio vektoriumi , kur yra i-ojo produkto kiekis. Visų prekių aibių X aibė vadinama erdve.

Individualaus vartotojo pasirinkimui būdingas pirmenybės santykis: manoma, kad vartotojas gali pasakyti apie bet kuriuos du rinkinius, kuris yra labiau pageidaujamas, arba jis nemato skirtumo tarp jų. Pirmenybės santykis yra pereinamasis: jei aibė yra geresnė už aibę, o aibė yra geresnė už aibę, tada aibė yra geriau nei aibė. Darysime prielaidą, kad vartotojų elgseną pilnai apibūdina individualaus vartotojo aksioma: kiekvienas individualus vartotojas priima sprendimą dėl vartojimo, pirkimų ir pan., remdamasis savo pirmenybių sistema.

6.1 Naudingumo funkcija

Vartotojų rinkinių X aibėje funkcija yra apibrėžta , kurios vertė vartotojo rinkinyje yra lygi vartotojo apskaičiuotam asmeniui šiam rinkiniui. Funkcija vadinama vartotojo naudingumo funkcija arba vartotojo pirmenybės funkcija. Tie. kiekvienas vartotojas turi savo naudingumo funkciją. Bet visą vartotojų aibę galima suskirstyti į tam tikras vartotojų klases (pagal amžių, turtinę padėtį ir pan.) ir kiekvienai klasei priskirti kokią nors, galbūt, vidutinę naudingumo funkciją.

Taigi funkcija yra vartotojo įvertinimas arba asmens poreikių tenkinimo lygis perkant duotą rinkinį. Jei rinkinys yra geresnis nei tam tikram asmeniui skirtas rinkinys, tada.

Naudingumo funkcijos savybės.

1.

Pirmosios naudingumo funkcijos dalinės išvestinės vadinamos produktų ribiniais naudingumais. Iš šios savybės išplaukia, kad padidėjus vienos prekės suvartojimui, o kitų produktų suvartojimui nesikeičiant, didėja vartotojų vertinimas. Vektorius yra funkcijos gradientas, jis parodo didžiausio funkcijos augimo kryptį. Funkcijos gradientas yra ribinių produktų naudingumo vektorius.

2.

Tie. bet kurios prekės ribinis naudingumas mažėja didėjant vartojimui.

3.

Tie. kiekvieno produkto ribinis naudingumas didėja didėjant kito produkto kiekiui.

Kai kurios naudingumo funkcijos.

1) Neoklasikinis:.

2) Kvadratinis: kur matrica yra neigiama apibrėžtoji ir dėl .

3) Logaritminė funkcija:.

6.2 Abejingumo linijos

Taikomose vartotojų pasirinkimo problemose ir modeliuose dažnai naudojamas konkretus dviejų prekių rinkinio atvejis, t.y. kai naudingumo funkcija priklauso nuo dviejų kintamųjų. Abejingumo linija – tai linija, jungianti vartotojų rinkinius, turinčius vienodą individo poreikių patenkinimo lygį. Iš esmės abejingumo linijos yra funkcijos lygio linijos. Abejingumo linijos lygtys: .

Pagrindinės abejingumo linijų savybės.

1. Abejingumo linijos, atitinkančios skirtingus poreikių tenkinimo lygius, nesiliečia ir nesikerta.

2. Abejingumo linijos mažėja.

3. Abejingumo linijos yra išgaubtos žemyn.

2 savybė reiškia svarbią apytikslę lygybę.

Šis santykis parodo, kiek individas turėtų padidinti (sumažinti) antrojo produkto vartojimą, tuo pačiu sumažindamas (padidindamas) pirmojo produkto suvartojimą vienu vienetu, nekeičiant savo poreikių patenkinimo lygio. Santykis vadinamas pirmojo produkto pakeitimo antruoju greičiu, o reikšmė vadinama ribine pirmojo produkto pakeitimo antruoju norma.

53 pavyzdys. Jei pirmosios prekės ribinis naudingumas yra 6, o antrosios - 2, tai sumažėjus pirmosios prekės suvartojimui vienu vienetu, antrosios prekės suvartojimą reikia padidinti 3 vienetais vienodas poreikių tenkinimo lygis.

6.3 Biudžeto rinkinys

Leisti - n produktų rinkinio kainų vektorius; I - asmens pajamos, kurias jis nori išleisti produktų rinkiniui įsigyti. Prekių rinkinių, kainuojančių ne daugiau nei I nurodytomis kainomis, aibė vadinama biudžetine aibe B. Be to, prekių rinkinių, kainuojančių I, aibė vadinama biudžetinės aibės B riba G. aibę B riboja riba G ir gamtiniai apribojimai.

Biudžeto rinkinys apibūdinamas nelygybių sistema:

Dviejų prekių aibės atveju biudžeto aibė B (1 pav.) yra trikampis koordinačių sistemoje, ribojamas koordinačių ašių ir tiesės.

6.4 Vartotojų paklausos teorija

Vartojimo teorijoje daroma prielaida, kad vartotojas visada siekia maksimaliai padidinti savo naudingumą ir vienintelis apribojimas jam yra ribotos pajamos I, kurias jis gali išleisti pirkdamas prekių rinkinį. Apskritai vartotojų pasirinkimo problema (racionalaus vartotojų elgesio rinkoje problema) formuluojama taip: rasti vartotojų rinkinį. , kuris maksimaliai padidina jo naudingumo funkciją esant tam tikram biudžeto apribojimui. Matematinis šios problemos modelis:

Jei yra dviejų produktų rinkinys:

Geometriškai šios problemos sprendimas yra sąlyčio taškas tarp biudžeto aibės G ribos ir abejingumo linijos.

Šios problemos sprendimas sumažinamas iki lygčių sistemos sprendimo:

(1)

Šios sistemos sprendimas yra vartotojo pasirinkimo problemos sprendimas.

Vartotojo pasirinkimo problemos sprendimas vadinamas paklausos tašku. Šis paklausos taškas priklauso nuo kainų ir pajamų I. Tai yra. paklausos taškas yra paklausos funkcija. Savo ruožtu paklausos funkcija yra n funkcijų rinkinys, kurių kiekviena priklauso nuo argumento:

Šios funkcijos vadinamos atitinkamų prekių paklausos funkcijomis.

54 pavyzdys. Dviejų rinkoje esančių prekių rinkiniui, žinomoms jų kainoms ir I pajamoms, suraskite paklausos funkcijas, jei naudingumo funkcija turi formą .

Sprendimas. Išskirkime naudingumo funkciją:

.

Pakeiskite gautas išraiškas (1) ir gaukite lygčių sistemą:

Tokiu atveju išlaidos kiekvienai prekei bus pusė vartotojo pajamų, o perkamos prekės suma lygi jai išleistai sumai, padalytai iš prekės kainos.

55 pavyzdys. Tegul naudingumo funkcija skirta pirmai prekei, antrajai,

pirmos prekės kaina, antrojo kaina. Pajamos . Kiek vartotojas turėtų pirkti, kad padidintų naudingumą?

Sprendimas. Raskime naudingumo funkcijų išvestines, pakeiskime jas į sistemą (1) ir išspręskime:

Šis prekių rinkinys yra optimalus vartotojui, siekiant maksimaliai padidinti naudingumą.

Bandymas turi būti atliktas pagal parinktį, pasirinktą pagal paskutinį įrašų knygos numerio skaitmenį atskirame bloknote. Kiekviena problema turi turėti sąlygą, išsamų sprendimą ir išvadą.

1. Įvadas į skaičiavimą

Užduotis 1. Raskite funkcijos sritį.

5.

2 uždavinys. Raskite funkcijų ribas.

.

Užduotis 3. Raskite funkcijos lūžio taškus ir nustatykite jų tipą.

1. 2. 3.

2 skyrius. Vieno kintamojo funkcijos diferencialinis skaičiavimas

4 užduotis. Raskite šių funkcijų išvestinius.

1.a); b) c) y =;

d) y = x 6 + + + 5; e) y = x tg x + ln sin x + e 3x;

f) y = 2 x - arcsin x.

2.a) ; b) y =; c) y =; d) y = x 2 - + 3; e) y = e cos; f) y =.

3.a) y = lnx; b) y =; c) y = ln;

4. a) y =; b) y = (e 5 x - 1) 6; c) y =; d) y =; e) y = x 8 ++ + 5; f) y = 3 x - arcsin x.

5.a) y = 2x 3 - + e x; b) y =; c) y =;

d) y =; e) y = 2 cos; f) y =.

6.a) y = lnx; b) y =; c) y = ln;

d) y =; e) y = x 7 + + 1; f) y = 2.

7.a) ; b) y =; c) y =; d) y = x 2 + xsinx +; e) y = e cos; f) y =.

8. a) y =; b) y = (3 x - 4) 6; c) y = sintg;

d) y = 3x 4 - - 9+ 9; e) y =;

f) y = x 2 + arcsin x - x.

9.a); b) ; c) y =; d) y = 5 sin 3 x; e) y = x 3 - - 6+ 3; f) y = 4x 4 + ln.

10.a) b) y =; c) y = (3 x - 4) 6; d) y =; e) y = x 2 - x; f) y = e sin 3 x + 2.

5 užduotis. Ištirkite funkciją ir sudarykite jos grafiką.

1. a) b) c).

2.a) b) v) .

3.a) b) v) .

4.b) v)

5.a) b) v) .

6.a) b) v) .

7. a) b) c).

8. a) b) c).

9.a) b) c).

10. a) b) v) .

6 užduotis. Raskite didžiausią ir mažiausią funkcijos reikšmę duotame atkarpoje.

1. .

3. .

6. .

8. .

9. .

10. .

3 skyrius. Integralinis skaičiavimas

7 uždavinys. Raskite neapibrėžtuosius integralus.

1.a) b);

2.a) b) c) d).

4. G)

5.a) ; b); v) ; G).

6.a) ; b); v); G)

7.a) ; b) ; v) ; G)

8.a) ; b); v) ; G) .

9.a) ; b) c); G).

10.a) b) v) ; G) .

8 uždavinys. Apskaičiuokite apibrėžtuosius integralus.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

9 uždavinys. Raskite netinkamus integralus arba įrodykite, kad jie skiriasi.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

10 uždavinys. Raskite kreivių apribotos srities plotą

1. .2. .

5. 6.

7. , .8..

10. , .

4 skyrius. Kelių kintamųjų funkcijos diferencialinis skaičiavimas.

Užduotis 11. Raskite funkcijos sritį (parodykite brėžinyje).

12 uždavinys. Ištirkite funkcijos tęstinumą

13 uždavinys. Raskite netiesiogiai apibrėžtos funkcijos išvestinę.

14 uždavinys. Apskaičiuokite apytikslę

1.a); b) ; v)

2.a) ; b); v) .

3.a) ; b) ; v) .

4.a) ; b) ; v) .

5. a); b) ; v) .

6. a); b); v) .

7. a); b) ; v) .

8.a); b) ; v)

9.a) ; b); v) .

10. a); b) ; v)

15 uždavinys. Ištirkite ekstremalių funkciją.

7. .

8. .

9. .

10. .

16 uždavinys. Raskite didžiausią ir mažiausią funkcijos reikšmę duotoje uždaroje srityje.

1.stačiakampyje

2.

3.stačiakampyje

4.parabolės apribotoje srityje

Ir abscisė.

5.kvadratas

6.trikampyje, apribotame koordinačių ašių ir tiesės

7.trikampyje, apribotame koordinačių ašių ir tiesės

8. trikampyje, apribotame koordinačių ašių ir tiesės

9.parabolės ribojamame regione

Ir abscisė.

10.parabolės ribojamame regione

Ir abscisė.

Pagrindinis

1. M.S. Crassus, B.P. Chuprynovas. Matematikos pagrindai ir jos taikymas ekonominiame ugdyme: vadovėlis. - 4-asis leidimas, isp. - M .: Delo, 2003 m.

2. M.S. Crassus, B.P. Chuprynovas. Matematika ekonomikos specialybėms: Vadovėlis. - 4-asis leidimas, isp. - M .: Delo, 2003 m.

3. M.S. Crassus, B.P. Chuprynovas. Matematika ekonomikos bakalauro laipsniui gauti. Vadovėlis. - 4-asis leidimas, isp. - M .: Delo, 2005 m.

4. Aukštoji matematika ekonomistams. Vadovėlis universitetams / N.Sh. Kremeris, B.A. Putko, I.M. Trišinas, M.N. Friedmanas; Red. prof. N.Sh. Kremer, – 2-asis leidimas, pataisytas. ir pridėkite. - M: VIENYBĖ, 2003 m.

5. Kremer N.Sh, Putko BA, Trishin IM, Fridman MN Aukštoji matematika ekonomikos specialybėms. Vadovėlis ir dirbtuvės (I ir II dalys) / Red. prof. N.Sh. Kremer, – 2-asis leidimas, pataisytas. ir pridėkite. - M: Aukštasis išsilavinimas, 2007. - 893p. - (Mokslų pagrindai)

6. Danko P.E., Popovas A.G., Koževnikova T.Ya. Aukštoji matematika pratimuose ir uždaviniuose. M. vidurinę mokyklą. 1999 m.

Papildomas

1. I.I. Bavrinas, V.L. Jūreiviai. Aukštoji matematika. „Vlados humanitarinės leidybos centras“, 2002 m.

2. I.A. Zaicevas. Aukštoji matematika. „Vidurinė mokykla“, 1998 m.

3. A.S. Solodovnikovas, V.A. Babaicevas, A.V. Brailovas, I.G. Šandra. Matematika ekonomikoje / iš dviejų dalių /. M. Finansai ir statistika. 1999 m.

studentams medicinos, vaikų, odontologijos

ir prevencinės medicinos fakultetai

laboratoriniams darbams

„Pagrindinės matematinės analizės sąvokos“

1. Mokslinis ir metodinis temos pagrindimas:

Išvestinės ir diferencinės sąvokos yra viena iš pagrindinių matematinės analizės sąvokų. Išvestinių skaičiavimas reikalingas sprendžiant daugelį fizikos ir matematikos uždavinių (randant greitį, pagreitį, slėgį ir kt.). Išvestinės sąvokos svarbą visų pirma lemia tai, kad funkcijos išvestinė charakterizuoja šios funkcijos kitimo greitį, kai keičiasi jos argumentas.

Diferencialo naudojimas leidžia atlikti apytikslius skaičiavimus, taip pat įvertinti klaidas.

Funkcijų išvestinių ir diferencialų radimo metodai ir jų taikymas yra pagrindinė diferencialinio skaičiavimo problema. Išvestinės sąvokos poreikis iškyla suformuluojant judėjimo greičio skaičiavimo ir kreivės liestinės kampo nustatymo problemą. Galima ir atvirkštinė problema: pagal greitį nustatykite nuvažiuotą atstumą, o pagal liestinės nuolydžio liestinę raskite atitinkamą funkciją. Ši atvirkštinė problema veda prie neapibrėžto integralo sampratos.

Apibrėžtinio integralo sąvoka naudojama daugelyje praktinių problemų, ypač plokštumos figūrų plotų skaičiavimo, kintamos jėgos atliekamo darbo apskaičiavimo ir funkcijos vidutinės reikšmės nustatymo uždaviniuose.

Įvairių fizikinių, cheminių, biologinių procesų ir reiškinių matematiniame aprašyme dažnai naudojamos lygtys, kuriose pateikiami ne tik tiriamieji dydžiai, bet ir įvairios šių dydžių eilės jų dariniai. Pavyzdžiui, pagal paprasčiausią bakterijų dauginimosi dėsnio versiją, dauginimosi greitis yra proporcingas bakterijų skaičiui tam tikru metu. Jei šis dydis žymimas N (t), tai pagal fizinę darinio reikšmę bakterijų dauginimosi greitis yra N (t) darinys, o remiantis aukščiau pateiktu dėsniu, galime parašyti santykis N "(t) = k ∙ N, kur k> 0 - proporcingumo koeficientas Gauta lygtis nėra algebrinė, nes joje yra ne tik nežinoma funkcija N (t), bet ir jos pirmosios eilės išvestinė.

2. Trumpa teorija:

1. Problemos, vedančios prie išvestinės sąvokos

1. Materialaus taško greičio v radimo problema... Tegul koks nors materialus taškas atlieka tiesinį judėjimą. Vienu metu t 1 taškas yra padėtyje M 1. Vienu metu t 2 nėščia M 2 . Pažymime intervalą M 1 , M 2 skersai ΔS; t 2 - t 1 = Δt... Ši vertė vadinama vidutiniu judėjimo greičiu. Norėdami rasti momentinį taško greitį tam tikroje padėtyje M 1 būtina Δt linkę į nulį. Matematiškai tai reiškia

, (1)

Taigi, norint rasti momentinį materialaus taško greitį, reikia apskaičiuoti funkcijos prieaugio santykio ribą ΔS prie argumento Δt prieaugio su sąlyga, kad Δt → 0.

2. Funkcijos grafiko liestinės polinkio kampo radimo problema.

1 pav

Apsvarstykite kokios nors funkcijos grafiką y = f (x). Koks yra pasvirimo kampas
liestinė taške M 1 ? Taške M 1 nubrėžkite funkcijos grafiko liestinę. Pasirinkite savavališką grafiko tašką M 2 ir nubrėžkite sekantą. Ji pasvirusi link ašies OI kampu α 1 ... Apsvarstykite ΔM 1 M 2 A:

, (2)

Jei taškas M 1 pataisyti ir nukreipti M 2 pereiti arčiau M 1 , tada sekantas M 1 M 2 eis į funkcijos grafiko liestinę taške M 1 ir tu gali parašyti:

, (3)

Taigi, reikia apskaičiuoti funkcijos prieaugio ir argumento prieaugio santykio ribą, jei argumento prieaugis linkęs į nulį.

Funkcijos y = f (x) prieaugio Δy santykio su argumento Δx prieaugiu riba duotame taške x 0 kadangi Δx linkęs į nulį, vadinama funkcijos išvestine tam tikrame taške.

Išvestinis žymėjimas: y ", f" (x), ... Pagal apibrėžimą

, (4)

kur Δx = x 2 -x 1 yra argumento padidėjimas (skirtumas tarp dviejų vėlesnių pakankamai artimų argumento reikšmių), Δy = y 2 -y 1 yra funkcijos padidėjimas (skirtumas tarp reikšmių funkcijos, atitinkančios šias argumento reikšmes).

Duotos funkcijos išvestinės radimas vadinamas jos diferenciacija... Pagrindinių elementariųjų funkcijų diferencijavimas atliekamas pagal paruoštas formules (žr. lentelę), taip pat naudojant taisykles:

Algebrinės sumos išvestinė funkcijos yra lygi šių funkcijų išvestinių sumai:

(u+ υ )"= u" + υ "

2. Dviejų funkcijų sandaugos išvestinė lygi antrosios funkcijos sandaugų sumai iš pirmosios ir pirmosios funkcijos iš antrosios išvestinės:

(u ∙υ ) "= tu"υ + uυ "

3. Dalinio išvestinė dviejų funkcijų yra lygi trupmenai, kurios skaitiklis yra skirtumas tarp vardiklio sandaugų iš skaitiklio išvestinės ir skaitiklio iš vardiklio išvestinės, o vardiklis yra vardiklio kvadratas:

Fizinė išvestinės reikšmė. (4) ir (1) palyginimas reiškia, kad momentinis materialaus taško tiesinio judėjimo greitis yra lygus jo koordinatės priklausomybės nuo laiko išvestinei.

Bendroji funkcijos išvestinės reikšmė yra ta, kad ji charakterizuoja funkcijos kitimo greitis (greitas). tam tikram argumento pakeitimui. Taip pat dariniu išreiškiamas fizinių, cheminių ir kitų procesų greitis, pavyzdžiui, kūno aušinimo greitis, cheminės reakcijos greitis, bakterijų dauginimosi greitis ir kt.

Išvestinės geometrinė reikšmė. Funkcijos grafike nubrėžtos liestinės polinkio kampo liestinės dydis vadinamas matematikoje liestinės nuolydis.

Diferencijuojamos funkcijos grafiko liestinės nuolydis tam tikru tašku yra skaitiniu požiūriu lygus funkcijos išvestinei šiame taške.

Šis teiginys vadinamas geometrinė išvestinės reikšmė.

Straipsnio turinys

MATEMATINĖ ANALIZĖ, matematikos šaka, teikianti įvairių kitimo procesų kiekybinio tyrimo metodus; nagrinėja kitimo greičio tyrimą (diferencialinis skaičiavimas) ir kreivių kontūrų ir paviršių apribotų figūrų kreivių ilgių, plotų ir tūrių nustatymą (integralinis skaičiavimas). Matematinės analizės uždaviniams būdinga tai, kad jų sprendimas siejamas su ribos samprata.

Matematinę analizę 1665 metais pradėjo I. Niutonas, o (apie 1675 m.) savarankiškai – G. Leibnicas, nors svarbius parengiamuosius darbus atliko I. Kepleris (1571–1630), F. Cavalieri (1598–1647), P. Ferma. (1601–1665), J. Wallis (1616–1703) ir I. Barrow (1630–1677).

Kad pristatymas būtų gyvesnis, pasitelksime grafikų kalbą. Todėl prieš skaitant šį straipsnį skaitytojui gali būti naudinga peržvelgti straipsnį ANALITINĖ GEOMETRIJOS.

DIFERENCINIS SKAIČIUS

Tangentai.

Fig. 1 parodytas kreivės fragmentas y = 2x – x 2, sudaryta tarp x= –1 ir x= 3. Pakankamai maži šios kreivės segmentai atrodo tiesūs. Kitaip tariant, jei R Ar yra savavališkas šios kreivės taškas, tada per šį tašką eina tam tikra linija, kuri yra kreivės apytikslis taškas mažoje kaimynystėje R, ir kuo mažesnė kaimynystė, tuo geresnis apytikslis. Tokia tiesi linija vadinama kreivės liestine taške R... Pagrindinė diferencialinio skaičiavimo užduotis yra sukurti bendrą metodą, leidžiantį rasti liestinės kryptį bet kuriame kreivės taške, kuriame yra liestinė. Nesunku įsivaizduoti kreivę su staigiu lūžiu (2 pav.). Jeigu R- tokios pertraukos viršus, tada galite nutiesti apytikslę tiesią liniją PT 1 - taško dešinėje R ir dar viena apytikslė linija RT 2 – taško kairėje R... Tačiau nėra vienos tiesios linijos, einančios per tašką R, kuris vienodai gerai priartėjo prie kreivės taško apylinkėse P tiek į dešinę, tiek į kairę, taigi ir liestinė taške P neegzistuoja.

Fig. 1 liestinė NUO nupieštas per kilmę O= (0,0). Šios linijos nuolydis yra 2, t.y. abscisei pasikeitus 1, ordinatės padidėja 2. Jei x ir y- savavališko taško koordinatės NUO, tada tolsta nuo O per atstumą X vienetų į dešinę, tolstame nuo O 2 dieną y vienetų aukštyn. Vadinasi, y/x= 2 arba y = 2x... Tai yra liestinės lygtis NUOį kreivę y = 2x – x 2 taške O.

Dabar reikia paaiškinti, kodėl iš eilučių, einančių per tašką, aibės O, buvo pasirinkta tiesi linija NUO... Kuo skiriasi tiesė, kurios nuolydis yra 2, ir kitos tiesės? Yra vienas paprastas atsakymas, ir mums sunku atsispirti pagundai panaudoti apskritimo liestinės analogiją: liestinę. NUO turi tik vieną bendrą tašką su kreive, o bet kuri kita ne vertikali tiesė, einanti per tašką O, kerta kreivę du kartus. Tai galima patikrinti taip.

Nuo išraiškos y = 2x – x 2 galima gauti atėmus X 2 iš y = 2x(tiesės lygtys NUO), tada vertės y yra mažiau žinių grafikui y tiesei visuose taškuose, išskyrus tašką x= 0. Todėl grafikas yra visur, išskyrus tašką O esantis žemiau NUO, o ši linija ir grafikas turi tik vieną bendrą tašką. Be to, jei y = mx- kokios nors kitos tiesės, einančios per tašką, lygtis O, tada tikrai yra du susikirtimo taškai. tikrai, mx = 2x – x 2 ne tik x= 0, bet ir už x = 2 – m... Ir tik tada, kai m= 2 abu susikirtimo taškai sutampa. Fig. 3 parodytas atvejis, kai m mažiau nei 2, taigi į dešinę nuo O yra antras susikirtimo taškas.

Ką NUO- vienintelė nevertikali tiesi linija, einanti per tašką O ir turintis tik vieną bendrą tašką su grafiku, o ne jo svarbiausią savybę. Iš tiesų, jei pažvelgsime į kitus grafikus, netrukus paaiškės, kad liestinės savybė, kurią pažymėjome bendruoju atveju, nėra įvykdyta. Pavyzdžiui, iš fig. 4 matyti, kad šalia taško (1,1) kreivės grafikas y = x 3 yra gerai apytikslė tiesia linija RT, kuris vis dėlto turi daugiau nei vieną bendrą dalyką. Tačiau norėtume apsvarstyti RTšio grafiko liestinė taške R... Todėl būtina rasti kitą būdą liestinei paryškinti nei ta, kuri mums taip pasitarnavo pirmame pavyzdyje.

Tarkime, kad per tašką O ir savavališkas taškas K = (h,k) kreivės grafike y = 2x – x 2 (5 pav.) nubrėžiama tiesi linija (vadinama sekantu). Į kreivės lygtį pakeičiant reikšmes x = h ir y = k, mes tai suprantame k = 2h – h 2, todėl sekanto nuolydis yra

Su labai mažais h prasmė m artimas 2. Be to, pasirenkant h pakankamai arti 0 galime padaryti m savavališkai arti 2. Galime pasakyti, kad m„Tendns to the limit“ lygus 2 kai h linkęs į nulį ar bet kokią ribą m lygus 2 už h linkę į nulį. Tai simboliškai parašyta taip:

Tada grafiko liestinė taške O apibrėžiamas kaip tiesė, einanti per tašką O, kurio nuolydis lygus šiai ribai. Šis liestinės apibrėžimas taikomas paprastai.

Parodykime šio metodo privalumus kitu pavyzdžiu: raskite kreivės grafiko liestinės nuolydį y = 2x – x 2 savavališkame taške P = (x,y), neapsiribodami pačiu paprasčiausiu atveju, kai P = (0,0).

Leisti K = (x + h, y + k) – antrasis diagramos taškas, esantis per atstumą hį dešinę R(6 pav.). Būtina rasti nuolydį k/h sekantas PQ... Taškas K yra per atstumą

virš ašies X.

Išplėsdami skliaustus randame:

Atimant iš šios lygties y = 2x – x 2, randame vertikalų atstumą nuo taško R iki taško K:

Todėl nuolydis m sekantas PQ yra lygus

Dabar kai h linkęs į nulį, m linkęs į 2-2 x; paskutinę reikšmę laikysime liestinės nuolydžiu PT... (Tas pats rezultatas bus gautas, jei h ima neigiamas reikšmes, kurios atitinka taško pasirinkimą K kairėje nuo P.) Atkreipkite dėmesį, kad už x= 0 rezultatas yra toks pat kaip ir ankstesnis.

2 - 2 išraiška x vadinamas 2 išvestiniu x – x 2. Senovėje išvestinė dar buvo vadinama „diferencialiniu santykiu“ ir „diferencialiniu koeficientu“. Jei 2 išraiška x – x 2 paskirti f(x), t.y.

tada išvestinę galima žymėti

Norėdami sužinoti funkcijos grafiko liestinės nuolydį y = f(x) tam tikru momentu turi būti pakeistas fў ( x) reikšmę, atitinkančią šį tašką X... Taigi nuolydis fў (0) = 2 už X = 0, fў (0) = 0 X= 1 ir fў (2) = –2 X = 2.

Taip pat žymimas vedinys adresuў , dy/dx, D x y ir Du.

Faktas, kad kreivė y = 2x – x 2 šalia tam tikro taško praktiškai nesiskiria nuo jo liestinės šiame taške, leidžia kalbėti apie liestinės nuolydį kaip apie "kreivės nuolydį" liesties taške. Taigi galime teigti, kad nagrinėjamos kreivės nuolydis taške (0,0) yra lygus 2. Taip pat galima teigti, kad ties tašku (0,0) x= 0 kitimo greitis y santykinai x yra 2. Taške (2,0) liestinės (ir kreivės) nuolydis yra –2. (Minuso ženklas reiškia, kad kaip x kintamasis y mažėja.) Taške (1,1) liestinė yra horizontali. Mes sakome kreivę y = 2x – x 2 šiuo metu turi stacionarią vertę.

Aukštos ir žemos.

Mes ką tik parodėme, kad kreivė f(x) = 2x – x 2 yra nejudantis taške (1,1). Nes fў ( x) = 2 – 2x = 2(1 – x), aišku, kad už x mažiau nei 1, fў ( x) yra teigiamas, todėl y dideja; adresu x, didelis 1, fў ( x) yra neigiamas, todėl y mažėja. Taigi, šalia taško (1,1), nurodyto fig. 6 raidė M, prasmė adresu auga iki taško M, stacionarus taške M ir mažėja po taško M... Šis taškas vadinamas „maksimuliu“, nes vertė adresušiuo metu viršija bet kurią savo vertę pakankamai mažoje jo kaimynystėje. Panašiai „minimalus“ apibrėžiamas kaip taškas, šalia kurio yra visos reikšmės y viršija skaičių adresušiuo metu. Taip pat gali atsitikti taip, kad nors išvestinė iš f(x) tam tikru momentu ir išnyksta, jo ženklas netoli šio taško nekinta. Toks taškas, kuris nėra nei maksimumas, nei minimumas, vadinamas vingio tašku.

Kaip pavyzdį suraskime stacionarų kreivės tašką

Šios funkcijos išvestinė yra

ir dingsta x = 0, X= 1 ir X= –1; tie. taškuose (0,0), (1, –2/15) ir (–1, 2/15). Jeigu X tada šiek tiek mažiau nei -1 fў ( x) yra neigiamas; jeigu X tada šiek tiek daugiau nei -1 fў ( x) yra teigiamas. Todėl taškas (–1, 2/15) yra maksimalus. Panašiai galima parodyti, kad taškas (1, –2/15) yra minimumas. Tačiau išvestinė fў ( x) yra neigiamas tiek prieš, tiek po taško (0,0). Todėl (0,0) yra vingio taškas.

Atliktas kreivės formos tyrimas, taip pat tai, kad kreivė kerta ašį X adresu f(x) = 0 (t. y. už X= 0 arba) leidžia pavaizduoti jo grafiką maždaug taip, kaip parodyta Fig. 7.

Apskritai, jei neįtrauksime neįprastų atvejų (kreivės, kuriose yra tiesių atkarpų arba begalinis lenkimų skaičius), yra keturios santykinės kreivės padėties ir liestinės šalia liestinės taško parinktys. R. (Cm... ryžių. 8, kur liestinė turi teigiamą nuolydį.)

1) Abiejose taško pusėse R kreivė yra virš liestinės (8 pav., a). Šiuo atveju jie sako, kad kreivė taške R išgaubtas žemyn arba įgaubtas.

2) Abiejose taško pusėse R kreivė yra žemiau liestinės (8 pav., b). Šiuo atveju sakoma, kad kreivė yra išgaubta aukštyn arba tiesiog išgaubta.

3) ir 4) Kreivė yra virš liestinės vienoje taško pusėje R o žemiau – kitoje. Tokiu atveju R- Vingio taškas.

Vertybių palyginimas fў ( x) abiejose pusėse R su jo verte taške R, galima nustatyti, kuris iš šių keturių atvejų turi būti sprendžiamas sprendžiant konkrečią problemą.

Programos.

Visa tai, kas išdėstyta pirmiau, yra svarbi įvairiose srityse. Pavyzdžiui, jei kūnas metamas vertikaliai aukštyn pradiniu 200 pėdų per sekundę greičiu, tada aukštis s per kurią jie bus išdėstyti t sekundžių, palyginti su pradiniu tašku

Veikdami taip pat, kaip ir nagrinėtuose pavyzdžiuose, mes nustatome

ši reikšmė išnyksta c. Darinys fў ( x) yra teigiamas iki c reikšmės ir neigiamas po šio laiko. Vadinasi, s padidėja iki, tada tampa nejudantis, o tada mažėja. Tai bendras kūno, mesto aukštyn, judėjimo aprašymas. Iš jo žinome, kada kūnas pasiekia aukščiausią tašką. Be to, pakeitimas t= 25/4 colio f(t), gauname 625 pėdas, didžiausią pakėlimą. Šioje užduotyje fў ( t) turi fizinę reikšmę. Ši išvestinė rodo greitį, kuriuo kūnas juda tuo momentu t.

Dabar panagrinėkime kitą taikymo tipą (9 pav.). Iš 75 cm 2 ploto kartono lakšto reikia pagaminti dėžutę kvadratiniu dugnu. Kokio dydžio turi būti ši dėžė, kad jos tūris būtų didžiausias? Jeigu X- dėžutės pagrindo šoną ir h- jo aukštis, tada dėžutės tūris yra V = x 2 h, o paviršiaus plotas yra 75 = x 2 + 4xh... Transformuodami lygtį, gauname:

Kilęs iš V pasirodo lygūs

ir dingsta X= 5. Tada

ir V= 125/2. Funkcijų grafikas V = (75x – x 3) / 4 parodyta pav. 10 (neigiamos reikšmės X praleistas kaip neturintis fizinės reikšmės šioje problemoje).

Dariniai.

Svarbi diferencialinio skaičiavimo užduotis – metodų, leidžiančių greitai ir patogiai rasti išvestines, sukūrimas. Pavyzdžiui, tai lengva apskaičiuoti

(Konstantos išvestinė, žinoma, lygi nuliui.) Nesunku išvesti bendrąją taisyklę:

kur n- bet koks sveikasis skaičius arba trupmena. Pavyzdžiui,

(Šis pavyzdys parodo, kokie naudingi yra trupmeniniai rodikliai.)

Štai keletas svarbiausių formulių:

Taip pat yra šios taisyklės: 1) jei kiekviena iš dviejų funkcijų g(x) ir f(x) turi išvestines, tai jų sumos išvestinė lygi šių funkcijų išvestinių sumai, o skirtumo išvestinė lygi išvestinių skirtumui, t.y.

2) dviejų funkcijų sandaugos išvestinė apskaičiuojama pagal formulę:

3) dviejų funkcijų santykio išvestinė turi formą

4) funkcijos išvestinė, padauginta iš konstantos, lygi konstantai, padaugintai iš šios funkcijos išvestinės, t.y.

Dažnai atsitinka taip, kad funkcijos reikšmės turi būti skaičiuojamos etapais. Pavyzdžiui, apskaičiuoti nuodėmę x 2, pirmiausia turime rasti u = x 2, tada apskaičiuokite skaičiaus sinusą u... Tokių sudėtingų funkcijų išvestinę randame naudodami vadinamąją „grandinės taisyklę“:

Mūsų pavyzdyje f(u) = nuodėmė u, fў ( u) = cos u, vadinasi,

Šios ir kitos panašios taisyklės leidžia iš karto išrašyti daugelio funkcijų išvestinius.

Tiesinės aproksimacijos.

Tai, kad, žinodami išvestinę, daugeliu atvejų galime pakeisti funkcijos grafiką šalia kurio nors jos liestinės taško šiame taške, yra labai svarbu, nes tiesiomis tiesėmis dirbti lengviau.

Ši idėja tiesiogiai taikoma apskaičiuojant apytiksles funkcijų reikšmes. Pavyzdžiui, gana sunku apskaičiuoti vertę kada x= 1,033. Bet jūs galite pasinaudoti tuo, kad skaičius 1,033 yra artimas 1 ir tiek. Uždaryti x= 1 galime pakeisti liestinės kreivės grafiką nepadarydami rimtos klaidos. Tokios liestinės nuolydis yra lygus išvestinės ( x 1/3) ў = (1/3) x–2/3, kai x = 1, ty 1/3. Kadangi taškas (1,1) yra kreivėje, o kreivės liestinės nuolydis šiame taške yra 1/3, liestinės lygtis turi tokią formą

Šioje linijoje adresu X = 1,033

Gauta vertė y turėtų būti labai arti tikrosios vertės y; ir iš tikrųjų tai tik 0,00012 daugiau nei tiesa. Matematinės analizės metu buvo sukurti metodai, skirti pagerinti tokio tipo tiesinio aproksimavimo tikslumą. Šie metodai užtikrina mūsų apytikslių skaičiavimų patikimumą.

Ką tik aprašyta procedūra siūlo naudingą žymėjimą. Leisti P- funkcijos grafike atitinkantis taškas f kintamasis X ir leiskite veikti f(x) yra diferencijuojamas. Pakeiskite kreivės grafiką šalia taško R jos liestinė, nubrėžta šioje vietoje. Jeigu X keisti pagal sumą h, tada liestinės ordinatė pasikeis reikšme h H f ў ( x). Jeigu h yra labai mažas, tada pastaroji reikšmė yra geras tikrojo ordinačių pokyčio aproksimacija y grafika. Jei vietoj h parašysime simbolį dx(tai ne gaminys!), o ordinatės pasikeitimas yžymėti dy, tada gauname dy = f ў ( x)dx, arba dy/dx = f ў ( x) (cm... ryžių. vienuolika). Todėl vietoj Dy arba f ў ( x) simbolis dažnai naudojamas išvestinei žymėti dy/dx... Šio žymėjimo patogumas daugiausia priklauso nuo aiškios grandinės taisyklės išvaizdos (sudėtingos funkcijos diferenciacijos); naujajame žymėjime ši formulė atrodo taip:

kur numanoma, kad adresu priklauso nuo u, a u savo ruožtu priklauso nuo X.

Didumas dy vadinamas diferencialu adresu; iš tikrųjų tai priklauso nuo du kintamieji, būtent: nuo X ir prieaugiais dx... Kai prieaugis dx labai mažas, dydis dy yra artimas atitinkamam vertės pokyčiui y... Tačiau manyti, kad prieaugis dx mažai, nereikia.

Išvestinė funkcija y = f(x) pažymėjome f ў ( x) arba dy/dx... Dažnai galima imti išvestinę išvestinę. Rezultatas vadinamas antruoju išvestiniu f (x) ir pažymėtas f ўў ( x) arba d 2 y/dx 2. Pavyzdžiui, jei f(x) = x 3 – 3x 2, tada f ў ( x) = 3x 2 – 6x ir f ўў ( x) = 6x- 6. Panašūs pavadinimai naudojami aukštesnės eilės išvestinėms priemonėms. Tačiau norint išvengti didelio brūkšnelių skaičiaus (lygaus išvestinės tvarkai), ketvirtą išvestinę (pavyzdžiui) galima parašyti kaip f (4) (x), ir išvestinė n-th order as f (n) (x).

Galima parodyti, kad kreivė taške yra išgaubta žemyn, jei antroji išvestinė yra teigiama, ir išgaubta aukštyn, jei antroji išvestinė yra neigiama.

Jei funkcija turi antrą išvestinę, tai kiekio pokytis y atitinkantį prieaugį dx kintamasis X, galima apytiksliai apskaičiuoti pagal formulę

Šis apytikslis apskaičiavimas paprastai yra geresnis už tą, kurį suteikia diferencialas fў ( x)dx... Tai atitinka kreivės dalies pakeitimą parabole, o ne tiesia linija.

Jei funkcija f(x) yra aukštesnių eilių išvestiniai, tada

Likusi dalis yra

kur x- tam tikras skaičius tarp x ir x + dx... Aukščiau pateiktas rezultatas vadinamas likučio Taylor formule. Jeigu f(x) turi visų eilių išvestinius, tada paprastai R n® 0 už n ® Ґ .

INTEGRALINIS SKAIČIUS

Kvadratai.

Tiriant kreivinės plokštumos figūrų sritis, atskleidžiami nauji matematinės analizės aspektai. Tokias problemas bandė spręsti net senovės graikai, kuriems, pavyzdžiui, apskritimo ploto nustatymas buvo viena iš sunkiausių užduočių. Archimedas pasiekė didelę sėkmę spręsdamas šią problemą, jam taip pat pavyko rasti parabolinės atkarpos plotą (12 pav.). Remdamasis labai sudėtingais samprotavimais, Archimedas įrodė, kad parabolinės atkarpos plotas yra 2/3 aprašyto stačiakampio ploto, todėl šiuo atveju lygus (2/3) (16). = 32/3. Kaip matysime vėliau, šį rezultatą nesunkiai galima gauti matematinės analizės metodais.

Niutono ir Leibnizo pirmtakai, daugiausia Kepleris ir Cavalieri, kreivių figūrų plotų apskaičiavimo problemą išsprendė vargu ar loginiu pavadintu metodu, kuris pasirodė itin vaisingas. Kai Wallis 1655 m. sujungė Keplerio ir Cavalieri metodus su Dekarto metodais (analitine geometrija) ir panaudojo naujai gimusią algebrą, Niutono pasirodymo scena buvo visiškai paruošta.

Wallis padalijo figūrą, kurios plotą reikėjo apskaičiuoti, į labai siauras juosteles, kurių kiekviena buvo maždaug laikoma stačiakampiu. Tada jis susumavo apytikslių stačiakampių plotus ir paprasčiausiais atvejais gavo reikšmę, į kurią linksta stačiakampių plotų suma, kai juostelių skaičius linkęs į begalybę. Fig. 13 pavaizduoti stačiakampiai, atitinkantys tam tikrą ploto po kreive padalijimą į juosteles y = x 2 .

Pagrindinė teorema.

Puikus Niutono ir Leibnizo atradimas leido pašalinti sunkų procesą, pereinant prie plotų sumos ribos. Tai buvo padaryta naujai pažvelgus į kvadrato koncepciją. Esmė ta, kad turime įsivaizduoti plotą po kreive, sukurtą ordinatėms judant iš kairės į dešinę, ir paklausti, kaip greitai keičiasi ordinačių nubraukiamas plotas. Raktą į atsakymą į šį klausimą gausime, jei atsižvelgsime į du ypatingus atvejus, kai plotas žinomas iš anksto.

Pradėkime nuo ploto po tiesinės funkcijos grafiku y = 1 + x nes šiuo atveju plotą galima apskaičiuoti naudojant elementariąją geometriją.

Leisti A(x) Ar plokštumos dalis, esanti tarp tiesės y = 1 + x ir segmentas OQ(14 pav.). Vairuojant QP teisinga sritis A(x) dideja. Kaip greitai? Į šį klausimą atsakyti nesunku, nes žinome, kad trapecijos plotas lygus jos aukščio sandaugai iš jos pagrindų sumos. Vadinasi,

Ploto kitimo greitis A(x) nustatomas pagal jo išvestinę

Mes tai matome Aў ( x) sutampa su ordinatėmis adresu taškų R... Ar tai sutapimas? Pabandykime patikrinti parabolę, parodytą Fig. 15. Kvadratas A (x) po parabole adresu = X 2 diapazone nuo 0 iki X yra lygus A(x) = (1 / 3)(x)(x 2) = x 3/3. Šios srities kitimo greitis nustatomas pagal išraišką

kuri tiksliai sutampa su ordinatėmis adresu judantis taškas R.

Jei manysime, kad ši taisyklė apskritai yra įvykdyta taip, kad

yra ploto po funkcijos grafiku kitimo greitis y = f(x), tai gali būti naudojama skaičiavimams ir kitoms sritims. Tiesą sakant, santykis Aў ( x) = f(x) išreiškia pagrindinę teoremą, kurią būtų galima suformuluoti taip: išvestinė arba ploto kitimo greitis kaip funkcija X, yra lygus funkcijos reikšmei f (x) taške X.

Pavyzdžiui, norint rasti sritį po funkcijos grafiku y = x 3 nuo 0 iki X(16 pav.), dedame

Galimas atsakymas:

nes vedinys iš X 4/4 tikrai lygu X 3. Be to, A(x) yra lygus nuliui X= 0, kaip turėtų būti, jei A(x) iš tikrųjų yra sritis.

Matematinė analizė įrodo, kad be aukščiau pateiktos išraiškos yra dar vienas atsakymas A(x), neegzistuoja. Parodykime, kad šis teiginys yra tikėtinas, naudodamiesi šiuo euristiniu (negriežtu) samprotavimu. Tarkime, yra koks nors antras sprendimas V(x). Jeigu A(x) ir V(x) „Pradėti“ vienu metu nuo nulio vertės ties X= 0 ir visą laiką keičiasi tuo pačiu greičiu, tada jų reikšmės yra Nr X negali tapti kitokiu. Jie visur turi būti vienodi; todėl yra tik vienas sprendimas.

Kaip galima pateisinti santykį? Aў ( x) = f(x) apskritai? Į šį klausimą galima atsakyti tik ištyrus ploto kitimo greitį kaip funkciją X apskritai. Leisti m- mažiausia funkcijos reikšmė f (x) diapazone nuo X prieš ( x + h), a M- didžiausia šios funkcijos reikšmė tame pačiame intervale. Tada ploto padidėjimas einant nuo Xį ( x + h) turi būti tarp dviejų stačiakampių sričių (17 pav.). Abiejų stačiakampių pagrindai yra vienodi h... Mažesnis stačiakampis turi aukštį m ir plotas mh, atitinkamai didesnis, M ir Mh... Sklype plotas prieš X(18 pav.) matyti, kad abscisei pasikeitus h, ordinatės (t. y. ploto) vertė padidinama suma, esančia tarp mh ir Mh... Sekantinis nuolydis šioje diagramoje yra tarp m ir M... kas atsitinka kada h linkęs į nulį? Jei funkcijos grafikas y = f(x) yra tęstinis (t. y. jame nėra nutrūkimų), tada M, ir m linkęs į f(x). Todėl nuolydis Aў ( x) ploto sklypas kaip funkcija nuo X yra lygus f(x). Būtent prie tokios išvados ir reikėjo prieiti.

Leibnicas pasiūlė plotą po kreive y = f(x) nuo 0 iki a paskirtis

Taikant griežtą požiūrį, šis vadinamasis apibrėžtas integralas turi būti apibrėžtas kaip tam tikrų sumų riba, kaip Wallis. Atsižvelgiant į aukščiau pateiktą rezultatą, aišku, kad šis integralas yra apskaičiuojamas, jei galime rasti tokią funkciją A(x), kuris išnyksta X= 0 ir turi išvestinę Aў ( x) lygus f (x). Tokios funkcijos radimas paprastai vadinamas integravimu, nors tikslingiau būtų šią operaciją vadinti antidiferenciacija, tai reiškia, kad ji tam tikra prasme yra atvirkštinė diferenciacijai. Polinomo atveju integravimas yra nesudėtingas. Pavyzdžiui, jei

kurią lengva patikrinti diferencijuojant A(x).

Norėdami apskaičiuoti plotą A 1 po kreive y = 1 + x + x 2/2, esantis tarp ordinačių 0 ir 1, mes tiesiog rašome

ir pakeičiant X= 1, gauname A 1 = 1 + 1/2 + 1/6 = 5/3. Kvadratas A(x) nuo 0 iki 2 yra lygus A 2 = 2 + 4/2 + 8/6 = 16/3. Kaip matyti iš fig. 19, plotas tarp 1 ir 2 ordinačių yra A 2 – A 1 = 11/3. Paprastai jis rašomas kaip apibrėžtas integralas

Apimtys.

Panašus samprotavimas leidžia stebėtinai paprasta apskaičiuoti apsisukimų kūnų tūrį. Parodykime tai rutulio tūrio apskaičiavimo pavyzdžiu – dar vieną klasikinę problemą, kurią senovės graikai, naudodami jiems žinomus metodus, sugebėjo išspręsti labai sunkiai.

Pasukite plokštumos dalį, esančią per ketvirtį spindulio apskritimo r, 360° kampu aplink ašį X... Dėl to gauname puslankį (20 pav.), kurio tūrį žymime V(x). Būtina nustatyti kursą, kuriuo V(x) didėjant x... Pereinama nuo XĮ X + h, nesunku patikrinti, ar garsumo padidėjimas yra mažesnis už garsumą p(r 2 – x 2)h apskrito cilindro spindulys ir aukštis h, ir daugiau nei apimtis p[r 2 – (x + h) 2 ]h cilindro spindulys ir aukštis h... Todėl funkcijos grafike V(x) sekanto nuolydis yra tarp p(r 2 – x 2) ir p[r 2 – (x + h) 2]. Kada h linkęs į nulį, nuolydis linkęs

At x = r mes gauname

pusrutulio tūriui, taigi 4 p r 3/3 viso rutulio tūrio.

Panašus metodas leidžia rasti kreivių ilgius ir lenktų paviršių plotus. Pavyzdžiui, jei a(x) - arkos ilgis PR pav. 21, tada mūsų užduotis yra apskaičiuoti aў( x). Euristiniame lygmenyje mes naudojame triuką, leidžiantį nesinaudoti įprastu perėjimu iki ribos, kuri būtina norint tiksliai įrodyti rezultatą. Tarkime, kad funkcijos kitimo greitis a(x) taške R yra toks pat, koks būtų, jei kreivė būtų pakeista jos liestine PT taške P... Bet iš pav. 21 galima tiesiogiai matyti žengiant h taško dešinėje arba kairėje X kartu RT prasmė a(x) keičiasi į

Todėl funkcijos kitimo greitis a(x) yra

Norėdami rasti pačią funkciją a(x), tereikia integruoti išraišką dešinėje lygybės pusėje. Pasirodo, daugumą funkcijų sunku integruoti. Todėl integralinio skaičiavimo metodų kūrimas sudaro didelę matematinės analizės dalį.

Antidariniai.

Kiekviena funkcija, kurios išvestinė yra lygi tam tikrai funkcijai f(x), vadinamas antidariniu (arba primityvu). f(x). Pavyzdžiui, X 3/3 yra funkcijos antidarinys X 2, nuo ( x 3/3) ў = x 2. Žinoma X 3/3 nėra vienintelis funkcijos antidarinys X 2 nuo x 3 /3 + C taip pat yra vedinys X 2 bet kuriai konstantai SU... Tačiau toliau mes sutiksime praleisti tokias priedų konstantas. Apskritai

kur n yra teigiamas sveikasis skaičius, nes ( x n + 1/(n+ 1)) ў = x n... Santykis (1) galioja dar bendresne prasme, jei n pakeisti bet kuriuo racionaliu skaičiumi k išskyrus -1.

Savavališka antiderivatinė funkcija tam tikrai funkcijai f(x) paprastai vadinamas neapibrėžtuoju integralu f(x) ir pažymėkite kaip

Pavyzdžiui, nuo (nuodėmė x) ў = cos x, formulė galioja

Daugeliu atvejų, kai yra tam tikros funkcijos neapibrėžto integralo formulė, ją galima rasti daugelyje plačiai paskelbtų neapibrėžtų integralų lentelių. Elementariųjų funkcijų integralai yra lentelės formos (tai laipsniai, logaritmai, eksponentinė funkcija, trigonometrinės funkcijos, atvirkštinės trigonometrinės funkcijos, taip pat jų baigtinės kombinacijos, gautos naudojant sudėties, atimties, daugybos ir dalybos operacijas). Naudodami lentelių integralus galite apskaičiuoti sudėtingesnių funkcijų integralus. Yra daug būdų, kaip apskaičiuoti neapibrėžtus integralus; labiausiai paplitęs iš jų yra kintamojo pakeitimo arba pakeitimo metodas. Tai susideda iš to, kad jei norime pakeisti neapibrėžtą integralą (2) x dėl tam tikros diferencijuojamos funkcijos x = g(u), kad integralas nesikeistų, būtina x pakeistas gў ( u)du... Kitaip tariant, lygybė

(2 pakaitalas x = u, iš kur 2 dx = du).

Štai dar vienas integravimo būdas – integravimo dalimis metodas. Jis pagrįstas jau žinoma formule

Integravus kairę ir dešinę puses ir atsižvelgiant į tai

Ši formulė vadinama integravimo dalimis formule.

Pavyzdys 2. Būtina rasti. Kadangi cos x= (nuodėmė x) ў, mes galime tai parašyti

Nuo (5), nustatymas u = x ir v= nuodėmė x, mes gauname

Ir nuo tada (–cos x) ў = nuodėmė x randame, kad ir

Reikia pabrėžti, kad apsiribojome tik labai trumpu įvadu į labai platų dalyką, kuriame sukaupta daugybė šmaikščių technikų.

Dviejų kintamųjų funkcijos.

Dėl kreivės y = f(x) svarstėme dvi užduotis.

1) Raskite kreivės liestinės nuolydį tam tikrame taške. Ši problema išspręsta apskaičiuojant išvestinės priemonės vertę fў ( x) nurodytame taške.

2) Raskite plotą po kreive virš ašies segmento X apribotas vertikaliomis linijomis X = a ir X = b... Ši problema išspręsta apskaičiuojant apibrėžtąjį integralą.

Kiekviena iš šių problemų turi analogą paviršiaus atveju z = f(x,y).

1) Raskite paviršiaus liestinės plokštumą tam tikrame taške.

2) Raskite tūrį žemiau paviršiaus virš plokštumos dalies hu apribotas kreivės SU, o iš šono – statmenai plokštumai xy einančios per ribinės kreivės taškus SU (cm... ryžių. 22).

Toliau pateikti pavyzdžiai parodo, kaip šios užduotys atliekamos.

Pavyzdys 4. Raskite paviršiaus liestinės plokštumą

taške (0,0,2).

Plokštuma apibrėžiama, jei pateiktos dvi joje esančios susikertančios tiesės. Viena iš šių eilučių ( l 1) įlipame į lėktuvą xz (adresu= 0), antrasis ( l 2) – plokštumoje yz (x = 0) (cm... ryžių. 23).

Visų pirma, jei adresu= 0, tada z = f(x,0) = 2 – 2x – 3x 2. Išvestinė atžvilgiu Xžymimas fў x(x,0) = –2 – 6x, adresu X= 0 reikšmė –2. Tiesiai l 1 pateikta lygtimis z = 2 – 2x, adresu= 0 – liestinė SU 1, paviršiaus susikirtimo su plokštuma linijos adresu= 0. Panašiai, jei X= 0, tada f(0,y) = 2 – y – y 2, ir išvestinė, susijusi su adresu turi formą

Nes fў y(0,0) = –1, kreivė SU 2 - paviršiaus susikirtimo su plokštuma linija yz- turi liestinę l 2 pateiktos lygtyse z = 2 – y, X= 0. Norimoje liestinės plokštumoje yra abi tiesės l 1 ir l 2 ir parašyta lygtimi

Tai yra plokštumos lygtis. Be to, gauname tiesias linijas l 1 ir l 2, nustatymas, atitinkamai, adresu= 0 ir X = 0.

Tai, kad (7) lygtis tikrai apibrėžia liestinės plokštumą, gali būti patikrinta euristiniu lygiu, jei pastebėsime, kad šioje lygtyje yra pirmosios eilės terminai, įtraukti į (6) lygtį, ir kad antrosios eilės terminai gali būti pavaizduoti forma -. Kadangi ši išraiška yra neigiama visoms reikšmėms X ir adresu, Be to X = adresu= 0, paviršius (6) yra visur žemiau plokštumos (7), išskyrus tašką R= (0,0,0). Galima sakyti, kad paviršius (6) taške yra išgaubtas į viršų R.

Pavyzdys 5. Raskite paviršiaus liestinės plokštumą z = f(x,y) = x 2 – y 2 iš pradžių 0.

Ant paviršiaus adresu= 0 mes turime: z = f(x,0) = x 2 ir fў x(x,0) = 2x... Ant SU 1, susikirtimo linijos, z = x 2. Taške O nuolydis yra fў x(0,0) = 0. Plokštumoje X= 0 mes turime: z = f(0,y) = –y 2 ir fў y(0,y) = –2y... Ant SU 2, sankirtos linijos, z = –y 2. Taške O kreivės nuolydis SU 2 yra lygus fў y(0,0) = 0. Kadangi liestinės į SU 1 ir SU 2 yra ašys X ir adresu, liestinės plokštuma, kurioje jie yra, yra plokštuma z = 0.

Tačiau šalia kilmės mūsų paviršius nėra vienoje liestinės plokštumos pusėje. Iš tiesų, kreivė SU 1 visur, išskyrus tašką 0, yra virš liestinės plokštumos ir kreivės SU 2 - atitinkamai žemiau jo. Paviršius kerta liestinės plokštumą z= 0 tiesiomis linijomis adresu = X ir adresu = –X... Teigiama, kad toks paviršius ištakoje turi balno tašką (24 pav.).

Daliniai dariniai.

Ankstesniuose pavyzdžiuose naudojome vedinius iš f (x,y) įjungta X ir pagal adresu... Dabar panagrinėkime tokius išvestinius dalykus plačiau. Pavyzdžiui, jei turime dviejų kintamųjų funkciją, F(x,y) = x 2 – xy, tada kiekviename taške galime apibrėžti du jo „dalinius išvestinius“, vieną išskirdami funkciją pagal X ir tvirtinimas adresu, kitą – diferencijuodami pagal adresu ir tvirtinimas X... Pirmasis iš šių darinių žymimas kaip fў x(x,y) arba ¶ f/¶ x; antra - kaip f f ў y... Jei abu mišrūs dariniai (pagal X ir adresu, įjungta adresu ir X) yra ištisiniai, tada ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x; mūsų pavyzdyje ¶ 2 f/¶ x¶ y= ¶ 2 f/¶ y¶ x = –1.

Dalinė išvestinė fў x(x,y) rodo funkcijos kitimo greitį f taške ( x,y) didėjimo kryptimi X, a fў y(x,y) Ar funkcijos kitimo greitis f kylančia kryptimi adresu... Funkcijų pasikeitimo greitis f taške ( X,adresu) tiesės, darančios kampą, kryptimi q su teigiama ašies kryptimi X, vadinamas funkcijos išvestine f link; jo reikšmė yra dviejų funkcijos dalinių išvestinių derinys f liestinės plokštumoje yra beveik lygus (mažoms dx ir dy) tikras pokytis z paviršiuje, tačiau diferencialą apskaičiuoti paprastai yra lengviau.

Formulė, kurią jau nagrinėjome iš kintamųjų keitimo metodo, žinomos kaip sudėtingos funkcijos arba grandinės taisyklės išvestinė, vienmačiu atveju, kai adresu priklauso nuo X, a X priklauso nuo t, turi tokią formą:

Dviejų kintamųjų funkcijoms panaši formulė yra:

Dalinės diferenciacijos sąvokas ir pavadinimus lengva apibendrinti iki aukštesnių matmenų. Visų pirma, jei paviršius netiesiogiai pateikiamas lygtimi f(x,y,z) = 0, paviršiaus liestinės plokštumos lygtis gali būti simetriškesnė: liestinės plokštumos taške ( x (x 2/4)], tada jis integruojamas X 0 prieš 1. Galutinis rezultatas – 3/4.

(10) formulė gali būti interpretuojama ir kaip vadinamasis dvigubas integralas, t.y. kaip elementariųjų „ląstelių“ tūrių sumos ribą. Kiekviena tokia ląstelė turi bazę D x D y ir aukštis, lygus paviršiaus aukščiui virš kurio nors stačiakampio pagrindo taško ( cm... ryžių. 26). Galima parodyti, kad abu požiūriai į (10) formulę yra lygiaverčiai. Dvigubi integralai naudojami svorio centrams ir daugeliui mechanikoje randamų momentų rasti.

Griežtesnis matematinio aparato pagrindimas.

Iki šiol skaičiavimo sąvokas ir metodus pristatėme intuityviu lygiu ir nedvejodami pasitelkėme geometrines figūras. Belieka trumpai panagrinėti griežtesnius metodus, kurie pasirodė XIX ir XX a.

XIX amžiaus pradžioje, pasibaigus „matematinės analizės kūrimo“ puolimo ir puolimo erai, išryškėjo jos pateisinimo klausimai. Abelio, Koši ir daugelio kitų iškilių matematikų darbuose buvo tiksliai apibrėžtos sąvokos „riba“, „nuolatinė funkcija“, „konverguojančios serijos“. Tai buvo būtina tam, kad matematinės analizės pagrindas būtų logiška tvarka, kad ji būtų patikima tyrimo priemonė. Išsamaus pagrindimo poreikis tapo dar akivaizdesnis po to, kai 1872 m. Weierstrassas atrado visur ištisines, bet niekur nesiskiriančias funkcijas (tokių funkcijų grafikas turi pertrauką kiekviename taške). Šis rezultatas padarė didžiulį įspūdį matematikams, nes aiškiai prieštaravo jų geometrinei intuicijai. Dar ryškesnis geometrinės intuicijos nepatikimumo pavyzdys buvo D. Peano sukonstruota ištisinė kreivė, visiškai užpildanti tam tikrą kvadratą, t.y. einantis per visus jo taškus. Iš šių ir kitų atradimų atsirado matematikos „aritmetizavimo“ programa, t.y. padaryti jį patikimesniu pagrįsti visas matematines sąvokas naudojant skaičiaus sąvoką. Beveik puritoniškas susilaikymas nuo aiškumo darbuose apie matematikos pagrindus turėjo istorinį pagrindimą.

Pagal šiuolaikinius loginio griežtumo kanonus neleistina kalbėti apie plotą po kreive. y = f(x) ir virš ašies segmento X, net f– ištisinė funkcija, prieš tai nenustačius tikslios sąvokos „plotas“ reikšmės ir nenustačius, kad tokiu būdu nustatytas plotas tikrai egzistuoja. Šią problemą 1854 metais sėkmingai išsprendė B. Riemannas, tiksliai apibrėžęs apibrėžtojo integralo sąvoką. Nuo tada sumavimo idėja, slypinti už apibrėžto integralo sąvokos, buvo daugelio gilių tyrimų ir apibendrinimų objektas. Dėl to šiandien galima suteikti reikšmę apibrėžtajam integralui, net jei integralas visur yra nenutrūkstamas. Naujos integracijos sampratos, prie kurių kūrimo labai prisidėjo A. Lebesgue'as (1875–1941) ir kiti matematikai, padidino šiuolaikinės matematinės analizės galią ir grožį.

Vargu ar būtų tikslinga gilintis į visas šias ir kitas sąvokas. Mes apsiribosime tik pateikdami griežtus ribos ir apibrėžtojo integralo apibrėžimus.

Apibendrinant, sakykime, kad matematinė analizė, būdama nepaprastai vertinga priemonė mokslininko ir inžinieriaus rankose, ir šiandien patraukia matematikų dėmesį kaip vaisingų idėjų šaltinis. Kartu atrodo, kad šiuolaikinė raida rodo, kad matematinė analizė vis labiau įsisavinama tokia dominuojanti XX amžiuje. tokios matematikos šakos kaip abstrakčioji algebra ir topologija.

Matematikoje visiškai neįmanoma išspręsti fizikinių uždavinių ar pavyzdžių, nežinant išvestinės ir jos skaičiavimo metodų. Išvestinė yra viena iš svarbiausių matematinės analizės sąvokų. Šiandienos straipsnį nusprendėme skirti šiai esminei temai. Kas yra išvestinė, kokia jos fizikinė ir geometrinė reikšmė, kaip apskaičiuoti funkcijos išvestinę? Visus šiuos klausimus galima sujungti į vieną: kaip suprasti išvestinę?

Geometrinė ir fizikinė išvestinės reikšmė

Tegul būna funkcija f (x) duota tam tikru intervalu (a, b) ... Taškai х ir х0 priklauso šiam intervalui. Pasikeitus x, pasikeičia ir pati funkcija. Argumento keitimas – skirtumas tarp jo vertybių x-x0 ... Šis skirtumas parašytas kaip delta x ir vadinamas argumentų prieaugiu. Funkcijos pakeitimas arba padidėjimas yra funkcijos reikšmių skirtumas dviejuose taškuose. Išvestinis apibrėžimas:

Funkcijos išvestinė taške yra funkcijos padidėjimo tam tikrame taške ir argumento prieaugio santykio riba, kai pastarasis linkęs į nulį.

Kitu atveju jis gali būti parašytas taip:

Kokia prasmė rasti tokią ribą? Ir štai kas:

funkcijos išvestinė taške yra lygi kampo tarp OX ašies ir funkcijos grafiko liestinės liestei taške.

Fizinė išvestinės reikšmė: kelio išvestinė laiko atžvilgiu lygi tiesinio judėjimo greičiui.

Iš tiesų, nuo mokyklos laikų visi žino, kad greitis yra privatus kelias. x = f (t) ir laikas t ... Vidutinis greitis per tam tikrą laikotarpį:

Norėdami sužinoti judėjimo greitį vienu metu t0 reikia apskaičiuoti ribą:

Pirma taisyklė: išimkite konstantą

Konstanta gali būti perkelta už išvestinės ženklo ribų. Be to, tai turi būti padaryta. Spręsdami matematikos pavyzdžius, laikykitės taisyklės - jei galite supaprastinti išraišką, būtinai supaprastinkite .

Pavyzdys. Apskaičiuokime išvestinę:

Antra taisyklė: funkcijų sumos išvestinė

Dviejų funkcijų sumos išvestinė yra lygi šių funkcijų išvestinių sumai. Tas pats pasakytina ir apie funkcijų skirtumo išvestinę.

Mes nepateiksime šios teoremos įrodymo, o apsvarstysime praktinį pavyzdį.

Raskite funkcijos išvestinę:

Trečia taisyklė: funkcijų sandaugos išvestinė

Dviejų diferencijuojamų funkcijų sandaugos išvestinė apskaičiuojama pagal formulę:

Pavyzdys: suraskite funkcijos išvestinę:

Sprendimas:

Čia svarbu pasakyti apie sudėtingų funkcijų išvestinių skaičiavimą. Sudėtinės funkcijos išvestinė yra lygi šios funkcijos išvestinės tarpinio argumento sandaugai ir tarpinio argumento išvestinei nepriklausomo kintamojo atžvilgiu.

Aukščiau pateiktame pavyzdyje mes atitinkame išraišką:

Šiuo atveju tarpinis argumentas yra 8 kartus didesnis už penktą laipsnį. Norėdami apskaičiuoti tokios išraiškos išvestinę, pirmiausia apskaičiuojame išorinės funkcijos išvestinę tarpinio argumento atžvilgiu, o tada padauginame iš tiesioginio tarpinio argumento išvestinės nepriklausomo kintamojo atžvilgiu.

Ketvirta taisyklė: dviejų funkcijų koeficiento išvestinė

Dviejų funkcijų dalinio išvestinės nustatymo formulė:

Mes bandėme jums papasakoti apie manekenų išvestinius produktus nuo nulio. Ši tema nėra tokia paprasta, kaip atrodo, todėl perspėkite: pavyzdžiuose dažnai yra spąstų, todėl būkite atsargūs skaičiuodami išvestines.

Jei turite klausimų šia ir kitomis temomis, galite susisiekti su studentų tarnyba. Per trumpą laiką padėsime išspręsti sunkiausią testą ir susidoroti su užduotimis, net jei dar niekada nedarėte išvestinių skaičiavimų.

Ant kurio išanalizavome paprasčiausius darinius, taip pat susipažinome su diferencijavimo taisyklėmis ir kai kuriomis išvestinių radimo technikomis. Taigi, jei nesate labai susipažinę su funkcijų išvestiniais arba kai kurie šio straipsnio punktai nėra visiškai aiškūs, pirmiausia perskaitykite aukščiau pateiktą pamoką. Prašau nusiteikti rimtai nuotaikai - medžiaga ne iš lengvųjų, bet vis tiek pasistengsiu ją pateikti paprastai ir prieinamai.

Praktikoje su kompleksinės funkcijos išvestine tenka susidurti labai dažnai, net sakyčiau, beveik visada, kai duodama užduotis surasti išvestines.

Lentelėje žiūrime į taisyklę (Nr. 5), kaip atskirti sudėtingą funkciją:

Supratimas. Visų pirma, atkreipkime dėmesį į įrašą. Čia mes turime dvi funkcijas – ir, be to, funkcija, vaizdžiai tariant, yra įterpta į funkciją. Tokio tipo funkcija (kai viena funkcija įdėta į kitą) vadinama sudėtinga funkcija.

Paskambinsiu funkcijai išorinė funkcija ir funkcija - vidinė (arba įdėta) funkcija.

! Šie apibrėžimai nėra teoriniai ir neturėtų būti įtraukti į galutinį užduočių planą. Aš naudoju neformalius posakius „išorinė funkcija“, „vidinė“ funkcija tik tam, kad jums būtų lengviau suprasti medžiagą.

Norėdami išsiaiškinti situaciją, apsvarstykite:

1 pavyzdys

Raskite funkcijos išvestinę

Po sinusu turime ne tik raidę „X“, o sveikojo skaičiaus išraišką, todėl iš lentelės išvestinės iš karto rasti nepavyks. Taip pat pastebime, kad čia neįmanoma taikyti pirmųjų keturių taisyklių, atrodo, kad skirtumas yra, bet faktas yra tas, kad negalima „išardyti“ sinuso:

Šiame pavyzdyje, jau iš mano paaiškinimų, intuityviai aišku, kad funkcija yra sudėtinga funkcija, o daugianomas yra vidinė funkcija (įdėjimas) ir išorinė funkcija.

Pirmas žingsnis, kuri turi būti atlikta ieškant kompleksinės funkcijos išvestinę, yra ta išsiaiškinti, kuri funkcija yra vidinė, o kuri išorinė.

Paprastų pavyzdžių atveju atrodo aišku, kad polinomas yra įdėtas po sinusu. Bet ką daryti, jei viskas nėra akivaizdu? Kaip tiksliai nustatyti, kuri funkcija yra išorinė, o kuri vidinė? Norėdami tai padaryti, siūlau naudoti šią techniką, kurią galima atlikti mintyse arba pagal juodraštį.

Įsivaizduokite, kad skaičiuotuvu turime apskaičiuoti išraiškos reikšmę (vietoj vieneto gali būti bet koks skaičius).

Ką skaičiuosime pirmiausia? Pirmiausia turėsite atlikti šį veiksmą:, todėl daugianomas bus vidinė funkcija:

Antra reikės rasti, todėl sinusas bus išorinė funkcija:

Po mūsų Išsiaiškinti su vidinėmis ir išorinėmis funkcijomis, laikas taikyti sudėtingos funkcijos diferencijavimo taisyklę .

Pradedame spręsti. Iš pamokos Kaip rasti išvestinę priemonę? prisimename, kad bet kurios išvestinės sprendinio dizainas visada prasideda taip - posakį įdedame skliausteliuose, o viršuje dešinėje darome brūkšnį:

Pirmas raskite išorinės funkcijos išvestinę (sinusą), pažiūrėkite į elementariųjų funkcijų išvestinių lentelę ir pastebėkite tai. Visos lentelės formulės yra taikomos, net jei "x" pakeičiamas sudėtinga išraiška, tokiu atveju:

Atkreipkite dėmesį, kad vidinė funkcija nepasikeitė, mes jo neliečiame.

Na, tai visiškai akivaizdu

Formulės taikymo rezultatas galutiniame projekte jis atrodo taip:

Pastovus veiksnys paprastai dedamas išraiškos pradžioje:

Jei kyla painiavos, užrašykite sprendimą ir dar kartą perskaitykite paaiškinimus.

2 pavyzdys

Raskite funkcijos išvestinę

3 pavyzdys

Raskite funkcijos išvestinę

Kaip visada, užrašome:

Išsiaiškinkime, kur turime išorinę funkciją, o kur – vidinę. Norėdami tai padaryti, pabandykite (protiškai arba juodraštyje) apskaičiuoti išraiškos reikšmę. Ką pirmiausia reikėtų padaryti? Visų pirma reikia apskaičiuoti, kam lygi bazė: tai reiškia, kad daugianomas yra vidinė funkcija:

Ir tik tada atliekamas eksponentas, todėl galios funkcija yra išorinė funkcija:

Pagal formulę , pirmiausia reikia rasti išorinės funkcijos išvestinę, šiuo atveju laipsnį. Lentelėje ieškome reikiamos formulės:. Dar kartą kartojame: bet kuri lentelės formulė galioja ne tik "x", bet ir sudėtingai išraiškai... Taigi kompleksinės funkcijos diferenciacijos taisyklės taikymo rezultatas Kitas:

Dar kartą pabrėžiu, kad imant išorinės funkcijos išvestinę, vidinė funkcija mums nesikeičia:

Dabar belieka rasti labai paprastą vidinės funkcijos išvestinį ir šiek tiek „šukuoti“ rezultatą:

4 pavyzdys

Raskite funkcijos išvestinę

Tai yra nepriklausomo sprendimo pavyzdys (atsakymas pamokos pabaigoje).

Kad būtų įtvirtintas kompleksinės funkcijos išvestinės supratimas, pateiksiu pavyzdį be komentarų, pabandykite tai išsiaiškinti patys, spėliokite, kur yra išorinė, o kur vidinė funkcija, kodėl taip buvo išspręstos užduotys?

5 pavyzdys

a) Raskite funkcijos išvestinę

b) Raskite funkcijos išvestinę

6 pavyzdys

Raskite funkcijos išvestinę

Čia mes turime šaknį, o norint atskirti šaknį, ji turi būti pavaizduota kaip laipsnis. Taigi pirmiausia pateikiame funkciją į diferencijavimui tinkamą formą:

Analizuodami funkciją, darome išvadą, kad trijų narių suma yra vidinė funkcija, o eksponentiškumas yra išorinė funkcija. Taikome kompleksinės funkcijos diferenciacijos taisyklę :

Laipsnis vėl vaizduojamas kaip radikalas (šaknis), o vidinės funkcijos išvestinei taikome paprastą sumos diferencijavimo taisyklę:

Paruošta. Taip pat galite suvesti išraišką į bendrą vardiklį skliausteliuose ir užrašyti viską viena trupmena. Žinoma, gražu, bet kai gaunami gremėzdiški ilgi vediniai, geriau to nedaryti (lengva susipainioti, padaryti bereikalingą klaidą, o mokytojui bus nepatogu tikrinti).

7 pavyzdys

Raskite funkcijos išvestinę

Tai yra nepriklausomo sprendimo pavyzdys (atsakymas pamokos pabaigoje).

Įdomu pastebėti, kad kartais vietoj sudėtingos funkcijos diferencijavimo taisyklės galima naudoti koeficiento diferencijavimo taisyklę. , tačiau toks sprendimas atrodys neįprastai kaip iškrypimas. Štai tipiškas pavyzdys:

8 pavyzdys

Raskite funkcijos išvestinę

Čia galite naudoti koeficiento diferencijavimo taisyklę , bet daug pelningiau išvestinę rasti taikant sudėtingos funkcijos diferenciacijos taisyklę:

Paruošiame funkciją diferencijuoti - minusą perkeliame už išvestinės ženklo ribų, o kosinusą keliame iki skaitiklio:

Kosinusas yra vidinė funkcija, eksponentiškumas yra išorinė funkcija.
Mes naudojame savo taisyklę :

Raskite vidinės funkcijos išvestinę, iš naujo nustatykite kosinusą žemyn:

Paruošta. Nagrinėjamame pavyzdyje svarbu nesupainioti ženkluose. Beje, pabandykite tai išspręsti taisykle , atsakymai turi sutapti.

9 pavyzdys

Raskite funkcijos išvestinę

Tai yra nepriklausomo sprendimo pavyzdys (atsakymas pamokos pabaigoje).

Iki šiol nagrinėjome atvejus, kai turėjome tik vieną sudėtingos funkcijos priedą. Praktinėse užduotyse dažnai galima rasti išvestinių, kur, kaip lėlytės, viena kitos viduje, vienu metu įdėtos 3 ar net 4-5 funkcijos.

10 pavyzdys

Raskite funkcijos išvestinę

Supraskime šios funkcijos priedus. Bandoma įvertinti išraišką naudojant testo reikšmę. Kaip suskaičiuotume skaičiuotuvą?

Pirmiausia turite rasti, o tai reiškia, kad arcsinusas yra giliausias lizdas:

Tada šis vieneto arcsinusas turėtų būti padalytas kvadratu:

Ir galiausiai pakelkite 7 į galią:

Tai reiškia, kad šiame pavyzdyje turime tris skirtingas funkcijas ir du priedus, o vidinė funkcija yra arcsinė, o tolimiausia funkcija yra eksponentinė funkcija.

Pradedame spręsti

Pagal taisyklę pirmiausia reikia paimti išorinės funkcijos išvestinę. Žiūrime į išvestinių lentelę ir randame eksponentinės funkcijos išvestinę: Vienintelis skirtumas yra tas, kad vietoj "x" turime sudėtingą išraišką, kuri nepaneigia šios formulės galiojimo. Taigi, kompleksinės funkcijos diferenciacijos taisyklės taikymo rezultatas Kitas.