Математикалық талдау.

Шеберхана.

Мамандығы бойынша университет студенттеріне:

«Мемлекеттік және муниципалды басқару»

Т.З. Павлова

Колпашево 2008 ж

1-тарау. Талдауға кіріспе

1.1 Функциялар. Жалпы қасиеттер

1.2 Шектер теориясы

1.3 Функцияның үздіксіздігі

2.1 Туындының анықтамасы

2.4 Функцияларды зерттеу

2.4.1 Толық функцияны зерттеу жоспары

2.4.2 Функцияларды зерттеу мысалдары

2.4.3. Функцияның сегменттегі ең үлкен және ең кіші мәні

2.5 Лопитал ережесі

3.1 Анықталмаған интеграл

3.1.1 Анықтамалар мен қасиеттер

3.1.2 Интегралдар кестесі

3.1.3 Интеграцияның негізгі әдістері

3.2 Анықталған интеграл

3.2.2 Анықталған интегралды есептеу әдістері

4-тарау. Бірнеше айнымалылардың функциялары

4.1 Негізгі ұғымдар

4.2 Бірнеше айнымалы функциялардың шектері мен үздіксіздігі

4.3.3 Толық дифференциал және оны жуықтап есептеуге қолдану

5-тарау. Классикалық оңтайландыру әдістері

6.1 Утилита функциясы.

6.2 Емдеу сызықтары

6.3 Бюджет жиынтығы

Үйге тапсырма

1.1 Функциялар. Жалпы қасиеттер

Сандық функция нақты сандардың D жиынында анықталады, егер айнымалының әрбір мәні y айнымалысының кейбір нақты анықталған нақты мәнімен байланысты болса, мұндағы D — функцияның анықталу облысы.

Функцияның аналитикалық көрінісі:

анық:;

жанама түрде:;

параметрлік түрде:

анықтау саласындағы әртүрлі формулалар:

Қасиеттер.

Жұп функциясы:. Мысалы, функциясы жұп, өйткені ...

Тақ функция: ... Мысалы, функция тақ, өйткені ...

Периодтық функция: , мұндағы T – функцияның периоды,. Мысалы, тригонометриялық функциялар.

Монотоникалық функция. Қандай да бір анықтау облысы үшін - функция өсуде, - кемуде. Мысалы, - өсу, және - кему.

Шектеулі функция. Егер М саны болса, онда. Мысалы, функциялар және, өйткені .

Мысал 1. Функциялардың анықталу облысын табыңыз.

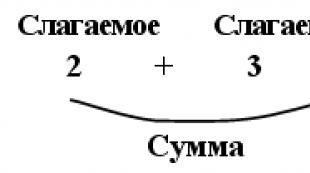
+ 2 – 3 +

1.2 Шектер теориясы

Анықтама 1... Функцияның шегі b саны, егер кез келген (- ерікті аз оң сан) үшін аргументтің осындай мәнін табуға болады, одан бастап теңсіздік қанағаттандырылады.

Белгі:.

Анықтама 2... Функцияның шегі b саны, егер кез келген үшін (еркін аз оң сан болса) теңсіздікті қанағаттандыратын x-тің барлық мәндері үшін теңсіздік орындалатындай оң сан болса.

Белгі:.

Анықтама 3.Функция немесе үшін шексіз аз деп аталады, егер немесе.

Қасиеттер.

1. Шексіз аз шамалардың ақырлы санының алгебралық қосындысы шексіз аз шама.

2. Шексіз аз шаманың шектелген функциясына көбейтіндісі (тұрақты, басқа шексіз аз шама) шексіз аз шама.

3. Шексіз аз шаманы шегі нөлге тең емес функцияға бөлудің бөлімі шексіз аз шама.

Анықтама 4.Функция шексіз үлкен, егер деп аталады.

Қасиеттер.

1. Шексіз үлкен шаманың шегі нөлге тең емес функцияның көбейтіндісі шексіз үлкен шама.

2. Шексіз үлкен шама мен шектелген функцияның қосындысы шексіз үлкен шама.

3. Шексіз үлкен шаманы шегі бар функцияға бөлудің бөлімі шексіз үлкен шама.

Теорема.(Шексіз аз шама мен шексіз үлкен шама арасындағы қатынас.) Егер функция () нүктесінде шексіз аз болса, онда функция () нүктесінде шексіз үлкен шама болады. Және керісінше, егер функция () нүктесінде шексіз үлкен болса, онда функция () нүктесінде шексіз кіші болады.

Шекті теоремалар.

1. Функцияның бірден артық шегі болуы мүмкін емес.

2. Бірнеше функциялардың алгебралық қосындысының шегі осы функциялардың шектерінің алгебралық қосындысына тең:

3. Бірнеше функциялардың көбейтіндісінің шегі осы функциялардың шектерінің көбейтіндісіне тең:

4. Дәреженің шегі шектің дәрежесіне тең:

5. Бөлгіш шегі бар болса, бөлгіш шегі шектердің бөліміне тең:

.

6. Бірінші тамаша шек.

Салдары:

7. Екінші керемет шек:

Салдары:

Эквивалентті шексіз аз мәндер үшін:

Лимиттерді есептеу.

Шектерді есептеу кезінде шектер туралы негізгі теоремалар, үздіксіз функциялардың қасиеттері және осы теоремалар мен қасиеттерден туындайтын ережелер қолданылады.

1-ереже.Осы нүктеде үздіксіз болатын функция нүктесіндегі шегін табу үшін оның шектік мәнін функцияда х аргументінің орнына шектік таңбаның астына қою керек.

Мысал 2. Табыңыз

2-ереже.Бөлшектің шегін тапқанда бөлгіштің шегі нөлге, ал алымының шегі нөлге тең емес болса, онда мұндай функцияның шегі болады.

Мысал 3. Табыңыз

3-ереже.Бөлшектің шегін тапқанда бөлгіштің шегі тең болса, ал алымының шегі нөлден өзгеше болса, онда мұндай функцияның шегі нөлге тең болады.

Мысал 4. Табыңыз

Көбінесе аргумент үшін шекті мәнді ауыстыру сияқты анықталмаған өрнектерге әкеледі

.

Бұл жағдайларда функцияның шегін табу белгісіздікті ашу деп аталады. Белгісіздікті ашу үшін шекке барар алдында бұл өрнекті түрлендіру қажет. Белгісіздіктерді ашу үшін әртүрлі әдістер қолданылады.

4-ереже... Типтің белгісіздігі бағыныңқы функцияны түрлендіру арқылы ашылады, осылайша алым мен бөлгіште шегі нөлге тең болатын көбейткішті таңдау үшін және сол арқылы бөлшекті азайтып, бөлімнің шегін табу керек. Ол үшін алым мен бөлгіш көбейтіледі немесе алым мен бөлгішке жалғанатын өрнектерге көбейтіледі.

5-ереже.Егер сублимиттік өрнекте тригонометриялық функциялар болса, онда бірінші керемет шек түрдің белгісіздігін көрсету үшін пайдаланылады.

.

6-ереже... Пішіннің белгісіздігін анықтау үшін ішкі шекті бөлшектің алымы мен бөлімін аргументтің ең жоғары дәрежесіне бөлу керек, содан кейін бөліктің шегін табу керек.

Ықтимал нәтижелер:

1) қажетті шек алым мен бөлгіш аргументінің ең жоғары дәрежелеріндегі коэффициенттердің қатынасына тең, егер бұл дәрежелер бірдей болса;

2) алым аргументінің дәрежесі бөлгіштің аргументінің дәрежесінен жоғары болса, шек шексіздікке тең;

3) алым аргументінің дәрежесі бөлгіштің аргументінің дәрежесінен төмен болса, шек нөлге тең болады.

а)

бері

Дәрежелер тең, бұл шек жоғары дәрежелердегі коэффициенттердің қатынасына тең, яғни. ...

б)

Алым, бөлгіш дәрежесі 1-ге тең, бұл шекті білдіреді

v)

Бөлгіштің дәрежесі 1-ге тең, ал бөлгіштің дәрежесі 0-ге тең.

7-ереже... Пішіннің белгісіздігін ашу үшін ішкі шекті бөлшектің алымы мен бөлімін жалғаулық өрнекке көбейту керек.

10-мысал.

8-ереже... Екінші керемет шек және оның салдары түрдің белгісіздігін ашу үшін қолданылады.

Мұны дәлелдеуге болады

11-мысал.

12-мысал.

13-мысал.

9-ереже... Сублиминалды функциясы шексіз азды қамтитын белгісіздіктерді ашқан кезде осы шексіздіктердің шегін ауыстыру қажет. оларға эквивалентті шексіз аз элементтердің шектері бойынша.

14-мысал.

15-мысал.

10-ереже. L'Hopital ережесі (2.6 қараңыз).

1.3 Функцияның үздіксіздігі

Аргумент ретінде функцияның шегі a-ға ұмтылатын болса, бар болса және осы нүктедегі функцияның мәніне тең болса, функция нүктеде үздіксіз болады.

Эквивалентті шарттар:

1. ;

3.

Үзіліс нүктесінің жіктелуі:

бірінші түрдегі үзіліс

Бір реттік – бір жақты шектеулер бар және тең;

Өлім (секіру) – бір жақты шектеулер тең емес;

екінші түрдегі үзіліс: нүктедегі функцияның шегі жоқ.

Мысал 16. Функцияның нүктедегі үзіліссіздігінің сипатын анықтаңыз немесе осы нүктедегі функцияның үзіліссіздігін дәлелдеңіз.

өйткені функция анықталмаған, сондықтан бұл нүктеде ол үздіксіз емес. Өйткені және сәйкесінше, , онда бірінші түрдегі алынбалы үзіліс нүктесі.

б)

(a) тапсырмасымен салыстырғанда функция нүктеде кеңейтілген , демек, бұл функция осы нүктеде үздіксіз.

Функция анықталмаған кезде;

.

Өйткені бір жақты шектердің бірі шексіз болса, онда ол екінші түрдегі үзілу нүктесі болып табылады.

2-тарау. Дифференциалдық есептеулер

2.1 Туындының анықтамасы

Туынды анықтамасы

Берілген функцияның туындысы деп аргумент өсімі нөлге ұмтылған кездегі функция өсімінің сәйкес аргумент өсіміне қатынасының шегін айтады:

Немесе .

Туындының механикалық мағынасы – функцияның өзгеру жылдамдығы. Туындының геометриялық мағынасы функция графигіне жанаманың көлбеу бұрышының тангенсі:

2.2 Дифференциацияның негізгі ережелері

Аты	Функция	Туынды
Тұрақты көбейткішке көбейту
Екі функцияның алгебралық қосындысы
Екі функцияның туындысы
Жеке екі функция
Күрделі функция

Негізгі элементар функциялардың туындылары

P / p No.	Функция атауы	Функция және оның туындысы
1	тұрақты
2	қуат функциясы ерекше жағдайлар
3	көрсеткіштік функция жеке оқиға
4	логарифмдік функция жеке оқиға
5	тригонометриялық функциялар
6	кері тригонометриялық

б)

2.3 Жоғары ретті туынды құралдар

Функцияның екінші ретті туындысы

Функцияның екінші ретті туындысы:

18-мысал.

а) Функцияның екінші ретті туындысын табыңыз.

Шешім. Алдымен бірінші ретті туындыны табайық .

Бірінші ретті туындының туындысын алайық.

Мысал 19. Функцияның үшінші ретті туындысын табыңыз.

2.4 Функцияларды зерттеу

2.4.1 Толық функцияны зерттеу жоспары:

Толық функционалдық оқу жоспары:

1. Бастауыш зерттеу:

Мәндердің доменін және диапазонын табыңыз;

Жалпы қасиеттерін табыңыз: паритет (тақтық), кезеңділік;

Координаталық осьтермен қиылысу нүктелерін табу;

Тұрақтылық аудандарын анықтаңыз.

2. Асимптоталар:

Тік асимптоталарды табыңыз, егер;

Көлбеу асимптоталарды табыңыз:.

Егер қандай да бір сан болса, онда – көлденең асимптоталар.

3. Зерттеуді қолдану:

Сыни нүктелерді табыңыз, сол. бар немесе жоқ нүктелер;

Арту аралықтарын анықтаңыз, сол. интервалдар, олардағы және кемімелі функциялар -;

Экстремалды анықтаңыз: өту кезінде таңбасын «+»-ден «-ге» өзгертетін нүктелер максимум нүктелер, «-»-ден «+»-ке дейін – минимум.

4. Зерттеуді қолдану:

Қай немесе жоқ нүктелерді табыңыз;

Дөңес аймақтарды табыңыз, яғни. ойыстардың болатын аралықтары;

Иілу нүктелерін табыңыз, яғни. өту кезінде белгісі өзгеретін нүктелер.

1. Зерттеудің жеке элементтері табылғанына қарай біртіндеп графикке салынады.

2. Функцияның графигін құруда қиындықтар туындаса, онда функцияның мәндері кейбір қосымша нүктелерде табылады.

3. Зерттеудің мақсаты – функцияның мінез-құлық сипатын сипаттау. Сондықтан нақты график емес, табылған элементтер (экстремалар, иілу нүктелері, асимптоталар және т.б.) анық көрсетілген оның жуықтауы құрастырылады.

4. Жоғарыда аталған жоспарды қатаң сақтау қажет емес; функция әрекетінің сипаттамалық элементтерін назардан тыс қалдырмау маңызды.

2.4.2 Функцияны зерттеу мысалдары:

1)

2) функциясы тақ:

.

3) Асимптоталар.

- тік асимптоталар, өйткені

Қиғаш асимптот.

5)

- иілу нүктесі.

2) функциясы тақ:

3) Асимптоталар: Тік асимптоталар жоқ.

Көлбеу:

- қиғаш асимптоталар

4) - функция артады.

- иілу нүктесі.

Бұл функцияның схемалық диаграммасы:

2) Жалпы функция

3) Асимптоталар

- қиғаш асимптоталар жоқ

- горизонталь асимптота at

- иілу нүктесі

Бұл функцияның схемалық диаграммасы:

2) Асимптоталар.

- тік асимптота, өйткені

- қиғаш асимптоталар жоқ

, - көлденең асимптота

Бұл функцияның схемалық диаграммасы:

2) Асимптоталар

- вертикальды асимптот, бері

- қиғаш асимптоталар жоқ

, - көлденең асимптота

3) - аралықтардың әрқайсысында функция азаяды.

Бұл функцияның схемалық диаграммасы:

Сегменттегі функцияның ең үлкен және ең кіші мәнін табу үшін диаграмманы пайдалануға болады:

1. Функцияның туындысын табыңыз.

2. Функцияның бар немесе жоқ критикалық нүктелерін табыңыз.

3. Берілген кесіндіге және оның ұштарына жататын критикалық нүктелердегі функцияның мәнін тауып, олардың ең үлкені мен ең кішісін таңдаңыз.

Мысал. Берілген кесіндідегі функцияның ең кіші және ең үлкен мәнін табыңыз.

25. арасында

2) - сыни нүктелер

26. арасында.

Туынды бұл жерде жоқ, бірақ 1 бұл интервалға жатпайды. Функция аралықта азаяды, яғни ең үлкен мән жоқ, бірақ ең кіші мән бар.

2.5 Лопитал ережесі

Теорема. Екі шексіз аз немесе шексіз үлкен функциялардың қатынасының шегі, егер соңғысы көрсетілген мағынада бар болса, олардың туындыларының қатынасының шегіне тең (ақырлы немесе шексіз).

Анау. түріндегі белгісіздіктерді ашқанда немесе мына формуланы қолдануға болады:

.

27.

3-тарау. Интегралдық есептеулер

3.1 Анықталмаған интеграл

3.1.1 Анықтамалар мен қасиеттер

Анықтама 1. Функция if үшін қарсы туынды деп аталады.

Анықтама 2. f (x) функциясының анықталмаған интегралы - осы функция үшін барлық қарсы туындылардың жиыны.

Белгіленуі: , мұндағы c - ерікті тұрақты.

Анықталмаған интегралдық қасиеттер

1. Анықталмаған интегралдың туындысы:

2. Анықталмаған интегралдың дифференциалы:

3. Дифференциалдың анықталмаған интегралы:

4. Екі функцияның қосындысының (айырымы) анықталмаған интегралы:

5. Тұрақты көбейткішті анықталмаған интеграл таңбасынан ары жылжыту:

3.1.2 Интегралдар кестесі

.1.3 Интеграцияның негізгі әдістері

1. Анықталмаған интегралдың қасиеттерін қолдану.

29-мысал.

2. Дифференциалдық белгінің астына әкелу.

30-мысал.

3. Айнымалыларды ауыстыру әдісі:

а) интегралда ауыстыру

қайда - бастапқыға қарағанда интегралдау оңай функция; - функцияға кері функция; функцияның қарсы туындысы болып табылады.

31-мысал.

б) түрдегі интегралды ауыстыру:

32-мысал.

33-мысал.

4. Бөлшектері бойынша интеграциялау әдісі:

34-мысал.

35-мысал.

Интегралды бөлек алайық

Біздің интегралымызға оралайық:

3.2 Анықталған интеграл

3.2.1 Анықталған интеграл түсінігі және оның қасиеттері

Анықтама.Қандай да бір интервалда үздіксіз функция берілсін. Оның графигін құрастырайық.

Жоғарыдан қисық сызықпен, солға және оңға түзу сызықтармен және төменнен а және b нүктелері арасында абсцисса осінің кесіндісімен шектелген фигураны қисық трапеция деп атайды.

S – аудан – қисық трапеция.

Аралықты нүктелермен бөліп, мынаны алыңыз:

Интегралдық қосынды:

Анықтама. Анықталған интеграл – интегралдық қосындының шегі.

Анықталған интегралдық қасиеттер:

1. Тұрақты коэффициентті интегралдық таңбадан шығаруға болады:

2. Екі функцияның алгебралық қосындысының интегралы осы функциялардың интегралдарының алгебралық қосындысына тең:

3. Егер интегралдау кесіндісі бөліктерге бөлінсе, онда бүкіл кесіндідегі интеграл пайда болған бөліктердің әрқайсысы үшін интегралдардың қосындысына тең болады, яғни кез келген a, b, c үшін:

4. Егер сегментте болса, онда

5. Интегралдың таңбасы өзгерген кезде интегралдау шегін ауыстыруға болады:

6.

7. Нүктедегі интеграл 0-ге тең:

8.

9. («орташа туралы») y = f (x) функциясы интегралдансын. Содан кейін , мұндағы, f (c) – f (x) мәнінің орташа мәні:

10. Ньютон-Лейбниц формуласы

,

мұндағы F (x) – f (x) үшін антитуынды.

3.2.2 Анықталған интегралды есептеу әдістері.

1. Тікелей интеграция

35-мысал.

а)

б)

v)

д)

2. Анықталған интегралдық таңба астындағы айнымалылардың өзгеруі .

36-мысал.

2. Анықталған интегралдағы бөліктер бойынша интегралдау .

37-мысал.

а)

б)

д)

3.2.3 Анықталған интегралдың қолданылуы

Сипаттама	Функция түрі	Формула
	декарттық координаттарда
қисық сектор ауданы	полярлық координаттарда
қисық трапеция аймағы	параметрлік формада
доғаның ұзындығы	декарттық координаттарда
доғаның ұзындығы	полярлық координаттарда
доғаның ұзындығы	параметрлік формада
дене көлемі айналу	декарттық координаттарда
берілген көлденеңімен дене көлемі көлденең қима

Мысал 38. Сызықтармен шектелген фигураның ауданын есептеңіз: және .

Шешімі:Осы функциялардың графиктерінің қиылысу нүктелерін табайық. Ол үшін функцияларды теңестіріп, теңдеуді шешеміз

Сонымен, қиылысу нүктелері және.

Формула арқылы фигураның ауданын табамыз

.

Біздің жағдайда

Жауабы: ауданы тең (шаршы бірлік).

4.1 Негізгі ұғымдар

Анықтама. Егер қандай да бір ережеге сәйкес z айнымалысының бір немесе бірнеше мәні белгілі жиыннан тәуелсіз сандардың әрбір жұбына тағайындалса, онда z айнымалысы екі айнымалының функциясы деп аталады.

Анықтама. z функциясының анықталу облысы z функциясы бар жұптар жиыны болып табылады.

Екі айнымалы функцияның анықталу облысы – Oxy координаталық жазықтықтағы нүктелер жиыны. z-координатасы қолданбалы деп аталады, содан кейін функцияның өзі Е 3 кеңістігінде қандай да бір бет ретінде бейнеленеді. Мысалы:

Мысал 39. Функцияның анықталу облысын табыңыз.

а)

Оң жақтағы өрнек тек үшін мағыналы. Демек, бұл функцияның анықталу облысы координаталар басының центрінде орналасқан R радиусы шеңбердің ішінде және шекарасында жатқан барлық нүктелердің жиыны болып табылады.

Бұл функцияның анықталу облысы түзу нүктелерін қоспағанда, жазықтықтың барлық нүктелері болып табылады, яғни. координаталық осьтер.

Анықтама. Функция деңгейінің сызықтары - форманың теңдеулерімен сипатталған координаталық жазықтықтағы қисықтардың тобы.

Мысал 40. Функция деңгейінің сызықтарын табыңыз .

Шешім. Берілген функцияның деңгей сызықтары теңдеумен сипатталған жазықтықтағы қисықтардың тобы болып табылады

Соңғы теңдеу радиусы О 1 (1, 1) нүктесінде орналасқан шеңберлер тобын сипаттайды. Осы функциямен сипатталған революция беті (параболоид) осьтен алыстаған сайын «тік» болады, ол х = 1, у = 1 теңдеулерімен берілген. (4-сурет).

4.2 Бірнеше айнымалы функциялардың шектері мен үздіксіздігі.

1. Шектер.

Анықтама. А саны функцияның шегі деп аталады, өйткені нүкте нүктеге ұмтылады, егер әрбір еркін аз сан үшін кез келген нүкте үшін шарт ақиқат болатындай сан болса және шарт ... Олар жазады: .

Мысал 41. Шектерді табыңыз:

анау. шектеу тәуелді, демек, ол жоқ.

2. Үздіксіздік.

Анықтама. Нүкте функцияның анықталу облысына тиесілі болсын. Сонда функция егер нүктеде үздіксіз деп аталады

(1)

оның үстіне нүкте ерікті түрде нүктеге ұмтылады.

Егер кез келген нүктеде (1) шарты орындалмаса, онда бұл нүкте функцияның үзіліс нүктесі деп аталады. Бұл келесі жағдайларда болуы мүмкін:

1) Функция нүктеде анықталмаған.

2) Шектеу жоқ.

3) Бұл шектеу бар, бірақ ол тең емес.

Мысал 42. Берілген функция нүктеде үзіліссіз болатынын анықтаңыз, егер.

Түсіндім демек, бұл функция нүктеде үздіксіз болады.

шегі k-ға тәуелді, яғни. ол берілген нүктеде жоқ, бұл функцияның осы нүктеде үзіліс бар екенін білдіреді.

4.3 Бірнеше айнымалы функциялардың туындылары мен дифференциалдары

4.3.1 Бірінші ретті жартылай туындылар

Х аргументіне қатысты функцияның ішінара туындысы у айнымалысының тұрақты мәні үшін бір х айнымалысының функциясының жай туындысы болып табылады және былай белгіленеді:

y аргументіне қатысты функцияның ішінара туындысы х айнымалысының тұрақты мәніндегі бір у айнымалысының функциясының жай туындысы болып табылады және былай белгіленеді:

Мысал 43. Функцияның дербес туындыларын табыңыз.

4.3.2 Екінші ретті жартылай туындылар

Екінші ретті жартылай туындылар бірінші ретті жартылай туынды туындылар болып табылады. Пішіннің екі айнымалы функциясы үшін екінші ретті ішінара туындының төрт түрі мүмкін:

Әртүрлі айнымалыларға қатысты дифференциалдау жүргізілетін екінші ретті жартылай туындылар аралас туындылар деп аталады. Екі рет дифференциалданатын функцияның екінші ретті аралас туындылары тең.

44-мысал. Екінші ретті дербес туындыларды табыңыз.

4.3.3 Толық дифференциал және оны жуықтап есептеуге қолдану.

Анықтама. Екі айнымалы функцияның бірінші ретті дифференциалы формула бойынша табылады

.

Мысал 45. Функцияның толық дифференциалын табыңыз.

Шешім. Жартылай туындыларды табайық:

.

x және y аргументтерінің шағын қадамдары үшін функция шамамен dz-ге тең өсімді алады, яғни. ...

Нүктедегі функцияның жуық мәнін табу формуласы, егер оның нүктедегі дәл мәні белгілі болса:

Мысал 46. Табыңыз .

Шешім. болсын,

Содан кейін формуланы қолданамыз

Жауап. .

Мысал 47. Шамамен есептеңіз.

Шешім. Функцияны қарастырайық. Бізде бар

Мысал 48. Шамамен есептеңіз.

Шешім. Функцияны қарастырыңыз ... Біз алып жатырмыз:

Жауап. .

4.3.4 Имплицитті функцияны дифференциалдау

Анықтама. Функция z-ге қатысты шешілмейтін теңдеу арқылы берілсе, ол жасырын деп аталады.

Мұндай функцияның жеке туындылары мына формулалар арқылы табылады:

49-мысал. Теңдеу арқылы берілген z функциясының жеке туындыларын табыңыз .

Шешім.

Анықтама. Функция у-ға қатысты шешілмейтін теңдеу арқылы берілсе, ол жасырын деп аталады.

Мұндай функцияның туындысы мына формула бойынша табылады:

.

Мысал 50. Осы функциялардың туындыларын табыңыз.

5.1 Бірнеше айнымалы функцияның жергілікті экстремумы

Анықтама 1. Функцияның егер нүктесінде максимумы бар

Анықтама 2. Функцияның егер нүктесінде минимумы бар нүктеге жеткілікті жақын және одан өзгеше барлық нүктелер үшін.

Экстремумның қажетті шарты. Егер функция нүктеде экстремумға жетсе, онда функцияның ішінара туындылары жойылады немесе осы нүктеде болмайды.

Жартылай туындылар жойылатын немесе жоқ нүктелер критикалық деп аталады.

Экстремумның жеткілікті белгісі. Функция критикалық нүктенің кейбір маңайында анықталсын және осы нүктеде үздіксіз екінші ретті ішінара туындылары болсын.

1) нүктесінде жергілікті максимумы бар, егер және;

2) нүктесінде жергілікті минимумы бар, егер және;

3) нүктесінде жергілікті экстремумы жоқ, егер;

Екі айнымалы функцияның экстремумын зерттеу схемасы.

1. Функцияның дербес туындыларын табыңыз: және.

2. Теңдеулер жүйесін шешіп, функцияның критикалық нүктелерін табыңдар.

3. Екінші ретті жартылай туындыларды табыңыз, олардың критикалық нүктелеріндегі мәндерін есептеңіз және жеткілікті шартты пайдаланып, экстремумның болуы туралы қорытынды жасаңыз.

4. Функцияның экстремумын табыңыз.

Мысал 51. Функцияның экстремумдарын табыңыз .

1) Дербес туындыларды табыңыз.

2) Теңдеулер жүйесін шешу

4) Екінші ретті жартылай туындыларды және олардың критикалық нүктелердегі мәндерін табыңыз:. Осы кезде біз аламыз:

демек, нүктеде экстремум жоқ. Осы кезде біз аламыз:

демек, нүктеде минимум бар.

5.2 Ғаламдық экстремум (функцияның ең жоғары және ең төменгі мәні)

Кейбір тұйық жиында үздіксіз болатын бірнеше айнымалы функцияның ең үлкен және ең кіші мәндеріне не экстремум нүктелерінде, не жиынның шекарасында қол жеткізіледі.

Ең жоғары және ең төменгі мәндерді табу схемасы.

1) Облыс ішінде жатқан критикалық нүктелерді табыңыз, осы нүктелердегі функцияның мәнін есептеңіз.

2) Аудан шекарасындағы функцияны зерттеңіз; егер шекара бірнеше түрлі сызықтардан тұрса, онда зерттеу әрбір учаске үшін бөлек жүргізілуі керек.

3) Функцияның алынған мәндерін салыстырып, ең үлкенін және ең кішісін таңдаңыз.

Мысал 52. Тіктөртбұрыштағы ең үлкен және ең кіші функция мәндерін табыңыз.

Шешім. 1) Функцияның критикалық нүктелерін табыңыз, ол үшін жеке туындыларын табамыз:, және теңдеулер жүйесін шешіңіз:

А сыни нүктесі алынды. Алынған нүкте көрсетілген аймақтың ішінде жатыр,

Аудан шекарасы төрт сегменттен тұрады: және. әрбір сегменттегі функцияның ең үлкен және ең кіші мәнін табыңыз.

4) Алынған нәтижелерді салыстырыңыз және оны нүктелерден табыңыз .

6-тарау. Тұтынушы таңдау моделі

Біз n түрлі тауар бар деп есептейміз. Сонда белгілі бір тауарлар жиыны n өлшемді вектормен белгіленеді , мұндағы i-ші туындының мөлшері. Х тауарлардың барлық жиынтықтарының жиынтығы кеңістік деп аталады.

Жеке тұтынушының таңдауы артықшылық қатынасымен сипатталады: тұтынушы қалаған кез келген екі жиынтық туралы айта алады немесе олардың арасындағы айырмашылықты көрмейді деп есептеледі. Артықшылық қатынасы өтпелі: егер жиын жиыннан артық болса, ал жиын жиыннан артық болса, онда жиын жиыннан жақсырақ болады. Тұтынушының мінез-құлқы жеке тұтынушының аксиомасымен толық сипатталады деп есептейміз: әрбір жеке тұтынушы өзінің қалаулар жүйесіне сүйене отырып, тұтыну, сатып алу және т.б. туралы шешім қабылдайды.

6.1 Утилита функциясы

X тұтынушылық жиындар жиынында функция анықталған , оның тұтыну жиынындағы құны тұтынушының осы жиынтық үшін жеке тұлғаның бағалауына тең. Функция тұтынушының қызметтік функциясы немесе тұтынушының қалауы функциясы деп аталады. Анау. әрбір тұтынушының өзінің пайдалы қызметі бар. Бірақ тұтынушылардың барлық жиынтығын тұтынушылардың белгілі бір кластарына бөлуге болады (жасы, мүліктік жағдайы және т.б. бойынша) және әрбір сыныпқа кейбір, мүмкін, орташаланған пайдалы функция тағайындалуы мүмкін.

Сонымен, функция дегеніміз тұтынушының бағалауы немесе берілген жиынтықты сатып алу кезіндегі жеке адамның қажеттіліктерін қанағаттандыру деңгейі. Берілген жеке адам үшін жиынтықтан артықшылық болса, онда.

Утилита функциясының қасиеттері.

1.

Пайдалылық функциясының алғашқы жартылай туындылары өнімдердің шекті пайдалылықтары деп аталады. Осы қасиеттен шығатыны, бір тауарды тұтыну көлемінің ұлғаюы, ал басқа өнімдердің тұтынуы өзгеріссіз қалуы тұтынушылардың бағасының өсуіне әкеледі. Вектор функцияның градиенті болып табылады, ол функцияның ең үлкен өсу бағытын көрсетеді. Функция үшін оның градиенті өнімдердің шекті утилиталарының векторы болып табылады.

2.

Анау. тұтыну өскен сайын кез келген тауардың шекті пайдалылығы төмендейді.

3.

Анау. әрбір өнімнің шекті пайдалылығы басқа өнімнің санына қарай артады.

Қызметтік функциялардың кейбір түрлері.

1) Неоклассикалық:.

2) Квадраттық: мұндағы матрица теріс анықталған және үшін .

3) Логарифмдік функция:.

6.2 Емдеу сызықтары

Қолданбалы есептер мен тұтынушы таңдау үлгілерінде екі тауар жиынтығының нақты жағдайы жиі пайдаланылады, яғни. қызметтік функция екі айнымалыға тәуелді болғанда. Индивидуалдылық сызығы – жеке адамның қажеттіліктерін қанағаттандыру деңгейі бірдей тұтынушылар жиынын қосатын сызық. Негізінде енжарлық сызықтары функция деңгейінің сызықтары болып табылады. Елеусіз сызықтың теңдеулері: .

Инференциялық сызықтардың негізгі қасиеттері.

1. Қажеттіліктерді қанағаттандырудың әртүрлі деңгейлеріне сәйкес келетін немқұрайлылық сызықтары жанаспайды және қиылыспайды.

2. Елеусіздік сызықтары азаяды.

3. Анықтамалық сызықтар төмен қарай дөңес.

2-қасиет маңызды шамамен теңдікті білдіреді.

Бұл арақатынас жеке адам өзінің қажеттіліктерін қанағаттандыру деңгейін өзгертпестен бірінші өнімнің тұтынуын бір бірлікке азайтқанда (ұлғайтқанда) екінші өнімді тұтынуды қаншалықты арттыруы (азайту) керектігін көрсетеді. Қатынас бірінші өнімді екіншіге ауыстыру жылдамдығы деп, ал мән бірінші өнімді екіншіге ауыстырудың шекті жылдамдығы деп аталады.

Мысал 53. Егер бірінші игіліктің шекті пайдалылығы 6, ал екіншісі - 2 болса, онда бірінші тауарды тұтыну бір бірлікке азайған кезде екінші игіліктің тұтынуын 3 бірлікке көбейту керек. қажеттіліктерді қанағаттандырудың бірдей деңгейі.

6.3 Бюджет жиынтығы

Болсын - n өнім жиынтығының баға векторы; I – жеке тұлғаның өнім жиынтығын сатып алуға жұмсауға дайын табысы. Берілген бағалар бойынша құны I-ден аспайтын тауарлар жиынтықтарының жиынтығы В бюджеттік жиыны деп аталады. Сонымен қатар, құны I болатын тауарлар жиыны В бюджеттік жиынының G шекарасы деп аталады. В жиыны G шекарасымен және табиғи шектеулермен шектеледі.

Бюджет жиынтығы теңсіздіктер жүйесімен сипатталады:

Екі тауар жиынтығы жағдайында В бюджеттік жиыны (1-сурет) координаталар жүйесіндегі координаталар осьтерімен және түзу сызықпен шектелген үшбұрыш болып табылады.

6.4 Тұтынушы сұранысының теориясы

Тұтыну теориясында тұтынушы әрқашан өзінің пайдалылығын барынша арттыруға ұмтылады және ол үшін жалғыз шектеу ол тауарлар жиынтығын сатып алуға жұмсай алатын шектеулі кіріс I болып табылады деп болжанады. Тұтынушылардың таңдау мәселесі (нарықтағы тұтынушылардың ұтымды мінез-құлқы мәселесі) жалпы түрде былай тұжырымдалады: тұтынушы жиынын табыңыз. , бұл берілген бюджеттік шектеу үшін оның пайдалылық функциясын барынша арттырады. Бұл есептің математикалық моделі:

Екі өнім жиынтығы жағдайында:

Геометриялық тұрғыдан бұл есептің шешімі G бюджеттік жиынының шекарасы мен енжарлық сызығының түйісу нүктесі болып табылады.

Бұл есептің шешімі теңдеулер жүйесін шешуге келтіріледі:

(1)

Бұл жүйенің шешімі тұтынушылардың таңдау мәселесін шешу болып табылады.

Тұтынушы таңдау мәселесін шешу сұраныс нүктесі деп аталады. Бұл сұраныс нүктесі баға мен табысқа байланысты I. Яғни. сұраныс нүктесі сұраныс функциясы болып табылады. Өз кезегінде сұраныс функциясы n функциялар жиынтығы болып табылады, олардың әрқайсысы аргументке байланысты:

Бұл функциялар сәйкес тауарлардың сұраныс функциялары деп аталады.

Мысал 54. Нарықтағы екі тауардың жиыны үшін белгілі бағалар мен кірістер I, егер пайдалылық функциясының формасы болса, сұраныс функцияларын табыңыз. .

Шешім. Утилитарлық функцияны ажыратайық:

.

Алынған өрнектерді (1) орнына қойып, теңдеулер жүйесін алыңыз:

Бұл жағдайда әрбір өнімге жұмсалатын шығын тұтынушы табысының жартысы болады, ал сатып алынған өнімнің сомасы өнімнің бағасына бөлінген соған жұмсалған сомаға тең болады.

Мысал 55. Пайдалылық бірінші игілікке, екіншісіне,

бірінші өнімнің бағасы, екіншісінің бағасы. Кіріс. Пайдалылықты арттыру үшін тұтынушы қанша сатып алуы керек?

Шешім. Пайдалы функциялардың туындыларын тауып, оларды (1) жүйеге қойып, оны шешейік:

Бұл тауарлар жиынтығы пайдалылықты арттыру тұрғысынан тұтынушы үшін оңтайлы болып табылады.

Сынақ жеке блокноттағы есепке алу кітапшасының нөмірінің соңғы санымен таңдалған нұсқаға сәйкес орындалуы керек. Әрбір мәселе шартты, егжей-тегжейлі шешімді және қорытындыны қамтуы керек.

1. Есепке кіріспе

Тапсырма 1. Функцияның анықталу облысын табыңыз.

5.

Есеп 2. Функциялардың шектерін табыңыз.

.

Тапсырма 3. Функцияның үзіліс нүктелерін тауып, олардың түрін анықтаңыз.

1. 2. 3.

2-тарау. Бір айнымалы функцияның дифференциалдық есебі

Тапсырма 4. Осы функциялардың туындыларын табыңыз.

1.a); б) в) у =;

г) у = x 6 + + + 5; д) y = x tg x + ln sin x + e 3x;

f) у = 2 х - доғасы х.

2.а) ; б) y =; в) y =; г) у = x 2 - + 3; e) y = e cos; f) y =.

3.a) y = lnx; б) y =; в) y = ln;

4. а) y =; б) у = (e 5 x - 1) 6; в) y =; d) y =; д) у = x 8 ++ + 5; f) у = 3 х - доғасы х.

5.а) y = 2x 3 - + e x; б) y =; в) y =;

d) y =; e) y = 2 cos; f) y =.

6.a) y = lnx; б) y =; в) y = ln;

d) y =; д) у = x 7 + + 1; f) y = 2.

7.a) ; б) y =; в) y =; г) y = x 2 + xsinx +; e) y = e cos; f) y =.

8. а) y =; б) у = (3 x - 4) 6; в) y = sintg;

г) у = 3х 4 - - 9+ 9; д) y =;

f) y = x 2 + arcsin x - x.

9.а); б) ; в) y =; г) y = 5 sin 3 x; д) у = x 3 - - 6+ 3; f) y = 4x 4 + ln.

10.a) б) y =; в) у = (3 x - 4) 6; d) y =; д) y = x 2 - x; f) y = e sin 3 x + 2.

Тапсырма 5. Функцияны зерттеп, графигін тұрғыз.

1. а) ә) в)

2.а) ә) v) .

3.а) ә) v) .

4.b) v)

5.a) b) v) .

6.a) b) v) .

7. a) b) c)

8. а) б) в)

9.a) b) c)

10. а) ә) v) .

Тапсырма 6. Берілген кесіндідегі функцияның ең үлкен және ең кіші мәнін табыңыз.

1. .

3. .

6. .

8. .

9. .

10. .

3-тарау. Интегралдық есептеулер

Есеп 7. Анықталмаған интегралды табыңыз.

1.а) б);

2.а) б) в) г)

4. G)

5.a) ; б); v) ; G).

6.a) ; б); v); G)

7.a) ; б) ; v) ; G)

8.a) ; б); v) ; G) .

9.a) ; б) в); G).

10.a) б) v) ; G) .

Есеп 8. Анықталған интегралдарды есептеңдер.

1.

2.

3.

4.

5.

6.

7. .

8.

9.

10.

Есеп 9. Дұрыс емес интегралды табыңыз немесе олардың ажырайтынын дәлелдеңіз.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Есеп 10. Қисықтармен шектелген ауданның ауданын табыңыз

1. .2. .

5. 6.

7. , .8..

10. , .

4-тарау. Бірнеше айнымалы функцияның дифференциалдық есебі.

Тапсырма 11. Функцияның анықталу облысын табыңыз (сызбада көрсетіңіз).

Есеп 12. for функциясының үздіксіздігін зерттеңіз

Есеп 13. Айқын анықталған функцияның туындысын табыңыз.

Есеп 14. Шамамен есептеңіз

1.a); b) ; v)

2.а) ; б); v) .

3.а) ; б) ; v) .

4.а) ; б) ; v) .

5. а); б) ; v) .

6. а); б); v) .

7. а); б) ; v) .

8.a); b) ; v)

9.a) ; б); v) .

10. a); b) ; v)

Есеп 15. Экстремум үшін функцияны зерттеңіз.

7. .

8. .

9. .

10. .

Есеп 16. Берілген тұйық облыстағы функцияның ең үлкен және ең кіші мәнін табыңыз.

1.тіктөртбұрышта

2.

3.тіктөртбұрышта

4.параболамен шектелген аймақта

Және абсцисса.

5.шаршы

6.координаталық осьтермен және түзумен шектелген үшбұрышта

7.координаталық осьтермен және түзумен шектелген үшбұрышта

8. координат осьтерімен және түзумен шектелген үшбұрышта

9.параболамен шектелген аймақта

Және абсцисса.

10.параболамен шектелген аймақта

Және абсцисса.

Басты

1. М.С. Крассус, Б.П. Чупрынов. Математика негіздері және оның экономикалық білім беруде қолданылуы: Оқу құралы. - 4-ші басылым, Исп. - М .: Дело, 2003 ж.

2. М.С. Крассус, Б.П. Чупрынов. Экономикалық мамандықтарға арналған математика: Оқу құралы. - 4-ші басылым, Исп. - М .: Дело, 2003 ж.

3. М.С. Крассус, Б.П. Чупрынов. Экономика бакалавры дәрежесіне арналған математика. Оқулық. - 4-ші басылым, Исп. - М.: Дело, 2005 ж.

4. Экономистер үшін жоғары математика. Жоғары оқу орындарына арналған оқулық / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Ред. проф. Н.Ш. Кремер, - 2-ші басылым, қайта қаралған. және қосыңыз. - М: БІРЛІК, 2003 ж.

5. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Экономикалық мамандықтарға арналған жоғары математика. Оқулық және практикум (I және II бөлімдер) / Ред. проф. Н.Ш. Кремер, - 2-ші басылым, қайта қаралған. және қосыңыз. - М: Жоғары білім, 2007. - 893б. - (Ғылым негіздері)

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Жаттығулар мен есептердегі жоғары математика. М. орта мектебі. 1999.

Қосымша

1. I.I. Баврин, В.Л. Теңізшілер. Жоғары математика. «Владос гуманитарлық баспа орталығы», 2002 ж.

2. И.А. Зайцев. Жоғары математика. «Орта мектеп», 1998 ж.

3. А.С. Солодовников, В.А. Бабайцев, А.В. Брайлов, И.Г. Шандра. Экономикадағы математика /екі бөлімде/. M. Қаржы және статистика. 1999.

студенттерге арналған медициналық, педиатриялық, стоматологиялық

және профилактикалық медицина факультеттері

зертханалық жұмысқа

«Математикалық талдаудың негізгі ұғымдары»

1. Тақырыптың ғылыми-әдістемелік негіздемесі:

Туынды және дифференциалдық ұғымдар математикалық талдаудың негізгі ұғымдарының бірі болып табылады. Туындыларды есептеу физика мен математиканың көптеген есептерін (жылдамдық, үдеу, қысымды табу және т.б. табу) кезінде қажет. Туынды ұғымының маңыздылығы, атап айтқанда, функцияның туындысы оның аргументі өзгерген кезде осы функцияның өзгеру жылдамдығын сипаттайтынымен анықталады.

Дифференциалды қолдану шамамен есептеулерді жүргізуге, сондай-ақ қателерді бағалауға мүмкіндік береді.

Функциялардың туындылары мен дифференциалдарын табу әдістері және оларды қолдану дифференциалдық есептеудің негізгі мәселесін құрайды. Туынды ұғымының қажеттілігі қозғалыс жылдамдығын есептеу және қисыққа жанаманың бұрышын табу есебін тұжырымдауға байланысты туындайды. Кері есеп те шығарылады: жылдамдық бойынша жүріп өткен жолды анықтаңыз және жанама еңістің тангенсі бойынша сәйкес функцияны табыңыз. Бұл кері есеп анықталмаған интеграл ұғымына әкеледі.

Анықталған интеграл ұғымы бірқатар практикалық есептерде, атап айтқанда жазық фигуралардың аудандарын есептеу, айнымалы күштің атқаратын жұмысын есептеу және функцияның орташа мәнін табу есептерінде қолданылады.

Әртүрлі физикалық, химиялық, биологиялық процестер мен құбылыстарды математикалық сипаттауда зерттелетін шамаларды ғана емес, сонымен бірге осы шамалардың әртүрлі ретті туындыларын қамтитын теңдеулер жиі қолданылады. Мысалы, бактериялардың көбею заңының қарапайым нұсқасы бойынша көбею жылдамдығы белгілі бір уақыттағы бактериялар санына пропорционал. Егер бұл шаманы N (t) деп белгілесе, онда туындының физикалық мағынасына сәйкес бактериялардың көбею жылдамдығы N (t) туындысы болып табылады және жоғарыдағы заңның негізінде мынаны жазуға болады: қатынасы N "(t) = k ∙ N, мұндағы k> 0 - пропорционалдық коэффициенті Алынған теңдеу алгебралық емес, өйткені ол тек белгісіз N (t) функциясын ғана емес, оның бірінші ретті туындысын да қамтиды.

2. Қысқаша теория:

1. Туынды ұғымға әкелетін есептер

1. Материалдық нүктенің v жылдамдығын табу есебі... Кейбір материалдық нүкте түзу сызықты қозғалыс жасасын. Бір уақытта т 1 нүктесі орнында М 1. Бір уақытта т 2 жүкті М 2 . интервалды белгілейік М 1 , М 2 бойымен ΔS; т 2 - т 1 = Δt... Мән қозғалыстың орташа жылдамдығы деп аталады. Нүктенің бір позициядағы лездік жылдамдығын табу М 1 қажетті Δtнөлге бейім. Математикалық тұрғыдан бұл дегеніміз

, (1)

Сонымен, материалдық нүктенің лездік жылдамдығын табу үшін функция өсімінің қатынасының шегін есептеу керек. ΔSшартымен Δt аргументінің өсіміне Δt → 0.

2. Функция графигіне жанаманың көлбеу бұрышын табу мәселесі.

1-сурет

Кейбір функцияның графигін қарастырайық y = f (x).Көлбеу бұрышы қандай
нүктедегі жанама М 1 ? Нүктеде М 1 функциясының графигіне жанама сызыңыз. Графиктен ерікті нүктені таңдаңыз М 2 және секантты сызыңыз. Ол оське қарай қисайтылған OHбұрышта α 1 ... Қарастырыңыз ΔM 1 М 2 A:

, (2)

Егер нүкте М 1 түзетіңіз және көрсетіңіз М 2 жақынырақ жылжытыңыз М 1 , содан кейін секант М 1 М 2 нүктедегі функцияның графигіне жанамаға барады М 1 және сіз жаза аласыз:

, (3)

Осылайша, егер аргумент өсімі нөлге ұмтылса, функция өсімінің аргумент өсіміне қатынасының шегін есептеу қажет.

y = f (x) функциясының Δy өсімінің берілген x нүктесіндегі Δx аргументінің өсімшесінің қатынасының шегі 0 Δx нөлге ұмтылатындықтан, берілген нүктедегі функцияның туындысы деп аталады.

Туынды белгісі: y ", f" (x), ... Анықтамасы бойынша

, (4)

мұндағы Δx = x 2 -x 1 - аргументтің өсімі (аргументтің екі келесі жеткілікті жақын мәндерінің арасындағы айырмашылық), Δy = y 2 -y 1 - функцияның өсімі (мәндер арасындағы айырмашылық ​аргументтің осы мәндеріне сәйкес функцияның).

Берілген функцияның туындысын табу оның деп аталады дифференциация... Негізгі элементар функцияларды саралау дайын формулалар бойынша жүзеге асырылады (кестені қараңыз), сонымен қатар ережелер:

Алгебралық қосындының туындысы функциялары осы функциялардың туындыларының қосындысына тең:

(u+ υ )"= u" + υ "

2. Екі функцияның туындысының туындысы екінші функцияның біріншінің туындысына және бірінші функцияның екіншісінің туындысына көбейтінділерінің қосындысына тең:

(u ∙υ ) "= u"υ + uυ "

3. Бөлімшенің туындысы екі функцияның бөлімі бөлшекке тең, оның алымы азайғыштың туындысы мен алымының азалғыштың туындысы бойынша көбейтінділерінің айырмасы болып табылады, ал бөлгіш азайғыштың квадраты болып табылады:

Туындының физикалық мағынасы. (4) және (1) тармақтарын салыстыру материалдық нүктенің түзу сызықты қозғалысының лездік жылдамдығы оның координатасының уақытқа тәуелділігінің туындысына тең екенін білдіреді.

Функцияның туындысының жалпы мағынасы оның сипаттауында функцияның өзгеру жылдамдығы (жылдамдығы).берілген аргументтің өзгеруі үшін. Физикалық, химиялық және басқа процестердің жылдамдығы, мысалы, дененің салқындату жылдамдығы, химиялық реакция жылдамдығы, бактериялардың көбею жылдамдығы және т.б., сондай-ақ туынды арқылы өрнектеледі.

Туындының геометриялық мағынасы.Функция графигіне түсірілген жанаманың көлбеу бұрышының тангенсінің шамасы математикада деп аталады. жанаманың еңісі.

Дифференциалданатын функцияның графигіне қандай да бір нүктедегі жанаманың көлбеуі сан жағынан осы нүктедегі функцияның туындысына тең.

Бұл мәлімдеме деп аталады туындының геометриялық мағынасы.

Мақаланың мазмұны

МАТЕМАТИКАЛЫҚ ТАЛДАУ,әртүрлі өзгерістер процестерін сандық зерттеу әдістерін қамтамасыз ететін математиканың бөлімі; өзгеру жылдамдығын (дифференциалдық есептеу) зерттеумен және қисық контурлармен және беттермен шектелген фигуралардың қисықтарының ұзындықтарын, аудандары мен көлемдерін анықтаумен (интегралдық есептеу) айналысады. Математикалық талдау есептері үшін олардың шешімі шек ұғымымен байланысты болуы тән.

Математикалық талдауды 1665 жылы И.Ньютон және (шамамен 1675 ж.) дербес Г.Лейбниц бастады, дегенмен маңызды дайындық жұмыстарын И.Кеплер (1571–1630), Ф.Кавальери (1598–1647), П.Ферма жүргізді. (1601– 1665), Дж.Уоллис (1616-1703) және И.Барроу (1630-1677).

Презентацияны жанды ету үшін біз графиктер тіліне жүгінеміз. Сондықтан оқырманға осы мақаланы оқымас бұрын АНАЛИТИКАЛЫҚ ГЕОМЕТРИЯ мақаласын қарап шығу пайдалы болуы мүмкін.

ДИФФЕРЕНЦИАЛДЫҚ ЕСЕПТЕР

Тангендер.

күріште. 1 қисық фрагментін көрсетеді ж = 2x – x 2, арасында жасалған x= –1 және x= 3. Бұл қисықтың жеткілікті түрде кішкентай сегменттері түзу көрінеді. Басқаша айтқанда, егер РБұл қисық сызықтың ерікті нүктесі болса, онда осы нүкте арқылы өтетін және нүктенің шағын маңындағы қисық сызықтың жуықтауы болатын қандай да бір түзу бар. Р, және көршілестік неғұрлым аз болса, соғұрлым жуықтау жақсырақ болады. Мұндай түзу нүктедегі қисыққа жанама деп аталады Р... Дифференциалдық есептеудің негізгі міндеті – жанама бар қисық сызықтың кез келген нүктесінде жанаманың бағытын табуға мүмкіндік беретін жалпы әдісті құру. Өткір үзіліспен қисық сызықты елестету қиын емес (2-сурет). Егер Р- мұндай үзілістің төбесі, содан кейін жуықтау түзуін салуға болады PT 1 - нүктенің оң жағында Ржәне басқа жуықтау сызығы RT 2 - нүктенің сол жағына Р... Бірақ нүкте арқылы өтетін жалғыз түзу жоқ Р, ол нүктенің маңайындағы қисыққа бірдей жақсы жақындады Поңға да, солға да, демек нүктедегі жанама Пжоқ.

күріште. 1 тангенс FROMбастау арқылы сызылады О= (0,0). Бұл сызықтың еңісі 2, яғни. абсцисса 1-ге өзгергенде ордината 2-ге артады.Егер xжәне ж- ерікті нүктенің координаталары FROM, содан кейін алыстау Оқашықтықта Xбірліктер оңға қарай, біз алыстаймыз О 2 бойынша жбірлік жоғары. Демек, ж/x= 2 немесе ж = 2x... Бұл жанама теңдеу FROMқисыққа ж = 2x – x 2 нүктесінде О.

Енді нүкте арқылы өтетін түзулердің жиынынан неге екенін түсіндіру керек О, бұл түзу сызық таңдалды FROM... Еңісі 2 түзу сызықтың басқа түзулерден айырмашылығы неде? Бір қарапайым жауап бар және біз шеңберге жанама ұқсастығын қолдану азғыруына қарсы тұру қиынға соғады: жанама FROMқисықпен бір ғана ортақ нүктесі бар, ал нүкте арқылы өтетін кез келген басқа тік емес түзу О, қисық сызықты екі рет қиып өтеді. Мұны келесідей тексеруге болады.

Өрнектен бері ж = 2x – x 2-ні азайту арқылы алуға болады X 2-ден ж = 2x(түзу сызықтың теңдеулері FROM), содан кейін мәндер жграфик бойынша білім аз жнүктеден басқа барлық нүктелердегі түзу үшін x= 0. Демек, график нүктеден басқа барлық жерде Отөменде орналасқан FROM, және бұл түзу мен графиктің бір ғана ортақ нүктесі бар. Оның үстіне, егер ж = mx- нүкте арқылы өтетін басқа түзудің теңдеуі О, онда міндетті түрде екі қиылысу нүктесі болады. Шынымен, mx = 2x – x 2 үшін ғана емес x= 0, бірақ сонымен бірге x = 2 – м... Және тек қашан м= 2 екі қиылысу нүктесі де сәйкес келеді. күріште. 3 жағдайды көрсетеді м 2-ден аз, сондықтан оңға қарай Оекінші қиылысу нүктесі бар.

Не FROM- нүкте арқылы өтетін жалғыз тік емес түзу Ожәне оның ең маңызды қасиеті емес, графпен ортақ бір ғана нүктесі бар. Шынында да, егер басқа графиктерге жүгінсек, жалпы жағдайда біз атап өткен тангенс қасиетінің орындалмайтыны көп ұзамай белгілі болады. Мысалы, күріштен. 4 (1,1) нүктесінің жанында қисық графигі екенін көруге болады ж = x 3 түзу сызықпен жақсы жақындатылған RT, дегенмен, онымен бірнеше ортақ нүкте бар. Дегенмен, біз қарастырғымыз келеді RTнүктесінде осы графикке жанама Р... Сондықтан бірінші мысалда бізге жақсы қызмет еткеннен гөрі жанаманы бөлектеудің басқа жолын табу керек.

Бұл нүкте арқылы делік Ожәне ерікті нүкте Q = (h,к) қисық графигінде ж = 2x – x 2 (5-сурет) түзу сызық (секант деп аталады) сызылған. Қисық теңдеуіне мәндерді ауыстыру x = hжәне ж = к, біз мұны аламыз к = 2h – h 2, демек, секанттың еңісі

Өте кішкентаймен hмағынасы мжақын 2. Оның үстіне, таңдау h 0-ге жеткілікті жақын біз жасай аламыз мерікті түрде 2-ге жақын. Біз мұны айта аламыз м«Шектеуге бейім» 2-ге тең болғанда hнөлге немесе қандай да бір шекке ұмтылады мүшін 2-ге тең hнөлге ұмтылады. Бұл символдық түрде былай жазылады:

Содан кейін нүктедегі графикке жанама Онүкте арқылы өтетін түзу ретінде анықталады О, осы шекке тең еңіспен. Тангенстің бұл анықтамасы әдетте қолданылады.

Бұл тәсілдің артықшылықтарын басқа мысалмен көрсетейік: қисық графигіне жанаманың еңісін табыңыз. ж = 2x – x 2 ерікті нүктеде П = (x,ж), ең қарапайым жағдаймен шектелмей, қашан П = (0,0).

Болсын Q = (x + h, ж + к) - қашықтықта орналасқан диаграммадағы екінші нүкте hоң жағында Р(6-сурет). Еңісті табу қажет к/hсекант PQ... Нүкте Qқашықтықта орналасқан

осьтің үстінде X.

Жақшаларды кеңейте отырып, біз табамыз:

Осы теңдеуден шегеру ж = 2x – x 2, нүктеден тік қашықтықты табамыз РНүктеге Q:

Сондықтан еңіс мсекант PQтең

Енді сол hнөлге ұмтылады, м 2 - 2-ге бейім x; соңғы мәнді тангенстің еңісі ретінде қабылдаймыз PT... (Дәл осындай нәтиже алынады, егер hнүктені таңдауға сәйкес келетін теріс мәндерді қабылдайды Qсол П.) Мынаны ескеріңіз x= 0 нәтиже алдыңғы нәтижемен бірдей.

2 - 2 өрнек x 2-нің туындысы деп аталады x – x 2. Бұрынғы уақытта туынды «дифференциалдық қатынас» және «дифференциалдық коэффициент» деп те аталды. Егер өрнек 2 x – x 2 белгілеу f(x), яғни.

онда туындыны белгілеуге болады

Функция графигіне жанаманың көлбеулігін анықтау үшін ж = f(x) белгілі бір уақытта ауыстырылуы керек fў ( x) осы нүктеге сәйкес мән X... Сонымен еңіс fў (0) = 2 үшін X = 0, fў (0) = 0 үшін X= 1 және fў (2) = –2 үшін X = 2.

Туынды да белгіленеді сағў , dy/dx, D x yжәне Ду.

Бұл қисық ж = 2x – x 2 берілген нүктенің жанында оның осы нүктедегі жанамасынан іс жүзінде айырмашылығы жоқ, жанама нүктесіндегі «қисық қисық еңісі» ретінде жанаманың еңісі туралы айтуға мүмкіндік береді. Сонымен, қарастырылып отырған қисықтың еңісі (0,0) нүктесінде 2 көлбеу болады деп айтуға болады. x= 0 өзгеру жылдамдығы жсалыстырмалы x 2. (2,0) нүктесінде жанаманың (және қисығының) еңісі –2. (Минус таңбасы мынаны білдіреді xайнымалы жазаяды.) (1,1) нүктесінде жанама горизонталь болады. Біз қисық айтамыз ж = 2x – x 2 осы нүктеде тұрақты мәнге ие.

Жоғары және төмен.

Біз жаңа ғана қисық екенін көрсеттік f(x) = 2x – x 2 (1,1) нүктесінде қозғалмайтын. Өйткені fў ( x) = 2 – 2x = 2(1 – x), үшін екені анық x 1-ден аз, fў ( x) оң, сондықтан жартады; сағ x, үлкен 1, fў ( x) теріс, демек жтөмендейді. Осылайша, суретте көрсетілген (1,1) нүктеге жақын жерде. 6 әріп М, мағынасы сағнүктеге дейін өседі М, нүктесінде қозғалмайтын Мжәне нүктеден кейін төмендейді М... Бұл нүкте «максимум» деп аталады, себебі мән сағбұл кезде оның жеткілікті шағын төңірегінде оның кез келген мәндерінен асып түседі. Сол сияқты, «минимум» барлық мәндері болатын маңайдағы нүкте ретінде анықталады жартық сағдәл осы сәтте. Бұл туынды болғанымен де орын алуы мүмкін f(x) белгілі бір нүктеде жойылады, оның белгісі осы нүктеге жақын жерде өзгермейді. Максимум да, минимум да болмайтын мұндай нүкте иілу нүктесі деп аталады.

Мысал ретінде қисықтың стационарлық нүктесін табайық

Бұл функцияның туындысы

және жоғалады x = 0, X= 1 және X= –1; анау. (0,0), (1, –2/15) және (–1, 2/15) нүктелерінде. Егер Xонда -1-ден сәл аз fў ( x) теріс; егер X-1-ден сәл артық fў ( x) оң. Демек, нүкте (–1, 2/15) максимум болып табылады. Сол сияқты, нүктенің (1, –2/15) минимум екенін көрсетуге болады. Бірақ туынды fў ( x) (0,0) нүктесінің алдында да, одан кейін де теріс. Демек, (0,0) - иілу нүктесі.

Қисықтың пішінін, сонымен қатар қисықтың осьпен қиылысу фактісін зерттеу жүргізілді. Xсағ f(x) = 0 (яғни, үшін X= 0 немесе) оның графигін шамамен суретте көрсетілгендей көрсетуге мүмкіндік береді. 7.

Жалпы, әдеттен тыс жағдайларды (түзу сызықты кесінділерден тұратын қисықтар немесе иілулердің шексіз саны) алып тастасақ, қисық пен жанама нүктесіне жақын жерде жанаманың салыстырмалы орналасуының төрт нұсқасы бар. Р. (См... күріш. 8, мұндағы жанама оң көлбеу болады.)

1) Нүктенің екі жағында Рқисық жанаманың үстінде жатыр (Cурет 8, а). Бұл жағдайда олар нүктедегі қисық деп айтады Ртөмен қарай дөңес немесе ойыс.

2) Нүктенің екі жағында Рқисық жанаманың астында орналасқан (Cурет 8, б). Бұл жағдайда қисық жоғары дөңес немесе жай дөңес деп аталады.

3) және 4) Қисық нүктенің бір жағында жанаманың үстінде орналасқан Ржәне төменде - екіншісінде. Бұл жағдайда Р- иілу нүктесі.

Мәндерді салыстыру fў ( x) екі жағында Рнүктедегі мәнімен Р, белгілі бір мәселеде осы төрт жағдайдың қайсысын шешу керектігін анықтауға болады.

Қолданбалар.

Жоғарыда айтылғандардың барлығы әртүрлі салаларда маңызды қолданбаларды табады. Мысалы, егер дене секундына 200 фут бастапқы жылдамдықпен тігінен жоғары лақтырылса, онда биіктік солар арқылы орналасатын болады тбастапқы нүктемен салыстырғанда секунд болады

Біз қарастырған мысалдардағыдай әрекет ете отырып, біз табамыз

бұл мән c кезінде жоғалады. Туынды fў ( x) c мәніне дейін оң және осы уақыттан кейін теріс. Демек, сдейін артады, содан кейін стационар болады, содан кейін азаяды. Бұл жоғары лақтырылған дененің қозғалысының жалпы сипаттамасы. Одан біз дененің ең биік нүктесіне жеткенін білеміз. Әрі қарай, ауыстыру т= 25/4 дюйм f(т), біз 625 фут аламыз, максималды көтеру. Бұл тапсырмада fў ( т) физикалық мағынаға ие. Бұл туынды дененің уақыт мезетінде қозғалатын жылдамдығын көрсетеді т.

Енді қосымшаның басқа түрін қарастырайық (9-сурет). Ауданы 75 см 2 картон парағынан шаршы түбі бар қорапты жасау қажет. Бұл қорап максималды көлемге ие болуы үшін қаншалықты үлкен болуы керек? Егер X- қораптың негізінің жағы және h- оның биіктігі, онда қораптың көлемі болады В = x 2 h, ал бетінің ауданы 75 = x 2 + 4хх... Теңдеуді түрлендірсек, мынаны аламыз:

Алады Втең болып шығады

және жоғалады X= 5. Содан кейін

және В= 125/2. Функция графигі В = (75x – x 3) / 4 суретте көрсетілген. 10 (теріс мәндер XБұл мәселеде физикалық мағынасы жоқ деп есептелмеген).

Туындылар.

Дифференциалдық есептеудің маңызды міндеті туындыларды тез және ыңғайлы табуға мүмкіндік беретін әдістерді құру болып табылады. Мысалы, оны есептеу оңай

(Тұрақтының туындысы, әрине, нөлге тең.) Жалпы ережені шығару қиын емес:

қайда n- кез келген бүтін немесе бөлшек. Мысалы,

(Бұл мысал бөлшек дәрежелердің қаншалықты пайдалы екенін көрсетеді.)

Мұнда ең маңызды формулалардың кейбірі берілген:

Сондай-ақ келесі ережелер бар: 1) егер екі функцияның әрқайсысы g(x) және f(x) туындылары бар, онда олардың қосындысының туындысы осы функциялардың туындыларының қосындысына тең, ал айырманың туындысы туындылардың айырмасына тең, яғни.

2) екі функцияның туындысының туындысы мына формуламен есептеледі:

3) екі функцияның қатынасының туындысы түрге ие болады

4) функцияның тұрақтыға көбейтіндісінің туындысы осы функцияның туындысына көбейтілген тұрақтыға тең, яғни.

Функцияның мәндерін кезең-кезеңімен есептеу қажет болатын жағдайлар жиі кездеседі. Мысалы, күнәні есептеу үшін x 2, алдымен табу керек u = x 2, содан кейін санның синусын есептеңіз u... Осындай күрделі функциялардың туындысын «тізбек ережесі» арқылы табамыз:

Біздің мысалда f(u) = күнә u, fў ( u) = cos u, демек,

Осы және басқа ұқсас ережелер көптеген функциялардың туындыларын бірден жазуға мүмкіндік береді.

Сызықтық жуықтаулар.

Туындыны біле отырып, біз көп жағдайда функцияның графигін осы нүктедегі оның жанамасының қандай да бір нүктесіне жақын жерде ауыстыра алатындығымыз үлкен маңызға ие, өйткені түзу сызықтармен жұмыс істеу оңайырақ.

Бұл идея функциялардың жуық мәндерін есептеуде тікелей қолдануды табады. Мысалы, қашан мәнді есептеу өте қиын x= 1,033. Бірақ сіз 1.033 саны 1-ге жақын және сол фактіні пайдалана аласыз. Жабық x= 1 біз жанама қисық сызығының графигін елеулі қателіксіз ауыстыра аламыз. Мұндай жанаманың еңісі туындының мәніне тең ( x 1/3) ў = (1/3) x–2/3 кезінде x = 1, яғни 1/3. (1,1) нүктесі қисық сызықта жататындықтан және осы нүктедегі қисыққа жанаманың көлбеуі 1/3 болғандықтан, жанама теңдеуі мынадай түрге ие болады.

Осы жолда X = 1,033

Алынған мән жшынайы мәнге өте жақын болуы керек ж; және, шын мәнінде, бұл шындықтан тек 0,00012 артық. Математикалық талдауда сызықтық жуықтаудың дәлдігін жақсарту үшін әдістер әзірленді. Бұл әдістер біздің шамамен есептеулеріміздің сенімділігін қамтамасыз етеді.

Жаңа сипатталған процедура пайдалы белгіні ұсынады. Болсын П- функцияның графигіне сәйкес нүкте fайнымалы Xжәне функцияға рұқсат етіңіз f(x) дифференциалданады. Қисықтың графигін нүктенің жанында ауыстырыңыз Роған жанама, осы нүктеде сызылған. Егер Xсомасына қарай өзгерту h, онда тангенстің ординатасы мән бойынша өзгереді hХ f ў ( x). Егер hөте аз болса, онда соңғы мән ординатадағы шынайы өзгеріске жақсы жуықтау болып табылады жграфика. Егер орнына hсимволын жазамыз dx(бұл туынды емес!), бірақ ординатадағы өзгеріс жбелгілеу dy, содан кейін аламыз dy = f ў ( x)dx, немесе dy/dx = f ў ( x) (см... күріш. он бір). Сондықтан, орнына Dyнемесе f ў ( x) символы көбінесе туындыны белгілеу үшін қолданылады dy/dx... Бұл белгілеудің ыңғайлылығы негізінен тізбек ережесінің айқын көрінуіне байланысты (күрделі функцияның дифференциациясы); жаңа белгілерде бұл формула келесідей болады:

бұл жерде бұл айтылған сағбайланысты u, а uөз кезегінде байланысты X.

Шамасы dyдифференциал деп аталады сағ; шын мәнінде байланысты екіайнымалылар, атап айтқанда: бастап Xжәне ұлғайту dx... Көбейту кезінде dxөте аз, шама dyмәндегі сәйкес өзгеріске жақын ж... Бірақ бұл өсім деп болжауға dxаз, қажет емес.

Туынды функция ж = f(x) белгіледік f ў ( x) немесе dy/dx... Туындының туындысын жиі алуға болады. Нәтиже екінші туындысы деп аталады f (x) және белгіленеді f ўў ( x) немесе г 2 ж/dx 2. Мысалы, егер f(x) = x 3 – 3x 2, содан кейін f ў ( x) = 3x 2 – 6xжәне f ўў ( x) = 6x- 6. Ұқсас белгілер жоғары дәрежелі туынды құралдар үшін қолданылады. Дегенмен, көп сызықшаларды болдырмау үшін (туындының ретіне тең) төртінші туындыны (мысалы) келесідей жазуға болады. f (4) (x) және туынды n- реті ретінде f (n) (x).

Егер екінші туынды оң болса, нүктедегі қисық төмен қарай дөңес, ал екінші туынды теріс болса жоғары қарай дөңес болатынын көрсетуге болады.

Егер функцияның екінші туындысы болса, онда шаманың өзгеруі жөсімге сәйкес келеді dxайнымалы X, шамамен формула бойынша есептеуге болады

Бұл жуықтау әдетте дифференциалмен берілгеннен жақсырақ fў ( x)dx... Ол қисық бөлігін түзу емес, параболамен ауыстыруға сәйкес келеді.

Егер функция f(x) жоғары дәрежелі туындылар бар, онда

Қалғаны

қайда x- арасында біраз сан xжәне x + dx... Жоғарыда келтірілген нәтиже қалдық Тейлор формуласы деп аталады. Егер f(x) барлық реттердің туындылары бар, содан кейін әдетте R n® 0 үшін n ® Ґ .

ИНТЕГРАЛДЫҚ ЕСЕПТЕР

Шаршы.

Қисық сызықты жазық фигуралардың аймақтарын зерттеу кезінде математикалық талдаудың жаңа аспектілері ашылады. Тіпті ежелгі гректер де мұндай мәселелерді шешуге тырысты, олар үшін, мысалы, шеңбердің ауданын анықтау ең қиын міндеттердің бірі болды. Архимед бұл мәселені шешуде үлкен жетістікке жетті, ол да параболалық сегменттің ауданын таба алды (12-сурет). Өте күрделі пайымдаулардың көмегімен Архимед параболалық кесіндінің ауданы сипатталған тіктөртбұрыштың 2/3 бөлігін құрайтынын дәлелдеді, сондықтан бұл жағдайда (2/3) (16) тең болады. = 32/3. Кейінірек көретініміздей, бұл нәтижені математикалық талдау әдістері арқылы оңай алуға болады.

Ньютон мен Лейбництің предшественниктері, негізінен Кеплер мен Кавальери қисық сызықты фигуралардың аудандарын есептеу мәселесін логикалық деп атауға қиын, бірақ өте жемісті болып шыққан әдіспен шешті. Уоллис 1655 жылы Кеплер мен Кавальери әдістерін Декарт әдістерімен (аналитикалық геометрия) біріктіріп, жаңадан туған алгебраны қолданғанда Ньютонның пайда болу кезеңі толығымен дайындалды.

Уоллис ауданы есептелуі қажет фигураны өте тар жолақтарға бөлді, олардың әрқайсысы шамамен тіктөртбұрыш болып саналды. Содан кейін ол жақындаған тіктөртбұрыштардың аудандарын қосты және ең қарапайым жағдайларда, жолақтар саны шексіздікке ұмтылған кезде тіктөртбұрыштардың аудандарының қосындысы бейім болатын мәнді алды. күріште. 13 қисық астындағы аумақтың жолақтарына кейбір бөлуге сәйкес тіктөртбұрыштарды көрсетеді ж = x 2 .

Негізгі теорема.

Ньютон мен Лейбництің ұлы ашылуы аумақтар қосындысының шегіне өтудің ауыр процесін жоққа шығаруға мүмкіндік берді. Бұл шаршы ұғымына жаңа көзқарастың арқасында жасалды. Мәселе мынада: ординатаның солдан оңға қарай жылжуы нәтижесінде пайда болатын қисық астындағы ауданды елестетіп, ординаталардың сыпырылған аймағының қаншалықты жылдам өзгеретінін сұрау керек. Ауданы алдын ала белгілі екі ерекше жағдайды қарастырсақ, бұл сұраққа жауаптың кілтін аламыз.

Сызықтық функцияның графигі астындағы ауданнан бастайық ж = 1 + xөйткені бұл жағдайда ауданды қарапайым геометрия арқылы есептеуге болады.

Болсын А(x) Түзу сызықтың арасына салынған жазықтықтың бөлігі ж = 1 + xжәне сегмент OQ(Cурет 14). Көлік жүргізу кезінде QPоң аймақ А(x) артады. Қаншалықты жылдам? Бұл сұраққа жауап беру қиын емес, өйткені біз трапецияның ауданы оның биіктігінің табандарының жарты қосындысына көбейтіндісіне тең екенін білеміз. Демек,

Ауданның өзгеру жылдамдығы А(x) оның туындысы арқылы анықталады

Біз мұны көреміз Аў ( x) ординатамен сәйкес келеді сағұпай Р... Бұл кездейсоқтық па? Суретте көрсетілген параболаны тексеріп көрейік. 15. Шаршы А (x) парабола астында сағ = X 0-ден 2-ге дейінгі аралықта Xтең А(x) = (1 / 3)(x)(x 2) = x 3/3. Бұл аймақтың өзгеру жылдамдығы өрнекпен анықталады

ол ординатамен дәл сәйкес келеді сағқозғалатын нүкте Р.

Егер бұл ереже жалпы түрде осылай орындалады деп есептесек

функцияның графигі астындағы ауданның өзгеру жылдамдығы болып табылады ж = f(x), онда оны есептеулер және басқа аймақтар үшін пайдалануға болады. Шын мәнінде, қатынас Аў ( x) = f(x) іргелі теореманы өрнектейді, оны келесідей тұжырымдауға болады: туынды немесе функция ретінде ауданның өзгеру жылдамдығы. X, функциясының мәніне тең f (x) нүктесінде X.

Мысалы, функцияның графигінің астындағы ауданды табу ж = x 3-ден 0-ге дейін X(Cурет 16), біз қойдық

Мүмкін жауап:

туындысынан бастап X 4/4 шынымен тең X 3. Оның үстіне, А(x) үшін нөлге тең X= 0, егер болуы керек болса А(x) шынымен де аумақ болып табылады.

Математикалық талдау жоғарыда көрсетілген өрнектен басқа басқа жауап екенін дәлелдейді А(x), жоқ. Төмендегі эвристикалық (қатаң емес) пайымдауды пайдаланып, бұл мәлімдеменің орынды екенін көрсетейік. Екінші шешім бар делік В(x). Егер А(x) және В(x) «Бастау» бір уақытта нөлдік мәннен бастап X= 0 және барлық уақытта бірдей жылдамдықпен өзгереді, содан кейін олардың мәндері жоқ Xбасқаша бола алмайды. Олар барлық жерде бірдей болуы керек; сондықтан бір ғана шешім бар.

Пропорцияны қалай негіздеуге болады? Аў ( x) = f(x) жалпы алғанда? Бұл сұраққа функция ретінде ауданның өзгеру жылдамдығын зерттеу арқылы ғана жауап беруге болады Xжалпы алғанда. Болсын м- функцияның ең кіші мәні f (x) аралығында Xбұрын ( x + h), а М- осы функцияның сол интервалдағы ең үлкен мәні. Содан кейін бастап бара жатқан ауданның ұлғаюы XКімге ( x + h) екі тіктөртбұрыштың аудандары арасында қоршалу керек (Cурет 17). Екі төртбұрыштың да табандары тең h... Кіші тіктөртбұрыштың биіктігі бар мжәне аумақ мх, сәйкесінше үлкенірек, Мжәне Мх... Ауданның учаскесі бойынша X(18-сурет) абсциссаның өзгеретінін көруге болады h, ординатаның мәні (яғни, аудан) арасына бекітілген мөлшерге артады. мхжәне Мх... Бұл графиктегі секанттық еңіс арасында мжәне М... қашан не болады hнөлге ұмтылады? Функцияның графигі болса ж = f(x) үздіксіз (яғни үзілістерді қамтымайды), онда М, және мбейім f(x). Сондықтан еңіс Аў ( x) функциясы ретінде ауданның учаскесі Xтең f(x). Дәл осындай қорытындыға келуге тура келді.

Лейбниц қисық астындағы ауданды ұсынды ж = f(x) 0-ден абелгілеу

Қатаң көзқараспен бұл анықталған интегралды Уоллис әдісімен белгілі бір соманың шегі ретінде анықтау керек. Жоғарыда келтірілген нәтижені ескере отырып, мұндай функцияны таба алатын болсақ, бұл интеграл есептелетіні анық А(x), ол жоғалады X= 0 және туындысы бар Аў ( x) тең f (x). Мұндай функцияны табу әдетте интеграция деп аталады, дегенмен бұл операцияны антидифференциация деп атаған дұрысырақ болар еді, яғни ол белгілі бір мағынада дифференциацияға кері. Көпмүше болған жағдайда интегралдау оңай болады. Мысалы, егер

дифференциациялау арқылы тексеру оңай А(x).

Ауданды есептеу үшін А 1 қисық астында ж = 1 + x + x 2/2, 0 және 1 ординаталарының арасына қоршалған, біз жай жазамыз

және алмастыру X= 1, аламыз А 1 = 1 + 1/2 + 1/6 = 5/3. Шаршы А(x) 0-ден 2-ге дейін тең А 2 = 2 + 4/2 + 8/6 = 16/3. Суреттен көрініп тұрғандай. 19, 1 және 2 ординаталарының арасындағы аудан А 2 – А 1 = 11/3. Ол әдетте анықталған интеграл ретінде жазылады

Томдар.

Ұқсас пайымдаулар революция денелерінің көлемдерін есептеуді таңқаларлықтай жеңілдетеді. Ежелгі гректер өздеріне белгілі әдістерді қолдана отырып, үлкен қиындықпен шешкен тағы бір классикалық есеп - доптың көлемін есептеу мысалында осыны көрсетейік.

Радиус шеңберінің төрттен бір бөлігінде орналасқан жазықтықтың бөлігін айналдырыңыз r, ось айналасында 360 ° бұрышта X... Нәтижесінде біз жарты шарды аламыз (20-сурет), оның көлемін біз белгілейміз В(x). жылдамдығын анықтау қажет В(x) артуымен x... Одан әрі қарай XКімге X + h, дыбыс өсімі дыбыс деңгейінен аз екенін тексеру оңай б(r 2 – x 2)hдөңгелек цилиндрдің радиусы мен биіктігі h, және көлемінен көп б[r 2 – (x + h) 2 ]hцилиндрдің радиусы мен биіктігі h... Сондықтан функцияның графигінде В(x) секанттың еңісі арасында б(r 2 – x 2) және б[r 2 – (x + h) 2]. Қашан hнөлге ұмтылады, еңіс ұмтылады

Сағат x = rБіз алып жатырмыз

жарты шардың көлемі үшін, демек 4 p rБүкіл доптың көлемі үшін 3/3.

Ұқсас әдіс қисықтардың ұзындықтарын және қисық беттердің аудандарын табуға мүмкіндік береді. Мысалы, егер а(x) - доғаның ұзындығы PRкүріште. 21, онда біздің міндетіміз есептеу аў( x). Эвристикалық деңгейде біз нәтижені қатаң дәлелдеу үшін қажетті шекке әдеттегі өтуге бармауға мүмкіндік беретін трюкті қолданамыз. Функцияның өзгеру жылдамдығы делік а(x) нүктесінде Рқисық оның жанамасымен ауыстырылса, дәл солай болады PTнүктесінде П... Бірақ суреттен. 21 қадам басқанда тікелей көрінеді hнүктенің оң немесе сол жағына Xбойымен RTмағынасы а(x) өзгереді

Демек, функцияның өзгеру жылдамдығы а(x) болып табылады

Функцияның өзін табу үшін а(x), тек теңдіктің оң жағындағы өрнекті біріктіру қажет. Көптеген функцияларды біріктіру қиын екені белгілі болды. Сондықтан интегралдық есептеу әдістерінің дамуы математикалық талдаудың үлкен бөлігін құрайды.

Антитуындылар.

Туындысы берілген функцияға тең әрбір функция f(x), үшін антитуынды (немесе қарабайыр) деп аталады f(x). Мысалы, X 3/3 - функцияның қарсы туындысы X 2, бері ( x 3/3) ў = x 2. Әрине X 3/3 функцияның жалғыз антитуындысы емес X 2 бері x 3 /3 + Cүшін де туынды болып табылады X 2 кез келген тұрақты үшін МЕН... Дегенмен, келесіде біз мұндай қосымша тұрақтыларды алып тастауға келісеміз. Жалпы алғанда

қайда nНатурал сан, өйткені ( x n + 1/(n+ 1)) ў = x n... (1) қатынасы одан да жалпы мағынада орындалады if nкез келген рационал санмен ауыстырыңыз к-1 қоспағанда.

Берілген функция үшін ерікті антитуынды функция f(x) әдетте анықталмаған интегралы деп аталады f(x) және оны ретінде белгілеңіз

Мысалы, бері (күнә x) ў = cos x, формула жарамды

Көптеген жағдайларда, берілген функцияның анықталмаған интегралы үшін формула болған кезде, оны анықталмаған интегралдардың көптеген кеңінен жарияланған кестелерінен табуға болады. Элементар функциялардың интегралдары кестелік (бұған дәрежелер, логарифмдер, көрсеткіштік функция, тригонометриялық функциялар, кері тригонометриялық функциялар, сонымен қатар қосу, алу, көбейту және бөлу амалдары арқылы алынған олардың ақырлы комбинациялары жатады). Кестелік интегралдарды пайдалана отырып, күрделірек функциялардың интегралдарын есептеуге болады. Анықталмаған интегралды есептеудің көптеген әдістері бар; олардың ең көп тарағаны айнымалы алмастыру немесе алмастыру әдісі. Ол анықталмаған интегралға ауыстырғымыз келсе (2) xкейбір дифференциалданатын функция бойынша x = g(u), интеграл өзгермеуі үшін қажет xауыстырылды gў ( u)ду... Басқаша айтқанда, теңдік

(2 ауыстыру x = u, қайдан 2 dx = ду).

Міне, тағы бір интеграция әдісі – бөліктер бойынша біріктіру әдісі. Ол бұрыннан белгілі формулаға негізделген

Сол және оң жақтарды біріктіріп, соны ескере отырып

Бұл формула бөліктер бойынша интегралдау формуласы деп аталады.

Мысал 2. Табу керек. Себебі cos x= (күнә x) ў, біз мұны жаза аламыз

(5) бастап, орнату u = xжәне v= күнә x, Біз алып жатырмыз

Содан бері (– cos x) ў = күнә xбіз оны табамыз және

Айта кету керек, біз көптеген тапқыр әдістер жинақталған өте кең тақырыпқа өте қысқаша кіріспемен ғана шектелдік.

Екі айнымалының функциялары.

Қисықтың арқасында ж = f(x) біз екі тапсырманы қарастырдық.

1) Берілген нүктедегі қисыққа жанаманың еңісін табыңыз. Бұл есеп туындының мәнін есептеу арқылы шешіледі fў ( x) көрсетілген нүктеде.

2) Ось сегментінің үстіндегі қисық астындағы ауданды табыңыз Xтік сызықтармен шектелген X = ажәне X = б... Бұл есеп анықталған интегралды есептеу арқылы шешіледі.

Осы мәселелердің әрқайсысының бетінің жағдайында аналогы бар z = f(x,ж).

1) Берілген нүктеде бетке жанама жазықтықты табыңыз.

2) Жазықтық бөлігінің үстіндегі беттің астындағы көлемді табыңыз хуқисықпен шектелген МЕН, ал бүйірден - жазықтыққа перпендикулярлар xyшекаралық қисық нүктелері арқылы өтетін МЕН (см... күріш. 22).

Келесі мысалдар бұл тапсырмалардың қалай орындалатынын көрсетеді.

Мысал 4. Бетке жанама жазықтықты табыңыз

нүктесінде (0,0,2).

Жазықтық анықталады, егер оның ішінде жатқан екі қиылысатын түзу берілсе. Осы жолдардың бірі ( л 1) Ұшаққа мінеміз xz (сағ= 0), екіншісі ( л 2) - жазықтықта yz (x = 0) (см... күріш. 23).

Ең алдымен, егер сағ= 0, онда z = f(x,0) = 2 – 2x – 3x 2. қатысты туынды Xарқылы белгіленеді fў x(x,0) = –2 – 6x, сағ X= 0 мәні –2 мәніне ие. Түзу л 1 теңдеулер арқылы берілген z = 2 – 2x, сағ= 0 - жанама МЕН 1, беттің жазықтықпен қиылысу сызықтары сағ= 0. Сол сияқты, егер X= 0, онда f(0,ж) = 2 – ж – ж 2, және қатысты туынды сағпішіні бар

Өйткені fў ж(0,0) = –1, қисық МЕН 2 – беттің жазықтықпен қиылысу сызығы yz- тангенсі бар л 2 теңдеулер арқылы берілген z = 2 – ж, X= 0. Қажетті жанама жазықтықта екі түзу де бар л 1 және л 2 және теңдеу арқылы жазылады

Бұл жазықтықтың теңдеуі. Сонымен қатар, біз түзу сызықтарды аламыз л 1 және л 2, сәйкесінше, сағ= 0 және X = 0.

(7) теңдеу шын мәнінде жанама жазықтықты анықтайтынын эвристикалық деңгейде тексеруге болады, егер бұл теңдеуде (6) теңдеуге енгізілген бірінші ретті мүшелер бар екенін және екінші ретті мүшелерді мына формулада көрсетуге болатынын байқасақ. нысаны -. Бұл өрнек барлық мәндер үшін теріс болғандықтан Xжәне сағ, Сонымен қатар X = сағ= 0, (6) беті нүктеден басқа (7) жазықтықтың астында барлық жерде жатыр Р= (0,0,0). (6) бетін нүктеде жоғары қарай дөңес деп айта аламыз Р.

Мысал 5. Бетке жанама жазықтықты табыңыз z = f(x,ж) = x 2 – ж 2 бастауында 0.

Бетінде сағ= 0 бізде: z = f(x,0) = x 2 және fў x(x,0) = 2x... Үстінде МЕН 1, қиылысу сызықтары, z = x 2. Нүктеде Оеңіс болып табылады fў x(0,0) = 0. Жазықтықта X= 0 бізде: z = f(0,ж) = –ж 2 және fў ж(0,ж) = –2ж... Үстінде МЕН 2, қиылысу сызықтары, z = –ж 2. Нүктеде Оқисықтың еңісі МЕН 2 тең fў ж(0,0) = 0. Жанамалары болғандықтан МЕН 1 және МЕН 2 осьтер Xжәне сағ, оларды қамтитын жанама жазықтық — жазықтық z = 0.

Дегенмен, бастауға жақын жерде біздің бетіміз жанама жазықтықтың бір жағында емес. Шынында да, қисық МЕН 0 нүктесінен басқа барлық жерде 1 жанама жазықтық пен қисық сызықтың үстінде жатыр МЕН 2 - тиісінше оның астында. Беткей жанама жазықтықпен қиылысады z= 0 түзу сағ = Xжәне сағ = –X... Мұндай беттің басында седла нүктесі бар деп аталады (24-сурет).

Жартылай туындылар.

Алдыңғы мысалдарда біз туынды сөздерді қолдандық f (x,ж) қосулы Xжәне арқылы сағ... Енді мұндай туындыларды жалпылама қарастырайық. Егер бізде екі айнымалы функция болса, мысалы, Ф(x,ж) = x 2 – xy, содан кейін біз әрбір нүктеде оның екі «жартылай туындыларын» анықтай аламыз, біреуін функцияға қатысты дифференциалдау арқылы Xжәне бекіту сағ, екіншісіне қатысты ажырату арқылы сағжәне бекіту X... Осы туындылардың біріншісі ретінде белгіленеді fў x(x,ж) немесе ¶ f/¶ x; екінші – қалай f f ў ж... Егер аралас туындылардың екеуі де болса ( Xжәне сағ, қосулы сағжәне X) үздіксіз болса, ¶ 2 f/¶ x¶ ж= ¶ 2 f/¶ ж¶ x; біздің мысалда ¶ 2 f/¶ x¶ ж= ¶ 2 f/¶ ж¶ x = –1.

Жартылай туынды fў x(x,ж) функцияның өзгеру жылдамдығын көрсетеді fнүктесінде ( x,ж) арттыру бағытында X, а fў ж(x,ж) Функцияның өзгеру жылдамдығы fкөтерілу бағыты сағ... Функцияның өзгеру жылдамдығы fнүктесінде ( X,сағ) бұрыш жасайтын түзу бағытында qосьтің оң бағытымен X, функциясының туындысы деп аталады fқарай; оның мәні функцияның екі жартылай туындыларының қосындысы болып табылады Жанама жазықтықтағы f дерлік тең (кіші dxжәне dy) шынайы өзгеріс zбетінде, бірақ дифференциалды есептеу әдетте оңайырақ.

Бір өлшемді жағдайда күрделі функцияның туындысы немесе тізбек ережесі ретінде белгілі айнымалыны өзгерту әдісінен қарастырған формула сағбайланысты X, а Xбайланысты т, пішіні бар:

Екі айнымалы функциялар үшін ұқсас формула:

Жоғары өлшемдерге ішінара дифференциалдау ұғымдары мен белгілеулерін жалпылау оңай. Атап айтқанда, егер бет жанама түрде теңдеу арқылы берілсе f(x,ж,z) = 0, бетке жанама жазықтықтың теңдеуін неғұрлым симметриялы түрде беруге болады: нүктедегі жанама жазықтықтың теңдеуі ( x (x 2/4)], содан кейін ол біріктіріледі X 0-ден 1-ге дейін. Соңғы нәтиже 3/4 құрайды.

Формула (10) қосарланған интеграл деп те түсіндіріледі, яғни. элементар «клеткалардың» көлемдерінің қосындысының шегі ретінде. Әрбір мұндай ұяшықта D негізі болады x D жжәне тікбұрышты негіздің кейбір нүктесінен жоғары бетінің биіктігіне тең биіктік ( см... күріш. 26). (10) формула бойынша екі көзқарастың да эквивалент екенін көрсетуге болады. Қос интегралдар ауырлық центрлерін және механикада кездесетін көптеген моменттерді табу үшін қолданылады.

Математикалық аппаратты неғұрлым қатаң негіздеу.

Осы уақытқа дейін біз интуитивті деңгейде есептеудің тұжырымдамалары мен әдістерін ұсындық және геометриялық пішіндерге жүгінуден тартынбадық. Бізге 19-20 ғасырларда пайда болған неғұрлым қатаң әдістерді қысқаша қарастыру қалады.

19-ғасырдың басында «математикалық талдау жасаудағы» шабуылдар мен шабуылдар дәуірі аяқталғанда, оны негіздеу сұрақтары алға шықты. Абель, Коши және басқа да бірқатар көрнекті математиктердің еңбектерінде «шектік», «үзіліссіз функция», «жиналғыш қатарлар» ұғымдарына нақты анықтама берілген. Бұл математикалық талдауды сенімді зерттеу құралына айналдыру үшін оның негізіне логикалық тәртіпті келтіру үшін қажет болды. Егжей-тегжейлі негіздеудің қажеттілігі 1872 жылы Вейерштрасс барлық жерде үздіксіз, бірақ ешбір жерде дифференциалданбайтын функцияларды ашқаннан кейін (мұндай функциялардың графигінде әр нүктеде үзіліс бар) одан да айқын болды. Бұл нәтиже математиктерге керемет әсер қалдырды, өйткені бұл олардың геометриялық интуициясына анық қайшы болды. Геометриялық интуицияның сенімсіздігінің одан да жарқын мысалы Д.Пеано құрастырған үздіксіз қисық болды, ол белгілі бір шаршыны толығымен толтырады, яғни. оның барлық нүктелері арқылы өтеді. Осы және басқа да ашылулар математиканы «арифметизациялау» бағдарламасын тудырды, т.б. сан ұғымын пайдалана отырып, барлық математикалық ұғымдарды негіздеу арқылы оны сенімдірек ету. Математика негіздері туралы еңбектердегі анықтықтан дерлік пуритандық тартыну өзінің тарихи негіздемесіне ие болды.

Логикалық қатаңдықтың заманауи канондарына сәйкес, қисық астындағы аудан туралы айтуға болмайды. ж = f(x) және ось сегментінің үстінде X, тіпті f- алдымен «аудан» терминінің нақты мағынасын анықтамай және осылайша анықталған аумақтың шынымен бар екенін дәлелдемейтін үздіксіз функция. Бұл мәселені 1854 жылы Б.Риман сәтті шешіп, анықталған интеграл ұғымына нақты анықтама берді. Содан бері белгілі бір интеграл түсінігінің астарында жинақтау идеясы көптеген терең зерттеулер мен жалпылаулардың нысаны болды. Нәтижесінде, бүгінгі таңда интеграл барлық жерде үзіліссіз болса да, белгілі бір интегралға мән беруге болады. Интеграцияның жаңа концепциялары, олардың жасалуына А.Лебесг (1875–1941) және басқа математиктер үлкен үлес қосты, қазіргі математикалық талдаудың күші мен сұлулығын арттырды.

Осы және басқа да ұғымдардың барлығына егжей-тегжейлі тоқталу дұрыс болмас еді. Біз шек пен анықталған интегралдың қатаң анықтамаларын берумен ғана шектелеміз.

Қорытындылай келе, математикалық талдау ғалым мен инженердің қолындағы аса құнды құрал бола отырып, бүгінгі күні де жемісті ойлардың қайнар көзі ретінде математиктердің назарын аударып отырғанын айта кетейік. Сонымен қатар, қазіргі заманғы даму математикалық талдаудың 20-шы ғасырда мұндай үстемдікке көбірек сіңіп бара жатқанын көрсететін сияқты. абстрактілі алгебра және топология сияқты математиканың салалары.

Туындыны және оны есептеу әдістерін білмейінше математикадағы физикалық есептерді немесе мысалдарды шешу мүлдем мүмкін емес. Туынды – математикалық талдаудың маңызды ұғымдарының бірі. Біз бүгінгі мақаланы осы іргелі тақырыпқа арнауды шештік. Туынды дегеніміз не, оның физикалық және геометриялық мағынасы қандай, функцияның туындысы қалай есептеледі? Барлық осы сұрақтарды біріктіруге болады: туындыны қалай түсінуге болады?

Туындының геометриялық және физикалық мағынасы

Функция болсын f (x) белгілі бір аралықта беріледі (а, б) ... Осы интервалға х және х0 нүктелері жатады. х өзгерген кезде функцияның өзі өзгереді. Аргументті өзгерту – оның мәндері арасындағы айырмашылық x-x0 ... Бұл айырмашылық былай жазылады дельта x және аргумент өсімі деп аталады. Функцияның өзгеруі немесе артуы - бұл функцияның екі нүктедегі мәндерінің айырмашылығы. Туынды анықтамасы:

Функцияның нүктедегі туындысы - берілген нүктедегі функция өсімінің соңғысы нөлге ұмтылған кездегі аргумент өсіміне қатынасының шегі.

Әйтпесе, оны былай жазуға болады:

Мұндай шекті табудың мәні неде? Міне, мыналар:

нүктедегі функцияның туындысы OX осі арасындағы бұрыштың тангенсіне және осы нүктедегі функция графигіне жанамаға тең.

Туындының физикалық мағынасы: жолдың уақытқа қатысты туындысы түзу сызықты қозғалыс жылдамдығына тең.

Шынында да, мектеп кезінен бәрі жылдамдықтың жеке жол екенін біледі. x = f (t) және уақыт т ... Белгілі бір уақыт аралығындағы орташа жылдамдық:

Бір уақыттағы қозғалыс жылдамдығын білу t0 шектеуді есептеу керек:

Бірінші ереже: тұрақтыны алыңыз

Тұрақты шаманы туындының белгісінен тыс жылжытуға болады. Оның үстіне мұны істеу керек. Математикадан мысалдарды шешкенде, ережеге сәйкес алыңыз - өрнекті жеңілдете алсаңыз, жеңілдетуді ұмытпаңыз .

Мысал. Туындыны есептейік:

Екінші ереже: функциялар қосындысының туындысы

Екі функцияның қосындысының туындысы осы функциялардың туындыларының қосындысына тең. Функциялар айырмасының туындысы үшін де солай.

Біз бұл теореманың дәлелін бермейміз, керісінше практикалық мысалды қарастырамыз.

Функцияның туындысын табыңыз:

Үшінші ереже: функциялар туындысының туындысы

Екі дифференциалданатын функцияның туындысының туындысы мына формуламен есептеледі:

Мысалы: функцияның туындысын табыңыз:

Шешімі:

Бұл жерде күрделі функциялардың туындыларын есептеу туралы айту маңызды. Күрделі функцияның туындысы осы функцияның аралық аргументке қатысты туындысының тәуелсіз айнымалыға қатысты аралық аргументтің туындысына көбейтіндісіне тең.

Жоғарыдағы мысалда біз өрнекті кездестіреміз:

Бұл жағдайда аралық аргумент бесінші дәрежеге 8x. Мұндай өрнектің туындысын есептеу үшін алдымен аралық аргументке қатысты сыртқы функцияның туындысын есептеп шығарамыз, содан кейін тәуелсіз айнымалыға қатысты тікелей аралық аргументтің туындысына көбейтеміз.

Төртінші ереже: екі функцияның туынды туындысы

Екі функцияның бөліндісінің туындысын анықтау формуласы:

Біз сізге нөлден бастап манекендерге арналған туындылар туралы айтуға тырыстық. Бұл тақырып көрінгендей қарапайым емес, сондықтан ескертіңіз: мысалдарда қателер жиі кездеседі, сондықтан туындыларды есептеу кезінде абай болыңыз.

Осы және басқа да тақырыптар бойынша кез келген сұрақтар бойынша студенттік қызметке хабарласуға болады. Қысқа уақыт ішінде біз сізге ең қиын сынақты шешуге және бұрын ешқашан туынды құралдарды есептеумен айналыспаған болсаңыз да, тапсырмаларды шешуге көмектесеміз.

Ол бойынша біз ең қарапайым туындыларды талдадық, сонымен қатар дифференциалдау ережелерімен және туындыларды табудың кейбір әдістерімен таныстық. Осылайша, егер сіз функциялардың туындыларымен онша таныс болмасаңыз немесе осы мақаланың кейбір тармақтары толығымен түсініксіз болса, алдымен жоғарыдағы сабақты оқып шығыңыз. Өтінемін, байсалды көңіл-күйді реттеңіз - материал оңай емес, бірақ мен оны қарапайым және қол жетімді етіп көрсетуге тырысамын.

Практикада күрделі функцияның туындысымен өте жиі айналысуға тура келеді, тіпті туындыларды табу тапсырмалары берілгенде дерлік дерлік дер едім.

Күрделі функцияны дифференциалдау үшін кестеден ережені (No5) қарастырамыз:

Түсіну. Ең алдымен, жазбаға назар аударайық. Мұнда бізде екі функция бар - және, оның үстіне, функция, бейнелеп айтқанда, функцияға енгізілген. Осындай түрдегі функция (бір функция екінші функцияның ішіне салынған кезде) күрделі функция деп аталады.

Мен функцияны шақырамын сыртқы функцияжәне функция - ішкі (немесе кірістірілген) функция.

! Бұл анықтамалар теориялық емес және тапсырмалардың соңғы дизайнында көрсетілмеуі керек. Мен "сыртқы функция", "ішкі" функция бейресми өрнектерді материалды түсінуді жеңілдету үшін ғана қолданамын.

Жағдайды түсіндіру үшін мыналарды қарастырыңыз:

1-мысал

Функцияның туындысын табыңыз

Синустың астында бізде «Х» әрпі ғана емес, бүтін өрнек бар, сондықтан кестеден туындыны бірден табу мүмкін болмайды. Сондай-ақ біз мұнда алғашқы төрт ережені қолдану мүмкін емес екенін байқаймыз, айырмашылық бар сияқты, бірақ синусын «бөліп тастау» мүмкін емес:

Бұл мысалда менің түсініктемелерімнен функцияның күрделі функция, ал көпмүшеліктің ішкі функция (ұя салу) және сыртқы функция екендігі интуитивті түрде анық болды.

Алғашқы қадам, ол күрделі функцияның туындысын табу кезінде орындалуы керек, бұл Қай функция ішкі, қайсысы сыртқы екенін анықтаңыз.

Қарапайым мысалдар жағдайында көпмүше синусының астында орналасқаны анық көрінеді. Бірақ бәрі анық болмаса ше? Қандай функция сыртқы, қайсысы ішкі екенін нақты қалай анықтауға болады? Ол үшін мен ойша немесе нобайда жасауға болатын келесі әдістемені қолдануды ұсынамын.

Калькулятордағы өрнектің мәнін есептеу керек деп елестетіңіз (бір санның орнына кез келген сан болуы мүмкін).

Алдымен нені есептейміз? Бірінші кезектекелесі әрекетті орындау керек:, сондықтан көпмүше ішкі функция болады:

Екіншідентабу керек, сондықтан синус сыртқы функция болады:

Бізден кейін Анықталдыішкі және сыртқы функциялары бар, күрделі функцияны дифференциалдау ережесін қолдану уақыты келді .

Біз шешім қабылдауға кірісеміз. Сабақтан Туындыны қалай табуға болады?Кез келген туындының шешімін жобалау әрқашан осылай басталатынын есте ұстаймыз - өрнекті жақшаға алып, жоғарғы оң жаққа штрих қоямыз:

Біріншісыртқы функцияның (синус) туындысын табыңыз, элементар функциялардың туындылары кестесін қараңыз және оны байқаңыз. Барлық кестелік формулалар "x" күрделі өрнекпен ауыстырылса да қолданылады, Бұл жағдайда:

Ішкі функцияны ескеріңіз өзгерген жоқ, оған тиіспейміз.

Жарайды, бұл анық

Формуланы қолдану нәтижесі соңғы дизайнда келесідей көрінеді:

Тұрақты көбейткіш әдетте өрнектің басына қойылады:

Егер қандай да бір түсініксіздік болса, шешімді жазып, түсініктемелерді қайта оқыңыз.

2-мысал

Функцияның туындысын табыңыз

3-мысал

Функцияның туындысын табыңыз

Әдеттегідей, біз жазамыз:

Бізде қай жерде сыртқы функция бар, ал қай жерде ішкі функция бар екенін анықтайық. Мұны істеу үшін (ойша немесе жобада) өрнектің мәнін есептеп көріңіз. Алдымен не істеу керек? Ең алдымен, негіз неге тең екенін есептеу керек: бұл көпмүше ішкі функция екенін білдіреді:

Және, сонда ғана дәрежеге шығару орындалады, демек, дәреже функциясы сыртқы функция болып табылады:

Формула бойынша , алдымен сыртқы функцияның туындысын, бұл жағдайда дәрежесін табу керек. Біз кестеден қажетті формуланы іздейміз:. Тағы да қайталаймыз: кез келген кестелік формула тек «х» үшін ғана емес, күрделі өрнек үшін де жарамды... Осылайша, күрделі функцияны дифференциалдау ережесін қолдану нәтижесі Келесі:

Мен сыртқы функцияның туындысын қабылдағанда, ішкі функция біз үшін өзгермейтінін тағы да атап өтемін:

Енді ішкі функцияның өте қарапайым туындысын табу және нәтижені аздап «тарақтау» қалады:

4-мысал

Функцияның туындысын табыңыз

Бұл тәуелсіз шешімнің мысалы (жауап оқулықтың соңында).

Күрделі функцияның туындысы туралы түсінікті бекіту үшін мен түсініктемесіз мысал келтіремін, оны өз беттеріңізше анықтауға тырысамын, сыртқы және ішкі функция қайда, неліктен тапсырмалар осылай шешілді?

5-мысал

а) Функцияның туындысын табыңыз

б) Функцияның туындысын табыңыз

6-мысал

Функцияның туындысын табыңыз

Мұнда бізде түбір бар және түбірді ажырату үшін оны дәреже ретінде көрсету керек. Осылайша, алдымен функцияны дифференциалдау үшін қолайлы пішінге келтіреміз:

Функцияны талдай отырып, үш мүшенің қосындысы ішкі функция, ал дәреже көрсеткіші сыртқы функция деген қорытындыға келеміз. Күрделі функцияны дифференциалдау ережесін қолданамыз :

Дәреже қайтадан радикал (түбір) түрінде көрсетіледі және ішкі функцияның туындысы үшін қосындыны дифференциалдаудың қарапайым ережесін қолданамыз:

Дайын. Сондай-ақ өрнекті жақшадағы ортақ бөлгішке әкеліп, барлығын бір бөлшекке жазуға болады. Жақсы, әрине, бірақ қиын ұзын туындылар алынғанда, мұны жасамаған дұрыс (шатастыру оңай, қажетсіз қателік жібереді және мұғалімге тексеру ыңғайсыз болады).

7-мысал

Функцияның туындысын табыңыз

Бұл тәуелсіз шешімнің мысалы (жауап оқулықтың соңында).

Бір қызығы, кейде күрделі функцияны дифференциалдау ережесінің орнына бөлікті дифференциалдау ережесін қолдануға болады. , бірақ мұндай шешім бұрмалау сияқты әдеттен тыс көрінеді. Міне, әдеттегі мысал:

8-мысал

Функцияның туындысын табыңыз

Мұнда бөлімді дифференциалдау ережесін қолдануға болады , бірақ күрделі функцияны дифференциалдау ережесі арқылы туындыны табу әлдеқайда тиімді:

Функцияны дифференциалдау үшін дайындаймыз - минусты туындының белгісінен тыс жылжытамыз және косинусты алымға көтереміз:

Косинус – ішкі функция, дәрежеге шығару – сыртқы функция.
Біз өз ережемізді қолданамыз :

Ішкі функцияның туындысын табыңыз, косинусты қайтадан төмендетіңіз:

Дайын. Қарастырылған мысалда белгілерде шатастырмау маңызды. Айтпақшы, оны ережемен шешуге тырысыңыз , жауаптары сәйкес болуы керек.

9-мысал

Функцияның туындысын табыңыз

Бұл тәуелсіз шешімнің мысалы (жауап оқулықтың соңында).

Осы уақытқа дейін біз күрделі функцияда бір ғана тіркеме болған жағдайларды қарастырдық. Практикалық тапсырмаларда сіз көбінесе туындыларды таба аласыз, оларда ұя салатын қуыршақтар сияқты бірінің ішінде бірінің ішінде 3 немесе тіпті 4-5 функция бірден кірістірілген.

10-мысал

Функцияның туындысын табыңыз

Осы функцияның қосымшаларын түсінейік. Сынақ мәнін пайдаланып өрнекті бағалауға тырысу. Калькуляторға қалай сенер едік?

Алдымен сіз табуыңыз керек, бұл доғаның ең терең ұясы екенін білдіреді:

Сонда бір доғасының квадраты болуы керек:

Соңында, 7-ні қуатқа көтеріңіз:

Яғни, бұл мысалда бізде үш түрлі функция және екі тіркеме бар, ал ішкі функция доға синусы, ал ең сыртқы функция көрсеткіштік функция.

Біз шешуге кірісеміз

Ережеге сәйкес алдымен сыртқы функцияның туындысын алу керек. Туындылар кестесін қарап, көрсеткіштік функцияның туындысын табамыз: Жалғыз айырмашылығы – «х» орнына күрделі өрнек берілген, бұл формуланың дұрыстығын жоққа шығармайды. Сонымен, күрделі функцияны дифференциалдау ережесін қолдану нәтижесі Келесі.