ხელოსნობა

პრობლემების სახეები დრეკადობის თეორიაში. დრეკადობის თეორიის ძირითადი განტოლებები. ამოცანების სახეები დრეკადობის თეორიაში რა არის ელასტიურობის კლასიკური თეორიის შესწავლის საგანი

რუსეთის სახელმწიფო უნივერსიტეტი

ნავთობი და გაზი მათ. I.M. გუბკინა

ტექნიკური მექანიკის დეპარტამენტი

ᲐᲑᲡᲢᲠᲐᲥᲢᲣᲚᲘ

"ელასტიურობის თეორია"

დაასრულა: პოლიაკოვი A.A.

შეამოწმა: ევდოკიმოვი A.P.

მოსკოვი 2011 წელი

ელასტიურობის თეორიის განტოლება

1. შესავალი

სტრესი-დაძაბულობის მდგომარეობის თეორია სხეულის წერტილში

2.1 სტრესის თეორია

2 დეფორმაციის თეორია

3 კავშირი დაძაბულ და დეფორმირებულ მდგომარეობას დრეკადი სხეულებისთვის

დრეკადობის თეორიის ძირითადი განტოლებები. პრობლემების სახეები დრეკადობის თეორიაში

1 დრეკადობის თეორიის ძირითადი განტოლებები

2 პრობლემების ტიპები დრეკადობის თეორიაში

4 დრეკადობის თეორიის განტოლებები გადაადგილებებში (ლამის განტოლებები)

ელასტიურობის თეორიის ვარიაციული პრინციპები

1 შესაძლო გადაადგილების პრინციპი (ლაგრანგის პრინციპი)

2 შესაძლო მდგომარეობების პრინციპი (კასტილანოს პრინციპი)

3 კავშირი ზუსტ ამოხსნასა და ლაგრანჟისა და კასტილიანოს პრინციპებზე დაყრდნობით მიღებულ ამონახსნებს შორის

გამოყენებული ლიტერატურის სია

1. შესავალი

სტრესებისა და დეფორმაციების თეორიები შექმნა ო.კოშიმ. ისინი ჩამოყალიბებულია 1822 წელს პარიზის მეცნიერებათა აკადემიაში წარდგენილ ნაშრომში, რომლის რეზიუმე გამოიცა 1823 წელს და რამდენიმე შემდგომი სტატია. ო. კოშიმ გამოიღო ელემენტარული ტეტრაედრის წონასწორობის სამი განტოლება, დაამტკიცა ტანგენციალური ძაბვების დაწყვილების კანონი, შემოიტანა ძირითადი ღერძებისა და ძირითადი ძაბვების ცნებები და გამოიტანა დიფერენციალური წონასწორობის განტოლებები (ჩვეულებრივ, ისინი არ გამოიყოფა სიძლიერის დროს. მასალები). მან ასევე გააცნო ნორმალური ძაბვის ზედაპირი (კოშის ოთხკუთხედი), რომელზედაც განლაგებულია რადიუსის ვექტორების ბოლოები, რომელთა მიმართულებები ემთხვევა ნორმალების მიმართულებას უბნებისკენ, ხოლო მნიშვნელობა უკუპროპორციულია კვადრატულ ფესვთან. ამ არეში ნორმალური სტრესის აბსოლუტური მნიშვნელობისაა და დადასტურდა, რომ ეს ზედაპირი არის მეორე რიგის ზედაპირი, რომელიც ორიენტირებულია საწყისზე. ნორმალური ძაბვის ზედაპირის ძირითად ღერძებად გადაქცევის შესაძლებლობა მიუთითებს სამი ერთმანეთის ძირითადი პერპენდიკულარული არეების არსებობაზე თითოეულ წერტილში.

მსგავსი ათვლის დაძაბულობის ზედაპირი შემოიღო რუსმა მექანიკოსმა გ.ვ. კოლოსოვი 1933 წელს

სივრცეში სტრესის მდგომარეობის გეომეტრიული ინტერპრეტაცია სტრესების ელიფსოიდის სახით მისცეს გ.ლამმა და ბ.კლაპეირონმა თავიანთ მემუარებში, წარდგენილი პარიზის მეცნიერებათა აკადემიაში 1828 წელს და გამოქვეყნდა 1833 წელს.

დაძაბულობის მდგომარეობის გეომეტრიული წარმოდგენა სიბრტყეზე ერთი რიგის პლატფორმებისთვის, რომელიც გადის მთავარ ღერძზე, დაძაბულობის წრის სახით, შემოგვთავაზა კ. კულმანმა თავის წიგნში 1866 წელს.

სტრესული მდგომარეობის ზოგადი შემთხვევისთვის, მისი ძალიან მკაფიო გეომეტრიული ინტერპრეტაცია სიბრტყეზე მისცა ო. მოჰრმა (ე.წ. წრიული მორის დიაგრამა) 1882 წელს. მისგან რამდენიმე მნიშვნელოვანი დასკვნის გაკეთება შეიძლება. ძირითადი ძაბვების კიდური, იმ უბნების პოზიცია, რომლებშიც ტანგენციალური ძაბვები მაქსიმალურია და ამ მაქსიმალური ათვლის დაძაბულობის მნიშვნელობების შესახებ.

ო. კოშიმ მისცა შტამების განმარტება, გამოიტანა მათი დამოკიდებულება გადაადგილებაზე მცირე დაძაბულობის კონკრეტულ შემთხვევაში (ეს დამოკიდებულებები, როგორც წესი, არ წარმოიქმნება მასალების სიმტკიცის დროს), განსაზღვრა ძირითადი დაძაბულობის და ძირითადი ცნებები. შტამების, და მიღებულია დაძაბულობის კომპონენტების დამოკიდებულება დაძაბულობის კომპონენტებზე, როგორც იზოტროპული, ასევე ანიზოტროპული ელასტიური სხეულისთვის. მასალების წინააღმდეგობისას, როგორც წესი, დადგენილია დაძაბულობის კომპონენტების დამოკიდებულება იზოტროპული სხეულის სტრესის კომპონენტებზე. მათ ჰუკის განზოგადებულ კანონს უწოდებენ, თუმცა, რა თქმა უნდა, ეს სახელი პირობითია, ვინაიდან რ.ჰუკმა არ იცოდა სტრესის ცნება.

ამ დამოკიდებულებებში, კოშიმ პირველად შემოიტანა ორი მუდმივი და ჩამოწერა დაძაბულობის დამოკიდებულება შტამებზე.

მ, ,

თუმცა მოგვიანებით ო.კოშიმ მიიღო L. Navier-ის კონცეფცია. მისი მიხედვით, ელასტიური სხეულები შედგება მოლეკულებისგან, რომელთა შორის დეფორმაციის დროს წარმოიქმნება ძალები, რომლებიც მოქმედებენ მოლეკულების დამაკავშირებელი სწორი ხაზების მიმართულებით და პროპორციულია მოლეკულებს შორის მანძილების ცვლილებისა. მაშინ ანისოტროპული სხეულის ზოგადი შემთხვევისთვის დრეკადობის მუდმივთა რიცხვი არის 15, ხოლო იზოტროპული სხეულისთვის ვიღებთ ერთ დრეკად მუდმივას. ამ ჰიპოთეზას იცავდა ს.პუასონი, დასაწყისში კი – გ.ლამი და ბ.კლაპეირონი. მასზე დაყრდნობით პუასონმა აღმოაჩინა, რომ განივი დაძაბულობის კოეფიციენტი არის 1/4.

დ. გრინმა 1839 წელს გამოიტანა კავშირი შტამებსა და სტრესებს შორის დრეკადი სხეულების მოლეკულური სტრუქტურის ჰიპოთეზის გამოყენების გარეშე. მან ისინი მოიპოვა ენერგიის კონსერვაციის პრინციპზე დაყრდნობით, შემოიტანა დრეკადობის პოტენციალის კონცეფცია და აჩვენა, რომ ექვსი დაძაბულობის კომპონენტის წრფივი დამოკიდებულების გამოყენებისას ძაბვის ექვს კომპონენტზე, 36 კოეფიციენტიდან 21 დამოუკიდებელია, ე.ი. ანისოტროპული სხეული, დრეკადობის მუდმივთა რიცხვი არის 21 იზოტროპული სხეულისთვის დრეკადობის მუდმივთა რაოდენობა ორამდე მცირდება. თეორიას, რომელშიც ანისოტროპული სხეულისთვის დრეკადობის მუდმივთა რიცხვი არის 15, ხოლო იზოტროპული სხეულისთვის 1, ზოგჯერ უწოდებდნენ "იშვიათად მუდმივობას" ან "უნიკონსტანტს", ხოლო თეორიას, რომელშიც ანისოტროპული სხეულის დრეკადობის მუდმივთა რაოდენობაა. 21, ხოლო იზოტროპული 2-ისთვის - "მრავალმუდმივი".

ამ თეორიების მომხრეებს შორის კამათმა აიძულა ფიზიკოსები ექსპერიმენტული კვლევისკენ.

G. Wertheim-მა ღერძულ დაძაბულობაში მინის და ლითონის მილების შიდა მოცულობების გაზომვების საფუძველზე დაადგინა 1848 წელს, რომ განივი დეფორმაციის კოეფიციენტი არ არის 1/4-ის ტოლი. იგი განსხვავებულად თვლიდა სხვადასხვა მასალისთვის, მაგრამ ბევრი მასალისთვის ეს იყო 1/3-თან ახლოს.

ᲓᲐ ᲛᲔ. კუპფერმა, 1853 წელს, ლითონის ღეროების დაჭიმვისა და ბრუნვის ტესტირებისას, ასევე აღმოაჩინა, რომ მოდულების თანაფარდობა ათვლისა და დაჭიმვისას არ შეესაბამება განივი დაძაბულობას ტოლი 1/4.

1855 წელს ფ.ნეიმანმა გამოსცადა მართკუთხა განივი კვეთის ნიმუშები მოსახვევად და გაზომა სხივის ორი სახის ბრუნვის კუთხეები (განივი ტრაპეციულ ფორმას იღებს). შედეგად მან აჩვენა, რომ განივი დეფორმაციის კოეფიციენტი არ არის 1/4-ის ტოლი. გ. კირჩჰოფი, ფ. ნეუმანის სტუდენტი, იმავე დასკვნამდე მივიდა 1859 წელს ჩატარებული ტესტების საფუძველზე მრგვალი სპილენძის ღეროების ერთობლივი ღუნვისა და ტორსიისთვის, ერთ ბოლოზე დალუქული და მეორეზე დატვირთული კონცენტრირებული ძალით. ღეროს გადახვევის კუთხის გაზომვა და მონაკვეთის ბრუნვის კუთხის გაზომვა.

ფოლადის სხვადასხვა კლასის განივი დეფორმაციის კოეფიციენტების დიდი ექსპერიმენტული კვლევა ჩაატარა გ.კირჩჰოფის ერთ-ერთმა სტუდენტმა, მ.ფ. ოკატოვი 1865 - 1866 წლებში შედეგები მოცემულია მის სადოქტორო დისერტაციაში. ერთკრისტალებისგან მოჭრილი წვრილი პრიზმების ტორსიული და ღუნვის ტესტები, ასევე კრისტალების შეკუმშვის ტესტები ერთგვაროვანი თანაბარი შეკუმშვის ქვეშ, ჩაატარა ვ. ვოიგტმა და აღწერა მის მრავალ სტატიაში, მოგვიანებით. გაერთიანდა 1910 წელს გამოცემულ წიგნში, მათ დაადასტურეს მრავალ მუდმივი თეორიის სისწორე.

ანისოტროპული სხეულებისთვის ჰუკის კანონის მათემატიკური სტრუქტურის ღრმა შესწავლა ჩაატარა მექანიკოსმა და ინჟინერმა იან რიჩლევსკიმ 1984 წელს, მის მიერ შემოღებული ელასტიური საკუთრივ მდგომარეობის კონცეფციის საფუძველზე. კერძოდ, მან აჩვენა, რომ 21 დრეკადობის მუდმივი წარმოადგენს ექვს ნამდვილ სიმყარის მოდულს, 12 სიხისტის გამანაწილებელს და სამ კუთხეს.

2. დაძაბულობა-დაძაბულობის მდგომარეობის თეორია სხეულის წერტილში

1 სტრესის თეორია

შინაგანი ძალის ფაქტორები, რომლებიც წარმოიქმნება ელასტიური სხეულის დატვირთვისას, ახასიათებს სხეულის კონკრეტული მონაკვეთის მდგომარეობას, მაგრამ არ პასუხობს კითხვას, თუ რომელი წერტილია ჯვრის მონაკვეთის ყველაზე დატვირთული, ან, როგორც ამბობენ, საშიში წერტილი. აქედან გამომდინარე, აუცილებელია გავითვალისწინოთ გარკვეული დამატებითი რაოდენობა, რომელიც ახასიათებს სხეულის მდგომარეობას მოცემულ წერტილში.

თუ სხეული, რომელზეც გარე ძალები გამოიყენება, წონასწორობაშია, მაშინ შინაგანი წინააღმდეგობის ძალები წარმოიქმნება მის ნებისმიერ მონაკვეთში. აღვნიშნოთ ელემენტარული ფართობზე მოქმედი შინაგანი ძალით, ხოლო ამ ფართობის ნორმალური მნიშვნელობით

სრული ძაბვა ეწოდება.

ზოგადად, მთლიანი სტრესი არ ემთხვევა მიმართულებით ნორმალურს ელემენტარულ ზონაში, ამიტომ უფრო მოსახერხებელია მისი კომპონენტებით მუშაობა კოორდინატთა ღერძების გასწვრივ -

თუ გარე ნორმა ემთხვევა რომელიმე კოორდინატულ ღერძს, მაგალითად, X ღერძს, მაშინ დაძაბულობის კომპონენტები მიიღებენ ფორმას, ხოლო კომპონენტი აღმოჩნდება მონაკვეთის პერპენდიკულარული და ეწოდება ნორმალური სტრესი, და კომპონენტები დევს მონაკვეთის სიბრტყე და ეწოდება ათვლის ძაბვები.

ნორმალური და ათვლის ძაბვის მარტივად გასარჩევად, ჩვეულებრივ გამოიყენება სხვა აღნიშვნები: - ნორმალური ძაბვა, - ათვლის.

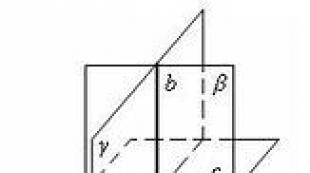
გარე ძალების მოქმედების ქვეშ მყოფი სხეულიდან გამოვყოთ უსასრულოდ პატარა პარალელეპიპედი, რომლის სახეები კოორდინატთა სიბრტყეების პარალელურია, ხოლო კიდეებს აქვს სიგრძე. ასეთი ელემენტარული პარალელეპიპედის თითოეულ სახეზე არის სამი სტრესის კომპონენტი, რომლებიც პარალელურია კოორდინატთა ღერძებთან. საერთო ჯამში, ექვს სახეზე ვიღებთ სტრესის 18 კომპონენტს.

ნორმალური სტრესები აღინიშნება როგორც , სადაც ინდექსი აღნიშნავს ნორმას შესაბამის სახეზე (ანუ მას შეუძლია მიიღოს მნიშვნელობები). ათვლის ძაბვებს აქვთ ფორმა; აქ პირველი მაჩვენებელი შეესაბამება იმ ადგილის ნორმას, რომელზეც მოქმედებს მოცემული ათვლის ძაბვა, ხოლო მეორე მიუთითებს იმ ღერძზე, რომლის პარალელურადაც მიმართულია ეს ძაბვა (ნახ. 1).

ნახ.1. ნორმალური და ათვლის ძაბვები

ამ ძაბვებისთვის მიღებულია შემდეგი ნიშნის წესი. ნორმალური სტრესი განიხილება დადებითად დაძაბულობაში, ან ექვივალენტურად, როდესაც იგი ემთხვევა გარე ნორმალის მიმართულებას იმ ადგილისკენ, რომელზეც ის მოქმედებს. ტანგენციალური სტრესი დადებითად ითვლება, თუ იმ ადგილზე, რომლის ნორმაც ემთხვევა მის პარალელურად კოორდინატთა ღერძის მიმართულებას, ის მიმართულია ამ ძაბვის შესაბამისი დადებითი კოორდინატთა ღერძისკენ.

სტრესის კომპონენტები სამი კოორდინატის ფუნქციებია. მაგალითად, ნორმალური სტრესი კოორდინატებით წერტილში შეიძლება აღინიშნოს

იმ წერტილში, რომელიც განსახილველისგან უსასრულოდ მცირე მანძილზეა, ძაბვა, პირველი რიგის უსასრულო ზომებამდე, შეიძლება გაფართოვდეს ტეილორის სერიაში:

პლატფორმებისთვის, რომლებიც სიბრტყის პარალელურად არიან, იცვლება მხოლოდ x-კოორდინატი და მატება, ამიტომ პარალელეპიპედის სახეზე, რომელიც სიბრტყეს ემთხვევა, ნორმალური ძაბვა იქნება. აქედან გამომდინარე, ძაბვის 18 კომპონენტიდან მხოლოდ ცხრაა უცნობი.

დრეკადობის თეორიაში დადასტურებულია ათვლის ძაბვების დაწყვილების კანონი, რომლის მიხედვითაც, ორი ურთიერთ პერპენდიკულარული უბნის გასწვრივ, ათვლის დაძაბულობის კომპონენტები, ამ უბნების გადაკვეთის ხაზებზე პერპენდიკულარული, ერთმანეთის ტოლია:

ტოლობები (2) მივყავართ იმ ფაქტს, რომ ცხრა სტრესული კომპონენტიდან, რომელიც ახასიათებს სტრესის მდგომარეობას სხეულის წერტილში, რჩება მხოლოდ ექვსი:

შეიძლება ნაჩვენები იყოს, რომ სტრესები (3) არა მხოლოდ ახასიათებს სხეულის სტრესულ მდგომარეობას მოცემულ წერტილში, არამედ განსაზღვრავს მას ცალსახად. ამ სტრესების კომბინაცია ქმნის სიმეტრიულ მატრიცას, რომელსაც სტრესის ტენსორი ეწოდება:

(4)

ტენზორის სკალარული სიდიდეზე გამრავლებისას მიიღება ახალი ტენსორი, რომლის ყველა კომპონენტი ჯერ უფრო დიდია, ვიდრე საწყისი ტენზორის კომპონენტები.

2 დეფორმაციის თეორია

გარე დატვირთვების გავლენით ელასტიური სხეული იცვლის ფორმას და დეფორმირდება. ამ შემთხვევაში, სხეულის წერტილები ახალ პოზიციას იკავებენ. დრეკადი სხეულის დეფორმაციის დასადგენად, ვადარებთ სხეულის წერტილების პოზიციებს დატვირთვის გამოყენებამდე და მის შემდეგ.

განვიხილოთ დატვირთული სხეულის წერტილი და მისი ახალი პოზიცია დატვირთვის გამოყენების შემდეგ. ვექტორს ეწოდება წერტილის გადაადგილების ვექტორი (ნახ. 2).

ნახ.2. წერტილის მოძრავი ვექტორი

შესაძლებელია ორი სახის გადაადგილება: მთლიანი სხეულის გადაადგილება დეფორმაციის გარეშე - ასეთ გადაადგილებებს თეორიული მექანიკა სწავლობს, როგორც აბსოლუტურად ხისტი სხეულის გადაადგილება, და სხეულის დეფორმაციასთან დაკავშირებული გადაადგილება - ასეთ გადაადგილებებს სწავლობს თეორია. ელასტიურობის.

მოდით, დანიშნოთ წერტილოვანი გადაადგილების ვექტორის პროგნოზები კოორდინატთა ღერძებზე შესაბამისად. ისინი უდრის სხვაობას წერტილების შესაბამის კოორდინატებს შორის და:

და არის კოორდინატების ფუნქციები:

სხეულის დეფორმაცია გამოწვეულია მისი სხვადასხვა წერტილების გადაადგილების სხვაობით. უსასრულოდ პატარა პარალელეპიპედი ელასტიური სხეულისგან ამოჭრილი კიდეებით თვითნებურ წერტილთან ახლოს, მისი წერტილების სხვადასხვა გადაადგილების გამო, დეფორმირებულია ისე, რომ იცვლება მისი კიდეების სიგრძე და სახეებს შორის თავდაპირველად სწორი კუთხეები დამახინჯებულია.

ნახაზი 3.3 გვიჩვენებს ამ პარალელეპიპედის ორ კიდეს: და კიდის სიგრძე ტოლია და კიდე არის

დეფორმაციის შემდეგ წერტილები იკავებენ პოზიციას.ამ შემთხვევაში წერტილი მიიღებს გადაადგილებას, რომლის კომპონენტები ნახაზის სიბრტყეში ტოლია, ხოლო წერტილიდან გამოყოფილი წერტილი უსასრულოდ მცირე მანძილზე მიიღებს გადაადგილებას. რომლის კომპონენტები განსხვავდებიან წერტილის გადაადგილების კომპონენტებისგან უსასრულო მნიშვნელობით კოორდინატის ცვლილების გამო

ნახ.3. წრფივი და კუთხოვანი დეფორმაციები

წერტილის გადაადგილების კომპონენტები განსხვავდებიან წერტილის გადაადგილების კომპონენტებისგან უსასრულო მნიშვნელობით კოორდინატის ცვლილების გამო.

ნეკნის პროექციის სიგრძე ღერძზე დეფორმაციის შემდეგ:

ნეკნის აბსოლუტური დრეკადობის პროექცია ღერძზე

შედარებითი დრეკადობა ღერძის გასწვრივ

(6)

ეწოდება წრფივი დეფორმაცია ღერძის მიმართულებით.

ანალოგიურად, ხაზოვანი დეფორმაციები ღერძების მიმართულებით და

(7)

განვიხილოთ პარალელეპიპედის კიდეებს შორის კუთხეების ცვლილება (ნახ. 3). სიბრტყეში ნეკნის ბრუნვის კუთხის ტანგენსი

დეფორმაციების სიმცირის გამო a, წრფივი დეფორმაცია შეიძლება იყოს უგულებელყოფილი მისი სიმცირის გამო ერთიანობასთან შედარებით და შემდეგ

ანალოგიურად, შეგიძლიათ განსაზღვროთ ნეკნის ბრუნვის კუთხე იმავე სიბრტყეში:

მართი კუთხის დამახინჯებას ეწოდება კუთხოვანი დეფორმაცია და განისაზღვრება, როგორც ნეკნების ბრუნვის კუთხეების ჯამი და:

(8)

ანალოგიურად, განისაზღვრება კუთხური დეფორმაციები ორ სხვა კოორდინატულ სიბრტყეში:

(9)

ფორმულები (6)-(9) იძლევა ექვს ძირითად დამოკიდებულებას წრფივი და კუთხოვანი დეფორმაციებისთვის გადაადგილების კომპონენტებზე. ამ დამოკიდებულებებს უწოდებენ კოშის განტოლებებს:

(10)

იმ ზღვარში, როდესაც პარალელეპიპედის კიდეების სიგრძე ნულისკენ მიისწრაფვის, კოშის მიმართებები განსაზღვრავს წრფივ და კუთხურ დეფორმაციებს წერტილის სიახლოვეს.

დადებითი ხაზოვანი დეფორმაციები შეესაბამება დრეკადებს, ხოლო უარყოფითი - შემოკლებებს. ცვლის კუთხე დადებითად ითვლება, როდესაც კუთხე შესაბამისი კოორდინატთა ღერძების დადებით მიმართულებებს შორის მცირდება და უარყოფითი - წინააღმდეგ შემთხვევაში.

დაძაბულობის ტენზორის მსგავსად, სხეულის დეფორმირებული მდგომარეობა მოცემულ წერტილში აღწერილია დაძაბულობის ტენსორის მიერ.

(11)

სტრესის ტენსორის მსგავსად, დაძაბულობის ტენსორი არის სიმეტრიული მატრიცა, რომელიც შეიცავს ცხრა კომპონენტს, რომელთაგან ექვსი განსხვავებულია.

2.3 კავშირი სტრესსა და დაძაბვას შორის ელასტიური სხეულებისთვის

სტრესსა და დაძაბულობას შორის ურთიერთობა ფიზიკურ ხასიათს ატარებს. შეზღუდული მცირე შტამებით, დაძაბულობასა და დაძაბულობას შორის ურთიერთობა შეიძლება ჩაითვალოს წრფივად.

ღეროს დაძაბულობაში ტესტირებისას (მასალების მექანიკური გამოცდა დეტალურად იქნება განხილული შემდეგ ნაწილში), პროპორციული ურთიერთობა დგინდება ნორმალურ სტრესსა და წრფივ დეფორმაციას შორის ერთი მიმართულებით, რასაც ჰუკის კანონი ჰქვია:

სადაც დრეკადობის მუდმივას ეწოდება გრძივი ელასტიურობის მოდული.

ანალოგიურად ექსპერიმენტული გზით დამყარდა კავშირი გრძივი და განივი მიმართულებით წრფივ დეფორმაციებს შორის:

სადაც - წრფივი დეფორმაცია განივი მიმართულებით, - მეორე დრეკადობის მუდმივი, რომელსაც ეწოდება პუასონის თანაფარდობა.

სუფთა ათვლის მექანიკურ ტესტებში დადგინდა პირდაპირპროპორციული კავშირი ათვლის ძაბვასა და კუთხურ დეფორმაციას შორის ამ დაძაბულობის მოქმედების სიბრტყეში, რომელსაც ჰუკის კანონი ათვლისას ეწოდა:

სადაც მნიშვნელობა არის მესამე დრეკადობის მუდმივი და ეწოდება ათვლის მოდული. თუმცა, ეს ელასტიური მუდმივი არ არის დამოუკიდებელი, რადგან პირველ ორთან ასოცირდება

დაძაბულობასა და დაძაბულობას შორის კავშირის დასადგენად, სხეულიდან ვირჩევთ უსასრულოდ პატარა პარალელეპიპედს (ნახ. 1) და განვიხილავთ მხოლოდ ნორმალური ძაბვების მოქმედებას. ეს იწვევს უფრო მაღალი ხარისხის სიმცირის დეფორმაციას.

განვსაზღვროთ ნეკნის დრეკადობა დაძაბულობის პარალელურად ამ დაძაბულობის მოქმედებით, ჰუკის კანონის მიხედვით (3.12) მოხდება ნეკნის ფარდობითი დრეკადობა.

სტრესი იწვევს მსგავს დრეკადობას ნეკნის პერპენდიკულარული მიმართულებით

ხოლო ნეკნის მიმართულებით - დამოკლება, რაც (13)-ის მიხედვით არის

ან დეფორმაციის გამოხატვის გათვალისწინებით

ანალოგიურად, განისაზღვრება ნეკნის შედარებითი დამოკლება სტრესის მოქმედების ქვეშ

ძალების მოქმედების დამოუკიდებლობის პრინციპიდან გამომდინარე, ნეკნის მთლიანი ფარდობითი დრეკადობა შეიძლება განისაზღვროს, როგორც თითოეული დაძაბულობის მოქმედების დრეკადობების ჯამი:

ანალოგიურად, შეიძლება განვსაზღვროთ წრფივი დეფორმაციები დანარჩენი ორი ღერძის მიმართულებით:

ჰუკის კანონის მიხედვით ათვლის (14), კუთხური დეფორმაციებისა და ათვლის ძაბვის ურთიერთობა შეიძლება დამოუკიდებლად იყოს წარმოდგენილი კოორდინატთა სიბრტყეების პარალელურად თითოეული სამი სიბრტყისთვის:

ამრიგად, მიღებულია ექვსი ფორმულა, რომლებიც გამოხატავს წრფივ კავშირს დაძაბულობასა და დაძაბულობის კომპონენტებს შორის იზოტროპულ დრეკად სხეულში და ეწოდება განზოგადებული ჰუკის კანონი:

(16)

3. დრეკადობის თეორიის ძირითადი განტოლებები. პრობლემების სახეები დრეკადობის თეორიაში

დრეკადობის თეორიის მთავარი ამოცანაა დაძაბულობა-დაძაბულობის მდგომარეობის განსაზღვრა სხეულის დატვირთვისა და დამაგრების მოცემული პირობების მიხედვით.

ძაბვის დაძაბულობის მდგომარეობა განისაზღვრება, თუ აღმოჩენილია დაძაბულობის ტენზორის(ებ)ის კომპონენტები და გადაადგილების ვექტორი, ცხრა ფუნქცია.

3.1 დრეკადობის თეორიის ძირითადი განტოლებები

ამ ცხრა ფუნქციის საპოვნელად, თქვენ უნდა ჩამოვწეროთ ელასტიურობის თეორიის ძირითადი განტოლებები, ან:

დიფერენციალური კეშიები

(17)

სად არის კოშის დეფორმაციების წრფივი ნაწილის ტენზორის კომპონენტები;

რადიუსის გასწვრივ გადაადგილების წარმოებულის ტენზორის კომპონენტები.

დიფერენციალური წონასწორობის განტოლებები

სად არის სტრესის ტენსორის კომპონენტები; არის სხეულის ძალის პროექცია j ღერძზე.

ჰუკის კანონი ხაზოვანი ელასტიური იზოტროპული სხეულისთვის

სად არის ლამის მუდმივები; იზოტროპული სხეულისთვის. აქ არის ნორმალური და ათვლის ძაბვები; დაძაბულობის და ათვლის კუთხეები, შესაბამისად.

ზემოაღნიშნული განტოლებები უნდა აკმაყოფილებდეს Saint-Venant დამოკიდებულებებს

ელასტიურობის თეორიაში პრობლემა წყდება, თუ ყველა ძირითადი განტოლება დაკმაყოფილებულია.

2 პრობლემების ტიპები დრეკადობის თეორიაში

სხეულის ზედაპირზე სასაზღვრო პირობები დაკმაყოფილებული უნდა იყოს და, სასაზღვრო პირობების ტიპებიდან გამომდინარე, ელასტიურობის თეორიაში სამი სახის პრობლემაა.

პირველი ტიპი. ძალები მოცემულია სხეულის ზედაპირზე. სასაზღვრო პირობები

მეორე ტიპი. პრობლემები, რომლებშიც გადაადგილება მითითებულია სხეულის ზედაპირზე. სასაზღვრო პირობები

მესამე ტიპი. ელასტიურობის თეორიის შერეული ამოცანები. ძალები მოცემულია სხეულის ზედაპირის ნაწილზე, გადაადგილება მოცემულია სხეულის ზედაპირის ნაწილზე. სასაზღვრო პირობები

პრობლემებს, რომლებშიც ძალები ან გადაადგილებები მითითებულია სხეულის ზედაპირზე, მაგრამ საჭიროა სხეულის შიგნით დაძაბულობა-დაძაბულობის მდგომარეობის და ის, რაც ზედაპირზე არ არის მითითებული, პირდაპირი პრობლემები ეწოდება. თუმცა, თუ სხეულის შიგნით მითითებულია ძაბვები, დეფორმაციები, გადაადგილებები და ა.შ. და საჭიროა დადგინდეს ის, რაც არ არის მითითებული სხეულის შიგნით, ასევე გადაადგილებები და ძაბვები სხეულის ზედაპირზე (ანუ პოვნა მიზეზები, რამაც გამოიწვია ასეთი სტრესი-დაძაბულობა)), მაშინ ასეთ პრობლემებს ინვერსიული ეწოდება.

4 დრეკადობის თეორიის განტოლებები გადაადგილებებში (ლამის განტოლებები)

გადაადგილებებში დრეკადობის თეორიის განტოლებების დასადგენად ვწერთ: დიფერენციალური წონასწორობის განტოლებები (18) ჰუკის კანონი ხაზოვანი დრეკადი იზოტროპული სხეულისთვის (19)

თუ გავითვალისწინებთ, რომ დეფორმაციები გამოიხატება გადაადგილების მიხედვით (17), ვწერთ:

ასევე უნდა გვახსოვდეს, რომ ათვლის კუთხე დაკავშირებულია გადაადგილებთან შემდეგი დამოკიდებულებით (17):

(23)

გამოხატვის (22) ჩანაცვლებით ტოლობის პირველ განტოლებაში (19), მივიღებთ, რომ ნორმალური ძაბვები

(24)

გაითვალისწინეთ, რომ აღნიშვნა u ამ შემთხვევაში არ ნიშნავს i-ზე შეჯამებას.

გამონათქვამის (23) ჩანაცვლებით ტოლობის მეორე განტოლებაში (19), მივიღებთ, რომ ათვლის ძაბვები

(25)

მოდით დავწეროთ წონასწორობის განტოლებები (18) გაფართოებული სახით j = 1-ისთვის

(26)

ნორმალური (24) და ტანგენციალური (25) ძაბვის განტოლების (26) გამოსახულებების ჩანაცვლებით, მივიღებთ

სადაც λ არის კოჭლის მუდმივი, რომელიც განისაზღვრება გამოსახულებით:

ჩვენ ვცვლით გამოხატულებას (28) განტოლებაში (27) და ვწერთ,

სადაც განისაზღვრება გამოხატულებით (22), ან გაფართოებული ფორმით

ჩვენ ვყოფთ გამოსახულებას (29) G-ზე და ვამატებთ მსგავს წევრებს და ვიღებთ ლამის პირველ განტოლებას:

(30)

სად არის ლაპლასის ოპერატორი (ჰარმონიული ოპერატორი), რომელიც განისაზღვრება როგორც

(31)

ანალოგიურად, შეგიძლიათ მიიღოთ:

(32)

განტოლებები (30) და (32) შეიძლება ჩაიწეროს შემდეგნაირად:

(33)

განტოლებები (33) ან (30) და (32) ლამის განტოლებებია. თუ სხეულის ძალები ნულოვანი ან მუდმივია, მაშინ

(34)

უფრო მეტიც, აღნიშვნა ამ შემთხვევაში არ გულისხმობს i-ზე შეჯამებას. Აქ

შეიძლება ნაჩვენები იყოს, რომ გადაადგილების ასეთი წარმოდგენა ჰარმონიული ფუნქციის მიხედვით აქცევს ლამის განტოლებებს (33) იდენტურად. ხშირად მათ პოპკოვიჩ-გროდსკის პირობებს უწოდებენ. ოთხი ჰარმონიული ფუნქცია არ არის აუცილებელი, რადგან φ0 შეიძლება გაუტოლდეს ნულს.

4. დრეკადობის თეორიის ვარიაციული პრინციპები.

1 შესაძლო გადაადგილების პრინციპი (ლაგრანგის პრინციპი)

ლაგრანგის პრინციპი. წონასწორობაში მყოფი სხეულისთვის, გარე და შინაგანი ძალების მუშაობა ნებისმიერ შესაძლო უსასრულო გადაადგილების ნამატებზე არის ნული.

კლაპეირონის თეორემის გამოყენებით, რომ ელასტიურად დეფორმირებული სხეულისთვის გადაადგილების ცვალებადობით მივიღებთ ლაგრანგის პრინციპს.

დეფორმირებადი სხეულების მექანიკაში შესაძლებელია ისეთი გადაადგილებები, რომლებიც აკმაყოფილებს სხეულზე დაწესებულ გარე და შინაგან შეზღუდვებს.

გარე კავშირები დამაგრების პირობაა, შიდა კავშირები უწყვეტობის პირობაა.

შიდა შეზღუდვების დასაკმაყოფილებლად აუცილებელია, რომ გადაადგილების მატება იყოს კოორდინატების უწყვეტი ერთმნიშვნელოვანი ფუნქციები.

ამ ფორმით, ლაგრანგის პრინციპი მოქმედებს ნებისმიერი დეფორმირებადი სხეულისთვის.

ელასტიური სხეულებისთვის მიიღეს რომ

(41)

შემდეგ (40), (41) გათვალისწინებით, შეიძლება დაიწეროს როგორც

(42)

სადაც W არის სპეციფიკური შტამი და

აქ U არის სხეულის მთელი პოტენციური ენერგიის ვარიაცია.

ჩვენ ვცვლით გამონათქვამს (43) (42) და რადგან ძალები არ იცვლება, ვწერთ ამას

(44)

განტოლება (44) არის ვარიაციური ლაგრანგის განტოლება.

თუ ძალები კონსერვატიულია, მაშინ პირველი ორი ინტეგრალი წარმოადგენს გარე ძალების პოტენციალის ცვლილებას დეფორმირებული მდგომარეობიდან დეფორმირებულზე გადასვლისას.

გარე ძალების პოტენციალი

(45)

სადაც - გარე ძალების შესაძლო მუშაობა დეფორმირებული მდგომარეობიდან დეფორმირებულ მდგომარეობაში გადასვლისას გამოითვლება იმ ვარაუდით, რომ გარე ძალები უცვლელი რჩება. სისტემის მთლიანი ენერგია

შემდეგ, გამონათქვამების (44) - (46) გათვალისწინებით, დაიწერება ლაგრანგის პრინციპი:

ანუ, სისტემის მთლიანი ენერგიის ცვალებადობა წონასწორობის მდგომარეობაში შესაძლო გადაადგილებაზე უდრის ნულს. გამოხატულება (47) არის ლაგრანჟის ვარიაციული განტოლება მხოლოდ კონსერვატიული ძალების მოქმედების შემთხვევაში.

სტაბილური წონასწორობის მდგომარეობაში, მთლიანი ენერგია P არის მინიმალური,

ლაგრანგის პრინციპი არის მინიმალური ენერგიის პრინციპი.

2 შესაძლო მდგომარეობების პრინციპი (კასტილანოს პრინციპი)

ჩვენ დავარქმევთ შესაძლო მდგომარეობებს, რომლებიც შეესაბამება გარე და შინაგან ძალებს, ანუ აკმაყოფილებენ წონასწორობის განტოლებებს.

განტოლება (57) წერს კასტილიანოს პრინციპს. სხეულის სტრესის მდგომარეობის შესაძლო ცვლილებებით, ცვალებადობა უდრის ინტეგრალს სხეულის ზედაპირის იმ ნაწილზე, რომელზეც გადაადგილებები მოცემულია შესაძლო ზედაპირული ძალებისა და გადაადგილების პროდუქტებიდან.

ლაგრანგის პრინციპზე დაყრდნობით, ვირჩევთ რამდენიმე ფუნქციას, ან მათ ერთობლიობას და ვინაიდან ფუნქციების ნაკრები შეზღუდულია, მივიღებთ სისტემის თავისუფლების ხარისხების უფრო მცირე რაოდენობას, რითაც მცირდება სტრუქტურის თავისუფლების ხარისხი. ანუ ენერგეტიკული გაგებით გამოსავალი უფრო ხისტი გამოდის ვიდრე ზუსტი.

თუ ავიღებთ ინტეგრალურ მახასიათებლებს, მაშინ სავარაუდო ამოხსნა უფრო ხისტი ინტეგრალურია.

სამაგრის შუაში განივი ძალით ჩამოკიდებული სხივის დატვირთვის პრობლემის გადაჭრისას (ნახ. 1), სავარაუდო ამოხსნა მისცემს უფრო მცირე გადაადგილებას ძალის ქვეშ, ვიდრე ზუსტი ამონახსნით.

ზუსტი გამოსავალი

კასტილიანოს ვარიაციული პრინციპის გამოყენებით ერთი და იგივე პრობლემის გადაჭრისას, რადგან უწყვეტობის პირობა არ არის დაკმაყოფილებული, სისტემა უფრო მეტ თავისუფლებას იღებს, ვიდრე სინამდვილეში.

ზუსტი გამოსავალი მდგომარეობს ამ ორ სავარაუდო მეთოდს შორის (ლაგრანჟი და კასტილიანო). ზოგჯერ სხვაობა მიღებულ ხსნარებს შორის მცირეა.

5. გამოყენებული ლიტერატურის სია

1. ალექსანდროვი ა.ვ., პოტაპოვი ვ.დ. ელასტიურობისა და პლასტიურობის თეორიის საფუძვლები. 400გვ.უმაღლესი სკოლა.1990წ.

2. ვერეტიმუს დ.კ. დრეკადობის თეორიის საფუძვლები ნაწილი I სტრესის თეორია მეთოდოლოგიური გზამკვლევი კურსის ,,ელასტიურობის და პლასტიურობის თეორიის საფუძვლები”. 2005.-37წ.

ვერეტიმუს დ.კ. დრეკადობის თეორიის საფუძვლები ნაწილი II დეფორმაციების თეორია. დაძაბულ და დეფორმირებულ მდგომარეობას შორის ურთიერთობა მეთოდოლოგიური გზამკვლევი კურსის „ელასტიურობისა და პლასტიურობის თეორიის საფუძვლები“ 2005.-53გვ.

ვერეტიმუს დ.კ. დრეკადობის თეორიის საფუძვლები ნაწილი III დრეკადობის თეორიის ძირითადი განტოლებები დრეკადობის თეორიის ამოცანების ტიპები კურსის მეთოდოლოგიური გზამკვლევი ,,ელასტიურობისა და პლასტიურობის თეორიის საფუძვლები” 2005.-45გვ.

მოსვენებულ სხეულებში ან მოძრაობენ ტვირთის მოქმედების ქვეშ.

1. დრეკადობის თეორიის პრობლემა

ამ თეორიის ამოცანაა დაწეროს მათემატიკური განტოლებები, რომელთა ამოხსნა იძლევა შემდეგ კითხვებზე პასუხის გაცემის საშუალებას:

როგორი იქნება კონკრეტული სხეულის დეფორმაციები, თუ მასზე მოცემული მნიშვნელობის იტვირთება ცნობილ ადგილებში?
როგორი იქნება დაძაბულობა სხეულში?

საკითხავია, სხეული დაინგრევა, გაუძლებს ამ დატვირთვებს, რომელიც მჭიდროდ არის დაკავშირებული ელასტიურობის თეორიასთან, მაგრამ, მკაცრად რომ ვთქვათ, მის კომპეტენციაში არ შედის.

უამრავი მაგალითია - დაწყებული დეფორმაციებისა და დაძაბულობის განსაზღვრიდან საყრდენებზე დატვირთულ სხივში, თვითმფრინავის, რაკეტის, წყალქვეშა ნავის სხეულში იგივე პარამეტრების გაანგარიშებამდე, მანქანის ბორბალში ტანკის ჯავშანში, როდესაც ჭურვი ხვდება, მთის ქედში ადტის დაგებისას, მაღალსართულიანი შენობის ჩარჩოში და ა.შ.

საინჟინრო პრობლემების შემთხვევაში, სტრუქტურებში ძაბვები და დაძაბულობები გამოითვლება გამარტივებული თეორიების მიხედვით, ლოგიკურად ეფუძნება დრეკადობის თეორიას. ეს თეორიები მოიცავს: მასალების სიმტკიცე, რომლის ამოცანაა ღეროების და სხივების გამოთვლა, აგრეთვე ძაბვების შეფასება, რომლებიც წარმოიქმნება მყარი ნივთიერებების კონტაქტური ურთიერთქმედების ზონებში; სტრუქტურული მექანიკა- ბარის სისტემების (მაგ. ხიდების) დიზაინი და ჭურვის თეორია- დეფორმაციისა და სტრესის მეცნიერების დამოუკიდებელი და კარგად განვითარებული დარგი, რომლის საგანია თხელკედლიანი გარსი - ცილინდრული, კონუსური, სფერული და რთული ფორმები.

2. დრეკადობის თეორიის ძირითადი ცნებები

ელასტიურობის თეორიის ძირითადი ცნებებია მცირე სიბრტყეებზე მოქმედი სტრესი, რომელიც სხეულში გონებრივად შეიძლება ჩაითვალოს მოცემული P წერტილის მეშვეობით, P წერტილის მცირე უბნის დეფორმაცია და თავად P წერტილის გადაადგილება. ზუსტად არის შემოღებული მექანიკური დაძაბულობის ტენსორი, მცირე დაძაბულობის ტენსორი და გადაადგილების ვექტორი u i.მოკლე აღნიშვნა, სად ინდექსები მე, ჯმიიღეთ მნიშვნელობები 1, 2, 3 (ან x, y, z)უნდა გავიგოთ, როგორც მატრიცა სახით:

ტენზორის მოკლე აღნიშვნა ანალოგიურად უნდა იქნას გაგებული.

თუ სხეულის ფიზიკურმა წერტილმა M დეფორმაციის გამო დაიკავა ახალი პოზიცია P სივრცეში, მაშინ გადაადგილების ვექტორი არის ვექტორი კომპონენტებით. (u x, u y, u z),ან მოკლედ, u i.მცირე დეფორმაციების თეორიაში კომპონენტები u iდა ითვლება მცირე რაოდენობით (მკაცრად რომ ვთქვათ, უსასრულოდ მცირე). ტენზორის კომპონენტები, რომელსაც ასევე ე.წ დაძაბულობის ტენსორი კოშიან ხაზოვანი დაძაბულობის ტენსორიდა ვექტორი u iდაკავშირებული დამოკიდებულებები:

ბოლო ჩანაწერიდან ჩანს, რომ , მაშასადამე, დეფორმაციის ტენსორი განსაზღვრებით სიმეტრიულია.

თუ ელასტიური სხეული გარე ძალების მოქმედებით წონასწორობაშია (ანუ მისი ყველა წერტილის სიჩქარე ნულის ტოლია), მაშინ სხეულის ნებისმიერი ნაწილი, რომელიც შეიძლება გონებრივად განცალკევდეს მისგან, ასევე წონასწორობაშია. სხეულიდან ამოღებულია უსასრულოდ პატარა მართკუთხა პარალელეპიპედი, რომლის სახეები დეკარტის სისტემის კოორდინატთა სიბრტყეების პარალელურია. კიდეების ზომების მქონე პარალელეპიპედის წონასწორობის მდგომარეობიდან dx, dy, dz,პროგნოზებში ძალთა ბალანსის პირობების გათვალისწინებით, შეგვიძლია მივიღოთ:

ანალოგიურად, მიიღება წონასწორობის განტოლებები, რომლებიც გამოხატავს პარალელეპიპედზე მოქმედი ყველა ძალის მთავარი მომენტის ტოლობას ნულამდე, დაყვანილი სახით:

ეს თანასწორობა ნიშნავს, რომ სტრესის ტენსორი არის სიმეტრიული ტენსორი და სტრესის ტენზორის უცნობი კომპონენტების რაოდენობა მცირდება 6-მდე. არსებობს მხოლოდ სამი წონასწორობის განტოლება, ე.ი. სტატიკის განტოლებები არ არის საკმარისი პრობლემის გადასაჭრელად. გამოსავალი არის ძაბვების გამოხატვა დაძაბულობების მიხედვით ჰუკის კანონის განტოლებების გამოყენებით, შემდეგ კი დაძაბულობის გამოხატვა გადაადგილების თვალსაზრისით. u iკოშის ფორმულების გამოყენებით და შეცვალეთ შედეგი წონასწორობის განტოლებაში. ამ შემთხვევაში მიიღება სამი დიფერენციალური წონასწორობის განტოლება სამი უცნობი ფუნქციის მიმართ u x u y u z,იმათ. უცნობის რაოდენობა შეესაბამება განტოლებების რაოდენობას. ამ განტოლებებს უწოდებენ ნავიე-კოშის განტოლებებს.

3. სასაზღვრო პირობები

დრეკადობის თეორიის პრობლემების გადაწყვეტა მცირდება დიფერენციალური განტოლებების სისტემის ინტეგრირებამდე ნაწილობრივ წარმოებულებში, რომლებიც განსაზღვრავენ დრეკადი სხეულის ქცევას შიდა წერტილებში. ეს განტოლებები ავსებს პირობებს ზედაპირზე, რომელიც ზღუდავს სხეულს. ეს პირობები განსაზღვრავს გარე ზედაპირული ძალების ამოცანებს ან სხეულის ზედაპირზე წერტილების გადაადგილებას. აქედან გამომდინარე, ჩვეულებრივ ჩამოყალიბებულია სამი ტიპის სასაზღვრო ამოცანები.

პირველი სასაზღვრო პრობლემა- კინემატიკური. სხეულის მოცულობაში გვხვდება გადაადგილების კომპონენტები, ისინი იძენენ გარკვეულ მნიშვნელობებს ზედაპირზე. სხეულის ზედაპირზე არსებულ მდგომარეობაში, ამგვარად დაყენებულია ზედაპირის განტოლებები და მასზე გადაადგილების კომპონენტების მნიშვნელობები.

მეორე სასაზღვრო პრობლემა- სტატიკური. ამ შემთხვევაში, სხეულის ზედაპირზე მოძრაობის შეზღუდვა არ არის დაწესებული და დაყენებულია ზედაპირის განტოლებები, რომლებიც მიმართავს ნორმალის კოსინუსებს ზედაპირზე და ზედაპირული დატვირთვის კომპონენტების მნიშვნელობებს.

იმ შემთხვევაში, როდესაც სხეულის ზედაპირი ემთხვევა კოორდინატულ სიბრტყეებს, სასაზღვრო პირობები შეიძლება ჩამოყალიბდეს უშუალოდ დაძაბულობის თვალსაზრისით. შემდეგ საკმარისია მიუთითოთ ზედაპირის განტოლება და დააყენოთ მასზე სტრესის კომპონენტების მნიშვნელობები.

მესამე სასაზღვრო პრობლემა- შერეული. ამ შემთხვევაში სხეულის ზედაპირის ერთ ნაწილზე დგება კინემატიკური პირობები, მეორეზე კი სტატიკური პირობები.

ეს სამი პრობლემა არ ამოწურავს სასაზღვრო პირობების მრავალფეროვნებას. მაგალითად, ზედაპირის ზოგიერთ უბანში, სამივე გადაადგილების კომპონენტი ან ზედაპირის დატვირთვის კომპონენტი შეიძლება არ იყოს მითითებული.

4. აგრეთვე

წყაროები

ტიმოშენკო S.P., Goodyear J.ელასტიურობის თეორია. მ.: ნაუკა, 1979. 560 გვ.

ელასტიურობის თეორია- უწყვეტი მექანიკის ფილიალი, რომელიც სწავლობს დატვირთვების ზემოქმედების ქვეშ მოსვენებული ან მოძრავი სხეულების გადაადგილებებს, დეფორმაციას და სტრესებს. ამ თეორიის მიზანია მათემატიკური განტოლებების გამომუშავება, რომელთა ამოხსნა იძლევა შემდეგ კითხვებზე პასუხის გაცემის საშუალებას: როგორი იქნება ამ კონკრეტული სხეულის დეფორმაცია, თუ მასზე მოცემული მნიშვნელობის დატვირთვები გამოიყენება ცნობილ ადგილებში? როგორი იქნება დაძაბულობა სხეულში? კითხვა, დაეცემა თუ არა სხეული ამ დატვირთვებს, მჭიდროდ არის დაკავშირებული ელასტიურობის თეორიასთან, მაგრამ, მკაცრად რომ ვთქვათ, არ შედის ამ თეორიის კომპეტენციაში.

შესაძლო მაგალითების რაოდენობა შეუზღუდავია - დაწყებული საყრდენებზე დატვირთული სხივის დეფორმაციებისა და დაძაბულობის განსაზღვრიდან დაწყებული, თვითმფრინავის, გემის, წყალქვეშა ნავის სტრუქტურაში, ვაგონის ბორბალში იგივე მნიშვნელობების გამოთვლამდე. ჯავშანტექნიკაში ჭურვის მოხვედრისას, მთის ქედში ადიტზე გავლისას, მაღალსართულიანი შენობის ჩარჩოში და ა.შ. აქ აუცილებელია დათქმის გაკეთება: თხელკედლიანი ელემენტებისაგან შემდგარი სტრუქტურები გამოითვლება გამარტივებული თეორიების მიხედვით, ლოგიკურად ელასტიურობის თეორიაზე დაყრდნობით; ასეთ თეორიებს მიეკუთვნება: მასალების გამძლეობის თეორია ტვირთის მოქმედებისადმი (ცნობილი „სოპრომატი“), რომლის ამოცანაა ძირითადად ღეროებისა და სხივების გამოთვლა; კონსტრუქციული მექანიკა - ბარის სისტემების გაანგარიშება (მაგალითად, ხიდები); და ბოლოს, ჭურვების თეორია, ფაქტობრივად, არის დამოუკიდებელი და ძალიან განვითარებული მეცნიერების სფერო დეფორმაციებისა და სტრესების შესახებ, რომლის საგანია ყველაზე მნიშვნელოვანი სტრუქტურული ელემენტები - თხელკედლიანი ჭურვები - ცილინდრული, კონუსური, სფერული. და უფრო რთული ფორმების მქონე. ამიტომ, ელასტიურობის თეორიაში, ჩვეულებრივ, განიხილება სხეულები, რომელთა არსებითი ზომები ძალიან არ განსხვავდება. ამრიგად, განიხილება მოცემული ფორმის ელასტიური სხეული, რომელზეც მოქმედებენ ცნობილი ძალები.

ელასტიურობის თეორიის ძირითადი ცნებებია მცირე უბნებზე მოქმედი სტრესები, რომლებიც შეიძლება გონებით განხორციელდეს სხეულში მოცემულ წერტილში. მ, წერტილის მცირე უბნის დეფორმაციები მდა თავად წერტილის გადატანა მ. უფრო ზუსტად, სტრესის ტენსორები ს იჯ, მცირე დაძაბულობის ტენსორი ე იჯდა გადაადგილების ვექტორი u i.

მოკლე აღნიშვნა ს იჯ, სადაც ინდექსები მე, ჯმიიღოს მნიშვნელობები 1, 2, 3 უნდა გავიგოთ, როგორც ფორმის მატრიცა:

ტენზორის მოკლე აღნიშვნა ე იჯ.

თუ სხეულის ფიზიკური წერტილი მდეფორმაციის გამო, სივრცეში ახალი პოზიცია დაიკავა მ, მაშინ გადაადგილების ვექტორი არის ვექტორი კომპონენტებით ( u x u y u z), ან, მოკლედ, u i. მცირე დეფორმაციების თეორიაში კომპონენტები u iდა ე მეითვლება მცირე რაოდენობით (მკაცრად რომ ვთქვათ, უსასრულოდ მცირე). e ტენზორის კომპონენტები იჯდა ვექტორი u ijდაკავშირებულია კოშის ფორმულებით, რომლებსაც აქვთ ფორმა:

ჩანს, რომ ე xy= ე yxდა, ზოგადად, ე იჯ= ე ჯიასე რომ, დაძაბულობის ტენსორი განსაზღვრებით სიმეტრიულია.

თუ ელასტიური სხეული გარე ძალების მოქმედებით წონასწორობაშია (ანუ მისი ყველა წერტილის სიჩქარე ნულის ტოლია), მაშინ სხეულის ნებისმიერი ნაწილი, რომელიც შეიძლება გონებრივად განცალკევდეს მისგან, ასევე წონასწორობაშია. სხეულიდან გამოდის პატარა (მკაცრად რომ ვთქვათ, უსასრულოდ მცირე) მართკუთხა პარალელეპიპედი, რომლის სახეები დეკარტის სისტემის კოორდინატთა სიბრტყის პარალელურია. ოქსიზი(ნახ. 1).

დაე, პარალელეპიპედის კიდეებს ჰქონდეს სიგრძე dx, დი, ძშესაბამისად (აქ, როგორც ყოველთვის dxარის დიფერენცია xდა ა.შ.). სტრესის თეორიის მიხედვით, პარალელეპიპედის სახეებზე მოქმედებენ სტრესის ტენზორის კომპონენტები, რომლებიც აღინიშნება:

ზღვარზე OADG:ს xx, ს xy, ს xz

ზღვარზე OABC:ს yx, ს წ.წ, ს yz

ზღვარზე DABE:ს zx, ს zy, ს ზზ

ხოლო კომპონენტები იგივე ინდექსებით (მაგალითად, s xx) მოქმედებენ სახის პერპენდიკულურად, ხოლო სხვადასხვა ინდექსის მქონეები მოქმედებენ ფართობის სიბრტყეში.

საპირისპირო სახეებზე, ამავე სახელწოდების სტრესის ტენზორის კომპონენტების მნიშვნელობები ოდნავ განსხვავებულია, ეს იმის გამო ხდება, რომ ისინი კოორდინატების ფუნქციებია და იცვლება წერტილიდან წერტილამდე (ყოველთვის, გარდა ცნობილი უმარტივესი შემთხვევებისა). და ცვლილების სიმცირე დაკავშირებულია პარალელეპიპედის მცირე ზომებთან, ასე რომ, შეგვიძლია ვივარაუდოთ, რომ თუ ზღვარზეა OABCძაბვა ს წ.წ, შემდეგ ზღვარზე GDEFძაბვა ს წ.წ+დს წ.წდა მცირე მნიშვნელობა ds წ.წზუსტად მისი სიმცირის გამო, მისი დადგენა შესაძლებელია ტეილორის სერიის გაფართოების გამოყენებით:

(აქ გამოიყენება ნაწილობრივი წარმოებულები, რადგან სტრესის ტენზორის კომპონენტები დამოკიდებულია x, წ, ზ).

ანალოგიურად, სტრესები ყველა სახეზე შეიძლება გამოიხატოს s-ის მიხედვით იჯდა დს იჯ. გარდა ამისა, სტრესებიდან ძალებზე გადასასვლელად, თქვენ უნდა გაამრავლოთ სტრესის სიდიდე იმ ადგილის ფართობზე, რომელზეც ის მოქმედებს (მაგალითად, ს. წ.წ+დს წ.წგავამრავლოთ dx dz). როდესაც პარალელეპიპედზე მოქმედი ყველა ძალა განისაზღვრება, შესაძლებელია, როგორც ეს ხდება სტატიკაში, ჩაიწეროს სხეულის წონასწორობის განტოლება, ხოლო ძირითადი ვექტორის ყველა განტოლებაში დარჩება მხოლოდ წარმოებულების ტერმინები, რადგან თავად ძაბვები. გააუქმოს ერთმანეთი და ფაქტორები dx dy dzმცირდება და შედეგად

ანალოგიურად, მიიღება წონასწორობის განტოლებები, რომლებიც გამოხატავენ პარალელეპიპედზე მოქმედი ყველა ძალის მთავარი მომენტის ტოლობას ნულამდე, რომლებიც მცირდება ფორმაში:

ეს ტოლობები ნიშნავს, რომ სტრესის ტენსორი არის სიმეტრიული ტენსორი. ამრიგად, 6 უცნობი კომპონენტისთვის ს იჯარსებობს სამი წონასწორობის განტოლება, ე.ი. სტატიკის განტოლებები არ არის საკმარისი პრობლემის გადასაჭრელად. გამოსავალი არის სტრესების გამოხატვა ს იჯდეფორმაციების მეშვეობით ე იჯჰუკის კანონის განტოლებების გამოყენებით, შემდეგ კი დეფორმაცია ე იჯგამოხატოს გადაადგილების თვალსაზრისით u iკოშის ფორმულების გამოყენებით და შეცვალეთ შედეგი წონასწორობის განტოლებით. ამ შემთხვევაში მიიღება სამი დიფერენციალური წონასწორობის განტოლება სამი უცნობი ფუნქციის მიმართ u x u y u z, ე.ი. უცნობის რაოდენობა უდრის განტოლებათა რაოდენობას. ამ განტოლებებს ლამის განტოლებებს უწოდებენ

სხეულის ძალები (წონა და ა.შ.) არ არის გათვალისწინებული

D არის ლაპლასის ოპერატორი, ე.ი.

ახლა ჩვენ უნდა დავაყენოთ სასაზღვრო პირობები სხეულის ზედაპირზე;

ამ პირობების ძირითადი ტიპები შემდეგია:

1. გადაადგილებები მოცემულია S 1 სხეულის ზედაპირის ცნობილ ნაწილზე, ე.ი. გადაადგილების ვექტორი ტოლია ცნობილი ვექტორის კომპონენტებით ( f x; ვ y; ვ z):

u x = ვ(xyz)

u y= ვ(xyz)

u z= ვ(xyz)

(f x, ვ წ, fzცნობილია კოორდინატთა ფუნქციები)

2. დანარჩენ ზედაპირზე ს 2 მოცემულია ზედაპირული ძალები. ეს ნიშნავს, რომ სხეულის შიგნით სტრესის განაწილება ისეთია, რომ სტრესის მნიშვნელობები ზედაპირის უშუალო სიახლოვეს, ხოლო ზღვარში - ზედაპირზე თითოეულ ელემენტარულ ზონაში ქმნის სტრესის ვექტორს, რომელიც ტოლია კომპონენტებით ცნობილი გარე დატვირთვის ვექტორთან. ( Fx ;Fy ; ფზ) ზედაპირული ძალები. მათემატიკურად ეს ასე იწერება: თუ წერტილში აზედაპირზე, ამ ზედაპირის ერთეულ ნორმალურ ვექტორს აქვს კომპონენტები n x, n y, ნზმაშინ ამ ეტაპზე ტოლობები (უცნობი) კომპონენტების მიმართ s იჯ:ე იჯ, მაშინ სამი უცნობისთვის ვიღებთ ექვს განტოლებას, ანუ ზედმეტად განსაზღვრულ სისტემას. ამ სისტემას გამოსავალი მხოლოდ იმ შემთხვევაში ექნება, თუ დამატებითი პირობები დაკმაყოფილდება ე იჯ. ეს პირობები არის თავსებადობის განტოლებები.

ამ განტოლებებს ხშირად უწოდებენ უწყვეტობის პირობებს, რაც გულისხმობს, რომ ისინი უზრუნველყოფენ სხეულის უწყვეტობას დეფორმაციის შემდეგ. ეს გამოთქმა ფიგურალურია, მაგრამ არაზუსტი: ეს პირობები უზრუნველყოფს უწყვეტი გადაადგილების ველის არსებობას, თუ დეფორმაციების (ან დაძაბულობის) კომპონენტები უცნობია. ამ პირობების შეუსრულებლობა იწვევს არა უწყვეტობის დარღვევას, არამედ პრობლემის გადაჭრის არარსებობას.

ამრიგად, ელასტიურობის თეორია უზრუნველყოფს დიფერენციალურ განტოლებებს და სასაზღვრო პირობებს, რომლებიც საშუალებას გვაძლევს ჩამოვაყალიბოთ სასაზღვრო ამოცანები, რომელთა გადაწყვეტა იძლევა სრულ ინფორმაციას განსახილველ სხეულებში ძაბვის, დაძაბულობისა და გადაადგილების განაწილების შესახებ. ასეთი პრობლემების გადაჭრის მეთოდები ძალიან რთულია და საუკეთესო შედეგები მიიღება ძლიერი კომპიუტერების გამოყენებით ანალიტიკური მეთოდების რიცხვით მეთოდებთან შერწყმით.

ვლადიმერ კუზნეცოვი

ელასტიურობის თეორიის საფუძვლები

ელასტიურობის თეორიის ღერძული სიმეტრიული პრობლემები

ელასტიურობის თეორიის საფუძვლები

ძირითადი დებულებები, დაშვებები და აღნიშვნა წონასწორობის განტოლებები ელემენტარული პარალელეპიპედისა და ელემენტარული ტეტრაედრისთვის. ნორმალური და ათვლის ძაბვები დახრილი პლატფორმის გასწვრივ

ძირითადი ძაბვების და ყველაზე დიდი ათვლის ძაბვების განსაზღვრა წერტილში. ხაზს უსვამს ოქტაედრულ უბნებს გადაადგილების კონცეფცია. დეფორმაციებისა და გადაადგილების მიმართება. ნათესავი

წრფივი დეფორმაცია თვითნებური მიმართულებით დეფორმაციის თავსებადობის განტოლებები. ჰუკის კანონი იზოტროპული სხეულისთვის სიბრტყის პრობლემა მართკუთხა კოორდინატებში სიბრტყის პრობლემა პოლარულ კოორდინატებში

ელასტიურობის თეორიის პრობლემების შესაძლო გადაწყვეტილებები. ამოცანების გადაწყვეტა გადაადგილებებში და სტრესებში ტემპერატურის ველის არსებობა. მოკლე დასკვნები განყოფილების შესახებ მარტივი ღერძის სიმეტრიული პრობლემები განტოლებები ცილინდრულ კოორდინატებში განტოლებები ცილინდრულ კოორდინატებში (გაგრძელება)

სქელკედლიანი სფერული ჭურჭლის დეფორმაცია სიბრტყეზე მოქმედი კონცენტრირებული ძალა

ელასტიური ნახევრად სივრცის დატვირთვის განსაკუთრებული შემთხვევები: წრის ფართობზე ერთგვაროვანი დატვირთვა, წრის არეში დატვირთვა "ნახევარსფეროს" გასწვრივ, შებრუნებული პრობლემა აბსოლუტურად ხისტი ბურთის ჩაღრმავება ელასტიურ ნახევარში. სივრცე. სქელკედლიანი მილების ბურთების ელასტიური კოლაფსის პრობლემა

Ზოგადი ინფორმაცია. მილის ელემენტის წონასწორობის განტოლება ერთ-ერთ წრეზე ზეწოლის ქვეშ ძაბვების შესწავლა. სიძლიერის პირობები ელასტიური დეფორმაციის დაძაბულობისთვის კომპოზიტურ მილებში. მრავალფენიანი მილების გაანგარიშების კონცეფცია გაანგარიშების მაგალითები

ფირფიტები, მემბრანები ძირითადი განმარტებები და ჰიპოთეზები

ფირფიტის მრუდი შუა ზედაპირის დიფერენციალური განტოლება მართკუთხა კოორდინატებში ფირფიტის ცილინდრული და სფერული მოხრა

მრგვალი ფირფიტის ღერძული სიმეტრიული მოღუნვის მომენტები. მრგვალი ფირფიტის შუა ზედაპირის დიფერენციალური განტოლება სასაზღვრო პირობები მრგვალ ფირფიტებში. ყველაზე დიდი სტრესები და გადახრები. სიძლიერის პირობები. თერმული სტრესები ფირფიტებში

მემბრანებში ძალების განსაზღვრა. ჯაჭვის ძალები და დაძაბულობა. გადახრისა და დაძაბულობის მიახლოებითი განსაზღვრა წრიულ დიაფრაგმებში გამოთვლის მაგალითები გაანგარიშების მაგალითები (გაგრძელება)

1.1 ძირითადი დებულებები, ვარაუდები და სიმბოლოები

დრეკადობის თეორია მიზნად ისახავს დრეკადი სხეულის დაძაბულობა-დაძაბულობის მდგომარეობის ანალიტიკურ შესწავლას. ელასტიურობის თეორიის დახმარებით შესაძლებელია წინააღმდეგობის დაშვებების გამოყენებით მიღებული გადაწყვეტილებების შემოწმება

მასალები და დადგენილია ამ გადაწყვეტილებების გამოყენების საზღვრები. ზოგჯერ ელასტიურობის თეორიის სექციები, რომლებშიც, როგორც მასალების წინააღმდეგობაში, განიხილება ნაწილის ვარგისიანობის საკითხი, მაგრამ საკმაოდ რთული მათემატიკური აპარატის გამოყენებით (ფირფიტების, ჭურვების, მასივების გაანგარიშება), მათ მოიხსენიებენ. როგორც ელასტიურობის გამოყენებითი თეორია.

ეს თავი ასახავს ელასტიურობის მათემატიკური ხაზოვანი თეორიის ძირითად ცნებებს. მათემატიკის გამოყენება ფიზიკური ფენომენების აღწერაში მოითხოვს მათ სქემატიზაციას. ელასტიურობის მათემატიკური თეორიაში ამოცანები წყდება ყველაზე მცირე რაოდენობის დაშვებით, რაც ართულებს ამოხსნისთვის გამოყენებულ მათემატიკურ მეთოდებს. ელასტიურობის ხაზოვანი თეორია ითვალისწინებს წრფივი კავშირის არსებობას კომპონენტის ძაბვებსა და დაძაბულობას შორის. რიგი მასალებისთვის (რეზინი, თუჯის ზოგიერთი კლასის), ასეთი დამოკიდებულება, თუნდაც მცირე დეფორმაციებით, არ შეიძლება იყოს მიღებული: დიაგრამა σ - ε ელასტიურობის ფარგლებში აქვს იგივე ფორმა როგორც დატვირთვისას, ასევე გადმოტვირთვისას, მაგრამ ორივე შემთხვევაში ის მრუდია. ასეთი მასალების შესწავლისას აუცილებელია ელასტიურობის არაწრფივი თეორიის დამოკიდებულებების გამოყენება.

IN ელასტიურობის მათემატიკური ხაზოვანი თეორია ეფუძნება შემდეგ დაშვებებს:

1. მედიუმის უწყვეტობაზე (განგრძობადობაზე). ამ შემთხვევაში ნივთიერების ატომისტური სტრუქტურა ან არსებობაარ არის გათვალისწინებული სიცარიელე.

2. იმ ბუნებრივ მდგომარეობაზე, რომლის საფუძველზეც მხედველობაში არ მიიღება სხეულის საწყისი დაძაბულობა (დეფორმირებული) მდგომარეობა, რომელიც წარმოიქმნა ძალის მოქმედებამდე, ანუ ივარაუდება, რომ სხეულის დატვირთვის მომენტში დეფორმაციები. და მის ნებისმიერ წერტილში ძაბვები ნულის ტოლია. საწყისი ძაბვების არსებობისას ეს დაშვება მართებულია, თუ მხოლოდ დრეკადობის ხაზოვანი თეორიის დამოკიდებულების გამოყენება შეიძლება მიღებულ ძაბვაზე (დამწყები და ზემოქმედების შედეგად წარმოქმნილი ჯამი).

3. ჰომოგენურობაზე, რის საფუძველზეც ვარაუდობენ, რომ სხეულის შემადგენლობა ყველა წერტილში ერთნაირია. მიუხედავად იმისა, რომ ლითონებისთვის ეს ვარაუდი არ იძლევა დიდ შეცდომებს, ბეტონისთვის, მცირე მოცულობის განხილვისას, შეიძლება გამოიწვიოს მნიშვნელოვანი შეცდომები.

4. სფერულ იზოტროპიაზე, რის საფუძველზეც ითვლება, რომმასალის მექანიკური თვისებები ყველა მიმართულებით ერთნაირია. ლითონის კრისტალებს ეს თვისება არ გააჩნიათ, მაგრამ მთლიანად ლითონისთვის, რომელიც შედგება დიდი რაოდენობით მცირე კრისტალებისაგან, შეგვიძლია ვივარაუდოთ, რომ ეს ჰიპოთეზა მართებულია. სხვადასხვა მიმართულებით სხვადასხვა მექანიკური თვისებების მქონე მასალებისთვის, როგორიცაა, მაგალითად, ლამინირებული პლასტმასისთვის, შემუშავებულია ორთოტროპული და ანისოტროპული მასალების ელასტიურობის თეორია.

5. იდეალური ელასტიურობის შესახებ, რომლის საფუძველზეც ვარაუდობენ დეფორმაციის სრული გაქრობა დატვირთვის მოხსნის შემდეგ. როგორც ცნობილია, რეალურ სხეულებში ნებისმიერი დატვირთვის დროს ხდება ნარჩენი დეფორმაცია. ამიტომ, ვარაუდი

6. კომპონენტის შტამებს შორის წრფივი ურთიერთობის შესახებ დახაზს უსვამს.

7. დეფორმაციების სიმცირეზე, რის საფუძველზეც ვარაუდობენ, რომ შედარებითი წრფივი და კუთხოვანი დეფორმაციები მცირეა ერთიანობასთან შედარებით. ისეთი მასალებისთვის, როგორიცაა რეზინი, ან ისეთი ელემენტები, როგორიცაა ხვეული ზამბარები, შემუშავებულია დიდი ელასტიური დეფორმაციების თეორია.

ელასტიურობის თეორიის ამოცანების გადაჭრისას ისინი იყენებენ თეორემას ამონახსნის უნიკალურობის შესახებ: თუ მოცემული გარე ზედაპირი და სხეულის ძალები წონასწორობაშია, ისინი შეესაბამება დაძაბულობისა და გადაადგილების ერთ სისტემას.ამონახსნის უნიკალურობის პოზიცია მართებულია, თუ მხოლოდ სხეულის ბუნებრივი მდგომარეობის ვარაუდი მოქმედებს (წინააღმდეგ შემთხვევაში შესაძლებელია ამონახსნების უსასრულო რაოდენობა) და დეფორმაციებისა და გარე ძალებს შორის წრფივი ურთიერთობის დაშვება.

ელასტიურობის თეორიის პრობლემების გადაჭრისას ხშირად გამოიყენება სენ-ვენანის პრინციპი: თუ ელასტიური სხეულის მცირე მონაკვეთზე გამოყენებული გარე ძალები შეიცვლება იმავე მონაკვეთზე მოქმედი ძალების სტატიკურად ექვივალენტური სისტემით (იგივე მთავარი ვექტორი და იგივე ძირითადი მომენტი), მაშინ ეს ჩანაცვლება გამოიწვევს მხოლოდ ადგილობრივი დეფორმაციების ცვლილებას. .

საკმარისად დაშორებულ ადგილებში, სადაც გარე დატვირთვები გამოიყენება, სტრესები ნაკლებად არის დამოკიდებული მათი გამოყენების მეთოდზე. დატვირთვა, რომელიც მასალების წინააღმდეგობის დროს სქემატურად გამოიხატა სენ-ვენანის პრინციპის საფუძველზე ძალის ან კონცენტრირებული მომენტის სახით, ფაქტობრივად ნორმალურია და ათვლის ძაბვები გადანაწილებულია ამა თუ იმ გზით. სხეულის ზედაპირის გარკვეული ფართობი. ამ შემთხვევაში, სტრესის სხვადასხვა განაწილება შეიძლება შეესაბამებოდეს იმავე ძალას ან ძალების წყვილს. სენ-ვენანის პრინციპიდან გამომდინარე, შეიძლება ჩაითვალოს, რომ ძალების ცვლილება სხეულის ზედაპირის მონაკვეთზე თითქმის არ მოქმედებს სტრესებზე იმ წერტილებზე, რომლებიც მდებარეობს ამ ძალების გამოყენების ადგილიდან საკმარისად დიდ მანძილზე (შედარებით დატვირთული ტერიტორიის ხაზოვანი ზომები).

სხეულში შერჩეული შესასწავლი ფართობის პოზიცია (ნახ. 1) განისაზღვრება მართკუთხა კოორდინატთა x, y და z ღერძების შერჩეულ სისტემაში ნორმალური N-ის მიმართულების კოსინუსებით ფართობის მიმართ.

თუ P არის A წერტილში არჩეულ ელემენტარულ ფართობზე მოქმედი შიდა ძალების შედეგი, მაშინ ჯამური ძაბვა p N ამ წერტილში ფართობის გასწვრივ ნორმალური N-თან განისაზღვრება, როგორც შეფარდების ზღვარი

შემდეგი ფორმა:

ვექტორი p N შეიძლება დაიშალოს სივრცეში სამ ურთიერთ პერპენდიკულარულ კომპონენტად.

2. კომპონენტებში σ N , τ N s და τ N t მიმართულებები ნორმალური ადგილის მიმართ (ნორმალური დაძაბულობა) და ორი ერთმანეთის პერპენდიკულარული ღერძი s და t (ნახ. 1b), რომლებიც მდებარეობს უბნის სიბრტყეში (ტანგენციალური). ხაზს უსვამს). ნახ. 1-ის მიხედვით, ბ

თუ სხეულის მონაკვეთი ან უბანი პარალელურია ერთ-ერთი საკოორდინატო სიბრტყის პარალელურად, მაგალითად y0z (ნახ. 2), მაშინ მესამე კოორდინატთა ღერძი x ნორმალური იქნება ამ არეზე და დაძაბულობის კომპონენტებს ექნებათ აღნიშვნები σ x , τ xy და τ xz.

ნორმალური სტრესი დადებითია, თუ ის დაჭიმულია და უარყოფითი, თუ კომპრესიულია. ათვლის დაძაბულობის ნიშანი განისაზღვრება შემდეგი წესით: თუ პოზიტიური (დაჭიმვის) ნორმალური ძაბვა უბნის გასწვრივ იძლევა დადებით პროექციას, მაშინ ტანგენციალური

დაძაბულობა ერთსა და იმავე ფართობზე დადებითად ითვლება, იმ პირობით, რომ იგი ასევე იძლევა დადებით პროექციას შესაბამის ღერძზე; თუ დაჭიმვის ნორმალური ძაბვა იძლევა უარყოფით პროექციას, მაშინ დადებითი ათვლის ძაბვა ასევე უნდა აძლევდეს უარყოფით პროექციას შესაბამის ღერძზე.

ნახ. 3, მაგალითად, ყველა სტრესის კომპონენტი, რომელიც მოქმედებს ელემენტარული პარალელეპიპედის სახეებზე, ემთხვევა კოორდინატულ სიბრტყეებს, დადებითია.

ელასტიური სხეულის წერტილში დაძაბულობის მდგომარეობის დასადგენად, საჭიროა ვიცოდეთ ჯამური ძაბვები p N სამი ერთმანეთის პერპენდიკულარული უბნისთვის, რომელიც გადის ამ წერტილში. ვინაიდან თითოეული მთლიანი სტრესი შეიძლება დაიყოს სამ კომპონენტად, სტრესის მდგომარეობა განისაზღვრება, თუ ცნობილია სტრესის ცხრა კომპონენტი. ეს კომპონენტები შეიძლება დაიწეროს მატრიცის სახით

ეწოდება სტრესის ტენსორის კომპონენტების მატრიცა წერტილში.

მატრიცის ყოველი ჰორიზონტალური ხაზი შეიცავს სტრესის სამ კომპონენტს, რომლებიც მოქმედებენ ერთსა და იმავე არეზე, რადგან პირველი ხატები (ნორმის სახელი) მათთვის იგივეა. ტენზორის ყოველი ვერტიკალური სვეტი შეიცავს სამ ძაბვას იმავე ღერძის პარალელურად, ვინაიდან მეორე ნიშნები (ღერძის სახელწოდება, რომლის პარალელურადაც მოქმედებს სტრესი) იგივეა.

1.2 ელემენტარული პარალელეპიპედის წონასწორობის განტოლებები

და ელემენტარული ტეტრაედონი

გამოვყოთ ელემენტარული პარალელეპიპედი ნეკნების ზომის dx, dy და dz დაძაბული დრეკადი სხეულის A წერტილში შესასწავლად (x, y და z კოორდინატებით) სამი ერთმანეთის პერპენდიკულარული წყვილი სიბრტყით (ნახ. 2). A წერტილის მიმდებარე სამ ორმხრივ პერპენდიკულარულ სახეზე (კოორდინატულ სიბრტყეებთან ყველაზე ახლოს) იმოქმედებს სამი სტრესის კომპონენტი - ნორმალური და ორი ტანგენციალური. ჩვენ ვვარაუდობთ, რომ ისინი დადებითია A წერტილის მიმდებარე სახეების გასწვრივ.

A წერტილიდან გამავალი სახიდან პარალელურ სახეზე გადასვლისას, ძაბვები იცვლება და იღებენ ნამატებს. მაგალითად, თუ სტრესის კომპონენტები σ x \u003d f 1 (x, y, z), τ xy \u003d f 2 (x, y, z,), τ xz \u003d f 3 (x, y,z,) , შემდეგ პარალელური სახის გასწვრივ, ერთი სახიდან მეორეზე გადასვლისას მხოლოდ ერთი x კოორდინატის გაზრდის გამო,

სტრესის კომპონენტები შესაძლებელია დაძაბულობის დადგენა ელემენტარული პარალელეპიპედის ყველა სახეზე, როგორც ნაჩვენებია ნახ. 3.

ელემენტარული პარალელეპიპედის სახეებზე დაძაბულობის გარდა, მასზე მოქმედებს სხეულის ძალები: წონის ძალები, ინერციული. მოდი ავღნიშნოთ ამ ძალების პროექციები, მოცულობის ერთეულზე, კოორდინატთა ღერძებზე X, Y და Z-ით. თუ ყველა ნორმალური, ტანგენციალური და მოცულობითი ძალების x ღერძზე პროექციების ჯამს გავუტოლებთ ნულს,

ვმოქმედებთ ელემენტარულ პარალელეპიპედზე, შემდეგ dxdydz ნამრავლით შემცირების შემდეგ ვიღებთ განტოლებას

y და z ღერძებზე ძალების პროგნოზირების მსგავსი განტოლებების შედგენის შემდეგ, ჩვენ ვწერთ სამ დიფერენციალურ განტოლებას ელემენტარული პარალელეპიპედის წონასწორობისთვის, რომელიც მიღებულია კოშის მიერ,

როდესაც პარალელეპიპედის ზომები ნულამდე მცირდება, ის იქცევა წერტილად, ხოლო σ და τ არის დაძაბულობის კომპონენტები სამი ერთმანეთის პერპენდიკულარული უბნის გასწვრივ, რომლებიც გადის A წერტილში.

თუ ელემენტარულ პარალელეპიპედზე მოქმედი ყველა ძალის მომენტების ჯამს გავატოლებთ x c ღერძთან, x ღერძის პარალელურად და გადის მის სიმძიმის ცენტრში, მივიღებთ განტოლებას.

ან, იმის გათვალისწინებით, რომ განტოლების მეორე და მეოთხე წევრი უფრო მცირე ზომისაა დანარჩენებთან შედარებით, dxdydz-ით შემცირების შემდეგ.

τ yz - τ zy = 0 ან τ yz = τ zy.

y c და z c ცენტრალური ღერძების მომენტების მსგავსი განტოლებების შედგენისას ვიღებთ სამ განტოლებას ათვლის დაძაბულობის დაწყვილების კანონისთვის.

τ xy = τ yx, τ yx = τ xy, τ zx = τ xz. (1.3)

ეს კანონი ჩამოყალიბებულია შემდეგნაირად:ტანგენციალური ძაბვები, რომლებიც მოქმედებენ ორმხრივ პერპენდიკულარულ უბნებზე და მიმართულია უბნების გადაკვეთის ხაზთან პერპენდიკულურად, ტოლია სიდიდით და იდენტური ნიშნით.

ამრიგად, T σ ტენზორის მატრიცის ცხრა სტრესის კომპონენტიდან ექვსი ერთმანეთის წყვილი ტოლია და წერტილში სტრესის მდგომარეობის დასადგენად საკმარისია მხოლოდ შემდეგი ექვსი სტრესის კომპონენტის პოვნა:

მაგრამ დადგენილი წონასწორობის პირობებმა მოგვცა მხოლოდ სამი განტოლება (1.2), რომელთაგან ექვსი უცნობი ვერ მოიძებნა. ამრიგად, სტრესის მდგომარეობის განსაზღვრის პირდაპირი პრობლემა, ზოგად შემთხვევაში, სტატიკურად განუსაზღვრელია. ამ სტატიკური განუსაზღვრელობის გამოსავლენად საჭიროა დამატებითი გეომეტრიული და ფიზიკური დამოკიდებულებები.

მოდით გავჭრათ ელემენტარული პარალელეპიპედი A წერტილში მისი სახეებისკენ დახრილი სიბრტყით; მოდით ამ სიბრტყის ნორმალურ N-ს ჰქონდეს მიმართულების კოსინუსები l, m და n. მიღებული გეომეტრიული ფიგურა (ნახ. 4) არის პირამიდა სამკუთხა ფუძით - ელემენტარული ტეტრაედონი. ჩვენ ვივარაუდებთ, რომ წერტილი A ემთხვევა კოორდინატების საწყისს, ხოლო ტეტრაედრის სამი ერთმანეთის პერპენდიკულარული სახე ემთხვევა კოორდინატთა სიბრტყეს.

განხილული იქნება ტეტრაედრის ამ სახეებზე მოქმედი სტრესის კომპონენტები

დადებითი. ისინი ნაჩვენებია ნახ. 4. აღნიშნეთ , და მთლიანი დაძაბულობის პროგნოზები p N, რომელიც მოქმედებს BCD ტეტრაედრის დახრილ სახეზე x, y და z ღერძებზე. დახრილი სახის BCD ფართობი აღინიშნება dF-ით. შემდეგ სახის ABC არე იქნება dFp, სახე ACD - dFl და სახე ADB - dFt.

მოდით შევადგინოთ ტეტრაედრის წონასწორობის განტოლება მის სახეებზე მოქმედი ყველა ძალის x-ღერძზე პროექციით; სხეულის ძალის პროექცია არ შედის საპროექციო განტოლებაში, ამიტომ

როგორია სიმცირის უმაღლესი რიგის მნიშვნელობა ზედაპირული ძალების პროგნოზებთან შედარებით:

y და z ღერძებზე ტეტრაედრონზე მოქმედი ძალების საპროექციო განტოლებების შედგენისას მივიღებთ კიდევ ორ მსგავს განტოლებას. შედეგად, ჩვენ გვექნება სამი წონასწორობის განტოლება ელემენტარული ტეტრაედრისთვის

მოდით, თვითნებური ფორმის სივრცითი სხეული გავყოთ ორმხრივი პერპენდიკულარული სიბრტყეების სისტემით хОу, yОz და хОz (ნახ. 5) ელემენტარულ პარალელეპიპედებად. სხეულის ზედაპირზე, ელემენტარული

ტეტრაედრები, (ზედაპირის მრუდი მონაკვეთები, მათი სიმცირის გამო, შეიძლება შეიცვალოს სიბრტყეებით). ამ შემთხვევაში, p N წარმოადგენს დატვირთვას ზედაპირზე, ხოლო განტოლებები (1.4) დაუკავშირებენ ამ დატვირთვას σ და τ ძაბვებს სხეულში, ანუ ისინი წარმოადგენენ დრეკადობის თეორიის პრობლემის სასაზღვრო პირობებს. ამ განტოლებებით განსაზღვრულ პირობებს უწოდებენ ზედაპირის პირობები.

უნდა აღინიშნოს, რომ ელასტიურობის თეორიაში გარე დატვირთვები წარმოდგენილია ნორმალური და ტანგენციალური სტრესებით, რომლებიც გამოიყენება ზოგიერთი კანონის მიხედვით სხეულის ზედაპირთან დამთხვევაზე.

1.3 ნორმალური და ათვლის ძაბვები ფერდობის გასწვრივ

საიტი

განვიხილოთ ელემენტარული ტეტრაედონი ABCD, რომლის სამი სახე კოორდინატთა სიბრტყეების პარალელურია, ხოლო ნორმალური N მეოთხე პირის მიმართ ქმნის კუთხეებს კოორდინატთა ღერძებით, რომელთა კოსინუსები ტოლია l, m და n-ის (ნახ. 6). . ჩვენ ვივარაუდებთ, რომ კოორდინატულ სიბრტყეში მდებარე უბნებზე მოქმედი ნორმალური და ათვლის ძაბვის კომპონენტები მოცემულია და განვსაზღვრავთ ძაბვებს BCD არეს. ჩვენ ვირჩევთ მართკუთხა კოორდინატთა ღერძების ახალ სისტემას x 1, y 1 და z 1, ისე რომ x 1 ღერძი ემთხვევა ნორმალურ N-ს,

დაძაბულობა-დაძაბულობის მდგომარეობა განისაზღვრება, თუ აღმოჩენილია დაძაბულობის ტენზორის () და გადაადგილების ვექტორის კომპონენტები, ცხრა ფუნქცია.

დრეკადობის თეორიის ძირითადი განტოლებები

დიფერენციალური კეშიები

სად არის კოშის დეფორმაციების წრფივი ნაწილის ტენზორის კომპონენტები;

რადიუსის გასწვრივ გადაადგილების წარმოებულის ტენზორის კომპონენტები.

დიფერენციალური წონასწორობის განტოლებები

ჰუკის კანონი ხაზოვანი ელასტიური იზოტროპული სხეულისთვის

ზემოაღნიშნული განტოლებები უნდა აკმაყოფილებდეს Saint-Venant დამოკიდებულებებს

პრობლემების სახეები დრეკადობის თეორიაში

პირველი ტიპი. ძალები მოცემულია სხეულის ზედაპირზე. სასაზღვრო პირობები

დრეკადობის თეორიის პირდაპირი და შებრუნებული ამოცანები

ელასტიურობის თეორიის განტოლებები გადაადგილებებში (ლამის განტოლებები)

გადაადგილებებში დრეკადობის თეორიის განტოლებების დასადგენად ვწერთ: დიფერენციალური წონასწორობის განტოლებები (18) ჰუკის კანონი წრფივი დრეკადობის იზოტროპული სხეულისთვის (19)