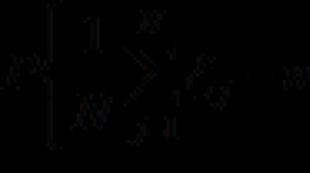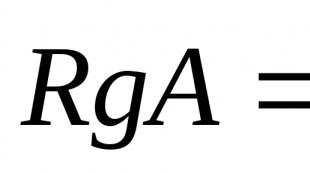Տարասեռ համակարգի ընդհանուր լուծում. Գծային հավասարումների միատարր համակարգեր Միատարր համակարգերի լուծում 0

Գծային հավասարումը կոչվում է միատարր, եթե նրա ազատ անդամը հավասար է զրոյի, իսկ հակառակ դեպքում՝ անհամասեռ։ Միատարր հավասարումներից բաղկացած համակարգը կոչվում է միատարր և ունի ընդհանուր ձև.

Ակնհայտ է, որ յուրաքանչյուր միատարր համակարգ հետևողական է և ունի զրոյական (չնչին) լուծում։ Հետևաբար, երբ կիրառվում է գծային հավասարումների միատարր համակարգերի նկատմամբ, հաճախ պետք է փնտրել ոչ զրոյական լուծումների առկայության հարցի պատասխանը։ Այս հարցի պատասխանը կարելի է ձևակերպել հետևյալ թեորեմի տեսքով.

Թեորեմ . Գծային հավասարումների համասեռ համակարգը ունի ոչ զրոյական լուծում, եթե և միայն այն դեպքում, եթե նրա աստիճանը փոքր է անհայտների թվից .

Ապացույց: Ենթադրենք, որ համակարգը, որի աստիճանը հավասար է, ունի ոչ զրոյական լուծում: Ակնհայտ է, որ այն չի գերազանցում: Այն դեպքում, երբ համակարգը ունի յուրահատուկ լուծում. Քանի որ միատարր գծային հավասարումների համակարգը միշտ ունի զրոյական լուծում, ապա զրոյական լուծումը կլինի այս եզակի լուծումը: Այսպիսով, ոչ զրոյական լուծումներ հնարավոր են միայն .

Եզրակացություն 1 : Հավասարումների միատարր համակարգը, որտեղ հավասարումների թիվը փոքր է անհայտների թվից, միշտ ունի ոչ զրոյական լուծում:

Ապացույց: Եթե ​​հավասարումների համակարգն ունի , ապա համակարգի աստիճանը չի գերազանցում հավասարումների թիվը, այսինքն. . Այսպիսով, պայմանը բավարարված է և, հետևաբար, համակարգն ունի ոչ զրոյական լուծում։

Եզրակացություն 2 : Անհայտներով հավասարումների միատարր համակարգը ունի ոչ զրոյական լուծում, եթե և միայն այն դեպքում, երբ նրա որոշիչը զրո է:

Ապացույց: Ենթադրենք, որ գծային միատարր հավասարումների համակարգը, որի մատրիցը որոշիչով ունի զրոյական լուծում: Այնուհետև, ըստ ապացուցված թեորեմի, և դա նշանակում է, որ մատրիցը եզակի է, այսինքն. .

Կրոնեկեր-Կապելի թեորեմ. SLU-ը հետևողական է, եթե և միայն այն դեպքում, եթե համակարգի մատրիցայի աստիճանը հավասար է այս համակարգի ընդլայնված մատրիցայի աստիճանին: ur համակարգը կոչվում է հետևողական, եթե այն ունի առնվազն մեկ լուծում:

Գծային հանրահաշվական հավասարումների միատարր համակարգ.

m գծային հավասարումների համակարգը n փոփոխականով կոչվում է գծային միատարր հավասարումների համակարգ, եթե բոլոր ազատ անդամները հավասար են 0-ի: Գծային միատարր հավասարումների համակարգը միշտ համահունչ է, քանի որ այն միշտ ունի առնվազն զրոյական լուծում: Գծային միատարր հավասարումների համակարգը ունի ոչ զրոյական լուծում, եթե և միայն այն դեպքում, երբ փոփոխականների համար նրա գործակիցների մատրիցայի աստիճանը փոքր է փոփոխականների թվից, այսինքն. A աստիճանի համար (n. Ցանկացած գծային համակցություն

Lin համակարգի լուծումներ. միատարր. ur-ii-ն նույնպես այս համակարգի լուծումն է:

Գծային անկախ լուծումների e1, e2,...,еk համակարգը կոչվում է հիմնարար, եթե համակարգի յուրաքանչյուր լուծում լուծումների գծային համակցություն է։ Թեորեմ. եթե գծային միատարր հավասարումների համակարգի փոփոխականների համար գործակիցների մատրիցայի r աստիճանը փոքր է n փոփոխականների թվից, ապա համակարգի լուծումների յուրաքանչյուր հիմնարար համակարգ բաղկացած է n-r լուծումներից։ Հետեւաբար, գծային համակարգի ընդհանուր լուծումը. մի օր ur-th-ն ունի c1e1+c2e2+...+skek ձևը, որտեղ e1, e2,..., ek լուծումների ցանկացած հիմնարար համակարգ է, c1, c2,...,ck կամայական թվեր են և k=n-r: n փոփոխականներով m գծային հավասարումների համակարգի ընդհանուր լուծումը հավասար է գումարին

դրան համապատասխան համակարգի ընդհանուր լուծումը միատարր է։ գծային հավասարումներ և այս համակարգի կամայական որոշակի լուծում:

7. Գծային տարածություններ. Ենթատարածություններ. Հիմք, չափս. Գծային պատյան. Գծային տարածությունը կոչվում է n-չափ, եթե այն պարունակում է գծային անկախ վեկտորների համակարգ, և ավելի մեծ թվով վեկտորների ցանկացած համակարգ գծային կախված է։ Համարը կոչվում է չափսեր (չափերի քանակը)գծային տարածություն և նշանակվում է . Այլ կերպ ասած, տարածության չափը այս տարածության գծային անկախ վեկտորների առավելագույն քանակն է: Եթե ​​այդպիսի թիվ գոյություն ունի, ապա տարածությունը կոչվում է վերջավոր ծավալային: Եթե ​​ցանկացած n բնական թվի համար տարածության մեջ կա համակարգ, որը բաղկացած է գծային անկախ վեկտորներից, ապա այդպիսի տարածությունը կոչվում է անվերջաչափ (գրված՝ ): Հետևյալում, եթե այլ բան նշված չէ, կդիտարկվեն վերջավոր չափերի տարածությունները:

n-չափ գծային տարածության հիմքը գծային անկախ վեկտորների կարգավորված հավաքածուն է ( հիմքի վեկտորներ).

Թեորեմ 8.1 վեկտորի ընդլայնման վերաբերյալ հիմքի առումով: Եթե ​​n-չափ գծային տարածության հիմքն է, ապա ցանկացած վեկտոր կարող է ներկայացվել որպես հիմքի վեկտորների գծային համակցություն.

V=v1*e1+v2*e2+…+vn+en
եւ, առավել եւս, միակ ճանապարհով, ի. գործակիցները որոշվում են եզակի.Այսինքն՝ տարածության ցանկացած վեկտոր կարող է ընդլայնվել հիմքի մեջ և առավել եւս՝ յուրօրինակ կերպով։

Իրոք, տարածության չափը . Վեկտորների համակարգը գծային անկախ է (սա հիմք է): Հիմքին որևէ վեկտոր ավելացնելուց հետո մենք ստանում ենք գծային կախված համակարգ (քանի որ այս համակարգը բաղկացած է n-չափ տարածության վեկտորներից): Օգտագործելով 7 գծային կախված և գծային անկախ վեկտորների հատկությունը՝ ստանում ենք թեորեմի եզրակացությունը.

Բարձրագույն մասնագիտական ​​կրթության դաշնային պետական ​​բյուջետային ուսումնական հաստատության Կալուգայի մասնաճյուղ

«Մոսկվայի պետական ​​տեխնիկական համալսարանի անվան N.E. Բաուման»

(Ն.Է. Բաումանի անվան Մոսկվայի պետական ​​տեխնիկական համալսարանի Խարկովի մասնաճյուղ)

Վլայկով Ն.Դ.

Միատարր SLAE-ների լուծում

Զորավարժությունների անցկացման ուղեցույցներ

անալիտիկ երկրաչափության ընթացքի վրա

Կալուգա 2011թ

Դասի նպատակները էջ 4

Դասի պլան էջ 4

Անհրաժեշտ տեսական տեղեկատվություն էջ 5

Գործնական մաս էջ 10

Լուսաբանված նյութի յուրացման մոնիտորինգ էջ 13

Տնային աշխատանք էջ 14

Ժամերի քանակը՝ 2

Դասի նպատակները.

Ստացված տեսական գիտելիքները համակարգել SLAE-ների տեսակների և դրանց լուծման մեթոդների մասին:

Ձեռք բերեք համասեռ SLAE-ների լուծման հմտություններ:

Դասի պլան:

Համառոտ ներկայացրեք տեսական նյութը:

Լուծել համասեռ SLAE:

Գտե՛ք համասեռ SLAE-ի լուծումների հիմնարար համակարգը:

Գտեք համասեռ SLAE-ի կոնկրետ լուծում:

Ձևակերպեք միատարր SLAE-ի լուծման ալգորիթմ:

Ստուգեք ձեր ընթացիկ տնային աշխատանքը:

Իրականացնել ստուգման աշխատանքներ.

Ներկայացրե՛ք հաջորդ սեմինարի թեման։

Ներկայացրե՛ք ընթացիկ տնային աշխատանքը:

Անհրաժեշտ տեսական տեղեկատվություն.

Մատրիցային աստիճան.

Def.Մատրիցայի աստիճանը այն թիվն է, որը հավասար է նրա ոչ զրոյական փոքրերի առավելագույն կարգին: Մատրիցայի աստիճանը նշվում է.

Եթե ​​քառակուսի մատրիցը ոչ եզակի է, ապա դրա աստիճանը հավասար է իր կարգին: Եթե ​​քառակուսի մատրիցը եզակի է, ապա դրա աստիճանը պակաս է իր կարգից:

Անկյունագծային մատրիցայի աստիճանը հավասար է նրա ոչ զրոյական անկյունագծային տարրերի թվին:

տես.Երբ մատրիցը փոխադրվում է, դրա վարկանիշը չի փոխվում, այսինքն.
.

տես.Մատրիցայի աստիճանը չի փոխվում նրա տողերի և սյունակների տարրական փոխակերպումներով:

Թեորեմը փոքր հիմքի վրա.

Def.Անչափահաս
մատրիցներ կոչվում է հիմնական, եթե երկու պայման կա.

ա) այն հավասար չէ զրոյի.

բ) դրա կարգը հավասար է մատրիցայի աստիճանին .

Մատրիցա կարող է ունենալ մի քանի հիմք անչափահասներ:

Մատրիցային տողեր և սյունակներ , որում գտնվում է ընտրված հիմնական մինորը, կոչվում են հիմնական։

տես.Թեորեմը փոքր հիմքի վրա. Մատրիցայի հիմնական տողերը (սյունակները): , համապատասխան ցանկացած իր հիմքում ընկած անչափահասներին
, գծային անկախ են։ Մատրիցայի ցանկացած տող (սյունակ): , ներառված չէ
, հիմքի տողերի (սյունակների) գծային համակցություններ են։

տես.Ցանկացած մատրիցի համար նրա աստիճանը հավասար է գծային անկախ տողերի (սյունակների) առավելագույն թվին։

Մատրիցայի աստիճանի հաշվարկ: Տարրական փոխակերպումների մեթոդ.

Օգտագործելով տողերի տարրական փոխակերպումները, ցանկացած մատրիցա կարող է կրճատվել էշելոնի ձևի: Քայլի մատրիցայի աստիճանը հավասար է ոչ զրոյական տողերի թվին: Դրա հիմքում ընկած է մինորը, որը գտնվում է ոչ զրոյական տողերի հատման կետում՝ տողերից յուրաքանչյուրում ձախից առաջին ոչ զրոյական տարրերին համապատասխանող սյունակների հետ։

ՍԼԱՈՒ. Հիմնական սահմանումներ.

Def.Համակարգ

(15.1)

Թվեր կոչվում են SLAE գործակիցներ: Թվեր
կոչվում են հավասարումների ազատ անդամներ։

SLAE մուտքը (15.1) կոչվում է կոորդինատ:

Def. SLAE-ն կոչվում է միատարր, եթե
. Հակառակ դեպքում այն ​​կոչվում է տարասեռ:

Def. SLAE-ի լուծումը անհայտ արժեքների մի շարք է, որը փոխարինելուց հետո համակարգի յուրաքանչյուր հավասարում վերածվում է ինքնության: SLAE-ի ցանկացած կոնկրետ լուծում կոչվում է նաև դրա հատուկ լուծում:

SLAE-ի լուծումը նշանակում է լուծել երկու խնդիր.

Պարզեք, թե արդյոք SLAE-ն ունի լուծումներ.

Գտեք բոլոր լուծումները, եթե դրանք կան:

Def. SLAE-ը կոչվում է հոդ, եթե այն ունի առնվազն մեկ լուծում: Հակառակ դեպքում այն ​​կոչվում է անհամատեղելի:

Def.Եթե ​​SLAE-ն (15.1) ունի լուծում և եզակի, ապա այն կոչվում է որոշակի, իսկ եթե լուծումը եզակի չէ, ապա այն կոչվում է անորոշ:

Def.Եթե ​​(15.1) հավասարման մեջ.
SLAE-ը կոչվում է քառակուսի:

SLAU ձայնագրման ձևեր.

Բացի կոորդինատային ձևից (15.1), SLAE գրառումները հաճախ օգտագործվում են դրա այլ ներկայացումներում:

(15.2)

Հարաբերությունը կոչվում է SLAE նշման վեկտորային ձև:

Եթե ​​հիմք ընդունենք մատրիցների արտադրյալը, ապա SLAE (15.1) կարելի է գրել հետևյալ կերպ.

(15.3)

կամ
.

SLAE-ի (15.1) նշումը (15.3) կոչվում է մատրիցա:

Միատարր SLAEs.

Միատարր համակարգ
գծային հանրահաշվական հավասարումների հետ անհայտները ձևի համակարգ է

Միատարր SLAE-ները միշտ համահունչ են, քանի որ միշտ կա զրոյական լուծում:

Ոչ զրոյական լուծման առկայության չափանիշ.Որպեսզի միատարր քառակուսի SLAE-ի համար գոյություն ունենա ոչ զրոյական լուծում, անհրաժեշտ է և բավարար, որ դրա մատրիցը լինի եզակի:

տես.Եթե ​​սյունակները
,
, …,
միատարր SLAE-ի լուծումներ են, ապա դրանց ցանկացած գծային համակցություն նույնպես այս համակարգի լուծումն է:

Հետևանք. Եթե ​​միատարր SLAE-ն ունի ոչ զրոյական լուծում, ապա այն ունի անսահման թվով լուծումներ:

Բնական է փորձել նման լուծումներ գտնել
,
, …,
համակարգեր, որպեսզի ցանկացած այլ լուծում ներկայացվի որպես դրանց գծային համակցություն և, առավել ևս, յուրօրինակ կերպով:

Def.Ցանկացած հավաքածու
գծային անկախ սյունակներ
,
, …,
, որոնք համասեռ SLAE-ի լուծույթներ են
, Որտեղ - անհայտների թիվը, և - իր մատրիցայի աստիճանը , կոչվում է այս միատարր SLAE-ի լուծումների հիմնարար համակարգ։

Գծային հավասարումների միատարր համակարգերը ուսումնասիրելիս և լուծելիս մենք համակարգի մատրիցայում կամրագրենք հիմնական մինորը: Հիմնական մինորը կհամապատասխանի հիմնական սյունակներին և, հետևաբար, հիմքի անհայտներին: Մնացած անհայտներին ազատ կանվանենք։

տես.Միատարր SLAE-ի ընդհանուր լուծման կառուցվածքի մասին. Եթե
,
, …,
- համասեռ SLAE-ի լուծումների կամայական հիմնարար համակարգ
, ապա դրա ցանկացած լուծում կարող է ներկայացվել ձևով

Որտեղ , …,- ոմանք մշտական ​​են:

Դա. համասեռ SLAE-ի ընդհանուր լուծումն ունի ձև

Գործնական մաս.

Դիտարկենք SLAE-ների հետևյալ տեսակների լուծումների հնարավոր հավաքածուները և դրանց գրաֆիկական մեկնաբանությունը:

;
;
.

Դիտարկենք այս համակարգերը լուծելու հնարավորությունը՝ օգտագործելով Քրամերի բանաձևերը և մատրիցային մեթոդը:

Բացատրեք Գաուսի մեթոդի էությունը:

Լուծե՛ք հետևյալ խնդիրները.

Օրինակ 1. Լուծե՛ք համասեռ SLAE: Գտեք FSR:

.

Եկեք գրենք համակարգի մատրիցը և հասցնենք այն աստիճանաբար:

.

համակարգը կունենա անսահման շատ լուծումներ։ FSR-ն բաղկացած կլինի
սյունակներ.

Եկեք դեն նետենք զրոյական տողերը և նորից գրենք համակարգը.

.

Հիմնական մինորը մենք կհամարենք վերին ձախ անկյունում: Դա.
- հիմնական անհայտները, և
- անվճար. Արտահայտենք
անվճար միջոցով
:

;

դնենք
.

Վերջապես մենք ունենք.

- պատասխանի կոորդինատիվ ձև, կամ

- պատասխանի մատրիցային ձև, կամ

- պատասխանի վեկտորային ձև (վեկտոր - սյունակները FSR սյունակներ են):

Միատարր SLAE-ի լուծման ալգորիթմ.

Գտեք FSR-ը և հետևյալ համակարգերի ընդհանուր լուծումը.

№2.225(4.39)

. Պատասխան.

№2.223(2.37)

. Պատասխան.

№2.227(2.41)

. Պատասխան.

Լուծեք համասեռ SLAE.

. Պատասխան.

Լուծեք համասեռ SLAE.

. Պատասխան.

Հաջորդ սեմինարի թեմայի ներկայացում.

Գծային անհամասեռ հավասարումների համակարգերի լուծում.

Ծածկված նյութի տիրապետման մոնիտորինգ:

Թեստային աշխատանք 3-5 րոպե: Հանդեսում կենտ թվերով մասնակցում է 4 աշակերտ՝ սկսած թիվ 10-ից

Հետևեք այս քայլերին. ; ;	Հետևեք այս քայլերին.
	Հաշվիր որոշիչը՝

Հետևեք այս քայլերին. չսահմանված	Հետևեք այս քայլերին.
Գտե՛ք այս մեկի հակադարձ մատրիցը.	Հաշվիր որոշիչը՝

Տնային աշխատանք:

1. Լուծել խնդիրները.

№ 2.224, 2.226, 2.228, 2.230, 2.231, 2.232.

2. Աշխատեք դասախոսությունների միջոցով հետևյալ թեմաներով.

Գծային հանրահաշվական հավասարումների համակարգեր (SLAEs). Ձայնագրման կոորդինատային, մատրիցային և վեկտորային ձևեր: SLAE-ների համատեղելիության Kronecker-Capelli չափանիշը. Տարասեռ SLAEs. Միատարր SLAE-ի ոչ զրոյական լուծման գոյության չափանիշ: Միատարր SLAE-ի լուծույթների հատկությունները. Միատարր SLAE-ի լուծումների հիմնարար համակարգը, դրա գոյության թեորեմը. Լուծումների նորմալ հիմնարար համակարգ: Միասեռ SLAE-ի ընդհանուր լուծման կառուցվածքի թեորեմ. Թեորեմ անհամասեռ SLAE-ի ընդհանուր լուծման կառուցվածքի վերաբերյալ.

Գծային հավասարումների համակարգ, որտեղ բոլոր ազատ անդամները հավասար են զրոյի, կոչվում է միատարր :

Ցանկացած միատարր համակարգ միշտ հետևողական է, քանի որ միշտ էլ եղել է զրո (չնչին ) լուծում. Հարց է առաջանում, թե ինչ պայմաններում միատարր համակարգը կունենա ոչ տրիվիալ լուծում:

Թեորեմ 5.2.Միատարր համակարգը ունի ոչ տրիվիալ լուծում, եթե և միայն այն դեպքում, երբ հիմքում ընկած մատրիցայի աստիճանը փոքր է նրա անհայտների թվից:

Հետևանք. Քառակուսի միատարր համակարգը ունի ոչ տրիվիալ լուծում, եթե և միայն այն դեպքում, եթե համակարգի հիմնական մատրիցայի որոշիչը հավասար չէ զրոյի:

Օրինակ 5.6.Որոշեք l պարամետրի արժեքները, որոնց դեպքում համակարգն ունի ոչ տրիվիալ լուծումներ և գտեք այս լուծումները.

Լուծում. Այս համակարգը կունենա ոչ տրիվիալ լուծում, երբ հիմնական մատրիցայի որոշիչը հավասար է զրոյի.

Այսպիսով, համակարգը ոչ տրիվիալ է, երբ l=3 կամ l=2: l=3-ի դեպքում համակարգի հիմնական մատրիցայի աստիճանը 1 է: Այնուհետև թողնելով միայն մեկ հավասարում և ենթադրելով, որ y=աԵվ զ=բ, ստանում ենք x=b-a, այսինքն.

l=2-ի համար համակարգի հիմնական մատրիցայի աստիճանը 2 է: Այնուհետև որպես հիմք ընտրելով փոքրը.

մենք ստանում ենք պարզեցված համակարգ

Այստեղից մենք գտնում ենք, որ x=z/4, y=z/2. Հավատալով զ=4ա, ստանում ենք

Միատարր համակարգի բոլոր լուծումների հավաքածուն ունի շատ կարևոր գծային սեփականություն : եթե X սյունակները 1 և X 2 - լուծումներ միատարր համակարգի AX = 0, ապա դրանց ցանկացած գծային համակցությունա X 1 + բ X 2 կլինի նաև այս համակարգի լուծումը. Իսկապես, քանի որ ԿԱՑԻՆ 1 = 0 Եվ ԿԱՑԻՆ 2 = 0 , Դա Ա(ա X 1 + բ X 2) = ա ԿԱՑԻՆ 1 + բ ԿԱՑԻՆ 2 = a · 0 + b · 0 = 0. Այս հատկության շնորհիվ է, որ եթե գծային համակարգն ունի մեկից ավելի լուծում, ապա այդ լուծումների անսահման թիվը կլինի:

Գծային անկախ սյունակներ Ե 1 , Ե 2 , Ե կ, որոնք միատարր համակարգի լուծույթներ են, կոչվում են լուծումների հիմնարար համակարգ գծային հավասարումների միատարր համակարգ, եթե այս համակարգի ընդհանուր լուծումը կարելի է գրել որպես այս սյունակների գծային համակցություն.

Եթե ​​միատարր համակարգն ունի nփոփոխականներ, և համակարգի հիմնական մատրիցայի աստիճանը հավասար է r, Դա կ = n-r.

Օրինակ 5.7.Գտե՛ք գծային հավասարումների հետևյալ համակարգի լուծումների հիմնարար համակարգը.

Լուծում. Գտնենք համակարգի հիմնական մատրիցայի աստիճանը.

Այսպիսով, այս հավասարումների համակարգի լուծումների բազմությունը կազմում է չափումների գծային ենթատարածություն n-r= 5 - 2 = 3. Եկեք որպես հիմք ընտրենք փոքրը

Այնուհետև, թողնելով միայն հիմնական հավասարումները (մնացածը կլինի այս հավասարումների գծային համակցությունը) և հիմնական փոփոխականները (մնացածը, այսպես կոչված, ազատ փոփոխականները տեղափոխում ենք աջ), մենք ստանում ենք հավասարումների պարզեցված համակարգ.

Հավատալով x 3 = ա, x 4 = բ, x 5 = գ, գտնում ենք

Հավատալով ա= 1, b = c= 0, մենք ստանում ենք առաջին հիմնական լուծումը. հավատալով բ= 1, a = c= 0, մենք ստանում ենք երկրորդ հիմնական լուծումը. հավատալով գ= 1, ա = բ= 0, մենք ստանում ենք երրորդ հիմնական լուծումը: Արդյունքում լուծումների նորմալ հիմնարար համակարգը ձև կընդունի

Օգտագործելով հիմնարար համակարգը, միատարր համակարգի ընդհանուր լուծումը կարելի է գրել այսպես

X = աԷ 1 + լինել 2 + cE 3. ա

Եկեք նշենք գծային հավասարումների անհամասեռ համակարգի լուծումների որոշ հատկություններ AX=Bև դրանց կապը համապատասխան միատարր հավասարումների համակարգի հետ AX = 0:

Անհամասեռ համակարգի ընդհանուր լուծումհավասար է AX = 0 համապատասխան համասեռ համակարգի ընդհանուր լուծման և անհամասեռ համակարգի կամայական որոշակի լուծման գումարին.. Իսկապես, թող Յ 0-ը անհամասեռ համակարգի կամայական որոշակի լուծում է, այսինքն. ԱՅ 0 = Բ, Եվ Յ- տարասեռ համակարգի ընդհանուր լուծում, այսինքն. ԱՅ=Բ. Մեկ հավասարությունը մյուսից հանելով՝ ստանում ենք
Ա(Ե-Յ 0) = 0, այսինքն. Ե-Յ 0-ը համապատասխան համասեռ համակարգի ընդհանուր լուծումն է ԿԱՑԻՆ=0. Հետևաբար, Ե-Յ 0 = X, կամ Y=Y 0 + X. Ք.Ե.Դ.

Թող անհամասեռ համակարգը ունենա AX = B ձև 1 + Բ 2 . Այնուհետև նման համակարգի ընդհանուր լուծումը կարելի է գրել X = X 1 + X 2 , որտեղ AX 1 = Բ 1 եւ AX 2 = Բ 2. Այս հատկությունն արտահայտում է ընդհանրապես ցանկացած գծային համակարգի (հանրահաշվական, դիֆերենցիալ, ֆունկցիոնալ և այլն) ունիվերսալ հատկություն։ Ֆիզիկայի մեջ այս հատկությունը կոչվում է սուպերպոզիցիոն սկզբունքըէլեկտրատեխնիկայում և ռադիոտեխնիկայում. սուպերպոզիցիայի սկզբունքը. Օրինակ, գծային էլեկտրական սխեմաների տեսության մեջ ցանկացած շղթայի հոսանքը կարելի է ստանալ որպես էներգիայի յուրաքանչյուր աղբյուրի կողմից առանձին-առանձին առաջացած հոսանքների հանրահաշվական գումար:

Գծային հավասարումների համասեռ համակարգ AX = 0միշտ միասին. Այն ունի ոչ տրիվիալ (ոչ զրոյական) լուծումներ, եթե r= կոչում Ա< n .

Միատարր համակարգերի համար հիմնական փոփոխականները (որոնց գործակիցները կազմում են հիմնական մինորը) արտահայտվում են ազատ փոփոխականների միջոցով՝ ձևի հարաբերություններով.

Հետո n-rԳծային անկախ վեկտորային լուծումները կլինեն.

և ցանկացած այլ լուծում դրանց գծային համակցությունն է: Վեկտորային լուծումներ ձևավորել նորմալացված հիմնարար համակարգ.

Գծային տարածության մեջ գծային հավասարումների համասեռ համակարգի լուծումների բազմությունը կազմում է չափերի ենթատարածություն n-r; - այս ենթատարածության հիմքը:

Համակարգ մհետ գծային հավասարումներ nանհայտ(կամ, գծային համակարգ

Այստեղ x 1 , x 2 , …, x n ա 11 , ա 12 , …, մի մն- համակարգային գործակիցներ - և բ 1 , բ 2 , … բ մ ա ijես) և անհայտ ( ժ

Համակարգը (1) կոչվում է միատարրբ 1 = բ 2 = … = բ մ= 0), հակառակ դեպքում - տարասեռ.

Համակարգը (1) կոչվում է քառակուսի, եթե համարը մթվին հավասար հավասարումներ nանհայտ.

Լուծումհամակարգեր (1) - հավաքածու nթվեր գ 1 , գ 2 , …, c n, այնպիսին, որ յուրաքանչյուրի փոխարինումը գ iփոխարեն x iհամակարգի մեջ (1) իր բոլոր հավասարումները վերածում է ինքնությունների:

Համակարգը (1) կոչվում է համատեղ ոչ համատեղ

Լուծումներ գ 1 (1) , գ 2 (1) , …, c n(1) և գ 1 (2) , գ 2 (2) , …, c n բազմազան

գ 1 (1) = գ 1 (2) , գ 2 (1) = գ 2 (2) , …, c n (1) = c n (2) .

որոշակի անորոշ. Եթե ​​կան ավելի շատ հավասարումներ, քան անհայտներ, այն կոչվում է վերասահմանված.

Գծային հավասարումների համակարգերի լուծում

Լուծելով մատրիցային հավասարումներ ~ Գաուսի մեթոդ

Գծային հավասարումների համակարգերի լուծման մեթոդները բաժանվում են երկու խմբի.

1. ճշգրիտ մեթոդներ, որոնք համակարգի արմատները հաշվարկելու վերջավոր ալգորիթմներ են (համակարգերի լուծում՝ օգտագործելով հակադարձ մատրիցա, Քրամերի կանոն, Գաուսի մեթոդ և այլն),

2. կրկնվող մեթոդներ, որոնք հնարավորություն են տալիս կոնվերգենտ իտերատիվ պրոցեսների միջոցով (իտերացիոն մեթոդ, Սեյդելի մեթոդ և այլն) ստանալ համակարգի լուծումը տրված ճշգրտությամբ։

Անխուսափելի կլորացման պատճառով նույնիսկ ճշգրիտ մեթոդների արդյունքները մոտավոր են։ Կրկնվող մեթոդների կիրառման ժամանակ, բացի այդ, ավելացվում է մեթոդի սխալը։

Կրկնվող մեթոդների արդյունավետ օգտագործումը զգալիորեն կախված է սկզբնական մոտարկման հաջող ընտրությունից և գործընթացի մերձեցման արագությունից:

Մատրիցային հավասարումների լուծում

Հաշվի առեք համակարգը nգծային հանրահաշվական հավասարումների նկատմամբ nանհայտ X 1 , X 2 , …, x n:

.

(15)

Մատրիցա Ա, որի սյունակները համապատասխան անհայտների գործակիցներն են, իսկ տողերը՝ համապատասխան հավասարման անհայտների գործակիցները, կոչվում է. համակարգի մատրիցա; մատրիցա-սյունակ բ, որի տարրերը համակարգի հավասարումների աջ կողմերն են, կոչվում է աջ կողմի մատրիցակամ պարզապես համակարգի աջ կողմը. Սյունակի մատրիցա X, որի տարրերն են անհայտ անհայտները, կոչվում է համակարգի լուծում.

Եթե ​​մատրիցա Ա- ոչ հատուկ, այսինքն՝ դետ A n e-ը հավասար է 0-ի, ապա համակարգը (13), կամ դրան համարժեք մատրիցային հավասարումը (14) ունի յուրահատուկ լուծում։

Փաստորեն, տրամադրվում է դետ A-ն հավասար չէ 0 կա հակադարձ մատրիցա Ա-1. (14) հավասարման երկու կողմերը բազմապատկելով մատրիցով Ա-1 մենք ստանում ենք.

(16)

Բանաձև (16) լուծում է տալիս (14) հավասարումը և այն եզակի է:

Հարմար է լուծել գծային հավասարումների համակարգերը՝ օգտագործելով ֆունկցիան լուծել.

լուծել ( Ա, բ)

Լուծման վեկտորը վերադարձվում է xայնպիսին է, որ Օ՜= բ.

Փաստարկներ:

Ա- քառակուսի, ոչ եզակի մատրիցա:

բ- վեկտոր, որն ունի նույն թվով տողեր, որքան տողերը մատրիցայում Ա .

Նկար 8-ը ցույց է տալիս երեք անհայտ երեք գծային հավասարումների համակարգի լուծումը:

Գաուսի մեթոդ

Գաուսի մեթոդը, որը նաև կոչվում է Գաուսի վերացման մեթոդ, բաղկացած է նրանից, որ համակարգը (13) անհայտների հաջորդական վերացման միջոցով վերածվում է եռանկյունաձև մատրիցով համարժեք համակարգի.

Մատրիցային նշումներում դա նշանակում է, որ նախ (Գաուսի մեթոդի ուղղակի մոտեցումը), տողերի վրա տարրական գործողություններով, համակարգի ընդլայնված մատրիցը կրճատվում է աստիճանական ձևի.

և այնուհետև (Գաուսի մեթոդի հակառակը) այս քայլի մատրիցը փոխակերպվում է այնպես, որ առաջին nսյունակներում մենք ստանում ենք միավորի մատրիցա.

.

Վերջին, ( n+ 1) այս մատրիցայի սյունակը պարունակում է (13) համակարգի լուծումը:

Mathcad-ում Գաուսի մեթոդի առաջ և հետընթաց շարժումները կատարվում են ֆունկցիայի միջոցով հղում(Ա).

Նկար 9-ը ցույց է տալիս Գաուսի մեթոդով գծային հավասարումների համակարգի լուծումը, որն օգտագործում է հետևյալ գործառույթները.

ռեֆ ( Ա)

Մատրիցայի քայլային ձևը վերադարձվում է Ա.

մեծացնել ( Ա, IN)

Վերադարձնում է տեղանքով ձևավորված զանգվածը Ա Եվ IN կողք կողքի. Զանգվածներ Ա Եվ IN պետք է ունենա նույն թվով տողեր:

ենթամատրիցան ( A, ir, jr, ic, jc)

Վերադարձնում է ենթամատրիցան, որը բաղկացած է բոլոր տարրերից irԸստ կրտսերեւ սյուներ հետ Հասկանալի էԸստ ժկ.Համոզվեք, որ դա ir կրտսերԵվ

Հասկանալի է jc,հակառակ դեպքում տողերի և/կամ սյունակների հերթականությունը կփոխվի:

Նկար 9.

Մեթոդի նկարագրությունը

n անհայտով n գծային հավասարումների համակարգի համար (կամայական դաշտում)

զրոյից տարբերվող Δ համակարգի մատրիցայի որոշիչով լուծումը գրվում է ձևով

(համակարգի մատրիցայի i-րդ սյունակը փոխարինվում է անվճար տերմինների սյունակով):
Մեկ այլ ձևով Կրամերի կանոնը ձևակերպված է հետևյալ կերպ. c1, c2, ..., cn ցանկացած գործակիցների համար գործում է հետևյալ հավասարությունը.

Այս ձևով Քրամերի բանաձևը վավեր է առանց ենթադրության, որ Δ-ն տարբերվում է զրոյից, նույնիսկ անհրաժեշտ չէ, որ համակարգի գործակիցները լինեն ինտեգրալ օղակի տարրեր (համակարգի որոշիչը կարող է լինել նույնիսկ գործակցի զրոյական բաժանարար։ մատանի): Կարող ենք նաև ենթադրել, որ կամ b1,b2,...,bn և x1,x2,...,xn բազմությունները, կամ c1,c2,...,cn բազմությունները չեն կազմված գործակցի օղակի տարրերից։ համակարգի, բայց այս օղակի վերևում գտնվող որոշ մոդուլ: Այս ձևով Քրամերի բանաձևն օգտագործվում է, օրինակ, Գրամի որոշիչի և Նակայամայի Լեմմայի բանաձևի ապացուցման մեջ։

35) Կրոնեկեր-Կապելի թեորեմ

Որպեսզի n անհայտներում m անհամասեռ գծային հավասարումների համակարգը հետևողական լինի, անհրաժեշտ է և բավարար, որ անհրաժեշտության ապացույցը: Թող (1.13) համակարգը լինի հետևողական, այսինքն՝ կան այդպիսի թվեր X 1 =α 1 , X 2 =α 2 , …, x n = α n,Ինչ (1.15) Ընդլայնված մատրիցայի վերջին սյունակից հանենք նրա առաջին սյունակը՝ բազմապատկելով α 1-ով, երկրորդը՝ α 2-ով, ..., n-րդը՝ բազմապատկած α n-ով, այսինքն՝ մատրիցայի վերջին սյունակից։ (1.14) մենք պետք է հանենք հավասարումների ձախ կողմերը (1.15): Այնուհետև մենք ստանում ենք մատրիցը որոնց աստիճանը տարրական փոխակերպումների արդյունքում չի փոխվի և . Բայց դա ակնհայտ է, հետևաբար՝ բավարարության ապացույց։ Հստակության համար թող մատրիցայի վերին ձախ անկյունում գտնվի r կարգի ոչ զրոյական մինոր. Սա նշանակում է, որ մատրիցայի մնացած տողերը կարելի է ստանալ որպես առաջին r տողերի գծային համակցություններ, այսինքն՝ մատրիցայի m-r տողերը կարող են ներկայացվել որպես առաջին r տողերի գումարներ՝ բազմապատկված որոշ թվերով։ Բայց հետո համակարգի առաջին r հավասարումները (1.13) անկախ են, իսկ մնացածը դրանց հետևանքներն են, այսինքն՝ առաջին r հավասարումների համակարգի լուծումը ինքնաբերաբար լուծում է մնացած հավասարումների։ Երկու հնարավոր դեպք կա. 1. r=n. Այնուհետև առաջին r հավասարումներից բաղկացած համակարգը ունի նույն թվով հավասարումներ և անհայտներ և հետևողական է, և դրա լուծումը եզակի է։ 2.ր (1.16) «Անվճար» անհայտ x r +1, x r +2, …, x n-ին կարող են տրվել ցանկացած արժեք: Այնուհետև անհայտները ստանում են համապատասխան արժեքներ x 1 , x 2 , …, x r. Համակարգը (1.13) այս դեպքում հետևողական է, բայց անորոշ: Մեկնաբանություն. r կարգի ոչ զրոյական փոքր, որտեղ r X 1 , X 2 , …, X r կոչվում են նաև հիմնական, մնացածը անվճար են։ Համակարգը (1.16) կոչվում է կրճատված: Եթե ​​նշվում են ազատ անհայտները x r +1 =գ 1 , x r +2 =գ 2 , …, x n = c n - r, ապա դրանցից կախված կլինեն հիմնական անհայտները, այսինքն՝ n անհայտ ունեցող m հավասարումների համակարգի լուծումը կունենա X = ( x 1 (գ 1 , …, c n - r), x 2 (գ 1 , …, c n - r), …, x r(գ 1 , …, c n - r), գ 1 , գ 2 , …, c n - r) T, որտեղ T նշանը նշանակում է փոխադրում: Համակարգի այս լուծումը կոչվում է ընդհանուր։

36) որոշակիություն, անորոշություն
Համակարգ մհետ գծային հավասարումներ nանհայտ(կամ, գծային համակարգ) գծային հանրահաշիվում ձևի հավասարումների համակարգ է

Այստեղ x 1 , x 2 , …, x n- անհայտներ, որոնք պետք է որոշվեն: ա 11 , ա 12 , …, մի մն- համակարգային գործակիցներ - և բ 1 , բ 2 , … բ մ- ազատ անդամներ - ենթադրվում է, որ հայտնի են: Գործակիցների ինդեքսներ ( ա ij) համակարգերը նշանակում են հավասարման թվեր ( ես) և անհայտ ( ժ), որի վրա համապատասխանաբար գտնվում է այս գործակիցը։

Համակարգը (1) կոչվում է միատարր, եթե նրա բոլոր ազատ անդամները հավասար են զրոյի ( բ 1 = բ 2 = … = բ մ= 0), հակառակ դեպքում - տարասեռ.

Համակարգը (1) կոչվում է համատեղ, եթե ունի գոնե մեկ լուծում, և ոչ համատեղ, եթե նա չունի մեկ լուծում:

(1) տիպի համատեղ համակարգը կարող է ունենալ մեկ կամ մի քանի լուծում:

Լուծումներ գ 1 (1) , գ 2 (1) , …, c n(1) և գ 1 (2) , գ 2 (2) , …, c n(2) կոչվում են (1) ձևի միացյալ համակարգեր բազմազան, եթե հավասարություններից գոնե մեկը խախտված է.

գ 1 (1) = գ 1 (2) , գ 2 (1) = գ 2 (2) , …, c n (1) = c n (2) .

(1) ձևի միացյալ համակարգ կոչվում է որոշակի, եթե այն ունի յուրահատուկ լուծում; եթե այն ունի առնվազն երկու տարբեր լուծում, ապա այն կոչվում է անորոշ

37) Գծային հավասարումների համակարգերի լուծում Գաուսի մեթոդով

Թող սկզբնական համակարգը այսպիսի տեսք ունենա

Մատրիցա Ակոչվում է համակարգի հիմնական մատրիցա, բ- անվճար անդամների սյունակ:

Այնուհետև, ըստ տողերի վրա տարրական փոխակերպումների հատկության, այս համակարգի հիմնական մատրիցը կարող է կրճատվել փուլային ձևի (նույն փոխակերպումները պետք է կիրառվեն ազատ տերմինների սյունակում).

Այնուհետև կոչվում են փոփոխականները հիմնական փոփոխականներ. Բոլոր մյուսները կոչվում են անվճար.

[խմբագրել]Համատեղելիության պայման

Բոլորի համար վերը նշված պայմանը կարող է ձևակերպվել որպես համատեղելիության անհրաժեշտ և բավարար պայման.

Հիշեցնենք, որ համատեղ համակարգի աստիճանը նրա հիմնական մատրիցի (կամ ընդլայնված մատրիցի) աստիճանն է, քանի որ դրանք հավասար են:

Ալգորիթմ

Նկարագրություն

Գաուսի մեթոդով SLAE-ների լուծման ալգորիթմը բաժանված է երկու փուլի.

§ Առաջին փուլում իրականացվում է այսպես կոչված ուղիղ շարժումը, երբ շարքերի վրայով տարրական փոխակերպումների միջոցով համակարգը բերվում է աստիճանական կամ եռանկյունաձև ձևի կամ պարզվում է, որ համակարգը անհամատեղելի է։ Մասնավորապես, մատրիցայի առաջին սյունակի տարրերից ընտրեք ոչ զրոյական մեկը, տեղափոխեք այն վերին դիրք՝ վերադասավորելով տողերը և ստացված առաջին տողը հանեք մնացած տողերից վերադասավորումից հետո՝ բազմապատկելով այն արժեքով։ հավասար է այս տողերից յուրաքանչյուրի առաջին տարրի և առաջին շարքի առաջին տարրի հարաբերությանը, դրանով իսկ զրոյացնելով դրա տակ գտնվող սյունակը: Այս փոխակերպումների ավարտից հետո առաջին տողը և առաջին սյունակը մտովի հատվում են և շարունակվում այնքան ժամանակ, մինչև մնա զրոյական չափի մատրիցա: Եթե ​​որևէ կրկնության դեպքում առաջին սյունակի տարրերի մեջ չկա ոչ զրոյական տարր, ապա անցեք հաջորդ սյունակ և կատարեք նմանատիպ գործողություն:

§ Երկրորդ փուլում իրականացվում է այսպես կոչված հակադարձ շարժումը, որի էությունը ստացված բոլոր հիմնական փոփոխականներն արտահայտելն է ոչ հիմնականներով և կառուցել լուծումների հիմնարար համակարգ, կամ, եթե բոլոր փոփոխականները հիմնական, ապա թվային կերպով արտահայտեք գծային հավասարումների համակարգի միակ լուծումը: Այս ընթացակարգը սկսվում է վերջին հավասարումից, որից համապատասխան հիմնական փոփոխականն արտահայտվում է (և կա միայն մեկը) և փոխարինվում է նախորդ հավասարումներով և այսպես շարունակ՝ բարձրանալով «աստիճաններով»։ Յուրաքանչյուր տող համապատասխանում է ճիշտ մեկ հիմնական փոփոխականի, ուստի յուրաքանչյուր քայլում, բացի վերջինից (վերևից), իրավիճակը ճշգրտորեն կրկնում է վերջին տողի դեպքը:

Գաուսի մեթոդը պահանջում է կարգուկանոն Օ(n 3) գործողություններ.

Այս մեթոդը հիմնված է.

38)Կրոնեկեր-Կապելի թեորեմ.
Համակարգը հետևողական է, եթե և միայն այն դեպքում, եթե նրա հիմնական մատրիցայի աստիճանը հավասար է իր ընդլայնված մատրիցայի աստիճանին:

Գծային միատարր հավասարումների համակարգեր- ունի ∑a k i x i = 0 ձև, որտեղ m > n կամ m Գծային հավասարումների միատարր համակարգը միշտ համահունչ է, քանի որ rangA = rangB: Այն ակնհայտորեն ունի զրոներից բաղկացած լուծում, որը կոչվում է չնչին.

Ծառայության նպատակը. Առցանց հաշվիչը նախատեսված է SLAE-ի ոչ աննշան և հիմնարար լուծում գտնելու համար: Ստացված լուծումը պահվում է Word ֆայլում (տես լուծման օրինակ):

Հրահանգներ. Ընտրեք մատրիցայի չափը.

Գծային միատարր հավասարումների համակարգերի հատկությունները

Որպեսզի համակարգը ունենա ոչ տրիվիալ լուծումներ, անհրաժեշտ է և բավարար, որ նրա մատրիցայի աստիճանը փոքր լինի անհայտների թվից։

Թեորեմ. m=n դեպքում համակարգը ունի ոչ տրիվիալ լուծում, եթե և միայն այն դեպքում, երբ այս համակարգի որոշիչը հավասար է զրոյի:

Թեորեմ. Համակարգի լուծումների ցանկացած գծային համակցություն նույնպես այդ համակարգի լուծումն է:
Սահմանում. Գծային միատարր հավասարումների համակարգի լուծումների բազմությունը կոչվում է լուծումների հիմնարար համակարգ, եթե այս բազմությունը բաղկացած է գծային անկախ լուծումներից, և համակարգի ցանկացած լուծում այս լուծումների գծային համակցությունն է։

Թեորեմ. Եթե ​​համակարգի մատրիցայի r աստիճանը փոքր է անհայտների n թվից, ապա գոյություն ունի լուծումների հիմնարար համակարգ, որը բաղկացած է (n-r) լուծումներից:

Գծային միատարր հավասարումների համակարգերի լուծման ալգորիթմ

1. Գտնելով մատրիցայի աստիճանը:
2. Մենք ընտրում ենք հիմնական անչափահասը: Տարբերում ենք կախյալ (հիմնական) և ազատ անհայտները։
3. Մենք խաչում ենք համակարգի այն հավասարումները, որոնց գործակիցները ներառված չեն բազիս-մինորում, քանի որ դրանք մյուսների հետևանքներն են (ըստ հիմնարար մինորի թեորեմի):
4. Ազատ անհայտներ պարունակող հավասարումների անդամները տեղափոխում ենք աջ կողմ։ Արդյունքում ստանում ենք r անհայտներով r հավասարումների համակարգ, որը համարժեք է տվյալին, որի որոշիչը զրոյական չէ։
5. Ստացված համակարգը լուծում ենք անհայտները վերացնելով։ Մենք գտնում ենք կախված փոփոխականներ արտահայտող հարաբերություններ ազատների միջոցով:
6. Եթե ​​մատրիցայի աստիճանը հավասար չէ փոփոխականների թվին, ապա մենք գտնում ենք համակարգի հիմնարար լուծումը:
7. Rang = n դեպքում մենք ունենք չնչին լուծում:

Օրինակ. Գտե՛ք վեկտորների համակարգի հիմքը (a 1, a 2,...,a m), դասավորե՛ք և արտահայտե՛ք վեկտորները հիմքի վրա: Եթե ​​a 1 =(0,0,1,-1), և 2 =(1,1,2,0), և 3 =(1,1,1,1), և 4 =(3,2,1) ,4), և 5 =(2,1,0,3):
Եկեք գրենք համակարգի հիմնական մատրիցը.

3-րդ տողը բազմապատկեք (-3-ով): 3-րդին ավելացնենք 4-րդ տողը.

0	0	1	-1
0	0	-1	1
0	-1	-2	1
3	2	1	4
2	1	0	3

4-րդ տողը բազմապատկեք (-2-ով): 5-րդ տողը բազմապատկենք (3-ով): 4-րդին ավելացնենք 5-րդ տողը.
Ավելացնենք 2-րդ տողը 1-ին.
Եկեք գտնենք մատրիցայի աստիճանը:
Այս մատրիցայի գործակիցներով համակարգը համարժեք է սկզբնական համակարգին և ունի ձև.
- x 3 = - x 4
- x 2 - 2x 3 = - x 4
2x 1 + x 2 = - 3x 4
Օգտագործելով անհայտները վերացնելու մեթոդը, մենք գտնում ենք ոչ տրիվիալ լուծում.
Մենք ստացանք x 1 , x 2 , x 3 կախյալ փոփոխականներն արտահայտող հարաբերություններ x 4 ազատների միջոցով, այսինքն՝ ընդհանուր լուծում գտանք.
x 3 = x 4
x 2 = - x 4
x 1 = - x 4