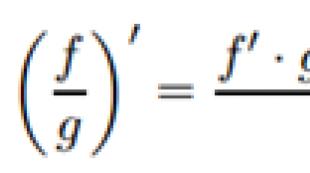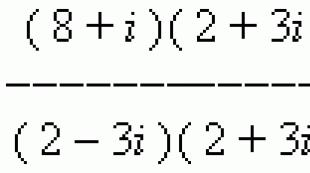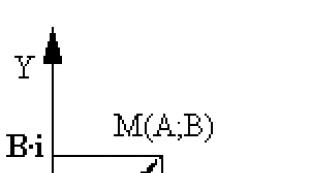किसी सम्मिश्र संख्या की घात के सभी मान ज्ञात कीजिए। जटिल आंकड़े। सम्मिश्र संख्या का बीजगणितीय रूप. सम्मिश्र संख्या की अवधारणा का परिचय
जटिल आंकड़े
काल्पनिक और जटिल आंकड़े। एब्सिस्सा और ऑर्डिनेट
जटिल संख्या। सम्मिश्र संख्याओं को संयुग्मित करें.
सम्मिश्र संख्याओं के साथ संक्रियाएँ. ज्यामितिक
जटिल संख्याओं का प्रतिनिधित्व. जटिल विमान.
एक सम्मिश्र संख्या का मापांक और तर्क। त्रिकोणमितीय
सम्मिश्र संख्या प्रपत्र. जटिल के साथ संचालन
त्रिकोणमितीय रूप में संख्याएँ. मोइवर फॉर्मूला.
के बारे में बुनियादी जानकारी काल्पनिक और जटिल आंकड़े "काल्पनिक और सम्मिश्र संख्याएँ" अनुभाग में दिए गए हैं। मामले के लिए द्विघात समीकरणों को हल करते समय एक नए प्रकार की इन संख्याओं की आवश्यकता उत्पन्न हुई
डी< 0 (здесь डीद्विघात समीकरण का विभेदक है)। लंबे समय तक, इन संख्याओं का भौतिक उपयोग नहीं हुआ, यही कारण है कि इन्हें "काल्पनिक" संख्याएँ कहा जाता था। हालाँकि, अब इनका उपयोग भौतिकी के विभिन्न क्षेत्रों में बहुत व्यापक रूप से किया जाता है।और प्रौद्योगिकी: इलेक्ट्रिकल इंजीनियरिंग, हाइड्रो- और वायुगतिकी, लोच का सिद्धांत, आदि।
जटिल आंकड़े इस प्रकार लिखे गए हैं:ए+बी. यहाँ एऔर बी – वास्तविक संख्या , ए मैं – काल्पनिक इकाई.इ। मैं 2 = –1. संख्या एबुलाया सूच्याकार आकृति का भुज, ए बी - समन्वयजटिल संख्याए + बी .दो सम्मिश्र संख्याएँए+बीऔर ए-द्वि बुलाया संयुग्मजटिल आंकड़े।
मुख्य समझौते:
1. वास्तविक संख्या
एफॉर्म में भी लिखा जा सकता हैजटिल संख्या:एक + 0 मैंया ए - 0 मैं. उदाहरण के लिए, प्रविष्टियाँ 5 + 0मैंऔर 5 - 0 मैंमतलब एक ही नंबर 5 .2. सम्मिश्र संख्या 0 + द्विबुलाया पूर्णतः काल्पनिक संख्या. रिकॉर्डिंगद्विमतलब 0 के समान है + द्वि.
3. दो सम्मिश्र संख्याएँए+बी औरसी + डियदि समान माना जाता हैए = सीऔर बी = डी. अन्यथा सम्मिश्र संख्याएँ समान नहीं हैं.
जोड़ना। सम्मिश्र संख्याओं का योगए+बीऔर सी + डिसम्मिश्र संख्या कहलाती है (ए+सी ) + (बी+डी ) मैं ।इस प्रकार, जब जोड़ा गया सम्मिश्र संख्याएँ, उनके भुज और निर्देशांक अलग-अलग जोड़े जाते हैं।
यह परिभाषा सामान्य बहुपदों से निपटने के नियमों का पालन करती है।
घटाव. दो सम्मिश्र संख्याओं के बीच का अंतरए+बी(कम) और सी + डि(घटाना) एक सम्मिश्र संख्या कहलाती है (एसी ) + (बी डी ) मैं ।
इस प्रकार, दो जटिल संख्याओं को घटाते समय, उनके भुज और निर्देशांक अलग-अलग घटाए जाते हैं।
गुणन. सम्मिश्र संख्याओं का गुणनफलए+बीऔर सी + डि सम्मिश्र संख्या कहलाती है.
(एसी-बीडी ) + (विज्ञापन+बीसी ) मैं ।यह परिभाषा दो आवश्यकताओं से उत्पन्न होती है:
1) संख्याएँ ए+बीऔर सी + डिबीजगणितीय की तरह गुणा करना चाहिएद्विपद,
2) संख्या मैंमुख्य संपत्ति है:मैं 2 = – 1.
उदाहरण ( ए + द्वि )(ए-द्वि) = ए 2 +बी 2 . इस तरह, काम
दो संयुग्मी सम्मिश्र संख्याएँ वास्तविक के बराबर होती हैं
सकारात्मक संख्या।
विभाजन। किसी सम्मिश्र संख्या को विभाजित करेंए+बी (विभाज्य) दूसरे कोसी + डि(विभाजक) - मतलब तीसरा नंबर ढूंढनाई + फाई(चैट), जिसे, जब एक भाजक से गुणा किया जाता हैसी + डि, जिसके परिणामस्वरूप लाभांश मिलता हैए + बी .
यदि भाजक शून्य नहीं है, तो विभाजन सदैव संभव है।
उदाहरण खोजें (8+मैं ) : (2 – 3 मैं) .
समाधान। आइए इस अनुपात को भिन्न के रूप में फिर से लिखें:
इसके अंश और हर को 2 + 3 से गुणा करनामैं
और सभी परिवर्तन करने के बाद, हमें मिलता है:
सम्मिश्र संख्याओं का ज्यामितीय निरूपण। वास्तविक संख्याओं को संख्या रेखा पर बिंदुओं द्वारा दर्शाया जाता है:
बात यहीं है एमतलब नंबर -3, बिंदुबीसंख्या 2 है, और हे- शून्य। इसके विपरीत, जटिल संख्याओं को निर्देशांक तल पर बिंदुओं द्वारा दर्शाया जाता है। इसके लिए, हम दोनों अक्षों पर समान पैमाने के साथ आयताकार (कार्टेशियन) निर्देशांक चुनते हैं। फिर सम्मिश्र संख्याए+बी एक बिंदु द्वारा दर्शाया जाएगा एब्सिस्सा के साथ पी ए और कोर्डिनेट बी (अंजीर देखें।) इस समन्वय प्रणाली को कहा जाता है जटिल विमान .
मापांक सम्मिश्र संख्या को सदिश की लंबाई कहा जाता हैसेशन, निर्देशांक पर एक सम्मिश्र संख्या को दर्शाते हुए ( विस्तृत) विमान। सम्मिश्र संख्या मापांकए+बीद्वारा निरूपित | ए+बी| या पत्र आर
एक द्विघात समीकरण पर विचार करें.
आइए इसकी जड़ों को परिभाषित करें।
ऐसी कोई वास्तविक संख्या नहीं है जिसका वर्ग -1 हो। लेकिन यदि सूत्र ऑपरेटर को परिभाषित करता है मैंएक काल्पनिक इकाई के रूप में, तो इस समीकरण का हल इस रूप में लिखा जा सकता है 
. जिसमें 
और 
- सम्मिश्र संख्याएँ, जिनमें -1 वास्तविक भाग है, 2 या दूसरे मामले में -2 काल्पनिक भाग है। काल्पनिक भाग भी एक वास्तविक (वास्तविक) संख्या है। काल्पनिक भाग को काल्पनिक इकाई से गुणा करने का अर्थ पहले से है काल्पनिक संख्या.
सामान्य तौर पर, एक सम्मिश्र संख्या का रूप होता है
जेड = एक्स + iy ,
कहाँ एक्स, वाईवास्तविक संख्याएँ हैं, एक काल्पनिक इकाई है। कई अनुप्रयुक्त विज्ञानों में, उदाहरण के लिए, इलेक्ट्रिकल इंजीनियरिंग, इलेक्ट्रॉनिक्स, सिग्नल सिद्धांत में, काल्पनिक इकाई को किसके द्वारा निरूपित किया जाता है? जे. वास्तविक संख्या एक्स = पुनः(z)और आप=मैं हूँ(z)बुलाया वास्तविक और काल्पनिक भागनंबर जेडअभिव्यक्ति कहलाती है बीजगणितीय रूपएक सम्मिश्र संख्या का अंकन.
कोई भी वास्तविक संख्या किसी सम्मिश्र संख्या के रूप में एक विशेष स्थिति होती है 
. एक काल्पनिक संख्या भी सम्मिश्र संख्या का एक विशेष मामला है। 
.
सम्मिश्र संख्याओं के समुच्चय की परिभाषा C
यह अभिव्यक्ति इस प्रकार है: सेट साथ, ऐसे तत्वों से मिलकर बना है एक्सऔर यवास्तविक संख्याओं के समुच्चय से संबंधित हैं आरऔर काल्पनिक इकाई है. ध्यान दें आदि.
दो सम्मिश्र संख्याएँ 
और 
समान हैं यदि और केवल यदि उनके वास्तविक और काल्पनिक भाग समान हैं, अर्थात। और ।
जटिल संख्याओं और कार्यों का व्यापक रूप से विज्ञान और प्रौद्योगिकी में उपयोग किया जाता है, विशेष रूप से, एसी सर्किट, एनालॉग इलेक्ट्रॉनिक्स, सिग्नल सिद्धांत और प्रसंस्करण, स्वचालित नियंत्रण सिद्धांत और अन्य व्यावहारिक विज्ञानों के यांत्रिकी, विश्लेषण और गणना में।
- सम्मिश्र संख्याओं का अंकगणित
दो जटिल संख्याओं के योग में उनके वास्तविक और काल्पनिक भागों को जोड़ना शामिल है, अर्थात।
तदनुसार, दो जटिल संख्याओं का अंतर
जटिल संख्या 
बुलाया जटिल संयुग्मसंख्या z=एक्स +i.y.
जटिल संयुग्म संख्याएँ z और z * काल्पनिक भाग के संकेतों में भिन्न हैं। यह तो स्पष्ट है
.
जटिल अभिव्यक्तियों के बीच कोई भी समानता तभी मान्य रहती है जब यह समानता सर्वत्र हो मैंद्वारा प्रतिस्थापित -
मैं, अर्थात। संयुग्मी संख्याओं की समानता पर जाएँ। नंबर मैंऔर –
मैंबीजगणितीय रूप से अप्रभेद्य हैं क्योंकि 
.
दो सम्मिश्र संख्याओं के गुणनफल (गुणन) की गणना इस प्रकार की जा सकती है:
दो सम्मिश्र संख्याओं का विभाजन:
उदाहरण:
- जटिल विमान
एक जटिल संख्या को एक आयताकार समन्वय प्रणाली में ग्राफ़िक रूप से दर्शाया जा सकता है। आइए हम समतल में एक आयताकार समन्वय प्रणाली स्थापित करें (एक्स, वाई).
धुरी पर बैलहम वास्तविक भागों की व्यवस्था करेंगे एक्स, यह कहा जाता है वास्तविक (वास्तविक) अक्ष, अक्ष पर ओए- काल्पनिक भाग यजटिल आंकड़े। वह नाम रखती है काल्पनिक धुरी. इसके अलावा, प्रत्येक जटिल संख्या विमान के एक निश्चित बिंदु से मेल खाती है, और ऐसे विमान को कहा जाता है जटिल विमान. बिंदु एजटिल तल वेक्टर के अनुरूप होगा ओए.
संख्या एक्सबुलाया सूच्याकार आकृति का भुजजटिल संख्या, संख्या य – तालमेल.
जटिल संयुग्म संख्याओं की एक जोड़ी को वास्तविक अक्ष के बारे में सममित रूप से स्थित बिंदुओं के रूप में प्रदर्शित किया जाता है।
 |
यदि विमान सेट पर ध्रुवीय समन्वय प्रणाली, फिर प्रत्येक सम्मिश्र संख्या जेडध्रुवीय निर्देशांक द्वारा निर्धारित। जिसमें मापांकनंबर 
बिंदु का ध्रुवीय त्रिज्या और कोण है 
- इसका ध्रुवीय कोण या सम्मिश्र संख्या तर्क जेड.
सम्मिश्र संख्या मापांक 
हमेशा गैर-नकारात्मक. किसी सम्मिश्र संख्या का तर्क विशिष्ट रूप से परिभाषित नहीं है। तर्क का मुख्य मान शर्त को पूरा करना चाहिए 
. जटिल तल का प्रत्येक बिंदु तर्क के कुल मूल्य से भी मेल खाता है। जिन तर्कों में 2π के गुणज का अंतर होता है उन्हें समान माना जाता है। संख्या तर्क शून्य परिभाषित नहीं है.
तर्क का मुख्य मूल्य अभिव्यक्तियों द्वारा निर्धारित किया जाता है:
यह तो स्पष्ट है
जिसमें
, 
.
जटिल संख्या प्रतिनिधित्व जेडजैसा
बुलाया त्रिकोणमितीय रूपजटिल संख्या।
उदाहरण.
- सम्मिश्र संख्याओं का घातांकीय रूप
में विघटन मैकलॉरिन श्रृंखलावास्तविक तर्क कार्यों के लिए 
की तरह लगता है:
एक जटिल तर्क के घातीय कार्य के लिए जेडअपघटन समान है
.
काल्पनिक तर्क के घातीय कार्य के लिए मैकलॉरिन श्रृंखला विस्तार को इस प्रकार दर्शाया जा सकता है
परिणामी पहचान कहलाती है यूलर फार्मूला.
एक नकारात्मक तर्क के लिए, ऐसा लगता है
इन अभिव्यक्तियों को मिलाकर, हम साइन और कोसाइन के लिए निम्नलिखित अभिव्यक्तियों को परिभाषित कर सकते हैं
.
जटिल संख्याओं के निरूपण के त्रिकोणमितीय रूप से, यूलर सूत्र का उपयोग करना
उपलब्ध ठोस(घातीय, ध्रुवीय) एक सम्मिश्र संख्या का रूप, अर्थात्। रूप में इसका प्रतिनिधित्व
,
कहाँ 
- आयताकार निर्देशांक वाले एक बिंदु के ध्रुवीय निर्देशांक ( एक्स,य).
सम्मिश्र संख्या का संयुग्म घातांकीय रूप में इस प्रकार लिखा जाता है।
घातांकीय रूप के लिए, जटिल संख्याओं के गुणन और विभाजन के लिए निम्नलिखित सूत्रों को परिभाषित करना आसान है
अर्थात् घातांकीय रूप में सम्मिश्र संख्याओं का गुणनफल और विभाजन बीजगणितीय रूप की तुलना में आसान होता है। गुणा करते समय, कारकों के मॉड्यूल को गुणा किया जाता है, और तर्क जोड़े जाते हैं। यह नियम किसी भी संख्या में कारकों पर लागू होता है। विशेष रूप से, किसी सम्मिश्र संख्या को गुणा करते समय जेडपर मैंवेक्टर जेड 90 तक वामावर्त घुमाता है
विभाजन में, अंश मापांक को हर मापांक से विभाजित किया जाता है, और हर तर्क को अंश तर्क से घटा दिया जाता है।
सम्मिश्र संख्याओं के घातांकीय रूप का उपयोग करके, कोई सुप्रसिद्ध त्रिकोणमितीय सर्वसमिकाओं के लिए व्यंजक प्राप्त कर सकता है। उदाहरण के लिए, पहचान से
यूलर सूत्र का उपयोग करके हम लिख सकते हैं
इस व्यंजक में वास्तविक और काल्पनिक भागों को बराबर करने पर, हमें कोणों के योग की कोज्या और ज्या के लिए व्यंजक प्राप्त होते हैं
- सम्मिश्र संख्याओं की घातें, मूल और लघुगणक
एक सम्मिश्र संख्या को एक प्राकृतिक घात तक बढ़ाना एनसूत्र के अनुसार तैयार किया गया है
उदाहरण. गणना करना 
.
एक संख्या की कल्पना करें त्रिकोणमितीय रूप में
’
घातांक सूत्र को लागू करने पर, हम पाते हैं
अभिव्यक्ति में मान डालना आर= 1, हमें तथाकथित मिलता है डी मोइवरे का सूत्र, जिससे आप अनेक कोणों की ज्याओं और कोज्याओं के व्यंजक निर्धारित कर सकते हैं।
जड़ एनएक सम्मिश्र संख्या की वां घात जेडयह है एनअभिव्यक्ति द्वारा निर्धारित विभिन्न मान
उदाहरण. पता लगाते हैं ।
ऐसा करने के लिए, हम सम्मिश्र संख्या () को त्रिकोणमितीय रूप में व्यक्त करते हैं
.
किसी सम्मिश्र संख्या के मूल की गणना करने के सूत्र के अनुसार, हमें प्राप्त होता है
सम्मिश्र संख्या का लघुगणक जेडएक संख्या है डब्ल्यू, जिसके लिए । किसी सम्मिश्र संख्या के प्राकृतिक लघुगणक में अनंत संख्या में मान होते हैं और इसकी गणना सूत्र द्वारा की जाती है
वास्तविक (कोसाइन) और काल्पनिक (साइन) भागों से मिलकर बनता है। इस तरह के तनाव को लंबाई के वेक्टर के रूप में दर्शाया जा सकता है उ म, प्रारंभिक चरण (कोण), कोणीय वेग से घूमता हुआ ω .
इसके अलावा, यदि जटिल कार्यों को जोड़ा जाता है, तो उनके वास्तविक और काल्पनिक भागों को भी जोड़ा जाता है। यदि किसी जटिल फलन को किसी अचर या वास्तविक फलन से गुणा किया जाता है, तो उसके वास्तविक और काल्पनिक भागों को एक ही कारक से गुणा किया जाता है। ऐसे जटिल कार्य का विभेदन/एकीकरण वास्तविक और काल्पनिक भागों के विभेदन/एकीकरण तक कम हो जाता है।
उदाहरण के लिए, जटिल तनाव अभिव्यक्ति का विभेदन
से गुणा करना है iω फ़ंक्शन f(z) का वास्तविक भाग है, और 
फ़ंक्शन का काल्पनिक भाग है. उदाहरण: 
.
अर्थ जेडजटिल z विमान में एक बिंदु और संबंधित मान द्वारा दर्शाया गया है डब्ल्यू- जटिल तल में एक बिंदु डब्ल्यू. प्रदर्शित होने पर डब्ल्यू = एफ(जेड)समतल रेखाएँ जेडविमान की पंक्तियों में गुजरें डब्ल्यू, एक तल की आकृतियों को दूसरे तल की आकृतियों में बदलना, लेकिन रेखाओं या आकृतियों का आकार महत्वपूर्ण रूप से बदल सकता है।
सम्मिश्र संख्या लिखने का बीजगणितीय रूप ................................................. ... ................... |
|||
सम्मिश्र संख्याओं का तल ................................................. ................................................... ................... ... |
|||
सम्मिश्र संयुग्म संख्याएँ ....................................................... ................ ................................................. .............. |
|||
बीजगणितीय रूप में सम्मिश्र संख्याओं के साथ संक्रियाएँ................................................... ................... .... |
|||
सम्मिश्र संख्याओं का योग................................................... ................................................... ................... |
|||
सम्मिश्र संख्याओं का घटाव................................................... ............ ....................................... ........... |
|||
सम्मिश्र संख्याओं का गुणन ……………………………… ............ ....................................... ......... |
|||
सम्मिश्र संख्याओं का विभाजन ……………………………… ................ ................................................. .............. ... |
|||
सम्मिश्र संख्या का त्रिकोणमितीय रूप ................................................. .................. .......... |
|||
त्रिकोणमितीय रूप में सम्मिश्र संख्याओं के साथ संक्रियाएँ................................................... ............ |
|||
सम्मिश्र संख्याओं का त्रिकोणमितीय रूप में गुणन................................................... .................................. |
|||
सम्मिश्र संख्याओं का त्रिकोणमितीय रूप में विभाजन................................................... ................... ... |
|||
किसी सम्मिश्र संख्या को धनात्मक पूर्णांक घात तक बढ़ाना |
|||
किसी सम्मिश्र संख्या से धनात्मक पूर्णांक घात का मूल निकालना |
|||
किसी सम्मिश्र संख्या को तर्कसंगत घात तक बढ़ाना .................................................. ................................... |
|||
जटिल शृंखला ................................................. .................. .................................. .................................................. |
|||
सम्मिश्र संख्या शृंखला ……………………………… ................ ................................................. .............. |
|||
जटिल तल में शक्ति श्रृंखला ................................................. .................. .................................. |
|||
जटिल तल में दो-तरफा शक्ति श्रृंखला ................................................. ...................... ... |
|||
एक जटिल चर के कार्य................................................... ………………………………… ................... |
|||
बुनियादी प्राथमिक कार्य …………………………………… ................... ................................................. ........... |
|||
यूलर सूत्र ................................................. .. .................................................. ................... |
|||
सम्मिश्र संख्या के निरूपण का घातांकीय रूप ……………………. ...... . |
|||
त्रिकोणमितीय और अतिशयोक्तिपूर्ण कार्यों के बीच संबंध ................................................. |
|||
लघुगणकीय फ़ंक्शन ................................................. .................. .................................. ................... ... |
|||
सामान्य घातांकीय और सामान्य शक्ति फलन................................................... ...................... ............... |
|||
एक जटिल चर के कार्यों का विभेदन................................................... ................... ... |
|||
कॉची-रीमैन स्थितियाँ ....................................................... .......... .................................................. ............ ............ |
|||
व्युत्पन्न की गणना के लिए सूत्र ................................................. .............. ................................. |
|||
विभेदन की संक्रिया के गुण ................................................. ............... ................................. |
|||
एक विश्लेषणात्मक फ़ंक्शन के वास्तविक और काल्पनिक भागों के गुण ....................................... ....... |
|||
किसी जटिल चर के किसी फ़ंक्शन को उसके वास्तविक या काल्पनिक से पुनर्प्राप्त करना |
|||
विधि संख्या 1. वक्ररेखीय इंटीग्रल का उपयोग करना................................................... ......... ....... |
|||
विधि संख्या 2. कॉची-रीमैन स्थितियों का प्रत्यक्ष अनुप्रयोग...................................... |
|||
विधि संख्या 3. वांछित फ़ंक्शन के व्युत्पन्न के माध्यम से ................................................... ................... ......... |
|||
एक जटिल चर के कार्यों का एकीकरण................................................... ................... ........... |
|||
कॉची का अभिन्न सूत्र ................................................. .................................................. . .. |
|||
टेलर और लॉरेंट श्रृंखला में कार्यों का विस्तार .................................................. .... ................................... |
|||
एक जटिल चर के फ़ंक्शन के शून्य और एकवचन बिंदु ....................................... ....... ...... |
|||
एक जटिल चर के फ़ंक्शन के शून्य .................................................. ................ ................................. |
|||
किसी सम्मिश्र चर के फलन के पृथक एकवचन बिंदु .................................................. ...... |
|||
14.3 एक जटिल चर के फ़ंक्शन के एकवचन बिंदु के रूप में अनंत पर बिंदु
निकासी ................................................. .................................................. . ....................................................... |
|||
अंतिम बिंदु पर कटौती .................................................. ......................................................... ............ ...... |
|||
अनंत पर एक बिंदु पर किसी फलन का अवशेष ................................................. ...................... ................. |
|||
अवशेषों का उपयोग करके अभिन्नों की गणना ……………………………… .................................................. |
|||
आत्मनिरीक्षण के लिए प्रश्न .................................................. .................. .................................. .................. ....... |
|||
साहित्य................................................. .................................................. . ................................ |
|||
विषय अनुक्रमणिका................................................. .................................................. . .............. |
|||
प्रस्तावना
किसी परीक्षा या मॉड्यूल प्रमाणन के सैद्धांतिक और व्यावहारिक भागों की तैयारी में समय और प्रयास को सही ढंग से आवंटित करना काफी कठिन है, खासकर जब से सत्र के दौरान हमेशा पर्याप्त समय नहीं होता है। और जैसा कि अभ्यास से पता चलता है, हर कोई इसका सामना नहीं कर सकता। परिणामस्वरूप, परीक्षा के दौरान, कुछ छात्र समस्याओं को सही ढंग से हल करते हैं, लेकिन सबसे सरल सैद्धांतिक प्रश्नों का उत्तर देना मुश्किल होता है, जबकि अन्य एक प्रमेय बना सकते हैं, लेकिन इसे लागू नहीं कर सकते।
कॉम्प्लेक्स वेरिएबल (टीएफवी) पाठ्यक्रम के कार्यों के सिद्धांत में परीक्षा की तैयारी के लिए वर्तमान पद्धति संबंधी सिफारिशें इस विरोधाभास को हल करने और पाठ्यक्रम की सैद्धांतिक और व्यावहारिक सामग्री की एक साथ पुनरावृत्ति सुनिश्चित करने का एक प्रयास है। सिद्धांत "अभ्यास के बिना सिद्धांत मृत है, सिद्धांत के बिना अभ्यास अंधा है" द्वारा निर्देशित, उनमें परिभाषाओं और फॉर्मूलेशन के स्तर पर पाठ्यक्रम की सैद्धांतिक स्थिति और प्रत्येक दिए गए सैद्धांतिक स्थिति के अनुप्रयोग को दर्शाने वाले उदाहरण शामिल हैं, और इस प्रकार इसे बनाते हैं। याद रखना और समझना आसान है।
प्रस्तावित कार्यप्रणाली अनुशंसाओं का उद्देश्य छात्र को बुनियादी स्तर पर परीक्षा की तैयारी में मदद करना है। दूसरे शब्दों में, एक विस्तारित कार्य मार्गदर्शिका संकलित की गई है जिसमें टीएफकेटी पाठ्यक्रम कक्षाओं में उपयोग किए जाने वाले मुख्य बिंदु शामिल हैं और होमवर्क करते समय और नियंत्रण गतिविधियों की तैयारी करते समय आवश्यक हैं। छात्रों के स्वतंत्र कार्य के अलावा, इस इलेक्ट्रॉनिक शैक्षिक प्रकाशन का उपयोग इलेक्ट्रॉनिक बोर्ड का उपयोग करके इंटरैक्टिव रूप में कक्षाएं संचालित करते समय या दूरस्थ शिक्षा प्रणाली में प्लेसमेंट के लिए किया जा सकता है।
कृपया ध्यान दें कि यह कार्य पाठ्यपुस्तकों या व्याख्यान नोट्स को प्रतिस्थापित नहीं करता है। सामग्री के गहन अध्ययन के लिए, मॉस्को स्टेट टेक्निकल यूनिवर्सिटी में प्रकाशित प्रकाशन के संबंधित अनुभागों को देखने की अनुशंसा की जाती है। एन.ई. बाउमन बुनियादी पाठ्यपुस्तक।
मैनुअल के अंत में अनुशंसित साहित्य की एक सूची और एक विषय सूचकांक है, जिसमें पाठ में हाइलाइट किए गए सभी शामिल हैं। बोल्ड इटैलिकशर्तें। सूचकांक में उन अनुभागों के हाइपरलिंक होते हैं जहां इन शब्दों को सख्ती से परिभाषित या वर्णित किया जाता है और जहां उनके उपयोग को दर्शाने के लिए उदाहरण दिए जाते हैं।
यह मैनुअल MSTU के सभी संकायों के द्वितीय वर्ष के छात्रों के लिए है। एन.ई. बौमन.
1. सम्मिश्र संख्या लिखने का बीजगणितीय रूप
फॉर्म z \u003d x + iy की रिकॉर्डिंग, जहां x, y वास्तविक संख्याएं हैं, i एक काल्पनिक इकाई है (यानी i 2 = - 1)
सम्मिश्र संख्या z का बीजीय रूप कहा जाता है। इस स्थिति में, x को सम्मिश्र संख्या का वास्तविक भाग कहा जाता है और इसे Re z (x = Re z) द्वारा दर्शाया जाता है, y को सम्मिश्र संख्या का काल्पनिक भाग कहा जाता है और इसे Im z (y = Im z) द्वारा दर्शाया जाता है।
उदाहरण। सम्मिश्र संख्या z = 4 - 3i का वास्तविक भाग Re z = 4 है, और काल्पनिक भाग Im z = - 3 है।
2. सम्मिश्र संख्याओं का तल
में एक जटिल चर के कार्यों के सिद्धांतों पर विचार करेंसम्मिश्र संख्या तल, जिसे या तो दर्शाया जाता है, या जटिल संख्याओं z, w, आदि को दर्शाने वाले अक्षरों का उपयोग किया जाता है।
सम्मिश्र तल का क्षैतिज अक्ष कहलाता है वास्तविक अक्ष, वास्तविक संख्याएँ z = x + 0 i = x इस पर स्थित हैं।
जटिल तल के ऊर्ध्वाधर अक्ष को काल्पनिक अक्ष कहा जाता है, यह है
3. जटिल संयुग्म संख्याएँ
संख्याएँ z = x + iy और z = x - iy कहलाती हैं जटिल सन्युग्म. जटिल तल पर, वे उन बिंदुओं के अनुरूप होते हैं जो वास्तविक अक्ष के बारे में सममित होते हैं।
4. बीजगणितीय रूप में सम्मिश्र संख्याओं के साथ संक्रियाएँ
4.1 सम्मिश्र संख्याओं का योग
दो सम्मिश्र संख्याओं का योग |
जेड 1 = एक्स 1 + आईवाई 1 |
तथा z 2 = x 2 + iy 2 एक सम्मिश्र संख्या कहलाती है |
|||||||||||
z1 + z2 |
= (x 1 + iy 1 ) + (x 2 + iy 2 ) = (x 1 + x 2 ) + i (y 1 + y 2 ) . |
कार्यवाही |
अतिरिक्त |
||||||||||
सम्मिश्र संख्याएँ बीजगणितीय द्विपदों को जोड़ने की क्रिया के समान है। |
|||||||||||||
उदाहरण। दो सम्मिश्र संख्याओं z 1 = 3 + 7i और z 2 का योग |
= −1 +2 i |
एक सम्मिश्र संख्या होगी |
|||||||||||
z 1 + z 2 = (3 +7 i ) +(−1 +2 i ) = (3 −1 ) +(7 +2 ) i = 2 +9 i . |
|||||||||||||
ज़ाहिर तौर से, |
एक जटिल में योग |
संयुग्मित |
है |
वैध |
|||||||||
z + z = (x + iy) + (x - iy) = 2 x = 2 Rez। |
|||||||||||||
4.2 सम्मिश्र संख्याओं का घटाव |
|||||||||||||
दो सम्मिश्र संख्याओं का अंतर z 1 = x 1 + iy 1 |
एक्स 2 +आईवाई 2 |
बुलाया |
विस्तृत |
||||||||||
संख्या z 1 - z 2 = (x 1 + iy 1 ) - (x 2 + iy 2 ) = (x 1 - x 2 ) + i (y 1 - y 2 ) । |
|||||||||||||
उदाहरण। दो सम्मिश्र संख्याओं के बीच का अंतर |
z 1 = 3 −4 i |
और z2 |
= −1 +2 i |
एक व्यापक होगा |
|||||||||
संख्या z 1 − z 2 = (3 − 4i ) − (− 1+ 2i ) = (3 − (− 1) ) + (− 4 − 2) i = 4 − 6i . |
|||||||||||||
अंतर |
जटिल सन्युग्म |
है |
|||||||||||
z - z = (x + iy) - (x - iy) = 2 iy = 2 i Im z। |
|||||||||||||
4.3 सम्मिश्र संख्याओं का गुणन |
|||||||||||||
दो सम्मिश्र संख्याओं का गुणनफल |
जेड 1 = एक्स 1 + आईवाई 1 |
और z 2 = x 2 + iy 2 |
जटिल कहा जाता है |
||||||||||
z 1z 2 = (x 1 + iy 1 )(x 2 + iy 2 ) = x 1x 2 + iy 1x 2 + iy 2 x 1 + i 2 y 1 y 2 |
= (x 1x 2 - y 1 y 2 ) + i (y 1x 2 + y 2 x ) । |
||||||||||||
इस प्रकार, सम्मिश्र संख्याओं के गुणन की संक्रिया बीजगणितीय द्विपदों के गुणन की संक्रिया के समान है, इस तथ्य को ध्यान में रखते हुए कि i 2 = − 1.
परिभाषा
सम्मिश्र संख्या का बीजगणितीय रूप सम्मिश्र संख्या \(\ z \) को \(\ z=x+i y \) के रूप में लिखना है, जहां \(\ x \) और \(\ y \) वास्तविक संख्याएं हैं, \ (\ i \ ) एक काल्पनिक इकाई है जो संबंध \(\ i^(2)=-1 \) को संतुष्ट करती है
संख्या \(\ x \) को सम्मिश्र संख्या \(\ z \) का वास्तविक भाग कहा जाता है और इसे \(\ x=\operatorname(Re) z \) से दर्शाया जाता है।
संख्या \(\ y \) को जटिल संख्या \(\ z \) का काल्पनिक भाग कहा जाता है और इसे \(\ y=\operatorname(Im) z \) से दर्शाया जाता है
उदाहरण के लिए:
सम्मिश्र संख्या \(\ z=3-2 i \) और उससे संबंधित संख्या \(\ \overline(z)=3+2 i \) को बीजगणितीय रूप में लिखा गया है।
काल्पनिक मान \(\ z=5 i \) बीजगणितीय रूप में लिखा गया है।
इसके अलावा, हल की जा रही समस्या के आधार पर, आप एक जटिल संख्या को त्रिकोणमितीय या घातीय संख्या में परिवर्तित कर सकते हैं।
संख्या \(\ z=\frac(7-i)(4)+13 \) को बीजगणितीय रूप में लिखें, इसके वास्तविक और काल्पनिक भागों के साथ-साथ संयुग्म संख्या भी ज्ञात करें।
भिन्नों का विभाजन शब्द और भिन्नों के योग के नियम को लागू करने पर, हम पाते हैं:
\(\ z=\frac(7-i)(4)+13=\frac(7)(4)+13-\frac(i)(4)=\frac(59)(4)-\frac( 1)(4) मैं \)
इसलिए, सम्मिश्र संख्या \(\ z=\frac(5 g)(4)-\frac(1)(4) i \) का वास्तविक भाग संख्या \(\ x=\operatorname(Re) z= है \frac(59) (4) \) , काल्पनिक भाग एक संख्या है \(\ y=\operatorname(Im) z=-\frac(1)(4) \)
संयुग्म संख्या: \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)
\(\ z=\frac(59)(4)-\frac(1)(4) i \), \(\ \operatorname(Re) z=\frac(59)(4) \), \(\ \operatorname(Im) z=-\frac(1)(4) \), \(\ \overline(z)=\frac(59)(4)+\frac(1)(4) i \)
बीजीय रूप में सम्मिश्र संख्याओं की क्रियाओं की तुलना
दो सम्मिश्र संख्याएँ \(\ z_(1)=x_(1)+i y_(1) \) बराबर हैं यदि \(\ x_(1)=x_(2) \), \(\ y_(1)= y_ (2)\)अर्थात् उनके वास्तविक और काल्पनिक भाग बराबर हैं।
निर्धारित करें कि x और y के लिए दो जटिल संख्याएं \(\ z_(1)=13+y i \) और \(\ z_(2)=x+5 i \) बराबर हैं।
परिभाषा के अनुसार, दो सम्मिश्र संख्याएँ समान होती हैं यदि उनके वास्तविक और काल्पनिक भाग समान हों, अर्थात। \(\ x=13 \), \(\ y=5 \).
जोड़ना
सम्मिश्र संख्याओं का योग \(\ z_(1)=x_(1)+i y_(1) \) वास्तविक और काल्पनिक भागों के सीधे योग द्वारा किया जाता है:
\(\ z_(1)+z_(2)=x_(1)+i y_(1)+x_(2)+i y_(2)=\left(x_(1)+x_(2)\right) +i\left(y_(1)+y_(2)\right)\)
सम्मिश्र संख्याओं का योग ज्ञात कीजिए \(\ z_(1)=-7+5 i \), \(\ z_(2)=13-4 i \)
सम्मिश्र संख्या \(\ z_(1)=-7+5 i \) का वास्तविक भाग संख्या \(\ x_(1)=\operatorname(Re) z_(1)=-7 \) है, काल्पनिक भाग संख्या \( \ y_(1)=\mathrm(Im) \), \(\ z_(1)=5 \) है। सम्मिश्र संख्या \(\ z_(2)=13-4 i \) के वास्तविक और काल्पनिक भाग \(\ x_(2)=\operatorname(Re) z_(2)=13 \) और \(\ y_ हैं (2 )=\operatorname(Im) z_(2)=-4 \) .
इसलिए, सम्मिश्र संख्याओं का योग है:
\(\ z_(1)+z_(2)=\left(x_(1)+x_(2)\right)+i\left(y_(1)+y_(2)\right)=(-7+ 13)+i(5-4)=6+i\)
\(\z_(1)+z_(2)=6+i \)
सम्मिश्र संख्याओं को जोड़ने के बारे में एक अलग लेख में और पढ़ें: सम्मिश्र संख्याओं को जोड़ना।
घटाव
जटिल संख्याओं \(\ z_(1)=x_(1)+i y_(1) \) और \(\ z_(2)=x_(2)+i y_(2) \) का घटाव प्रत्यक्ष द्वारा किया जाता है वास्तविक और काल्पनिक भागों का घटाव:
\(\ z_(1)-z_(2)=x_(1)+i y_(1)-\left(x_(2)+i y_(2)\right)=x_(1)-x_(2) +\left(i y_(1)-i y_(2)\right)=\left(x_(1)-x_(2)\right)+i\left(y_(1)-y_(2)\right )\)
सम्मिश्र संख्याओं का अंतर ज्ञात कीजिए \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \)
सम्मिश्र संख्याओं के वास्तविक और काल्पनिक भाग ज्ञात कीजिए \(\ z_(1)=17-35 i \), \(\ z_(2)=15+5 i \) :
\(\ x_(1)=\operatorname(Re) z_(1)=17, x_(2)=\operatorname(Re) z_(2)=15 \)
\(\ y_(1)=\operatorname(Im) z_(1)=-35, y_(2)=\operatorname(Im) z_(2)=5 \)
अतः सम्मिश्र संख्याओं का अंतर है:
\(\ z_(1)-z_(2)=\left(x_(1)-x_(2)\right)+i\left(y_(1)-y_(2)\right)=(17-15 )+i(-35-5)=2-40 i \)
\(\ z_(1)-z_(2)=2-40 i \) गुणा
सम्मिश्र संख्याओं \(\ z_(1)=x_(1)+i y_(1) \) और \(\ z_(2)=x_(2)+i y_(2) \) का गुणन सीधे द्वारा किया जाता है काल्पनिक इकाई \(\ i^(2)=-1 \) के गुण को ध्यान में रखते हुए, बीजगणितीय रूप में संख्याएँ उत्पन्न करना :
\(\ z_(1) \cdot z_(2)=\left(x_(1)+i y_(1)\right) \cdot\left(x_(2)+i y_(2)\right)=x_ (1) \cdot x_(2)+i^(2) \cdot y_(1) \cdot y_(2)+\left(x_(1) \cdot i y_(2)+x_(2) \cdot i y_(1)\दाएं)= \)
\(\ =\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2 ) \cdot y_(1)\दाएं) \)
सम्मिश्र संख्याओं का गुणनफल ज्ञात कीजिए \(\ z_(1)=1-5 i \)
सम्मिश्र संख्याओं का सम्मिश्र:
\(\ z_(1) \cdot z_(2)=\left(x_(1) \cdot x_(2)-y_(1) \cdot y_(2)\right)+i\left(x_(1) \cdot y_(2)+x_(2) \cdot y_(1)\right)=(1 \cdot 5-(-5) \cdot 2)+i(1 \cdot 2+(-5) \cdot 5 )=15-23 मैं \)
\(\ z_(1) \cdot z_(2)=15-23 i \) विभाजन
सम्मिश्र संख्या गुणनखंड \(\ z_(1)=x_(1)+i y_(1) \) और \(\ z_(2)=x_(2)+i y_(2) \) को गुणा करके निर्धारित किया जाता है हर के साथ संयुग्मित संख्या का अंश और हर:
\(\ \frac(z_(1))(z_(2))=\frac(x_(1)+i y_(1))(x_(2)+i y_(2))=\frac(\left (x_(1)+i y_(1)\right)\left(x_(2)-i y_(2)\right))(\left(x_(2)+i y_(2)\right)\left (x_(2)-i y_(2)\right))=\frac(x_(1) \cdot x_(2)+y_(1) \cdot y_(2))(x_(2)^(2) +y_(2)^(2))+i \frac(x_(2) \cdot y_(1)-x_(1) \cdot y_(2))(x_(2)^(2)+y_(2) )^(2)) \)
संख्या 1 को सम्मिश्र संख्या \(\ z=1+2 i \) से विभाजित करना।
चूँकि वास्तविक संख्या 1 का काल्पनिक भाग शून्य है, गुणनखंड है:
\(\ \frac(1)(1+2 i)=\frac(1 \cdot 1)(1^(2)+2^(2))-i \frac(1 \cdot 2)(1^( 2)+2^(2))=\frac(1)(5)-i \frac(2)(5) \)
\(\ \frac(1)(1+2 i)=\frac(1)(5)-i \frac(2)(5) \)
शिक्षण योजना।
1. संगठनात्मक क्षण.
2. सामग्री की प्रस्तुति.
3. गृहकार्य.
4. पाठ का सारांश।
कक्षाओं के दौरान
I. संगठनात्मक क्षण.
द्वितीय. सामग्री की प्रस्तुति.
प्रेरणा।
वास्तविक संख्याओं के समुच्चय का विस्तार इस तथ्य में निहित है कि वास्तविक संख्याओं में नई संख्याएँ (काल्पनिक) जोड़ी जाती हैं। इन संख्याओं का परिचय वास्तविक संख्याओं के समुच्चय में ऋणात्मक संख्या से मूल निकालने की असंभवता से जुड़ा है।
सम्मिश्र संख्या की अवधारणा का परिचय.
जिन काल्पनिक संख्याओं को हम वास्तविक संख्याओं से पूरक करते हैं उन्हें इस प्रकार लिखा जाता है द्वि, कहाँ मैंकाल्पनिक इकाई है, और मैं 2 = - 1.
इसके आधार पर, हमें सम्मिश्र संख्या की निम्नलिखित परिभाषा प्राप्त होती है।
परिभाषा. सम्मिश्र संख्या रूप की अभिव्यक्ति है ए+बी, कहाँ एऔर बीवास्तविक संख्याएँ हैं. इस मामले में, निम्नलिखित शर्तें पूरी होती हैं:
ए) दो सम्मिश्र संख्याएँ ए 1 + बी 1 आईऔर ए 2 + बी 2 आईयदि और केवल यदि के बराबर ए 1 = ए 2, बी1=बी2.
बी) सम्मिश्र संख्याओं का योग नियम द्वारा निर्धारित होता है:
(ए 1 + बी 1 आई) + (ए 2 + बी 2 आई) = (ए 1 + ए 2) + (बी 1 + बी 2) आई.
ग) सम्मिश्र संख्याओं का गुणन नियम द्वारा निर्धारित होता है:
(ए 1 + बी 1 आई) (ए 2 + बी 2 आई) = (ए 1 ए 2 - बी 1 बी 2) + (ए 1 बी 2 - ए 2 बी 1) आई.
सम्मिश्र संख्या का बीजगणितीय रूप.
प्रपत्र में सम्मिश्र संख्या लिखना ए+बीसम्मिश्र संख्या का बीजगणितीय रूप कहा जाता है, जहाँ ए- वास्तविक भाग द्विकाल्पनिक भाग है, और बीएक वास्तविक संख्या है.
जटिल संख्या ए+बीइसे शून्य के बराबर माना जाता है यदि इसके वास्तविक और काल्पनिक भाग शून्य के बराबर हों: ए=बी=0
जटिल संख्या ए+बीपर बी = 0एक वास्तविक संख्या मानी जाती है ए: ए + 0आई = ए.
जटिल संख्या ए+बीपर ए = 0पूर्णतः काल्पनिक कहा जाता है और निरूपित किया जाता है द्वि: 0 + द्वि = द्वि.
दो सम्मिश्र संख्याएँ z = ए + द्विऔर = ए - द्वि, जो केवल काल्पनिक भाग के चिन्ह में भिन्न होते हैं, संयुग्म कहलाते हैं।
बीजगणितीय रूप में सम्मिश्र संख्याओं पर क्रियाएँ।
निम्नलिखित संक्रियाएँ जटिल संख्याओं पर बीजगणितीय रूप में निष्पादित की जा सकती हैं।
1) जोड़.
परिभाषा. सम्मिश्र संख्याओं का योग जेड 1 = ए 1 + बी 1 आईऔर जेड 2 = ए 2 + बी 2 आईसम्मिश्र संख्या कहलाती है जेड, जिसका वास्तविक भाग वास्तविक भागों के योग के बराबर है जेड 1और z2, और काल्पनिक भाग संख्याओं के काल्पनिक भागों का योग है जेड 1और z2, वह है जेड = (ए 1 + ए 2) + (बी 1 + बी 2)आई.
नंबर जेड 1और z2पद कहलाते हैं.
सम्मिश्र संख्याओं के योग में निम्नलिखित गुण होते हैं:
1º. क्रमपरिवर्तनशीलता: z1 + z2 = z2 + z1.
2º. साहचर्य: (जेड 1 + जेड 2) + जेड 3 = जेड 1 + (जेड 2 + जेड 3)।
3º. जटिल संख्या -ए -द्विसम्मिश्र संख्या का विपरीत कहा जाता है z = ए + द्वि. सम्मिश्र संख्या सम्मिश्र संख्या के विपरीत जेड, निरूपित -जेड. सम्मिश्र संख्याओं का योग जेडऔर -जेडशून्य के बराबर: z + (-z) = 0
उदाहरण 1: जोड़ें (3 - आई) + (-1 + 2आई).
(3 - i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) घटाव.
परिभाषा।सम्मिश्र संख्या से घटाएँ जेड 1जटिल संख्या z2 जेड,क्या जेड + जेड 2 = जेड 1.
प्रमेय. जटिल संख्याओं का अंतर मौजूद है और, इसके अलावा, अद्वितीय है।
उदाहरण 2: घटाना (4 - 2आई) - (-3 + 2आई).
(4 - 2आई) - (-3 + 2आई) = (4 - (-3)) + (-2 - 2) आई = 7 - 4आई.
3) गुणन.
परिभाषा. सम्मिश्र संख्याओं का गुणनफल जेड 1 =ए 1 +बी 1 आईऔर जेड 2 = ए 2 + बी 2 आईसम्मिश्र संख्या कहलाती है जेड, समानता द्वारा परिभाषित: जेड = (ए 1 ए 2 - बी 1 बी 2) + (ए 1 बी 2 + ए 2 बी 1)i.
नंबर जेड 1और z2कारक कहलाते हैं।
सम्मिश्र संख्याओं के गुणन में निम्नलिखित गुण होते हैं:
1º. क्रमपरिवर्तनशीलता: z 1 z 2 = z 2 z 1.
2º. साहचर्य: (जेड 1 जेड 2)जेड 3 = जेड 1 (जेड 2 जेड 3)
3º. जोड़ के संबंध में गुणन की वितरणशीलता:
(जेड 1 + जेड 2) जेड 3 = जेड 1 जेड 3 + जेड 2 जेड 3.
4º. z = (ए + बीआई) (ए - बीआई) = ए 2 + बी 2एक वास्तविक संख्या है.
व्यवहार में, सम्मिश्र संख्याओं का गुणन योग को योग से गुणा करने और वास्तविक और काल्पनिक भागों को अलग करने के नियम के अनुसार किया जाता है।
निम्नलिखित उदाहरण में, सम्मिश्र संख्याओं को दो तरीकों से गुणा करने पर विचार करें: नियम से और योग को योग से गुणा करके।
उदाहरण 3: गुणा करें (2 + 3i) (5 - 7i).
1 रास्ता. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15) )मैं = 31 + मैं.
2 रास्ते। (2 + 3i) (5 - 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 - 14i + 15i + 21 = 31 + i.
4) प्रभाग.
परिभाषा. किसी सम्मिश्र संख्या को विभाजित करें जेड 1एक जटिल संख्या के लिए z2, का अर्थ है ऐसी सम्मिश्र संख्या ज्ञात करना जेड, क्या जेड जेड 2 = जेड 1.
प्रमेय.जटिल संख्याओं का भागफल मौजूद है और अद्वितीय है यदि z2 ≠ 0 + 0i.
व्यवहार में, सम्मिश्र संख्याओं का भागफल अंश और हर को हर के संयुग्मक से गुणा करके पाया जाता है।
होने देना जेड 1 = ए 1 + बी 1 आई, जेड 2 = ए 2 + बी 2 आई, तब
.
निम्नलिखित उदाहरण में, हम सूत्र द्वारा विभाजन करते हैं और हर के संयुग्मक द्वारा गुणन के नियम का पालन करते हैं।
उदाहरण 4. भागफल ज्ञात कीजिए 
.
5) एक धनात्मक पूर्णांक घात तक बढ़ाना।
क) काल्पनिक एकता की शक्तियाँ।
समानता का लाभ उठा रहे हैं मैं 2 = -1, काल्पनिक इकाई की किसी भी सकारात्मक पूर्णांक शक्ति को परिभाषित करना आसान है। अपने पास:
मैं 3 = मैं 2 मैं = -मैं,
मैं 4 = मैं 2 मैं 2 = 1,
मैं 5 = मैं 4 मैं = मैं,
मैं 6 = मैं 4 मैं 2 = -1,
मैं 7 = मैं 5 मैं 2 = -मैं,
मैं 8 = मैं 6 मैं 2 = 1वगैरह।
इससे पता चलता है कि डिग्री मान में, कहाँ एन- एक धनात्मक पूर्णांक, सूचक बढ़ने पर समय-समय पर दोहराया जाता है 4 .
इसलिए संख्या बढ़ानी है मैंएक सकारात्मक पूर्णांक घात के लिए, घातांक को इससे विभाजित करें 4 और सीधा मैंउस घात के लिए जिसका प्रतिपादक विभाजन का शेष भाग है।
उदाहरण 5 गणना करें: (आई 36 + आई 17) आई 23.
मैं 36 = (मैं 4) 9 = 1 9 = 1,
मैं 17 = मैं 4 × 4+1 = (मैं 4) 4 × मैं = 1 मैं = मैं।
मैं 23 = मैं 4 × 5+3 = (मैं 4) 5 × मैं 3 = 1 मैं 3 = - मैं।
(आई 36 + आई 17) आई 23 = (1 + आई) (- आई) = - आई + 1 = 1 - आई।
बी) एक जटिल संख्या को एक सकारात्मक पूर्णांक शक्ति तक बढ़ाना एक द्विपद को संबंधित शक्ति तक बढ़ाने के नियम के अनुसार किया जाता है, क्योंकि यह समान जटिल कारकों को गुणा करने का एक विशेष मामला है।
उदाहरण 6 गणना करें: (4+2आई)3
(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
