Creation

Find the area of a rhombus using the formula log in with. Four formulas that can be used to calculate the area of a rhombus. Properties of a rhombus. Trapezoid area formulas

Mathematics is a school subject that is studied by everyone, regardless of class profile. However, she is not everyone's favorite. Sometimes undeservedly. This science constantly presents students with challenges that allow their brains to develop. Mathematics does a great job of keeping children's thinking skills alive. One of its sections copes especially well with this - geometry.

Any of the topics that are studied in it is worthy of attention and respect. Geometry is a way to develop spatial imagination. An example is the topic about the areas of shapes, in particular rhombuses. These puzzles can lead to dead ends if you don't understand the details. Because different approaches to finding the answer are possible. It is easier for some to remember different versions of the formulas that are written below, while others are able to obtain them themselves from previously learned material. In any case, there are no hopeless situations. If you think a little, you will definitely find a solution.

It is necessary to answer this question in order to understand the principles of obtaining formulas and the flow of reasoning in problems. After all, in order to understand how to find the area of a rhombus, you need to clearly understand what kind of figure it is and what its properties are.

For the convenience of considering a parallelogram, which is a quadrilateral with pairwise parallel sides, we will take it as a “parent”. He has two “children”: a rectangle and a rhombus. Both of them are parallelograms. If we continue the parallels, then this is a “surname”. This means that in order to find the area of a rhombus, you can use the already studied formula for a parallelogram.

But, like all children, the rhombus also has something of its own. This makes it slightly different from the "parent" and allows it to be viewed as a separate figure. After all, a rectangle is not a rhombus. Returning to the parallels - they are like brother and sister. They have a lot in common, but they are still different. These differences are their special properties that need to be used. It would be strange to know about them and not apply them in solving problems.

If we continue the analogy and recall another figure - a square, then it will be a continuation of a rhombus and a rectangle. This figure combines all the properties of both.

Properties of a rhombus

There are five of them and they are listed below. Moreover, some of them repeat the properties of a parallelogram, while some are inherent only to the figure in question.

A rhombus is a parallelogram that has taken on a special shape. It follows from this that its sides are pairwise parallel and equal. Moreover, they are not equal in pairs, but that’s all. As it would be for a square.
The diagonals of this quadrilateral intersect at an angle of 90º. This is convenient and greatly simplifies the flow of reasoning when solving problems.
Another property of diagonals: each of them is divided by the point of intersection into equal segments.
The angles of this figure lying opposite each other are equal.
And the last property: the diagonals of a rhombus coincide with the bisectors of the angles.

Notations adopted in the considered formulas

In mathematics, you solve problems using common letter expressions called formulas. The topic about squares is no exception.

In order to move on to the notes that will tell you how to find the area of a rhombus, you need to agree on the letters that replace all the numerical values of the elements of the figure.

Now it's time to write the formulas.

The problem data includes only the diagonals of the rhombus

The rule states that to find an unknown quantity, you need to multiply the lengths of the diagonals, and then divide the product in half. The result of division is the area of the rhombus through the diagonals.

The formula for this case will look like this:

Let this formula be number 1.

The problem gives the side of a rhombus and its height

To calculate the area, you will need to find the product of these two quantities. This is perhaps the simplest formula. Moreover, it is also known from the topic about the area of a parallelogram. Such a formula has already been studied there.

Mathematical notation:

The number of this formula is 2.

Known side and acute angle

In this case, you need to square the size of the side of the rhombus. Then find the sine of the angle. And with the third action, calculate the product of the two resulting quantities. The answer will be the area of the rhombus.

Literal expression:

Its serial number is 3.

Given quantities: radius of inscribed circle and acute angle

To calculate the area of a rhombus, you need to find the square of the radius and multiply it by 4. Determine the value of the sine of the angle. Then divide the product by the second quantity.

The formula takes the following form:

It will be numbered 4.

The problem involves the side and radius of an inscribed circle

To determine how to find the area of a rhombus, you will need to calculate the product of these quantities and the number 2.

The formula for this problem will look like this:

Its serial number is 5.

Examples of possible tasks

Problem 1

One of the diagonals of a rhombus is 8 cm, and the other is 14 cm. You need to find the area of the figure and the length of its side.

Solution

To find the first quantity, you will need formula 1, in which D 1 = 8, D 2 = 14. Then the area is calculated as follows: (8 * 14) / 2 = 56 (cm 2).

The diagonals divide the rhombus into 4 triangles. Each of them will definitely be rectangular. This must be used to determine the value of the second unknown. The side of the rhombus will become the hypotenuse of the triangle, and the legs will be the halves of the diagonals.

Then a 2 = (D 1 /2) 2 + (D 2 /2) 2. After substituting all the values, we get: a 2 = (8 / 2) 2 + (14 / 2) 2 = 16 + 49 = 65. But this is the square of the side. This means we need to take the square root of 65. Then the side length will be approximately 8.06 cm.

Answer: area is 56 cm2 and side is 8.06 cm.

Problem 2

The side of a rhombus has a value equal to 5.5 dm, and its height is 3.5 dm. Find the area of the figure.

Solution

In order to find the answer, you will need formula 2. In it, a = 5.5, H = 3.5. Then, replacing the letters in the formula with numbers, we find that the desired value is 5.5 * 3.5 = 19.25 (dm 2).

Answer: The area of a rhombus is 19.25 dm2.

Problem 3

The acute angle of a certain rhombus is 60º, and its smaller diagonal is 12 cm. You need to calculate its area.

Solution

To get the result, you will need formula number 3. In it, instead of A will be 60, and the value A unknown.

To find the side of a rhombus, you will need to remember the theorem of sines. In a right triangle A will be the hypotenuse, the shorter leg is equal to half the diagonal, and the angle is divided in half (known from the property where the bisector is mentioned).

Then the side A will be equal to the product of the leg and the sine of the angle.

The leg needs to be calculated as D/2 = 12/2 = 6 (cm). Sine (A/2) will be equal to its value for an angle of 30º, that is, 1/2.

After performing simple calculations, we obtain the following value for the side of the rhombus: a = 3 (cm).

Now the area is the product of 3 2 and the sine of 60º, that is, 9 * (√3)/2 = (9√3)/2 (cm 2).

Answer: the required value is (9√3)/2 cm 2.

Results: everything is possible

Here we looked at some options for how to find the area of a rhombus. If it is not directly clear in a problem which formula to use, then you need to think a little and try to connect previously studied topics. In other topics there will definitely be a hint that will help connect known quantities with those in the formulas. And the problem will be solved. The main thing is to remember that everything previously learned can and should be used.

In addition to the proposed tasks, inverse problems are also possible, when using the area of a figure you need to calculate the value of some element of a rhombus. Then you need to use the equation that is closest to the condition. And then transform the formula, leaving an unknown quantity on the left side of the equality.

A rhombus is a special figure in geometry. Thanks to its special properties, there is not one, but several formulas that can be used to calculate the area of a rhombus. What are these properties and what are the most common formulas for finding the area of this figure? Let's figure it out.

What geometric figure is called a rhombus?

Before you find out what the area of a rhombus is, it’s worth finding out what kind of figure it is.

From the time of Euclidean geometry, a rhombus is a symmetrical quadrilateral, all four sides of which are equal in length and parallel in pairs.

Origin of the term

The name of this figure came to most modern languages from Greek, through the mediation of Latin. The “progenitor” of the word “rhombus” was the Greek noun ῥόμβος (tambourine). Although it is difficult for twentieth-century residents, accustomed to round tambourines, to imagine them in any other shape, among the Hellenes these musical instruments were traditionally made not round, but diamond-shaped.

In most modern languages, this mathematical term is used as in Latin: rombus. However, in English, rhombuses are sometimes called diamond (diamond or diamond). This figure received this nickname because of its special shape, reminiscent of a precious stone. As a rule, a similar term is not used for all rhombuses, but only for those in which the angle of intersection of its two sides is equal to sixty or forty-five degrees.

This figure was first mentioned in the works of the Greek mathematician who lived in the first century of the new era - Heron of Alexandria.

What properties does this geometric figure have?

To find the area of a rhombus, first of all you need to know what features this geometric figure has.

Under what conditions is a parallelogram a rhombus?

As you know, every rhombus is a parallelogram, but not every parallelogram is a rhombus. To accurately state that the presented figure is indeed a rhombus, and not a simple parallelogram, it must correspond to one of the three main features that distinguish a rhombus. Or all three at once.

The diagonals of a parallelogram intersect at an angle of ninety degrees.
Diagonals divide angles in two, acting as their bisectors.
Not only parallel, but also adjacent sides have the same length. This, by the way, is one of the main differences between a rhombus and a parallelogram, since the second figure has only parallel sides that are equal in length, but not adjacent ones.

Under what conditions is a rhombus a square?

According to its properties, in some cases a rhombus can simultaneously become a square. To clearly confirm this statement, simply rotate the square in any direction by forty-five degrees. The resulting figure will be a rhombus, each of the angles of which is equal to ninety degrees.

Also, to confirm that the square is a rhombus, you can compare the characteristics of these figures: in both cases, all sides are equal, and the diagonals are bisectors and intersect at an angle of ninety degrees.

How to find out the area of a rhombus using its diagonals

In the modern world, you can find almost all the materials to perform the necessary calculations on the Internet. Thus, there are a lot of resources equipped with programs for automatically calculating the area of a particular figure. Moreover, if (as in the case of a rhombus) there are several formulas for this, then it is possible to choose which one is most convenient to use. However, first of all, you need to be able to calculate the area of a rhombus yourself without the help of a computer and navigate the formulas. There are many of them for the rhombus, but the most famous of them are four.

One of the simplest and most common ways to find out the area of this figure is if you have information about the length of its diagonals. If the problem has this data, then you can apply the following formula to find the area: S = KM x LN/2 (KM and LN are the diagonals of the rhombus KLMN).

You can check the reliability of this formula in practice. Let's say that a rhombus KLMN has the length of one of its diagonals KM - 10 cm, and the second LN - 8 cm. Then we substitute these data into the above formula and get the following result: S = 10 x 8/ 2 = 40 cm 2.

Formula for calculating the area of a parallelogram

There is another formula. As stated above in the definition of a rhombus, it is not just a quadrilateral, but also a parallelogram, and has all the features of this figure. In this case, to find its area, it is quite advisable to use the formula used for a parallelogram: S = KL x Z. In this case, KL is the length of the side of the parallelogram (rhombus), and Z is the length of the height drawn to this side.

In some problems, the length of the side is not provided, but the perimeter of the rhombus is known. Since the formula for finding it was indicated above, you can use it to find out the length of the side. So, the perimeter of the figure is 10 cm. The length of the side can be found by inverting the perimeter formula and dividing 10 by 4. The result will be 2.5 cm - this is the desired length of the side of the rhombus.

Now it’s worth trying to substitute this number into the formula, knowing that the length of the height drawn to the side is also equal to 2.5 cm. Now let’s try to put these values into the above formula for the area of a parallelogram. It turns out that the area of the rhombus is S = 2.5 x 2.5 = 6.25 cm 2.

Other ways to calculate the area of a rhombus

Those who have already mastered sines and cosines can use formulas containing them to find the area of a rhombus. A classic example is the following formula: S = KM 2 x Sin KLM. In this case, the area of the figure is equal to the product of the two sides of the rhombus multiplied by the sine of the angle between them. And since all the sides in a rhombus are the same, it is easier to immediately square one side, as was shown in the formula.

We check this scheme in practice, and not just for a rhombus, but for a square, which, as you know, has all right angles, which means they are equal to ninety degrees. Let's say one of the sides is 15 cm. It is also known that the sine of an angle of 90° is equal to one. Then, according to the formula, S = 15 x 15 x Sin 90° = 255x1 = 255 cm 2.

In addition to the above, in some cases another formula is used, using sine to determine the area of a rhombus: S = 4 x R 2 /Sin KLM. In this embodiment, the radius of a circle inscribed in a rhombus is used. It is raised to the power of the square and multiplied by four. And the entire result is divided by the sine of the angle closest to the inscribed figure.

As an example, for simplicity of calculations, let’s take a square again (the sine of its angle will always be equal to one). The radius of the circle inscribed in it is 4.4 cm. Then the area of the rhombus will be calculated as follows: S = 4 x 4.4 2 / Sin 90 ° = 77.44 cm 2

The above formulas for finding the radius of a rhombus are far from the only ones of their kind, but they are the easiest to understand and carry out calculations.

is a parallelogram in which all sides are equal, then all the same formulas apply to it as for a parallelogram, including the formula for finding the area through the product of height and sides.

The area of a rhombus can be found by also knowing its diagonals. The diagonals divide the rhombus into four absolutely identical right triangles. If we sort them to get a rectangle, then its length and width will be equal to one whole diagonal and half of the second diagonal. Therefore, the area of a rhombus is found by multiplying the diagonals of the rhombus, reduced by two (as the area of the resulting rectangle).

If you only have an angle and a side at your disposal, then you can use the diagonal as an assistant and draw it opposite the known angle. Then it will divide the rhombus into two congruent triangles, the areas of which will add up to give us the area of the rhombus. The area of each of the triangles will be equal to half the product of the square of the side and the sine of the known angle, as the area of an isosceles triangle. Since there are two such triangles, the coefficients are reduced, leaving only the side to the second power and the sine:

If you inscribe a circle inside a rhombus, then its radius will relate to the side at an angle of 90°, which means that twice the radius will be equal to the height of the rhombus. Substituting instead of height h=2r into the previous formula, we get area S=ha=2ra

If, along with the radius of the inscribed circle, not a side, but an angle is given, then you must first find the side by drawing the height in such a way as to obtain a right triangle with a given angle. Then side a can be found from trigonometric relations using the formula . Substituting this expression into the same standard formula for the area of a rhombus, we get

A rhombus (from the ancient Greek ῥόμβος and from the Latin rombus “tambourine”) is a parallelogram, which is characterized by the presence of sides of equal length. When the angles are 90 degrees (or a right angle), such a geometric figure is called a square. A rhombus is a geometric figure, a type of quadrilateral. It can be both a square and a parallelogram.

Origin of this term

Let's talk a little about the history of this figure, which will help us uncover a little of the mysterious secrets of the ancient world. The familiar word for us, often found in school literature, “rhombus,” originates from the ancient Greek word “tambourine.” In Ancient Greece, these musical instruments were produced in a diamond or square shape (as opposed to modern devices). Surely you noticed that the card suit - diamonds - has a rhombic shape. The formation of this suit goes back to the times when round diamonds were not used in everyday life. Consequently, the rhombus is the oldest historical figure that was invented by mankind long before the advent of the wheel.

For the first time, such a word as “rhombus” was used by such famous personalities as Heron and the Pope of Alexandria.

Properties of a rhombus

Since the sides of a rhombus are opposite each other and are parallel in pairs, then the rhombus is undoubtedly a parallelogram (AB || CD, AD || BC).
Rhombic diagonals intersect at right angles (AC ⊥ BD), and therefore are perpendicular. Therefore, the intersection bisects the diagonals.
The bisectors of rhombic angles are the diagonals of the rhombus (∠DCA = ∠BCA, ∠ABD = ∠CBD, etc.).
From the identity of parallelograms it follows that the sum of all the squares of the diagonals of a rhombus is the number of the square of the side, which is multiplied by 4.

Signs of a diamond

A rhombus is a parallelogram when it meets the following conditions:

All sides of a parallelogram are equal.
The diagonals of a rhombus intersect a right angle, that is, they are perpendicular to each other (AC⊥BD). This proves the rule of three sides (the sides are equal and at an angle of 90 degrees).
The diagonals of a parallelogram divide the angles equally because the sides are equal.

Area of a rhombus

The area of a rhombus is equal to the number that is half the product of all its diagonals.
Since a rhombus is a kind of parallelogram, the area of the rhombus (S) is the product of the side of the parallelogram and its height (h).
In addition, the area of a rhombus can be calculated using the formula, which is the product of the squared side of the rhombus and the sine of the angle. The sine of the angle is alpha - the angle located between the sides of the original rhombus.
A formula that is the product of twice the angle alpha and the radius of the inscribed circle (r) is considered quite acceptable for the correct solution.

What is Rhombus? A rhombus is a parallelogram in which all sides are equal.

RHOMBUS, a figure on a plane, a quadrilateral with equal sides. A rhombus is a special case of a PARALLELOGRAM, in which either two adjacent sides are equal, or the diagonals intersect at right angles, or the diagonal bisects the angle. A rhombus with right angles is called a square.

The classic formula for the area of a rhombus is to calculate the value through the height. The area of a rhombus is equal to the product of a side and the height drawn to that side.

1. The area of a rhombus is equal to the product of a side and the height drawn to this side:

\[ S = a \cdot h \]

2. If the side of a rhombus is known (all sides of a rhombus are equal) and the angle between the sides, then the area can be found using the following formula:

\[ S = a^(2) \cdot sin(\alpha) \]

3. The area of a rhombus is also equal to the half product of the diagonals, that is:

\[ S = \dfrac(d_(1) \cdot d_(2) )(2) \]

4. If the radius r of a circle inscribed in a rhombus and the side of the rhombus a are known, then its area is calculated by the formula:

\[ S = 2 \cdot a \cdot R \]

Properties of a rhombus

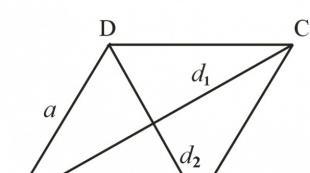
In the figure above, \(ABCD\) is a rhombus, \(AC = DB = CD = AD\) . Since a rhombus is a parallelogram, it has all the properties of a parallelogram, but there are also properties inherent only to a rhombus.

You can fit a circle into any rhombus. The center of a circle inscribed in a rhombus is the intersection point of its diagonals. Circle radius equal to half the height of the rhombus:

\[ r = \frac( AH )(2) \]