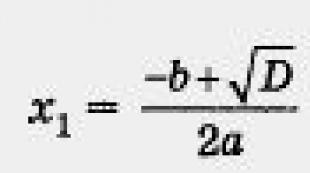Rubber bracelets

Find the area between lines online. Finding the area of the figure bounded by the lines y=f(x), x=g(y). Arc length of a flat curve

Let the function be non-negative and continuous on the interval . Then, according to the geometric meaning of a certain integral, the area of a curvilinear trapezoid bounded from above by the graph of this function, from below by the axis , from the left and right by straight lines and (see Fig. 2) is calculated by the formula

Example 9 Find the area of a figure bounded by a line and axis.

Solution. Function Graph is a parabola whose branches point downwards. Let's build it (Fig. 3). To determine the limits of integration, we find the points of intersection of the line (parabola) with the axis (straight line). To do this, we solve the system of equations

We get: , where , ; Consequently, , .

Rice. 3

The area of the figure is found by the formula (5):

If the function is non-positive and continuous on the segment , then the area of the curvilinear trapezoid, bounded from below by the graph of this function, from above by the axis, from the left and right by straight lines and , is calculated by the formula

. (6)

If the function is continuous on a segment and changes sign at a finite number of points, then the area of the shaded figure (Fig. 4) is equal to the algebraic sum of the corresponding definite integrals:

Rice. four

Example 10 Calculate the area of \u200b\u200bthe figure bounded by the axis and the graph of the function for .

Rice. 5

Solution. Let's make a drawing (Fig. 5). The desired area is the sum of the areas and . Let's find each of these areas. First, we determine the limits of integration by solving the system We get , . Consequently:

;

Thus, the area of the shaded figure is

(sq. units).

Rice. 6

Let, finally, the curvilinear trapezoid is bounded from above and below by the graphs of functions continuous on the segment and ,
and on the left and right - straight and (Fig. 6). Then its area is calculated by the formula

. (8)

Example 11. Find the area of the figure enclosed by the lines and .

Solution. This figure is shown in Fig. 7. We calculate its area using formula (8). Solving the system of equations, we find , ; Consequently, , . On the segment we have: . Hence, in formula (8) we take as x, and as - . We get:

(sq. units).

More complex problems of calculating areas are solved by breaking the figure into non-intersecting parts and calculating the area of the whole figure as the sum of the areas of these parts.

Rice. 7

Example 12. Find the area of the figure bounded by the lines , , .

Solution. Let's make a drawing (Fig. 8). This figure can be considered as a curvilinear trapezoid bounded from below by the axis , from the left and right - by straight lines and , from above - by graphs of functions and . Since the figure is bounded from above by the graphs of two functions, to calculate its area, we will divide this straight figure into two parts (1 is the abscissa of the intersection point of the lines and). The area of each of these parts is found by the formula (4):

(sq. units); (sq. units). Consequently:

(sq. units).

Rice. eight

X= j( at)

Rice. 9

In conclusion, we note that if a curvilinear trapezoid is bounded by straight lines and , the axis and continuous on the curve (Fig. 9), then its area is found by the formula

Volume of a body of revolution

Let a curvilinear trapezoid bounded by a graph of a function continuous on a segment, an axis, straight lines and rotate around the axis (Fig. 10). Then the volume of the resulting body of revolution is calculated by the formula

. (9)

Example 13 Calculate the volume of a body obtained by rotating around the axis of a curvilinear trapezoid bounded by a hyperbola , straight lines , and the axis .

Solution. Let's make a drawing (Fig. 11).

It follows from the condition of the problem that , . By formula (9) we obtain

Rice. ten

Rice. eleven

The volume of a body obtained by rotation around an axis OU curvilinear trapezoid bounded by straight lines y = c and y = d, axis OU and a graph of a function continuous on a segment (Fig. 12), is determined by the formula

. (10)

X= j( at)

Rice. 12

Example 14. Calculate the volume of a body obtained by rotation around an axis OU curvilinear trapezoid bounded by lines X 2 = 4at, y= 4, x = 0 (Fig. 13).

Solution. In accordance with the condition of the problem, we find the limits of integration: , . By formula (10) we obtain:

Rice. 13

Arc length of a flat curve

Let the curve given by the equation , where , lie in a plane (Fig. 14).

Rice. fourteen

Definition. The length of an arc is understood as the limit to which the length of a polyline inscribed in this arc tends when the number of links of the polyline tends to infinity, and the length of the largest link tends to zero.

If the function and its derivative are continuous on the segment , then the arc length of the curve is calculated by the formula

. (11)

Example 15. Calculate the length of the arc of the curve enclosed between the points for which .

Solution. From the condition of the problem we have . By formula (11) we obtain:

4. Improper integrals
with infinite limits of integration

When introducing the concept of a definite integral, it was assumed that the following two conditions are satisfied:

a) limits of integration a and are finite;

b) the integrand is bounded on the segment .

If at least one of these conditions is not met, then the integral is called improper.

Let us first consider improper integrals with infinite limits of integration.

Definition. Let the function be defined and continuous on the interval , then and unbounded on the right (Fig. 15).

If the improper integral converges, then this area is finite; if the improper integral diverges, then this area is infinite.

Rice. fifteen

An improper integral with an infinite lower limit of integration is defined similarly:

. (13)

This integral converges if the limit on the right side of equality (13) exists and is finite; otherwise the integral is said to be divergent.

An improper integral with two infinite limits of integration is defined as follows:

, (14)

where с is any point of the interval . The integral converges only if both integrals converge on the right side of equality (14).

;

G) = [select the full square in the denominator: ] = [replacement:

] =

Hence, the improper integral converges and its value is equal to .

Enter the function for which you want to find the integral

The calculator provides a DETAILED solution of definite integrals.

This calculator solves the definite integral of the function f(x) with the given upper and lower limits.

Examples

With the use of degree
(square and cube) and fractions

(x^2 - 1)/(x^3 + 1)

Square root

Sqrt(x)/(x + 1)

cube root

Cbrt(x)/(3*x + 2)

Using sine and cosine

2*sin(x)*cos(x)

Arcsine

X*arcsin(x)

Arc cosine

x*arccos(x)

Application of the logarithm

X*log(x, 10)

natural logarithm

Exhibitor

Tg(x)*sin(x)

Cotangent

Ctg(x)*cos(x)

Irrational fractions

(sqrt(x) - 1)/sqrt(x^2 - x - 1)

Arctangent

X*arctg(x)

Arc tangent

X*arсctg(x)

Hyberbolic sine and cosine

2*sh(x)*ch(x)

Hyberbolic tangent and cotangent

ctgh(x)/tgh(x)

Hyberbolic arcsine and arccosine

X^2*arcsinh(x)*arccosh(x)

Hyberbolic arctangent and arccotangent

X^2*arctgh(x)*arctgh(x)

Rules for entering expressions and functions

Expressions can consist of functions (notations are given in alphabetical order): absolute(x) Absolute value x
(module x or |x|) arccos(x) Function - arc cosine of x arccosh(x) Arc cosine hyperbolic from x arcsin(x) Arcsine from x arcsinh(x) Arcsine hyperbolic from x arctg(x) Function - arc tangent from x arctgh(x) The arc tangent is hyperbolic from x e e a number that is approximately equal to 2.7 exp(x) Function - exponent from x(which is e^x) log(x) or log(x) Natural logarithm of x
(To obtain log7(x), you need to enter log(x)/log(7) (or, for example, for log10(x)=log(x)/log(10)) pi The number is "Pi", which is approximately equal to 3.14 sin(x) Function - Sine of x cos(x) Function - Cosine of x sinh(x) Function - Hyperbolic sine of x cash(x) Function - Hyperbolic cosine of x sqrt(x) The function is the square root of x sqr(x) or x^2 Function - Square x tg(x) Function - Tangent from x tgh(x) Function - Hyperbolic tangent of x cbrt(x) The function is the cube root of x

You can use the following operations in expressions: Real numbers enter in the form 7.5 , not 7,5 2*x- multiplication 3/x- division x^3- exponentiation x + 7- addition x - 6- subtraction
Other features: floor(x) Function - rounding x down (example floor(4.5)==4.0) ceiling(x) Function - rounding x up (example ceiling(4.5)==5.0) sign(x) Function - Sign x erf(x) Error function (or probability integral) laplace(x) Laplace function

Calculating the area of a figure This is perhaps one of the most difficult problems in area theory. In school geometry, they are taught to find the areas of basic geometric shapes such as, for example, a triangle, a rhombus, a rectangle, a trapezoid, a circle, etc. However, one often has to deal with the calculation of the areas of more complex figures. It is in solving such problems that it is very convenient to use integral calculus.

Definition.

Curvilinear trapezoid some figure G is called, bounded by the lines y = f(x), y = 0, x = a and x = b, and the function f(x) is continuous on the segment [a; b] and does not change its sign on it (Fig. 1). The area of a curvilinear trapezoid can be denoted by S(G).

The definite integral ʃ a b f(x)dx for the function f(x), which is continuous and non-negative on the segment [a; b], and is the area of the corresponding curvilinear trapezoid.

That is, to find the area of \u200b\u200bthe figure G, bounded by the lines y \u003d f (x), y \u003d 0, x \u003d a and x \u003d b, it is necessary to calculate the definite integral ʃ a b f (x) dx.

In this way, S(G) = ʃ a b f(x)dx.

If the function y = f(x) is not positive on [a; b], then the area of the curvilinear trapezoid can be found by the formula S(G) = -ʃ a b f(x)dx.

Example 1

Calculate the area of \u200b\u200bthe figure bounded by the lines y \u003d x 3; y = 1; x = 2.

Solution.

The given lines form the figure ABC, which is shown by hatching on rice. 2.

The desired area is equal to the difference between the areas of the curvilinear trapezoid DACE and the square DABE.

Using the formula S = ʃ a b f(x)dx = S(b) – S(a), we find the limits of integration. To do this, we solve a system of two equations:

(y \u003d x 3,
(y = 1.

Thus, we have x 1 \u003d 1 - the lower limit and x \u003d 2 - the upper limit.

So, S = S DACE - S DABE = ʃ 1 2 x 3 dx - 1 = x 4 /4| 1 2 - 1 \u003d (16 - 1) / 4 - 1 \u003d 11/4 (square units).

Answer: 11/4 sq. units

Example 2

Calculate the area of \u200b\u200bthe figure bounded by lines y \u003d √x; y = 2; x = 9.

Solution.

The given lines form the figure ABC, which is bounded from above by the graph of the function

y \u003d √x, and from below the graph of the function y \u003d 2. The resulting figure is shown by hatching on rice. 3.

The desired area is equal to S = ʃ a b (√x - 2). Let's find the limits of integration: b = 9, to find a, we solve the system of two equations:

(y = √x,
(y = 2.

Thus, we have that x = 4 = a is the lower limit.

So, S = ∫ 4 9 (√x – 2)dx = ∫ 4 9 √x dx –∫ 4 9 2dx = 2/3 x√x| 4 9 - 2x| 4 9 \u003d (18 - 16/3) - (18 - 8) \u003d 2 2/3 (square units).

Answer: S = 2 2/3 sq. units

Example 3

Calculate the area of \u200b\u200bthe figure bounded by the lines y \u003d x 3 - 4x; y = 0; x ≥ 0.

Solution.

Let's plot the function y \u003d x 3 - 4x for x ≥ 0. To do this, we find the derivative y ':

y’ = 3x 2 – 4, y’ = 0 at х = ±2/√3 ≈ 1.1 are critical points.

If we draw the critical points on the real axis and place the signs of the derivative, we get that the function decreases from zero to 2/√3 and increases from 2/√3 to plus infinity. Then x = 2/√3 is the minimum point, the minimum value of the function y is min = -16/(3√3) ≈ -3.

Let's determine the intersection points of the graph with the coordinate axes:

if x \u003d 0, then y \u003d 0, which means that A (0; 0) is the point of intersection with the Oy axis;

if y \u003d 0, then x 3 - 4x \u003d 0 or x (x 2 - 4) \u003d 0, or x (x - 2) (x + 2) \u003d 0, from where x 1 \u003d 0, x 2 \u003d 2, x 3 \u003d -2 (not suitable, because x ≥ 0).

Points A(0; 0) and B(2; 0) are the intersection points of the graph with the Ox axis.

The given lines form the OAB figure, which is shown by hatching on rice. four.

Since the function y \u003d x 3 - 4x takes on (0; 2) a negative value, then

S = |ʃ 0 2 (x 3 – 4x)dx|.

We have: ʃ 0 2 (x 3 - 4x)dx = (x 4 /4 - 4x 2 /2)| 0 2 \u003d -4, from where S \u003d 4 square meters. units

Answer: S = 4 sq. units

Example 4

Find the area of the figure bounded by the parabola y \u003d 2x 2 - 2x + 1, the straight lines x \u003d 0, y \u003d 0 and the tangent to this parabola at the point with the abscissa x 0 \u003d 2.

Solution.

First, we compose the equation of the tangent to the parabola y \u003d 2x 2 - 2x + 1 at the point with the abscissa x₀ \u003d 2.

Since the derivative y' = 4x - 2, then for x 0 = 2 we get k = y'(2) = 6.

Find the ordinate of the touch point: y 0 = 2 2 2 – 2 2 + 1 = 5.

Therefore, the tangent equation has the form: y - 5 \u003d 6 (x - 2) or y \u003d 6x - 7.

Let's build a figure bounded by lines:

y \u003d 2x 2 - 2x + 1, y \u003d 0, x \u003d 0, y \u003d 6x - 7.

Г y \u003d 2x 2 - 2x + 1 - parabola. Points of intersection with the coordinate axes: A(0; 1) - with the Oy axis; with the Ox axis - there are no intersection points, because the equation 2x 2 - 2x + 1 = 0 has no solutions (D< 0). Найдем вершину параболы:

x b \u003d 2/4 \u003d 1/2;

y b \u003d 1/2, that is, the vertex of the parabola point B has coordinates B (1/2; 1/2).

So, the figure whose area is to be determined is shown by hatching on rice. 5.

We have: S O A B D \u003d S OABC - S ADBC.

Find the coordinates of point D from the condition:

6x - 7 = 0, i.e. x \u003d 7/6, then DC \u003d 2 - 7/6 \u003d 5/6.

We find the area of triangle DBC using the formula S ADBC = 1/2 · DC · BC. In this way,

S ADBC = 1/2 5/6 5 = 25/12 sq. units

S OABC = ʃ 0 2 (2x 2 - 2x + 1)dx = (2x 3 /3 - 2x 2 /2 + x)| 0 2 \u003d 10/3 (square units).

Finally we get: S O A B D \u003d S OABC - S ADBC \u003d 10/3 - 25/12 \u003d 5/4 \u003d 1 1/4 (sq. units).

Answer: S = 1 1/4 sq. units

We have reviewed examples finding the areas of figures bounded by given lines. To successfully solve such problems, you need to be able to build lines and graphs of functions on a plane, find the points of intersection of lines, apply a formula to find the area, which implies the ability and skills to calculate certain integrals.

site, with full or partial copying of the material, a link to the source is required.

Solution.

The first and most important moment of the decision is the construction of a drawing.

Let's make a drawing:

The equation y=0 sets the x-axis;

- x=-2 and x=1 - straight, parallel to the axis OU;

- y \u003d x 2 +2 - a parabola whose branches are directed upwards, with a vertex at the point (0;2).

Comment. To construct a parabola, it is enough to find the points of its intersection with the coordinate axes, i.e. putting x=0 find the intersection with the axis OU and solving the corresponding quadratic equation, find the intersection with the axis Oh .

The vertex of a parabola can be found using the formulas:

You can draw lines and point by point.

On the interval [-2;1] the graph of the function y=x 2 +2 located over axis Ox , that's why:

Answer: S \u003d 9 square units

After the task is completed, it is always useful to look at the drawing and figure out if the answer is real. In this case, "by eye" we count the number of cells in the drawing - well, about 9 will be typed, it seems to be true. It is quite clear that if we had, say, the answer: 20 square units, then, obviously, a mistake was made somewhere - 20 cells clearly do not fit into the figure in question, at most a dozen. If the answer turned out to be negative, then the task was also solved incorrectly.

What to do if the curvilinear trapezoid is located under axle Oh?

b) Calculate the area of a figure bounded by lines y=-e x , x=1 and coordinate axes.

Solution.

Let's make a drawing.

If a curvilinear trapezoid completely under the axle Oh , then its area can be found by the formula:

Answer: S=(e-1) sq. unit" 1.72 sq. unit

Attention! Don't confuse the two types of tasks:

1) If you are asked to solve just a definite integral without any geometric meaning, then it can be negative.

2) If you are asked to find the area of a figure using a definite integral, then the area is always positive! That is why the minus appears in the formula just considered.

In practice, most often the figure is located in both the upper and lower half-planes.

With) Find the area of a plane figure bounded by lines y \u003d 2x-x 2, y \u003d -x.

Solution.

First you need to make a drawing. Generally speaking, when constructing a drawing in area problems, we are most interested in the intersection points of lines. Let's find the points of intersection of the parabola and the line. This can be done in two ways. The first way is analytical.

We solve the equation:

So the lower limit of integration a=0 , the upper limit of integration b=3 .

We build the given lines: 1. Parabola - vertex at the point (1;1); axis intersection Oh - points(0;0) and (0;2). 2. Straight line - the bisector of the 2nd and 4th coordinate angles. And now Attention! If on the interval [ a;b] some continuous function f(x) greater than or equal to some continuous function g(x), then the area of the corresponding figure can be found by the formula: .

And it does not matter where the figure is located - above the axis or below the axis, but it is important which chart is HIGHER (relative to another chart), and which one is BELOW. In the example under consideration, it is obvious that on the segment the parabola is located above the straight line, and therefore it is necessary to subtract from

It is possible to construct lines point by point, while the limits of integration are found out as if "by themselves". Nevertheless, the analytical method of finding the limits still sometimes has to be used if, for example, the graph is large enough, or the threaded construction did not reveal the limits of integration (they can be fractional or irrational).

The desired figure is limited by a parabola from above and a straight line from below.

On the segment , according to the corresponding formula:

Answer: S \u003d 4.5 sq. units

Calculate the area of a figure bounded by lines.

Solution.

We find the points of intersection of the given lines. To do this, we solve the system of equations:

To find the abscissas of the points of intersection of the given lines, we solve the equation:

We find: x 1 = -2, x 2 = 4.

So, these lines, which are a parabola and a straight line, intersect at points A(-2; 0), B(4; 6).

These lines form a closed figure, the area of \u200b\u200bwhich is calculated using the above formula:

According to the Newton-Leibniz formula, we find:

Find the area of an area bounded by an ellipse.

Solution.

From the ellipse equation for the I quadrant we have . From here, according to the formula, we obtain

Let's apply the substitution x = a sin t, dx = a cos t dt. New limits of integration t = α and t = β are determined from the equations 0 = a sin t, a = a sin t. Can be put α = 0 and β = π /2.

We find one fourth of the required area

From here S = pab.

Find the area of a figure bounded by linesy = - x 2 + x + 4 andy = - x + 1.

Solution.

Find the intersection points of the lines y = -x 2 + x + 4, y = -x+ 1, equating the ordinates of the lines: - x 2 + x + 4 = -x+ 1 or x 2 - 2x- 3 = 0. Find the roots x 1 = -1, x 2 = 3 and their corresponding ordinates y 1 = 2, y 2 = -2.

Using the figure area formula, we get

Find the area enclosed by the parabolay = x 2 + 1 and directx + y = 3.

Solution.

Solving the system of equations

find the abscissas of the intersection points x 1 = -2 and x 2 = 1.

Assuming y 2 = 3 - x and y 1 = x 2 + 1, based on the formula we get

Calculate the area contained within the Bernoulli lemniscater 2 = a 2 cos 2 φ .

Solution.

In the polar coordinate system, the area of the figure bounded by the arc of the curve r = f(φ ) and two polar radii φ 1 = ʅ and φ 2 = ʆ , is expressed by the integral

Due to the symmetry of the curve, we first determine one-fourth of the desired area

Therefore, the total area is S = a 2 .

Calculate the arc length of an astroidx 2/3 + y 2/3 = a 2/3 .

Solution.

We write the equation of the astroid in the form

(x 1/3) 2 + (y 1/3) 2 = (a 1/3) 2 .

Let's put x 1/3 = a 1/3 cos t, y 1/3 = a 1/3 sin t.

From here we obtain the parametric equations of the astroid

x = a cos 3 t, y = a sin 3 t, (*)

where 0 ≤ t ≤ 2π .

In view of the symmetry of the curve (*), it suffices to find one fourth of the arc length L corresponding to the parameter change t from 0 to π /2.

We get

dx = -3a cos 2 t sin t dt, dy = 3a sin 2 t cos t dt.

From here we find

Integrating the resulting expression in the range from 0 to π /2, we get

From here L = 6a.

Find the area bounded by the spiral of Archimedesr = aφ and two radius vectors that correspond to polar anglesφ 1 andφ 2 (φ 1 < φ 2 ).

Solution.

Area bounded by a curve r = f(φ ) is calculated by the formula , where α and β - limits of change of the polar angle.

Thus, we get

(*)

From (*) it follows that the area bounded by the polar axis and the first turn of the Archimedes spiral ( φ 1 = 0; φ 2 = 2π ):

Similarly, we find the area bounded by the polar axis and the second turn of the Archimedes spiral ( φ 1 = 2π ; φ 2 = 4π ):

The required area is equal to the difference of these areas

Calculate the volume of a body obtained by rotation around an axisOx figure bounded by parabolasy = x 2 andx = y 2 .

Solution.

Let's solve the system of equations

and get x 1 = 0, x 2 = 1, y 1 = 0, y 2 = 1, whence the intersection points of the curves O(0; 0), B(eleven). As can be seen in the figure, the desired volume of the body of revolution is equal to the difference between the two volumes formed by rotation around the axis Ox curvilinear trapezoids OCBA and ODBA:

Calculate the area bounded by the axisOx and sinusoidy = sinx on segments: a); b) .

Solution.

a) On the segment, the function sin x preserves the sign, and therefore by the formula , assuming y= sin x, we find

b) On the segment , function sin x changes sign. For the correct solution of the problem, it is necessary to divide the segment into two and [ π , 2π ], in each of which the function retains its sign.

According to the rule of signs, on the segment [ π , 2π ] area is taken with a minus sign.

As a result, the desired area is equal to

Determine the volume of the body bounded by the surface obtained from the rotation of the ellipsearound the major axisa .

Solution.

Given that the ellipse is symmetrical about the coordinate axes, it is enough to find the volume formed by rotation around the axis Ox area OAB, equal to one quarter of the area of the ellipse, and double the result.

Let us denote the volume of the body of revolution through V x; then, based on the formula, we have , where 0 and a- abscissas of points B and A. From the equation of the ellipse we find . From here

Thus, the required volume is equal to . (When the ellipse rotates around the minor axis b, the volume of the body is )

Find the area bounded by parabolasy 2 = 2 px andx 2 = 2 py .

Solution.

First, we find the coordinates of the intersection points of the parabolas in order to determine the integration interval. Transforming the original equations, we obtain and . Equating these values, we get or x 4 - 8p 3 x = 0.

x 4 - 8p 3 x = x(x 3 - 8p 3) = x(x - 2p)(x 2 + 2px + 4p 2) = 0.