Ko je uveo derivat? Šta je derivacija Definicija i značenje funkcije izvoda. Geometrijsko značenje derivacije funkcije u tački
Zadatak B9 daje graf funkcije ili derivacije iz kojeg trebate odrediti jednu od sljedećih veličina:
- Vrijednost derivacije u nekoj tački x 0,
- Maksimalne ili minimalne tačke (ekstremalne tačke),
- Intervali rastućih i opadajućih funkcija (intervali monotonosti).
Funkcije i derivacije predstavljene u ovom problemu su uvijek kontinuirane, čineći rješenje mnogo lakšim. Unatoč činjenici da zadatak pripada dijelu matematičke analize, mogu ga obaviti i najslabiji učenici, jer ovdje nije potrebno duboko teorijsko znanje.
Da biste pronašli vrijednost derivacije, ekstremnih tačaka i intervala monotonosti, postoje jednostavni i univerzalni algoritmi - svi će biti razmotreni u nastavku.
Pažljivo pročitajte uslove zadatka B9 da ne napravite glupe greške: ponekad naiđete na prilično dugačke tekstove, ali postoji nekoliko važnih uslova koji utiču na tok rešenja.
Proračun vrijednosti derivata. Metoda u dve tačke
Ako je problemu zadan graf funkcije f(x), tangentan na ovaj graf u nekoj tački x 0, i potrebno je pronaći vrijednost derivacije u ovoj tački, primjenjuje se sljedeći algoritam:
- Pronađite dvije “adekvatne” tačke na tangentnom grafu: njihove koordinate moraju biti cijeli broj. Označimo ove tačke kao A (x 1 ; y 1) i B (x 2 ; y 2). Ispravno zapišite koordinate - ovo je ključna točka u rješenju, a svaka greška ovdje će dovesti do pogrešnog odgovora.
- Poznavajući koordinate, lako je izračunati prirast argumenta Δx = x 2 − x 1 i prirast funkcije Δy = y 2 − y 1 .
- Konačno, nalazimo vrijednost izvoda D = Δy/Δx. Drugim riječima, trebate podijeliti prirast funkcije s prirastom argumenta - i to će biti odgovor.
Napomenimo još jednom: tačke A i B moraju se tražiti upravo na tangenti, a ne na grafu funkcije f(x), kao što se često dešava. Tangentna linija će nužno sadržavati najmanje dvije takve točke - inače problem neće biti ispravno formuliran.
Razmotrite tačke A (−3; 2) i B (−1; 6) i pronađite priraštaje:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.
Nađimo vrijednost izvoda: D = Δy/Δx = 4/2 = 2.
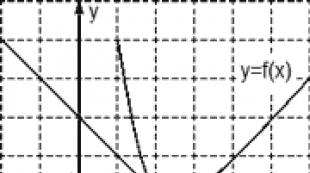
Zadatak. Na slici je prikazan grafik funkcije y = f(x) i tangenta na nju u tački sa apscisom x 0. Pronađite vrijednost izvoda funkcije f(x) u tački x 0 .
Razmotrite tačke A (0; 3) i B (3; 0), pronađite priraštaje:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.
Sada nalazimo vrijednost izvoda: D = Δy/Δx = −3/3 = −1.
Zadatak. Na slici je prikazan grafik funkcije y = f(x) i tangenta na nju u tački sa apscisom x 0. Pronađite vrijednost izvoda funkcije f(x) u tački x 0 .
Razmotrite tačke A (0; 2) i B (5; 2) i pronađite priraštaje:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.
Ostaje pronaći vrijednost derivacije: D = Δy/Δx = 0/5 = 0.
Iz posljednjeg primjera možemo formulirati pravilo: ako je tangenta paralelna s osom OX, derivacija funkcije u tački tangentnosti je nula. U ovom slučaju ne morate ništa da brojite - samo pogledajte grafikon.
Obračun maksimalnih i minimalnih bodova
Ponekad, umjesto grafa funkcije, zadatak B9 daje graf derivacije i zahtijeva pronalaženje maksimalne ili minimalne tačke funkcije. U ovoj situaciji metoda u dvije točke je beskorisna, ali postoji drugi, još jednostavniji algoritam. Prvo, hajde da definišemo terminologiju:
- Tačka x 0 naziva se maksimalnom tačkom funkcije f(x) ako u nekom susjedstvu ove tačke vrijedi sljedeća nejednakost: f(x 0) ≥ f(x).
- Tačka x 0 naziva se minimalnom tačkom funkcije f(x) ako u nekom susjedstvu ove tačke vrijedi sljedeća nejednakost: f(x 0) ≤ f(x).
Da biste pronašli maksimalnu i minimalnu točku iz grafa derivacije, samo slijedite ove korake:
- Ponovo nacrtajte graf derivata, uklanjajući sve nepotrebne informacije. Kao što pokazuje praksa, nepotrebni podaci samo ometaju odluku. Stoga označavamo nule derivacije na koordinatnoj osi - i to je to.
- Saznajte predznake izvoda na intervalima između nula. Ako je za neku tačku x 0 poznato da je f'(x 0) ≠ 0, tada su moguće samo dvije opcije: f'(x 0) ≥ 0 ili f'(x 0) ≤ 0. Predznak izvoda je lako odrediti iz originalnog crteža: ako graf derivacije leži iznad ose OX, tada je f'(x) ≥ 0. I obrnuto, ako graf derivacije leži ispod ose OX, tada je f'(x) ≤ 0.
- Ponovo provjeravamo nule i predznake derivacije. Gdje se predznak mijenja iz minusa u plus je minimalna tačka. Suprotno tome, ako se predznak derivacije promijeni iz plusa u minus, ovo je maksimalna tačka. Brojanje se uvijek vrši s lijeva na desno.
Ova šema radi samo za kontinuirane funkcije - nema drugih u problemu B9.
Zadatak. Na slici je prikazan graf derivacije funkcije f(x) definisane na intervalu [−5; 5]. Pronađite minimalnu tačku funkcije f(x) na ovom segmentu.
Oslobodimo se nepotrebnih informacija i ostavimo samo granice [−5; 5] i nule izvoda x = −3 i x = 2.5. Također primjećujemo znakove:
Očigledno, u tački x = −3 predznak izvoda se mijenja iz minusa u plus. Ovo je minimalna tačka.
Zadatak. Na slici je prikazan graf derivacije funkcije f(x) definisane na intervalu [−3; 7]. Pronađite maksimalnu tačku funkcije f(x) na ovom segmentu.
Precrtajmo graf, ostavljajući samo granice [−3; 7] i nule izvoda x = −1,7 i x = 5. Zabilježimo predznake izvoda na rezultirajućem grafu. Imamo:
![]()
Očigledno, u tački x = 5 znak derivacije se mijenja sa plusa na minus - ovo je maksimalna tačka.
Zadatak. Na slici je prikazan graf derivacije funkcije f(x), definisane na intervalu [−6; 4]. Odrediti broj maksimalnih tačaka funkcije f(x) koje pripadaju segmentu [−4; 3].
Iz uslova zadatka proizilazi da je dovoljno razmotriti samo dio grafa ograničen segmentom [−4; 3]. Stoga gradimo novi graf na kojem označavamo samo granice [−4; 3] i nule izvoda unutar njega. Naime, tačke x = −3,5 i x = 2. Dobijamo:
![]()
Na ovom grafu postoji samo jedna maksimalna tačka x = 2. U toj tački se predznak derivacije menja sa plus na minus.
Mala napomena o tačkama sa necelobrojnim koordinatama. Na primjer, u posljednjem zadatku razmatrana je tačka x = −3,5, ali sa istim uspjehom možemo uzeti x = −3,4. Ako je problem pravilno sastavljen, takve promjene ne bi trebale utjecati na odgovor, jer točke „bez određenog mjesta stanovanja“ ne učestvuju direktno u rješavanju problema. Naravno, ovaj trik neće raditi s cijelim točkama.
Pronalaženje intervala rastućih i opadajućih funkcija
U takvom problemu, kao što su tačke maksimuma i minimuma, predlaže se korištenje grafa derivacije za pronalaženje područja u kojima se sama funkcija povećava ili smanjuje. Prvo, hajde da definišemo šta je povećanje i smanjenje:
- Kaže se da funkcija f(x) raste na segmentu ako je za bilo koje dvije tačke x 1 i x 2 iz ovog segmenta tačna sljedeća tvrdnja: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Drugim riječima, što je veća vrijednost argumenta, veća je vrijednost funkcije.
- Kaže se da je funkcija f(x) opadajuća na segmentu ako je za bilo koje dvije tačke x 1 i x 2 iz ovog segmenta tačna sljedeća tvrdnja: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2) . One. Veća vrijednost argumenta odgovara manjoj vrijednosti funkcije.
Formulirajmo dovoljne uslove za povećanje i smanjenje:
- Da bi kontinuirana funkcija f(x) porasla na segmentu, dovoljno je da njen izvod unutar segmenta bude pozitivan, tj. f’(x) ≥ 0.
- Da bi se kontinuirana funkcija f(x) smanjila na segmentu , dovoljno je da njen izvod unutar segmenta bude negativan, tj. f’(x) ≤ 0.
Prihvatimo ove izjave bez dokaza. Tako dobijamo šemu za pronalaženje intervala rasta i opadanja, koja je u mnogome slična algoritmu za izračunavanje ekstremnih tačaka:
- Uklonite sve nepotrebne informacije. U originalnom grafu derivacije nas prvenstveno zanimaju nule funkcije, pa ćemo ostaviti samo njih.
- Označite predznake izvoda na razmacima između nula. Gdje je f’(x) ≥ 0, funkcija raste, a gdje je f’(x) ≤ 0, ona opada. Ako problem postavlja ograničenja na varijablu x, dodatno ih označavamo na novom grafu.
- Sada kada znamo ponašanje funkcije i ograničenja, ostaje da izračunamo količinu potrebnu za zadatak.
Zadatak. Na slici je prikazan graf derivacije funkcije f(x) definisane na intervalu [−3; 7.5]. Naći intervale opadanja funkcije f(x). U svom odgovoru navedite zbir cijelih brojeva uključenih u ove intervale.
Kao i obično, hajde da ponovo nacrtamo graf i označimo granice [−3; 7.5], kao i nule izvoda x = −1.5 i x = 5.3. Zatim bilježimo znakove derivacije. Imamo:
![]()
Pošto je izvod negativan na intervalu (− 1,5), ovo je interval opadajuće funkcije. Ostaje da se zbroje svi cijeli brojevi koji se nalaze unutar ovog intervala:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Zadatak. Na slici je prikazan grafik derivacije funkcije f(x), definisane na intervalu [−10; 4]. Naći intervale povećanja funkcije f(x). U svom odgovoru navedite dužinu najvećeg od njih.
Oslobodimo se nepotrebnih informacija. Ostavimo samo granice [−10; 4] i nule izvoda kojih je ovoga puta bilo četiri: x = −8, x = −6, x = −3 i x = 2. Označimo predznake izvoda i dobijemo sljedeću sliku:
Zanimaju nas intervali rastuće funkcije, tj. gdje je f’(x) ≥ 0. Postoje dva takva intervala na grafu: (−8; −6) i (−3; 2). Izračunajmo njihove dužine:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.
Pošto treba da nađemo dužinu najvećeg intervala, kao odgovor zapisujemo vrednost l 2 = 5.
Neka je funkcija definirana u tački i nekom njenom susjedstvu. Dajmo argumentu povećanje tako da tačka spada u domen definicije funkcije. Funkcija će se tada povećati.
DEFINICIJA. Derivat funkcije u tački naziva se granica omjera prirasta funkcije u ovoj tački i priraštaja argumenta, at (ako ova granica postoji i konačna je), tj.
Označiti: ,,,.
Derivat funkcije u tački desno (lijevo) pozvao
(ako ova granica postoji i konačna je).
Označeno sa: , – derivacija u tački desno,
, je derivacija u tački lijevo.
Očigledno je tačna sljedeća teorema.
TEOREMA. Funkcija ima derivaciju u tački ako i samo ako u ovoj tački derivacije funkcije s desne i lijeve strane postoje i jednake su jedna drugoj. Štaviše
Sljedeća teorema uspostavlja vezu između postojanja derivacije funkcije u tački i kontinuiteta funkcije u toj tački.
TEOREMA (neophodan uslov za postojanje derivacije funkcije u tački). Ako funkcija ima izvod u nekoj tački, tada je funkcija u toj tački kontinuirana.
DOKAZ
Neka postoji. Onda
![]() ,
,
gdje je infinitezimalno na.
Komentar
derivat funkcije i označiti
diferencijacija funkcije .
GEOMETRIJSKO I FIZIČKO ZNAČENJE
1) Fizičko značenje izvedenice. Ako su funkcija i njen argument fizičke veličine, onda je derivacija stopa promjene varijable u odnosu na varijablu u nekoj tački. Na primjer, ako je udaljenost koju prijeđe tačka u vremenu, onda je njen izvod brzina u trenutku. Ako je količina struje koja teče kroz poprečni presjek provodnika u trenutku, onda je brzina promjene količine električne energije u trenutku, tj. trenutna snaga u datom trenutku.
2) Geometrijsko značenje derivacije.
Neka je neka kriva, biti tačka na krivulji. 
Svaka prava linija koja siječe najmanje dvije tačke se naziva secant .
Tangenta na krivu u tački naziva se granična pozicija sekante ako tačka teži ka, krećući se duž krive.
Iz definicije je očigledno da ako tangenta na krivu postoji u tački, onda je ona jedina
Razmotrimo krivu (tj. graf funkcije). Neka ima ne-vertikalnu tangentu u tački. Njegova jednačina: (jednačina prave linije koja prolazi kroz tačku i ima ugaoni koeficijent). 
Po definiciji nagiba
gdje je ugao nagiba prave linije prema osi.
Neka je ugao nagiba sekanse prema osi, gdje. Pošto je tangenta, onda kada
dakle,
Dakle, dobili smo to – ugaoni koeficijent tangente na graf funkcije u tački(geometrijsko značenje derivacije funkcije u tački). Dakle, jednadžba tangente na krivu u nekoj tački može se napisati u obliku
Komentar . Prava linija koja prolazi kroz tačku okomitu na tangentu povučenu na krivu u toj tački naziva se normalna na krivu u tački . Kako su ugaoni koeficijenti okomitih pravih linija povezani relacijom, jednadžba normale na krivu u nekoj tački će imati oblik
![]() , Ako .
, Ako .
Ako je , tada će tangenta na krivu u tački imati oblik
i normalno.
TANGENTNE I NORMALNE JEDNAČINE
Tangentna jednadžba
Neka je funkcija data jednadžbom y=f(x), potrebno je da napišete jednačinu tangenta u tački x 0. Iz definicije derivata:
y/(x)=limΔ x→0Δ yΔ x
Δ y=f(x+Δ x)−f(x).
Jednačina tangenta na graf funkcije: y=kx+b (k,b=konst). Iz geometrijskog značenja izvedenice: f/(x 0)=tgα= k Jer x 0 i f(x 0)∈ prava, zatim jednačina tangenta je napisano kao: y−f(x 0)=f/(x 0)(x−x 0) , ili
y=f/(x 0)· x+f(x 0)−f/(x 0)· x 0.

Normalna jednačina
Normalno- je okomito na tangenta(vidi sliku). Na osnovu ovoga:
tgβ= tg(2π−α)= ctgα=1 tgα=1 f/(x 0)
Jer ugao nagiba normale je ugao β1, tada imamo:
tgβ1= tg(π−β)=− tgβ=−1 f/(x).
tačka ( x 0,f(x 0))∈ normalno, jednačina ima oblik:
y−f(x 0)=−1f/(x 0)(x−x 0).
DOKAZ
Neka postoji. Onda
![]() ,
,
gdje je infinitezimalno na.
Ali to znači da je kontinuirano u tački (vidi geometrijsku definiciju kontinuiteta). ∎
Komentar . Kontinuitet funkcije u tački nije dovoljan uslov za postojanje derivacije ove funkcije u tački. Na primjer, funkcija je kontinuirana, ali nema izvod u tački. stvarno,
i stoga ne postoji.
Očigledno, korespondencija je funkcija definirana na nekom skupu. Zovu je derivat funkcije i označiti
Operacija nalaženja funkcije njene derivacije se zove diferencijacija funkcije .
Derivat zbira i razlike
Neka su date funkcije f(x) i g(x) čiji su nam izvodi poznati. Na primjer, možete uzeti elementarne funkcije o kojima smo gore govorili. Tada možete pronaći derivaciju zbira i razlike ovih funkcija:
(f + g)’ = f ’ + g ’
(f − g)’ = f ’ − g ’
Dakle, derivacija zbira (razlike) dvije funkcije jednaka je zbiru (razlici) izvoda. Možda ima više termina. Na primjer, (f + g + h)’ = f’ + g’ + h’.
Strogo govoreći, u algebri ne postoji koncept „oduzimanja“. Postoji koncept „negativnog elementa“. Dakle, razlika f − g se može prepisati kao zbir f + (−1) g, a onda ostaje samo jedna formula - derivacija zbira.
Sadržaj članka
DERIVAT– derivacija funkcije y = f(x), dat u određenom intervalu ( a, b) u tački x ovog intervala naziva se granica kojoj teži omjer prirasta funkcije f u ovom trenutku na odgovarajući prirast argumenta kada inkrement argumenta teži nuli.
Izvod se obično označava na sljedeći način:
Druge oznake se također široko koriste:
Trenutna brzina.
Pusti poentu M kreće se pravolinijski. Razdaljina s pokretna tačka, računajući od neke početne pozicije M 0 , zavisi od vremena t, tj. s postoji funkcija vremena t: s= f(t). Neka u nekom trenutku t pokretna tačka M bio na distanci s sa početne pozicije M 0, a u nekom sljedećem trenutku t+D t našla u poziciji M 1 - na daljinu s+D s sa početne pozicije ( vidi sliku.).
Dakle, tokom određenog vremenskog perioda D t razdaljina s promijenjen za iznos D s. U ovom slučaju kažu da je tokom vremenskog intervala D t magnitude s primljeno povećanje D s.
Prosječna brzina ne može u svim slučajevima tačno okarakterizirati brzinu kretanja tačke M u određenom trenutku t. Ako, na primjer, tijelo na početku intervala D t kretao vrlo brzo, a na kraju vrlo sporo, tada prosječna brzina neće moći odraziti naznačene karakteristike kretanja točke i dati predstavu o pravoj brzini njenog kretanja u ovom trenutku t. Da biste preciznije izrazili pravu brzinu koristeći prosječnu brzinu, potrebno je da uzmete kraći vremenski period D t. Najpotpunije karakterizira brzinu kretanja tačke u ovom trenutku t granica kojoj teži prosječna brzina u D t® 0. Ovo ograničenje se naziva trenutna brzina:
Dakle, brzina kretanja u datom trenutku naziva se granica omjera prirasta putanje D s na vremensko povećanje D t, kada vremenski prirast teži nuli. Jer
Geometrijsko značenje izvedenice. Tangenta na graf funkcije.
Konstrukcija tangentnih linija jedan je od onih problema koji su doveli do rađanja diferencijalnog računa. Prvi objavljeni rad vezan za diferencijalni račun, koji je napisao Leibniz, nosio je naslov Nova metoda maksimuma i minimuma, kao i tangente, za koje ni razlomke ni iracionalne veličine nisu prepreka, i posebna vrsta računa za to.
Neka je kriva grafik funkcije y =f(x) u pravougaonom koordinatnom sistemu ( cm. pirinač.).
Po nekoj vrijednosti x funkcija je bitna y =f(x). Ove vrijednosti x I y tačka na krivoj odgovara M 0(x, y). Ako je argument x dati povećanje D x, zatim novu vrijednost argumenta x+D x odgovara novoj funkcijskoj vrijednosti y+ D y = f(x + D x). Odgovarajuća tačka krive će biti tačka M 1(x+D x,y+D y). Ako nacrtate sekantu M 0M 1 i označeno sa j kut formiran transverzalom s pozitivnim smjerom ose Ox, odmah je jasno iz slike da .
Ako sada D x teži nuli, a zatim tački M 1 se kreće duž krivulje, približavajući se tački M 0, i ugao j promjene sa D x. At Dx® 0 ugao j teži određenoj granici a i pravoj liniji koja prolazi kroz tačku M 0 i komponenta s pozitivnim smjerom x-ose, ugao a, bit će željena tangenta. Njen nagib je:
dakle, f´( x) = tga
one. vrijednost derivata f´( x) za datu vrijednost argumenta x jednak je tangentu ugla koji formira tangenta na graf funkcije f(x) u odgovarajućoj tački M 0(x,y) sa pozitivnim smjerom ose Ox.
Diferencijalnost funkcija.
Definicija. Ako je funkcija y = f(x) ima derivaciju u tački x = x 0, tada je funkcija u ovom trenutku diferencibilna.
Kontinuitet funkcije koja ima izvod. Teorema.
Ako je funkcija y = f(x) se može razlikovati u nekom trenutku x = x 0, onda je u ovoj tački kontinuirano.
Dakle, funkcija ne može imati izvod u tačkama diskontinuiteta. Suprotan zaključak je netačan, tj. iz činjenice da je u nekom trenutku x = x 0 funkcija y = f(x) je kontinuirano ne znači da je u ovom trenutku diferencijabilno. Na primjer, funkcija y = |x| kontinuirano za sve x(–Ґ x x = 0 nema izvod. U ovom trenutku nema tangente na graf. Postoje desna i lijeva tangenta, ali se ne poklapaju.
Neke teoreme o diferencijabilnim funkcijama. Teorema o korijenima derivacije (Rolleova teorema). Ako je funkcija f(x) je kontinuiran na segmentu [a,b], diferenciran je u svim unutrašnjim tačkama ovog segmenta i na krajevima x = a I x = b ide na nulu ( f(a) = f(b) = 0), zatim unutar segmenta [ a,b] postoji barem jedna tačka x= With, a c b, u kojem je izvod fў( x) ide na nulu, tj. fў( c) = 0.
Teorema konačnog priraštaja (Lagrangeova teorema). Ako je funkcija f(x) je kontinuiran na intervalu [ a, b] i diferencibilan je u svim unutrašnjim tačkama ovog segmenta, zatim unutar segmenta [ a, b] postoji barem jedna tačka With, a c b to
f(b) – f(a) = fў( c)(b– a).
Teorema o omjeru prirasta dvije funkcije (Cauchyjev teorem). Ako f(x) I g(x) – dvije funkcije kontinuirane na segmentu [a, b] i diferenciran na svim unutrašnjim tačkama ovog segmenta, i gў( x) ne nestaje nigdje unutar ovog segmenta, zatim unutar segmenta [ a, b] postoji takva tačka x = With, a c b to
Derivati raznih redova.
Neka funkcija y =f(x) je diferencibilan na nekom intervalu [ a, b]. Vrijednosti derivata f ў( x), općenito govoreći, zavise od x, tj. derivat f ў( x) je također funkcija x. Prilikom diferenciranja ove funkcije dobijamo takozvani drugi izvod funkcije f(x), što je označeno f ўў ( x).
Derivat n- th red funkcije f(x) se naziva derivat (prvog reda) izvoda n- 1- th i označen je simbolom y(n) = (y(n– 1))ŭ.
Diferencijali raznih redova.
Funkcijski diferencijal y = f(x), Gdje x– nezavisna varijabla, da dy = f ў( x)dx, neke funkcije iz x, ali od x samo prvi faktor može zavisiti f ў( x), drugi faktor ( dx) je prirast nezavisne varijable x i ne zavisi od vrednosti ove varijable. Jer dy postoji funkcija iz x, tada možemo odrediti diferencijal ove funkcije. Diferencijal diferencijala funkcije naziva se drugi diferencijal ili diferencijal drugog reda ove funkcije i označava se d 2y:
d(dx) = d 2y = f ўў( x)(dx) 2 .
Diferencijal n- prvog reda naziva se prvi diferencijal diferencijala n- 1- red:
d n y = d(d n–1y) = f(n)(x)dx(n).
Parcijalni derivat.
Ako funkcija ne zavisi od jednog, već od nekoliko argumenata x i(i varira od 1 do n,i= 1, 2,… n),f(x 1,x 2,… x n), tada se u diferencijalni račun uvodi koncept parcijalnog izvoda, koji karakterizira brzinu promjene funkcije nekoliko varijabli kada se promijeni samo jedan argument, npr. x i. Parcijalni izvod 1. reda u odnosu na x i je definiran kao običan derivat, a pretpostavlja se da su svi argumenti osim x i, zadržati konstantne vrijednosti. Za parcijalne izvode uvodi se notacija
Ovako definisane parcijalne derivacije 1. reda (kao funkcije istih argumenata) mogu, zauzvrat, imati i parcijalne izvode, to su parcijalne derivacije drugog reda, itd. Takvi derivati uzeti iz različitih argumenata nazivaju se mješoviti. Kontinuirane mješovite derivacije istog reda ne zavise od reda diferencijacije i jednake su jedna drugoj.
Anna Chugainova
(\large\bf Derivat funkcije)
Razmotrite funkciju y=f(x), specificirano na intervalu (a, b). Neka x- bilo koja fiksna tačka intervala (a, b), A Δx- proizvoljan broj takav da je vrijednost x+Δx takođe pripada intervalu (a, b). Ovaj broj Δx naziva se povećanjem argumenta.
Definicija. Povećanje funkcije y=f(x) u tački x, što odgovara inkrementu argumenta Δx, pozovimo broj
Δy = f(x+Δx) - f(x).
Vjerujemo u to Δx ≠ 0. Razmotrite u datoj fiksnoj tački x omjer prirasta funkcije u ovoj tački i odgovarajućeg prirasta argumenta Δx
Ovu relaciju ćemo nazvati relacijom razlike. Pošto vrednost x smatramo fiksnim, odnos razlike je funkcija argumenta Δx. Ova funkcija je definirana za sve vrijednosti argumenata Δx, koji pripada nekoj dovoljno maloj okolini tačke Δx=0, osim same tačke Δx=0. Dakle, imamo pravo da razmotrimo pitanje postojanja granice navedene funkcije na Δx → 0.
Definicija. Derivat funkcije y=f(x) na datoj fiksnoj tački x nazvan limit at Δx → 0 odnos razlike, tj
Pod uslovom da ovo ograničenje postoji.
Oznaka. y′(x) ili f′(x).
Geometrijsko značenje derivacije: Derivat funkcije f(x) na ovom mjestu x jednak tangentu ugla između osa Ox i tangenta na graf ove funkcije u odgovarajućoj tački:
f′(x 0) = \tgα.
Mehaničko značenje izvedenice: Derivat putanje u odnosu na vrijeme jednak je brzini pravolinijskog kretanja tačke:
Jednadžba tangente na pravu y=f(x) u tački M 0 (x 0 ,y 0) poprima oblik
y-y 0 = f′(x 0) (x-x 0).
Normala na krivu u nekoj tački je okomita na tangentu u istoj tački. Ako f′(x 0)≠ 0, zatim jednadžba normale na pravu y=f(x) u tački M 0 (x 0 ,y 0) je napisano ovako:

Koncept diferencijabilnosti funkcije
Neka funkcija y=f(x) definisano u određenom intervalu (a, b), x- neka fiksna vrijednost argumenta iz ovog intervala, Δx- bilo koji porast argumenta takav da vrijednost argumenta x+Δx ∈ (a, b).
Definicija. Funkcija y=f(x) naziva se diferencibilnim u datoj tački x, ako se povećava Δy ovu funkciju u tački x, što odgovara inkrementu argumenta Δx, može se predstaviti u obliku
Δy = A Δx +αΔx,
Gdje A- neki broj neovisan od Δx, A α - argument funkcija Δx, što je beskonačno malo na Δx→ 0.
Budući da je proizvod dvije infinitezimalne funkcije αΔx je infinitezimal višeg reda od Δx(svojstvo 3 beskonačno male funkcije), tada možemo napisati:
Δy = A Δx +o(Δx).
Teorema. Da bi funkcija y=f(x) bio diferenciran u datoj tački x, potrebno je i dovoljno da ima konačan izvod u ovoj tački. Gde A=f′(x), to je
Δy = f′(x) Δx +o(Δx).
Operacija pronalaženja derivacije se obično naziva diferencijacijom.
Teorema. Ako je funkcija y=f(x) x, onda je u ovom trenutku kontinuirano.
Komentar. Iz kontinuiteta funkcije y=f(x) na ovom mjestu x, općenito govoreći, diferencijabilnost funkcije ne slijedi f(x) na ovom mjestu. Na primjer, funkcija y=|x|- kontinuirano u jednoj tački x=0, ali nema derivat.
Pojam diferencijalne funkcije
Definicija. Funkcijski diferencijal y=f(x) proizvod derivacije ove funkcije i prirasta nezavisne varijable se poziva x:
dy = y′ Δx, df(x) = f′(x) Δx.
Za funkciju y=x dobijamo dy=dx=x′Δx = 1· Δx= Δx, to je dx=Δx- diferencijal nezavisne varijable jednak je inkrementu ove varijable.
Dakle, možemo pisati
dy = y′ dx, df(x) = f′(x) dx
![]()
Diferencijal dy i prirast Δy funkcije y=f(x) na ovom mjestu x, oba odgovaraju istom prirastu argumenta Δx, generalno govoreći, nisu jednake jedna drugoj.
Geometrijsko značenje diferencijala: Diferencijal funkcije jednak je inkrementu ordinate tangente na graf ove funkcije kada se argument povećava Δx.
Pravila diferencijacije
Teorema. Ako svaka od funkcija u(x) I v(x) diferencibilan u datoj tački x, zatim zbir, razlika, proizvod i količnik ovih funkcija (kvocijent pod uslovom da v(x)≠ 0) su također diferencijabilne u ovom trenutku, a formule vrijede:

Razmotrite složenu funkciju y=f(φ(x))≡ F(x), Gdje y=f(u), u=φ(x). U ovom slučaju u pozvao međuargument, x - nezavisna varijabla.
Teorema. Ako y=f(u) I u=φ(x) su diferencibilne funkcije njihovih argumenata, zatim derivacija kompleksne funkcije y=f(φ(x)) postoji i jednak je proizvodu ove funkcije u odnosu na međuargument i derivaciji međuargumenata u odnosu na nezavisnu varijablu, tj.
![]()
Komentar. Za složenu funkciju koja je superpozicija tri funkcije y=F(f(φ(x))), pravilo diferencijacije ima oblik
y′ x = y′ u u′ v v′ x,
gdje su funkcije v=φ(x), u=f(v) I y=F(u)- diferencibilne funkcije njihovih argumenata.
Teorema. Neka funkcija y=f(x) raste (ili opada) i kontinuirano je u nekom susjedstvu tačke x 0. Neka je, pored toga, ova funkcija diferencibilna u naznačenoj tački x 0 i njegov derivat u ovom trenutku f′(x 0) ≠ 0. Zatim u nekom susjedstvu odgovarajuće tačke y 0 =f(x 0) inverz je definiran za y=f(x) funkcija x=f -1 (y), a naznačena inverzna funkcija je diferencibilna u odgovarajućoj tački y 0 =f(x 0) i za njegov derivat u ovom trenutku y formula je važeća

Tabela derivata

Invarijantnost oblika prvog diferencijala
Razmotrimo diferencijal kompleksne funkcije. Ako y=f(x), x=φ(t)- funkcije njihovih argumenata su diferencibilne, zatim derivacija funkcije y=f(φ(t)) izraženo formulom
y′ t = y′ x x′ t.
A-prioritet dy=y′ t dt, onda dobijamo
dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx,
dy = y′ x dx.
Dakle, dokazali smo
Svojstvo invarijantnosti oblika prvog diferencijala funkcije: kao u slučaju kada je argument x je nezavisna varijabla, au slučaju kada je argument x sama je diferencijabilna funkcija nove varijable, diferencijala dy funkcije y=f(x) jednaka je derivaciji ove funkcije pomnoženoj s diferencijalom argumenta dx.
Primjena diferencijala u aproksimativnim proračunima
Pokazali smo da je diferencijal dy funkcije y=f(x), općenito govoreći, nije jednako priraštaju Δy ovu funkciju. Međutim, do beskonačno male funkcije višeg reda malenosti od Δx, vrijedi približna jednakost
Δy ≈ dy.
Omjer se naziva relativna greška jednakosti ove jednakosti. Jer Δy-dy=o(Δx), tada relativna greška ove jednakosti postaje onoliko mala koliko se želi sa smanjenjem |Δh|.
S obzirom na to Δy=f(x+δ x)-f(x), dy=f′(x)Δx, dobijamo f(x+δ x)-f(x) ≈ f′(x)Δx ili
f(x+δ x) ≈ f(x) + f′(x)Δx.
Ova približna jednakost dopušta s greškom o(Δx) zamijeniti funkciju f(x) u malom kraju tačke x(tj. za male vrijednosti Δx) linearna funkcija argumenta Δx, stoji na desnoj strani.
Derivati višeg reda
Definicija. Drugi izvod (ili izvod drugog reda) funkcije y=f(x) naziva se derivat njegovog prvog izvoda.
Zapis za drugi izvod funkcije y=f(x):
Mehaničko značenje druge izvedenice. Ako je funkcija y=f(x) opisuje zakon kretanja materijalne tačke u pravoj liniji, zatim drugi izvod f″(x) jednako ubrzanju pokretne tačke u trenutku vremena x.
Slično se određuju i treći i četvrti izvod.
Definicija. n th derivat (ili derivat n-ti red) funkcije y=f(x) naziva se derivatom toga n-1 th derivat:
y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′.
Oznake: y″′, y IV, y V itd.
Geometrijsko značenje derivacije
|
DEFINICIJA TANGENTE NA KRIVU Tangenta na krivu y=ƒ(x) u tački M naziva se granični položaj sekante povučene kroz tačku M i tačka uz nju M 1 kriva, pod uslovom da je tačka M 1 približava se neograničeno duž krivulje do tačke M. GEOMETRIJSKO ZNAČENJE DERIVATA Derivat funkcije y=ƒ(x) u tački X 0 je numerički jednako tangentu ugla nagiba prema osi Oh tangenta na krivu y=ƒ(x) u tački M (x 0; ƒ(x 0)). |
Varijacija DOTIC DO KRIVINE Tačkasto na krivini y=ƒ(x) upravo M naziva se granični položaj linije povučene kroz tačku M i sledeća tačka sa njom M 1 krivo, izvan uma, kakva poenta M 1 kriva se neizbežno približava tački M. GEOMETRICAL ZMIST POKHIDNOI Slične funkcije y=ƒ(x) upravo x 0 brojčano jednak tangenti nagiba na os Oh dotic, izveden do krivine y=ƒ(x) upravo M (x 0; ƒ(x 0)). |
Praktično značenje izvedenice
Razmotrimo šta praktično znači veličina koju smo pronašli kao derivaciju određene funkcije.
Kao prvo, derivat- ovo je osnovni koncept diferencijalnog računa, koji karakteriše brzinu promjene funkcije u datoj tački.
Šta je "stopa promjene"? Zamislimo funkciju f(x) = 5. Bez obzira na vrijednost argumenta (x), njegova vrijednost se ni na koji način ne mijenja. Odnosno, stopa njegove promjene je nula.
Sada razmotrite funkciju f(x) = x. Derivat od x je jednak jedan. Zaista, lako je primijetiti da za svaku promjenu argumenta (x) za jedan, vrijednost funkcije također raste za jedan.
Sa stanovišta primljenih informacija, pogledajmo sada tablicu izvoda jednostavnih funkcija. Na osnovu toga, fizičko značenje pronalaženja derivacije funkcije odmah postaje jasno. Ovo razumevanje bi trebalo da olakša rešavanje praktičnih problema.
Prema tome, ako izvod pokazuje brzinu promjene funkcije, onda dvostruki izvod pokazuje ubrzanje.
2080.1947