كلمات معقدةالنطق

614 قطريًا لشكل شبه منحرف مستطيل. أقطار شبه منحرف. خصائص خط موازٍ لقواعد شبه منحرف

مرة أخرى مثلث فيثاغورس :))) إذا تم تعيين قطعة من القطر الكبير من القاعدة الكبيرة إلى نقطة التقاطع x ، فمن التشابه الواضح للمثلثات القائمة الزاوية مع نفس الزوايا ، يتبع ذلك x / 64 = 36 / x ، ومن ثم x = 48 ؛ 48/64 = 3/4 ، وبالتالي فإن جميع المثلثات القائمة الزاوية المكونة من القواعد والأقطار والجانب العمودي على القاعدة تشبه المثلث ذي الأضلاع 3،4،5. الاستثناء الوحيد هو مثلث مكون من قطع قطرية وجانب مائل ، لكننا لسنا مهتمين به :). (لتوضيح ذلك ، التشابه المعني هو مجرد دوال مثلثية أخرى للزوايا :) نحن نعلم بالفعل ظل الزاوية بين القطر الكبير والقاعدة الكبيرة ، وهو 3/4 ، مما يعني أن الجيب هو 3/5 ، وجيب التمام هو 4/5 :)) يمكنك الكتابة على الفور

الإجابات. القاعدة السفلية 80 ستكون 60 ، والقمة ستكون 45. (36 * 5/4 = 45 ، 64 * 5/4 = 80 ، 100 * 3/5 = 60)

مهام مماثلة:

1. قاعدة المنشور مثلث ، طول ضلعه 2 سم ، والاثنان الآخران 3 سم ، وحافة الضلع 4 سم وتصنع زاوية 45 مع مستوى القاعدة. أوجد حافة يساوي مكعب بحجم.

2. قاعدة المنشور المائل هي مثلث متساوي الأضلاع مع الجانب أ ؛ أحد الوجوه الجانبية متعامد مع مستوى القاعدة وهو معين قطري أصغر يساوي c. أوجد حجم المنشور.

3. في المنشور المائل ، القاعدة عبارة عن مثلث قائم الزاوية ، ووتره هو c ، وزاوية واحدة حادة هي 30 ، والحافة الجانبية تساوي k وتصنع زاوية 60 مع مستوى القاعدة. أوجد الحجم من المنشور.

1. أوجد ضلع المربع إذا كان قطره 10 سم

2. في شبه منحرف متساوي الساقين ، تكون الزاوية المنفرجة 135 درجة أقل من القاعدة 4 سم ، والارتفاع 2 سم ، فأوجد مساحة شبه المنحرف؟

3. ارتفاع شبه المنحرف هو 3 أضعاف ارتفاع إحدى القاعدتين ، ولكن نصف حجم الأخرى. أوجد قاعدة شبه المنحرف والارتفاع إذا كانت مساحة شبه المنحرف 168 سم مربع؟

4. في المثلث ABC ، الزاوية A = الزاوية B = 75 درجة. أوجد BC إذا كانت مساحة المثلث 36 سم تربيع.

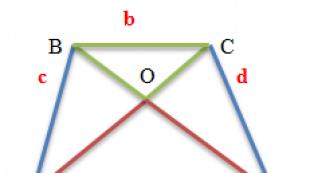
1. في شبه المنحرف ABCD مع الجانبين AB و CD ، تتقاطع الأقطار عند النقطة O

أ) قارن بين مناطق المثلثات ABD و ACD

ب) قارن مساحات المثلثات ABO و CDO

ج) إثبات أن OA * OB = OC * OD

2. تشير قاعدة المثلث متساوي الساقين إلى الضلع الجانبي بالرمز 4: 3 والارتفاع المرسوم على القاعدة هو 30 سم ، أوجد الأجزاء التي يقسم فيها هذا الارتفاع على منصف الزاوية عند القاعدة.

3. خط AM - مماس لدائرة ، ووتر AB لهذه الدائرة. أثبت أن زاوية MAB تقاس بنصف القوس AB الموجود داخل الزاوية MAB.

الجزء الذي يربط بين نقاط المنتصف للأقطار شبه المنحرفة يساوي نصف فرق القاعدة
تتشابه المثلثات المكونة من قواعد شبه المنحرف وأجزاء الأقطار حتى نقطة تقاطعها
تتشكل المثلثات من مقاطع من أقطار شبه منحرف ، تقع جوانبها على الجوانب الجانبية من شبه المنحرف - متساوية (لها نفس المنطقة)
إذا قمت بتمديد الجوانب الجانبية من شبه المنحرف باتجاه القاعدة الأصغر ، فإنها تتقاطع عند نقطة واحدة مع الخط المستقيم الذي يربط بين نقاط المنتصف للقواعد
الجزء الذي يربط بين قواعد شبه منحرف ويمر عبر نقطة تقاطع أقطار شبه منحرف مقسوم على هذه النقطة بنسبة تساوي نسبة أطوال قواعد شبه المنحرف
المقطع الموازي لقواعد شبه المنحرف والمرسوم عبر نقطة تقاطع الأقطار يُقسَّم على هذه النقطة إلى النصف ، وطوله يساوي 2ab / (أ + ب) ، حيث أ و ب هما القاعدتان من شبه منحرف

خصائص القطعة المستقيمة التي تربط بين نقاط المنتصف للأقطار شبه المنحرفة

نقوم بتوصيل نقاط المنتصف لأقطار شبه منحرف ABCD ، ونتيجة لذلك لدينا قطعة LM.
الجزء الذي يربط بين نقاط المنتصف للأقطار شبه المنحرفة ، تقع على خط الوسط شبه المنحرف.

هذا المقطع بالتوازي مع قاعدة شبه منحرف.

طول المقطع الذي يربط بين نقاط المنتصف لأقطار شبه المنحرف يساوي نصف فرق قواعده.

LM = (AD - BC) / 2
أو
LM = (أ-ب) / 2

خواص المثلثات المتكونة من أقطار شبه منحرف

المثلثات التي تتكون من قواعد شبه منحرف ونقطة تقاطع أقطار شبه منحرف - متشابهة.
المثلثات BOC و AOD متشابهة. نظرًا لأن الزاويتين BOC و AOD عموديان ، فإنهما متساويتان.
الزاويتان OCB و OAD هما داخليان بالعرض مع خطوط متوازية AD و BC (قواعد شبه المنحرف متوازية مع بعضها البعض) والخط القاطع AC ، وبالتالي ، فإنهما متساويتان.
زوايا OBC و ODA متساوية لنفس السبب (تقاطع داخلي).

نظرًا لأن الزوايا الثلاث لمثلث واحد تساوي الزوايا المقابلة للمثلث الآخر ، فإن هذه المثلثات متشابهة.

ماذا يتبع من هذا؟

لحل المشكلات في الهندسة ، يتم استخدام تشابه المثلثات على النحو التالي. إذا عرفنا قيم أطوال العنصرين المتناظرين لمثلثين متشابهين ، فسنجد معامل التشابه (نقسم أحدهما على الآخر). من أين ترتبط أطوال جميع العناصر الأخرى ببعضها البعض بنفس القيمة بالضبط.

خصائص المثلثات الموجودة على جانب شبه منحرف وأقطارها

لنفترض وجود مثلثين على الجانبين الجانبيين لشبه المنحرف AB و CD. هذه هي مثلثات AOB و COD. على الرغم من حقيقة أن أحجام الجوانب الفردية لهذه المثلثات قد تكون مختلفة تمامًا ، ولكن مناطق المثلثات التي شكلتها الجوانب ونقطة تقاطع الأقطار شبه المنحرفة هيأي أن المثلثات متساوية في الحجم.

إذا قمت بتمديد جوانب شبه المنحرف باتجاه القاعدة الأصغر ، فستكون نقطة تقاطع الجانبين تتطابق مع خط مستقيم يمر عبر نقاط المنتصف للقواعد.

وبالتالي ، يمكن تمديد أي شبه منحرف إلى مثلث. حيث:

تتشابه المثلثات المكونة من قواعد شبه منحرف مع قمة مشتركة عند تقاطع الجوانب الجانبية الممتدة
الخط المستقيم الذي يربط بين نقاط المنتصف لقواعد شبه المنحرف هو ، في نفس الوقت ، متوسط المثلث المُنشأ

خصائص الخط الذي يربط بين القواعد شبه المنحرفة

إذا قمت برسم مقطع ، تقع نهاياته على قواعد شبه منحرف ، والتي تقع عند نقطة تقاطع أقطار شبه منحرف (KN) ، ثم نسبة الأجزاء المكونة لها من جانب القاعدة إلى نقطة تقاطع الأقطار (KO / ON) ستكون مساوية لنسبة قواعد شبه المنحرف(قبل الميلاد / ميلادي).

KO / ON = BC / AD

هذه الخاصية تأتي من تشابه المثلثات المقابلة (انظر أعلاه).

خصائص خط موازٍ لقواعد شبه منحرف

إذا قمت برسم مقطع موازٍ لقواعد شبه المنحرف وتمر عبر نقطة تقاطع أقطار شبه المنحرف ، فسيكون لها الخصائص التالية:

المسافة المحددة مسبقًا (كم) يقسم نقطة تقاطع الأقطار شبه المنحرفة إلى النصف
طول القطعةالمرور عبر نقطة تقاطع أقطار شبه المنحرف وبالتوازي مع القواعد يساوي KM = 2ab / (أ + ب)

صيغ لإيجاد أقطار شبه منحرف

أ ، ب- قاعدة شبه منحرف

ج ، د- الجوانب الجانبية من شبه منحرف

د 1 د 2- أقطار شبه منحرف

α β - زوايا ذات قاعدة أكبر شبه منحرف

صيغ لإيجاد أقطار شبه منحرف من خلال القواعد والجوانب والزوايا في القاعدة

تعكس المجموعة الأولى من الصيغ (1-3) إحدى الخصائص الرئيسية للأقطار شبه المنحرفة:

1. مجموع مربعات أقطار شبه منحرف يساوي مجموع مربعات الأضلاع زائد ضعف حاصل ضرب قاعدته. يمكن إثبات خاصية أقطار شبه منحرف هذه كنظرية منفصلة

2 ... يتم الحصول على هذه الصيغة عن طريق تحويل الصيغة السابقة. يتم طرح مربع القطر الثاني من خلال علامة التساوي ، وبعد ذلك يتم استخراج الجذر التربيعي من الجانبين الأيسر والأيمن للتعبير.

3 ... هذه الصيغة لإيجاد طول قطري شبه منحرف مماثلة للصيغة السابقة ، مع وجود اختلاف في وجود قطر آخر على الجانب الأيسر من التعبير.

المجموعة التالية من الصيغ (4-5) متشابهة في المعنى وتعبر عن نسبة مماثلة.

مجموعة الصيغ (6-7) تسمح لك بإيجاد قطري شبه المنحرف إذا كانت القاعدة الأكبر لشبه المنحرف ، جانب واحد والزاوية عند القاعدة معروفة.

صيغ لإيجاد أقطار شبه منحرف بدلالة الارتفاع

ملحوظة... يقدم هذا الدرس حلاً للمشكلات الهندسية المتعلقة بأشكال شبه المنحرف. إذا لم تجد حلاً لمشكلة هندسية من النوع الذي تهتم به - اطرح سؤالاً في المنتدى.

مهمة.
يتقاطع أقطار شبه المنحرف ABCD (AD | | BC) عند النقطة O. أوجد طول القاعدة BC لشبه المنحرف إذا كانت القاعدة AD = 24 سم ، وطول AO = 9 سم ، وطول OC = 6 سم.

حل.
حل هذه المشكلة من الناحية الأيديولوجية مطابق تمامًا للمشاكل السابقة.

تتشابه المثلثات AOD و BOC في ثلاث زوايا - AOD و BOC عموديان ، والزوايا الأخرى متساوية في أزواج ، حيث أنها تتكون من تقاطع خط مستقيم واحد وخطين متوازيين.

نظرًا لأن المثلثات متشابهة ، فإن جميع أبعادها الهندسية مرتبطة ببعضها البعض ، كأبعاد هندسية للقطاعات AO و OC المعروفة لنا من بيان المشكلة. هذا هو

AO / OC = AD / BC
9/6 = 24 / ق
BC = 24 * 6/9 = 16

إجابة: 16 سم

مهمة .
في شبه المنحرف ABCD ، من المعروف أن AD = 24 ، BC = 8 ، AC = 13 ، BD = 5√17. أوجد مساحة شبه المنحرف.

حل .
لإيجاد ارتفاع شبه المنحرف من رءوس القاعدة الأصغر B و C ، نخفض ارتفاعين إلى القاعدة الأكبر. نظرًا لأن شبه المنحرف غير متساوٍ ، فإننا نشير إلى الطول AM = a ، والطول KD = b ( لا ينبغي الخلط بينه وبين التدوين في الصيغةإيجاد مساحة شبه منحرف). نظرًا لأن قواعد شبه المنحرف متوازية ، وحذفنا ارتفاعين متعامدين على القاعدة الأكبر ، فإن MBCK هي مستطيل.

وسائل
AD = AM + BC + KD
أ + 8 + ب = 24
أ = 16 - ب

المثلثان DBM و ACK مستطيلان ، لذلك تتشكل زواياهما اليمنى من ارتفاعات شبه منحرف. دعونا نشير إلى ارتفاع شبه المنحرف بمقدار h. ثم حسب نظرية فيثاغورس

H 2 + (24 - a) 2 = (5√17) 2
و
ح 2 + (24 - ب) 2 = 13 2

نأخذ في الاعتبار أن أ = 16 - ب ، ثم في المعادلة الأولى
ح 2 + (24-16 + ب) 2 = 425
ح 2 = 425 - (8 + ب) 2

لنعوض بقيمة مربع الارتفاع في المعادلة الثانية التي حصلت عليها نظرية فيثاغورس. نحن نحصل:
425 - (8 + ب) 2 + (24 - ب) 2 = 169
- (64 + 16 ب + ب) 2 + (24 - ب) 2 = -256
-64 - 16 ب - ب 2 + 576 - 48 ب + ب 2 = -256
-64 ب = -768
ب = 12

لذا دينار كويتي = 12
أين
ح 2 = 425 - (8 + ب) 2 = 425 - (8 + 12) 2 = 25
ح = 5

أوجد مساحة شبه المنحرف من خلال ارتفاعه ونصف مجموع القاعدتين
، حيث a b هي قاعدة شبه المنحرف ، h هي ارتفاع شبه المنحرف
S = (24 + 8) * 5/2 = 80 سم 2

إجابة: مساحة شبه المنحرف 80 سم 2.

إذا كانت الأقطار في شبه منحرف متساوي الساقين متعامدة ، فستكون المادة النظرية التالية مفيدة في حل المشكلة.

1. إذا كانت الأقطار في شبه منحرف متساوي الساقين متعامدة ، فإن ارتفاع شبه المنحرف يساوي نصف مجموع القاعدتين.

ارسم الخط CF الموازي لـ BD عبر النقطة C وامتد الخط AD إلى التقاطع مع CF.

رباعي الزوايا BCFD - متوازي الأضلاع (BC∥ DF كقاعدة شبه منحرف ، BD∥ CF بالبناء). ومن ثم ، CF = BD ، DF = BC و AF = AD + BC.

المثلث ACF مستطيل (إذا كان الخط عموديًا على أحد الخطين المتوازيين ، فإنه يكون عموديًا على الخط الآخر أيضًا). نظرًا لأن الأقطار في شبه منحرف متساوي الساقين متساوية ، و CF = BD ، ثم CF = AC ، أي أن المثلث ACF متساوي الساقين مع قاعدة AF. ومن ثم ، فإن ارتفاع CN لها هو أيضًا الوسيط. وبما أن وسيط المثلث القائم الزاوية المرسوم على الوتر يساوي نصفه ، إذن

والتي يمكن كتابتها بشكل عام كـ

حيث h هو ارتفاع شبه المنحرف ، و a و b هما قاعدته.

2. إذا كانت الأقطار في شبه منحرف متساوي الساقين متعامدة ، فإن ارتفاعها يساوي خط الوسط.

بما أن الخط الأوسط من شبه المنحرف m يساوي نصف مجموع القواعد ، إذن

3. إذا كانت الأقطار في شبه منحرف متساوي الساقين متعامدة ، فإن مساحة شبه المنحرف تساوي مربع ارتفاع شبه المنحرف (أو مربع نصف مجموع القاعدتين ، أو مربع خط الوسط ).

نظرًا لأن مساحة شبه المنحرف تم العثور عليها بواسطة الصيغة

والارتفاع ونصف مجموع القواعد والخط الأوسط لشبه منحرف متساوي الساقين بأقطار متعامدة متساوية مع بعضها البعض:

4. إذا كانت الأقطار في شبه منحرف متساوي الساقين متعامدة ، فإن مربع قطرها يساوي نصف مربع مجموع القواعد ، بالإضافة إلى ضعف مربع الارتفاع ومربع خط الوسط.

نظرًا لأن مساحة الشكل الرباعي المحدب يمكن العثور عليها من خلال أقطارها والزاوية بينهما بواسطة الصيغة