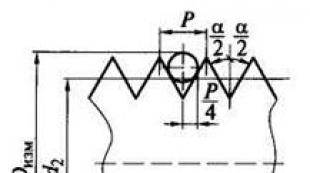
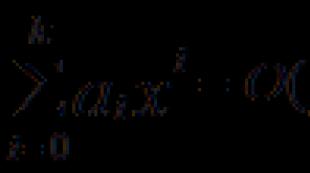ទ្រឹស្តីបទដ៏ធំរបស់កសិដ្ឋាន។ យើងលាតត្រដាង! ទ្រឹស្តីបទចុងក្រោយរបស់ Fermat បានបង្ហាញឱ្យឃើញ? តើទ្រឹស្តីបទកសិដ្ឋានស្តាប់ទៅដូចអ្វី?

Pierre de Fermat អាន "នព្វន្ធ" របស់ Diophantus នៃ Alexandria និងឆ្លុះបញ្ចាំងពីបញ្ហារបស់វា មានទម្លាប់សរសេរលទ្ធផលនៃការឆ្លុះបញ្ចាំងរបស់គាត់ក្នុងទម្រង់នៃការកត់សម្គាល់ខ្លីៗនៅក្នុងគែមនៃសៀវភៅ។ ប្រឆាំងនឹងបញ្ហាទីប្រាំបីនៃ Diophantus នៅក្នុងគែមនៃសៀវភៅ Fermat បានសរសេរថា: " ផ្ទុយទៅវិញ វាមិនអាចទៅរួចទេក្នុងការបំប្លែងគូបមួយទៅជាគូបពីរ ឬពីរការ៉េទៅជាពីរការ៉េ ហើយជាទូទៅគ្មានដឺក្រេធំជាងការេទៅជាថាមពលពីរដែលមាននិទស្សន្តដូចគ្នា។ ខ្ញុំបានរកឃើញភស្តុតាងដ៏អស្ចារ្យនៃរឿងនេះ ប៉ុន្តែរឹមទាំងនេះតូចចង្អៀតពេកសម្រាប់វា។» / E.T.Bell "អ្នកបង្កើតគណិតវិទ្យា"។ M., 1979, p.69/. ខ្ញុំសូមនាំមកជូនលោកអ្នកនូវភស្តុតាងបឋមនៃទ្រឹស្តីបទកសិដ្ឋាន ដែលអាចយល់បានដោយសិស្សវិទ្យាល័យណាមួយដែលចូលចិត្តគណិតវិទ្យា។

ចូរយើងប្រៀបធៀបការអត្ថាធិប្បាយរបស់ Fermat លើបញ្ហា Diophantine ជាមួយនឹងទម្រង់ទំនើបនៃទ្រឹស្តីបទដ៏អស្ចារ្យរបស់ Fermat ដែលមានទម្រង់សមីការ។
« សមីការ

x n + y n = z n(ដែល n ជាចំនួនគត់ធំជាងពីរ)

មិនមានដំណោះស្រាយក្នុងចំនួនគត់វិជ្ជមានទេ។»

សេចក្តីអធិប្បាយគឺនៅក្នុងការតភ្ជាប់ឡូជីខលជាមួយកិច្ចការ ស្រដៀងទៅនឹងការភ្ជាប់តក្កវិជ្ជានៃ predicate ជាមួយប្រធានបទ។ អ្វីដែលត្រូវបានបញ្ជាក់ដោយបញ្ហានៃ Diophantus ផ្ទុយទៅវិញត្រូវបានបញ្ជាក់ដោយការអត្ថាធិប្បាយរបស់ Fermat ។

ការអត្ថាធិប្បាយរបស់ Fermat អាចត្រូវបានបកស្រាយដូចខាងក្រោមៈ ប្រសិនបើសមីការបួនជ្រុងជាមួយចំនួនមិនស្គាល់ចំនួនបីមានដំណោះស្រាយគ្មានកំណត់លើសំណុំនៃចំនួនបីដងនៃលេខពីតាហ្គោរ នោះ ផ្ទុយទៅវិញ សមីការដែលមានចំនួនមិនស្គាល់ចំនួនបីក្នុងដឺក្រេធំជាងការេ។

មិនមានសូម្បីតែតម្រុយនៃការតភ្ជាប់របស់វាជាមួយបញ្ហា Diophantine នៅក្នុងសមីការ។ ការ​អះអាង​របស់​គាត់​ទាមទារ​ភស្តុតាង ប៉ុន្តែ​វា​មិន​មាន​លក្ខខណ្ឌ​ដែល​វា​ធ្វើ​តាម​ថា​វា​គ្មាន​ដំណោះស្រាយ​ក្នុង​ចំនួន​គត់​វិជ្ជមាន។

វ៉ារ្យ៉ង់នៃភស្តុតាងនៃសមីការដែលស្គាល់ចំពោះខ្ញុំត្រូវបានកាត់បន្ថយទៅជាក្បួនដោះស្រាយខាងក្រោម។

1. សមីការនៃទ្រឹស្តីបទរបស់ Fermat ត្រូវបានគេយកជាការសន្និដ្ឋានរបស់វា សុពលភាពដែលត្រូវបានផ្ទៀងផ្ទាត់ដោយមានជំនួយពីភស្តុតាង។
2. សមីការដូចគ្នាត្រូវបានគេហៅថា ដំបូងសមីការដែលភស្តុតាងរបស់វាត្រូវតែដំណើរការ។

លទ្ធផល​គឺ​ជា​ការ​បង្រៀន​ភាសា​វិទ្យា​មួយ​: ប្រសិនបើសមីការមិនមានដំណោះស្រាយក្នុងចំនួនគត់វិជ្ជមានទេ នោះវាគ្មានដំណោះស្រាយក្នុងចំនួនគត់វិជ្ជមានទេ។ភស្ដុតាង​នៃ​តិះដៀល​គឺ​ច្បាស់​ជា​ខុស ហើយ​គ្មាន​ន័យ​អ្វី​ឡើយ។ ប៉ុន្តែវាត្រូវបានបង្ហាញដោយភាពផ្ទុយគ្នា។

• ការសន្មត់មួយត្រូវបានធ្វើឡើងដែលផ្ទុយពីអ្វីដែលបានបញ្ជាក់ដោយសមីការដែលត្រូវបង្ហាញ។ វាមិនគួរផ្ទុយនឹងសមីការដើមឡើយ ប៉ុន្តែវាកើតឡើង។ ដើម្បីបញ្ជាក់នូវអ្វីដែលទទួលយកដោយគ្មានភស្តុតាង និងទទួលយកដោយគ្មានភស្តុតាង នូវអ្វីដែលតម្រូវឱ្យបង្ហាញនោះ វាគ្មានន័យទេ។
• ដោយផ្អែកលើការសន្មត់ដែលបានទទួលយក ប្រតិបត្តិការ និងសកម្មភាពគណិតវិទ្យាត្រឹមត្រូវពិតប្រាកដត្រូវបានអនុវត្ត ដើម្បីបញ្ជាក់ថាវាផ្ទុយនឹងសមីការដើម ហើយមិនពិត។

ដូច្នេះហើយ អស់រយៈពេល 370 ឆ្នាំមកនេះ ភស្តុតាងនៃសមីការនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat នៅតែជាសុបិនដែលមិនអាចទៅរួចរបស់អ្នកឯកទេស និងអ្នកដែលស្រឡាញ់គណិតវិទ្យា។

ខ្ញុំបានយកសមីការជាការសន្និដ្ឋាននៃទ្រឹស្តីបទ ហើយបញ្ហាទីប្រាំបីនៃ Diophantus និងសមីការរបស់វាជាលក្ខខណ្ឌនៃទ្រឹស្តីបទ។

"ប្រសិនបើសមីការ x 2 + y 2 = z 2 (1) មានសំណុំនៃដំណោះស្រាយគ្មានកំណត់លើសំណុំនៃចំនួនបីដងនៃលេខ Pythagorean បន្ទាប់មក ផ្ទុយទៅវិញសមីការ x n + y n = z n កន្លែងណា n > ២ (2) មិនមានដំណោះស្រាយលើសំណុំនៃចំនួនគត់វិជ្ជមានទេ។"

ភស្តុតាង។

ក)មនុស្សគ្រប់គ្នាដឹងថាសមីការ (1) មានដំណោះស្រាយគ្មានកំណត់លើសំណុំនៃចំនួនបីដងនៃលេខពីតាហ្គោរ។ ចូរយើងបញ្ជាក់ថា គ្មានលេខបីនៃ Pythagorean ដែលជាដំណោះស្រាយចំពោះសមីការ (1) គឺជាដំណោះស្រាយចំពោះសមីការ (2) នោះទេ។

ដោយផ្អែកលើច្បាប់នៃភាពបញ្ច្រាសនៃសមភាព ភាគីនៃសមីការ (1) ត្រូវបានផ្លាស់ប្តូរគ្នា។ លេខ Pythagorean (z, x, y) អាច​ត្រូវ​បាន​បកស្រាយ​ថា​ជា​ប្រវែង​នៃ​ជ្រុង​នៃ​ត្រីកោណ​កែង​មួយ និង​ការ​ការ៉េ (x2, y2, z2) អាច​ត្រូវ​បាន​បកស្រាយ​ថា​ជា​តំបន់​នៃ​ការេ​ដែល​បាន​សាងសង់​នៅ​លើ​អ៊ីប៉ូតេនុស និង​ជើង​របស់​វា​។

យើងគុណការេនៃសមីការ (1) ដោយកម្ពស់បំពាន ម៉ោង :

z 2 h = x 2 h + y 2 h (3)

សមីការ (3) អាច​ត្រូវ​បាន​បកស្រាយ​ថា​ជា​សមភាព​នៃ​បរិមាណ​នៃ​ប៉ារ៉ាឡែល​ភីព​ទៅ​ជា​ផលបូក​នៃ​បរិមាណ​នៃ​ប៉ារ៉ាឡែល​ពីរ។

សូមឱ្យកម្ពស់នៃ parallelepipeds បី h = z :

z 3 = x 2 z + y 2 z (4)

បរិមាណនៃគូបត្រូវបាន decomposed ជាពីរភាគនៃ parallelepipeds ពីរ។ យើងទុកបរិមាណគូបមិនផ្លាស់ប្តូរ ហើយកាត់បន្ថយកម្ពស់នៃ parallelepiped ដំបូងទៅ x ហើយកម្ពស់នៃ parallelepiped ទីពីរនឹងត្រូវបានកាត់បន្ថយទៅ y . បរិមាណគូបធំជាងផលបូកនៃបរិមាណគូបពីរ៖

z 3 > x 3 + y 3 (5)

នៅលើសំណុំនៃចំនួនបីដងនៃលេខ Pythagorean ( x, y, z ) នៅ n=3 មិនអាចមានដំណោះស្រាយចំពោះសមីការ (២) ទេ។ ដូច្នេះហើយ នៅលើសំណុំនៃចំនួនបីដងនៃលេខ Pythagorean វាមិនអាចទៅរួចទេក្នុងការបំបែកគូបមួយទៅជាគូបពីរ។

អនុញ្ញាតឱ្យនៅក្នុងសមីការ (3) កម្ពស់នៃ parallelepipeds បី h = z2 :

z 2 z 2 = x 2 z 2 + y 2 z 2 (6)

បរិមាណនៃ parallelepiped ត្រូវបាន decomposed ទៅជាផលបូកនៃបរិមាណនៃ parallelepipeds ពីរ។
យើងទុកផ្នែកខាងឆ្វេងនៃសមីការ (6) មិនផ្លាស់ប្តូរ។ នៅផ្នែកខាងស្តាំរបស់វាមានកម្ពស់ z2 កាត់បន្ថយទៅ X នៅក្នុងពាក្យដំបូងនិងរហូតដល់ នៅ 2 នៅក្នុងអាណត្តិទីពីរ។

សមីការ (៦) ប្រែទៅជាវិសមភាព៖

បរិមាណនៃ parallelepiped ត្រូវបាន decomposed ជាពីរភាគនៃ parallelepipeds ពីរ។

យើងទុកផ្នែកខាងឆ្វេងនៃសមីការ (8) មិនផ្លាស់ប្តូរ។
នៅផ្នែកខាងស្តាំនៃកម្ពស់ zn-2 កាត់បន្ថយទៅ xn-2 នៅក្នុងពាក្យដំបូងនិងកាត់បន្ថយ y n-2 នៅក្នុងអាណត្តិទីពីរ។ សមីការ (៨) ប្រែទៅជាវិសមភាព៖

z n > x n + y n

(9)

នៅលើសំណុំនៃចំនួនបីដងនៃ Pythagorean មិនអាចមានដំណោះស្រាយតែមួយនៃសមីការ (2) ទេ។

អាស្រ័យហេតុនេះ លើសំណុំនៃចំនួនបីដងនៃលេខ Pythagorean សម្រាប់ទាំងអស់គ្នា n > ២ សមីការ (២) មិនមានដំណោះស្រាយទេ។

ទទួលបាន "ភស្តុតាងក្រោយអព្ភូតហេតុ" ប៉ុន្តែសម្រាប់តែបីដងប៉ុណ្ណោះ។ លេខ Pythagorean. នេះ​គឺជា កង្វះភស្តុតាងនិងហេតុផលសម្រាប់ការបដិសេធ P. Fermat ពីគាត់។

ខ)អនុញ្ញាតឱ្យយើងបង្ហាញថាសមីការ (2) មិនមានដំណោះស្រាយលើសំណុំនៃចំនួនបីដងនៃលេខដែលមិនមែនជាពីថាហ្គោរ ដែលជាក្រុមនៃចំនួនបីដងនៃលេខពីតាហ្កោរដែលយកតាមអំពើចិត្ត។ z=13, x=12, y=5 និងក្រុមគ្រួសារនៃចំនួនគត់វិជ្ជមានបីដង z=21, x=19, y=16

ទាំងបីនៃចំនួនបីគឺជាសមាជិកនៃគ្រួសាររបស់ពួកគេ:

	(13, 12, 12); (13, 12,11);…; (13, 12, 5) ;…; (13,7, 1);…; (13,1, 1)	(10)
	(21, 20, 20); (21, 20, 19);…;(21, 19, 16);…;(21, 1, 1)	(11)

ចំនួនសមាជិកនៃគ្រួសារ (10) និង (11) គឺស្មើនឹងពាក់កណ្តាលនៃផលិតផល 13 គុណនឹង 12 និង 21 ដោយ 20 ពោលគឺ 78 និង 210។

សមាជិកនីមួយៗនៃគ្រួសារ (10) មាន z = ១៣ និងអថេរ X និង នៅ 13 > x > 0 , 13 > y > 0 1

សមាជិកនីមួយៗនៃគ្រួសារ (11) មាន z = ២១ និងអថេរ X និង នៅ ដែលយកតម្លៃចំនួនគត់ 21 > x > 0 , 21 > y > 0 . អថេរថយចុះជាលំដាប់ដោយ 1 .

បីដងនៃលេខនៃលំដាប់ (10) និង (11) អាចត្រូវបានតំណាងជាលំដាប់នៃវិសមភាពនៃសញ្ញាបត្រទីបី៖

	13 3 < 12 3 + 12 3 ;13 3 < 12 3 + 11 3 ;…; 13 3 < 12 3 + 8 3 ; 13 3 > 12 3 + 7 3 ;…; 13 3 > 1 3 + 1 3
	21 3 < 20 3 + 20 3 ; 21 3 < 20 3 + 19 3 ; …; 21 3 < 19 3 + 14 3 ; 21 3 > 19 3 + 13 3 ;…; 21 3 > 1 3 + 1 3

និងក្នុងទម្រង់នៃវិសមភាពនៃសញ្ញាបត្រទីបួន៖

	13 4 < 12 4 + 12 4 ;…; 13 4 < 12 4 + 10 4 ; 13 4 > 12 4 + 9 4 ;…; 13 4 > 1 4 + 1 4
	21 4 < 20 4 + 20 4 ; 21 4 < 20 4 + 19 4 ; …; 21 4 < 19 4 + 16 4 ;…; 21 4 > 1 4 + 1 4

ភាពត្រឹមត្រូវនៃវិសមភាពនីមួយៗត្រូវបានផ្ទៀងផ្ទាត់ដោយការបង្កើនចំនួនដល់អំណាចទីបី និងទីបួន។

គូប​នៃ​ចំនួន​ធំ​ជាង​នេះ​មិន​អាច​ត្រូវ​បាន​បំបែក​ជា​ពីរ​គូប​នៃ​ចំនួន​តូច​ជាង​។ វាគឺតិចជាង ឬធំជាងផលបូកនៃគូបនៃចំនួនតូចជាងទាំងពីរ។

bi-square នៃចំនួនធំជាងមិនអាចបំបែកទៅជា bi-squares នៃចំនួនតូចជាងនោះទេ។ វាគឺតិចជាង ឬធំជាងផលបូកនៃទ្វេការេនៃចំនួនតូចជាង។

នៅពេលដែលនិទស្សន្តកើនឡើង វិសមភាពទាំងអស់ លើកលែងតែវិសមភាពខាងឆ្វេងបំផុត មានអត្ថន័យដូចគ្នា៖

វិសមភាព ពួកគេទាំងអស់មានអត្ថន័យដូចគ្នា៖ កម្រិតនៃចំនួនធំគឺធំជាងផលបូកនៃដឺក្រេនៃចំនួនតូចជាងពីរដែលមាននិទស្សន្តដូចគ្នា៖

	13n> 12n + 12n ; 13n > 12n + 11n ;…; 13n > 7n + 4n ;…; 13n > 1n + 1n	(12)
	21n> 20n + 20n ; 21n > 20n + 19n ;…; ;…; 21n > 1n + 1n	(13)

ពាក្យខាងឆ្វេងបំផុតនៃលំដាប់ (12) (13) គឺជាវិសមភាពខ្សោយបំផុត។ ភាពត្រឹមត្រូវរបស់វាកំណត់ភាពត្រឹមត្រូវនៃវិសមភាពជាបន្តបន្ទាប់ទាំងអស់នៃលំដាប់ (12) សម្រាប់ ន > ៨ និងលំដាប់ (១៣) សម្រាប់ ន > ១៤ .

មិនអាចមានសមភាពក្នុងចំណោមពួកគេទេ។ គុណលក្ខណៈបីនៃចំនួនគត់វិជ្ជមាន (21,19,16) មិនមែនជាដំណោះស្រាយចំពោះសមីការ (2) នៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat នោះទេ។ ប្រសិនបើចំនួនគត់វិជ្ជមានបីដងដោយបំពានមិនមែនជាដំណោះស្រាយចំពោះសមីការទេ នោះសមីការមិនមានដំណោះស្រាយលើសំណុំនៃចំនួនគត់វិជ្ជមាន ដែលត្រូវបង្ហាញ។

ជាមួយ)ការអត្ថាធិប្បាយរបស់ Fermat លើបញ្ហា Diophantus ចែងថាវាមិនអាចទៅរួចទេក្នុងការរលួយ។ ជាទូទៅ គ្មានអំណាចធំជាងការ៉េទេ អំណាចពីរដែលមាននិទស្សន្តដូចគ្នា។».

ថើបថាមពលធំជាងការ៉េពិតជាមិនអាចបំបែកទៅជាថាមពលពីរដែលមាននិទស្សន្តដូចគ្នា។ ខ្ញុំមិនថើបទេ។ថាមពលធំជាងការ៉េអាចបំបែកទៅជាថាមពលពីរដែលមាននិទស្សន្តដូចគ្នា។

ណាមួយដែលបានជ្រើសរើសដោយចៃដន្យចំនួនបីនៃចំនួនគត់វិជ្ជមាន (z, x, y) អាច​ជា​របស់​គ្រួសារ​មួយ ដែល​សមាជិក​នីមួយៗ​មាន​ចំនួន​ថេរ z និងលេខពីរតិចជាង z . សមាជិកនីមួយៗនៃគ្រួសារអាចត្រូវបានតំណាងក្នុងទម្រង់នៃវិសមភាព ហើយវិសមភាពលទ្ធផលទាំងអស់អាចត្រូវបានតំណាងជាលំដាប់នៃវិសមភាពមួយ៖

z n< (z — 1) n + (z — 1) n ; z n < (z — 1) n + (z — 2) n ; …; z n >1n + 1n

(14)

លំដាប់នៃវិសមភាព (14) ចាប់ផ្តើមដោយវិសមភាពដែលផ្នែកខាងឆ្វេងមានតិចជាង ផ្នែក​ខាងស្តាំប៉ុន្តែបញ្ចប់ដោយវិសមភាពដែលផ្នែកខាងស្តាំតិចជាងផ្នែកខាងឆ្វេង។ ជាមួយនឹងការកើនឡើងនិទស្សន្ត n > ២ ចំនួនវិសមភាពនៅខាងស្តាំនៃលំដាប់ (14) កើនឡើង។ ជាមួយនឹងនិទស្សន្ត n=k វិសមភាពទាំងអស់នៃផ្នែកខាងឆ្វេងនៃលំដាប់ផ្លាស់ប្តូរអត្ថន័យរបស់វាហើយទទួលយកអត្ថន័យនៃវិសមភាពនៃផ្នែកខាងស្តាំនៃវិសមភាពនៃលំដាប់ (14) ។ ជាលទ្ធផលនៃការកើនឡើងនៃនិទស្សន្តនៃវិសមភាពទាំងអស់ ផ្នែកខាងឆ្វេងគឺធំជាងផ្នែកខាងស្តាំ៖

z k > (z-1) k + (z-1) k ; z k > (z-1) k + (z-2) k ;… ; zk > 2k + 1k ; zk > 1k + 1k

(15)

ជាមួយនឹងការកើនឡើងបន្ថែមទៀតនៅក្នុងនិទស្សន្ត n>k គ្មានវិសមភាពណាមួយផ្លាស់ប្តូរអត្ថន័យរបស់វា ហើយមិនប្រែទៅជាសមភាពនោះទេ។ នៅលើមូលដ្ឋាននេះ វាអាចត្រូវបានអះអាងថា ណាមួយដែលយកចំនួនបីនៃចំនួនគត់វិជ្ជមានតាមអំពើចិត្ត។ (z, x, y) នៅ n > ២ , z > x , z > y

ក្នុង​ចំនួន​បី​តាម​អំពើ​ចិត្ត​នៃ​ចំនួន​គត់​វិជ្ជមាន z អាចជាចំនួនធម្មជាតិដ៏ធំតាមអំពើចិត្ត។ សម្រាប់​ទាំងអស់ លេខធម្មជាតិដែលមិនមានទៀតទេ z ទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ត្រូវបានបញ្ជាក់។

ឃ)មិនថាលេខធំប៉ុនណាទេ។ z នៅក្នុងស៊េរីធម្មជាតិនៃចំនួនមុនវាមានចំនួនគត់ធំ ប៉ុន្តែមានកំណត់ ហើយបន្ទាប់ពីវាមានចំនួនគត់គ្មានកំណត់។

ចូរ​យើង​បង្ហាញ​ថា​សំណុំ​គ្មាន​កំណត់​ទាំងមូល​នៃ​ចំនួន​ធម្មជាតិ​ធំ​ជាង z បង្កើតជាបីដងនៃចំនួនដែលមិនមែនជាដំណោះស្រាយចំពោះសមីការនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ឧទាហរណ៍ បីដងតាមអំពើចិត្តនៃចំនួនគត់វិជ្ជមាន (z+1,x,y) , ម្ល៉ោះ z + 1 > x និង z + 1 > y សម្រាប់តម្លៃទាំងអស់នៃនិទស្សន្ត n > ២ មិនមែនជាដំណោះស្រាយចំពោះសមីការនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat នោះទេ។

ចំនួនគត់វិជ្ជមានដែលបានជ្រើសរើសដោយចៃដន្យ (z + 1, x, y) អាច​ជា​ក្រុម​គ្រួសារ​នៃ​ចំនួន​បី​ដង ដែល​សមាជិក​នីមួយៗ​មាន​ចំនួន​ថេរ z + 1 និងលេខពីរ X និង នៅ យកតម្លៃខុសគ្នា តូចជាង z + 1 . សមាជិកគ្រួសារអាចត្រូវបានតំណាងថាជាវិសមភាពដែលផ្នែកខាងឆ្វេងថេរគឺតិចជាង ឬធំជាងផ្នែកខាងស្តាំ។ វិសមភាពអាចត្រូវបានរៀបចំតាមលំដាប់លំដោយនៃវិសមភាព៖

ជាមួយនឹងការកើនឡើងបន្ថែមទៀតនៅក្នុងនិទស្សន្ត n>k ដល់ភាពគ្មានទីបញ្ចប់ គ្មានវិសមភាពនៅក្នុងលំដាប់ (17) ផ្លាស់ប្តូរអត្ថន័យរបស់វា ហើយមិនក្លាយជាសមភាពទេ។ នៅក្នុងលំដាប់ (16) វិសមភាពដែលកើតចេញពីចំនួនគត់វិជ្ជមានបីដងដែលយកតាមអំពើចិត្ត (z + 1, x, y) , អាចនៅក្នុងផ្នែកខាងស្តាំរបស់វានៅក្នុងទម្រង់ (z + 1) n > x n + y n ឬនៅខាងឆ្វេងរបស់វាក្នុងទម្រង់ (z+1)n< x n + y n .

ក្នុងករណីណាក៏ដោយ បីដងនៃចំនួនគត់វិជ្ជមាន (z + 1, x, y) នៅ n > ២ , z + 1 > x , z + 1 > y នៅក្នុងលំដាប់ (16) គឺជាវិសមភាព ហើយមិនអាចជាសមភាពបានទេ ពោលគឺវាមិនអាចជាដំណោះស្រាយចំពោះសមីការនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat នោះទេ។

វាងាយស្រួលនិងសាមញ្ញក្នុងការយល់ពីប្រភពដើមនៃលំដាប់នៃវិសមភាពអំណាច (16) ដែលវិសមភាពចុងក្រោយនៃផ្នែកខាងឆ្វេងនិងវិសមភាពទីមួយនៃផ្នែកខាងស្តាំគឺជាវិសមភាពនៃន័យផ្ទុយ។ ផ្ទុយទៅវិញ វាមិនមែនជាការងាយស្រួល និងពិបាកសម្រាប់សិស្សសាលា សិស្សវិទ្យាល័យ និងសិស្សវិទ្យាល័យ ក្នុងការយល់ដឹងពីរបៀបដែលលំដាប់នៃវិសមភាព (17) ត្រូវបានបង្កើតឡើងពីលំដាប់នៃវិសមភាព (16) ដែលវិសមភាពទាំងអស់មានអត្ថន័យដូចគ្នា។

នៅក្នុងលំដាប់ (16) ការបង្កើនកម្រិតចំនួនគត់នៃវិសមភាពដោយ 1 ប្រែវិសមភាពចុងក្រោយនៅផ្នែកខាងឆ្វេងទៅជាវិសមភាពទីមួយនៃអត្ថន័យផ្ទុយនៅខាងស្តាំ។ ដូច្នេះចំនួនវិសមភាពនៅផ្នែកទីប្រាំបួននៃលំដាប់មានការថយចុះ ខណៈដែលចំនួនវិសមភាពនៅផ្នែកខាងស្តាំកើនឡើង។ រវាងវិសមភាពអំណាចចុងក្រោយ និងទីមួយនៃអត្ថន័យផ្ទុយគ្នា វាមានសមភាពអំណាចមួយដោយគ្មានបរាជ័យ។ សញ្ញាបត្ររបស់វាមិនអាចជាចំនួនគត់បានទេ ព្រោះមានតែលេខដែលមិនមែនជាចំនួនគត់រវាងលេខធម្មជាតិពីរជាប់គ្នា។ សមភាពថាមពលនៃដឺក្រេដែលមិនមែនជាចំនួនគត់ យោងទៅតាមលក្ខខណ្ឌនៃទ្រឹស្តីបទ មិនអាចចាត់ទុកថាជាដំណោះស្រាយចំពោះសមីការ (1) បានទេ។

ប្រសិនបើនៅក្នុងលំដាប់ (16) យើងបន្តបង្កើនដឺក្រេដោយ 1 ឯកតា នោះវិសមភាពចុងក្រោយនៃផ្នែកខាងឆ្វេងរបស់វានឹងប្រែទៅជាវិសមភាពដំបូងនៃអត្ថន័យផ្ទុយនៃផ្នែកខាងស្តាំ។ ជាលទ្ធផលនឹងមិនមានវិសមភាពនៅផ្នែកខាងឆ្វេងនិងវិសមភាពតែផ្នែកខាងស្តាំប៉ុណ្ណោះដែលនឹងជាលំដាប់នៃការបង្កើនវិសមភាពអំណាច (17) ។ ការកើនឡើងបន្ថែមទៀតនៃដឺក្រេចំនួនគត់របស់ពួកគេដោយ 1 ឯកតាគ្រាន់តែពង្រឹងវិសមភាពថាមពលរបស់វាប៉ុណ្ណោះ ហើយមិនរាប់បញ្ចូលជាក្រុមនូវលទ្ធភាពនៃសមភាពក្នុងដឺក្រេចំនួនគត់។

ដូច្នេះ ជាទូទៅ គ្មានអំណាចចំនួនគត់នៃចំនួនធម្មជាតិ (z+1) នៃលំដាប់នៃវិសមភាពអំណាច (17) អាចត្រូវបានបំបែកទៅជាចំនួនគត់ពីរដែលមាននិទស្សន្តដូចគ្នា។ ដូច្នេះ សមីការ (1) មិនមានដំណោះស្រាយលើសំណុំនៃចំនួនធម្មជាតិគ្មានកំណត់ ដែលត្រូវបញ្ជាក់។

ដូច្នេះទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ត្រូវបានបញ្ជាក់ជាទូទៅទាំងអស់៖

• នៅក្នុងផ្នែក A) សម្រាប់កូនបីទាំងអស់។ (z, x, y) លេខ Pythagorean (ការរកឃើញរបស់ Fermat គឺជាភស្តុតាងអព្ភូតហេតុពិត)
• នៅក្នុងផ្នែក C) សម្រាប់សមាជិកទាំងអស់នៃគ្រួសារនៃបីដង (z, x, y) លេខ pythagorean,
• នៅក្នុងផ្នែក C) សម្រាប់លេខបីទាំងអស់។ (z, x, y) មិនមែនលេខធំទេ។ z
• នៅក្នុងផ្នែក D) សម្រាប់លេខបី (z, x, y) ស៊េរីលេខធម្មជាតិ។

ការផ្លាស់ប្តូរត្រូវបានធ្វើឡើងនៅថ្ងៃទី 05.09.2010

ទ្រឹស្ដីមួយណាដែលអាចនិងមិនអាចបញ្ជាក់បានដោយការផ្ទុយ

វចនានុក្រមពន្យល់នៃលក្ខខណ្ឌគណិតវិទ្យាកំណត់ភស្តុតាងដោយការផ្ទុយនៃទ្រឹស្តីបទដែលផ្ទុយទៅនឹងទ្រឹស្តីបទបញ្ច្រាស។

“ការបញ្ជាក់ដោយភាពផ្ទុយគ្នា គឺជាវិធីសាស្រ្តនៃការបញ្ជាក់ទ្រឹស្តីបទ (ប្រយោគ) ដែលមាននៅក្នុងការបញ្ជាក់មិនមែនជាទ្រឹស្តីបទរបស់វានោះទេ ប៉ុន្តែទ្រឹស្តីបទដែលស្មើនឹង (សមមូល) ទ្រឹស្ដីបញ្ច្រាស (បញ្ច្រាសទៅផ្ទុយ) ។ ភស្តុតាងដោយភាពផ្ទុយគ្នាត្រូវបានប្រើនៅពេលណាដែលទ្រឹស្តីបទផ្ទាល់ពិបាកបញ្ជាក់ ប៉ុន្តែការបញ្ច្រាសផ្ទុយគឺងាយស្រួលជាង។ នៅពេលបញ្ជាក់ដោយភាពផ្ទុយគ្នា ការសន្និដ្ឋាននៃទ្រឹស្តីបទត្រូវបានជំនួសដោយការបដិសេធរបស់វា ហើយដោយការវែកញែកមួយមកដល់ការបដិសេធនៃលក្ខខណ្ឌ ពោលគឺឧ។ ទៅភាពផ្ទុយគ្នា ផ្ទុយពីអ្វីដែលត្រូវបានផ្តល់ឱ្យ ការកាត់បន្ថយភាពមិនសមហេតុផលនេះ បង្ហាញទ្រឹស្តីបទ។

ភ័ស្តុតាងដោយភាពផ្ទុយគ្នាត្រូវបានគេប្រើជាញឹកញាប់នៅក្នុងគណិតវិទ្យា។ ភ័ស្តុតាងដោយភាពផ្ទុយគ្នាគឺផ្អែកលើច្បាប់នៃមជ្ឈិមដែលដកចេញដែលមាននៅក្នុងការពិតនៃសេចក្តីថ្លែងការណ៍ពីរ (សេចក្តីថ្លែងការណ៍) A និង A (ការបដិសេធរបស់ A) មួយក្នុងចំណោមពួកគេគឺពិតនិងមួយទៀតមិនពិត។/ វចនានុក្រមពន្យល់នៃពាក្យគណិតវិទ្យា៖ មគ្គុទ្ទេសក៍សម្រាប់គ្រូ / O. V. Manturov [និងអ្នកដទៃ]; ed ។ V. A. Ditkina.- M.: Enlightenment, 1965.- 539 p.: ill.-C.112/.

វាមិនមែនជាការប្រសើរជាងក្នុងការប្រកាសដោយបើកចំហថាវិធីសាស្រ្តនៃភស្តុតាងដោយភាពផ្ទុយគ្នាមិនមែនជាវិធីសាស្រ្តគណិតវិទ្យានោះទេ ទោះបីជាវាត្រូវបានគេប្រើនៅក្នុងគណិតវិទ្យាក៏ដោយ ថាវាជាវិធីសាស្ត្រតក្កវិជ្ជា និងជាកម្មសិទ្ធិរបស់តក្កវិជ្ជា។ តើវាត្រឹមត្រូវទេក្នុងការនិយាយថាភស្តុតាងដោយភាពផ្ទុយគ្នាគឺ "ប្រើនៅពេលណាដែលទ្រឹស្តីបទផ្ទាល់ពិបាកបញ្ជាក់" នៅពេលដែលការពិតវាត្រូវបានប្រើប្រសិនបើ ហើយប្រសិនបើគ្មានការជំនួសសម្រាប់វា។

លក្ខណៈនៃទំនាក់ទំនងរវាងទ្រឹស្តីបទផ្ទាល់ និងបញ្ច្រាសក៏សមនឹងទទួលបានការយកចិត្តទុកដាក់ពិសេសផងដែរ។ "ទ្រឹស្តីបទបញ្ច្រាសសម្រាប់ទ្រឹស្តីបទដែលបានផ្តល់ឱ្យ (ឬទ្រឹស្តីបទដែលបានផ្តល់ឱ្យ) គឺជាទ្រឹស្តីបទដែលលក្ខខណ្ឌគឺជាការសន្និដ្ឋាន ហើយការសន្និដ្ឋានគឺជាលក្ខខណ្ឌនៃទ្រឹស្តីបទដែលបានផ្តល់ឱ្យ។ ទ្រឹស្តីបទនេះទាក់ទងនឹងទ្រឹស្តីបទសន្ទនាត្រូវបានគេហៅថា ទ្រឹស្តីបទផ្ទាល់ (ដើម)។ ក្នុងពេលជាមួយគ្នានោះ ទ្រឹស្តីបទសន្ទនាទៅទ្រឹស្តីបទសន្ទនានឹងជាទ្រឹស្តីបទដែលបានផ្តល់ឱ្យ។ ដូច្នេះទ្រឹស្តីបទដោយផ្ទាល់ និងច្រាសត្រូវបានគេហៅថាទៅវិញទៅមក។ ប្រសិនបើទ្រឹស្តីបទផ្ទាល់ (ដែលបានផ្តល់ឱ្យ) គឺពិត នោះទ្រឹស្តីបទសន្ទនាមិនតែងតែពិតនោះទេ។ ឧទាហរណ៍ ប្រសិនបើ quadrilateral គឺជា rhombus នោះអង្កត់ទ្រូងរបស់វាគឺកាត់កែងគ្នាទៅវិញទៅមក (ទ្រឹស្តីបទផ្ទាល់)។ ប្រសិនបើអង្កត់ទ្រូងក្នុងចតុកោណកែងកាត់កែងទៅវិញទៅមក នោះចតុកោណជារាងមូល - នេះមិនពិតទេ ពោលគឺទ្រឹស្តីបទសន្ទនាមិនពិត។/ វចនានុក្រមពន្យល់នៃពាក្យគណិតវិទ្យា៖ មគ្គុទ្ទេសក៍សម្រាប់គ្រូ / O. V. Manturov [និងអ្នកដទៃ]; ed ។ V. A. Ditkina.- M.: Enlightenment, 1965.- 539 p.: ill.-C.261 /.

លក្ខណៈនៃទំនាក់ទំនងរវាងទ្រឹស្តីបទផ្ទាល់ និងច្រាសនេះ មិនគិតពីការពិតដែលថាលក្ខខណ្ឌនៃទ្រឹស្តីបទផ្ទាល់ត្រូវបានគេយកដូចដែលបានផ្តល់ឱ្យដោយគ្មានភស្តុតាង ដូច្នេះថាភាពត្រឹមត្រូវរបស់វាមិនត្រូវបានធានានោះទេ។ លក្ខខណ្ឌនៃទ្រឹស្តីបទបញ្ច្រាសមិនត្រូវបានគេយកដូចដែលបានផ្តល់ឱ្យទេព្រោះវាជាការសន្និដ្ឋាននៃទ្រឹស្តីបទផ្ទាល់ដែលបានបង្ហាញឱ្យឃើញ។ ភាពត្រឹមត្រូវរបស់វាត្រូវបានបញ្ជាក់ដោយភស្តុតាងនៃទ្រឹស្តីបទផ្ទាល់។ ភាពខុសគ្នានៃឡូជីខលដ៏សំខាន់នេះរវាងលក្ខខណ្ឌនៃទ្រឹស្តីបទផ្ទាល់ និងច្រាស ប្រែទៅជាការសម្រេចចិត្តនៅក្នុងសំណួរថាតើទ្រឹស្ដីមួយណាអាច និងដែលមិនអាចបញ្ជាក់បានដោយវិធីសាស្ត្រឡូជីខលពីផ្ទុយ។

ចូរសន្មតថាមានទ្រឹស្តីបទផ្ទាល់នៅក្នុងចិត្ត ដែលអាចបញ្ជាក់បានដោយវិធីសាស្ត្រគណិតវិទ្យាធម្មតា ប៉ុន្តែវាពិតជាពិបាកណាស់។ យើងបង្កើតវាជាទម្រង់ទូទៅក្នុងទម្រង់ខ្លីមួយដូចខាងក្រោម៖ ពី កគួរតែ អ៊ី . និមិត្តសញ្ញា ក មានតម្លៃនៃលក្ខខណ្ឌដែលបានផ្តល់ឱ្យនៃទ្រឹស្តីបទ ទទួលយកដោយគ្មានភស្តុតាង។ និមិត្តសញ្ញា អ៊ី គឺជាការសន្និដ្ឋាននៃទ្រឹស្តីបទដែលត្រូវបង្ហាញ។

យើងនឹងបញ្ជាក់ទ្រឹស្តីបទផ្ទាល់ដោយភាពផ្ទុយគ្នា ឡូជីខលវិធីសាស្រ្ត។ វិធីសាស្រ្តឡូជីខលបង្ហាញទ្រឹស្តីបទដែលមាន មិនមែនគណិតវិទ្យាទេ។លក្ខខណ្ឌ, និង ឡូជីខលលក្ខខណ្ឌ។ វាអាចត្រូវបានទទួលបានប្រសិនបើលក្ខខណ្ឌគណិតវិទ្យានៃទ្រឹស្តីបទ ពី កគួរតែ អ៊ី បន្ថែមជាមួយលក្ខខណ្ឌផ្ទុយ ពី កវាមិនធ្វើតាមទេ។ អ៊ី .

ជាលទ្ធផល លក្ខខណ្ឌផ្ទុយគ្នាឡូជីខលនៃទ្រឹស្តីបទថ្មីត្រូវបានទទួល ដែលរួមមានពីរផ្នែក៖ ពី កគួរតែ អ៊ី និង ពី កវាមិនធ្វើតាមទេ។ អ៊ី . លក្ខខណ្ឌលទ្ធផលនៃទ្រឹស្តីបទថ្មីត្រូវគ្នាទៅនឹងច្បាប់ឡូជីខលនៃមជ្ឈិមដែលដកចេញ ហើយត្រូវគ្នាទៅនឹងភស្តុតាងនៃទ្រឹស្តីបទដោយភាពផ្ទុយគ្នា។

យោងតាមច្បាប់ ផ្នែកមួយនៃលក្ខខណ្ឌផ្ទុយគឺមិនពិត ផ្នែកមួយទៀតគឺពិត និងទីបីត្រូវបានដកចេញ។ ភ័ស្តុតាងដោយភាពផ្ទុយគ្នា មានភារកិច្ច និងគោលដៅផ្ទាល់របស់វា ដើម្បីកំណត់ថាតើផ្នែកណាមួយនៃផ្នែកទាំងពីរនៃលក្ខខណ្ឌនៃទ្រឹស្តីបទគឺមិនពិត។ ដរាបណាផ្នែកមិនពិតនៃលក្ខខណ្ឌត្រូវបានកំណត់ វានឹងត្រូវបានបង្កើតឡើងថាផ្នែកផ្សេងទៀតគឺជាផ្នែកពិត ហើយផ្នែកទីបីត្រូវបានដកចេញ។

យោង​ទៅ​តាម វចនានុក្រមពន្យល់ពាក្យគណិតវិទ្យា “ភ័ស្តុតាងគឺជាការវែកញែក ក្នុងអំឡុងពេលដែលការពិត ឬមិនពិតនៃសេចក្តីថ្លែងការណ៍ណាមួយ (ការវិនិច្ឆ័យ សេចក្តីថ្លែងការណ៍ ទ្រឹស្តីបទ) ត្រូវបានបង្កើតឡើង”. ភស្តុតាង ផ្ទុយមានការពិភាក្សានៅក្នុងវគ្គដែលវាត្រូវបានបង្កើតឡើង ភាពមិនពិត(ភាពមិនសមហេតុផល) នៃការសន្និដ្ឋានដែលកើតឡើងពី មិនពិតលក្ខខណ្ឌនៃទ្រឹស្តីបទត្រូវបានបង្ហាញ។

បានផ្តល់ឱ្យ៖ ពី កគួរតែ អ៊ីនិងពី កវាមិនធ្វើតាមទេ។ អ៊ី .

បញ្ជាក់៖ ពី កគួរតែ អ៊ី .

ភស្តុតាង៖ លក្ខខណ្ឌ​ឡូជីខល​នៃ​ទ្រឹស្តីបទ​មាន​ភាពផ្ទុយគ្នា​ដែល​ទាមទារ​ការដោះស្រាយ​របស់វា។ ភាពផ្ទុយគ្នានៃលក្ខខណ្ឌត្រូវតែស្វែងរកដំណោះស្រាយរបស់វានៅក្នុងភស្តុតាង និងលទ្ធផលរបស់វា។ លទ្ធផលប្រែថាមិនពិត ប្រសិនបើការវែកញែកគ្មានកំហុស និងគ្មានកំហុស។ ហេតុផលសម្រាប់ការសន្និដ្ឋានមិនពិតជាមួយនឹងការវែកញែកត្រឹមត្រូវអាចគ្រាន់តែជាលក្ខខណ្ឌផ្ទុយគ្នាប៉ុណ្ណោះ៖ ពី កគួរតែ អ៊ី និង ពី កវាមិនធ្វើតាមទេ។ អ៊ី .

មិនមានស្រមោលនៃការសង្ស័យថាផ្នែកមួយនៃលក្ខខណ្ឌមិនពិតទេ ហើយមួយទៀតនៅក្នុងករណីនេះគឺជាការពិត។ ផ្នែកទាំងពីរនៃលក្ខខណ្ឌមានប្រភពដើមដូចគ្នា ត្រូវបានទទួលយកដូចដែលបានផ្តល់ឱ្យ សន្មតថាអាចធ្វើទៅបានស្មើគ្នា ដែលអាចទទួលយកបានស្មើគ្នា។ល។ ផ្សេងទៀត។ ដូច្នេះ ក្នុង​កម្រិត​ដូចគ្នា ពី កគួរតែ អ៊ី ហើយប្រហែលជា ពី កវាមិនធ្វើតាមទេ។ អ៊ី . សេចក្តីថ្លែងការណ៍ ពី កគួរតែ អ៊ី ប្រហែល មិនពិតបន្ទាប់មកសេចក្តីថ្លែងការណ៍ ពី កវាមិនធ្វើតាមទេ។ អ៊ី នឹងក្លាយជាការពិត។ សេចក្តីថ្លែងការណ៍ ពី កវាមិនធ្វើតាមទេ។ អ៊ី ប្រហែលជាមិនពិត បន្ទាប់មកសេចក្តីថ្លែងការណ៍ ពី កគួរតែ អ៊ី នឹងក្លាយជាការពិត។

ដូច្នេះវាមិនអាចទៅរួចទេក្នុងការបញ្ជាក់ទ្រឹស្តីបទផ្ទាល់ដោយវិធីសាស្ត្រផ្ទុយ។

ឥឡូវនេះយើងនឹងបង្ហាញទ្រឹស្តីបទផ្ទាល់ដូចគ្នាដោយវិធីសាស្ត្រគណិតវិទ្យាធម្មតា។

បានផ្តល់ឱ្យ៖ ក .

បញ្ជាក់៖ ពី កគួរតែ អ៊ី .

ភស្តុតាង។

1. ពី កគួរតែ ខ

2. ពី ខគួរតែ វ (យោងទៅតាមទ្រឹស្តីបទដែលបានបញ្ជាក់ពីមុន)) ។

3. ពី វគួរតែ ជី (យោងទៅតាមទ្រឹស្តីបទដែលបានបង្ហាញពីមុន) ។

4. ពី ជីគួរតែ ឃ (យោងទៅតាមទ្រឹស្តីបទដែលបានបង្ហាញពីមុន) ។

5. ពី ឃគួរតែ អ៊ី (យោងទៅតាមទ្រឹស្តីបទដែលបានបង្ហាញពីមុន) ។

ដោយផ្អែកលើច្បាប់នៃអន្តរកាល។ ពី កគួរតែ អ៊ី . ទ្រឹស្តីបទផ្ទាល់ត្រូវបានបង្ហាញដោយវិធីសាស្ត្រធម្មតា។

អនុញ្ញាតឱ្យទ្រឹស្តីបទផ្ទាល់ដែលបានបញ្ជាក់មានទ្រឹស្តីបទសន្ទនាត្រឹមត្រូវ៖ ពី អ៊ីគួរតែ ក .

ចូរយើងបញ្ជាក់វាដោយធម្មតា។ គណិតវិទ្យាវិធីសាស្រ្ត។ ភ័ស្តុតាងនៃទ្រឹស្តីបទបញ្ច្រាសអាចត្រូវបានបង្ហាញជាទម្រង់និមិត្តសញ្ញាជាក្បួនដោះស្រាយនៃប្រតិបត្តិការគណិតវិទ្យា។

បានផ្តល់ឱ្យ៖ អ៊ី

បញ្ជាក់៖ ពី អ៊ីគួរតែ ក .

ភស្តុតាង។

1. ពី អ៊ីគួរតែ ឃ

2. ពី ឃគួរតែ ជី (ដោយទ្រឹស្តីបទបញ្ច្រាសដែលបានបញ្ជាក់ពីមុន) ។

3. ពី ជីគួរតែ វ (ដោយទ្រឹស្តីបទបញ្ច្រាសដែលបានបញ្ជាក់ពីមុន) ។

4. ពី វវាមិនធ្វើតាមទេ។ ខ (ការសន្ទនាមិនពិត)។ នោះ​ហើយ​ជា​មូល​ហេតុ​ដែល ពី ខវាមិនធ្វើតាមទេ។ ក .

ក្នុងស្ថានភាពនេះ វាគ្មានន័យទេក្នុងការបន្តភស្តុតាងគណិតវិទ្យានៃទ្រឹស្តីបទបញ្ច្រាស។ ហេតុផលសម្រាប់ស្ថានភាពគឺឡូជីខល។ វាមិនអាចទៅរួចទេក្នុងការជំនួសទ្រឹស្ដីបញ្ច្រាសដែលមិនត្រឹមត្រូវជាមួយនឹងអ្វីទាំងអស់។ ដូច្នេះ ទ្រឹស្តីបទបញ្ច្រាសនេះមិនអាចបញ្ជាក់ដោយវិធីសាស្ត្រគណិតវិទ្យាធម្មតាបានទេ។ ក្តីសង្ឃឹមទាំងអស់គឺដើម្បីបញ្ជាក់ទ្រឹស្តីបទបញ្ច្រាសនេះដោយភាពផ្ទុយគ្នា។

ដើម្បីបញ្ជាក់វាដោយភាពផ្ទុយគ្នា វាត្រូវបានទាមទារដើម្បីជំនួសលក្ខខណ្ឌគណិតវិទ្យារបស់វាជាមួយនឹងលក្ខខណ្ឌផ្ទុយគ្នាឡូជីខល ដែលនៅក្នុងអត្ថន័យរបស់វាមានពីរផ្នែក - មិនពិត និងពិត។

ទ្រឹស្តីបទបញ្ច្រាសទាមទារ៖ ពី អ៊ីវាមិនធ្វើតាមទេ។ ក . ស្ថានភាពរបស់នាង អ៊ី , ពីការសន្និដ្ឋាន ក , គឺជាលទ្ធផលនៃការបញ្ជាក់ទ្រឹស្តីបទផ្ទាល់ដោយវិធីសាស្ត្រគណិតវិទ្យាធម្មតា។ លក្ខខណ្ឌនេះត្រូវតែរក្សាទុក និងបំពេញបន្ថែមជាមួយសេចក្តីថ្លែងការណ៍ ពី អ៊ីគួរតែ ក . ជាលទ្ធផលនៃការបន្ថែម លក្ខខណ្ឌផ្ទុយនៃទ្រឹស្តីបទបញ្ច្រាសថ្មីត្រូវបានទទួល៖ ពី អ៊ីគួរតែ ក និង ពី អ៊ីវាមិនធ្វើតាមទេ។ ក . ផ្អែកលើនេះ។ ឡូជីខលលក្ខខណ្ឌផ្ទុយ ទ្រឹស្តីបទសន្ទនាអាចត្រូវបានបញ្ជាក់ដោយត្រឹមត្រូវ។ ឡូជីខលហេតុផលតែប៉ុណ្ណោះ, និងតែមួយគត់, ឡូជីខលវិធីសាស្រ្តផ្ទុយ។ នៅក្នុងភ័ស្តុតាងដោយភាពផ្ទុយគ្នា សកម្មភាព និងប្រតិបត្តិការគណិតវិទ្យាណាមួយគឺស្ថិតនៅក្រោមឥទ្ធិពលនៃតក្កវិជ្ជា ដូច្នេះហើយមិនរាប់បញ្ចូលនោះទេ។

នៅក្នុងផ្នែកដំបូងនៃសេចក្តីថ្លែងការណ៍ផ្ទុយ ពី អ៊ីគួរតែ ក លក្ខខណ្ឌ អ៊ី ត្រូវបានបង្ហាញដោយភស្តុតាងនៃទ្រឹស្តីបទផ្ទាល់។ នៅក្នុងផ្នែកទីពីរ ពី អ៊ីវាមិនធ្វើតាមទេ។ ក លក្ខខណ្ឌ អ៊ី ត្រូវបានសន្មត់ និងទទួលយកដោយគ្មានភស្តុតាង។ មួយក្នុងចំណោមពួកគេគឺមិនពិត ហើយមួយទៀតគឺពិត។ វាត្រូវបានទាមទារដើម្បីបញ្ជាក់ថាមួយណាមិនពិត។

យើងបញ្ជាក់ដោយត្រឹមត្រូវ។ ឡូជីខលការវែកញែក និងរកឃើញថាលទ្ធផលរបស់វាគឺជាការសន្និដ្ឋានមិនពិត និងមិនសមហេតុផល។ ហេតុផលសម្រាប់ការសន្និដ្ឋានឡូជីខលមិនពិតគឺជាលក្ខខណ្ឌឡូជីខលផ្ទុយគ្នានៃទ្រឹស្តីបទដែលមានពីរផ្នែក - មិនពិតនិងពិត។ ផ្នែកមិនពិតអាចគ្រាន់តែជាសេចក្តីថ្លែងការណ៍មួយ។ ពី អ៊ីវាមិនធ្វើតាមទេ។ ក , ដែលក្នុងនោះ អ៊ី ទទួលយកដោយគ្មានភស្តុតាង។ នេះគឺជាអ្វីដែលសម្គាល់វាពី អ៊ី សេចក្តីថ្លែងការណ៍ ពី អ៊ីគួរតែ ក ដែលត្រូវបានបញ្ជាក់ដោយភស្តុតាងនៃទ្រឹស្តីបទផ្ទាល់។

ដូច្នេះសេចក្តីថ្លែងការណ៍គឺពិត៖ ពី អ៊ីគួរតែ ក ដែលត្រូវបញ្ជាក់។

សេចក្តីសន្និដ្ឋាន៖ មានតែទ្រឹស្តីបទសន្ទនានោះប៉ុណ្ណោះដែលត្រូវបានបញ្ជាក់ដោយវិធីសាស្ត្រតក្កវិជ្ជាពីផ្ទុយ ដែលមានទ្រឹស្តីបទផ្ទាល់បញ្ជាក់ដោយវិធីសាស្ត្រគណិតវិទ្យា ហើយដែលមិនអាចបញ្ជាក់បានដោយវិធីសាស្ត្រគណិតវិទ្យា។

ការសន្និដ្ឋានដែលទទួលបានទទួលបានសារៈសំខាន់ពិសេសមួយទាក់ទងនឹងវិធីសាស្រ្តនៃភស្តុតាងដោយភាពផ្ទុយគ្នានៃទ្រឹស្តីបទដ៏អស្ចារ្យរបស់ Fermat ។ ភាគច្រើនលើសលប់នៃការព្យាយាមដើម្បីបង្ហាញថាវាមិនផ្អែកលើវិធីសាស្រ្តគណិតវិទ្យាធម្មតានោះទេប៉ុន្តែនៅលើវិធីសាស្រ្តឡូជីខលនៃការបញ្ជាក់ដោយភាពផ្ទុយគ្នា។ ភស្តុតាងនៃទ្រឹស្តីបទដ៏អស្ចារ្យរបស់ Fermat Wiles គឺមិនមានករណីលើកលែងនោះទេ។

លោក Dmitry Abrarov នៅក្នុងអត្ថបទរបស់គាត់ "ទ្រឹស្តីបទរបស់ Fermat: បាតុភូតនៃភស្តុតាងរបស់ Wiles" បានបោះពុម្ពការអត្ថាធិប្បាយស្តីពីភស្តុតាងនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ដោយ Wiles ។ យោងតាមលោក Abrarov Wiles បង្ហាញទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ដោយមានជំនួយពីការរកឃើញដ៏គួរឱ្យកត់សម្គាល់មួយដោយគណិតវិទូអាល្លឺម៉ង់ Gerhard Frey (ខ. 1944) ទាក់ទងនឹងដំណោះស្រាយសក្តានុពលមួយចំពោះសមីការរបស់ Fermat ។ x n + y n = z n កន្លែងណា n > ២ ជាមួយនឹងសមីការខុសគ្នាទាំងស្រុងមួយទៀត។ សមីការ​ថ្មី​នេះ​ត្រូវ​បាន​ផ្តល់​ឱ្យ​ដោយ​ខ្សែ​កោង​ពិសេស (ហៅ​ថា​ខ្សែកោង​រាង​អេលីប Frey)។ ខ្សែកោង Frey ត្រូវបានផ្តល់ដោយសមីការសាមញ្ញបំផុត៖
.

“វាគឺច្បាស់ណាស់ Frey ដែលបានប្រៀបធៀបទៅនឹងគ្រប់ដំណោះស្រាយ (a, ខ, គ)សមីការរបស់ Fermat នោះគឺជាលេខដែលបំពេញទំនាក់ទំនង a n + b n = c nខ្សែកោងខាងលើ។ ក្នុងករណីនេះ ទ្រឹស្តីបទចុងក្រោយរបស់ Fermat នឹងធ្វើតាម។(ដកស្រង់ពី៖ Abrarov D. "ទ្រឹស្តីបទ Fermat: បាតុភូតនៃភស្តុតាង Wiles")

ម្យ៉ាងវិញទៀត Gerhard Frey បានផ្តល់យោបល់ថា សមីការនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat x n + y n = z n កន្លែងណា n > ២ មានដំណោះស្រាយជាចំនួនគត់វិជ្ជមាន។ ដំណោះស្រាយដូចគ្នាគឺដោយការសន្មតរបស់ Frey ដំណោះស្រាយនៃសមីការរបស់គាត់។
y 2 + x (x − a n) (y + b n) = 0 ដែលត្រូវបានផ្តល់ឱ្យដោយខ្សែកោងរាងអេលីបរបស់វា។

Andrew Wiles បានទទួលយកការរកឃើញដ៏អស្ចារ្យនេះរបស់ Frey ហើយជាមួយនឹងជំនួយរបស់វា តាមរយៈ គណិតវិទ្យាវិធីសាស្រ្តបានបង្ហាញថាការរកឃើញនេះ ពោលគឺខ្សែកោងរាងអេលីបរបស់ Frey មិនមានទេ។ ដូច្នេះ គ្មានសមីការ និងដំណោះស្រាយរបស់វាដែលត្រូវបានផ្តល់ដោយខ្សែកោងរាងអេលីបដែលមិនមាននោះទេ។ ដូច្នេះ Wiles គួរតែសន្និដ្ឋានថាមិនមានសមីការនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat និងទ្រឹស្តីបទរបស់ Fermat នោះទេ។ ទោះជាយ៉ាងណាក៏ដោយ គាត់ទទួលយកការសន្និដ្ឋានតិចតួចជាងនេះថា សមីការនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat មិនមានដំណោះស្រាយនៅក្នុងចំនួនគត់វិជ្ជមាននោះទេ។

វាអាចជាការពិតដែលមិនអាចប្រកែកបានដែល Wiles បានទទួលយកការសន្មត់ដែលផ្ទុយពីអត្ថន័យផ្ទាល់ទៅនឹងអ្វីដែលបានចែងដោយទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ។ វាតម្រូវឱ្យ Wiles បង្ហាញទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ដោយភាពផ្ទុយគ្នា។ ចូរយើងធ្វើតាមគំរូរបស់គាត់ ហើយមើលថាតើមានអ្វីកើតឡើងពីឧទាហរណ៍នេះ។

ទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ចែងថាសមីការ x n + y n = z n កន្លែងណា n > ២ , មិនមានដំណោះស្រាយក្នុងចំនួនគត់វិជ្ជមានទេ។

យោងទៅតាមវិធីសាស្រ្តឡូជីខលនៃភស្តុតាងដោយភាពផ្ទុយគ្នា សេចក្តីថ្លែងការណ៍នេះត្រូវបានរក្សាទុក ទទួលយកថាបានផ្តល់ឱ្យដោយគ្មានភស្តុតាង ហើយបន្ទាប់មកបន្ថែមដោយសេចក្តីថ្លែងការណ៍ផ្ទុយគ្នាក្នុងអត្ថន័យ: សមីការ x n + y n = z n កន្លែងណា n > ២ មានដំណោះស្រាយជាចំនួនគត់វិជ្ជមាន។

សេចក្តីថ្លែងការណ៍សម្មតិកម្មក៏ត្រូវបានទទួលយកដូចដែលបានផ្តល់ឱ្យដោយគ្មានភស្តុតាង។ សេចក្តីថ្លែងការណ៍ទាំងពីរដែលត្រូវបានពិចារណាតាមទស្សនៈនៃច្បាប់មូលដ្ឋាននៃតក្កវិជ្ជាគឺអាចទទួលយកបានស្មើគ្នា មានសិទ្ធិស្មើគ្នា និងអាចធ្វើទៅបានស្មើគ្នា។ តាមរយៈការវែកញែកត្រឹមត្រូវ វាត្រូវបានទាមទារដើម្បីបង្កើតមួយណាមិនពិត ដើម្បីបញ្ជាក់ថាសេចក្តីថ្លែងការណ៍ផ្សេងទៀតគឺពិត។

ការវែកញែកត្រឹមត្រូវបញ្ចប់ដោយការសន្និដ្ឋានមិនពិត មិនសមហេតុសមផល ហេតុផលសមហេតុសមផលដែលអាចគ្រាន់តែជាលក្ខខណ្ឌផ្ទុយគ្នានៃទ្រឹស្តីបទដែលកំពុងត្រូវបានបង្ហាញ ដែលមានពីរផ្នែកនៃអត្ថន័យផ្ទុយគ្នាដោយផ្ទាល់។ ពួកគេគឺជាមូលហេតុឡូជីខលនៃការសន្និដ្ឋានមិនសមហេតុផលដែលជាលទ្ធផលនៃភស្តុតាងដោយភាពផ្ទុយគ្នា។

ទោះជាយ៉ាងណាក៏ដោយ នៅក្នុងដំណើរការនៃហេតុផលត្រឹមត្រូវតាមតក្កវិជ្ជា មិនមានសញ្ញាតែមួយត្រូវបានរកឃើញទេ ដែលវាអាចបង្កើតសេចក្តីថ្លែងការណ៍ជាក់លាក់ណាមួយមិនពិត។ វាអាចជាសេចក្តីថ្លែងការណ៍មួយ៖ សមីការ x n + y n = z n កន្លែងណា n > ២ មានដំណោះស្រាយជាចំនួនគត់វិជ្ជមាន។ នៅលើមូលដ្ឋានដូចគ្នាវាអាចជាសេចក្តីថ្លែងការណ៍: សមីការ x n + y n = z n កន្លែងណា n > ២ , មិនមានដំណោះស្រាយក្នុងចំនួនគត់វិជ្ជមានទេ។

ជាលទ្ធផលនៃហេតុផលអាចមានការសន្និដ្ឋានតែមួយ: ទ្រឹស្តីបទចុងក្រោយរបស់ Fermat មិនអាចត្រូវបានបញ្ជាក់ដោយភាពផ្ទុយគ្នានោះទេ។.

វា​នឹង​ជា​បញ្ហា​ខុស​គ្នា​ខ្លាំង​ណាស់​ប្រសិន​បើ​ទ្រឹស្តីបទ​ចុង​ក្រោយ​របស់ Fermat ជា​ទ្រឹស្តីបទ​បញ្ច្រាស​ដែល​មាន​ទ្រឹស្តីបទ​ផ្ទាល់​ដែល​បង្ហាញ​ដោយ​វិធីសាស្ត្រ​គណិតវិទ្យា​ធម្មតា។ ក្នុងករណីនេះវាអាចត្រូវបានបញ្ជាក់ដោយភាពផ្ទុយគ្នា។ ហើយដោយសារវាជាទ្រឹស្តីបទផ្ទាល់ ភស្តុតាងរបស់វាត្រូវតែផ្អែកលើមិនផ្អែកលើវិធីសាស្រ្តឡូជីខលនៃភស្តុតាងដោយភាពផ្ទុយគ្នា ប៉ុន្តែនៅលើវិធីសាស្រ្តគណិតវិទ្យាធម្មតា។

យោងតាមលោក D. Abrarov អ្នកសិក្សា V. I. Arnold ដែលជាគណិតវិទូជនជាតិរុស្សីដ៏ល្បីល្បាញបំផុតបានប្រតិកម្មទៅនឹងភស្តុតាងរបស់ Wiles "សង្ស័យយ៉ាងសកម្ម" ។ អ្នកសិក្សាបាននិយាយថា "នេះមិនមែនជាគណិតវិទ្យាពិតទេ គណិតវិទ្យាពិតគឺធរណីមាត្រ ហើយមានទំនាក់ទំនងខ្លាំងជាមួយរូបវិទ្យា"។

ដោយភាពផ្ទុយគ្នា វាមិនអាចទៅរួចទេក្នុងការបញ្ជាក់ថាសមីការនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat មិនមានដំណោះស្រាយ ឬថាវាមានដំណោះស្រាយ។ កំហុសរបស់ Wiles មិនមែនជាគណិតវិទ្យាទេ ប៉ុន្តែជាឡូជីខល - ការប្រើប្រាស់ភស្តុតាងដោយភាពផ្ទុយគ្នា ដែលការប្រើប្រាស់របស់វាគ្មានន័យ និងមិនបញ្ជាក់ពីទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ។

ទ្រឹស្តីបទចុងក្រោយរបស់ Fermat មិនត្រូវបានបង្ហាញឱ្យឃើញទេ ទោះបីជាមានជំនួយពីធម្មតាក៏ដោយ។ វិធីសាស្រ្តគណិតវិទ្យា, ប្រសិនបើវាត្រូវបានផ្តល់ឱ្យ: សមីការ x n + y n = z n កន្លែងណា n > ២ មិនមានដំណោះស្រាយក្នុងចំនួនគត់វិជ្ជមានទេ ហើយប្រសិនបើវាត្រូវបានទាមទារដើម្បីបញ្ជាក់នៅក្នុងវា៖ សមីការ x n + y n = z n កន្លែងណា n > ២ , មិនមានដំណោះស្រាយក្នុងចំនួនគត់វិជ្ជមានទេ។ ក្នុងទម្រង់នេះ មិនមែនជាទ្រឹស្តីបទទេ ប៉ុន្តែជាទ្រឹស្ដីដែលមិនមានអត្ថន័យ។

ចំណាំ។ភស្តុតាង BTF របស់ខ្ញុំត្រូវបានពិភាក្សានៅលើវេទិកាមួយ។ អ្នកចូលរួមម្នាក់នៅក្នុង Trotil ដែលជាអ្នកឯកទេសខាងទ្រឹស្តីលេខបានធ្វើសេចក្តីថ្លែងការណ៍ដែលមានសិទ្ធិដូចខាងក្រោមដែលមានចំណងជើងថា: "ការរៀបរាប់សង្ខេបអំពីអ្វីដែល Mirgorodsky បានធ្វើ" ។ ខ្ញុំដកស្រង់វាដោយពាក្យសំដី៖

« ក. គាត់​បាន​បញ្ជាក់​ថា​ប្រសិន​បើ​ z 2 \u003d x 2 + y បន្ទាប់មក z n > x n + y n . នេះ​គឺ​ជា​ការ​ពិត​ដែល​ល្បី​និង​ច្បាស់​លាស់។

វ. គាត់បានយកបីដង - Pythagorean និង Non-Pythagorean ហើយបានបង្ហាញដោយការរាប់សាមញ្ញថាសម្រាប់ក្រុមគ្រួសារជាក់លាក់ចំនួនបីដង (78 និង 210 បំណែក) BTF ត្រូវបានអនុវត្ត (ហើយសម្រាប់វាតែប៉ុណ្ណោះ)។

ជាមួយ។ ហើយបន្ទាប់មកអ្នកនិពន្ធបានលុបចោលការពិតដែលថាពី < នៅក្នុងសញ្ញាបត្របន្តបន្ទាប់អាចជា = , មិន​ត្រឹម​តែ > . ឧទាហរណ៍សាមញ្ញមួយគឺការផ្លាស់ប្តូរ n=1 v n=2 នៅក្នុង Pythagorean បីដង។

ឃ. ចំណុចនេះមិនរួមចំណែកអ្វីសំខាន់ដល់ភស្តុតាង BTF ទេ។ សេចក្តីសន្និដ្ឋាន៖ BTF មិនត្រូវបានបញ្ជាក់ទេ។

ខ្ញុំនឹងពិចារណាចំណុចសន្និដ្ឋានរបស់គាត់ដោយចំណុច។

ក.នៅក្នុងវា BTF ត្រូវបានបង្ហាញសម្រាប់សំណុំគ្មានកំណត់ទាំងមូលនៃចំនួនបីដងនៃលេខ Pythagorean ។ បញ្ជាក់ដោយវិធីសាស្ត្រធរណីមាត្រ ដែលតាមខ្ញុំជឿ មិនត្រូវបានរកឃើញដោយខ្ញុំទេ ប៉ុន្តែបានរកឃើញឡើងវិញ។ ហើយវាត្រូវបានបើកដូចដែលខ្ញុំជឿដោយ P. Fermat ខ្លួនឯង។ Fermat ប្រហែលជាមានគំនិតនេះនៅពេលគាត់បានសរសេរថា:

"ខ្ញុំបានរកឃើញភស្តុតាងដ៏អស្ចារ្យនៃរឿងនេះ ប៉ុន្តែរឹមទាំងនេះតូចចង្អៀតពេកសម្រាប់វា" ការសន្មត់របស់ខ្ញុំនេះគឺផ្អែកលើការពិតដែលថានៅក្នុងបញ្ហា Diophantine ប្រឆាំងនឹងដែលនៅក្នុងរឹមនៃសៀវភៅ Fermat បានសរសេរថាយើងកំពុងនិយាយអំពីដំណោះស្រាយចំពោះសមីការ Diophantine ដែលជាចំនួនបីដងនៃ Pythagorean ។

សំណុំនៃចំនួនបីដងនៃ Pythagorean គ្មានដែនកំណត់ គឺជាដំណោះស្រាយចំពោះសមីការ Diophatian ហើយនៅក្នុងទ្រឹស្តីបទរបស់ Fermat ផ្ទុយទៅវិញ គ្មានដំណោះស្រាយណាមួយអាចជាដំណោះស្រាយចំពោះសមីការនៃទ្រឹស្តីបទ Fermat នោះទេ។ ហើយភ័ស្តុតាងអព្ភូតហេតុពិតប្រាកដរបស់ Fermat មានឥទ្ធិពលផ្ទាល់លើការពិតនេះ។ ក្រោយមក Fermat អាចពង្រីកទ្រឹស្តីបទរបស់គាត់ទៅសំណុំនៃចំនួនធម្មជាតិទាំងអស់។ នៅលើសំណុំនៃលេខធម្មជាតិទាំងអស់ BTF មិនមែនជាកម្មសិទ្ធិរបស់ "សំណុំនៃទ្រឹស្តីបទដ៏ស្រស់ស្អាតពិសេស" ទេ។ នេះ​ជា​ការ​សន្មត់​របស់​ខ្ញុំ ដែល​មិន​អាច​បញ្ជាក់​បាន ឬ​មិន​អាច​ប្រកែក​បាន​ឡើយ។ វាអាចទទួលយកបាន និងបដិសេធ។

វ.នៅក្នុងកថាខណ្ឌនេះ ខ្ញុំសូមបញ្ជាក់ថា ទាំងក្រុមគ្រួសារនៃលេខបីពីថាហ្គោរដែលបានយកតាមអំពើចិត្ត និងក្រុមគ្រួសារនៃលេខបីដងដែលមិនមែនជាពីតាហ្គោរ BTF ត្រូវបានគេពេញចិត្ត។ នេះគឺជាតំណភ្ជាប់ចាំបាច់ ប៉ុន្តែមិនគ្រប់គ្រាន់ និងមធ្យមនៅក្នុងភស្តុតាងរបស់ខ្ញុំអំពី BTF ឧទាហរណ៍ដែលខ្ញុំបានយកពីក្រុមគ្រួសារនៃចំនួនបីដងនៃ Pythagorean និងក្រុមគ្រួសារនៃលេខបីដែលមិនមែនជា Pythagorean មានអត្ថន័យនៃឧទាហរណ៍ជាក់លាក់ដែលសន្មតនិងមិនរាប់បញ្ចូលអត្ថិភាពនៃឧទាហរណ៍ផ្សេងទៀតស្រដៀងគ្នា។

សេចក្តីថ្លែងការណ៍របស់ Trotil ថាខ្ញុំ "បង្ហាញដោយការរាប់សាមញ្ញថាសម្រាប់គ្រួសារជាក់លាក់ចំនួនបី (78 និង 210 បំណែក) BTF ត្រូវបានបំពេញ (ហើយសម្រាប់តែវាប៉ុណ្ណោះ) គឺគ្មានមូលដ្ឋាន។ គាត់មិនអាចបដិសេធការពិតដែលថាខ្ញុំក៏អាចយកឧទាហរណ៍ផ្សេងទៀតនៃ Pythagorean និង non-pythagorean triples ដើម្បីទទួលបានគ្រួសារជាក់លាក់មួយនិងបីផ្សេងទៀត។

អ្វីក៏ដោយដែលខ្ញុំយកបីគូ ការពិនិត្យមើលភាពសមស្របរបស់ពួកគេសម្រាប់ការដោះស្រាយបញ្ហាអាចត្រូវបានអនុវត្តតាមគំនិតរបស់ខ្ញុំបានតែតាមវិធី "ការរាប់លេខសាមញ្ញ" ប៉ុណ្ណោះ។ វិធីសាស្រ្តផ្សេងទៀតមិនត្រូវបានគេស្គាល់ចំពោះខ្ញុំទេ ហើយមិនត្រូវបានទាមទារ។ ប្រសិនបើគាត់មិនចូលចិត្ត Trotil នោះគាត់គួរតែណែនាំវិធីសាស្រ្តមួយផ្សេងទៀតដែលគាត់មិនធ្វើ។ ដោយមិនផ្តល់អ្វីជាថ្នូរនឹងការថ្កោលទោស "ការរាប់បញ្ចូលសាមញ្ញ" មិនត្រឹមត្រូវទេ ដែលក្នុងករណីនេះមិនអាចជំនួសបានទេ។

ជាមួយ។ខ្ញុំបានលុបចោល = រវាង< и < на основании того, что в доказательстве БТФ рассматривается уравнение z 2 \u003d x 2 + y (1) ដែលសញ្ញាបត្រ n > ២ — ទាំងមូលលេខវិជ្ជមាន។ ពីសមភាពរវាងវិសមភាពវាដូចខាងក្រោម ជាកាតព្វកិច្ចការពិចារណាសមីការ (1) ជាមួយនឹងតម្លៃមិនមែនចំនួនគត់នៃសញ្ញាបត្រ n > ២ . ការរាប់ Trotil បង្ខំការពិចារណាលើសមភាពរវាងវិសមភាព, ការពិចារណាជាក់ស្តែង ចាំបាច់នៅក្នុងភស្តុតាង BTF ការពិចារណានៃសមីការ (1) ជាមួយ មិនមែនចំនួនគត់តម្លៃសញ្ញាបត្រ n > ២ . ខ្ញុំបានធ្វើវាសម្រាប់ខ្លួនខ្ញុំ ហើយបានរកឃើញសមីការនោះ (1) ជាមួយ មិនមែនចំនួនគត់តម្លៃសញ្ញាបត្រ n > ២ មានដំណោះស្រាយបីលេខ៖ z, (z-1), (z-1) ជាមួយនិទស្សន្តដែលមិនមែនជាចំនួនគត់។

Grigory Perelman ។ បដិសេធន៍

Vasily Maksimov

នៅខែសីហាឆ្នាំ 2006 ឈ្មោះរបស់គណិតវិទូដ៏ល្អបំផុតនៅលើភពផែនដីត្រូវបានប្រកាសដែលបានទទួលមេដាយ Fields ដ៏មានកិត្យានុភាពបំផុត - ប្រភេទនៃ analogue នៃរង្វាន់ណូបែលដែលអ្នកគណិតវិទូតាមគំនិតរបស់ Alfred Nobel ត្រូវបានដកហូត។ មេដាយ Fields - បន្ថែមពីលើផ្លាកសញ្ញានៃកិត្តិយស អ្នកឈ្នះរង្វាន់ត្រូវបានផ្តល់ជាមូលប្បទានប័ត្រមួយសម្រាប់ដប់ប្រាំពាន់ដុល្លារកាណាដា - ត្រូវបានផ្តល់ដោយសមាជអន្តរជាតិនៃគណិតវិទូរៀងរាល់បួនឆ្នាំម្តង។ វាត្រូវបានបង្កើតឡើងដោយអ្នកវិទ្យាសាស្ត្រជនជាតិកាណាដា John Charles Fields ហើយត្រូវបានផ្តល់រង្វាន់ជាលើកដំបូងក្នុងឆ្នាំ 1936 ។ ចាប់តាំងពីឆ្នាំ 1950 មក មេដាយ Fields ត្រូវបានផ្តល់រង្វាន់ជាទៀងទាត់ដោយស្តេចនៃប្រទេសអេស្ប៉ាញសម្រាប់ការរួមចំណែករបស់គាត់ក្នុងការអភិវឌ្ឍន៍វិទ្យាសាស្ត្រគណិតវិទ្យា។ ពីមួយទៅបួនអ្នកវិទ្យាសាស្ត្រដែលមានអាយុក្រោមសែសិបឆ្នាំអាចក្លាយជាម្ចាស់ពានរង្វាន់។ គណិតវិទូចំនួន 44 នាក់បានទទួលរង្វាន់រួចហើយ រួមទាំងជនជាតិរុស្សីប្រាំបីនាក់ផងដែរ។

Grigory Perelman ។ Henri Poincare ។

ក្នុងឆ្នាំ 2006 បុរសជនជាតិបារាំង Wendelin Werner ជនជាតិអូស្ត្រាលី Terence Tao និងជនជាតិរុស្ស៊ីពីរនាក់គឺ Andrey Okounkov ដែលធ្វើការនៅសហរដ្ឋអាមេរិក និង Grigory Perelman អ្នកវិទ្យាសាស្ត្រមកពីទីក្រុង St. Petersburg បានក្លាយជាជ័យលាភី។ ទោះជាយ៉ាងណាក៏ដោយនៅពេលចុងក្រោយវាត្រូវបានគេដឹងថា Perelman បានបដិសេធពានរង្វាន់ដ៏មានកិត្យានុភាពនេះ - ដូចដែលអ្នករៀបចំបានប្រកាស "សម្រាប់ហេតុផលនៃគោលការណ៍" ។

ទង្វើ​ហួសហេតុ​បែប​នេះ​របស់​គណិតវិទូ​រុស្ស៊ី​មិន​បាន​ធ្វើ​ឲ្យ​មនុស្ស​ដែល​ស្គាល់​គាត់​ភ្ញាក់​ផ្អើល​ឡើយ។ នេះមិនមែនជាលើកទីមួយទេដែលគាត់បដិសេធរង្វាន់គណិតវិទ្យា ដោយពន្យល់ពីការសម្រេចចិត្តរបស់គាត់ដោយការពិតដែលថាគាត់មិនចូលចិត្តព្រឹត្តិការណ៍ដ៏ឧឡារិក និងការឃោសនាហួសហេតុជុំវិញឈ្មោះរបស់គាត់។ កាលពី 10 ឆ្នាំមុន ក្នុងឆ្នាំ 1996 Perelman បានបដិសេធមិនទទួលរង្វាន់របស់សភាគណិតវិទ្យាអឺរ៉ុប ដោយលើកឡើងពីការពិតដែលថាគាត់មិនទាន់បានបញ្ចប់ការងារលើបញ្ហាវិទ្យាសាស្ត្រដែលត្រូវបានតែងតាំងសម្រាប់ពានរង្វាន់ ហើយនេះមិនមែនជាករណីចុងក្រោយនោះទេ។ គណិតវិទូជនជាតិរុស្សី ហាក់ដូចជាបានកំណត់គោលដៅជីវិតរបស់គាត់ ដើម្បីធ្វើអោយមនុស្សភ្ញាក់ផ្អើល ដោយប្រឆាំងនឹងមតិសាធារណៈ និងសហគមន៍វិទ្យាសាស្ត្រ។

Grigory Yakovlevich Perelman កើតនៅថ្ងៃទី 13 ខែមិថុនាឆ្នាំ 1966 នៅ Leningrad ។ តាំង​ពី​តូច​គាត់​ចូល​ចិត្ត​វិទ្យាសាស្ត្រ​ពិត​ប្រាកដ ដោយ​មាន​ភាព​ប៉ិន​ប្រសប់ គាត់​បាន​បញ្ចប់​ការ​សិក្សា​ថ្នាក់​លេខ ២៣៩ ដ៏​ល្បី។ វិទ្យាល័យជាមួយនឹងការសិក្សាស៊ីជម្រៅនៃគណិតវិទ្យា គាត់បានឈ្នះការប្រកួតគណិតវិទ្យាជាច្រើន៖ ឧទាហរណ៍ ក្នុងឆ្នាំ 1982 ក្នុងនាមជាផ្នែកមួយនៃក្រុមសិស្សសាលាសូវៀត គាត់បានចូលរួមក្នុងព្រឹត្តិការណ៍អូឡាំពិកគណិតវិទ្យាអន្តរជាតិ ដែលប្រារព្ធឡើងនៅទីក្រុង Budapest ។ Perelman ដោយគ្មានការប្រឡងត្រូវបានចុះឈ្មោះនៅក្នុងនាយកដ្ឋានមេកានិចនិងគណិតវិទ្យានៃសាកលវិទ្យាល័យ Leningrad ជាកន្លែងដែលគាត់បានសិក្សា "ល្អឥតខ្ចោះ" ដោយបន្តឈ្នះក្នុងការប្រកួតប្រជែងគណិតវិទ្យានៅគ្រប់កម្រិត។ បន្ទាប់ពីបញ្ចប់ការសិក្សាពីសាកលវិទ្យាល័យដោយកិត្តិយស គាត់បានចូលរៀនថ្នាក់បរិញ្ញាបត្រនៅនាយកដ្ឋាន St. Petersburg នៃវិទ្យាស្ថានគណិតវិទ្យា Steklov ។ អ្នកគ្រប់គ្រងរបស់គាត់គឺជាគណិតវិទូដ៏ល្បីល្បាញ Academician Alexandrov ។ ដោយបានការពារនិក្ខេបបទថ្នាក់បណ្ឌិតរបស់គាត់ លោក Grigory Perelman នៅតែនៅវិទ្យាស្ថាននេះ ក្នុងបន្ទប់ពិសោធន៍ធរណីមាត្រ និងសណ្ឋានដី។ ត្រូវបានគេស្គាល់សម្រាប់ការងាររបស់គាត់លើទ្រឹស្តីនៃលំហ Alexandrov គាត់អាចស្វែងរកភស្តុតាងសម្រាប់សម្មតិកម្មសំខាន់ៗមួយចំនួន។ ទោះបីជាមានការផ្តល់ជូនជាច្រើនពីសាកលវិទ្យាល័យឈានមុខគេលោកខាងលិចក៏ដោយ Perelman ចូលចិត្តធ្វើការនៅក្នុងប្រទេសរុស្ស៊ី។

ជោគជ័យដ៏ល្បីបំផុតរបស់គាត់គឺដំណោះស្រាយក្នុងឆ្នាំ 2002 នៃការស្មានរបស់ Poincare ដ៏ល្បីល្បាញដែលបានបោះពុម្ពផ្សាយក្នុងឆ្នាំ 1904 ហើយចាប់តាំងពីពេលនោះមកនៅតែមិនមានភស្តុតាង។ Perelman បានធ្វើការលើវាអស់រយៈពេលប្រាំបីឆ្នាំ។ សម្មតិកម្ម Poincaré ត្រូវបានចាត់ទុកថាជាអាថ៌កំបាំងគណិតវិទ្យាដ៏អស្ចារ្យបំផុត ហើយដំណោះស្រាយរបស់វាត្រូវបានចាត់ទុកថាជាសមិទ្ធិផលដ៏សំខាន់បំផុតនៅក្នុងវិទ្យាសាស្ត្រគណិតវិទ្យា៖ វានឹងជំរុញការសិក្សាអំពីបញ្ហានៃមូលដ្ឋានគ្រឹះរូបវិទ្យា និងគណិតវិទ្យានៃសកលលោកភ្លាមៗ។ គំនិតភ្លឺស្វាងបំផុតនៅលើភពផែនដីបានទស្សន៍ទាយដំណោះស្រាយរបស់វាក្នុងរយៈពេលពីរបីទសវត្សរ៍ប៉ុណ្ណោះ ហើយវិទ្យាស្ថាន Clay Institute of Mathematics នៅទីក្រុង Cambridge រដ្ឋ Massachusetts បានធ្វើឱ្យបញ្ហា Poincaré ក្លាយជាបញ្ហាគណិតវិទ្យាមួយក្នុងចំណោមបញ្ហាគណិតវិទ្យាដែលគួរឱ្យចាប់អារម្មណ៍បំផុតទាំងប្រាំពីរនៃសហស្សវត្សរ៍ ដែលនីមួយៗត្រូវបានសន្យាមួយលាន។ រង្វាន់ប្រាក់ដុល្លារ (បញ្ហារង្វាន់សហសវត្សរ៍) ។

សម្មតិកម្ម (ជួនកាលគេហៅថាបញ្ហា) របស់គណិតវិទូជនជាតិបារាំង Henri Poincaré (1854–1912) ត្រូវបានរៀបចំដូចខាងក្រោមៈ លំហរបីវិមាត្រដែលបិទជិតណាមួយគឺមានលក្ខណៈ homeomorphic ទៅជាស្វ៊ែរបីវិមាត្រ។ សម្រាប់ការបញ្ជាក់ គំរូដ៏ល្អមួយត្រូវបានប្រើប្រាស់៖ ប្រសិនបើអ្នករុំផ្លែប៉ោមជាមួយនឹងក្រុមកៅស៊ូ បន្ទាប់មកជាគោលការណ៍ ដោយទាញកាសែតជាមួយគ្នា អ្នកអាចច្របាច់ផ្លែប៉ោមទៅជាចំណុចមួយ។ ប្រសិនបើអ្នករុំនំដូណាត់ជាមួយនឹងកាសែតដដែលនោះ អ្នកមិនអាចច្របាច់វាចូលទៅក្នុងចំណុចមួយដោយមិនហែកនំដូណាត់ ឬកៅស៊ូនោះទេ។ នៅក្នុងបរិបទនេះ ផ្លែប៉ោមមួយត្រូវបានគេហៅថាជាតួរលេខ "ភ្ជាប់ដោយឯកឯង" ប៉ុន្តែនំដូណាត់មិនត្រូវបានភ្ជាប់យ៉ាងសាមញ្ញនោះទេ។ ស្ទើរតែមួយរយឆ្នាំមុន Poincaré បានបង្កើតថា ស្វ៊ែរពីរវិមាត្រត្រូវបានតភ្ជាប់យ៉ាងសាមញ្ញ ហើយបានស្នើថា ស្វ៊ែរបីវិមាត្រក៏ត្រូវបានតភ្ជាប់យ៉ាងសាមញ្ញផងដែរ។ គណិតវិទូដែលពូកែជាងគេលើពិភពលោក មិនអាចបង្ហាញការសន្និដ្ឋាននេះបានឡើយ។

ដើម្បីមានលក្ខណៈគ្រប់គ្រាន់សម្រាប់ពានរង្វាន់វិទ្យាស្ថាន Clay Institute Perelman គ្រាន់តែត្រូវការបោះពុម្ពដំណោះស្រាយរបស់គាត់នៅក្នុងទិនានុប្បវត្តិវិទ្យាសាស្ត្រមួយហើយប្រសិនបើក្នុងរយៈពេលពីរឆ្នាំគ្មាននរណាម្នាក់អាចរកឃើញកំហុសក្នុងការគណនារបស់គាត់ទេនោះដំណោះស្រាយនឹងត្រូវបានចាត់ទុកថាត្រឹមត្រូវ។ ទោះជាយ៉ាងណាក៏ដោយ Perelman បានងាកចេញពីច្បាប់តាំងពីដំបូងមកម្ល៉េះ ដោយបានបោះពុម្ពដំណោះស្រាយរបស់គាត់នៅលើគេហទំព័របោះពុម្ពជាមុននៃមន្ទីរពិសោធន៍វិទ្យាសាស្ត្រ Los Alamos ។ ប្រហែលជាគាត់ភ័យខ្លាចថាកំហុសបានចូលទៅក្នុងការគណនារបស់គាត់ - រឿងស្រដៀងគ្នានេះបានកើតឡើងរួចហើយនៅក្នុងគណិតវិទ្យា។ នៅឆ្នាំ 1994 គណិតវិទូជនជាតិអង់គ្លេស Andrew Wiles បានស្នើដំណោះស្រាយចំពោះទ្រឹស្តីបទរបស់ Fermat ដ៏ល្បីល្បាញ ហើយប៉ុន្មានខែក្រោយមកវាបានប្រែក្លាយថាកំហុសបានចូលទៅក្នុងការគណនារបស់គាត់ (ទោះបីជាវាត្រូវបានកែតម្រូវនៅពេលក្រោយក៏ដោយ ហើយអារម្មណ៍នៅតែកើតឡើង)។ នៅតែមិនទាន់មានការបោះពុម្ពផ្សាយជាផ្លូវការនូវភស្តុតាងនៃការសន្និដ្ឋានរបស់ Poincare នោះទេ ប៉ុន្តែមានមតិអនុញ្ញាតពីគណិតវិទូដ៏ល្អបំផុតនៅលើភពផែនដី ដោយបញ្ជាក់ពីភាពត្រឹមត្រូវនៃការគណនារបស់ Perelman ។

មេដាយ Fields ត្រូវបានផ្តល់ទៅឱ្យ Grigory Perelman យ៉ាងជាក់លាក់សម្រាប់ការដោះស្រាយបញ្ហា Poincaré។ ប៉ុន្តែ​អ្នក​វិទ្យាសាស្ត្រ​រុស្ស៊ី​រូប​នេះ​បាន​បដិសេធ​ចំពោះ​រង្វាន់​ដែល​គាត់​ពិត​ជា​សម​នឹង​ទទួល។ លោក John Ball ប្រធានសហភាពគណិតវិទ្យាពិភពលោក (WCM) បាននិយាយនៅក្នុងសន្និសីទសារព័ត៌មានមួយថា "Grigory បានប្រាប់ខ្ញុំថា គាត់មានអារម្មណ៍ឯកោពីសហគមន៍គណិតវិទ្យាអន្តរជាតិ នៅខាងក្រៅសហគមន៍នេះ ដូច្នេះហើយគាត់មិនចង់ទទួលបានពានរង្វាន់ទេ" ។ ម៉ាឌ្រីដ។

មានពាក្យចចាមអារ៉ាមថា Grigory Perelman នឹងចាកចេញពីវិទ្យាសាស្ត្រទាំងអស់គ្នា៖ កាលពីប្រាំមួយខែមុនគាត់បានចាកចេញពីវិទ្យាស្ថានគណិតវិទ្យា Steklov ដើមកំណើតរបស់គាត់ ហើយពួកគេនិយាយថាគាត់នឹងលែងធ្វើគណិតវិទ្យាទៀតហើយ។ ប្រហែលជាអ្នកវិទ្យាសាស្ត្ររុស្ស៊ីជឿថាតាមរយៈការបង្ហាញពីសម្មតិកម្មដ៏ល្បីល្បាញគាត់បានធ្វើអ្វីគ្រប់យ៉ាងដែលគាត់អាចធ្វើបានសម្រាប់វិទ្យាសាស្ត្រ។ ប៉ុន្តែតើអ្នកណានឹងនិយាយអំពីរថភ្លើងនៃការគិតរបស់អ្នកវិទ្យាសាស្ត្រដ៏ភ្លឺស្វាងនិងមនុស្សអស្ចារ្យបែបនេះ? .. Perelman បដិសេធការអត្ថាធិប្បាយណាមួយហើយគាត់បានប្រាប់កាសែត The Daily Telegraph ថា "គ្មានអ្វីដែលខ្ញុំអាចនិយាយបានគឺជាផលប្រយោជន៍សាធារណៈតិចតួចបំផុត" ។ ទោះជាយ៉ាងណាក៏ដោយការបោះពុម្ពផ្សាយវិទ្យាសាស្ត្រឈានមុខគេមានឯកច្ឆ័ន្ទក្នុងការវាយតម្លៃរបស់ពួកគេនៅពេលដែលពួកគេបានរាយការណ៍ថា "Grigory Perelman ដោយបានដោះស្រាយទ្រឹស្តីបទ Poincare បានឈរនៅលើស្មើជាមួយនឹងទេពកោសល្យដ៏អស្ចារ្យបំផុតនៃអតីតកាលនិងបច្ចុប្បន្ន" ។

ទស្សនាវដ្ដី អក្សរសាស្ត្រ សារព័ត៌មាន និងគ្រឹះស្ថានបោះពុម្ពប្រចាំខែ។

ថារង្វាន់ Abel ឆ្នាំ 2016 នឹងទៅដល់ Andrew Wiles សម្រាប់ភស្តុតាងរបស់គាត់អំពីការទស្សន៍ទាយ Taniyama-Shimura សម្រាប់ខ្សែកោងរាងពងក្រពើ semistable និងភស្តុតាងនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ដែលបន្តពីការស្មាននេះ។ បច្ចុប្បន្ននេះបុព្វលាភគឺ 6 លានក្រូនន័រវេស ពោលគឺប្រហែល 50 លានរូប្លិ៍។ យោងតាមលោក Wiles ពានរង្វាន់នេះបានមកជា "ការភ្ញាក់ផ្អើលពេញលេញ" សម្រាប់គាត់។

ទ្រឹស្តីបទរបស់ Fermat ដែលបានបង្ហាញជាង 20 ឆ្នាំមុន នៅតែទាក់ទាញចំណាប់អារម្មណ៍របស់គណិតវិទូ។ មួយផ្នែក នេះគឺដោយសារតែរូបមន្តរបស់វា ដែលអាចយល់បានសូម្បីតែសិស្សសាលា៖ ដើម្បីបញ្ជាក់ថាសម្រាប់លេខធម្មជាតិ n>2 មិនមានបីដងនៃចំនួនគត់ដែលមិនមែនជាសូន្យដែល a n + b n = c n ។ Pierre de Fermat បានសរសេរកន្សោមនេះនៅក្នុងរឹមនៃ Diophantus' Arithmetic ដោយមានចំណងជើងគួរឱ្យកត់សម្គាល់ថា "ខ្ញុំបានរកឃើញភស្តុតាងដ៏អស្ចារ្យមួយ [នៃការអះអាងនេះ] សម្រាប់រឿងនេះ ប៉ុន្តែគែមនៃសៀវភៅនេះគឺតូចចង្អៀតពេកសម្រាប់វា" ។ មិនដូចរឿងនិទានគណិតវិទ្យាភាគច្រើនទេ រឿងនេះគឺពិត។

ការធ្វើបទបង្ហាញនៃពានរង្វាន់នេះគឺជាឱកាសដ៏ល្អមួយដើម្បីរំលឹករឿងកំប្លែងចំនួនដប់ដែលទាក់ទងនឹងទ្រឹស្តីបទរបស់ Fermat ។

1.

មុនពេល Andrew Wiles បង្ហាញទ្រឹស្តីបទរបស់ Fermat វាត្រូវបានគេហៅយ៉ាងត្រឹមត្រូវថា ការសន្និដ្ឋាន នោះគឺជាសម្មតិកម្មរបស់ Fermat ។ ការពិតគឺថាទ្រឹស្តីបទមួយ តាមនិយមន័យ គឺជាសេចក្តីថ្លែងការណ៍ដែលបានបញ្ជាក់រួចមកហើយ។ ទោះយ៉ាងណាក៏ដោយ សម្រាប់ហេតុផលមួយចំនួន គ្រាន់តែឈ្មោះបែបនេះជាប់គាំងទៅនឹងសេចក្តីថ្លែងការណ៍នេះ។

2.

ប្រសិនបើយើងដាក់ n = 2 នៅក្នុងទ្រឹស្តីបទរបស់ Fermat នោះសមីការបែបនេះមានដំណោះស្រាយជាច្រើនគ្មានទីបញ្ចប់។ ដំណោះស្រាយទាំងនេះត្រូវបានគេហៅថា "បីដង Pythagorean" ។ ពួកគេបានទទួលឈ្មោះនេះ ដោយសារតែពួកគេត្រូវគ្នាទៅនឹងត្រីកោណមុំខាងស្តាំ ដែលជ្រុងត្រូវបានបញ្ជាក់ដោយសំណុំនៃលេខបែបនេះ។ អ្នកអាចបង្កើត Pythagorean បីដងដោយប្រើរូបមន្តទាំងបីនេះ (m 2 - n 2, 2mn, m 2 + n 2) ។ វាចាំបាច់ក្នុងការជំនួសតម្លៃខុសគ្នានៃ m និង n ទៅក្នុងរូបមន្តទាំងនេះហើយជាលទ្ធផលយើងនឹងទទួលបានបីដងដែលយើងត្រូវការ។ ទោះជាយ៉ាងណាក៏ដោយរឿងសំខាន់នៅទីនេះគឺត្រូវប្រាកដថាលេខលទ្ធផលនឹងធំជាងសូន្យ - ប្រវែងមិនអាចត្រូវបានបង្ហាញជាលេខអវិជ្ជមានបានទេ។

ដោយវិធីនេះ វាងាយស្រួលមើលថា ប្រសិនបើលេខទាំងអស់នៅក្នុង Pythagorean បីត្រូវបានគុណនឹងលេខមួយចំនួនដែលមិនមែនជាសូន្យនោះ Pythagorean ថ្មីបីនឹងត្រូវបានទទួល។ ដូច្នេះវាសមហេតុផលក្នុងការសិក្សាបីដង ដែលលេខទាំងបីក្នុងចំនួនសរុបមិនមានការបែងចែកធម្មតាទេ។ គ្រោងការណ៍ដែលយើងបានពិពណ៌នាធ្វើឱ្យវាអាចទទួលបានបីដងបែបនេះ - នេះមិនមែនជាលទ្ធផលសាមញ្ញទេ។

3.

នៅថ្ងៃទី 1 ខែមីនា ឆ្នាំ 1847 នៅឯកិច្ចប្រជុំនៃបណ្ឌិត្យសភាវិទ្យាសាស្ត្រទីក្រុងប៉ារីស គណិតវិទូពីរនាក់ក្នុងពេលតែមួយគឺ Gabriel Lame និង Augustin Cauchy បានប្រកាសថាពួកគេជិតឈានដល់ការបង្ហាញពីទ្រឹស្តីបទដ៏គួរឱ្យកត់សម្គាល់មួយ។ ពួកគេ​បាន​រត់​ប្រណាំង​ដើម្បី​ផ្សព្វផ្សាយ​ភស្តុតាង។ អ្នកសិក្សាភាគច្រើនបានអបអរសាទរចំពោះ Lame ពីព្រោះ Cauchy គឺជាអ្នកនិយមសាសនាដែលមិនស្មោះត្រង់នឹងខ្លួនឯង (ហើយជាការពិតណាស់ គណិតវិទូក្រៅម៉ោងដ៏អស្ចារ្យ)។ ទោះជាយ៉ាងណាក៏ដោយ ការប្រកួតនេះមិនមានគោលដៅបញ្ចប់នោះទេ - តាមរយៈមិត្តរបស់គាត់ Joseph Liouville ដែលជាគណិតវិទូជនជាតិអាឡឺម៉ង់ Ernst Kummer បានជូនដំណឹងដល់អ្នកសិក្សាថាមានកំហុសមួយ និងដូចគ្នានៅក្នុងភស្តុតាងនៃ Cauchy និង Lame ។

នៅសាលា វាត្រូវបានបង្ហាញថាការបំបែកលេខទៅជាកត្តាសំខាន់គឺមានតែមួយគត់។ គណិតវិទូទាំងពីរនាក់បានជឿថា ប្រសិនបើអ្នកក្រឡេកមើលការរលាយនៃចំនួនគត់រួចហើយនៅក្នុងករណីស្មុគស្មាញ នោះទ្រព្យសម្បត្តិនេះ - ភាពប្លែកពីគេ - នឹងត្រូវបានរក្សាទុក។ ទោះយ៉ាងណាក៏ដោយវាមិនមែនទេ។

គួរកត់សម្គាល់ថាប្រសិនបើយើងពិចារណាតែ m + i n នោះការរលួយគឺមានតែមួយគត់។ លេខបែបនេះត្រូវបានគេហៅថា Gaussian ។ ប៉ុន្តែការងាររបស់ Lame និង Cauchy ទាមទារកត្តានៅក្នុងវិស័យ cyclotomic ។ ជាឧទាហរណ៍ ទាំងនេះគឺជាលេខដែល m និង n គឺសមហេតុផល ហើយខ្ញុំពេញចិត្តនឹងទ្រព្យសម្បត្តិ i^k = 1 ។

4.

ទ្រឹស្តីបទរបស់ Fermat សម្រាប់ n = 3 មានអត្ថន័យធរណីមាត្រច្បាស់លាស់។ ចូរយើងស្រមៃថាយើងមានគូបតូចៗជាច្រើន។ ឧបមាថាយើងបានប្រមូលគូបធំពីរពីពួកគេ។ ក្នុងករណីនេះពិតណាស់ភាគីនឹងជាចំនួនគត់។ តើវាអាចទៅរួចទេក្នុងការស្វែងរកគូបធំពីរដែលដោយបានបំបែកពួកវាចូលទៅក្នុងគូបតូចៗនៃសមាសធាតុរបស់វា យើងអាចប្រមូលគូបធំមួយចេញពីពួកវាបានដែរឬទេ? ទ្រឹស្ដីរបស់ Fermat និយាយថា នេះមិនអាចធ្វើបានទេ។ វាគួរឱ្យអស់សំណើចដែលប្រសិនបើអ្នកសួរសំណួរដូចគ្នាសម្រាប់បីគូប ចម្លើយគឺបាទ។ ជាឧទាហរណ៍ មានលេខបួនបួន ដែលត្រូវបានរកឃើញដោយគណិតវិទូដ៏អស្ចារ្យ Srinivas Ramanujan៖

3 3 + 4 3 + 5 3 = 6 3

5.

Leonhard Euler ត្រូវបានកត់សម្គាល់នៅក្នុងប្រវត្តិសាស្រ្តនៃទ្រឹស្តីបទ Fermat ។ គាត់ពិតជាមិនបានជោគជ័យក្នុងការបញ្ជាក់សេចក្តីថ្លែងការណ៍ (ឬសូម្បីតែចូលទៅជិតភស្តុតាង) ប៉ុន្តែគាត់បានបង្កើតសម្មតិកម្មថាសមីការ

x 4 + y 4 + z 4 = u 4

មិនមានដំណោះស្រាយជាចំនួនគត់ទេ។ ការប៉ុនប៉ងទាំងអស់ដើម្បីស្វែងរកដំណោះស្រាយដោយផ្ទាល់ចំពោះសមីការបែបនេះបានប្រែទៅជាគ្មានផ្លែផ្កា។ វាមិនមែនរហូតដល់ឆ្នាំ 1988 ដែល Nahum Elkies នៃសាកលវិទ្យាល័យ Harvard អាចស្វែងរកគំរូផ្ទុយ។ វាមើលទៅដូចនេះ៖

2 682 440 4 + 15 365 639 4 + 18 796 760 4 = 20 615 673 4 .

ជាធម្មតារូបមន្តនេះត្រូវបានចងចាំក្នុងបរិបទនៃការពិសោធន៍លេខ។ តាមក្បួនក្នុងគណិតវិទ្យាវាមើលទៅដូចនេះ: មានរូបមន្តមួយចំនួន។ គណិតវិទូពិនិត្យរូបមន្តនេះក្នុងករណីសាមញ្ញ បញ្ចុះបញ្ចូលខ្លួនឯងអំពីការពិត និងបង្កើតសម្មតិកម្មមួយចំនួន។ បន្ទាប់មកគាត់ (ទោះបីជាជាញឹកញាប់និស្សិតបញ្ចប់ការសិក្សា ឬនិស្សិតមួយចំនួនរបស់គាត់) សរសេរកម្មវិធីមួយដើម្បីពិនិត្យមើលថារូបមន្តត្រឹមត្រូវសម្រាប់គ្រប់គ្រាន់។ លេខធំដែលមិនអាចរាប់បានដោយដៃ (យើងកំពុងនិយាយអំពីការពិសោធន៍បែបនេះជាមួយលេខបឋម)។ ជាការពិតណាស់ នេះមិនមែនជាភស្តុតាងទេ ប៉ុន្តែជាហេតុផលដ៏ល្អដើម្បីប្រកាសសម្មតិកម្ម។ សំណង់ទាំងអស់នេះគឺផ្អែកលើការសន្មតសមហេតុផលថាប្រសិនបើមានឧទាហរណ៍ផ្ទុយទៅនឹងរូបមន្តសមហេតុផលមួយចំនួននោះយើងនឹងរកឃើញវាឱ្យបានលឿនល្មម។

ការស្មានរបស់អយល័ររំឭកយើងថាជីវិតមានភាពចម្រុះជាងការស្រមើស្រមៃរបស់យើងទៅទៀត៖ ឧទាហរណ៍ដំបូងអាចមានទំហំធំតាមអំពើចិត្ត។

6.

ជាការពិត Andrew Wiles មិនបានព្យាយាមបញ្ជាក់ទ្រឹស្តីបទរបស់ Fermat ទេ - គាត់កំពុងដោះស្រាយបញ្ហាដែលពិបាកជាងនេះ ហៅថា ការសន្និដ្ឋាន Taniyama-Shimura ។ មានថ្នាក់គួរឱ្យកត់សម្គាល់ពីរនៃវត្ថុនៅក្នុងគណិតវិទ្យា។ ទម្រង់ទីមួយត្រូវបានគេហៅថាទម្រង់ម៉ូឌុល ហើយជាមុខងារសំខាន់មួយនៅលើលំហ Lobachevsky។ មុខងារទាំងនេះមិនផ្លាស់ប្តូរក្នុងអំឡុងពេលចលនានៃយន្តហោះនេះទេ។ ទីពីរត្រូវបានគេហៅថា "ខ្សែកោងរាងអេលីប" ហើយជាខ្សែកោងដែលផ្តល់ដោយសមីការនៃដឺក្រេទីបីនៅក្នុងប្លង់ស្មុគស្មាញ។ វត្ថុទាំងពីរគឺមានប្រជាប្រិយភាពយ៉ាងខ្លាំងនៅក្នុងទ្រឹស្តីលេខ។

នៅទសវត្សរ៍ឆ្នាំ 1950 គណិតវិទូដែលមានទេពកោសល្យពីរនាក់ Yutaka Taniyama និង Goro Shimura បានជួបគ្នានៅក្នុងបណ្ណាល័យនៃសាកលវិទ្យាល័យតូក្យូ។ នៅពេលនោះ មិនមានគណិតវិទ្យាពិសេសនៅសកលវិទ្យាល័យទេ៖ វាគ្រាន់តែមិនមានពេលវេលាដើម្បីងើបឡើងវិញក្រោយសង្រ្គាម។ ជាលទ្ធផល អ្នកវិទ្យាសាស្ត្របានសិក្សាដោយប្រើសៀវភៅសិក្សាចាស់ៗ ហើយពិភាក្សាក្នុងសិក្ខាសាលាដែលបញ្ហានៅអឺរ៉ុប និងសហរដ្ឋអាមេរិកត្រូវបានចាត់ទុកថាត្រូវបានដោះស្រាយ ហើយមិនពាក់ព័ន្ធជាពិសេសនោះទេ។ វាគឺជា Taniyama និង Shimura ដែលបានរកឃើញថាមានការឆ្លើយឆ្លងគ្នារវាងទម្រង់ម៉ូឌុល និងមុខងាររាងអេលីប។

ពួកគេបានសាកល្បងការសន្និដ្ឋានរបស់ពួកគេលើថ្នាក់សាមញ្ញមួយចំនួននៃខ្សែកោង។ វាបានប្រែក្លាយថាវាដំណើរការ។ ដូច្នេះ​ពួកគេ​បាន​ស្នើ​ថា​ការ​តភ្ជាប់​នេះ​តែងតែ​មាន។ នេះជារបៀបដែលសម្មតិកម្ម Taniyama-Shimura បានបង្ហាញខ្លួន ហើយបីឆ្នាំក្រោយមក Taniyama បានធ្វើអត្តឃាត។ នៅឆ្នាំ 1984 គណិតវិទូជនជាតិអាឡឺម៉ង់ Gerhard Frey បានបង្ហាញថាប្រសិនបើទ្រឹស្តីបទរបស់ Fermat ខុស នោះការសន្និដ្ឋាន Taniyama-Shimura គឺខុស។ វាបានបន្តពីនេះថាអ្នកដែលបង្ហាញការសន្និដ្ឋាននេះក៏នឹងបញ្ជាក់ទ្រឹស្តីបទ។ ហើយនោះជាអ្វីដែល Wiles បានធ្វើ - ទោះបីជាមិនមានលក្ខណៈទូទៅក៏ដោយ។

7.

Wiles បានចំណាយពេលប្រាំបីឆ្នាំដើម្បីបញ្ជាក់ពីការស្មាន។ ហើយក្នុងអំឡុងពេលត្រួតពិនិត្យ អ្នកត្រួតពិនិត្យបានរកឃើញកំហុសមួយនៅក្នុងវា ដែល "បានសម្លាប់" ភស្តុតាងភាគច្រើន ដោយចាត់ទុកជាមោឃៈពេញមួយឆ្នាំនៃការងារ។ អ្នកត្រួតពិនិត្យម្នាក់ឈ្មោះ Richard Taylor បានធ្វើការជួសជុលរន្ធជាមួយ Wiles ។ ខណៈពេលដែលពួកគេកំពុងធ្វើការ សារមួយបានលេចចេញមកថា Elkies ដែលជាមនុស្សដូចគ្នាដែលបានរកឃើញឧទាហរណ៍ផ្ទុយទៅនឹងការសន្និដ្ឋានរបស់អយល័រ ក៏បានរកឃើញឧទាហរណ៍ផ្ទុយទៅនឹងទ្រឹស្តីបទរបស់ Fermat (ក្រោយមកវាបានប្រែក្លាយថានេះគឺជារឿងកំប្លែងរបស់ April Fool)។ Wiles បានធ្លាក់ចូលទៅក្នុងការធ្លាក់ទឹកចិត្តហើយមិនចង់បន្ត - រន្ធនៅក្នុងភស្តុតាងមិនអាចបិទតាមមធ្យោបាយណាមួយឡើយ។ Taylor បាន​និយាយ​ជាមួយ Wiles ក្នុង​ការ​ចំបាប់​មួយ​ខែ​ទៀត។

អព្ភូតហេតុមួយបានកើតឡើង ហើយនៅចុងបញ្ចប់នៃគណិតវិទូរដូវក្តៅបានគ្រប់គ្រងការទម្លាយមួយ - នេះជារបៀបដែលស្នាដៃ "ខ្សែកោងរាងពងក្រពើម៉ូឌុល និងទ្រឹស្តីបទចុងក្រោយរបស់ Fermat" ដោយ Andrew Wiles (pdf) និង "ទ្រឹស្ដីចិញ្ចៀននៃពិជគណិត Hecke មួយចំនួន" ដោយ Richard Taylor និង Andrew Wiles កើត។ នេះជាភស្តុតាងត្រឹមត្រូវ។ វាត្រូវបានបោះពុម្ពនៅឆ្នាំ 1995 ។

8.

នៅឆ្នាំ 1908 គណិតវិទូ Paul Wolfskel បានទទួលមរណភាពនៅ Darmstadt ។ បន្ទាប់ពីខ្លួនគាត់គាត់បានទុកឆន្ទៈមួយដែលគាត់បានផ្តល់ឱ្យសហគមន៍គណិតវិទ្យារយៈពេល 99 ឆ្នាំដើម្បីស្វែងរកភស្តុតាងនៃទ្រឹស្តីបទចុងក្រោយរបស់ Fermat ។ អ្នកនិពន្ធនៃភស្តុតាងគួរតែទទួលបាន 100 ពាន់ពិន្ទុ (ដោយវិធីនេះអ្នកនិពន្ធនៃឧទាហរណ៍ផ្ទុយនឹងមិនបានទទួលអ្វីទេ) ។ យោងតាមរឿងព្រេងដ៏ពេញនិយមមួយ វាគឺជាសេចក្តីស្រឡាញ់ដែលបានជំរុញឱ្យគណិតវិទូ Wolfskell ធ្វើអំណោយបែបនេះ។ នេះជារបៀបដែល Simon Singh ពិពណ៌នាអំពីរឿងព្រេងនៅក្នុងសៀវភៅរបស់គាត់ Fermat's Last Theorem:

រឿងនេះចាប់ផ្តើមដោយ Wolfskehl ចាប់ផ្តើមជក់ចិត្តនឹងនារីដ៏ស្រស់ស្អាតម្នាក់ដែលអត្តសញ្ញាណមិនធ្លាប់មាន។ ចំពោះការសោកស្តាយរបស់ Wolfskel ស្ត្រីអាថ៌កំបាំងបានបដិសេធគាត់។ ធ្លាក់​ក្នុង​ភាព​អស់​សង្ឃឹម​យ៉ាង​ខ្លាំង​រហូត​សម្រេច​ចិត្ត​ធ្វើ​អត្តឃាត។ Wolfskel គឺជាបុរសដែលងប់ងល់ ប៉ុន្តែមិនមានការរំជើបរំជួល ហេតុដូច្នេះហើយបានចាប់ផ្ដើមធ្វើការបកស្រាយអំពីការស្លាប់របស់គាត់គ្រប់លម្អិត។ គាត់​បាន​កំណត់​ថ្ងៃ​ធ្វើ​អត្តឃាត ហើយ​បាន​សម្រេច​ចិត្ត​បាញ់​ចំ​ក្បាល​ដោយ​ការ​វាយ​ប្រហារ​លើក​ដំបូង​នៅ​ពាក់​កណ្តាល​អធ្រាត្រ។ ក្នុងអំឡុងពេលប៉ុន្មានថ្ងៃដែលនៅសេសសល់ Wolfskel បានសម្រេចចិត្តរៀបចំកិច្ចការរបស់គាត់ឱ្យមានសណ្តាប់ធ្នាប់ដែលដំណើរការល្អហើយនៅថ្ងៃចុងក្រោយគាត់បានធ្វើឆន្ទៈហើយសរសេរសំបុត្រទៅមិត្តភក្តិជិតស្និទ្ធនិងសាច់ញាតិ។

Wolfskehl បានធ្វើការដោយភាពខ្នះខ្នែងដែលគាត់បានបញ្ចប់អាជីវកម្មរបស់គាត់មុនពាក់កណ្តាលអធ្រាត្រ ហើយដើម្បីបំពេញម៉ោងដែលនៅសេសសល់ គាត់បានទៅបណ្ណាល័យ ជាកន្លែងដែលគាត់ចាប់ផ្តើមមើលទិនានុប្បវត្តិគណិតវិទ្យា។ មិនយូរប៉ុន្មានគាត់បានឃើញក្រដាសបុរាណរបស់ Kummer ដែលពន្យល់ពីមូលហេតុដែល Cauchy និង Lame បរាជ័យ។ ការងាររបស់ Kummer គឺជាការបោះពុម្ពគណិតវិទ្យាដ៏សំខាន់បំផុតមួយនៃសតវត្សរបស់ខ្លួន ហើយជាការអានដ៏ល្អបំផុតសម្រាប់គណិតវិទូដែលគិតអំពីការធ្វើអត្តឃាត។ Wolfskel ដោយប្រុងប្រយ័ត្នតាមបន្ទាត់តាមការគណនារបស់ Kummer ។ ដោយមិននឹកស្មានដល់ វាហាក់ដូចជា Wolfskel ដែលគាត់បានរកឃើញគម្លាតមួយ៖ អ្នកនិពន្ធបានធ្វើការសន្មត់ជាក់លាក់មួយ ហើយមិនបានបញ្ជាក់ពីជំហាននេះក្នុងការវែកញែករបស់គាត់នោះទេ។ Wolfskehl ឆ្ងល់ថាតើគាត់ពិតជាបានរកឃើញគម្លាតធ្ងន់ធ្ងរឬប្រសិនបើការសន្មត់របស់ Kummer គឺត្រឹមត្រូវ។ ប្រសិនបើគម្លាតត្រូវបានរកឃើញ នោះវាមានឱកាសដែលទ្រឹស្តីបទចុងក្រោយរបស់ Fermat អាចត្រូវបានបង្ហាញថាងាយស្រួលជាងការគិតជាច្រើន។

Wolfskehl អង្គុយនៅតុ វិភាគដោយប្រុងប្រយ័ត្ននូវផ្នែក "កំហុស" នៃការវែកញែករបស់ Kummer ហើយចាប់ផ្តើមគូសវាសនូវភស្តុតាងខ្នាតតូច ដែលត្រូវបានគេសន្មត់ថាគាំទ្រការងាររបស់ Kummer ឬបង្ហាញពីភាពមិនពិតនៃការសន្មត់ដែលគាត់បានធ្វើ ហើយជាលទ្ធផល។ បដិសេធរាល់អំណះអំណាងរបស់គាត់។ នៅពេលព្រឹកព្រលឹម Wolfskehl បានបញ្ចប់ការគណនារបស់គាត់។ ដំណឹងអាក្រក់ (គណិតវិទ្យា) គឺថា ភស្តុតាងរបស់ Kummer ត្រូវបានព្យាបាល ហើយទ្រឹស្តីបទចុងក្រោយរបស់ Fermat នៅតែមិនទាន់អាចទៅដល់បាន។ ប៉ុន្តែមានដំណឹងល្អ៖ ពេលវេលាសម្រាប់ការធ្វើអត្តឃាតបានកន្លងផុតទៅហើយ ហើយ Wolfskehl មានមោទនភាពយ៉ាងខ្លាំងដែលគាត់បានស្វែងរក និងបំពេញចន្លោះនៅក្នុងការងាររបស់ Ernest Kummer ដ៏អស្ចារ្យ ដែលភាពអស់សង្ឃឹមនិងភាពសោកសៅរបស់គាត់បានកំចាត់ចោលខ្លួនឯង។ គណិតវិទ្យាបានផ្តល់ឱ្យគាត់នូវការស្រេកឃ្លាននៃជីវិត។

ទោះយ៉ាងណាក៏ដោយមានកំណែជំនួស។ យោងទៅតាមនាង Wolfskel បានរៀនគណិតវិទ្យា (ហើយតាមពិតទ្រឹស្តីបទរបស់ Fermat) ដោយសារតែជំងឺក្រិនសរសៃឈាមរីកចម្រើនដែលរារាំងគាត់ពីការធ្វើអ្វីដែលគាត់ស្រឡាញ់ - ជាវេជ្ជបណ្ឌិត។ ហើយគាត់បានទុកលុយឱ្យគណិតវិទូដើម្បីកុំឱ្យចាកចេញពីប្រពន្ធរបស់គាត់ដែលគាត់ស្អប់នៅពេលចុងបញ្ចប់នៃជីវិតរបស់គាត់។

9.

ការប៉ុនប៉ងដើម្បីបញ្ជាក់ទ្រឹស្តីបទរបស់ Fermat ដោយវិធីសាស្រ្តបឋមបាននាំឱ្យមានការលេចឡើងនៃថ្នាក់ទាំងមូល មនុស្សចម្លែកត្រូវបានគេហៅថា "អ្នកនិយមនិយម" ។ ពួកគេបានធ្វើអ្វីដែលពួកគេបានធ្វើ ចំនួនទឹកប្រាក់ដ៏អស្ចារ្យភស្តុតាង ហើយមិនអស់សង្ឃឹមទាល់តែសោះ នៅពេលដែលរកឃើញកំហុសនៅក្នុងភស្តុតាងទាំងនេះ។

នៅមហាវិទ្យាល័យមេកានិក និងគណិតវិទ្យានៃសាកលវិទ្យាល័យរដ្ឋម៉ូស្គូ មានតួអង្គរឿងព្រេងនិទានឈ្មោះ Dobretsov ។ គាត់​បាន​ប្រមូល​វិញ្ញាបនបត្រ​ពី​នាយកដ្ឋាន​ផ្សេងៗ ហើយ​ដោយ​ប្រើ​វា​បាន​ទម្លាយ​ដល់​មេខមាត។ នេះ​ធ្វើ​ឡើង​ដើម្បី​ស្វែង​រក​ជន​រង​គ្រោះ​តែ​ប៉ុណ្ណោះ។ ដូចម្ដេចគាត់បានជួបនិស្សិតបញ្ចប់ការសិក្សាវ័យក្មេង (អ្នកសិក្សានាពេលអនាគត Novikov) ។ គាត់នៅក្នុងភាពឆោតល្ងង់របស់គាត់បានចាប់ផ្តើមសិក្សាដោយប្រុងប្រយ័ត្ននូវឯកសារដែល Dobretsov រអិលគាត់ដោយពាក្យដែលពួកគេនិយាយថានេះគឺជាភស្តុតាង។ បន្ទាប់ពីមួយទៀត "នេះគឺជាកំហុស ... " Dobretsov បានយកជង់ហើយដាក់ក្នុងកាបូបយួររបស់គាត់។ ពីកាតាបទីពីរ (បាទ គាត់បានដើរជុំវិញ mekhmat ជាមួយនឹងបាវពីរ) គាត់បានយកគំនរទីពីរចេញ ដកដង្ហើមធំ ហើយនិយាយថា៖ "អញ្ចឹង តោះមើលជម្រើស 7 B"។

ដោយវិធីនេះ ភាគច្រើននៃភស្តុតាងទាំងនេះចាប់ផ្តើមដោយឃ្លា "តោះផ្លាស់ទីពាក្យមួយទៅផ្នែកខាងស្តាំនៃសមភាព ហើយធ្វើកត្តាវា" ។

10.

រឿងអំពីទ្រឹស្តីបទនឹងមានភាពមិនពេញលេញដោយគ្មានខ្សែភាពយន្តដ៏អស្ចារ្យ "The Mathematician and the Devil"។

វិសោធនកម្ម

ផ្នែកទី 7 នៃអត្ថបទនេះពីដើមបាននិយាយថា Naum Elkies បានរកឃើញឧទាហរណ៍ផ្ទុយទៅនឹងទ្រឹស្តីបទរបស់ Fermat ដែលក្រោយមកបានប្រែជាខុស។ នេះ​មិន​ពិត​ទេ៖ សារ​អំពី​ឧទាហរណ៍​គឺ​ជា​រឿង​កំប្លែង​របស់ April Fool។ យើងសុំទោសចំពោះភាពមិនត្រឹមត្រូវ។

Andrey Konyaev