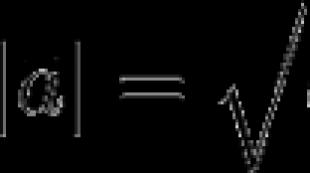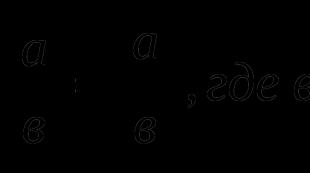អនុវិទ្យាល័យ MBOU №17 Ivanov

« សមីការម៉ូឌុល»
ការអភិវឌ្ឍន៍វិធីសាស្រ្ត

ចងក្រង

គ្រូគណិតវិទ្យា

Lebedeva N.V.

20010

កំណត់ចំណាំពន្យល់

ជំពូកទី 1 សេចក្តីផ្តើម

ផ្នែកទី 2. លក្ខណៈពិសេសចម្បង ផ្នែកទី 3. ការបកស្រាយធរណីមាត្រនៃគំនិតនៃម៉ូឌុលនៃចំនួនមួយ។ ផ្នែកទី 4. ក្រាហ្វនៃអនុគមន៍ y = |x| ផ្នែកទី 5 អនុសញ្ញា

ជំពូក 2

ផ្នែកទី 1. សមីការនៃទម្រង់ |F(х)| = m (ប្រូតូហ្សូអា) ផ្នែកទី 2. សមីការនៃទម្រង់ F(|х|) = m ផ្នែកទី 3. សមីការនៃទម្រង់ |F(х)| = G(x) ផ្នែកទី 4. សមីការនៃទម្រង់ |F(х)| = ± F(x) (ស្អាត) ផ្នែកទី 5. សមីការនៃទម្រង់ |F(х)| = |G(x)| ផ្នែកទី 6. ឧទាហរណ៍នៃការដោះស្រាយសមីការមិនស្តង់ដារ ផ្នែកទី 7. សមីការនៃទម្រង់ |F(х)| + |G(x)| = 0 ផ្នែកទី 8. សមីការនៃទម្រង់ |а 1 x ± в 1 | ± |a 2 x ± ក្នុង 2 | ± …|a n x ± ក្នុង n| = ម ផ្នែកទី 9. សមីការដែលមានម៉ូឌុលច្រើន។

ជំពូកទី 3. ឧទាហរណ៍នៃការដោះស្រាយសមីការផ្សេងៗជាមួយម៉ូឌុល។

ផ្នែកទី 1. សមីការត្រីកោណមាត្រ ផ្នែកទី 2. សមីការអិចស្ប៉ូណង់ស្យែល ផ្នែកទី 3. សមីការលោការីត ផ្នែកទី 4. សមីការមិនសមហេតុផល ផ្នែកទី 5. ភារកិច្ចនៃភាពស្មុគស្មាញកម្រិតខ្ពស់ ចម្លើយចំពោះលំហាត់ គន្ថនិទ្ទេស

កំណត់ចំណាំពន្យល់។

គោលគំនិតនៃតម្លៃដាច់ខាត (ម៉ូឌុល) នៃចំនួនពិត គឺជាលក្ខណៈសំខាន់មួយរបស់វា។ គំនិតនេះត្រូវបានប្រើប្រាស់យ៉ាងទូលំទូលាយនៅក្នុងផ្នែកផ្សេងៗនៃវិទ្យាសាស្ត្ររូបវិទ្យា គណិតវិទ្យា និងបច្ចេកទេស។ នៅក្នុងការអនុវត្តនៃការបង្រៀនមុខវិជ្ជាគណិតវិទ្យានៅអនុវិទ្យាល័យអនុលោមតាមកម្មវិធីរបស់ក្រសួងការពារជាតិនៃសហព័ន្ធរុស្ស៊ីគំនិតនៃ "តម្លៃដាច់ខាតនៃលេខ" ត្រូវបានជួបប្រទះម្តងហើយម្តងទៀត: នៅថ្នាក់ទី 6 និយមន័យនៃម៉ូឌុល។ អត្ថន័យធរណីមាត្ររបស់វាត្រូវបានណែនាំ។ នៅថ្នាក់ទី 8 គំនិតនៃកំហុសដាច់ខាតត្រូវបានបង្កើតឡើង ដំណោះស្រាយនៃសមីការសាមញ្ញបំផុត និងវិសមភាពដែលមានម៉ូឌុលត្រូវបានពិចារណា លក្ខណៈសម្បត្តិនៃឫសការ៉េនព្វន្ធត្រូវបានសិក្សា។ នៅថ្នាក់ទី 11 គំនិតត្រូវបានរកឃើញនៅក្នុងផ្នែក "ឫស នសញ្ញាបត្រ” ។បទពិសោធន៍នៃការបង្រៀនបង្ហាញថាសិស្សតែងតែជួបប្រទះការលំបាកក្នុងការដោះស្រាយកិច្ចការដែលទាមទារចំណេះដឹងអំពីសម្ភារៈនេះ ហើយជារឿយៗរំលងដោយមិនចាប់ផ្តើមបញ្ចប់។ នៅក្នុងអត្ថបទនៃភារកិច្ចប្រឡងសម្រាប់វគ្គសិក្សានៃថ្នាក់ទី 9 និងទី 11 ភារកិច្ចស្រដៀងគ្នាក៏ត្រូវបានរួមបញ្ចូលផងដែរ។ លើសពីនេះ លក្ខខណ្ឌតម្រូវដែលសាកលវិទ្យាល័យដាក់លើនិស្សិតបញ្ចប់ការសិក្សាគឺខុសគ្នា ពោលគឺមានកម្រិតខ្ពស់ជាងតម្រូវការនៃកម្មវិធីសិក្សារបស់សាលា។ សម្រាប់ជីវិតនៅក្នុងសង្គមសម័យទំនើប ការបង្កើតទម្រង់នៃការគិតបែបគណិតវិទ្យា ដែលបង្ហាញឱ្យឃើញពីជំនាញផ្លូវចិត្តជាក់លាក់ គឺមានសារៈសំខាន់ខ្លាំងណាស់។ នៅក្នុងដំណើរការនៃការដោះស្រាយបញ្ហាជាមួយម៉ូឌុល សមត្ថភាពក្នុងការអនុវត្តបច្ចេកទេសដូចជា ទូទៅ និងការបង្កើត ការវិភាគ ចំណាត់ថ្នាក់ និងប្រព័ន្ធ ភាពស្រដៀងគ្នាត្រូវបានទាមទារ។ ដំណោះស្រាយនៃភារកិច្ចបែបនេះអនុញ្ញាតឱ្យអ្នកពិនិត្យមើលចំណេះដឹងនៃផ្នែកសំខាន់ៗនៃវគ្គសិក្សារបស់សាលាកម្រិតនៃការគិតឡូជីខលនិងជំនាញដំបូងនៃការស្រាវជ្រាវ។ ការងារនេះត្រូវបានឧទ្ទិសដល់ផ្នែកមួយ - ដំណោះស្រាយនៃសមីការដែលមានម៉ូឌុល។ វាមានបីជំពូក។ ជំពូកទីមួយណែនាំអំពីគោលគំនិតជាមូលដ្ឋាន និងការគណនាទ្រឹស្តីសំខាន់ៗបំផុត។ ជំពូកទី 2 ស្នើប្រភេទសមីការជាមូលដ្ឋានចំនួនប្រាំបួនដែលមានម៉ូឌុល ពិចារណាវិធីសាស្រ្តសម្រាប់ដោះស្រាយពួកវា និងវិភាគឧទាហរណ៍នៃកម្រិតផ្សេងគ្នានៃភាពស្មុគស្មាញ។ ជំពូកទីបីផ្តល់នូវសមីការស្មុគស្មាញ និងមិនមានស្តង់ដារ (ត្រីកោណមាត្រ អិចស្ប៉ូណង់ស្យែល លោការីត និងអសមហេតុផល)។ សម្រាប់ប្រភេទនៃសមីការនីមួយៗមានលំហាត់សម្រាប់ដំណោះស្រាយឯករាជ្យ (ចម្លើយ និងការណែនាំត្រូវបានភ្ជាប់)។ គោលបំណងសំខាន់នៃការងារនេះគឺផ្តល់ជំនួយជាវិធីសាស្រ្តដល់គ្រូបង្រៀនក្នុងការរៀបចំមេរៀន និងក្នុងការរៀបចំវគ្គសិក្សាស្រេចចិត្ត។ សម្ភារៈក៏អាចប្រើជាជំនួយការបង្រៀនសម្រាប់សិស្សវិទ្យាល័យផងដែរ។ កិច្ចការដែលបានស្នើឡើងក្នុងការងារគឺគួរឱ្យចាប់អារម្មណ៍ ហើយមិនតែងតែងាយស្រួលក្នុងការដោះស្រាយនោះទេ ដែលធ្វើឱ្យវាអាចធ្វើឱ្យការលើកទឹកចិត្តក្នុងការសិក្សារបស់សិស្សកាន់តែមានមនសិការ សាកល្បងសមត្ថភាពរបស់ពួកគេ និងកែលម្អកម្រិតនៃការរៀបចំនិស្សិតបញ្ចប់ការសិក្សាសម្រាប់ចូលសាកលវិទ្យាល័យ។ ការជ្រើសរើសដោយឡែកនៃលំហាត់ដែលបានស្នើឡើងបង្កប់ន័យការផ្លាស់ប្តូរពីកម្រិតបន្តពូជនៃការបញ្ចូលសម្ភារៈទៅជាការច្នៃប្រឌិត ក៏ដូចជាឱកាសដើម្បីបង្រៀនពីរបៀបអនុវត្តចំណេះដឹងរបស់ពួកគេក្នុងការដោះស្រាយបញ្ហាដែលមិនមានស្តង់ដារ។

ជំពូក 1. សេចក្តីផ្តើម។

ផ្នែកទី 1. ការកំណត់តម្លៃដាច់ខាត .

និយមន័យ : តម្លៃដាច់ខាត (ម៉ូឌុល) នៃចំនួនពិត កត្រូវបានគេហៅថាលេខមិនអវិជ្ជមាន៖ កឬ - ក. ការកំណត់: │ ក │ ធាតុអានដូចខាងក្រោមៈ "ម៉ូឌុលនៃលេខ a" ឬ "តម្លៃដាច់ខាតនៃលេខ a"

│ a ប្រសិនបើ a > 0

│a│ = │ 0 ប្រសិនបើ a = 0 (1)

│ - a, ប្រសិនបើ a
ឧទាហរណ៍: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

ពង្រីកម៉ូឌុលកន្សោម៖

ក) │x − 8│ ប្រសិនបើ x > 12 ខ) │2x + 3│ ប្រសិនបើ x ≤ −2 │x - 8│= x − 8 │ 2x + 3│= − 2x − 3

ផ្នែកទី 2. លក្ខណៈសម្បត្តិមូលដ្ឋាន។

ពិចារណាអំពីលក្ខណៈសម្បត្តិជាមូលដ្ឋាននៃតម្លៃដាច់ខាត។ អចលនទ្រព្យលេខ ១៖ លេខទល់មុខមានម៉ូឌុលស្មើគ្នា i.e. │а│=│-а│ចូរយើងបង្ហាញពីភាពត្រឹមត្រូវនៃសមភាព។ ចូរយើងសរសេរនិយមន័យនៃលេខ - ក : │- ក│= (2) ចូរយើងប្រៀបធៀបសំណុំ (1) និង (2) ។ ជាក់ស្តែង និយមន័យនៃតម្លៃដាច់ខាតនៃលេខ កនិង - កផ្គូផ្គង។ អាស្រ័យហេតុនេះ │а│=│-а│
នៅពេលពិចារណាលើលក្ខណៈសម្បត្តិខាងក្រោម យើងបង្ខាំងខ្លួនយើងទៅនឹងការបង្កើតរបស់ពួកគេ ដោយសារភស្តុតាងរបស់ពួកគេត្រូវបានផ្តល់ឱ្យ អចលនទ្រព្យលេខ ២៖ តម្លៃដាច់ខាតនៃផលបូកនៃចំនួនកំណត់នៃចំនួនពិតមិនលើសពីផលបូកនៃតម្លៃដាច់ខាតនៃពាក្យ៖ អចលនទ្រព្យលេខ ៣៖ តម្លៃដាច់ខាតនៃភាពខុសគ្នារវាងចំនួនពិតពីរមិនត្រូវលើសពីផលបូកនៃតម្លៃដាច់ខាតរបស់វាទេ៖ │а - в│ ≤│а│+│в│ អចលនទ្រព្យលេខ ៤៖ តម្លៃដាច់ខាតនៃផលិតផលនៃចំនួនកំណត់នៃចំនួនពិតគឺស្មើនឹងផលិតផលនៃតម្លៃដាច់ខាតនៃកត្តា៖ │а · в│=│а│·│в│ អចលនទ្រព្យលេខ ៥៖ តម្លៃដាច់ខាតនៃកូតានៃចំនួនពិតគឺស្មើនឹងកូតានៃតម្លៃដាច់ខាតរបស់ពួកគេ៖

ផ្នែកទី 3. ការបកស្រាយធរណីមាត្រនៃគំនិតនៃម៉ូឌុលនៃចំនួនមួយ។

ចំនួនពិតនីមួយៗអាចត្រូវបានភ្ជាប់ជាមួយចំណុចនៅលើបន្ទាត់លេខ ដែលនឹងក្លាយជាតំណាងធរណីមាត្រនៃចំនួនពិតនេះ។ ចំណុចនីមួយៗនៅលើបន្ទាត់លេខត្រូវគ្នាទៅនឹងចម្ងាយរបស់វាពីប្រភពដើមពោលគឺឧ។ ប្រវែងនៃផ្នែកពីប្រភពដើមទៅចំណុចដែលបានផ្តល់ឱ្យ។ ចម្ងាយនេះតែងតែត្រូវបានចាត់ទុកថាជាតម្លៃមិនអវិជ្ជមាន។ ដូច្នេះប្រវែងនៃផ្នែកដែលត្រូវគ្នានឹងជាការបកស្រាយធរណីមាត្រនៃតម្លៃដាច់ខាតនៃចំនួនពិតដែលបានផ្តល់ឱ្យ។

រូបភាពធរណីមាត្រដែលបានបង្ហាញបញ្ជាក់យ៉ាងច្បាស់អំពីទ្រព្យសម្បត្តិលេខ 1 ពោលគឺឧ។ ម៉ូឌុលនៃលេខផ្ទុយគឺស្មើគ្នា។ ពីទីនេះ សុពលភាពនៃសមភាពងាយយល់៖ │x - a│= │a - x│ ។ វាក៏កាន់តែច្បាស់ផងដែរក្នុងការដោះស្រាយសមីការ │х│= m ដែល m ≥ 0 គឺ x 1.2 = ± m ។ ឧទាហរណ៍: 1) │х│= 4 x 1.2 = ± 4 2) │х − 3│= 1
x 1.2 = 2; ៤

ផ្នែកទី 4. ក្រាហ្វនៃអនុគមន៍ y \u003d │х│

ដែននៃអនុគមន៍នេះគឺជាចំនួនពិតទាំងអស់។

ផ្នែកទី 5. និមិត្តសញ្ញា។

នៅពេលអនាគត នៅពេលពិចារណាឧទាហរណ៍នៃការដោះស្រាយសមីការ អនុសញ្ញាខាងក្រោមនឹងត្រូវបានប្រើ៖ (-សញ្ញាប្រព័ន្ធ [-កំណត់សញ្ញា នៅពេលដោះស្រាយប្រព័ន្ធសមីការ (វិសមភាព) ចំនុចប្រសព្វនៃដំណោះស្រាយនៃសមីការ (វិសមភាព) ដែលរួមបញ្ចូលក្នុងប្រព័ន្ធត្រូវបានរកឃើញ។ នៅពេលដោះស្រាយសំណុំសមីការ (វិសមភាព) ដំណោះស្រាយនៃសមីការ (វិសមភាព) ដែលរួមបញ្ចូលក្នុងសំណុំត្រូវបានរកឃើញ។

ជំពូក 2

នៅក្នុងជំពូកនេះ យើងនឹងពិនិត្យមើលវិធីពិជគណិតដើម្បីដោះស្រាយសមីការដែលមានម៉ូឌុលមួយ ឬច្រើន។

ផ្នែកទី 1. សមីការនៃទម្រង់ │F (х) │= m

សមីការនៃប្រភេទនេះត្រូវបានគេហៅថាសាមញ្ញបំផុត។ វាមានដំណោះស្រាយប្រសិនបើ m ≥ 0 ។ តាមនិយមន័យនៃម៉ូឌុល សមីការដើមគឺស្មើនឹងការរួមបញ្ចូលគ្នានៃសមីការពីរ៖ │ ច(x)│=ម
ឧទាហរណ៍:
№1. ដោះស្រាយសមីការ៖ │7x − 2│= 9


ចម្លើយ៖ x 1 = - ១; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = −1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 \u003d 0; x 2 = −3 ចម្លើយ៖ ផលបូកនៃឫសគឺ - ២.№3
│x 4 −5x 2 + 2│= 2 x 4 − 5x 2 = 0 x 4 − 5x 2 + 4 = 0 x 2 (x 2 − 5) = 0 កំណត់ x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – តម្លៃទាំងពីរបំពេញលក្ខខណ្ឌ m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 ចម្លើយ៖ ចំនួនឫសនៃសមីការ ៧. លំហាត់៖
№1. ដោះស្រាយសមីការ និងចង្អុលបង្ហាញផលបូកនៃឫស៖ │x - 5│= 3 №2 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសតូច៖ │x 2 + x │ \u003d 0 №3 . ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសធំ៖ │x 2 - 5x + 4 │ \u003d 4 №4 .ដោះស្រាយសមីការ និងចង្អុលបង្ហាញឫសទាំងមូល៖ │2x 2 - 7x + 6│ \u003d 1 №5 .ដោះស្រាយសមីការ និងចង្អុលបង្ហាញចំនួនឫស៖ │x 4 − 13x 2 + 50 │ = 14

ផ្នែកទី 2. សមីការនៃទម្រង់ F(│х│) = m

អាគុយម៉ង់មុខងារនៅផ្នែកខាងឆ្វេងគឺស្ថិតនៅក្រោមសញ្ញាម៉ូឌុលខណៈពេលដែលផ្នែកខាងស្តាំគឺឯករាជ្យនៃអថេរ។ ចូរយើងពិចារណាវិធីពីរយ៉ាងនៃការដោះស្រាយសមីការនៃប្រភេទនេះ។ 1 វិធី៖តាមនិយមន័យនៃតម្លៃដាច់ខាត សមីការដើមគឺស្មើនឹងចំនួនសរុបនៃប្រព័ន្ធពីរ។ នៅក្នុងលក្ខខណ្ឌនីមួយៗត្រូវបានដាក់លើកន្សោមម៉ូឌុលរង។ ច(│х│) =ម
ដោយសារមុខងារ F(│х│) គឺសូម្បីតែនៅលើដែនទាំងមូលនៃនិយមន័យ ឫសនៃសមីការ F(х) = m និង F(-х) = m គឺជាគូនៃលេខផ្ទុយ។ ដូច្នេះវាគ្រប់គ្រាន់ដើម្បីដោះស្រាយប្រព័ន្ធមួយ (នៅពេលពិចារណាឧទាហរណ៍ក្នុងវិធីនេះ ដំណោះស្រាយនៃប្រព័ន្ធមួយនឹងត្រូវបានផ្តល់ឱ្យ) ។ 2 វិធី៖ការអនុវត្តវិធីសាស្រ្តនៃការណែនាំអថេរថ្មី។ ក្នុងករណីនេះ ការរចនា │х│= a ត្រូវបានណែនាំ ដែល a ≥ 0. វិធីសាស្រ្តនេះគឺមិនសូវមានពន្លឺនៅក្នុងការរចនា។
ឧទាហរណ៍: №1 . ដោះស្រាយសមីការ៖ 3x 2 − 4│x│ = − 1 ចូរប្រើការណែនាំនៃអថេរថ្មី។ សម្គាល់ │х│= a ដែល a ≥ 0. យើងទទួលបានសមីការ 3a 2 − 4a + 1 = 0 D = 16 − 12 = 4 a 1 = 1 a 2 = 1 / 3 យើងត្រលប់ទៅអថេរដើម៖ │х │ = 1 និង │х│ = 1/3 ។ សមីការនីមួយៗមានឫសពីរ។ ចម្លើយ៖ x 1 = 1; X 2 = - ១; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. ដោះស្រាយសមីការ៖ 5x 2 + 3│x│- 1 \u003d 1/2 │x│ + 3x 2
ចូរយើងស្វែងរកដំណោះស្រាយនៃប្រព័ន្ធកំណត់ដំបូង៖ 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 ចំណាំថា x 2 ធ្វើ មិនបំពេញលក្ខខណ្ឌ x ≥ 0 ។ តាមដំណោះស្រាយ ប្រព័ន្ធទីពីរនឹងជាលេខផ្ទុយ x 1 ។ ចម្លើយ៖ x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . ដោះស្រាយសមីការ៖ x 4 - │х│= 0 បញ្ជាក់ │х│= a ដែល a ≥ 0. យើងទទួលបានសមីការ a 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d 0 a 2 \u003d 1 យើងត្រឡប់ទៅអថេរដើមវិញ៖ │х│=0 និង │х│= 1 x = 0; ± ១ ចម្លើយ៖ x 1 = 0; X 2 = 1; X 3 = - 1.
លំហាត់៖ №6. ដោះស្រាយសមីការ៖ 2│х│ - 4.5 = 5 - 3/8 │х│ №7 . ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីចំនួនឫស៖ 3x 2 - 7│x│ + 2 = 0 №8 . ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីដំណោះស្រាយទាំងមូល៖ x 4 + │х│ - 2 = 0

ផ្នែកទី 3. សមីការនៃទម្រង់ │F(х)│ = G(х)

ផ្នែកខាងស្តាំនៃសមីការនៃប្រភេទនេះអាស្រ័យលើអថេរមួយ ហើយដូច្នេះវាមានដំណោះស្រាយប្រសិនបើផ្នែកខាងស្តាំគឺជាអនុគមន៍ G(x) ≥ 0។ សមីការដើមអាចត្រូវបានដោះស្រាយតាមពីរវិធី៖ 1 វិធី៖ស្តង់ដារដោយផ្អែកលើការបង្ហាញនៃម៉ូឌុលដោយផ្អែកលើនិយមន័យរបស់វា និងមាននៅក្នុងការផ្លាស់ប្តូរសមមូលទៅនឹងការរួមបញ្ចូលគ្នានៃប្រព័ន្ធពីរ។ │ ច(x)│ =ជី(X)

វាសមហេតុផលក្នុងការប្រើវិធីនេះក្នុងករណីកន្សោមស្មុគស្មាញសម្រាប់អនុគមន៍ G(x) និងកន្សោមស្មុគ្រស្មាញតិចសម្រាប់អនុគមន៍ F(x) ព្រោះវាត្រូវបានគេសន្មត់ថាដើម្បីដោះស្រាយវិសមភាពជាមួយអនុគមន៍ F(x)។ 2 វិធី៖វាមាននៅក្នុងការផ្លាស់ប្តូរទៅជាប្រព័ន្ធសមមូលដែលលក្ខខណ្ឌមួយត្រូវបានដាក់នៅខាងស្តាំ។ │ ច(x)│= ជី(x)

វិធីសាស្ត្រនេះងាយស្រួលប្រើជាង ប្រសិនបើកន្សោមសម្រាប់អនុគមន៍ G(x) មានភាពស្មុគស្មាញតិចជាងអនុគមន៍ F(x) ចាប់តាំងពីដំណោះស្រាយនៃវិសមភាព G(x) ≥ 0 ត្រូវបានសន្មត់។ បន្ថែមពីលើនេះ នៅក្នុងករណី នៃម៉ូឌុលជាច្រើន វិធីសាស្ត្រនេះត្រូវបានណែនាំឱ្យប្រើជម្រើសទីពីរ។ ឧទាហរណ៍: №1. ដោះស្រាយសមីការ៖ │x + 2│ = 6 −2x
(1 វិធី) ចម្លើយ៖ x = ១ 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(២ ផ្លូវ) ចំលើយ៖ ផលិតផលឫសគឺ ៣.
№3. ដោះស្រាយសមីការ ក្នុងចម្លើយសរសេរផលបូកនៃឫស៖
│x - 6 │ \u003d x 2 - 5x + 9

ចម្លើយ៖ ផលបូកនៃឫសគឺ ៤.
លំហាត់៖ №9. │x + 4│= − 3x №10. ដោះស្រាយសមីការ ក្នុងចម្លើយបង្ហាញពីចំនួនដំណោះស្រាយ៖ │x 2 + x - 1 │ \u003d 2x - 1 №11 . ដោះស្រាយសមីការ ក្នុងចម្លើយបង្ហាញពីផលិតផលនៃឫស៖ │x + 3 │ \u003d x 2 + x - 6

ផ្នែកទី 4. សមីការនៃទម្រង់ │F(x)│= F(x) និង │F(x)│= - F(x)

សមីការនៃប្រភេទនេះជួនកាលត្រូវបានគេហៅថា "ស្រស់ស្អាត" ។ ដោយសារផ្នែកខាងស្តាំនៃសមីការអាស្រ័យទៅលើអថេរ ដំណោះស្រាយមានប្រសិនបើ ហើយប្រសិនបើផ្នែកខាងស្តាំមិនអវិជ្ជមាន។ ដូច្នេះសមីការដើមគឺស្មើនឹងវិសមភាព៖
│F(x)│= F(x) F(x) ≥ 0 និង │F(x)│= - F(x) F(x) ឧទាហរណ៍: №1 . ដោះស្រាយសមីការ ក្នុងចម្លើយបង្ហាញពីចំនួនគត់តូចជាង៖ │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0.6 ចម្លើយ៖ x = ១№2. ដោះស្រាយសមីការ ក្នុងចម្លើយបង្ហាញពីប្រវែងនៃគម្លាត៖ │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] ចម្លើយ៖ ប្រវែងនៃគម្លាតគឺ 6 ។№3 . ដោះស្រាយសមីការ ក្នុងចំលើយបង្ហាញពីចំនួននៃដំណោះស្រាយចំនួនគត់៖ │2 + x − x 2 │ = 2 + x − x 2 2 + x − x 2 ≥ 0 x 2 − x − 2 ≤ 0 [ − 1 ; 2] ចម្លើយ៖ ៤ ដំណោះស្រាយទាំងមូល។№4 . ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីឫសធំបំផុត៖
│4 - x -
│ = 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1.2 \u003d
≈ 1,4

ចម្លើយ៖ x = ៣.

លំហាត់៖ №12. ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីឫសទាំងមូល៖ │x 2 + 6x + 8 │ = x 2 + 6x + 8 №13. ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីចំនួននៃដំណោះស្រាយចំនួនគត់៖ │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីចំនួនគត់ដែលមិនមែនជាឫសគល់នៃសមីការ៖

ផ្នែកទី 5. សមីការនៃទម្រង់ │F(x)│= │G(x)│

ដោយសារផ្នែកទាំងពីរនៃសមីការមិនអវិជ្ជមាន ដំណោះស្រាយពាក់ព័ន្ធនឹងការពិចារណាលើករណីពីរ៖ កន្សោមម៉ូឌុលរងគឺស្មើគ្នា ឬផ្ទុយគ្នាក្នុងសញ្ញា។ ដូច្នេះសមីការដើមគឺស្មើនឹងការរួមបញ្ចូលគ្នានៃសមីការពីរ៖ │ ច(x)│= │ ជី(x)│
ឧទាហរណ៍: №1. ដោះស្រាយសមីការ ក្នុងចម្លើយបង្ហាញឫសទាំងមូល៖ │x + 3│ \u003d │2x - 1│
ចម្លើយ៖ ចំនួនគត់ root x = 4 ។№2. ដោះស្រាយសមីការ៖ │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
ចម្លើយ៖ x = ២.№3 . ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីផលគុណនៃឫស៖




ឫសគល់នៃសមីការ 4x 2 + 2x - 1 \u003d 0 x 1.2 \u003d - 1±√5 / 4 ចម្លើយ៖ ផលិតផលឫសគឺ ០.២៥ ។ លំហាត់៖ №15 . ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីដំណោះស្រាយទាំងមូល៖ │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីឫសតូចជាង៖ │5x - 3│=│7 - x│ №17 . ដោះស្រាយសមីការ ក្នុងចម្លើយសរសេរផលបូកនៃឫស៖

ផ្នែកទី 6. ឧទាហរណ៍នៃការដោះស្រាយសមីការមិនស្តង់ដារ

នៅក្នុងផ្នែកនេះ យើងពិចារណាឧទាហរណ៍នៃសមីការមិនស្តង់ដារ នៅក្នុងដំណោះស្រាយដែលតម្លៃដាច់ខាតនៃការបញ្ចេញមតិត្រូវបានបង្ហាញតាមនិយមន័យ។ ឧទាហរណ៍:

№1. ដោះស្រាយសមីការ ក្នុងចម្លើយបង្ហាញពីផលបូកនៃឫស៖ x │x│- 5x - 6 \u003d 0
ចម្លើយ៖ ផលបូកនៃឫសគឺ ១ №2. . ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីឫសតូច៖ x 2 - 4x
- 5 = 0
ចម្លើយ៖ ឫសតូច x = − ៥ ។ №3. ដោះស្រាយសមីការ៖

ចម្លើយ៖ x = −1 ។ លំហាត់៖ №18. ដោះស្រាយសមីការ ហើយសរសេរផលបូកនៃឫស៖ x │3x + 5│ = 3x 2 + 4x + 3
№19. ដោះស្រាយសមីការ៖ x 2 - 3x \u003d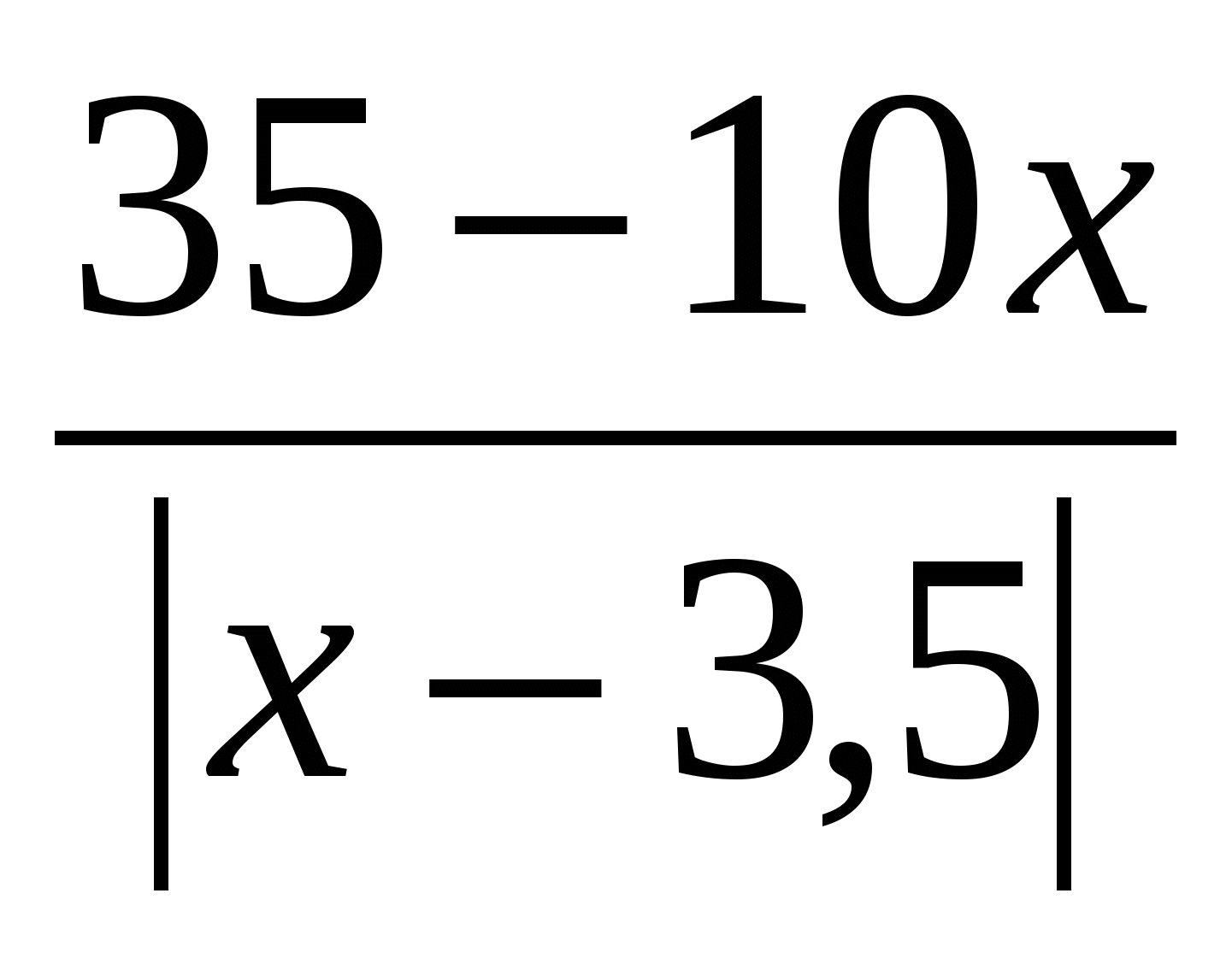

№20. ដោះស្រាយសមីការ៖

ផ្នែកទី 7. សមីការនៃទម្រង់ │F(x)│+│G(x)│=0

វាងាយស្រួលក្នុងការឃើញថានៅផ្នែកខាងឆ្វេងនៃសមីការនៃប្រភេទនេះ ផលបូកនៃបរិមាណមិនអវិជ្ជមាន។ ដូច្នេះ សមីការដើមមានដំណោះស្រាយប្រសិនបើ និងលុះត្រាតែពាក្យទាំងពីរក្នុងពេលដំណាលគ្នាស្មើនឹងសូន្យ។ សមីការគឺស្មើនឹងប្រព័ន្ធសមីការ៖ │ ច(x)│+│ ជី(x)│=0
ឧទាហរណ៍: №1 . ដោះស្រាយសមីការ៖
ចម្លើយ៖ x = ២. №2. ដោះស្រាយសមីការ៖ ចម្លើយ៖ x = ១. លំហាត់៖ №21. ដោះស្រាយសមីការ៖ №22 . ដោះស្រាយសមីការ ក្នុងចម្លើយសរសេរផលបូកនៃឫស៖ №23 . ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីចំនួនដំណោះស្រាយ៖

ផ្នែកទី 8. សមីការនៃទម្រង់

ដើម្បីដោះស្រាយសមីការនៃប្រភេទនេះ វិធីសាស្ត្រនៃចន្លោះពេលត្រូវបានប្រើ។ ប្រសិនបើវាត្រូវបានដោះស្រាយដោយការពង្រីកជាបន្តបន្ទាប់នៃម៉ូឌុលនោះយើងទទួលបាន នសំណុំនៃប្រព័ន្ធ ដែលស្មុគស្មាញ និងរអាក់រអួល។ ពិចារណាអំពីក្បួនដោះស្រាយនៃវិធីសាស្ត្រចន្លោះពេល៖ ១). ស្វែងរកតម្លៃអថេរ Xដែលម៉ូឌុលនីមួយៗស្មើនឹងសូន្យ (សូន្យនៃកន្សោមម៉ូឌុលរង)៖
២). តម្លៃ​ដែល​បាន​រក​ឃើញ​ត្រូវ​បាន​សម្គាល់​លើ​បន្ទាត់​លេខ​ដែល​ត្រូវ​បាន​បែង​ចែក​ជា​ចន្លោះ​ពេល (ចំនួន​ចន្លោះ​ពេល​រៀង​គ្នា​គឺ​ស្មើ​នឹង ន+1 ) ៣). កំណត់ជាមួយនឹងសញ្ញាណាមួយដែលម៉ូឌុលនីមួយៗត្រូវបានបង្ហាញនៅចន្លោះពេលនីមួយៗដែលទទួលបាន (នៅពេលបង្កើតដំណោះស្រាយអ្នកអាចប្រើបន្ទាត់លេខសម្គាល់សញ្ញានៅលើវា) 4) ។ សមីការដើមគឺស្មើនឹងសំណុំ ន+1 ប្រព័ន្ធនីមួយៗ ដែលសមាជិកភាពនៃអថេរត្រូវបានចង្អុលបង្ហាញ Xចន្លោះពេលមួយ។ ឧទាហរណ៍: №1 . ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីឫសធំបំផុត៖
១). ចូររកលេខសូន្យនៃកន្សោមម៉ូឌុល៖ x = 2; x = −3 ២). យើងសម្គាល់តម្លៃដែលបានរកឃើញនៅលើបន្ទាត់លេខ ហើយកំណត់ជាមួយនឹងសញ្ញាអ្វីដែលម៉ូឌុលនីមួយៗត្រូវបានបង្ហាញនៅលើចន្លោះពេលដែលទទួលបាន៖
x – 2 x – 2 x – 2 – - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- គ្មានដំណោះស្រាយ សមីការមានឫសពីរ។ ចម្លើយ៖ ឫសធំបំផុតគឺ x = 2 ។ №2. ដោះស្រាយសមីការ សរសេរឫសទាំងមូលនៅក្នុងចម្លើយ៖
១). ចូរយើងស្វែងរកលេខសូន្យនៃកន្សោមម៉ូឌុលរង៖ x = 1.5; x = − 1 2). យើងសម្គាល់តម្លៃដែលបានរកឃើញនៅលើបន្ទាត់លេខ ហើយកំណត់ជាមួយនឹងសញ្ញាអ្វីដែលម៉ូឌុលនីមួយៗត្រូវបានបង្ហាញនៅលើចន្លោះពេលដែលទទួលបាន៖ x + 1 x + 1 x + 1 - + +
-1 1.5 х 2х − 3 2х − 3 2х − 3 - - +
3).
ប្រព័ន្ធចុងក្រោយមិនមានដំណោះស្រាយទេ ដូច្នេះសមីការមានឫសពីរ។ នៅពេលដោះស្រាយសមីការ អ្នកគួរតែយកចិត្តទុកដាក់លើសញ្ញា "-" នៅពីមុខម៉ូឌុលទីពីរ។ ចម្លើយ៖ ចំនួនគត់ root x = 7 ។ №3. ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីផលបូកនៃឫស៖ ១). ចូរយើងស្វែងរកលេខសូន្យនៃកន្សោមម៉ូឌុលរង៖ x = 5; x = 1; x = − 2 ២). យើងសម្គាល់តម្លៃដែលបានរកឃើញនៅលើបន្ទាត់លេខ ហើយកំណត់ជាមួយនឹងសញ្ញាអ្វីដែលម៉ូឌុលនីមួយៗត្រូវបានបង្ហាញនៅលើចន្លោះពេលដែលទទួលបាន៖ x - 5 x - 5 x - 5 x - 5 - - - +
−2 1 5 x x – 1 x – 1 x – 1 x – 1 – − + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
សមីការមានឫសពីរ x = 0 និង 2 ។ ចម្លើយ៖ ផលបូកនៃឫសគឺ ២. №4 . ដោះស្រាយសមីការ៖ ១). ចូរយើងស្វែងរកលេខសូន្យនៃកន្សោមម៉ូឌុល៖ x = 1; x = 2; x = 3. 2). អនុញ្ញាតឱ្យយើងកំណត់សញ្ញាដែលម៉ូឌុលនីមួយៗត្រូវបានពង្រីកនៅលើចន្លោះពេលដែលទទួលបាន។ ៣).
យើងរួមបញ្ចូលគ្នានូវដំណោះស្រាយនៃប្រព័ន្ធបីដំបូង។ ចម្លើយ៖ ; x = ៥.
លំហាត់៖ №24. ដោះស្រាយសមីការ៖
№25. ដោះស្រាយសមីការ ក្នុងចម្លើយសរសេរផលបូកនៃឫស៖ №26. ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីឫសតូចជាង៖ №27. ដោះស្រាយសមីការ ផ្តល់ឫសធំនៅក្នុងចម្លើយរបស់អ្នក៖

ផ្នែកទី 9. សមីការដែលមានម៉ូឌុលច្រើន។

សមីការដែលមានម៉ូឌុលច្រើនសន្មតថាវត្តមាននៃតម្លៃដាច់ខាតនៅក្នុងកន្សោមម៉ូឌុលរង។ គោលការណ៍ជាមូលដ្ឋាននៃការដោះស្រាយសមីការនៃប្រភេទនេះគឺការបង្ហាញជាបន្តបន្ទាប់នៃម៉ូឌុលដោយចាប់ផ្តើមជាមួយ "ខាងក្រៅ" ។ នៅក្នុងវគ្គនៃដំណោះស្រាយ បច្ចេកទេសដែលបានពិភាក្សានៅក្នុងផ្នែកលេខ 1 លេខ 3 ត្រូវបានប្រើ។

ឧទាហរណ៍: №1. ដោះស្រាយសមីការ៖
ចម្លើយ៖ x = 1; - ដប់មួយ №2. ដោះស្រាយសមីការ៖
ចម្លើយ៖ x = 0; ៤; - ៤. №3. ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីផលគុណនៃឫស៖
ចំលើយ៖ ផលិតផលឫសគឺ ៨. №4. ដោះស្រាយសមីការ៖
សម្គាល់សមីការប្រជាជន (1) និង (2) ហើយពិចារណាដំណោះស្រាយនៃពួកវានីមួយៗដាច់ដោយឡែកពីគ្នាសម្រាប់ភាពងាយស្រួលនៃការរចនា។ ដោយសារសមីការទាំងពីរមានម៉ូឌុលច្រើនជាងមួយ វាកាន់តែងាយស្រួលក្នុងការអនុវត្តការផ្លាស់ប្តូរសមមូលទៅជាសំណុំនៃប្រព័ន្ធ។ (1)

(2)


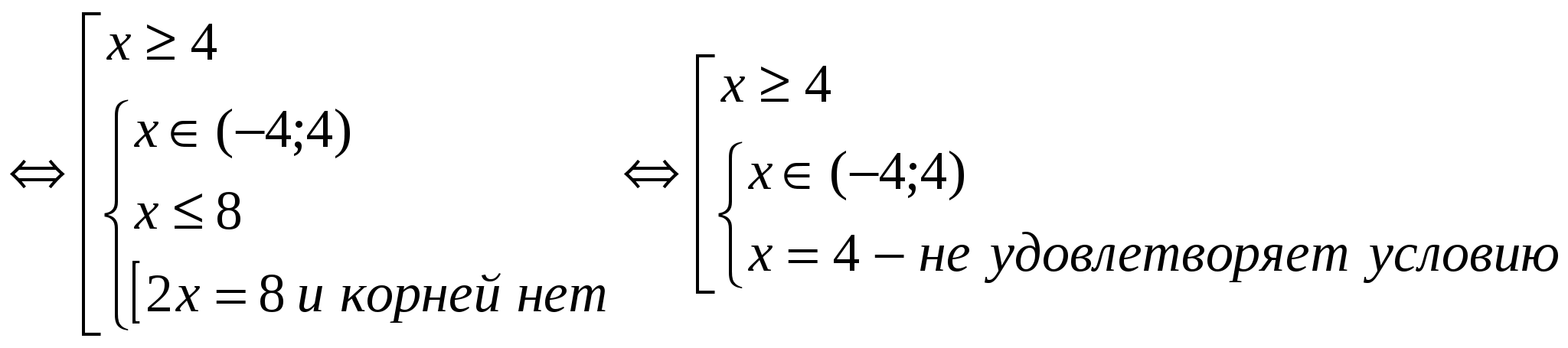ចម្លើយ៖
លំហាត់៖ №36. ដោះស្រាយសមីការ ក្នុងចម្លើយបង្ហាញពីផលបូកនៃឫស៖ 5 │3x-5│ \u003d 25 x №37. ដោះស្រាយសមីការប្រសិនបើមានឫសច្រើនជាងមួយ ក្នុងចម្លើយបង្ហាញពីផលបូកនៃឫស៖ │x + 2│ x - 3x - 10 = 1 №38. ដោះស្រាយសមីការ៖ 3 │2x -4│ \u003d 9 │x│ №39. ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីចំនួនឫសសម្រាប់៖ 2 │ sin x │ = √2 №40 . ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីចំនួនឫស៖

ផ្នែកទី 3. សមីការលោការីត។

មុននឹងដោះស្រាយសមីការខាងក្រោម ចាំបាច់ត្រូវពិនិត្យមើលលក្ខណៈសម្បត្តិរបស់លោការីត និងអនុគមន៍លោការីត។ ឧទាហរណ៍: №1. ដោះស្រាយសមីការនៅក្នុងចម្លើយបង្ហាញពីផលិតផលនៃឫស៖ កំណត់ហេតុ 2 (x + 1) 2 + កំណត់ហេតុ 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ − 1

ករណីទី 1៖ ប្រសិនបើ x ≥ − 1 បន្ទាប់មក log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – បំពេញលក្ខខណ្ឌ x ≥ - 1 2 ករណី៖ ប្រសិនបើ x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 កំណត់ហេតុ 2 (-(x+1) 3) = កំណត់ហេតុ 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = − 5– បំពេញលក្ខខណ្ឌ x - 1
ចម្លើយ៖ ផលិតផលឫសគឺ ១៥.
№2. ដោះស្រាយសមីការ ចម្លើយបង្ហាញពីផលបូកនៃឫស៖ lg
O.D.Z.

ចម្លើយ៖ ផលបូកនៃឫសគឺ ០.៥។
№3. ដោះស្រាយសមីការ៖ កំណត់ហេតុ ៥
O.D.Z.

ចម្លើយ៖ x = ៩ ។ №4. ដោះស្រាយសមីការ៖ │2 + log 0.2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 ចូរយើងប្រើរូបមន្តសម្រាប់ផ្លាស់ទីទៅមូលដ្ឋានផ្សេងទៀត។ │2 - កំណត់ហេតុ 5 x│+ 3 = │1 + កំណត់ហេតុ 5 x│
│2 - log 5 x│- │1 + log 5 x│= − 3 ចូររកលេខសូន្យនៃកន្សោមម៉ូឌុល៖ x = 25; x \u003d លេខទាំងនេះបែងចែកតំបន់នៃតម្លៃដែលអាចអនុញ្ញាតបានទៅជាបីចន្លោះ ដូច្នេះសមីការគឺស្មើនឹងចំនួនសរុបនៃប្រព័ន្ធទាំងបី។
ចម្លើយ :)