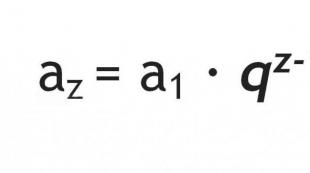Ზღაპრები

კონუსის კონცეფცია. კონუსი, როგორც გეომეტრიული ფიგურა, რა არის კონუსის გენერატრიქსის სიგრძე

რომლებიც გამოდიან ერთი წერტილიდან (კონუსის ზემოდან) და რომლებიც გადიან ბრტყელ ზედაპირზე.

ეს ხდება, რომ კონუსი არის სხეულის ნაწილი, რომელსაც აქვს შეზღუდული მოცულობა და მიიღება თითოეული სეგმენტის გაერთიანებით, რომელიც აკავშირებს ბრტყელი ზედაპირის წვეროსა და წერტილებს. ეს უკანასკნელი, ამ შემთხვევაში, არის კონუსის საფუძველი, და ამბობენ, რომ კონუსი ეყრდნობა ამ ბაზას.

როდესაც კონუსის საფუძველი მრავალკუთხედია, ის უკვე არის პირამიდა .

წრიული კონუსი- ეს არის სხეული, რომელიც შედგება წრისგან (კონუსის ფუძე), წერტილი, რომელიც არ დევს ამ წრის სიბრტყეში (კონუსის ზედა ნაწილი და ყველა სეგმენტი, რომელიც აკავშირებს კონუსის ზედა წერტილს). ბაზა).

სეგმენტები, რომლებიც აკავშირებენ კონუსის წვეროსა და ფუძის წრის წერტილებს, ეწოდება კონუსის ფორმირება. კონუსის ზედაპირი შედგება ფუძისა და გვერდითი ზედაპირისგან.

გვერდითი ზედაპირის ფართობი სწორია ნ- ნახშირბადის პირამიდა ჩაწერილი კონუსში:

S n =½P n l n,

სად P n- პირამიდის ფუძის პერიმეტრი და ლ ნ- აპოთემა.

იგივე პრინციპით: ჩამოჭრილი კონუსის გვერდითი ზედაპირის ფართობისთვის ბაზის რადიუსებით R 1, R 2და ფორმირება ლვიღებთ შემდეგ ფორმულას:

S=(R 1 +R 2)l.

სწორი და ირიბი წრიული კონუსები თანაბარი ფუძით და სიმაღლით. ამ სხეულებს აქვთ იგივე მოცულობა:

კონუსის თვისებები.

როდესაც ფუძის ფართობს აქვს ზღვარი, ეს ნიშნავს, რომ კონუსის მოცულობას ასევე აქვს ზღვარი და უდრის სიმაღლის პროდუქტის მესამე ნაწილს და ფუძის ფართობს.

სად ს- ბაზის ფართობი, ჰ- სიმაღლე.

ამრიგად, თითოეულ კონუსს, რომელიც ეყრდნობა ამ ფუძეს და აქვს წვერო, რომელიც მდებარეობს ფუძის პარალელურად სიბრტყეზე, აქვს თანაბარი მოცულობა, რადგან მათი სიმაღლეები იგივეა.

ლიმიტის მქონე თითოეული კონუსის სიმძიმის ცენტრი მდებარეობს ფუძიდან სიმაღლის მეოთხედზე.
სწორი წრიული კონუსის წვეროზე მყარი კუთხე შეიძლება გამოისახოს შემდეგი ფორმულით:

სად α - კონუსის გახსნის კუთხე.

ასეთი კონუსის გვერდითი ზედაპირის ფართობი, ფორმულა:

და მთლიანი ზედაპირის ფართობი (ანუ გვერდითი ზედაპირისა და ფუძის ფართობების ჯამი), ფორმულა:

S=πR(l+R),

სად რ- ბაზის რადიუსი, ლ- გენერატორის სიგრძე.

წრიული კონუსის მოცულობა, ფორმულა:

შეკვეცილი კონუსისთვის (არა მხოლოდ სწორი ან წრიული), მოცულობა, ფორმულა:

სად S 1და S 2- ზედა და ქვედა ბაზის ფართობი,

თდა ჰ- დისტანციები ზედა და ქვედა ბაზის სიბრტყიდან ზევით.

სიბრტყის გადაკვეთა მარჯვენა წრიულ კონუსთან ერთ-ერთი კონუსური მონაკვეთია.

ამ გაკვეთილზე ჩვენ გავეცნობით ისეთ ფიგურას, როგორიცაა კონუსი. შევისწავლოთ კონუსის ელემენტები და მისი მონაკვეთების ტიპები. და ჩვენ გავარკვევთ, რომელ ფიგურასთან აქვს კონუსს მრავალი საერთო თვისება.

ნახ.1. კონუსის ფორმის ობიექტები

მსოფლიოში უამრავი ნივთი კონუსის ფორმისაა. ხშირად ჩვენ არც კი ვამჩნევთ მათ. გზის კონუსები გამაფრთხილებელი საგზაო სამუშაოების შესახებ, ციხესიმაგრეებისა და სახლების სახურავები, ნაყინის გირჩები - ყველა ეს ობიექტი კონუსის ფორმისაა (იხ. სურ. 1).

ბრინჯი. 2. მართკუთხა სამკუთხედი

განვიხილოთ თვითნებური მართკუთხა სამკუთხედი ფეხებით და (იხ. სურ. 2).

ბრინჯი. 3. სწორი წრიული კონუსი

მოცემული სამკუთხედის ერთ-ერთი ფეხის გარშემო შემობრუნებით (განზოგადების დაკარგვის გარეშე, ეს იყოს ფეხი), ჰიპოტენუზა აღწერს ზედაპირს, ხოლო ფეხი აღწერს წრეს. ამრიგად, მიიღება სხეული, რომელსაც ეწოდება მარჯვენა წრიული კონუსი (იხ. სურ. 3).

ბრინჯი. 4. გირჩების სახეები

რადგან ვსაუბრობთ სწორ წრიულ კონუსზე, როგორც ჩანს, არსებობს არაპირდაპირი და არაწრიული? თუ კონუსის ფუძე არის წრე, მაგრამ წვერო არ არის დაპროექტებული ამ წრის ცენტრში, მაშინ ასეთ კონუსს ეწოდება დახრილი. თუ ფუძე არის არა წრე, არამედ თვითნებური ფიგურა, მაშინ ასეთ სხეულს ზოგჯერ კონუსსაც უწოდებენ, მაგრამ, რა თქმა უნდა, არა წრიულს (იხ. სურ. 4).

ამრიგად, ჩვენ კვლავ მივდივართ ჩვენთვის უკვე ნაცნობ ანალოგამდე ცილინდრებთან მუშაობისას. სინამდვილეში, კონუსი არის რაღაც პირამიდის მსგავსი, უბრალოდ, პირამიდას აქვს მრავალკუთხედი ძირში, ხოლო კონუსს (რომელსაც განვიხილავთ) აქვს წრე (იხ. სურ. 5).

კონუსის შიგნით ჩასმული ბრუნვის ღერძის სეგმენტს (ჩვენს შემთხვევაში ეს არის ფეხი) კონუსის ღერძი ეწოდება (იხ. სურ. 6).

ბრინჯი. 5. კონუსი და პირამიდა

ბრინჯი. 6. - კონუსის ღერძი

ბრინჯი. 7. კონუსის ძირი

მეორე ფეხის () ბრუნვის შედეგად წარმოქმნილ წრეს კონუსის ფუძე ეწოდება (იხ. სურ. 7).

და ამ ფეხის სიგრძე არის კონუსის ფუძის რადიუსი (ან, უფრო მარტივად, კონუსის რადიუსი) (იხ. სურ. 8).

ბრინჯი. 8. - კონუსის რადიუსი

ბრინჯი. 9. - კონუსის ზევით

ბრუნვის ღერძზე მდებარე მბრუნავი სამკუთხედის მახვილი კუთხის წვეროს ეწოდება კონუსის წვერო (იხ. სურ. 9).

ბრინჯი. 10. - კონუსის სიმაღლე

კონუსის სიმაღლე არის სეგმენტი, რომელიც გამოყვანილია კონუსის ზემოდან მის ფუძესთან პერპენდიკულარულად (იხ. სურ. 10).

აქ შეიძლება გაგიჩნდეთ შეკითხვა: მაშინ რით განსხვავდება ბრუნვის ღერძის სეგმენტი კონუსის სიმაღლისგან? ფაქტობრივად, ისინი ემთხვევა მხოლოდ სწორი კონუსის შემთხვევაში, თუ დახრილ კონუსს დააკვირდებით, შეამჩნევთ, რომ ეს ორი სრულიად განსხვავებული სეგმენტია (იხ. სურ. 11).

ბრინჯი. 11. სიმაღლე დახრილ კონუსში

დავუბრუნდეთ სწორ კონუსს.

ბრინჯი. 12. კონუსის გენერატორები

კონუსის წვეროს დამაკავშირებელ სეგმენტებს მისი ფუძის წრის წერტილებთან ეწოდება კონუსის გენერატორები. სხვათა შორის, მარჯვენა კონუსის ყველა გენერატორი ტოლია ერთმანეთის (იხ. სურ. 12).

ბრინჯი. 13. ბუნებრივი კონუსის მსგავსი საგნები

ბერძნულიდან თარგმნილი კონოსი ნიშნავს "ფიჭვის გირჩს". ბუნებაში არის საკმარისი ობიექტები, რომლებსაც აქვთ კონუსის ფორმა: ნაძვი, მთა, ჭიანჭველა და ა.შ. (იხ. სურ. 13).

მაგრამ ჩვენ მიჩვეული ვართ იმ ფაქტს, რომ კონუსი სწორია. მას აქვს თანაბარი გენერატრიკები და მისი სიმაღლე ემთხვევა ღერძს. ასეთ კონუსს სწორ კონუსს ვუწოდებდით. სასკოლო გეომეტრიის კურსებში, როგორც წესი, განიხილება სწორი კონუსები და ნაგულისხმევად, ნებისმიერი კონუსი ითვლება სწორ წრიულ კონუსად. მაგრამ ჩვენ უკვე ვთქვით, რომ არსებობს არა მხოლოდ სწორი, არამედ დახრილი კონუსები.

ბრინჯი. 14. პერპენდიკულარული მონაკვეთი

დავუბრუნდეთ სწორ კონუსებს. კონუსის „გაჭრა“ ღერძზე პერპენდიკულარული სიბრტყით (იხ. სურ. 14).

რა ფიგურა იქნება ჭრილზე? რა თქმა უნდა, ეს არის წრე! გავიხსენოთ, რომ სიბრტყე მიემართება ღერძის პერპენდიკულარულად და, შესაბამისად, ფუძის პარალელურად, რომელიც არის წრე.

ბრინჯი. 15. დახრილი მონაკვეთი

ახლა მოდით თანდათან გადავუხვიოთ მონაკვეთის სიბრტყე. შემდეგ ჩვენი წრე თანდათანობით გადაიქცევა უფრო წაგრძელებულ ოვალურად. მაგრამ მხოლოდ მანამ, სანამ მონაკვეთის სიბრტყე არ დაეჯახება ფუძის წრეს (იხ. სურ. 15).

ბრინჯი. 16. სექციების სახეები სტაფილოს მაგალითის გამოყენებით

მათ, ვისაც სამყაროს ექსპერიმენტულად შესწავლა უყვარს, შეუძლია ამის გადამოწმება სტაფილოსა და დანის დახმარებით (სცადეთ სტაფილოს ნაჭრების მოჭრა სხვადასხვა კუთხით) (იხ. სურ. 16).

ბრინჯი. 17. კონუსის ღერძული მონაკვეთი

კონუსის მონაკვეთს სიბრტყით, რომელიც გადის მის ღერძზე, ეწოდება კონუსის ღერძულ მონაკვეთს (იხ. სურ. 17).

ბრინჯი. 18. ტოლკუთხედი სამკუთხედი - სექციური ფიგურა

აქ ვიღებთ სრულიად განსხვავებულ სექციურ ფიგურას: სამკუთხედს. ეს სამკუთხედი ტოლფერდაა (იხ. სურ. 18).

ამ გაკვეთილზე ვისწავლეთ ცილინდრული ზედაპირის, ცილინდრის ტიპების, ცილინდრის ელემენტების და ცილინდრის მსგავსება პრიზმასთან.

კონუსის გენერატორი არის 12 სმ და დახრილია ფუძის სიბრტყეზე 30 გრადუსიანი კუთხით. იპოვნეთ კონუსის ღერძული განივი ფართობი.

გამოსავალი

განვიხილოთ საჭირო ღერძული მონაკვეთი. ეს არის ტოლფერდა სამკუთხედი, რომელშიც გვერდები 12 გრადუსია და ფუძის კუთხე 30 გრადუსია. შემდეგ შეგიძლიათ გააგრძელოთ სხვადასხვა გზით. ან შეგიძლიათ დახაზოთ სიმაღლე, იპოვოთ იგი (ჰიპოტენუზის ნახევარი, 6), შემდეგ საფუძველი (პითაგორას თეორემის გამოყენებით) და შემდეგ ფართობი.

ბრინჯი. 19. პრობლემის ილუსტრაცია

ან დაუყოვნებლივ იპოვნეთ კუთხე წვეროზე - 120 გრადუსი - და გამოთვალეთ ფართობი, როგორც გვერდების ნახევრად ნამრავლი და მათ შორის კუთხის სინუსი (პასუხი იგივე იქნება).

გეომეტრია. სახელმძღვანელო 10-11 კლასებისთვის. ატანასიანი ლ.ს. და სხვა მე-18 გამოცემა. - მ.: განათლება, 2009. - 255გვ.
გეომეტრია მე-11 კლასი ა.ვ. პოგორელოვი, მ.: განათლება, 2002 წ
სამუშაო რვეული გეომეტრიაზე მე-11 კლასი ვ.ფ. ბუტუზოვი, იუ.ა. გლაზკოვი

Yaklass.ru ().
Uztest.ru ().
Bitclass.ru ().

Საშინაო დავალება

) - სხეული ევკლიდეს სივრცეში, რომელიც მიღებულია ერთი წერტილიდან გამომავალი ყველა სხივის გაერთიანებით ( მწვერვალებიკონუსი) და გადის ბრტყელ ზედაპირზე. ზოგჯერ კონუსი არის ისეთი სხეულის ნაწილი, რომელსაც აქვს შეზღუდული მოცულობა და მიიღება ბრტყელი ზედაპირის წვეროსა და წერტილების დამაკავშირებელი ყველა სეგმენტის გაერთიანებით (ეს უკანასკნელი ამ შემთხვევაში ე.წ. საფუძველიკონუსი და კონუსი ე.წ დახრილიამის საფუძველზე). თუ კონუსის ფუძე მრავალკუთხედია, ასეთი კონუსი არის პირამიდა.

ენციკლოპედიური YouTube

1 / 4

✪ როგორ გააკეთოთ კონუსი ქაღალდისგან.

სუბტიტრები

დაკავშირებული განმარტებები

წვეროსა და ფუძის საზღვრის დამაკავშირებელ სეგმენტს ეწოდება კონუსის გენერაცია.
კონუსის გენერატორების გაერთიანებას ეწოდება გენერატრიქსი(ან მხარე) კონუსის ზედაპირი. კონუსის ფორმირების ზედაპირი კონუსური ზედაპირია.
წვეროდან ფუძის სიბრტყეზე პერპენდიკულარულად ჩამოშვებულ სეგმენტს (ისევე როგორც ასეთი სეგმენტის სიგრძეს) ე.წ. კონუსის სიმაღლე.
კონუსის კუთხე- კუთხე ორ მოპირდაპირე გენერატს შორის (კუთხე კონუსის მწვერვალზე, კონუსის შიგნით).
თუ კონუსის ფუძეს აქვს სიმეტრიის ცენტრი (მაგალითად, ეს არის წრე ან ელიფსი) და კონუსის წვეროს ორთოგონალური პროექცია ფუძის სიბრტყეზე ემთხვევა ამ ცენტრს, მაშინ კონუსი ე.წ. პირდაპირი. ამ შემთხვევაში, ბაზის ზედა და ცენტრის დამაკავშირებელი სწორი ხაზი ეწოდება კონუსის ღერძი.
ირიბი (მიდრეკილი) კონუსი - კონუსი, რომლის წვერის ორთოგონალური პროექცია ფუძეზე არ ემთხვევა მის სიმეტრიის ცენტრს.
წრიული კონუსი- კონუსი, რომლის საფუძველი წრეა.
სწორი წრიული კონუსი(ხშირად უბრალოდ კონუსს უწოდებენ) შეიძლება მიღებულ იქნეს მართკუთხა სამკუთხედის ბრუნვით ფეხის შემცველი ხაზის გარშემო (ეს ხაზი წარმოადგენს კონუსის ღერძს).
ელიფსზე, პარაბოლაზე ან ჰიპერბოლაზე დაყრდნობილ კონუსს შესაბამისად უწოდებენ ელიფსური, პარაბოლურიდა ჰიპერბოლური კონუსი(ბოლო ორს აქვს უსასრულო მოცულობა).
კონუსის ნაწილს, რომელიც დევს ფუძესა და ფუძის პარალელურ სიბრტყეს შორის და მდებარეობს ზედა და ფუძეს შორის, ე.წ. შეკვეცილი კონუსი, ან კონუსური ფენა.

Თვისებები

თუ ფუძის ფართობი სასრულია, მაშინ კონუსის მოცულობა ასევე სასრულია და უდრის სიმაღლისა და ფუძის ფართობის ნამრავლის მესამედს.

V = 1 3 S H , (\displaystyle V=(1 \3-ზე მეტი)SH,)

სად ს- ბაზის ფართობი, ჰ- სიმაღლე. ამრიგად, ყველა კონუსს, რომელიც ეყრდნობა მოცემულ ფუძეს (სასრული ფართობის) და აქვს წვერო, რომელიც მდებარეობს მოცემულ სიბრტყეზე ფუძის პარალელურად, აქვს თანაბარი მოცულობა, რადგან მათი სიმაღლეები ტოლია.

სასრული მოცულობის ნებისმიერი კონუსის სიმძიმის ცენტრი მდებარეობს ფუძიდან სიმაღლის მეოთხედზე.
მართი წრიული კონუსის წვეროზე მყარი კუთხე ტოლია

2 π (1 − cos ⁡ α 2) , (\displaystyle 2\pi \left(1-\cos (\alpha \2-ზე მეტი)\მარჯვნივ),)სადაც α არის კონუსის გახსნის კუთხე.

ასეთი კონუსის გვერდითი ზედაპირის ფართობი ტოლია

S = π R l, (\displaystyle S=\pi Rl,)

და მთლიანი ზედაპირის ფართობი (ანუ გვერდითი ზედაპირისა და ფუძის ფართობების ჯამი)

S = π R (l + R), (\displaystyle S=\pi R(l+R),)სად რ- ბაზის რადიუსი, l = R 2 + H 2 (\displaystyle l=(\sqrt (R^(2)+H^(2))))- გენერატრიქსის სიგრძე.

წრიული (არ არის აუცილებელი სწორი) კონუსის მოცულობა ტოლია

V = 1 3 π R 2 H. (\displaystyle V=(1 \3-ზე მეტი)\pi R^(2)H.)

შეკვეცილი კონუსისთვის (არ არის აუცილებელი სწორი და წრიული), მოცულობა უდრის:

V = 1 3 (H S 2 - h S 1) , (\ჩვენების სტილი V=(1 \3-ზე მეტი)(HS_(2)-hS_(1)),)

სადაც S 1 და S 2 არის ზედა (ზემოსთან ყველაზე ახლოს) და ქვედა ბაზის არეები, შესაბამისად, თდა ჰ- დისტანციები ზედა და ქვედა ბაზის სიბრტყიდან, შესაბამისად, ზევით.

სიბრტყის გადაკვეთა მარჯვენა წრიულ კონუსთან არის ერთ-ერთი კონუსური მონაკვეთი (არადეგენერაციულ შემთხვევებში - ელიფსი, პარაბოლა ან ჰიპერბოლა, ჭრის სიბრტყის პოზიციიდან გამომდინარე).

კონუსის განტოლება

განტოლებები, რომლებიც განსაზღვრავენ მარჯვენა წრიული კონუსის გვერდით ზედაპირს გახსნის კუთხით 2Θ, წვერო საწყისთან და ღერძი ემთხვევა ღერძს ოზი :

სფერულ კოორდინატულ სისტემაში კოორდინატებით ( რ, φ, θ) :

θ = Θ. (\displaystyle \theta =\Theta.)

ცილინდრულ კოორდინატულ სისტემაში კოორდინატებით ( რ, φ, ზ) :

z = r ⋅ ctg ⁡ Θ (\displaystyle z=r\cdot \ოპერატორის სახელი (ctg) \Theta)ან r = z ⋅ tan⁡ Θ . (\displaystyle r=z\cdot \ოპერატორის სახელი (tg) \Theta .)

დეკარტის კოორდინატთა სისტემაში კოორდინატებთან (x, წ, ზ) :

z = ± x 2 + y 2 ⋅ cot ⁡ Θ . (\displaystyle z=\pm (\sqrt (x^(2)+y^(2)))\cdot \ოპერატორის სახელი (ctg) \Theta .)ეს განტოლება კანონიკური ფორმით იწერება როგორც

სად არის მუდმივები ა, თანგანისაზღვრება პროპორციით c / a = cos ⁡ Θ / sin ⁡ Θ . (\displaystyle c/a=\cos \Theta /\sin \Theta.)ეს აჩვენებს, რომ მარჯვენა წრიული კონუსის გვერდითი ზედაპირი მეორე რიგის ზედაპირია (მას ე.წ კონუსური ზედაპირი). ზოგადად, მეორე რიგის კონუსური ზედაპირი ეყრდნობა ელიფსს; შესაფერის დეკარტის კოორდინატულ სისტემაში (ღერძი ოჰდა OUელიფსის ღერძების პარალელურად, კონუსის წვერო ემთხვევა საწყისს, ელიფსის ცენტრი დევს ღერძზე ოზი) მის განტოლებას აქვს ფორმა

x 2 a 2 + y 2 b 2 − z 2 c 2 = 0 , (\displaystyle (\frac (x^(2))(a^(2)))+(\frac (y^(2))( b^(2)))-(\frac (z^(2))(c^(2)))=0,)

და ა/კდა ბ/კელიფსის ნახევრადღერძების ტოლი. ყველაზე ზოგად შემთხვევაში, როდესაც კონუსი ეყრდნობა თვითნებურ ბრტყელ ზედაპირზე, შეიძლება აჩვენოს, რომ კონუსის გვერდითი ზედაპირის განტოლება (მისი წვერო საწყისთან) მოცემულია განტოლებით. f (x, y, z) = 0, (\displaystyle f(x,y,z)=0,)სად არის ფუნქცია f (x, y, z) (\displaystyle f(x,y,z))არის ერთგვაროვანი, ანუ აკმაყოფილებს მდგომარეობას f (α x, α y, α z) = α n f (x, y, z) (\displaystyle f(\alpha x,\alpha y,\alpha z)=\alpha ^(n)f(x,y ,ზ))ნებისმიერი რეალური რიცხვისთვის α.

სკანირება

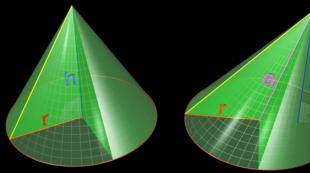
მარჯვენა წრიული კონუსი, როგორც ბრუნვის სხეული, იქმნება მართკუთხა სამკუთხედით, რომელიც ბრუნავს ერთ-ერთ ფეხის გარშემო, სადაც თ- კონუსის სიმაღლე ფუძის ცენტრიდან ზევით - არის მართკუთხა სამკუთხედის ფეხი, რომლის გარშემოც ხდება ბრუნვა. მართკუთხა სამკუთხედის მეორე ფეხი რ- რადიუსი კონუსის ბაზაზე. მართკუთხა სამკუთხედის ჰიპოტენუზა არის ლ- კონუსის ფორმირება.

კონუსური სკანირების შესაქმნელად შეიძლება გამოყენებულ იქნას მხოლოდ ორი რაოდენობა რდა ლ. ბაზის რადიუსი რგანსაზღვრავს კონუსის ფუძის წრეს განვითარებაში, ხოლო კონუსის გვერდითი ზედაპირის სექტორი განისაზღვრება გვერდითი ზედაპირის გენერატრიქსით. ლ, რომელიც არის გვერდითი ზედაპირის სექტორის რადიუსი. სექტორის კუთხე φ (\displaystyle \varphi)კონუსის გვერდითი ზედაპირის განვითარებაში განისაზღვრება ფორმულით:

φ = 360° ( რ/ლ) .

კონუსი (უფრო ზუსტად, წრიული კონუსი) არის სხეული, რომელიც შედგება წრისგან - კონუსის ფუძე, წერტილი, რომელიც არ დევს ამ წრის სიბრტყეში - კონუსის ზევით და კონუსის ზედა დამაკავშირებელი ყველა სეგმენტისაგან. ფუძის წერტილებთან (ნახ. 1) კონუსის ზედა ნაწილის ფუძის წრის წერტილებთან დამაკავშირებელ ხაზოვან სეგმენტებს კონუსის გენერატორები ეწოდება. კონუსის ყველა გენერატორი ერთმანეთის ტოლია. კონუსის ზედაპირი შედგება ფუძისა და გვერდითი ზედაპირისგან.
ბრინჯი. 1
კონუსს სწორი ეწოდება, თუ კონუსის ზედა ნაწილის დამაკავშირებელი სწორი ხაზი ფუძის ცენტრთან პერპენდიკულარულია ფუძის სიბრტყის მიმართ. ვიზუალურად, სწორი წრიული კონუსი შეიძლება წარმოვიდგინოთ, როგორც სხეული, რომელიც მიიღება მართკუთხა სამკუთხედის ღერძის სახით ფეხის გარშემო ბრუნვით (ნახ. 2).
ბრინჯი. 2
კონუსის სიმაღლე არის პერპენდიკულური, რომელიც ჩამოდის მისი ზემოდან ფუძის სიბრტყემდე. სწორი კონუსისთვის, სიმაღლის საფუძველი ემთხვევა ფუძის ცენტრს. მარჯვენა წრიული კონუსის ღერძი არის სწორი ხაზი, რომელიც შეიცავს მის სიმაღლეს.
კონუსის მონაკვეთი სიბრტყით, რომელიც გადის მის წვეროზე, არის ტოლფერდა სამკუთხედი, რომლის გვერდები ქმნის კონუსს (ნახ. 3). კერძოდ, ტოლფერდა სამკუთხედი არის კონუსის ღერძული მონაკვეთი. ეს არის მონაკვეთი, რომელიც გადის კონუსის ღერძზე (ნახ. 4).
ბრინჯი. 3 ნახ. 4

კონუსის ზედაპირის ფართობი
კონუსის გვერდითი ზედაპირი, ისევე როგორც ცილინდრის გვერდითი ზედაპირი, შეიძლება გადაბრუნდეს სიბრტყეზე მისი ერთ-ერთი გენერატორის გასწვრივ გაჭრით (ნახ. 2, ა, ბ). კონუსის გვერდითი ზედაპირის განვითარება არის წრიული სექტორი (ნახ. 2.6), რომლის რადიუსი უდრის კონუსის გენერატრიქსს, ხოლო სექტორის რკალის სიგრძე არის კონუსის ფუძის გარშემოწერილობა.
კონუსის გვერდითი ზედაპირის ფართობი აღებულია მისი განვითარების არეალად. გამოვხატოთ კონუსის გვერდითი ზედაპირის S ფართობი მისი გენერატორის l და ფუძის r რადიუსის მიხედვით.
წრიული სექტორის ფართობი - კონუსის გვერდითი ზედაპირის განვითარება (ნახ. 2) - უდრის (Pl2a)/360, სადაც a არის ABA რკალის ხარისხი", შესაბამისად.
გვერდი = (Pl2a)/360. (*)
გამოვხატოთ a l-ით და r-ით. ვინაიდან რკალის სიგრძე ABA" უდრის 2Pr (კონუსის ფუძის გარშემოწერილობა), მაშინ 2Pr = Pla/180, საიდანაც a=360r/l. ამ გამონათქვამის ჩანაცვლება ფორმულით (*), მივიღებთ:
Sside = Prl. (**)
ამრიგად, კონუსის გვერდითი ზედაპირის ფართობი უდრის ფუძისა და გენერატორის წრეწირის ნახევარს.
კონუსის მთლიანი ზედაპირის ფართობი არის გვერდითი ზედაპირისა და ფუძის ფართობების ჯამი. კონუსის მთლიანი ზედაპირის Scon ფართობის გამოსათვლელად მიიღება ფორმულა: Scon = Pr (l + r). (***)

ფრუსტუმი
ავიღოთ თვითნებური კონუსი და დავხატოთ საჭრელი სიბრტყე მისი ღერძის პერპენდიკულარულად. ეს სიბრტყე კვეთს კონუსს წრეში და ყოფს კონუსს ორ ნაწილად. ერთ-ერთი ნაწილი არის კონუსი, ხოლო მეორეს ეწოდება შეკვეცილი კონუსი. თავდაპირველი კონუსის ფუძეს და ამ კონუსის სიბრტყით ჭრის შედეგად მიღებულ წრეს უწოდებენ შეკვეცილი კონუსის ფუძეებს, ხოლო მათი ცენტრების შემაერთებელ სეგმენტს - შეჭრილი კონუსის სიმაღლეს.

კონუსური ზედაპირის იმ ნაწილს, რომელიც ესაზღვრება შეკვეცილ კონუსს, ეწოდება მის ლატერალურ ზედაპირს, ხოლო ფუძეებს შორის ჩასმული კონუსური ზედაპირის გენერატრიულ სეგმენტებს - შეკვეცილი კონუსის გენერატორები. შეკვეცილი კონუსის ყველა გენერატორი ერთმანეთის ტოლია (ეს თავად დაამტკიცეთ).
შეკვეცილი კონუსის გვერდითი ზედაპირის ფართობი უდრის ფუძეების და გენერატორის წრეების სიგრძის ჯამის ნახევრის ნამრავლს: Sside = П (r + r1) l.

დამატებითი ინფორმაცია კონუსის შესახებ
1. გეოლოგიაში არსებობს ცნება "გულშემატკივართა". ეს არის მიწის ფორმა, რომელიც წარმოიქმნება კლასტური ქანების (კენჭები, ხრეში, ქვიშა) დაგროვებით, რომლებიც მთის მდინარეების მიერ მთისწინა დაბლობზე ან უფრო ბრტყელ, განიერ ხეობაში გადატანილია.
2. ბიოლოგიაში არსებობს "ზრდის კონუსის" ცნება. ეს არის მცენარის გასროლისა და ფესვის წვერი, რომელიც შედგება სასწავლო ქსოვილის უჯრედებისგან.
3. „კონუსები“ არის პროსობრანული ქვეკლასის ზღვის მოლუსკების ოჯახი. ჭურვი კონუსურია (2–16 სმ), ღია ფერის. არსებობს 500-ზე მეტი სახის გირჩები. ისინი ცხოვრობენ ტროპიკებსა და სუბტროპიკებში, არიან მტაცებლები და აქვთ შხამიანი ჯირკვალი. გირჩების ნაკბენი ძალიან მტკივნეულია. ცნობილია გარდაცვალების შემთხვევები. ჭურვები გამოიყენება როგორც დეკორაციები და სუვენირები.
4. სტატისტიკის მიხედვით, ყოველწლიურად 1 მილიონ მოსახლეზე 6 ადამიანი იღუპება დედამიწაზე ელვის დარტყმის შედეგად (უფრო ხშირად სამხრეთის ქვეყნებში). ეს არ მოხდებოდა ყველგან რომ იყოს ელვისებური ღეროები, რადგან იქმნება უსაფრთხოების კონუსი. რაც უფრო მაღალია ელვისებური ჯოხი, მით უფრო დიდია ასეთი კონუსის მოცულობა. ზოგიერთი ადამიანი ცდილობს დაიმალოს ხის ქვეშ გამონადენისგან, მაგრამ ხე არ არის გამტარი, მასზე გროვდება მუხტები და ხე შეიძლება იყოს ძაბვის წყარო.
5. ფიზიკაში გვხვდება „მყარი კუთხის“ ცნება. ეს არის კონუსის ფორმის კუთხე, რომელიც მოჭრილია ბურთად. მყარი კუთხის ერთეული არის 1 სტერადიანი. 1 სტერადიანი არის მყარი კუთხე, რომლის რადიუსის კვადრატი უდრის სფეროს იმ ნაწილის ფართობს, რომელსაც ის წყვეტს. თუ ამ კუთხეში მოვათავსებთ 1 კანდელას (1 სანთლის) სინათლის წყაროს, მივიღებთ 1 ლუმენის მანათობელ ნაკადს. კინოკამერის ან პროჟექტორის შუქი კონუსის სახით ვრცელდება.